Similar presentations:
Кинематика твердого тела введение
1. ГЛАВА 2 КИНЕМАТИКА ТВЕРДОГО ТЕЛА ВВЕДЕНИЕ
Две основные задачи кинематики твердого телаЗадание движения твердого тела и определение
кинематических характеристик тела в целом.
Определение кинематических характеристик движения
отдельных точек тела.
Задать движение твердого тела – значит, указать
способ определения положения любой точки тела в
любой момент времени по отношению к выбранной
системе отсчета.
Замечание. Количество точек в твердом теле бесконечно
велико, однако их перемещения не являются независимыми,
а связаны условием неизменности расстояний между этими
точками. Это позволяет существенно упростить построение
теории движения твердого тела.
1
2. Кинематика твердого тела
Положение твердого тела в пространстве общем случаеопределяется заданием 6 независимых между собой параметров.
Пусть известна зависимость от времени декартовых координат трех точек твердого тела, не
лежащих на одной прямой:
M3
d
z
23
d13
x
M1
xk xk (t ), yk yk (t ), zk zk (t ) (k 1,2,3)
M2
d12
y
Тогда в любой момент времени должны
выполняться соотношения:
( x2 x1 ) 2 ( y2 y1 ) 2 ( z2 z1 ) 2 d122 const ,
2
2
2
2
( x3 x1 ) ( y3 y1 ) ( z3 z1 ) d13 const ,
(*)
2
2
2
2
( x3 x2 ) ( y3 y2 ) ( z3 z2 ) d 23 const.
Следовательно, из 9 координат, задающих положения трех рассматриваемых
точек тела в пространстве, независимы лишь 6, а 3 оставшиеся можно
определить из системы (*). Любая другая точка, лежащая на том же теле,
должна находиться на неизменном расстоянии от точек М1,М2,М3, поэтому три
координаты этой точки должны удовлетворять трем уравнениям вида (*).
Замечание. В качестве 6 независимых параметров, определяющих положение твердого тела
в пространстве, не обязательно выбираются декартовы координаты, а в некоторых частных
случаях движения твердого тела число задаваемых параметров может быть и меньше 6.
2
3. Кинематика твердого тела
Различают следующие 5 видов движения твердого тела:поступательное движение,
простейшие движения
вращательное движение,
плоское (плоскопараллельное) движение,
сферическое движение,
общий случай движения свободного твердого тела.
Каждый из перечисленных видов движения характеризуется
определенными, только ему присущими признаками.
Приступая к изучению движения твердого тела, следует прежде
всего установить к какому из перечисленных выше видов движения оно
относится, а далее использовать хорошо разработанную теорию
кинематики твердого тела.
3
4. Кинематика твердого тела
Теорема ГрасгофаПроекции векторов скоростей точек твердого тела на прямую,
соединяющую эти точки, равны.
Доказательство
B
AB rB rA , AB ( xB x A , yB y A , z B z A ) .
2
AB
r
A
rB
O
A
AB ( xB x A ) 2 ( yB y A ) 2 ( z B z A ) 2 const .
2
d
( AB ) 2 (( xB x A ) ( xB x A ) ( yB y A ) ( yB y A )
dt
( z B z A ) ( z B z A )) 0.
xB ( xB xA ) yB ( yB y A ) zB ( zB z A )
xA ( xB xA ) y A ( yB y A ) z A ( zB z A ).
VB AB VA AB , VB AB cos(VB AB) VA AB cos(VA AB) ,
VB cos(VB AB) VA cos(VA AB ) .
4
5. Теорема Грасгофа
Грасгоф ФранцBorn
1826-07-11
Died
1893-10-26
Немецкий механик и машиностроитель. Родился в Дюссельдорфе.
С 15 лет работал слесарем, затем посещал ремесленную школу.
Окончил Берлинский ремесленный институт (1845).
С 1854 — преподаватель математики и механики там же,
в 1863 возглавил кафедру прикладной механики в Политехникуме
в Карлсруэ.
Основное направление исследований — прикладная механика.
Был сторонником аналитических методов в механике. Работал также в
области гидравлики, машиноведения, теплотехники.
Его главный труд — «Теоретическое машиноведение» (т. 1—3,
1875—1890),в котором он развил учение Ф. Рело о кинематических
парах и кинематических цепях. Разработал теорию регуляторов.
Известна теорема Грасгофа о существовании кривошипа в плоском
четырехзвеннике.
5
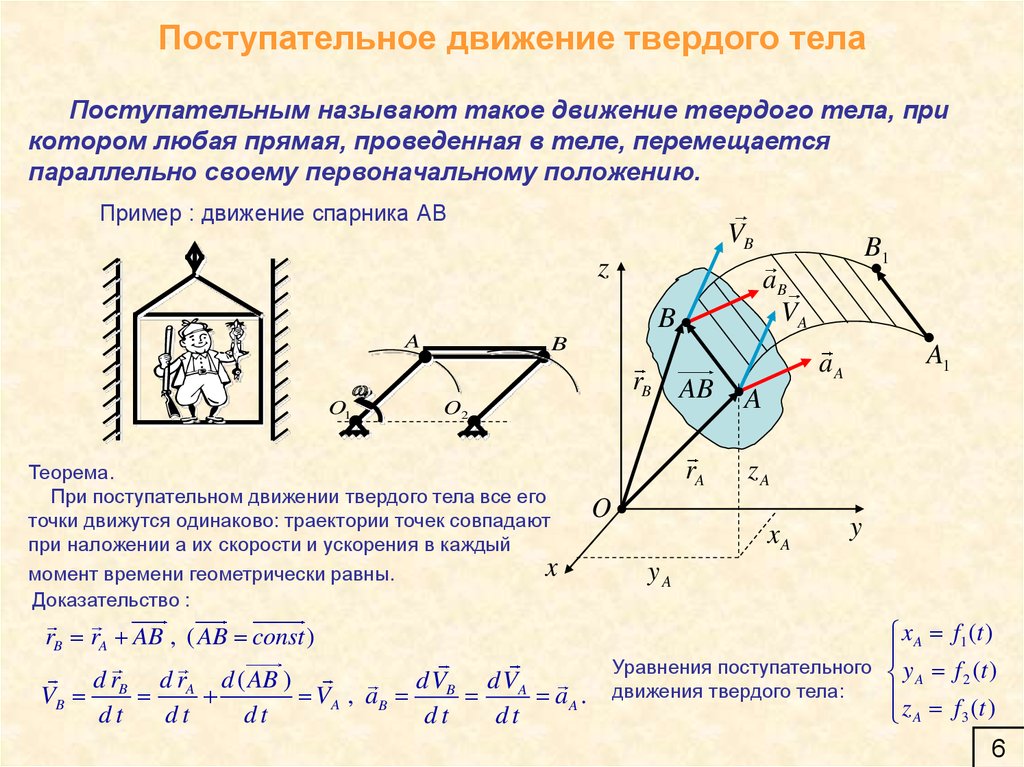
6. Поступательное движение твердого тела
Поступательным называют такое движение твердого тела, прикотором любая прямая, проведенная в теле, перемещается
параллельно своему первоначальному положению.
Пример : движение спарника АВ
z
B
A
B
rB
O1
O2
Теорема.
При поступательном движении твердого тела все его
точки движутся одинаково: траектории точек совпадают
при наложении а их скорости и ускорения в каждый
x
момент времени геометрически равны.
Доказательство :
rB rA AB , ( AB const )
VB
.
VB
d rB d rA d ( AB )
dV
d VA
VA , a B B
aA .
dt
dt
dt
dt
dt
O
AB
rA
B1
aB
VA
.
A1
aA
A
zA
xA
y
yA
x A f1 (t )
Уравнения поступательного y f (t )
A
2
движения твердого тела:
z f (t )
3
A
6
7. КИНЕМАТИКА ТВЕРДОГО ТЕЛА
ПРИМЕР ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯA
vA
aA
rA
rA
rBA
rBA
B
rB
rB
vB
aB
C
7
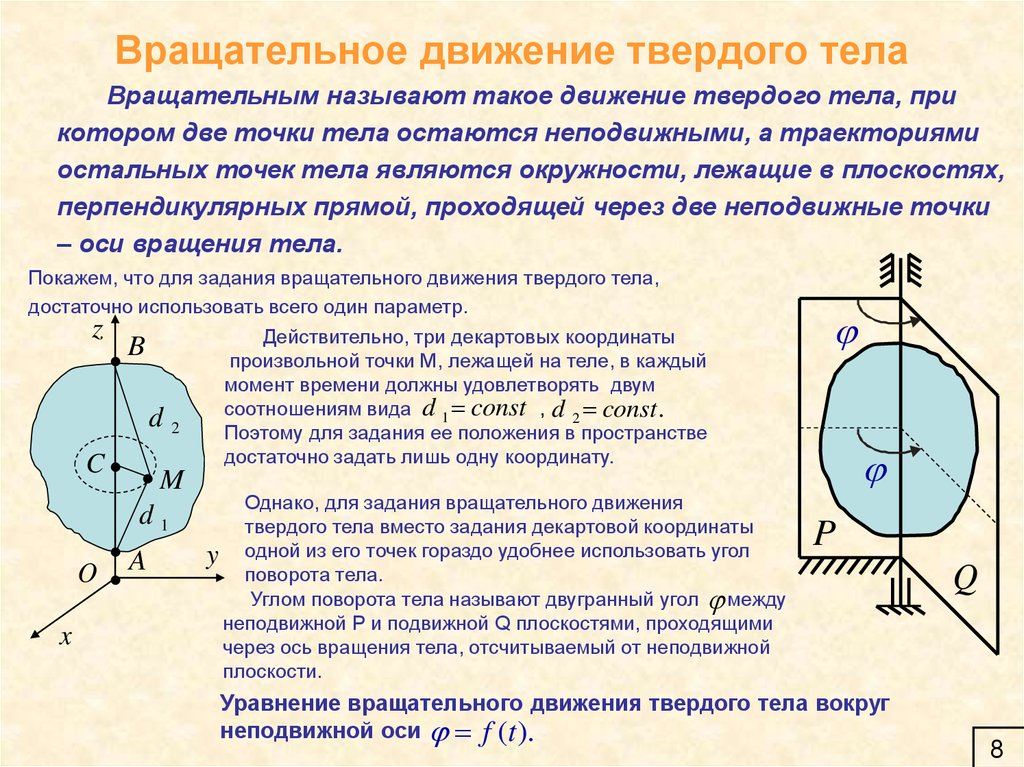
8. Вращательное движение твердого тела
Вращательным называют такое движение твердого тела, прикотором две точки тела остаются неподвижными, а траекториями
остальных точек тела являются окружности, лежащие в плоскостях,
перпендикулярных прямой, проходящей через две неподвижные точки
– оси вращения тела.
Покажем, что для задания вращательного движения твердого тела,
достаточно использовать всего один параметр.
z
Действительно, три декартовых координаты
B
произвольной точки М, лежащей на теле, в каждый
момент времени должны удовлетворять двум
соотношениям вида d 1 const , d 2 const.
d2
Поэтому для задания ее положения в пространстве
достаточно задать лишь одну координату.
C
.
..
..
M
d1
O
x
A
Однако, для задания вращательного движения
твердого тела вместо задания декартовой координаты
y одной из его точек гораздо удобнее использовать угол
поворота тела.
Углом поворота тела называют двугранный угол между
неподвижной P и подвижной Q плоскостями, проходящими
через ось вращения тела, отсчитываемый от неподвижной
плоскости.
P
Уравнение вращательного движения твердого тела вокруг
неподвижной оси f (t ).
Q
8
9. Угловая скорость вращающегося твердого тела.
Пусть в момент времени t угол поворота телавремени t+∆t угол поворота тела
(t t ) .
(t ), а в момент -
Тогда за промежуток времени ∆t приращение угла
поворота (t t ) (t ).
Средняя угловая скорость вращения тела:
.
. . скорость поворота тела:
Мгновенная угловая
.
.
t
d
lim
.
ср
t 0
.
Размерность угловой скорости в системе СИ:
t
dt
рад 1
с .
сек
В технике для характеристики скорости вращающегося
об
.
твердого тела часто используют число оборотов в минуту n
мин
n
.
Связь между и n дается формулой :
30
9
10. Угловое ускорение вращающегося твердого тела.
Пусть в момент времени t угловая скорость тела (t ),а в момент времени t+∆t
(t t ) .
Тогда за промежуток времени ∆t приращение угловой скорости тела
(t t ) (t ).
Среднее угловое ускорение тела
ср .
t
d d 2
Мгновенное угловое ускорение тела
lim
2 .
t 0 t
dt dt
Размерность углового ускорения в системе СИ
рад 2
с .
2
сек
Часто используемые законы вращательного движения:
равнопеременное const ,
вращение
0 t ,
1 2
0 0 t t ;
гармонические колебания 0 sin(kt ).
2
10
0,
равномерное const ,
0
вращение
t ;
0
0
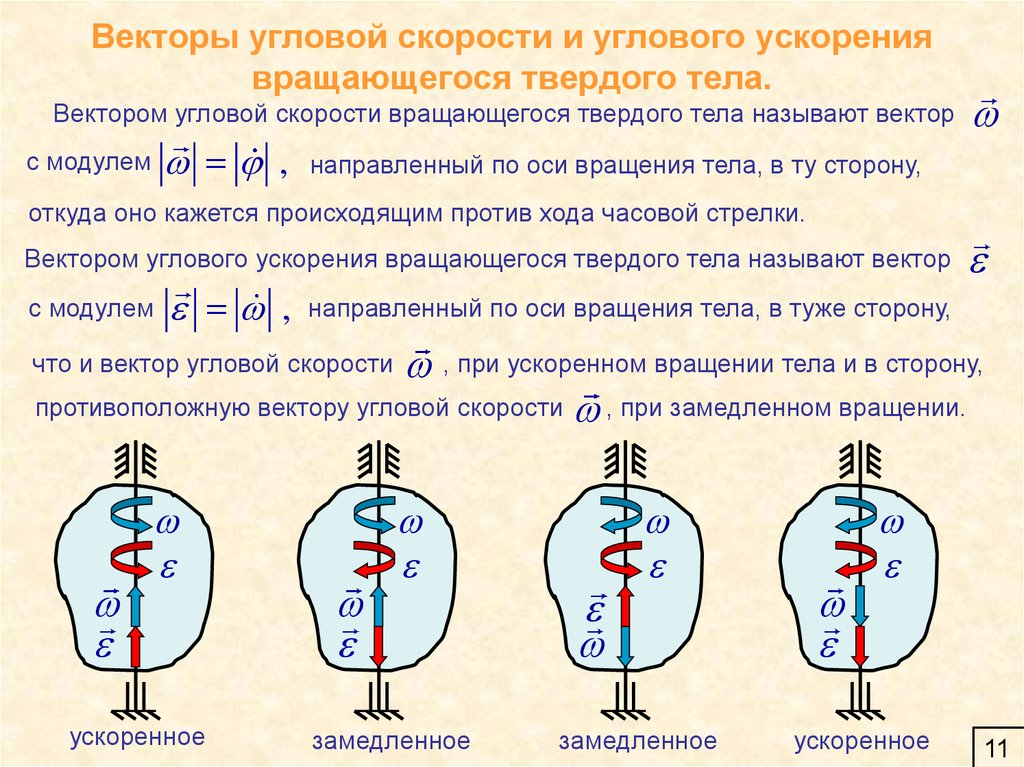
11. Векторы угловой скорости и углового ускорения вращающегося твердого тела.
Вектором угловой скорости вращающегося твердого тела называют вектор,
с модулем
направленный по оси вращения тела, в ту сторону,
откуда оно кажется происходящим против хода часовой стрелки.
Вектором углового ускорения вращающегося твердого тела называют вектор
с модулем
,
направленный по оси вращения тела, в туже сторону,
, при ускоренном вращении тела и в сторону,
противоположную вектору угловой скорости , при замедленном вращении.
что и вектор угловой скорости
ускоренное
замедленное
замедленное
ускоренное
11
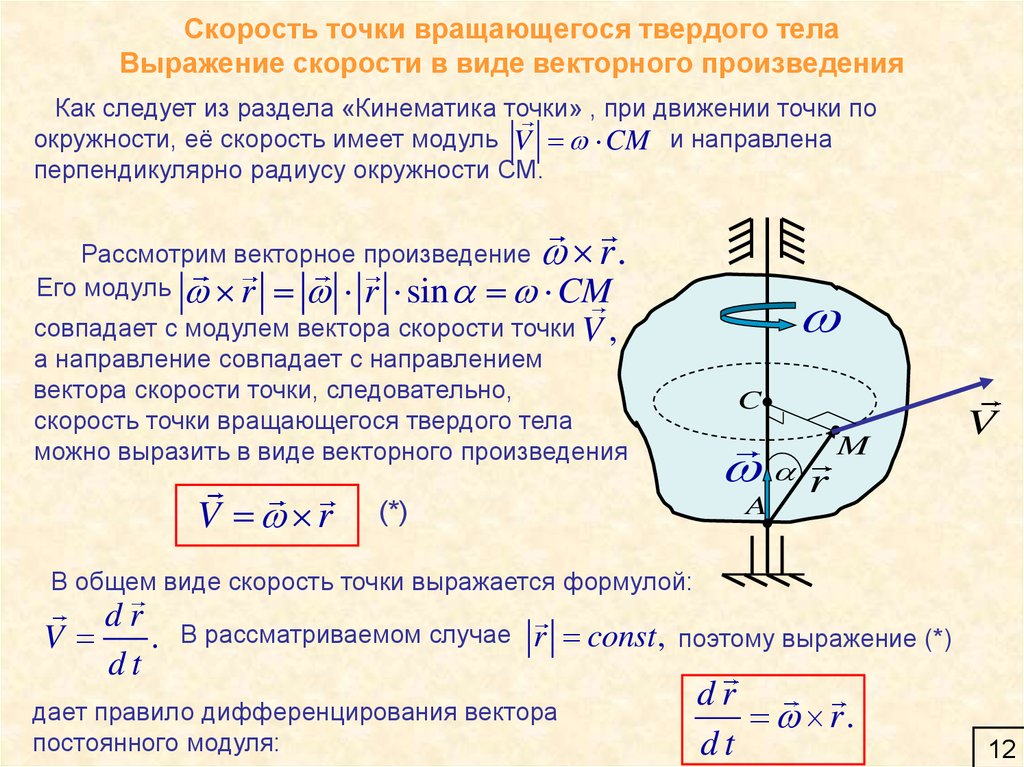
12. Скорость точки вращающегося твердого тела Выражение скорости в виде векторного произведения
Как следует из раздела «Кинематика точки» , при движении точки поокружности, её скорость имеет модуль V CM и направлена
перпендикулярно радиусу окружности СМ.
Рассмотрим векторное произведение
r.
Его модуль r r sin CM
совпадает с модулем вектора скорости точки V ,
а направление совпадает с направлением
вектора скорости точки, следовательно,
скорость точки вращающегося твердого тела
можно выразить в виде векторного произведения
V r
. .
r
.
C
M
V
A
(*)
В общем виде скорость точки выражается формулой:
dr
V
.
dt
В рассматриваемом случае
r const ,
дает правило дифференцирования вектора
постоянного модуля:
поэтому выражение (*)
dr
r.
dt
12
13. Ускорение точки вращающегося твердого тела. Тангенциальное и нормальное ускорения. Их выражение в виде векторных произведений.
Для нахождения ускорения точки вращающегося твердого телапродифференцируем по времени выражение скорости (*),
учитывая, что
dV d ( r ) d
dr
r const : a
r .
dt
dt
dt
dt
Выясним смысл отдельных слагаемых, входящих в полученное выражение
d
r r a
dt
- тангенциальное (касательное) ускорение, совпадающее с вектором
скорости точки при ускоренном вращении тела и направленное
противоположно вектору скорости точки при замедленном вращении;
dr
V r an
dt
- нормальное(центростремительное) ускорение,
направленное к оси вращения тела при любом
характере вращения.
V
M
.
C. a
n
13
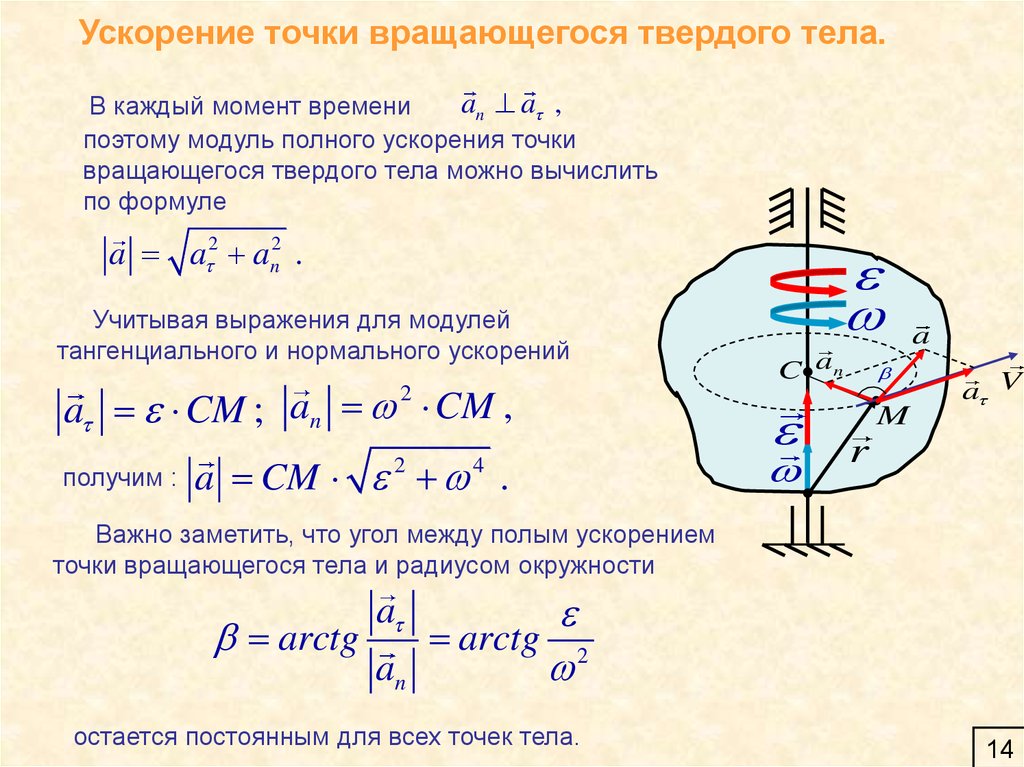
14.
Ускорение точки вращающегося твердого тела.an a ,
В каждый момент времени
поэтому модуль полного ускорения точки
вращающегося твердого тела можно вычислить
по формуле
a a 2 an2 .
Учитывая выражения для модулей
тангенциального и нормального ускорений
a CM ; an CM ,
2
получим :
a CM 2 4 .
. .
r
.
C an
M
a
a V
Важно заметить, что угол между полым ускорением
точки вращающегося тела и радиусом окружности
arctg
arctg 2
an
a
остается постоянным для всех точек тела.
14
15. ОСНОВНЫЕ ФОРМУЛЫ КИНЕМАТИКИ ТВЕРДОГО ТЕЛА
1. СКОРОСТЬ ТОЧКИ ВРАЩАЮЩЕГОСЯ ТВЕРДОГО ТЕЛАV R ,V R
Вектор скорости точки направлен
в сторону вращения тела.
2. УСКОРЕНИЕ ТОЧКИ ВРАЩАЮЩЕГОСЯ ТВЕРДОГО ТЕЛА
a R , a R
an R , an R
2
a R 2 4
Здесь
R
Тангенциальное (касательное) ускорение
точки направлено так же как вектор скорости
при ускоренном вращении тела и противоположно вектору скорости при замедленном
вращении тела.
Нормальное (центростремительное)
ускорение всегда направлено к оси вращения
тела.
Полное ускорение точки.
- кратчайшее расстояние от точки до оси вращения тела.
15
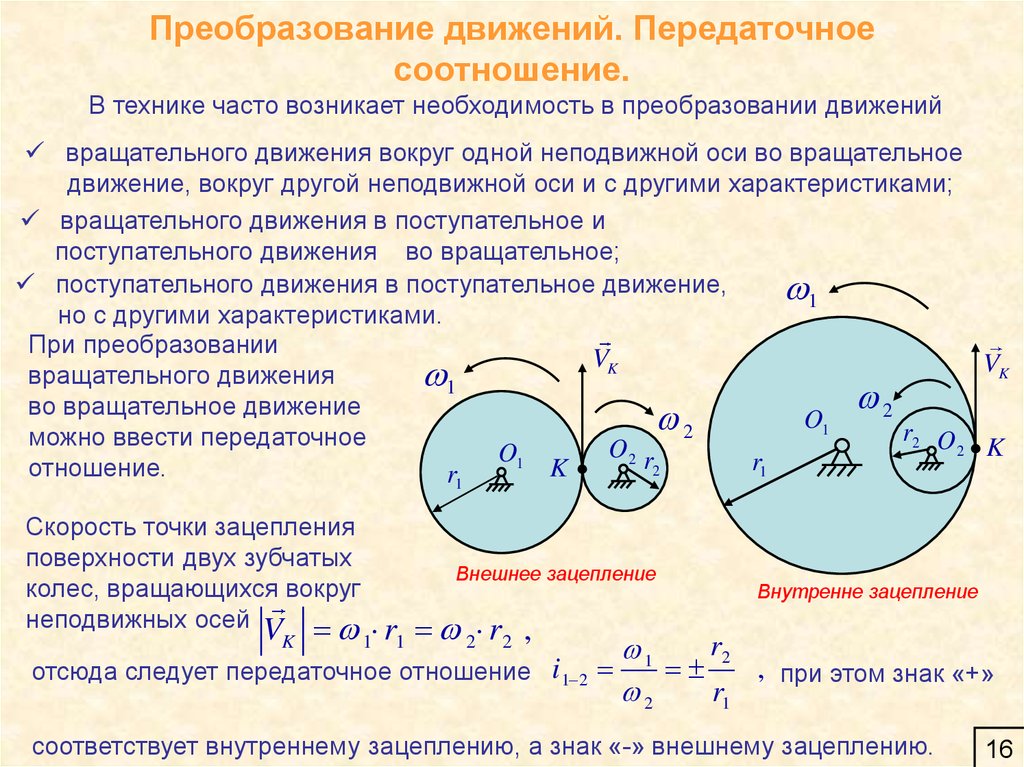
16. Преобразование движений. Передаточное соотношение.
В технике часто возникает необходимость в преобразовании движенийвращательного движения вокруг одной неподвижной оси во вращательное
движение, вокруг другой неподвижной оси и с другими характеристиками;
вращательного движения в поступательное и
поступательного движения во вращательное;
поступательного движения в поступательное движение,
1
но с другими характеристиками.
При преобразовании
VK
VK
вращательного движения
1
2
во вращательное движение
O1
2
r2 O
можно ввести передаточное
2 K
O
O1
2 r
r
2
K
отношение.
1
r1
.
.
Скорость точки зацепления
поверхности двух зубчатых
колес, вращающихся вокруг
неподвижных осей V
K
Внешнее зацепление
r1 2 r2 ,
1
отсюда следует передаточное отношение i 1 2
Внутренне зацепление
r2
1
, при этом знак «+»
2
r1
соответствует внутреннему зацеплению, а знак «-» внешнему зацеплению.
16
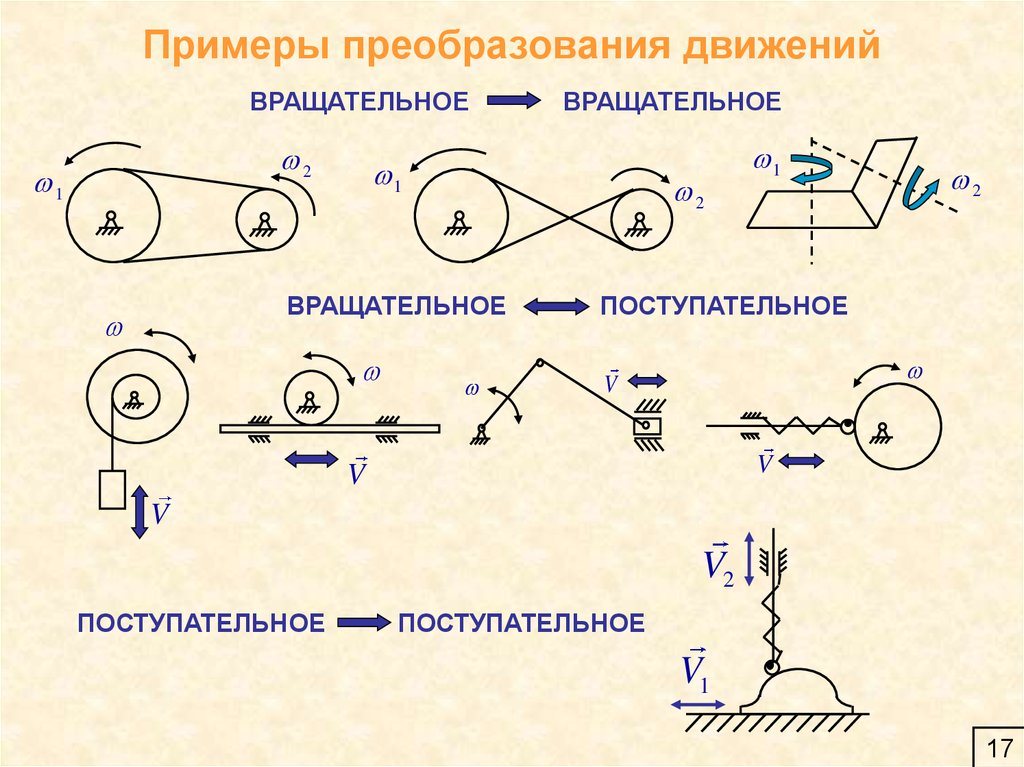
17. Примеры преобразования движений
ВРАЩАТЕЛЬНОЕ2
1
1
2
ВРАЩАТЕЛЬНОЕ
ВРАЩАТЕЛЬНОЕ
1
2
ПОСТУПАТЕЛЬНОЕ
V
.
V
V
V
V2
ПОСТУПАТЕЛЬНОЕ
ПОСТУПАТЕЛЬНОЕ
V1
.
17










 physics
physics








