Плоскопараллельное движение твердого тела

1. §3 ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА

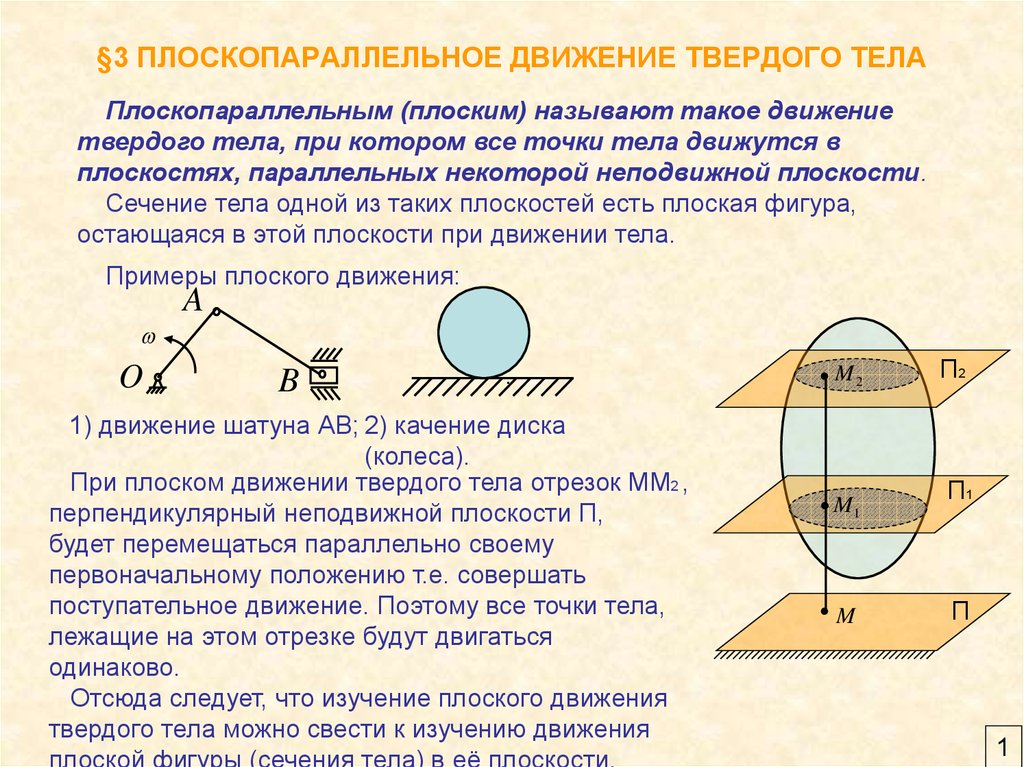
Плоскопараллельным (плоским) называют такое движение
твердого тела, при котором все точки тела движутся в
плоскостях, параллельных некоторой неподвижной плоскости.
Сечение тела одной из таких плоскостей есть плоская фигура,
остающаяся в этой плоскости при движении тела.
Примеры плоского движения:
O
A
B
.
1) движение шатуна АВ; 2) качение диска
(колеса).
При плоском движении твердого тела отрезок ММ2 ,
перпендикулярный неподвижной плоскости П,
будет перемещаться параллельно своему
первоначальному положению т.е. совершать
поступательное движение. Поэтому все точки тела,
лежащие на этом отрезке будут двигаться
одинаково.
Отсюда следует, что изучение плоского движения
твердого тела можно свести к изучению движения
плоской фигуры (сечения тела) в её плоскости.
.
M2
.
M1
.
M
П2
П1
П
1

2. Движение плоской фигуры в её плоскости

y
B
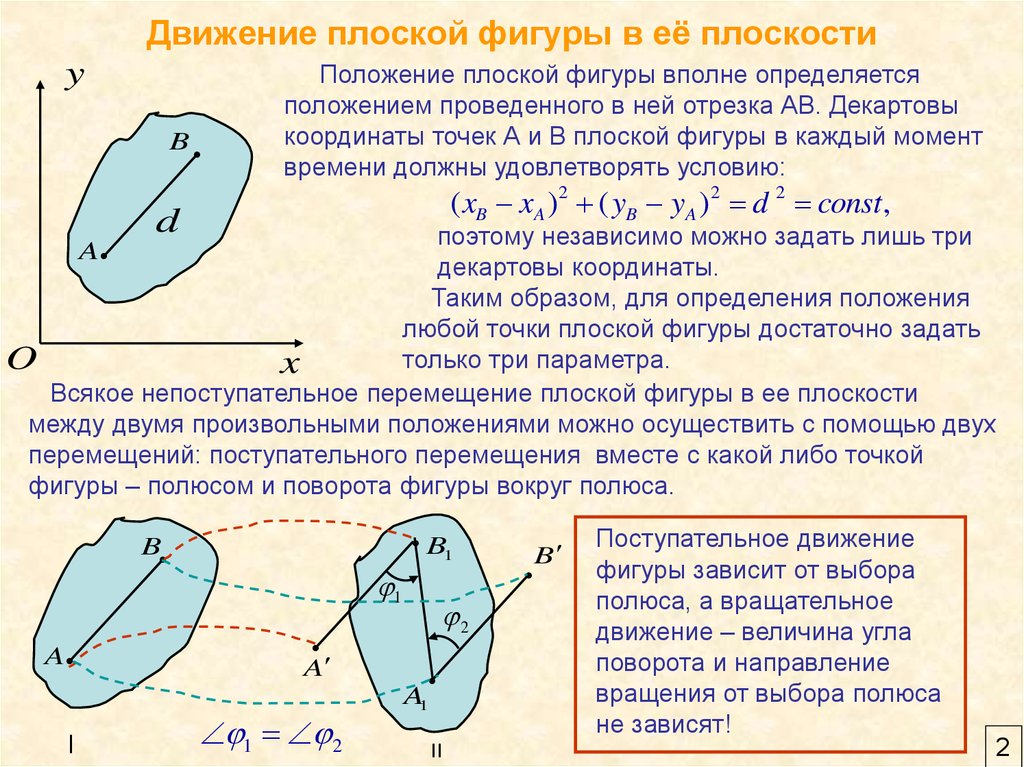
Положение плоской фигуры вполне определяется
положением проведенного в ней отрезка АВ. Декартовы
координаты точек А и В плоской фигуры в каждый момент
времени должны удовлетворять условию:
( xB xA )2 ( yB yA )2 d 2 const ,
d
поэтому независимо можно задать лишь три
декартовы координаты.
Таким образом, для определения положения
любой точки плоской фигуры достаточно задать
только три параметра.
O
x
Всякое непоступательное перемещение плоской фигуры в ее плоскости
между двумя произвольными положениями можно осуществить с помощью двух
перемещений: поступательного перемещения вместе с какой либо точкой
фигуры – полюсом и поворота фигуры вокруг полюса.
A
B
A
І
B
1
A
1 2
1
2
A1
‫װ‬
B
Поступательное движение
фигуры зависит от выбора
полюса, а вращательное
движение – величина угла
поворота и направление
вращения от выбора полюса
не зависят!
2

3.

УРАВНЕНИЯ ПЛОСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
y
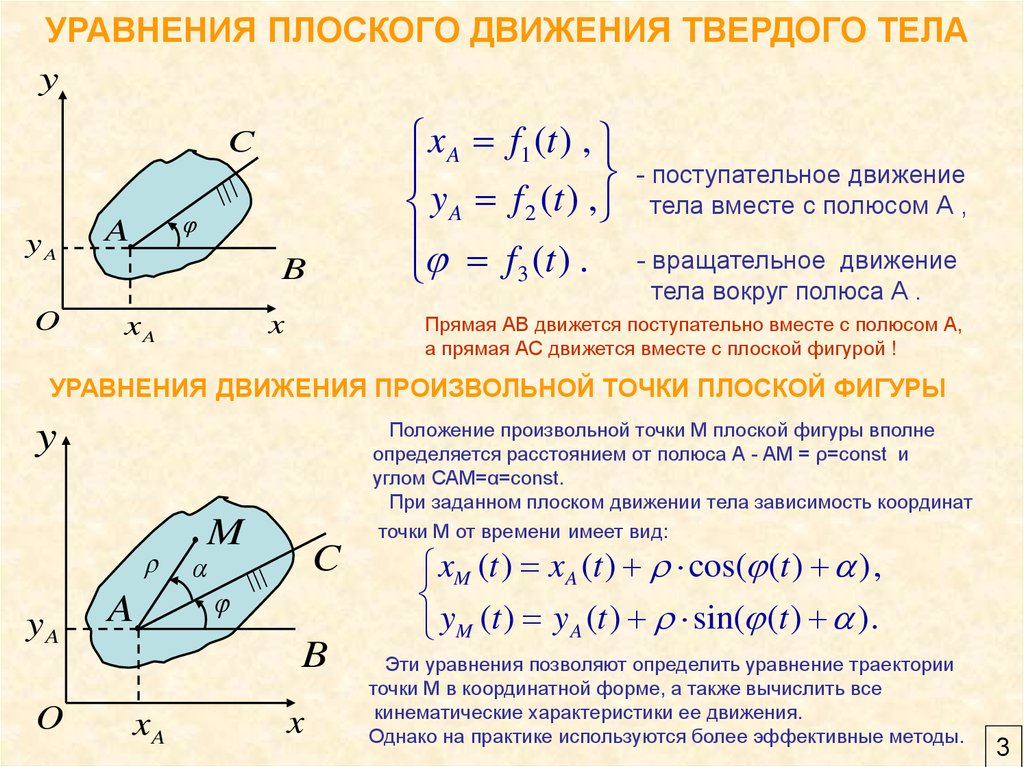
x A f1 (t ) ,
y A f 2 (t ) ,
f (t ) .
3
C
yA
O
A
B
- вращательное движение
тела вокруг полюса А .
Прямая АВ движется поступательно вместе с полюсом А,
а прямая АС движется вместе с плоской фигурой !
x
xA
- поступательное движение
тела вместе с полюсом А ,
УРАВНЕНИЯ ДВИЖЕНИЯ ПРОИЗВОЛЬНОЙ ТОЧКИ ПЛОСКОЙ ФИГУРЫ
Положение произвольной точки М плоской фигуры вполне
определяется расстоянием от полюса А - АМ = ρ=const и
углом САМ=α=const.
При заданном плоском движении тела зависимость координат
точки М от времени имеет вид:
y
yA
O
A
xA
M
C
B
x
xM (t ) x A (t ) cos( (t ) ),
yM (t ) y A (t ) sin( (t ) ).
Эти уравнения позволяют определить уравнение траектории
точки М в координатной форме, а также вычислить все
кинематические характеристики ее движения.
Однако на практике используются более эффективные методы.
3

4. ТЕОРЕМА О СКОРОСТЯХ ТОЧЕК ПЛОСКОЙ ФИГУРЫ

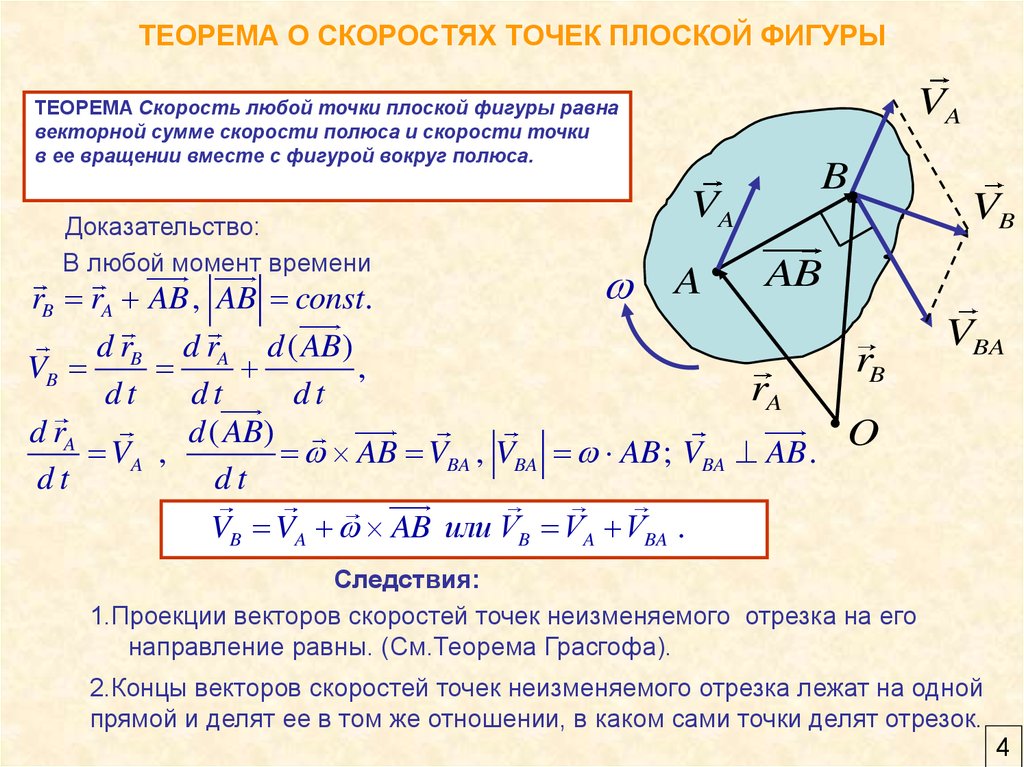
VA
ТЕОРЕМА Скорость любой точки плоской фигуры равна
векторной сумме скорости полюса и скорости точки
в ее вращении вместе с фигурой вокруг полюса.
Доказательство:
В любой момент времени
VA
A
B
VB
AB
rB rA AB , AB const.
d rB d rA d ( AB)
rB
VB
,
rA
dt
dt
dt
d rA
d ( AB)
O
VA ,
AB VBA , VBA AB ; VBA AB .
dt
dt
VBA
VB VA AB или VB VA VBA .
Следствия:
1.Проекции векторов скоростей точек неизменяемого отрезка на его
направление равны. (См.Теорема Грасгофа).
2.Концы векторов скоростей точек неизменяемого отрезка лежат на одной
прямой и делят ее в том же отношении, в каком сами точки делят отрезок.
4

5. МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ

Мгновенным центром скоростей (МЦС) называют точку плоской фигуры,
скорость которой в данный момент времени равна нулю.
Если в некоторый момент времени угловая скорость плоской фигуры
отлична от нуля, то МЦС существует.
Доказательство:
Пусть VA 0 , 0 .
Отложим от направления вектора скорости точки А - VA
в направлении вращения плоской фигуры прямой угол и
Проведем полупрямую АВ, на которой отложим
отрезок АР = V .
B
VPA
A
Определим скорость точки Р по теореме о скоростях точек
плоской фигуры :
VP VA VPA , VPA AP VA VA .
P VA
A
2
VA
VPA AP и направлен в сторону вращения фигуры,
поэтому VPA VA , но тогда V V V 0.
P
A
A
Вектор
Найдена точка Р, скорость которой в данный момент времени равна нулю,
а, следовательно, доказано существование мгновенного центра скоростей.
5

6. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ

Примем МЦС - точку Р за полюс и определим скорости нескольких точек
фигуры по теореме о скоростях точек плоской фигуры :
V
V
0 ; V
0 ; V
VA VP VAP VAP VP 0 ; VAP AP , VAP AP ,
VB VP VBP VBP
VC VP VCP VCP
VB
P
P
BP
BP , VBP BP ,
CP
CP , VCP CP и т. д.
BP VC CP VB
BP
,
,
,
AP VA
AP VC CP
VA
VA
AP
VB
BP
VC
CP
.
В каждый момент времени скорости точек плоской фигуры
распределены так, как если бы фигура в этот момент
времени вращалась вокруг МЦС : векторы скоростей
точек плоской фигуры направлены перпендикулярно
отрезкам, соединяющим эти точки с МЦС, а их модули
относятся так же как расстояния от этих точек до МЦС.
Таким образом, можно ввести понятие о поле скоростей
точек плоской фигуры.
VB
VA
B
A
VC
С
P
Замечание. МЦС в разные моменты времени занимает различные положения как
относительно движущейся плоской фигуры так и относительно неподвижной плоскости
6

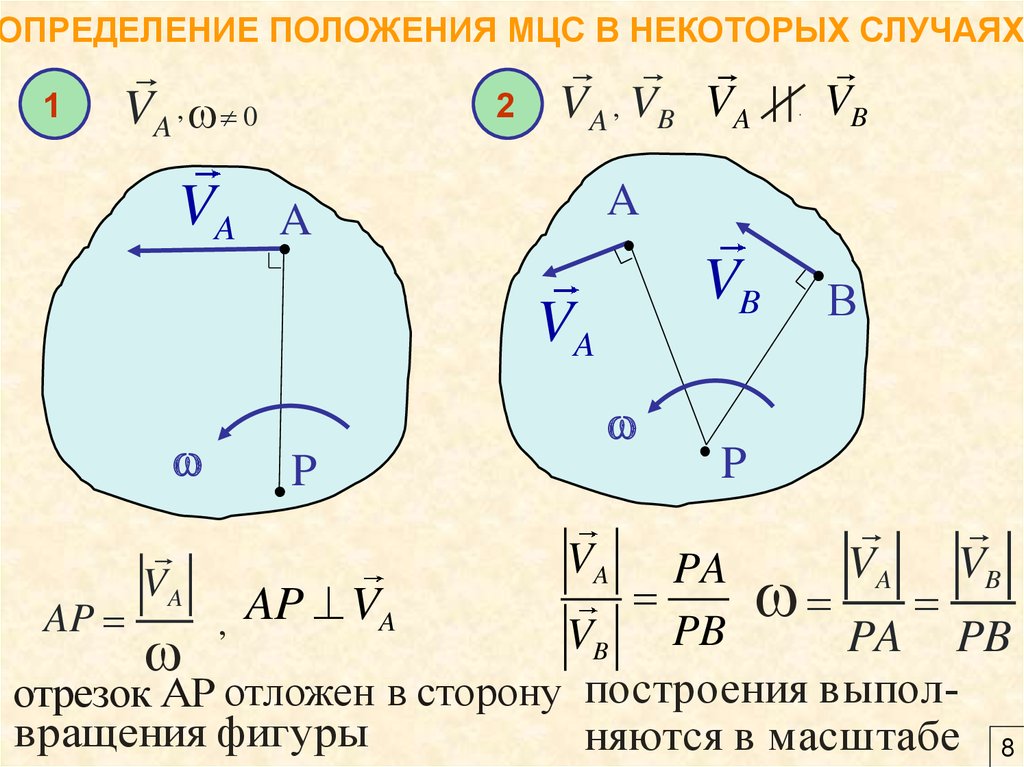
7. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ МЦС В НЕКОТОРЫХ СЛУЧАЯХ

№
1
Известно
VA ,
0
Построение положения МЦС
AP
VA
,
A
AP VA
3
VA , VB
V A не VB
VA , VB
VA
AB
AB
VB
VA
4
VA
VA 0
=
•A
VA
VB
PA PB
построения выполняются в масштабе
VA
PA ,
PB
VB
VB
VA
PA
VB
•B
•A
VB
•B
P
VB
•B
•P
V
A
•B
= 0
МЦС
VB построения выполняются
в масштабе
PB
•A
•P
VA
VA
5
P
VA
PA ,
PB
VB
VB
VA = VB
VA
отрезок АР
отложен в сторону
вращения фигуры
2
B
VB
VA
D
AP=0 (точка А - МЦС)
A
VB
B
A
VC
C
A
VD
E
VE
7

8.

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ МЦС В НЕКОТОРЫХ СЛУЧАЯХ
1
VA , 0
VA
2
VA , VB VA
A
A
VA
P
VA
VB
VB
В
P
VA
VB
PA
AP
V
A
AP
,
PB
V
PA PB
B
отрезок АР отложен в сторону построения выполвращения фигуры
няются в масштабе 8
VA

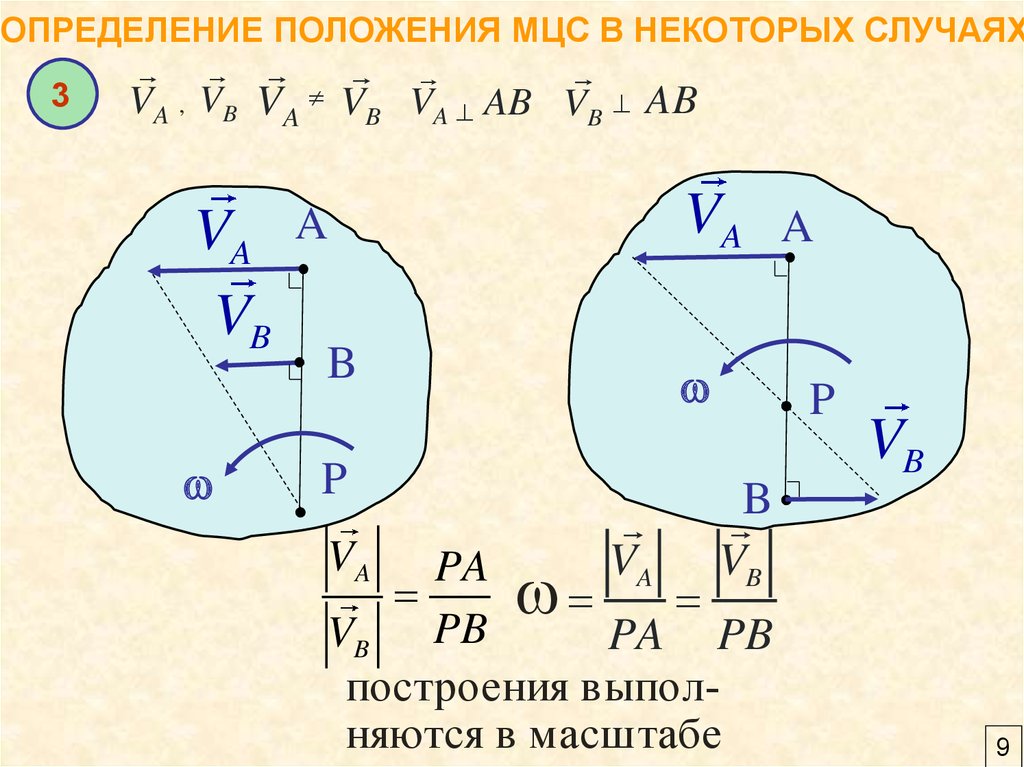
9.

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ МЦС В НЕКОТОРЫХ СЛУЧАЯХ
3
VA , VB VA VB VA AB VB AB
VA
VB
VA
B
A
V
P
VA
P
B
VB
PA
VB PB
PA PB
построения выполняются в масштабе
A
A
VB
9

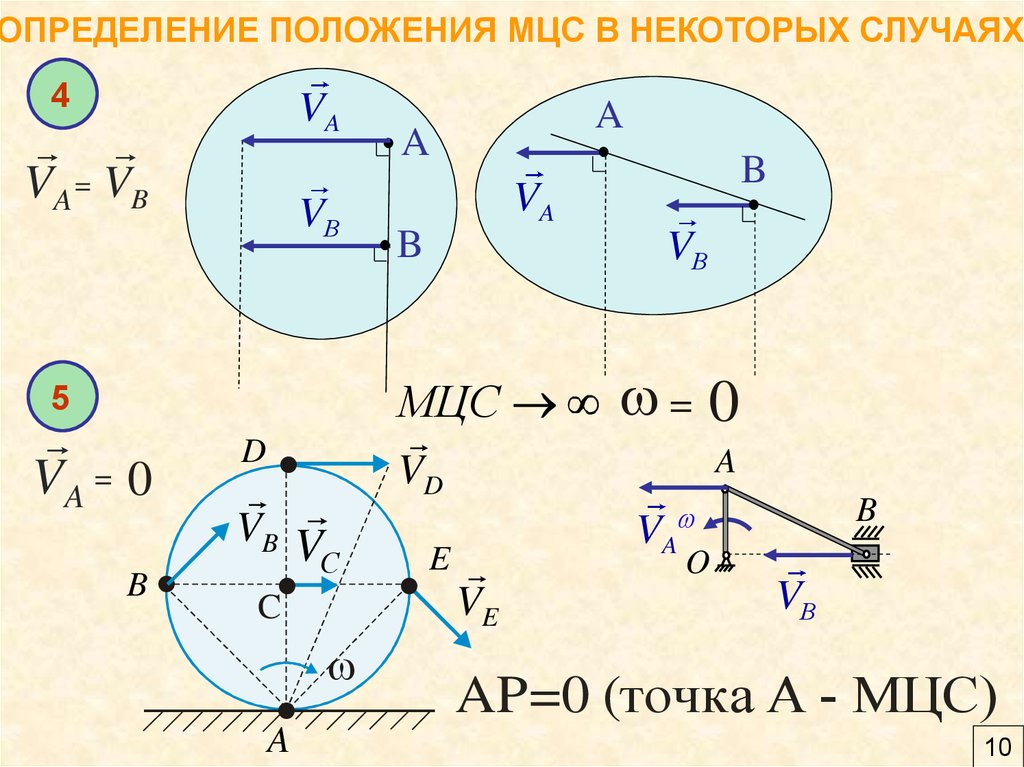
10.

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ МЦС В НЕКОТОРЫХ СЛУЧАЯХ
4
VA
V A = VB
VВ
VA
VA = 0
D
CC
•A
B
= 0
A
VD
VB V
C
С
VВ
МЦС
5
B
A
B
A
VA
E
VE
O
B
VВ
AP=0 (точка А - МЦС)
10

11. ОПРЕДЕЛЕНИЕ УГЛОВОЙ СКОРОСТИ ПЛОСКОЙ ФИГУРЫ В НЕКОТОРЫХ СЛУЧАЯХ

Замечание.
В случае, когда скорости двух точек
плоской фигуры параллельны (случай 3),
угловую скорость плоской
фигуры удобно определять, используя
искусственный прием «остановки»:
если мысленно перемещать фигуру
поступательно со скоростью точки А
(или точки В), но в направлении,
противоположном направлению скорости
этой точки, то выбранная точка А
(или точка В) остановится т.е. станет
МЦС плоской фигуры, а скорость другой
точки фигуры возрастет (уменьшится)
на величину скорости выбранной точки.
При этом угловая скорость фигуры
может быть определена по формуле:
VB VA
если
AB
или по формуле
VA VB ,
VB
VA
Рис.1
VB
•B
•P
V
A
(рис.1)
VB VA
AB
если
•B
•A
•P
A
Рис.2
VA VB . (рис.2)
11

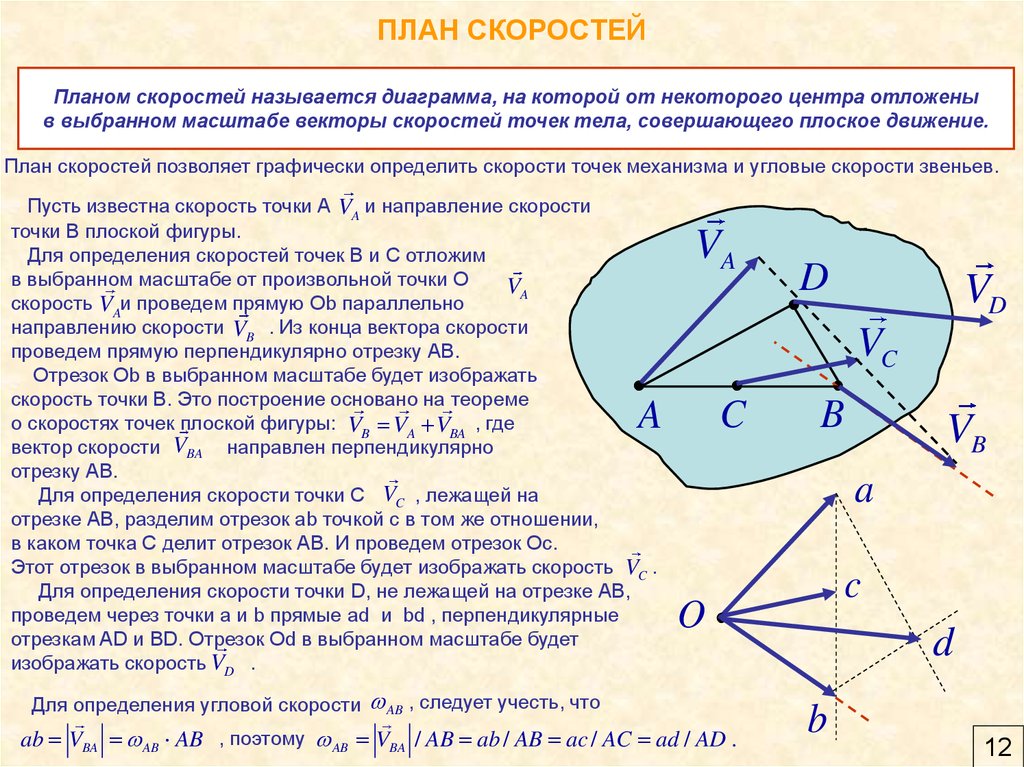
12. ПЛАН СКОРОСТЕЙ

Планом скоростей называется диаграмма, на которой от некоторого центра отложены
в выбранном масштабе векторы скоростей точек тела, совершающего плоское движение.
План скоростей позволяет графически определить скорости точек механизма и угловые скорости звеньев.
Пусть известна скорость точки А VA и направление скорости
точки В плоской фигуры.
Для определения скоростей точек В и С отложим
в выбранном масштабе от произвольной точки О
VA
скорость VAи проведем прямую Ob параллельно
направлению скорости VB . Из конца вектора скорости
проведем прямую перпендикулярно отрезку АВ.
Отрезок Оb в выбранном масштабе будет изображать
скорость точки В. Это построение основано на теореме
о скоростях точек плоской фигуры: VB VA VBA , где
вектор скорости VBA направлен перпендикулярно
отрезку АВ.
Для определения скорости точки С VC , лежащей на
отрезке АВ, разделим отрезок аb точкой с в том же отношении,
в каком точка С делит отрезок АВ. И проведем отрезок Ос.
Этот отрезок в выбранном масштабе будет изображать скорость VC .
Для определения скорости точки D, не лежащей на отрезке АВ,
проведем через точки а и b прямые ad и bd , перпендикулярные
отрезкам AD и BD. Отрезок Оd в выбранном масштабе будет
изображать скорость VD .
VA
D
A C B
Для определения угловой скорости
VD
VC
VB
a
O
AB , следует учесть, что
ab VBA AB AB , поэтому AB VBA / AB ab / AB ac / AC ad / AD .
c
d
b
12

13. ТЕОРЕМА ОБ УСКОРЕНИЯХ ТОЧЕК ПЛОСКОЙ ФИГУРЫ

ТЕОРЕМА. Ускорение любой точки плоской фигуры равно векторной
сумме ускорения полюса и ускорения точки в ее вращении вместе с
фигурой вокруг полюса.
Доказательство.
Дифференцируя по времени выражение для скорости точки плоской фигуры
VB VA AB ,
где
d VA
aA
dt
получим:
d AB
d VB d VA d
aB
AB
,
dt
dt
dt
dt
ускорение полюса – точки А ,
d
AB AB aBA
тангенциальное ускорение точки В во вращении
вокруг полюса А,
dt
при этом aBA
AB , aBA
AB .
AB a
d AB
dt
при этом
n
BA
нормальное ускорение точки В
во вращении вокруг полюса А,
n
n
n
aBA
2 AB , aBA
II AB . Следует отметить, что aBA
aBA
.
13

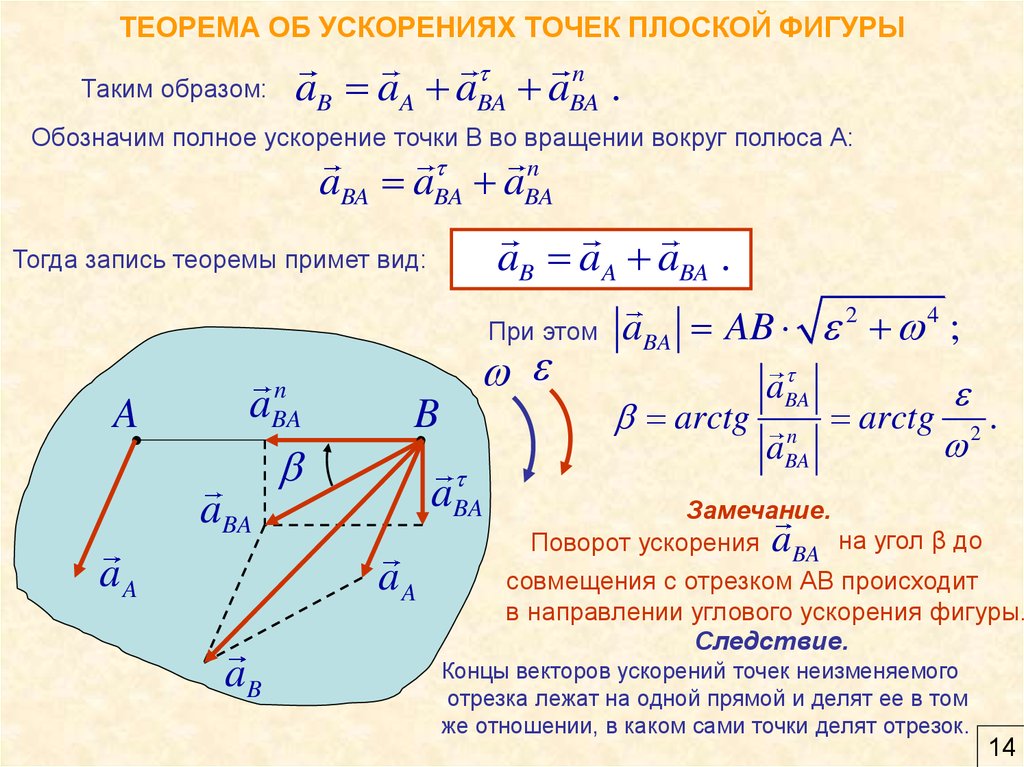
14. ТЕОРЕМА ОБ УСКОРЕНИЯХ ТОЧЕК ПЛОСКОЙ ФИГУРЫ

Таким образом:
n
aB aA aBA
aBA
.
Обозначим полное ускорение точки В во вращении вокруг полюса А:
n
aBA aBA aBA
aB aA aBA .
Тогда запись теоремы примет вид:
При этом
A
a
n
BA
B
aBA
aA
aA
aB
aBA
aBA AB 2 4 ;
arctg
aBA
n
aBA
arctg 2 .
Замечание.
Поворот ускорения a BA на угол β до
совмещения с отрезком АВ происходит
в направлении углового ускорения фигуры.
Следствие.
Концы векторов ускорений точек неизменяемого
отрезка лежат на одной прямой и делят ее в том
же отношении, в каком сами точки делят отрезок.
14

15. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ

Мгновенным центром ускорений (МЦУ) называют точку плоской
фигуры, ускорение которой в данный момент времени равно нулю.
Если в некоторый момент времени угловая скорость или угловое ускорение
плоской фигуры отличны от нуля, то МЦУ существует.
B
Доказательство.
aQA Q a A
Пусть aA 0 , 0 , 0 .
Отложим от направления вектора ускорения точки А - a A
в направлении углового ускорения плоской фигуры ε угол
arctg
2
и проведем полупрямую АВ, на которой.
отложим отрезок AQ a A /
.
2
4
Определим ускорение точки Q по теореме об ускорениях
точек плоской фигуры :
A
aA
aQ aA aQA , aQA 2 4 AQ 2 4 a A / 2 4 a A .
Вектор aQA составляет с отрезком АQ угол β и направлен в сторону
углового
у
ускорения плоской фигуры, поэтому aQA aA, , но тогда
у aQ a A a A 0
Найдена точка Q, ускорение которой в данный момент времени равно нулю,
а, следовательно, доказано существование мгновенного центра ускорений.
15

16. РАСПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ

Примем МЦУ - точку Q за полюс и определим ускорения нескольких точек
фигуры по теореме об ускорениях точек плоской фигуры :
a A aQ a AQ a AQ aQ 0 ; a AQ 2 4 AQ , (a AQ , AQ ) ,
aB aQ aBQ aBQ aQ 0 ; aBQ 2 4 BQ , (aBQ , BQ ) ,
aC aQ aCQ aCQ aQ 0 ; aCQ 2 4 CQ , (aCQ , CQ ) и т.д.
aB
aA
BQ aC CQ aB
BQ
,
,
.
AQ a A
AQ aC CQ
В каждый момент времени ускорения точек плоской фигуры
распределены так как если бы фигура в этот момент
времени вращалась вокруг МЦУ : векторы ускорений точек
плоской фигуры составляют с отрезками, соединяющими
эти точки с МЦУ угол arctg ( / 2 ), а их модули
относятся так же как расстояния от этих точек до МЦУ.
Таким образом, можно ввести понятие о поле ускорений
точек плоской фигуры.
aB
B
A
aA
aC
С
Q
Замечание. МЦУ в разные моменты времени занимает различные положения как
относительно движущейся плоской фигуры так и относительно неподвижной плоскости
16

17.

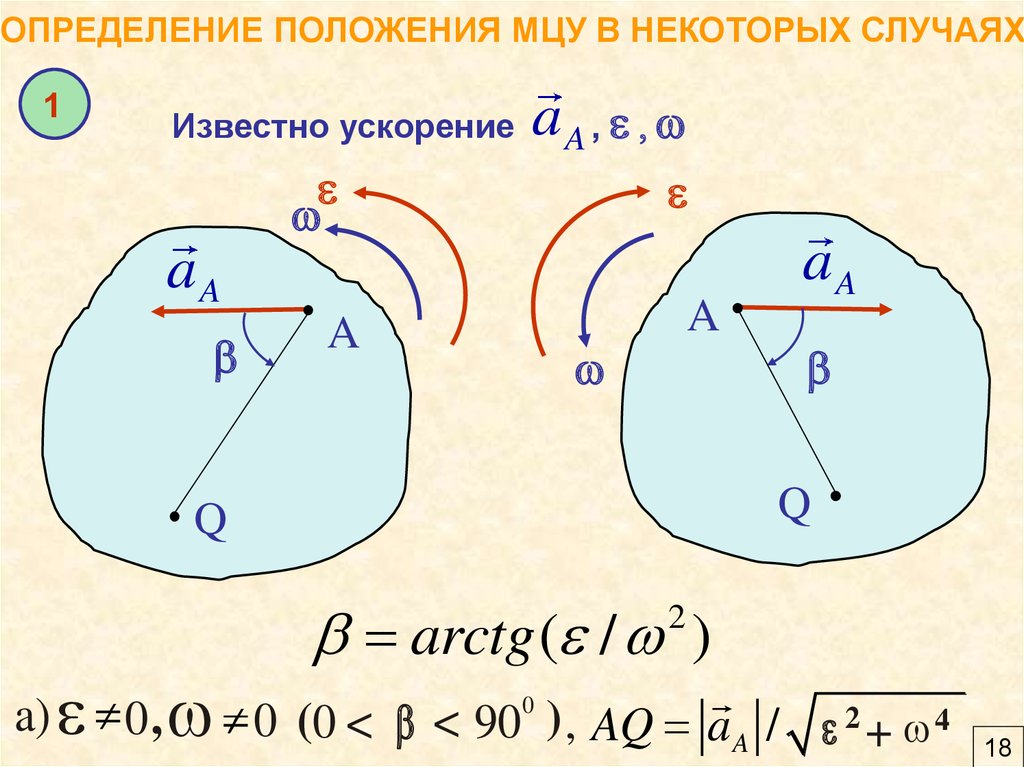
ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ МЦУ В НЕКОТОРЫХ СЛУЧАЯХ
1
Известно ускорение
aA , ,
aA
A
A
aA
Q
Q
arctg ( / )
2
a) 0 , 0 (0 < < 900 ) , AQ aA / 2 + 4
18

18.

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ МЦУ В НЕКОТОРЫХ СЛУЧАЯХ
1
A
aA
A
Q
aA
Q
b) = 0 , 0 , ( b= 0
AQ a / 2
A
0
) , c) 0,
0
(
,
b
=0
= 90 ) ,
AQ aA /
19

19.

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ МЦУ В НЕКОТОРЫХ СЛУЧАЯХ
1
A
aB
B
С
aA
aC
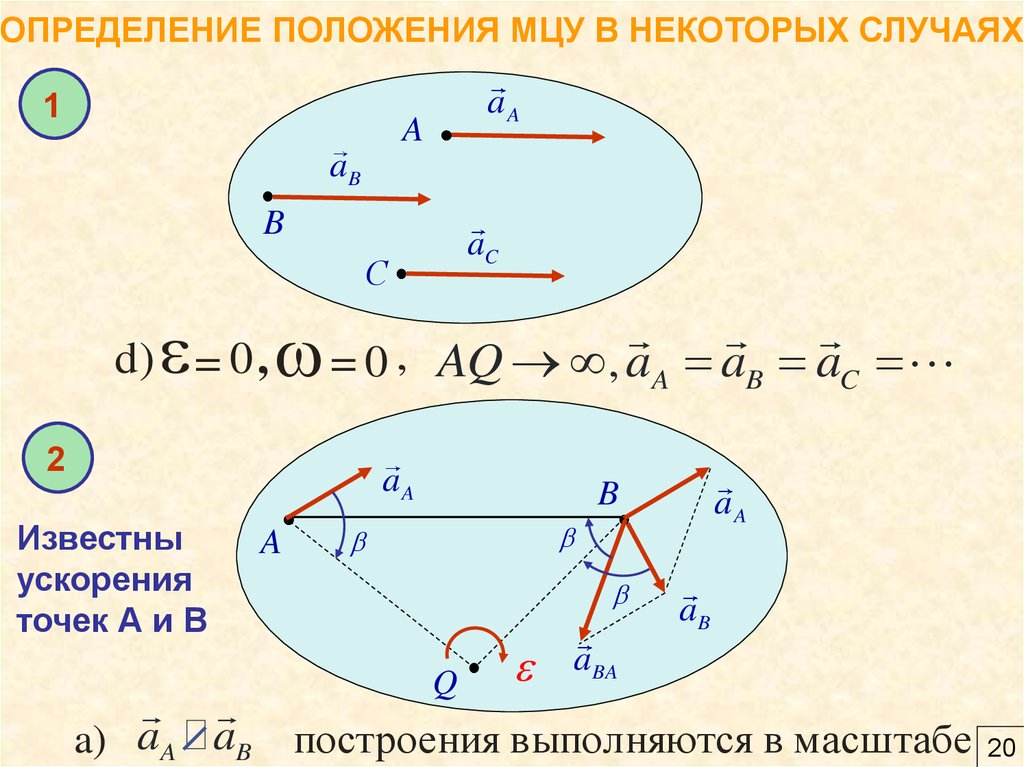
d) = 0, = 0 , AQ ® Ґ , aA aB aC L
2
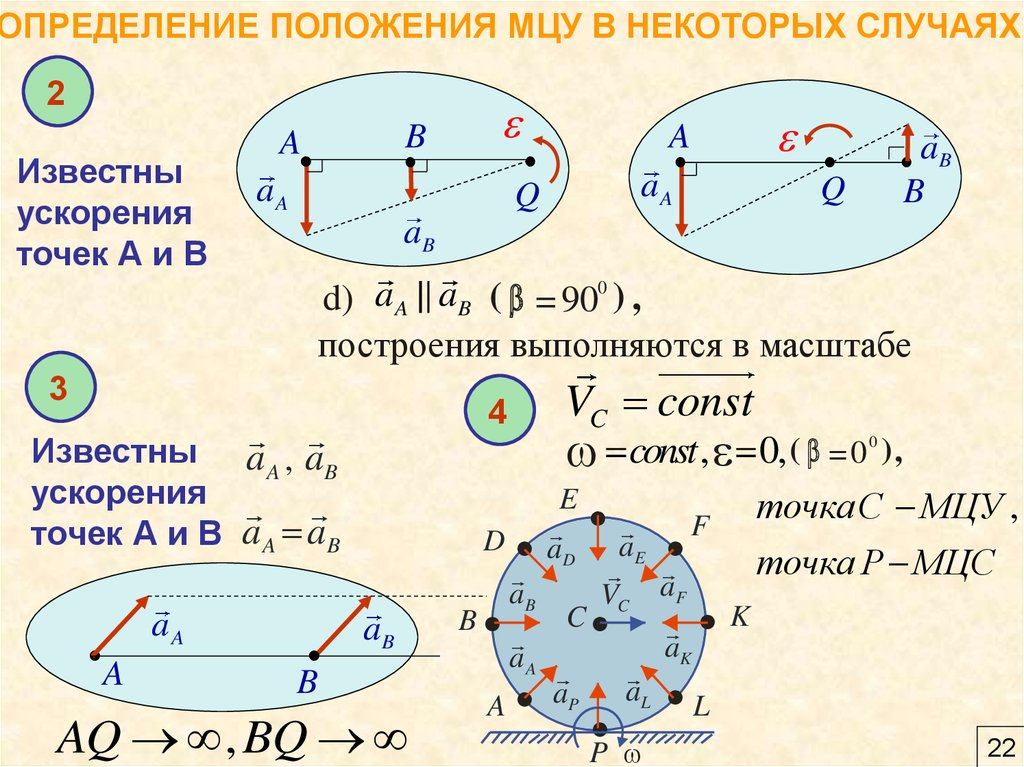
Известны
ускорения
точек А и В
A
aA
B
Q
aA
aB
aBA
a) aA P aB построения выполняются в масштабе
20

20.

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ МЦУ В НЕКОТОРЫХ СЛУЧАЯХ
2
A
B
Известны
ускорения
точек А и В
aA
aB
Q
A
aA
Q
aB
B
0
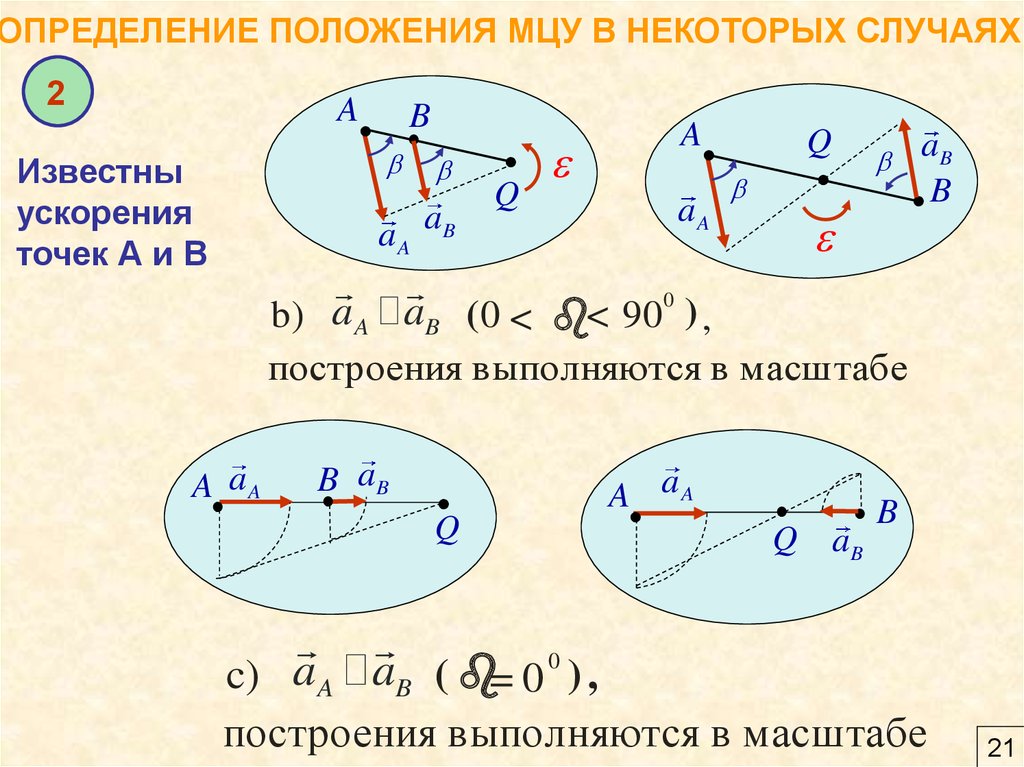
b) a A P aB ( 0 < b< 90 ) ,
построения выполняются в масштабе
A aA
B aB
Q
A aA
Q aB
B
c) a A P aB ( b= 0 0 ) ,
построения выполняются в масштабе
21

21.

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ МЦУ В НЕКОТОРЫХ СЛУЧАЯХ
2
Известны
ускорения
точек А и В
aA
A
aA
A
aA
Q
aB
B
Q
aB
d) a A aB ( = 900 ) ,
построения выполняются в масштабе
3
Известны
ускорения
точек А и В
B
A
a A , aB
a A aB
VC const
const , 0, ( = 0
4
D
aB
B
AQ ® Ґ , BQ ® Ґ
B
aB
E
aD
• a
VC
E
F
aF
aK
A
P
),
точкаС МЦУ ,
точка Р МЦС
•K
• a
a
A• a
•L
•P
C
0
L
22

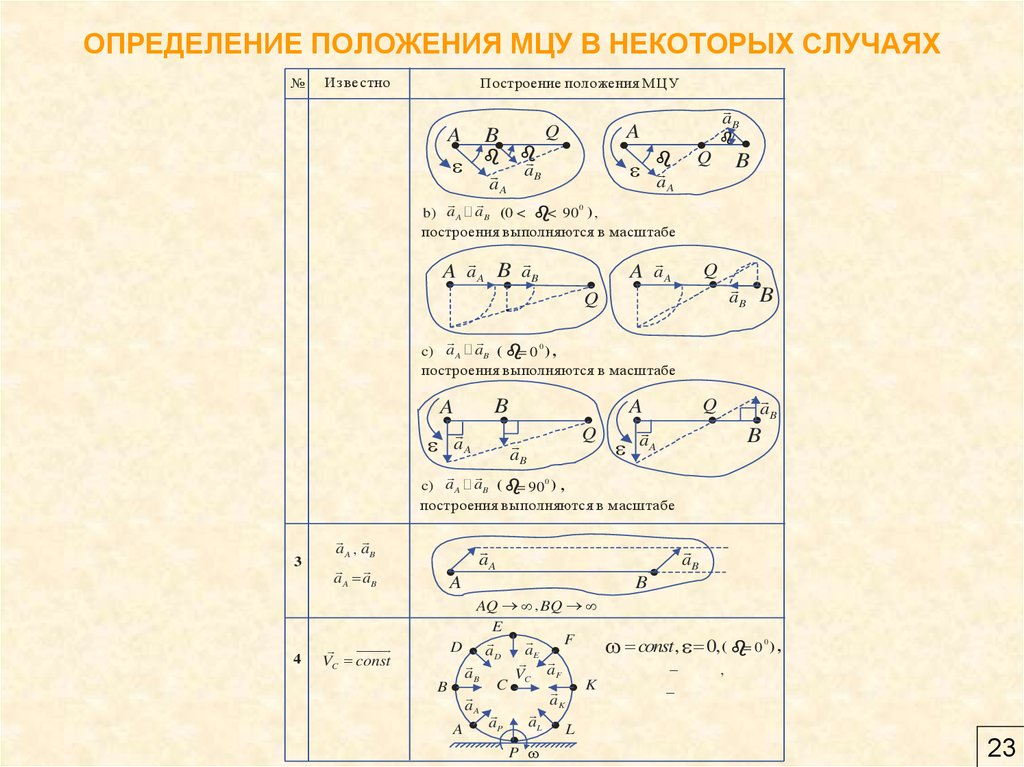
22. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ МЦУ В НЕКОТОРЫХ СЛУЧАЯХ

№
Изве стно
Построение положения МЦУ
Q
B
A
b
b
A
aB
aA
b
a
•Q
aB
b
B
A
0
b) a A P aB (0 < b< 90 ) ,
построения выполняются в масштабе
A a A B aB
Q
A aA
Q
aB
•B
c) a A P aB ( b= 0 0 ) ,
построения выполняются в масштабе
B
A
•
aA
Q
aB
aB
Q
A
•
aA
B
c) a A P aB ( b= 90 0 ) ,
построения выполняются в масштабе
3
4
a A , aB
a A aB
uuuuu
VC const
aA
•A
B
AQ ® Ґ , BQ ® Ґ
E
F
D
aE
aD
aB
V aF
K
C C
B
aK
aA
aL
aP
A
L
aB
•P
const , 0, ( b= 0
0
),
,
23

23. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ

Замечания.
1) МЦУ и МЦС - разные точки плоской фигуры.
Пример. Колесо катится без проскальзывания
по прямолинейному пути так, что скорость
его центра С VC const . Тогда точка касания
колеса с поверхностью – точка Р будет являться
МЦС, а центр колеса – точка С будет являться МЦУ.
Действительно a
C
aC a , где
n
C
aM
M
n
M
a
aM
C VC
aP
P n
d VC
aC
0, VC const , aCn 0 , т.к. траектория точки С – прямая.
dt
2) В данном примере
VC VC
d
const ,
0 , arctg 2 0,
PC R
dt
поэтому ускорения всех точек обода колеса направлены к центру колеса С и
имеют модули, равные 2 R VC2 R .
3) Если VC const , то угловое ускорение колеса можно вычислить
aC
по формуле :
.
R
24