Similar presentations:
Плоскопараллельное движение твердого тела
1. ТЕМА 6. Плоскопараллельное движение твердого тела.
2. Вопрос №1. Уравнения плоскопараллельного движения
Плоскопараллельное (плоское) движение твердого тела –такое его движение, при котором все его точки перемещаются
параллель но некоторой фиксированной плоскости.
Из определения следует, что перпендикуляр МА остается
параллелен своему начальному положению. По теореме о
поступательном движении траектории, скорости и ускорения точек М
и А совпадают.
Для изучения движения всего тела достаточно изучить, как
движется в плоскости Оху сечение S этого тела или некоторая плоская
фигура S.
3.
Примеры плоскопараллельного движения:скольжение стержня
качение цилиндра
4.
Для задания движения плоской фигуры введемподвижную систему координат, совершающую
поступательное движение с точкой А.
Точку А, выбранную для определения положения
фигуры S, будем в дальнейшем называть полюсом
5.
Положение плоской фигуры можно задать двумякоординатами полюса и одним углом между
отрезком, жестко связанным с телом, и
направлением одной из неподвижных осей:
x A f1 t , y A f 2 t , f3 t
уравнения движения плоской фигуры
Первые два уравнения представляют собой
уравнения поступательного движения полюса.
Третье
уравнение
описывает
вращательное
движение тела вокруг полюса.
6.
Основные кинематические характеристикиплоскопараллельного движения:
1) Скорость и ускорение поступательного полюса.
2
2
vA xA (t ) y A (t ) aA
2
2
xA (t ) yA (t )
2) Угловая скорость и угловое ускорение
вращательного движения вокруг полюса.
(t ) , (t ).
7. Вопрос №2. Определение скоростей точек плоской фигуры
Теорема: Скорость любой точки тела приплоском движении находится как сумма скорости
полюса
и скорости данной точки во
вращательном движении вокруг полюса.
v B v A v BA
где
vBA
AB , vBA AB
8.
9.
(1)10.
(1)11.
12.
13. Вопрос №3. Теорема о проекциях скоростей двух точек тела
Проекции скоростей двух точек плоской фигуры напрямую, проходящую через эти точки, равны между
собой.
пр AB v A пр AB vB
VВ
А
А
VВА
В
VА
х
Доказательство:
v B v A v BA , пр AB v B пр AB v A пр AB v BA ,
v A cos vB cos
0
14. Вопрос № 4. Определение скорости точек плоской фигуры с помощью мгновенного центра скоростей
Мгновенный центр скоростей – точка плоскойфигуры, скорость которой в данный момент
времени равна нулю.
Теорема:
При непоступательном движении плоской
фигуры существует жестко связанная с ней точка,
скорость которой в данный момент движения
равна нулю.
15.
Доказательство:Отложим перпендикуляр к скорости в точке
А и выберем на нем точку на расстоянии:
А
VРА
Р
VА
VА
следовательно: v p v A v PA
Теорема доказана.
АР =
vA
.
По
теореме
скоростях:
v p v A v PA ,
где v PA AP v A .
0.
о
16. Мгновенный центр скоростей плоской фигуры, способы его нахождения.
Выбирая мгновенный центр скоростей за полюс,нетрудно убедиться, что скорость любой точки плоской
фигуры находится как скорость во вращательном
движении вокруг МЦС.
VВ
vB vР vBP ,
В
vP 0,
С
Р
VС
vB BP
17.
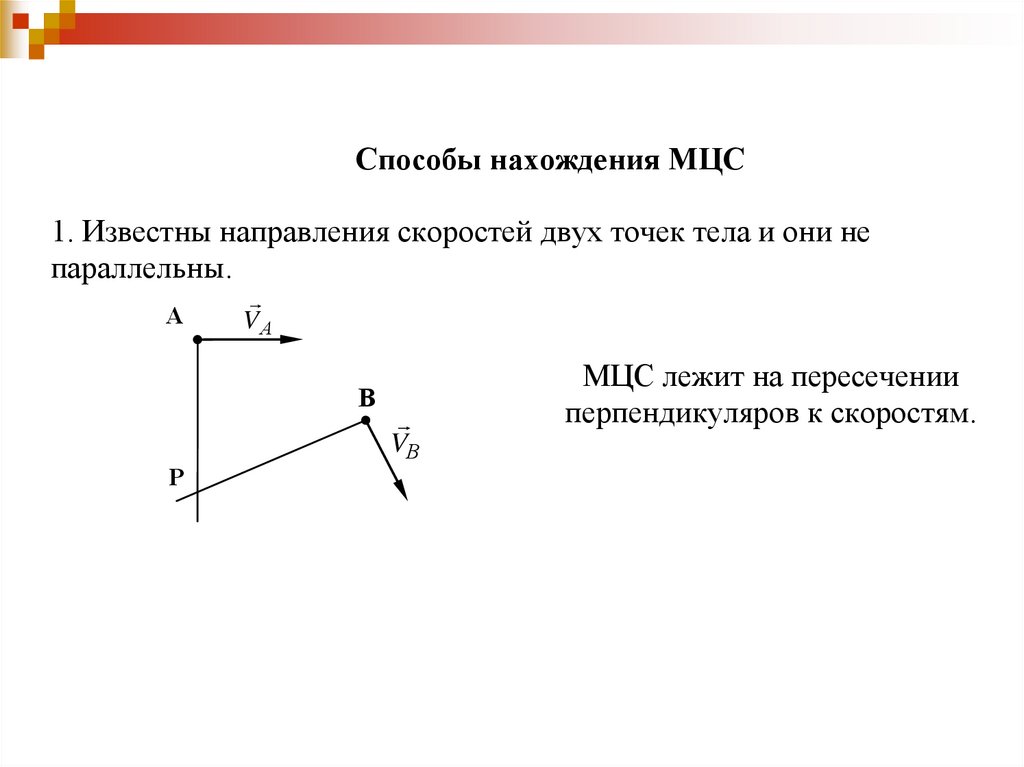
Способы нахождения МЦС1. Известны направления скоростей двух точек тела и они не
параллельны.
А
VА
В
Р
VВ
МЦС лежит на пересечении
перпендикуляров к скоростям.
18.
Способы нахождения МЦС2. Известны направления скоростей двух точек тела и они
параллельны.
а)
б)
А
VА
В
VВ
Р
А
VА
Р
VВ
В
19.
VАв)
А
α
VВ
В
v A cos vB cos ,
т.е.v A vB и 0.
α
МЦС не существует (находится
в бесконечности), то тело совершает
мгновеннопоступательное движение. Угловая скорость равна нулю,
скорости всех точек тела одинаковы.
Р
3. Качение без скольжения
неподвижной поверхности (нет
проскальзывания). МЦС находится
в точке касания
тела с
неподвижной поверхностью.
20. Вопрос № 5. Определение ускорения точек плоской фигуры
Теорема:Ускорение точки плоской фигуры равно сумме
ускорения полюса и ускорения данной точки во
вращательном движении вокруг полюса.
n
aB a A aBA aBA .
21.
aBA AB ABn
aBA
2
AB
AB
ε
В
n
а ВА
А
аА
а BA
22.
nn
aB a A a A aBA aBA .
n n
n
aB aB a A a A aBA aBA .





















 physics
physics








