Кинематика плоского движения твердого тела (лекция 9)

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра строительная механика
Теоретическая механика
Тема 11.
Кинематика плоского
движения твердого тела.
Лукашевич Надежда Кимовна
к.т.н., доцент
Сойту Наталья Юрьевна
к.т.н., доцент

2. Лекция 9.

Тема 11. Кинематика плоского движения твердого тела.
11.1. Определение плоского движения твердого тела.
Уравнения движения.
11.2. Разложение плоского движения на поступательное и вращательное.
11.3. Теорема Эйлера о сложении скоростей.
11.4. Мгновенный центр скоростей (МЦС).
11.5. Определение скоростей точек плоской фигуры через МЦС.
11.6. Примеры применения МЦС к определению скоростей
11.7. Теорема Эйлера о сложении ускорений.
2

3.

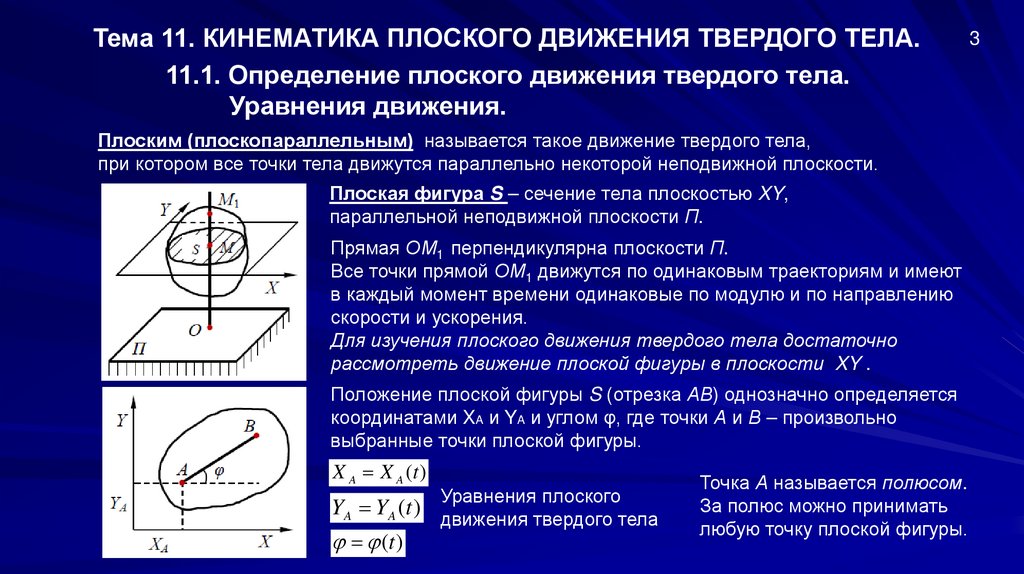
Тема 11. КИНЕМАТИКА ПЛОСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА.
11.1. Определение плоского движения твердого тела.
Уравнения движения.
Плоским (плоскопараллельным) называется такое движение твердого тела,
при котором все точки тела движутся параллельно некоторой неподвижной плоскости.
Плоская фигура S – сечение тела плоскостью XY,
параллельной неподвижной плоскости П.
Прямая ОМ1 перпендикулярна плоскости П.
Все точки прямой ОМ1 движутся по одинаковым траекториям и имеют
в каждый момент времени одинаковые по модулю и по направлению
скорости и ускорения.
Для изучения плоского движения твердого тела достаточно
рассмотреть движение плоской фигуры в плоскости XY .
Положение плоской фигуры S (отрезка АВ) однозначно определяется
координатами XA и YA и углом φ, где точки А и В – произвольно
выбранные точки плоской фигуры.
X A X A (t )
YA YA (t )
(t )
Уравнения плоского
движения твердого тела
Точка А называется полюсом.
За полюс можно принимать
любую точку плоской фигуры.
3

4.

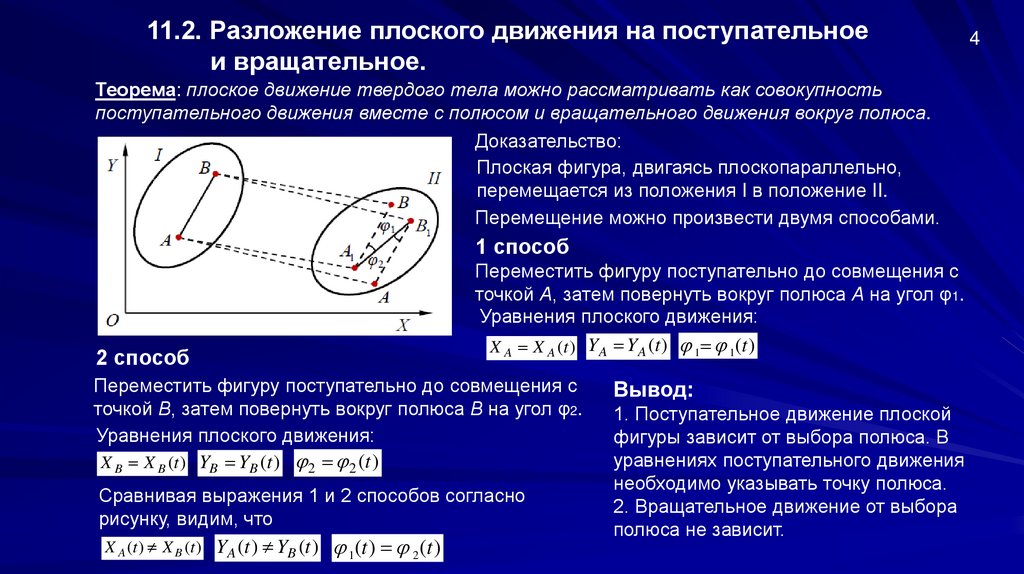
11.2. Разложение плоского движения на поступательное
и вращательное.
Теорема: плоское движение твердого тела можно рассматривать как совокупность
поступательного движения вместе с полюсом и вращательного движения вокруг полюса.
Доказательство:
Плоская фигура, двигаясь плоскопараллельно,
перемещается из положения I в положение II.
Перемещение можно произвести двумя способами.
1 способ
2 способ
Переместить фигуру поступательно до совмещения с
точкой А, затем повернуть вокруг полюса А на угол φ1.
Уравнения плоского движения:
X A X A (t ) YA YA (t ) 1 1(t )
Переместить фигуру поступательно до совмещения с
точкой В, затем повернуть вокруг полюса В на угол φ2.
Уравнения плоского движения:
X B X B (t ) YB YB (t ) 2 2 (t )
Сравнивая выражения 1 и 2 способов согласно
рисунку, видим, что
X A (t ) X B (t ) YA (t ) YB (t ) 1(t ) 2 (t )
Вывод:
1. Поступательное движение плоской
фигуры зависит от выбора полюса. В
уравнениях поступательного движения
необходимо указывать точку полюса.
2. Вращательное движение от выбора
полюса не зависит.
4

5.

11.3. Теорема Эйлера о сложении скоростей.
Теорема Эйлера: скорость любой точки плоской фигуры равна
геометрической сумме скорости полюса и скорости точки в ее вращении
вместе с плоской фигурой вокруг полюса VB VA VBA
Доказательство:
А и В – точки тела, движущегося плоскопараллельно.
rB rA rAB
Возьмем производную по времени
d rB
VB
dt
d rB d rA d rAB
dt
dt
dt
d rA
VA
dt
d rAB
VBА (т.к. у rAB меняется только направление)
dt
VBА – скорость вращения точки В вокруг полюса А.
Модуль скорости VBA AB или VBA AB sin 90 , следовательно VBA rAB
Вектор VBА направлен перпендикулярно вектору rAB в сторону угловой скорости.
Окончательно получим VB VA VBA
5

6.

Следствие 1 (правило проекций): проекции скоростей двух точек твердого
тела на прямую, проходящую через эти точки, равны.
Доказательство:
А и В – точки твердого тела,
движущегося плоскопараллельно.
По теореме Эйлера
VB VA VBA
Спроецируем на прямую АВ
Пр АВVB Пр АВV A Пр АВVBA
Учитывая, что Пр АВVBA 0 , получим Пр АВVB Пр АВV A
11.4. Мгновенный центр скоростей (МЦС).
Мгновенный центр скоростей (МЦС) – это точка, скорость которой в данный
момент времени равна нулю.
Теорема о существовании мгновенного центра скоростей: для тела,
движущегося плоскопараллельно, в каждый момент времени можно построить
мгновенный центр скоростей.
6

7.

Доказательство:
Примем точку А за полюс и найдем такую точку Р, для которой
скорость вращения вокруг полюса А равна скорости полюса с
противоположным знаком .
VPA VA
Точка лежит на перпендикуляре к скорости V A на расстоянии АР.
VPА AP , тогда AP VPA
Скорость точки Р по теореме Эйлера VP VA VPA VA VA 0 , следовательно Р – МЦС.
11.5. Определение скоростей точек плоской фигуры через МЦС.
Плоская фигура движется плоскопараллельно.
Примем точку Р за полюс.
Скорость точки А по теореме Эйлера VA VP VAP VAP ,
так как VP 0 (согласно определению МЦС)
Аналогично определяется скорость любой другой точки.
VB VP VBP VBP VС VP VСP VСP
Угловая скорость плоской фигуры
VA
AP
Скорости точек В и С VB BP VC CP
Плоское движение можно рассматривать как мгновенное вращение вокруг оси,
проходящей через МЦС перпендикулярно плоской фигуре.
7

8.

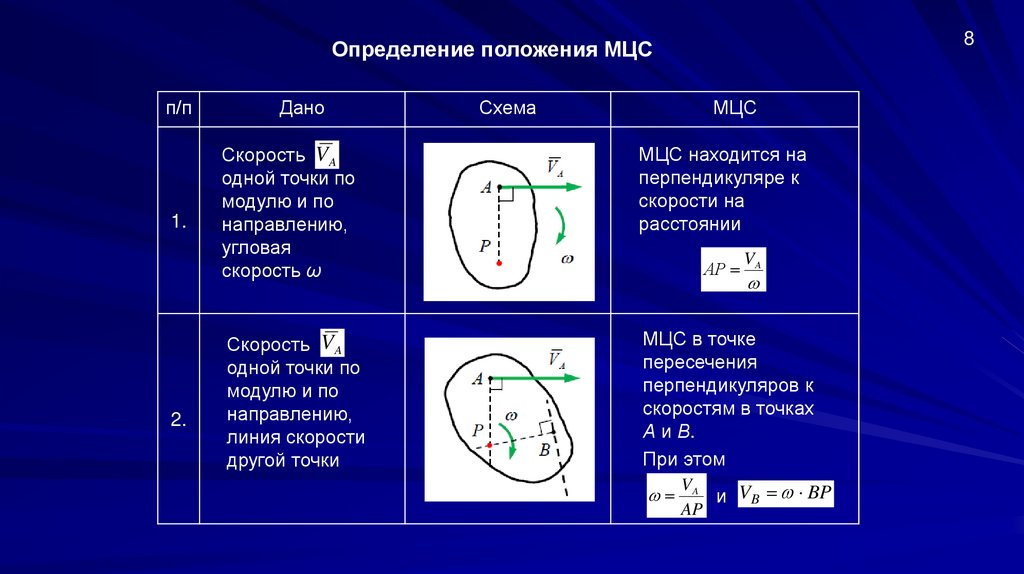
8
Определение положения МЦС
п/п
1.
2.
Дано
Схема
МЦС
Скорость VA
одной точки по
модулю и по
направлению,
угловая
скорость ω
МЦС находится на
перпендикуляре к
скорости на
расстоянии
Скорость V A
одной точки по
модулю и по
направлению,
линия скорости
другой точки
МЦС в точке
пересечения
перпендикуляров к
скоростям в точках
А и В.
При этом
АР
VA
VA
и VB BP
AP

9.

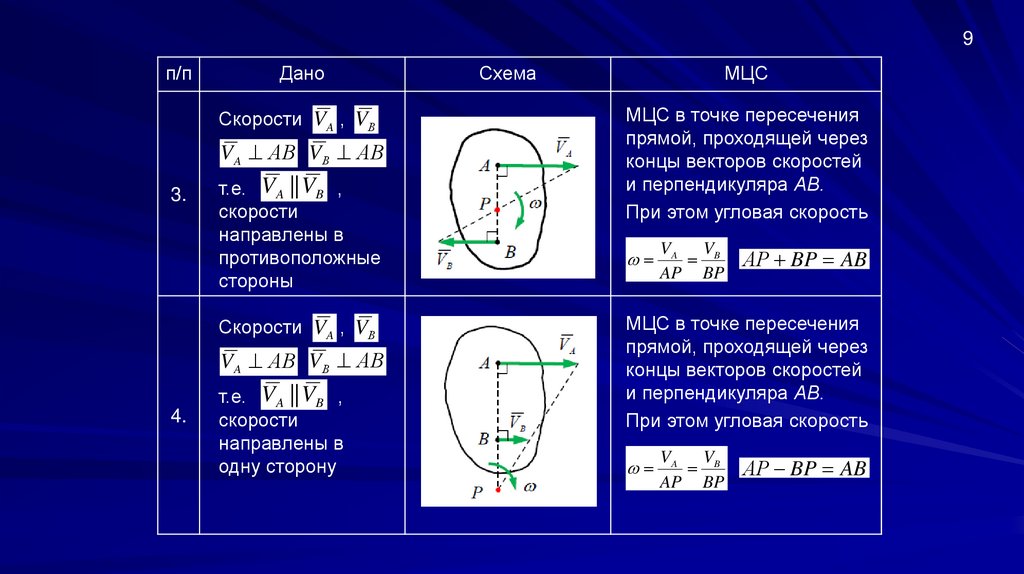
9
п/п
Дано
Скорости VA , VВ
VA АВ VВ АВ
3.
т.е. VA || VB ,
скорости
направлены в
противоположные
стороны
Скорости VA , VВ
VA АВ VВ АВ
4.
т.е. VA || VB ,
скорости
направлены в
одну сторону
Схема
МЦС
МЦС в точке пересечения
прямой, проходящей через
концы векторов скоростей
и перпендикуляра АВ.
При этом угловая скорость
VA VB
AP BP
АP BP AB
МЦС в точке пересечения
прямой, проходящей через
концы векторов скоростей
и перпендикуляра АВ.
При этом угловая скорость
VA VB
AP BP
АP BP AB

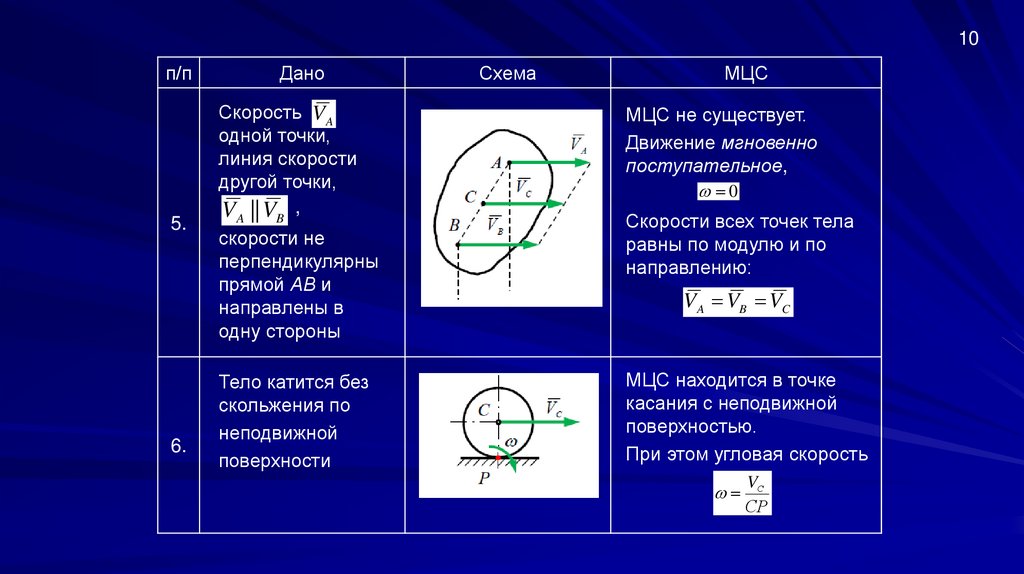
10.

10
п/п
5.
6.
Дано
Скорость VA
одной точки,
линия скорости
другой точки,
VA || VB ,
скорости не
перпендикулярны
прямой АВ и
направлены в
одну стороны
Тело катится без
скольжения по
неподвижной
поверхности
Схема
МЦС
МЦС не существует.
Движение мгновенно
поступательное,
0
Скорости всех точек тела
равны по модулю и по
направлению:
VA VB VC
МЦС находится в точке
касания с неподвижной
поверхностью.
При этом угловая скорость
VС
СP

11.

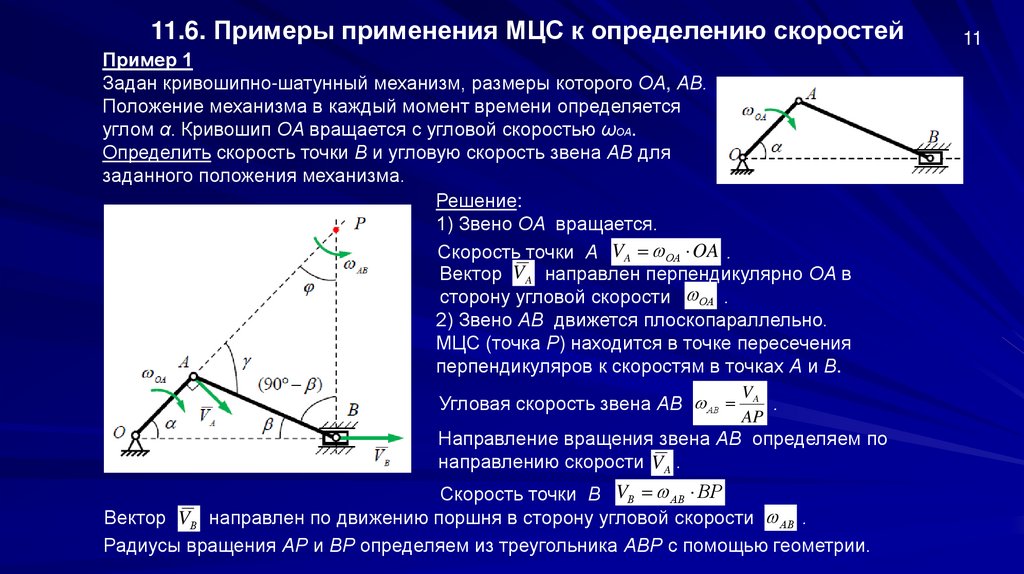
11.6. Примеры применения МЦС к определению скоростей
Пример 1
Задан кривошипно-шатунный механизм, размеры которого ОА, АВ.
Положение механизма в каждый момент времени определяется
углом α. Кривошип ОА вращается с угловой скоростью ωОА.
Определить скорость точки В и угловую скорость звена АВ для
заданного положения механизма.
Решение:
1) Звено ОА вращается.
Скорость точки А VA ОА OA .
Вектор V A направлен перпендикулярно ОА в
сторону угловой скорости ОА .
2) Звено АВ движется плоскопараллельно.
МЦС (точка Р) находится в точке пересечения
перпендикуляров к скоростям в точках А и В.
Угловая скорость звена АВ АВ
VA
.
AP
Направление вращения звена АВ определяем по
направлению скорости VA .
Скорость точки В VВ АВ ВР
Вектор VВ направлен по движению поршня в сторону угловой скорости АВ .
Радиусы вращения АР и ВР определяем из треугольника АВР с помощью геометрии.
11

12.

Пример 2.
12
Ступенчатое колесо катится по неподвижной поверхности.
Заданы радиусы колеса R и r , угол и скорость центра колеса Vc.
Определить угловую скорость колеса и скорости точек A, B, D, K.
Решение:
Колесо движется плоскопараллельно.
МЦС (точка Р) находится в точке касания с поверхностью.
VC VC
CP r
Направление угловой скорости колеса определяем
по направлению скорости VС
Угловая скорость колеса
Скорости точек V A AP ; VB BP ; VD DP ; VK KP .
Мгновенные радиусы вращения
AP AC CP R r
BP CB CP R r
Окончательно получим
VA ( R r )
Из треугольника DPC по теореме косинусов
VB ( R r )
DP DC 2 CP2 2 DC CP cos(90 ) R 2 r 2 2 R r cos(90 )
VD R 2 r 2 2 R r cos(90 )
Из треугольника КРС по теореме Пифагора
VK R 2 r 2
KP KC 2 CP2 R 2 r 2

13.

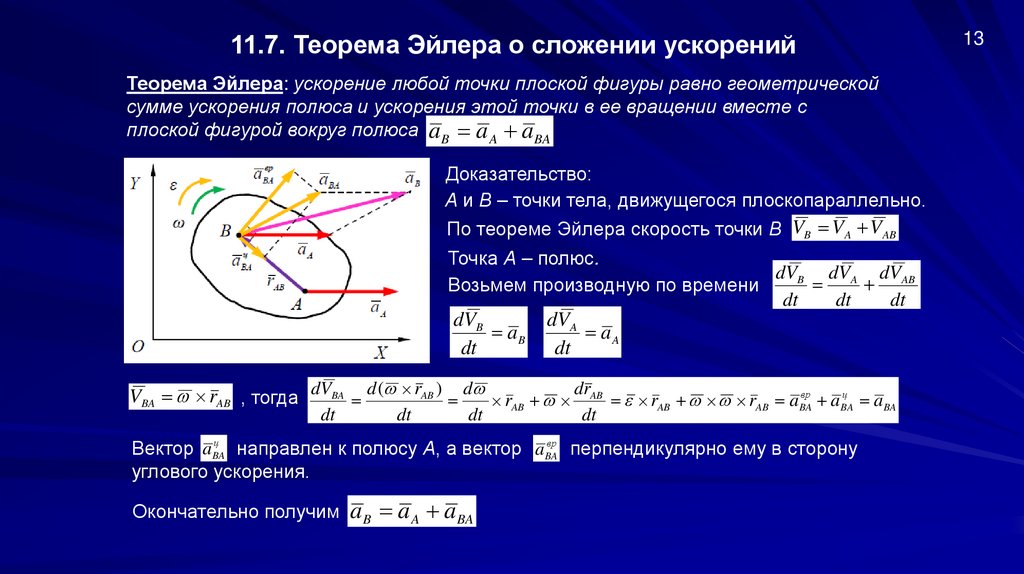
11.7. Теорема Эйлера о сложении ускорений
Теорема Эйлера: ускорение любой точки плоской фигуры равно геометрической
сумме ускорения полюса и ускорения этой точки в ее вращении вместе с
плоской фигурой вокруг полюса a B a A a BA
Доказательство:
А и В – точки тела, движущегося плоскопараллельно.
По теореме Эйлера скорость точки В VB VA VAB
Точка А – полюс.
dVB dVA dVAB
Возьмем производную по времени
dt
dt
dt
dVB
aB
dt
dVA
aA
dt
вр
ц
VBA rAB , тогда dVBA d ( rAB ) d rAB drAB rAB rAB aBA
aBA
aBA
dt
dt
dt
dt
ц
вр
Вектор aBA
направлен к полюсу А, а вектор aBA
перпендикулярно ему в сторону
углового ускорения.
Окончательно получим a B a A a BA
13

14.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра строительная механика
Авторы:
Лукашевич Надежда Кимовна
Сойту Наталья Юрьевна
tehmeh@spbgasu.ru