Кинематика плоского (плоскопараллельного) движения твердого тела

1.

А.И. Родионов
Теоретическая механика.
Ч.1. КИНЕМАТИКА

2.

Лекция 5.
Кинематика плоского (плоскопараллельного)
движения твердого тела.
§2.1. Основные понятия.
Движение твердого тела называется плоским
(плоскопараллельным), если все точки твердого тела
движутся в плоскостях, параллельных базовой
плоскости.
Плоское движение изучаем по причинам:
1) движение обладает многими свойствами
произвольного движения, но описывается математически
гораздо проще;
2) огромный класс механизмов современной техники
совершает именно плоское движение;

3.

3) довольно часто встречается в повседневной жизни;
4) динамику системы будем изучать в основном на
примере плоских механизмов.
§5.1. Теоремы о движении плоской фигуры.
Действительно, если движение твердого тела плоское, то
перпендикуляры к секущим плоскостям перемещаются
параллельно друг другу. Тогда
d
dt
d
dt
Тр ( A1 ) Тр ( A2 ) VA VA1 a A1 a A1
аналогично получим, что
Тр( В1 ) Тр( В2 ) VB1 VB2 aB1 aB2
Но
точки А не равна траектории точки В. Поэтому,
траектория
V А VВ. И так далее.

4.

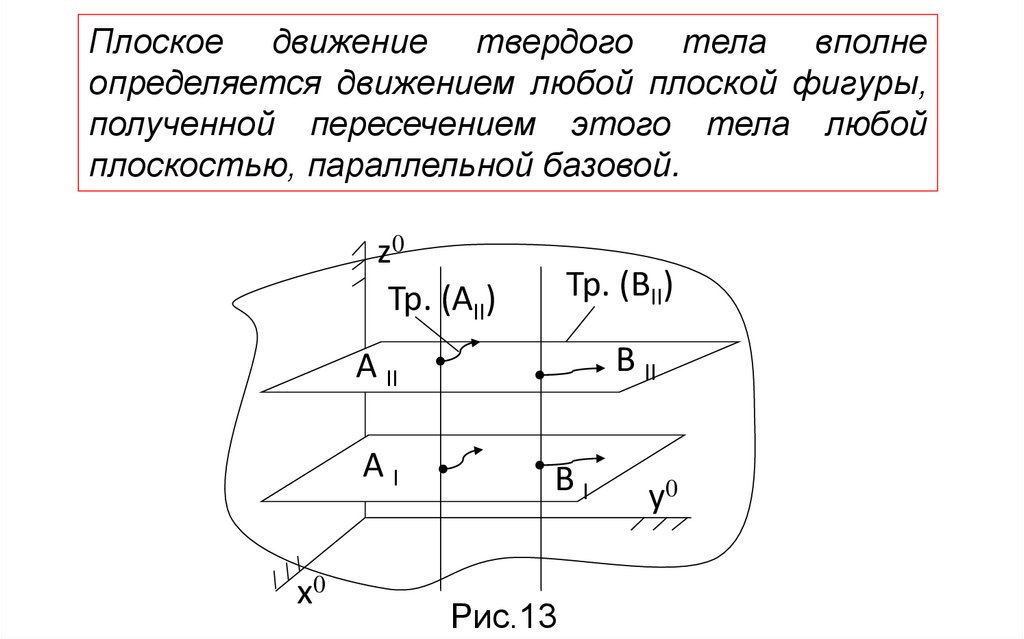
Плоское движение твердого тела вполне
определяется движением любой плоской фигуры,
полученной пересечением этого тела любой
плоскостью, параллельной базовой.
z0
Тр. (АII)
Тр. (BII)
B II
A II
AI
x0
BI
Рис.13
y0

5.

§5.1.2 Теорема о конечном перемещении плоской фигуры.
Докажем, что
конечное перемещение плоской фигуры можно
осуществить совокупностью (геометрической суммой)
двух перемещений: поступательного вместе с полюсом
(зависит от выбора полюса) и поворота вокруг оси,
перпендикулярной плоскости фигуры и проходящие
через полюс. (не зависит от выбора полюса).
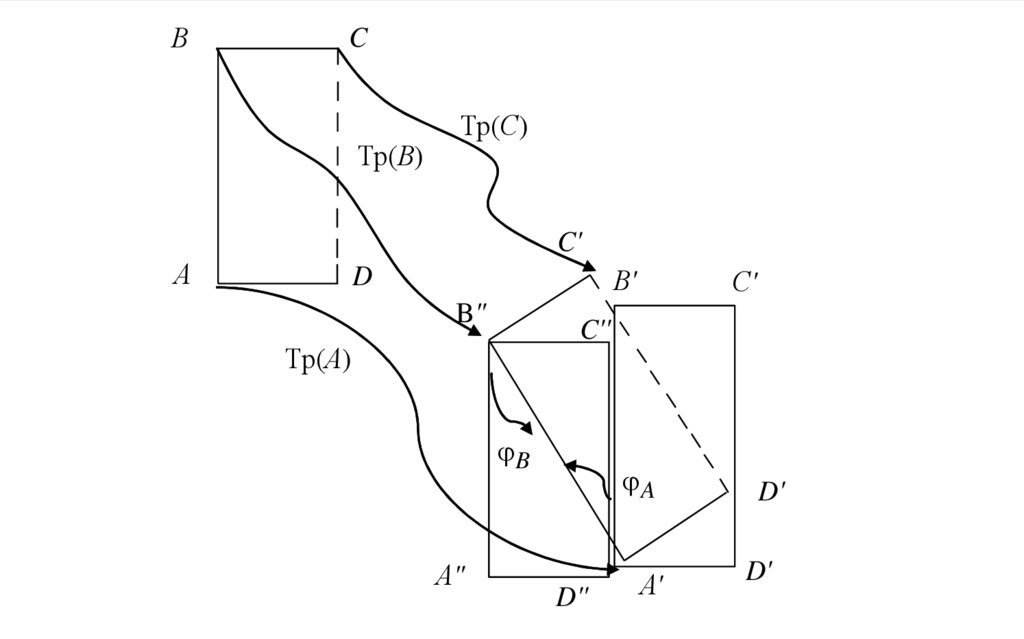
Возьмем за полюс на Рис.14. точку А и переместим
прямоугольник поступательно вместе с полюсом А. Тогда он
займет следующее положение, а потом развернем плоскую
фигуру на угол А вокруг некоторой оси, проходящей через
точку A' и перпендикулярный плоскости фигуры.

6.

В
C
Тр(В)
Тр(С)
C'
А
В'
D
B"
C''
Тр(А)
B
А"
С'
D''
A
D'
А'
D'

7.

Возьмем за полис другую точку, например точку , и
переместим поступательно прямоугольник вместе с точкой ,
затем развернем её на угол вокруг оси, проходящей через
точку и перпендикулярно
фигуры. Заметим, что
плоскости
A" B' // A"' B" , то
Тр( А) Тр( B) VА VВ , a A aB. Но так
как
A B , А B k , A B k ( А, B ).
Здесь k перпендикулярно к плоскости фигуры.
Т.о. конечное поступательное перемещение плоской
фигуры зависит от выбора полюса. А ее поворот как
целого не зависит от выбора полюса.

8.

Представив конечное перемещение плоской фигуры, как
последовательную совокупность бесконечно малых, приходим
к выводу о том, что плоское движение твердого тела имеет
три степени свободы: две поступательных с полюсом и
одну вращательную вокруг мгновенной оси, проходящей
через полюс s 3 1 0 1 0 1
Xc
Yc
§5.1.3 Теорема Шаля.
Плоскую фигуру можно переместить из одного
положения в любое другое положение на плоскости
одним поворотом этой фигуры вокруг некоторого
неподвижного центра.

9.

В
Е
В1
А1
А
D
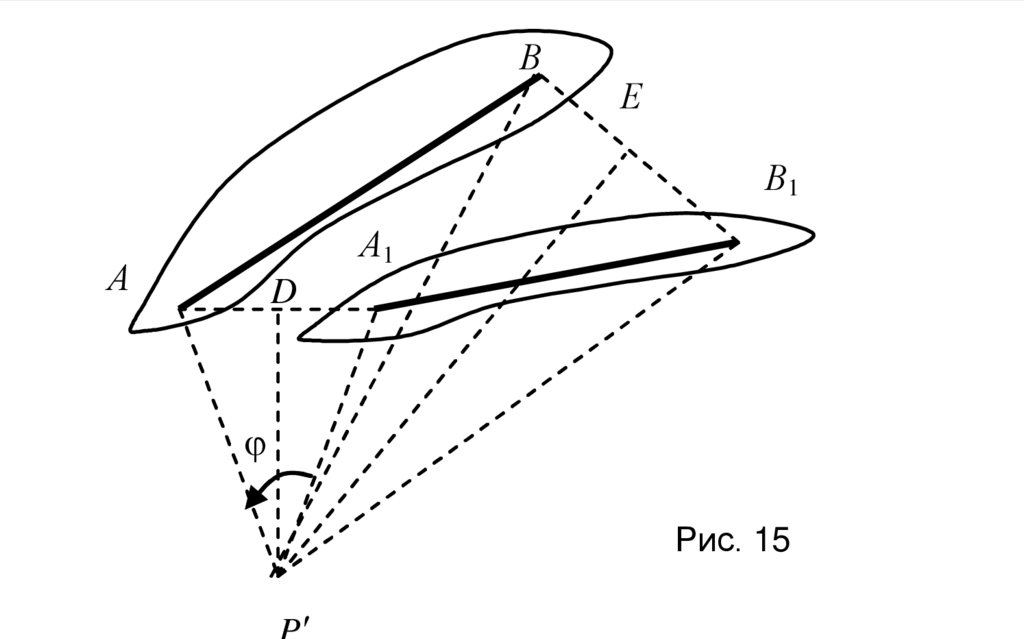
Рис. 15

10.

Положим, что отрезок, соединяющий точки А и В плоской
фигуры занимает на плоскости в два различных момента
времени положения АВ и А1В1. Разделим отрезок АА1и ВВ1
пополам. Из середин этих отрезков D и Е восстановим
перпендикуляры к отрезкам и продолжим их до пересечения в
точке P. Покажем, что эта точка неподвижной плоскости
является центром поворота для данного конечного
перемещения плоской фигуры. ACB A1CB1 по трем сторонам,
отсюда имеем ACB A1CB1 Отняв от обеих частей этого
ACB
, ACA1 BCB1
равенства ACB
, получим ACB ACB
1
1
1 ACB
1
1
где φ - абсолютная величина рассматриваемого угла. Таким
образом, перемещения двух точек фигуры, и, следовательно,
всей плоской фигуры из первого положение во второе можно
осуществить поворотом на угол φ вокруг центра поворота P.

11.

Поворот плоской фигуры как целого позволяет переместить
эту фигуру из первого положение во второе.
Рассматривая конечный поворот, как совокупность
бесконечно малых поворотов, плоское движение можно
представить в момент t как мгновенный поворот
вокруг мгновенного центра поворота точки P’.
Если перпендикуляры, восстановленные из середин отрезков,
сливаются, то центр поворота лежит на пересечении
продолжений отрезков АВ и А1В1.

12.

§5.2. Аналитический способ задания плоского движения.
Уравнение плоского движения.
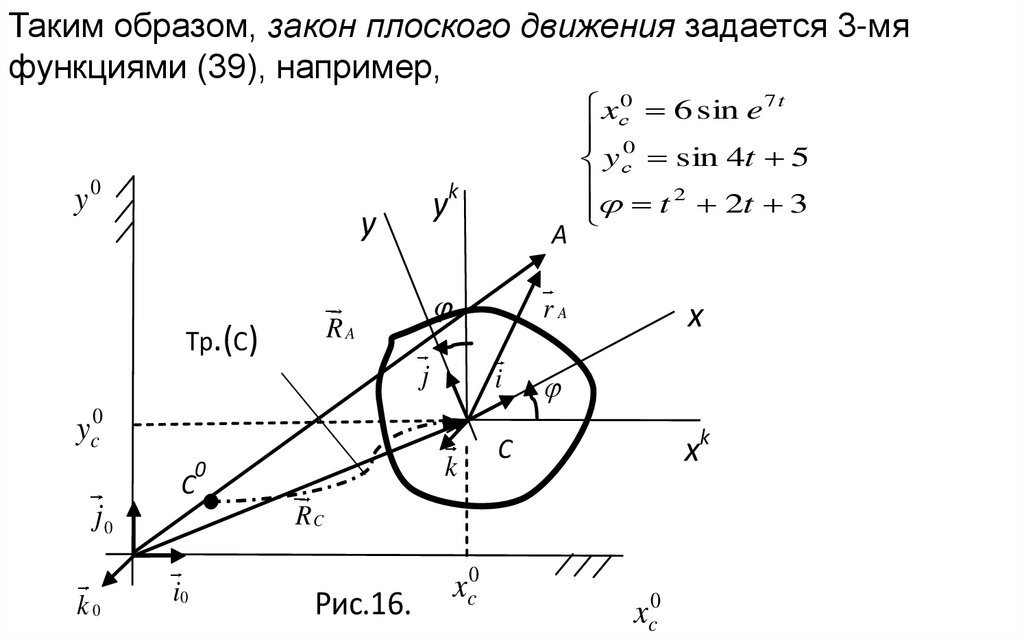
Введем в точке С оси х, у, которые “вморожены” в твердое
тело и движутся вместе с ним. Эти оси в момент t=0 в точке С0
совпадают с осями Кенига. В соответствии с только что
доказанной теоремой для аналитического описания плоского
движения твердого тела, нужно задать следующие функции и
координаты точки С в проекции на оси х0,у0
0
0
yc yc t
t
0
0
xc xc t
(39)

13.

Таким образом, закон плоского движения задается 3-мя
функциями (39), например,
y0
yk
y
RA
Тр.(С)
rA
j
i
yc0
k
0
C
j0
k0
A
xс0 6 sin e 7 t
0
yс sin 4t 5
2
t
2t 3
x
xk
C
RC
i0
Рис.16.
xc0
xc0

14.

Заметим, что
RA RC rA
(40)
rA CA(t ) CA const t
причем в силу неизменности расстояний между точками
плоской фигуры в процессе ее движения. А точка А
совершает чисто вращательное движение вокруг оси,
проходящей через точку С и перпендикулярно плоской
фигуре. Орт k 0 параллелен k t

15.

§5.3. Теорема о скоростях точек плоской фигуры
(теорема о сложении скоростей).
Скорость
любой
точки
А
плоской
фигуры,
совершающей
плоское
движение
геометрически
складывается из скорости полюса (С) и скорости
вращения точки А относительно С.
Действительно
d
d (CA)
(40) VA VC
VC rA
dt
dt
Таким образом,
VA VC VA / C VC rA
(41)

16.

что и требовалось доказать. Заметим, что при выводе
формулы (41) нигде учитывался плоский характер движения
тела. Поэтому, эта формула остается справедливой и для
произвольного движения твердого тела и является
следствием неизменности расстояний между точками в
процессе движения тела.
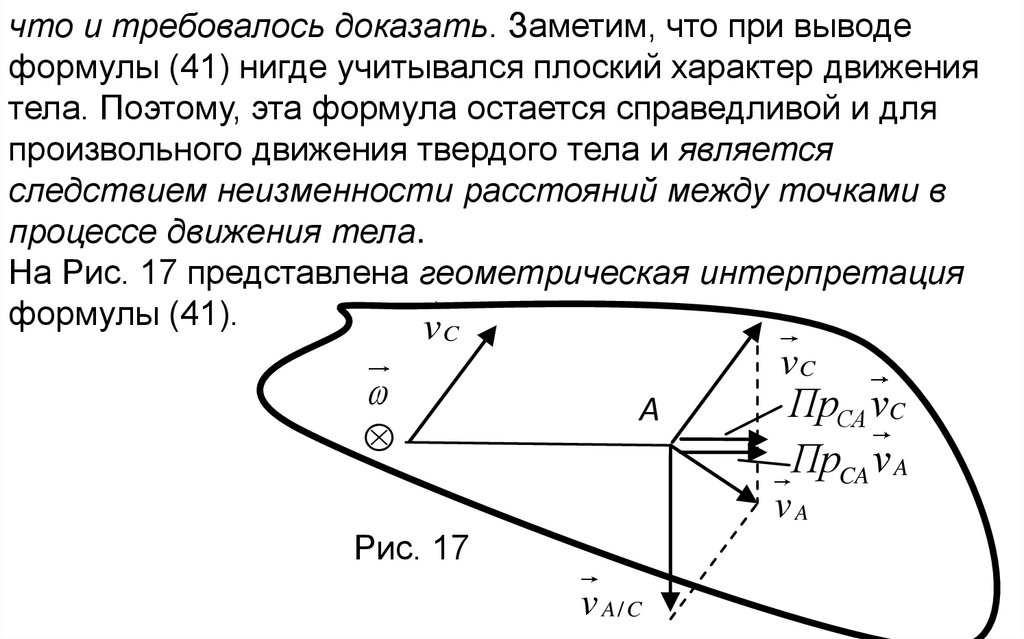
На Рис. 17 представлена геометрическая интерпретация
формулы (41).
vC
vC
А
ПрСА vC
ПрCA v A
vA
Рис. 17
v A/ C

17.

§5.4. Теорема Грасгофа о проекциях скоростей двух точек
твердого тела на линию их соединяющую.
Проекции скоростей двух точек твердого тела на
линию их соединяющую равны:
ПРABVA ПРABVB
(42)
Действительно, из Рис.15. следует, что
Пр АВVB Пр ABVA Пр АВVB / A , но VB / A AB,
и, поэтому, проекции равны. Заметим, что в отличие от
произвольного движения твердого тела для плоского
движения всегда будет иметь место формула
VA / C CA sin( / 2) CA
(43)

18.

§5.5. Мгновенный центр скоростей. Мгновенный центр
поворота.
Назовем плоскость xy в которой лежит плоская
фигура подвижной плоскостью, а плоскость x0y0 —
неподвижной плоскостью. Тогда точку плоской
фигуры или подвижной плоскости, скорость которой
в данный момент времени равна нулю, называют
мгновенным центром скоростей (·P) или МЦС.
Сопряженную ей точку неподвижной плоскости —
мгновенным центром поворота (·P’). Именно
относительно оси проходящей через эту точку и
совершается мгновенный поворот твердого тела
как целого.

19.

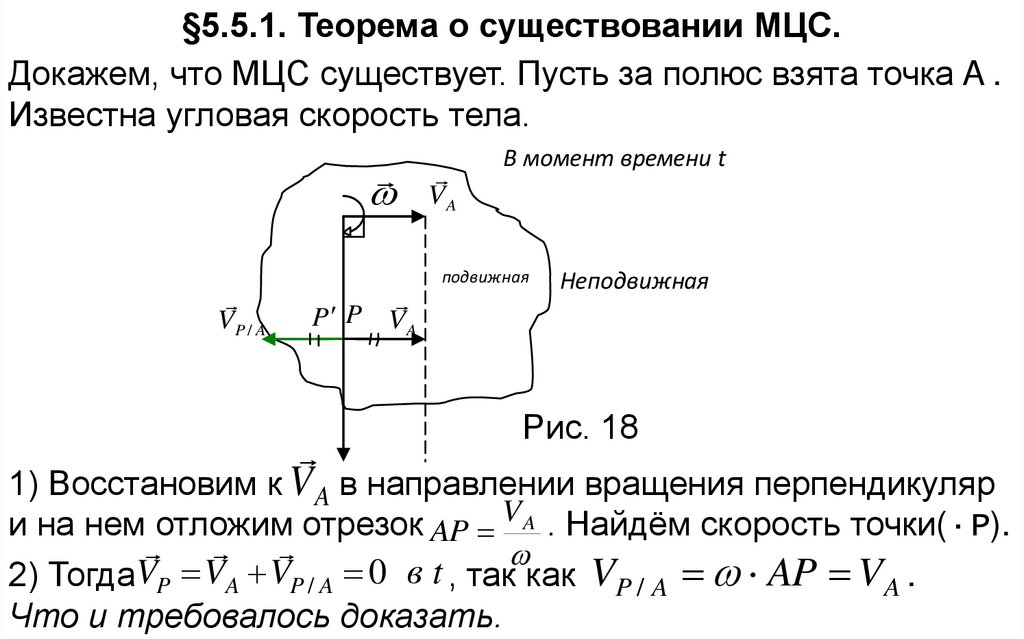
§5.5.1. Теорема о существовании МЦС.
Докажем, что МЦС существует. Пусть за полюс взята точка A .
Известна угловая скорость тела.
VP / A
P P VA
VA
В момент времени t
подвижная
Неподвижная
плоскость
Рис. 18
1) Восстановим к V A в направлении вращения перпендикуляр
и на нем отложим отрезок AP V A . Найдём скорость точки(·P).
2) ТогдаVP VA VP / A 0 в t , так как VP / A AP V A .
Что и требовалось доказать.

20.

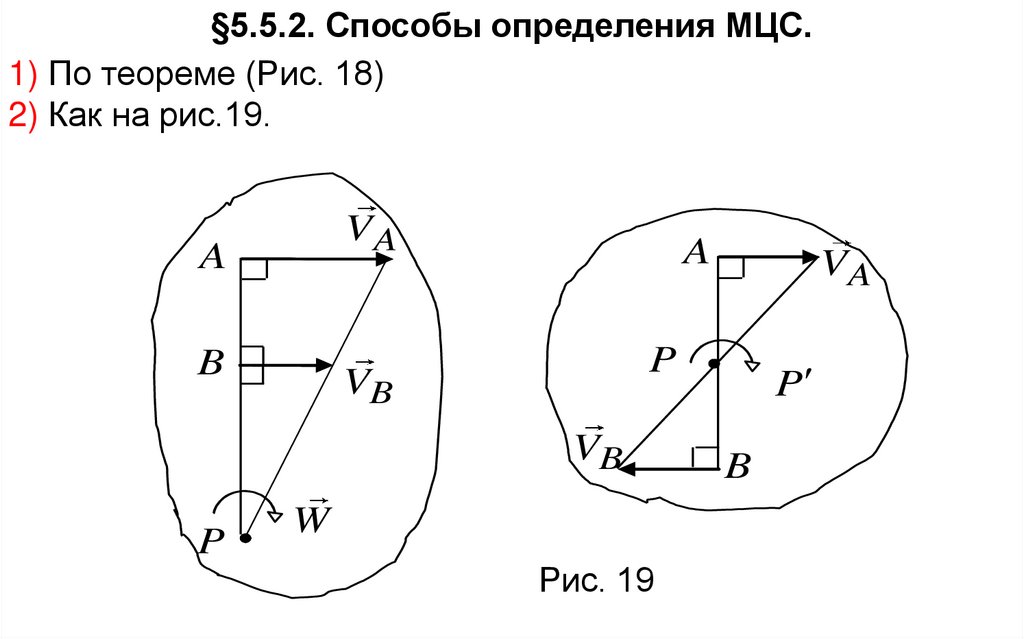
§5.5.2. Способы определения МЦС.
1) По теореме (Рис. 18)
2) Как на рис.19.
VA
A
B
A
P
VB
VB
P
VA
W
Рис. 19
P
B

21.

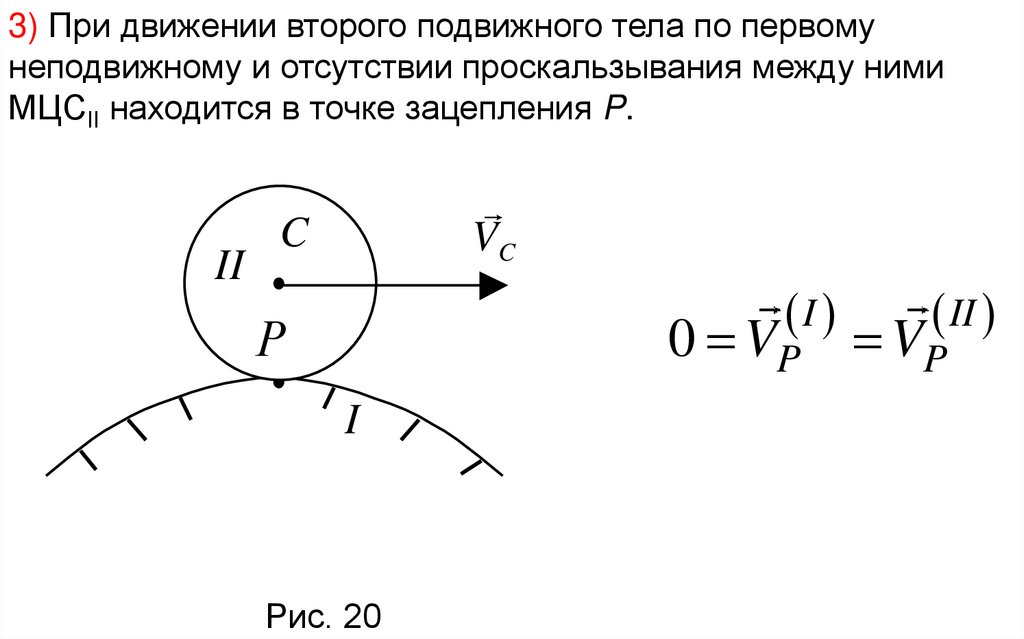
3) При движении второго подвижного тела по первому
неподвижному и отсутствии проскальзывания между ними
МЦСІІ находится в точке зацепления P.
II
VC
C
I
II
0 VP VP
Р
I
Рис. 20

22.

Известны
скорости хотя бы двух точек фигуры, либо известна
линия V одной из точек и скорость другой. Тогда МЦС
находится на пересечении перпендикуляров к скоростям. Этот
случай позволяет ввести крестовую формулу(44) для
вычисления скоростей точек плоской фигуры.
VA AP
VD DP VB BP
Vc CP
Рис. 21

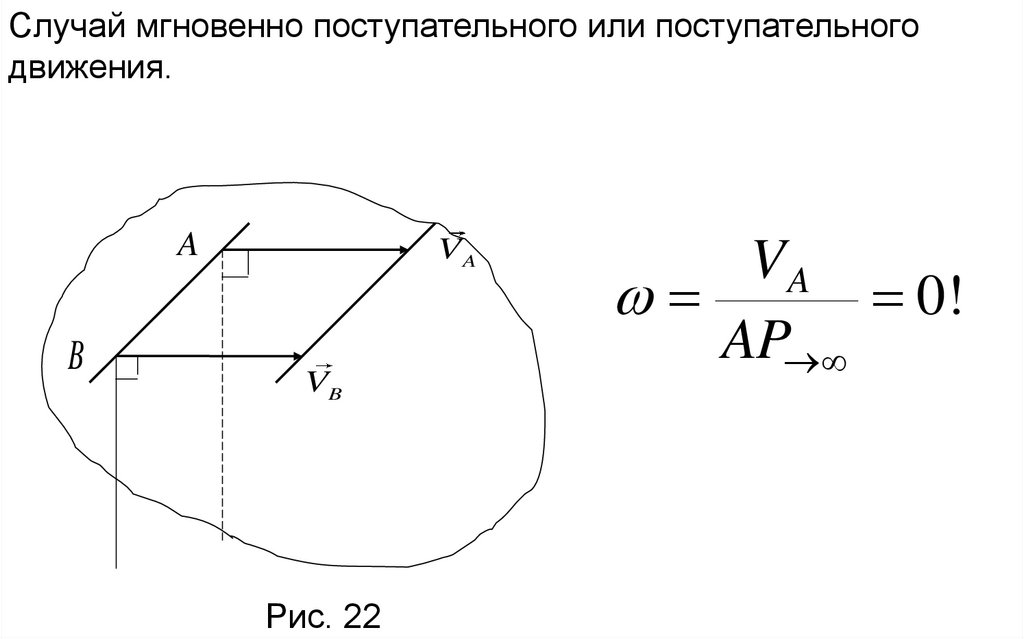
23.

Случай мгновенно поступательного или поступательного
движения.
A
B
VA
VB
Рис. 22
VA
0!
AP

24.

§5.6. Кинематика катящегося без проскальзывания колеса.
A
VA
VA/C
VC
VB
VB / C
B
VC
C
VC
W
D
P
W
P
VD

25.

A
VA / C
VB / C
B
C
C
W
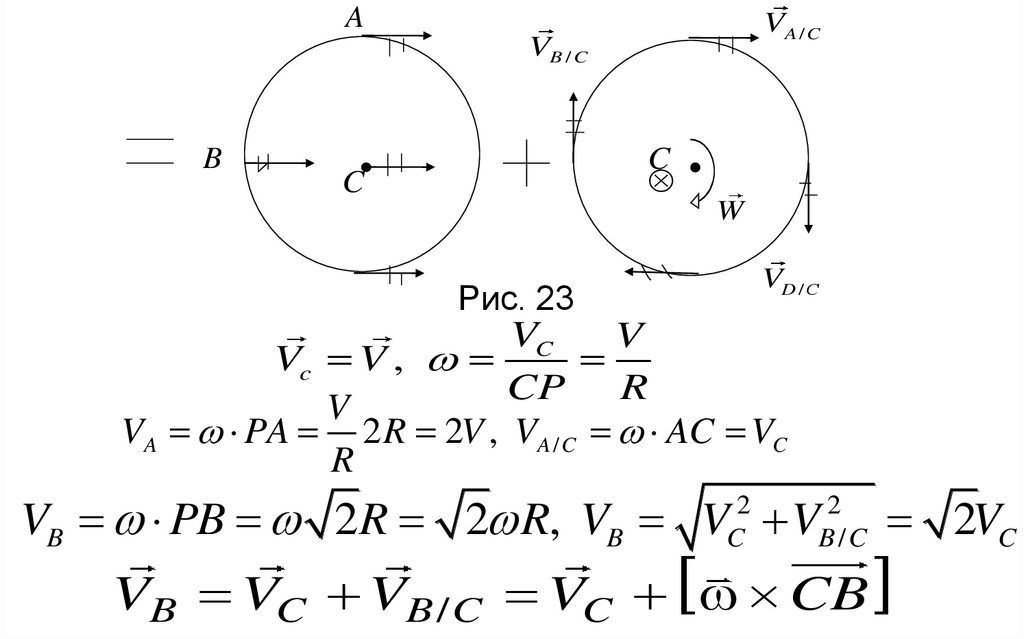
Рис. 23
VD / С
VC
V
Vc V ,
CP R
V
VA PA 2 R 2V , VA / C AC VC
R
VB PB 2R 2 R, VB VC2 VB2/ C 2VC
VB VC VB / C VC CB