Плоское (плоскопараллельное) движение твердого тела

1.

Плоское (плоскопараллельное)
движение
твердого тела
Плоскопараллельным или плоским движением называется
движение твердого тела, при котором его точки перемещаются
в плоскостях,
параллельных некоторой неподвижной плоскости

2.

3.

Примеры:
1) колесо на прямом участке пути;
2) Скольжение стержня;
3) движение шатуна в кривошипно-ползунном механизме (следующий слайд)
Движение шатуна в кривошипноползунном механизме

4.

5.

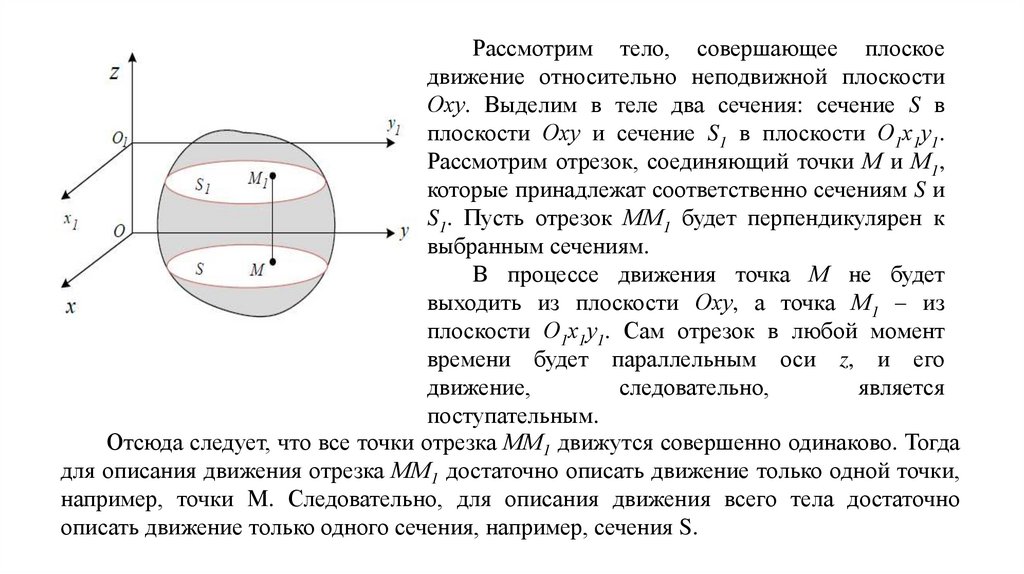
Рассмотрим тело, совершающее плоское
движение относительно неподвижной плоскости
Оху. Выделим в теле два сечения: сечение S в
плоскости Оху и сечение S1 в плоскости О1х1у1.
Рассмотрим отрезок, соединяющий точки М и М1,
которые принадлежат соответственно сечениям S и
S1. Пусть отрезок ММ1 будет перпендикулярен к
выбранным сечениям.
В процессе движения точка М не будет
выходить из плоскости Оху, а точка М1 – из
плоскости О1х1у1. Сам отрезок в любой момент
времени будет параллельным оси z, и его
движение,
следовательно,
является
поступательным.
Отсюда следует, что все точки отрезка ММ1 движутся совершенно одинаково. Тогда
для описания движения отрезка ММ1 достаточно описать движение только одной точки,
например, точки М. Следовательно, для описания движения всего тела достаточно
описать движение только одного сечения, например, сечения S.

6.

Плоское движение тела можно разложить на поступательное
и вращательное относительно выбранного центра.
На рисунке показано, что тело из положения I можно
переместить в положение II двумя способами.
1. Перемещаем тело поступательно так, чтобы прямая АВ,
перемещаясь параллельно первоначальному положению,
заняла в пространстве положение А2В1. После этого
повернем тело вокруг точки В1 на угол 1.
2. Переместим тело поступательно из положения I так,
чтобы прямая АВ совместилась с прямой А1В2, ей
параллельной. После этого будем вращать тело вокруг
точки А1 до тех пор, пока точка В2 не попадет в точку В1.
Поскольку А1В2||А2В1 и то углы 1 = 2. Следовательно, чтобы занять положение II, тело может
совершить различные поступательные движения (в зависимости от выбранного полюса), а
вращение, как при первом, так и при втором способе, будет одинаковым.
Следовательно, движение плоской фигуры можно представить как совокупность двух
мгновенных движений: поступательного вместе с полюсом - точка А и вращательного
вокруг полюса

7.

Рассмотрим движение плоской фигуры. Для этого
выберем неподвижную систему координат Оху. Выберем
на плоской фигуре точку А, которую будем называть
полюсом и проведем через нее систему координат,
которая будет двигаться вместе с телом.
Положение точки А в любой момент времени
определяется координатами полюса. Само тело при этом
может поворачиваться вокруг полюса. Величину этого
поворота определяет угол (угол между осями х и х1).
xA = xA(t),
yA = yA(t),
- уравнения движения плоской фигуры
= (t)
При задании плоского движения за полюс может приниматься любая точка
тела. Следовательно, вид первых двух уравнений движения зависит от выбора
полюса. Закон изменения угла от выбора полюса не зависит.

8.

Определения скорости точек тела, совершающего плоское движение
Теорема о сложении скоростей при
плоском движении. Скорость любой точки
тела при плоском движении находится как
сумма скорости полюса и скорости данной
точки во вращательном движении вокруг
полюса.
Точка А выбрана как
полюс
VB VA VBA
За полюс обычно принимают ту точку, скорость и ускорение
которой известны.

9.

Следствие
из
теоремы.
Проекции
скоростей
двух
точек пр
VA пр
VB
x
x
плоской
фигуры
на
направление
вектора,
соединяющего эти точки,
равны между собой.
Если лестница начнет скользить, то скорости
точек А и В будут связаны соотношением (через
проекции на отрезок АВ)
v A cos vB cos
2

10.

Мгновенный центр скоростей (МЦС)
Теорема. При непоступательном
движении плоской фигуры существует
жестко связанная с ней точка, скорость
которой в данный момент движения
равна нулю. Эта точка является
мгновенным центром скоростей.

11.

12.

Выбирая мгновенный центр скоростей за полюс, нетрудно
убедиться, что скорость любой точки плоской фигуры
находится как скорость во вращательном движении вокруг
МЦС
VB VP VBP
VP 0
VB VBP BP
VC VCP CP
VC CP
VB BP
VC
VB
CP BP
т.е. скорости пропорциональны расстояниям до мгновенного
центра скоростей. Через мгновенный центр скоростей проходит
мгновенная ось вращения тела.

13.

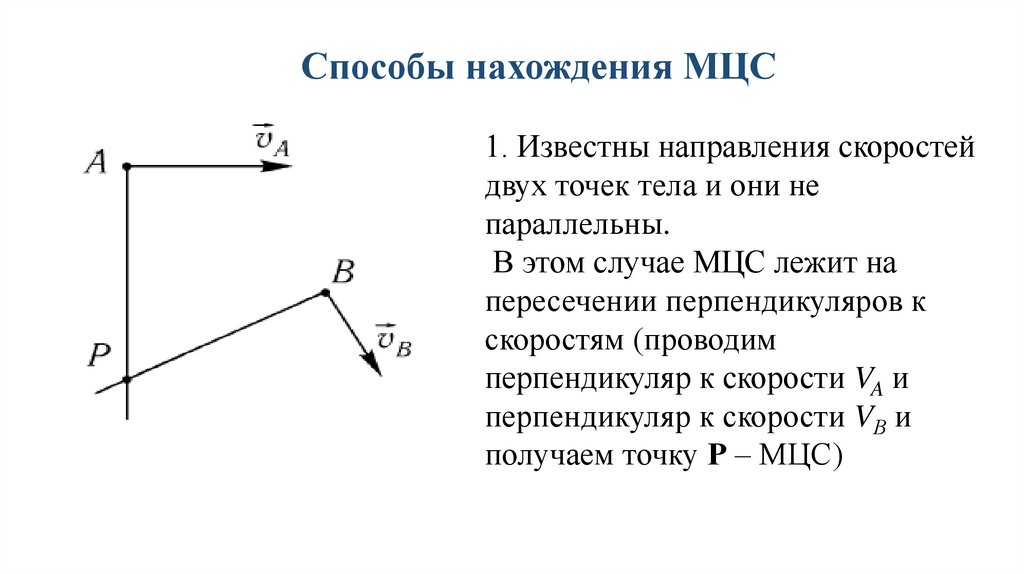
Способы нахождения МЦС
1. Известны направления скоростей
двух точек тела и они не
параллельны.
В этом случае МЦС лежит на
пересечении перпендикуляров к
скоростям (проводим
перпендикуляр к скорости VA и
перпендикуляр к скорости VВ и
получаем точку Р – МЦС)

14.

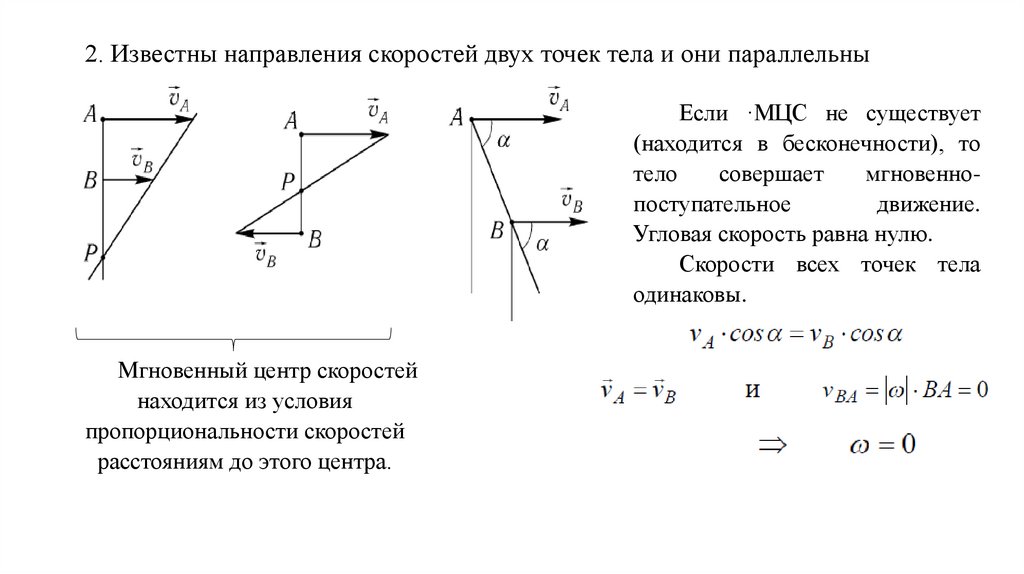
2. Известны направления скоростей двух точек тела и они параллельны
Если ·МЦС не существует
(находится в бесконечности), то
тело
совершает
мгновеннопоступательное
движение.
Угловая скорость равна нулю.
Скорости всех точек тела
одинаковы.
Мгновенный центр скоростей
находится из условия
пропорциональности скоростей
расстояниям до этого центра.

15.

Способы нахождения МЦС
3. Качение без скольжения по неподвижной
поверхности (нет проскальзывания). МЦС
находится в точке касания тела с неподвижной
поверхностью
Угловая скорость
v A vB vC
AP BP CP

16.

Пример. Суммирующие механизмы применяют для сложения
движений.
На рисунке две параллельные рейки 1 и 2 движутся в одну сторону с
постоянными скоростями v1 и v2 .
Между рейками зажат диск радиуса r , катящийся по рейкам без
скольжения.
Найти скорость средней рейки 3, присоединенной к оси C диска, а
также угловую скорость диска.

17.

Диск совершает плоскопараллельное
движение.
Скорости точек A и B равны скоростям
реек
Мгновенный центр скоростей диска находим
по известным направлениям скоростей точек
A и B. Из рисунка видно, что скорость точки
C находится как средняя линия трапеции,
основаниями которой служат скорости точек
A и B . Следовательно

18.

Для определения угловой скорости диска запишем теорему об
определении скоростей точек тела при плоском движении
Проектируя данное равенство на горизонтальную
ось, получим:

19.

Определение ускорений точек тела при плоском движении
Теорема. Ускорение точки плоской
фигуры равно сумме ускорения полюса и
ускорения
данной
точки
во
вращательном движении вокруг полюса.
aB a A aBA
aB a A a a
BA
n
BA

20.

Следствие из теоремы. Концы векторов ускорений точек плоской фигуры,
лежащих на одной прямой, также лежат на одной прямой и делят ее на отрезки,
пропорциональные расстояниям между точками.
Концы векторов ускорений точек aBA и aСA
лежат на одной прямой ABC и делят ее на
отрезки пропорциональные расстояниям
между точками:
aBA 2 4 AB, aCA 2 4 AC.
Концы векторов ускорений полюса A,
изображенных в точках B и C, лежат также
лежат на одной прямой.
Нетрудно доказать из подобия треугольников, что концы векторов суммарных
ускорений точек B и C также лежат на одной прямой, и делят эту прямую на
части, пропорциональные расстояниям между точками.

21.

Мгновенный центр ускорений (МЦУ)
Теорема. При любом непоступательном
движении плоской фигуры существует жестко
связанная с ней точка, ускорение которой в
данный момент движения равно нулю. Эта точка
называется мгновенным центром ускорений.