Теоретическая механика

1.

Преподаватель: Зюзин Евгений Александрович
Кафедра: Теоретической и геотехнической механики, а.4102 – 4104
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Разделы: Кинематика, Статика, Динамика
Рекомендуемая литература:
1. Мещерский, И. В. «Сборник задач по теоретической механике»
2. Яблонский, А. А. «Сборник задач для курсового проектирования по
теоретической механике»
3. Хямяляйнен, В. А. «Теоретическая механика»
4. Тарг, С. М. Краткий курс теоретической механики.
5. Бать, М. И. Теоретическая механика в примерах и задачах. В 2-х т.

2.

Оформление расчетно-графических работ (РГР)
формат A4 (вертикально)
поля: слева - 20 мм, справа, снизу, сверху - 5 мм
Штамп (на 1 странице)
Расчетно-графические работы для специальностей ГБ, ЭХ, ЭМ
по «сборнику задач…» [2] : К1, К3, С1, Д10
для специальности МА: К1, К3, К7, С3, Д10, Д14 (Д15)

3.

КИНЕМАТИКА
К и н е м а т и к а – раздел теоретической механики, в котором
изучаются геометрические свойства движения тел без учета их
масс и действующих на них сил
Механическим движением называется перемещение тела
относительно некоторой системы отсчета (системы координат)
Пространство и время в механике считаются абсолютными
Пространство рассматривается как трехмерное евклидово
Время является непрерывно изменяющейся величиной
0 t

4.

Кинематические характеристики
движения точки
Т р а е к т о р и я – геометрическое место последовательных
положений движущейся точки в рассматриваемой системе отсчета.
С к о р о с т ь ( v) – векторая величина, определяющая быстроту и
направление движения в данной системе отсчета.
a)
У с к о р е н и е (
– векторая величина, характеризующая
скорость изменения скорости по величине и направлению.
Способы задания
движения точки
1. В Е К Т О Р Н Ы Й.
2. К О О Р Д И Н А Т Н Ы Й.
3. Е С Т Е С Т В Е Н Н Ы Й.

5.

Способы задания движения точки
1. Векторный способ
а) скорость точки
M1
Vср
V
Δr
M
r+Δr
r
O
r r (t )
- уравнение движения точки
r
v ср
t
dr
v
dt
v lim v ср
t 0
Скорость точки направлена по касательной к траектории в
данной точке.
Размерность скорости : [v] = см/с, м/с

6.

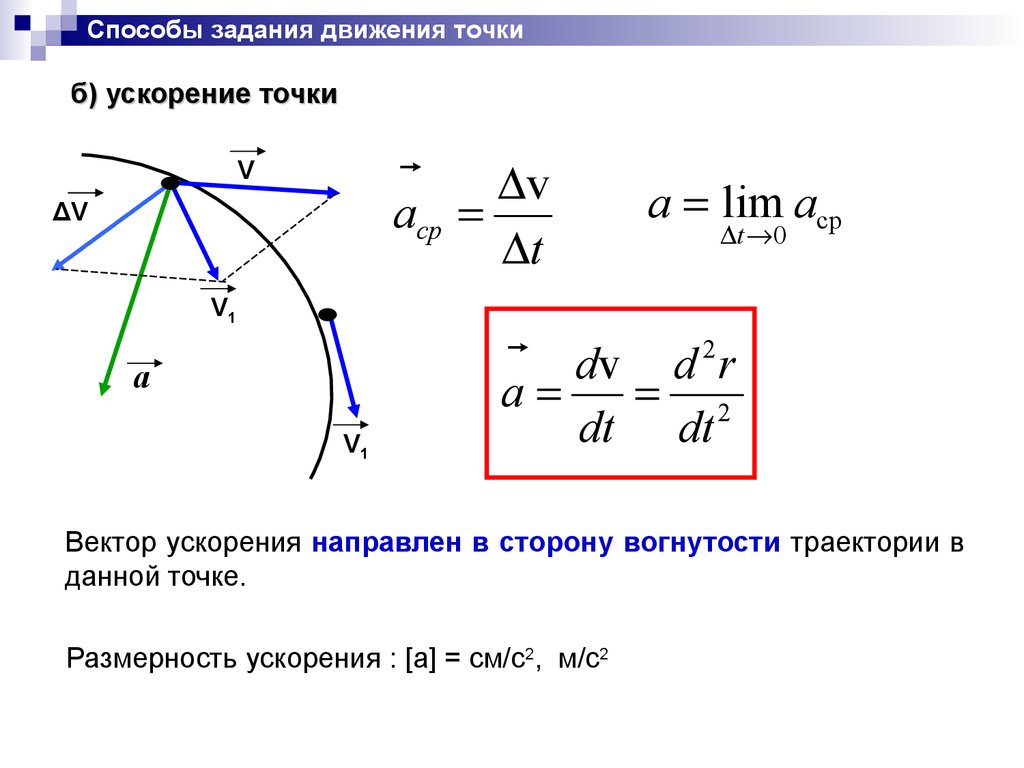
Способы задания движения точки
б) ускорение точки
v
aср
t
V
ΔV
V1
a
V1
a lim aср
t 0
2
dv d r
a
2
dt dt
Вектор ускорения направлен в сторону вогнутости траектории в
данной точке.
Размерность ускорения : [a] = см/с2, м/с2

7.

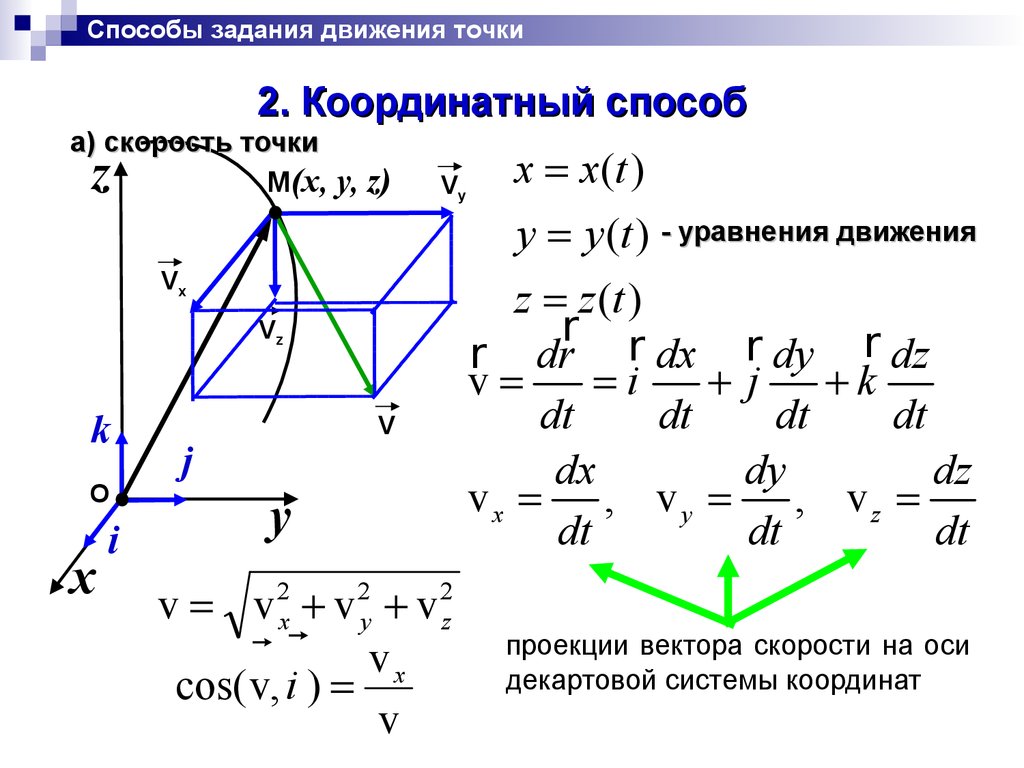
Способы задания движения точки
2. Координатный способ
а) скорость точки
M(x,
z
y, z)
Vy
x x(t )
y y (t ) - уравнения движения
Vx
Vz
k
O
x
i
V
j
y
v v 2x v 2y v 2z
vx
cos( v, i )
v
z z (t )
r r
dx r dy r dz
r dr
v
i
j
k
dt
dt
dt
dt
dx
dy
dz
vx , v y , vz
dt
dt
dt
проекции вектора скорости на оси
декартовой системы координат

8.

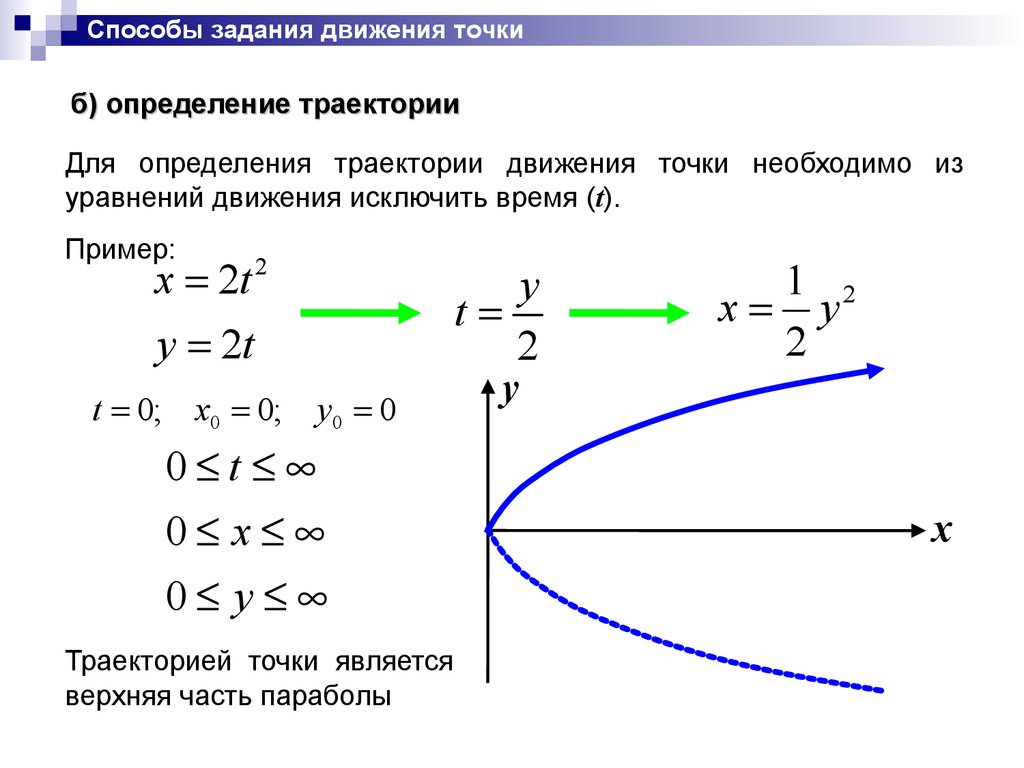
Способы задания движения точки
б) определение траектории
Для определения траектории движения точки необходимо из
уравнений движения исключить время (t).
Пример:
x 2t 2
y
t
2
y 2t
t 0; x0 0;
y0 0
0 t
0 x
0 y
Траекторией точки является
верхняя часть параболы
1 2
x y
2
y
x

9.

Способы задания движения точки
в) ускорение точки
dv dv y dv
dv d
a
v xi v y j v z k x i
j z k
dt dt
dt
dt
dt
dv y d dy d 2 y
dv x d dx d 2 x
dv z d dz d 2 z
ax
2 ; a y
2 ; az
2
dt
dt dt dt
dt
dt dt dt
dt
dt dt dt
ax , a y , az
проекции ускорений точки на оси декартовой
системы координат
| a | a x2 a y2 a z2
ax
ay
az
cos(a , i ) ; cos(a , j ) ; cos(a , k ) ;
a
a
a

10.

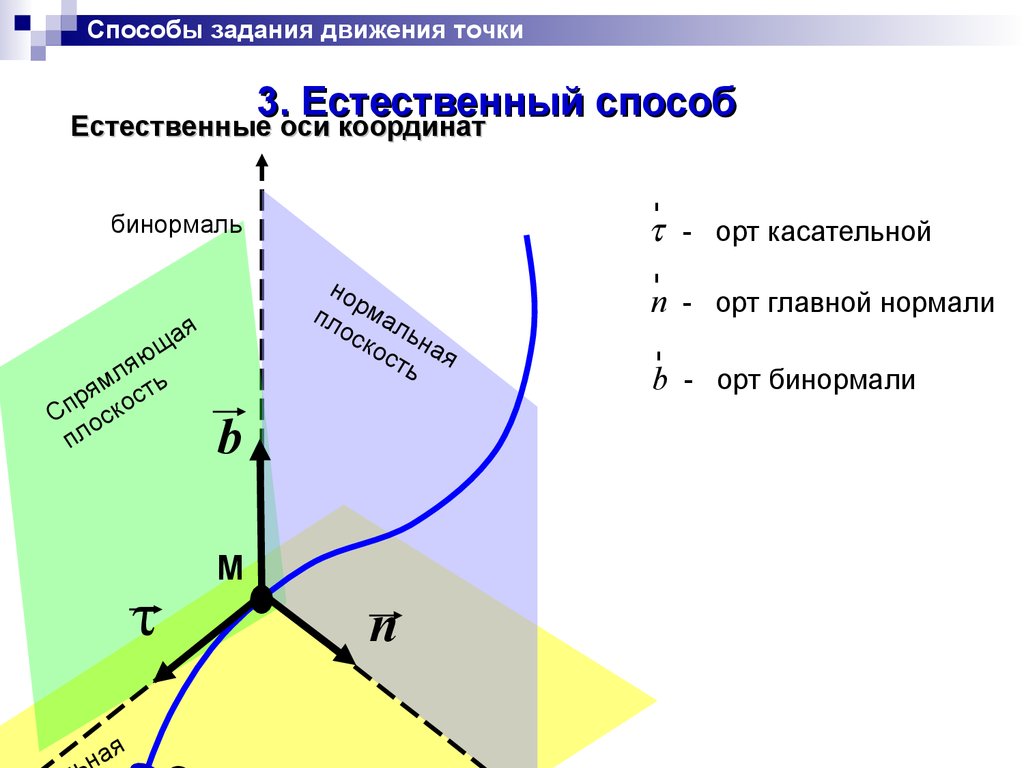
Способы задания движения точки
3. Естественный способ
Естественные оси координат
бинормаль
ая
щ
яю
л
ям сть
р
Сп оско
пл
τ
ая
но
пл рмал
ос
ко ьная
сть
b
М
n
r
- орт касательной
r
n - орт главной нормали
r
b - орт бинормали

11.

Способы задания движения точки
OM s s (t )
а) скорость точки
уравнение движения точки
_
О
+
М
τ
dr ds dr
v
dt dt ds
v
т.к.
dr
ds
r
О1
ds
v
dt
r
r
dr
r
lim
1
ds S 0 s
орт касательной
алгебраическая величина скорости
r ds r
v
dt

12.

Способы задания движения точки
со
пл пр
ос ик
ко ас
ст аю
ь щ
ая
ся
б) ускорение точки
an
- +
a
aτ
α
n
М
О
tg
a
an
τ
r
к
- вектор кривизны кривой в
данной точке, характеризует
поворот касательной к кривой
r
r d
к
ds
r 1 s
к n
- радиус кривизны кривой,
радиус вписанной окружности в
данной точке
ur
r
2
r d V d ds r d s r ds d
a
2
dt dt dt dt
dt dt
r
2
2
d s r ds d ds d 2s r ds r
2
2 к
dt
dt dt ds dt
dt
2
2
d s r ds 1 r dV r V 2 r r r
2 n
n a a n
dt
dt
dt

13.

Способы задания движения точки
a
a a an
- касательное ускорение, векторная величина, характеризует
быстроту изменения скорости по модулю
dv d 2 s
a
2
dt dt
an
a a 2 an2
a
axVx a yVy azVz
V
- нормальное ускорение, векторная величина, характеризует
быстроту изменения скорости по направлению
v2
an
an
axVy a yVx
V

14.

Годограф вектора скорости
z
M2
v1
r2
M1
r1
x
v2
vn
rn
z1
M3
v1
v2
y
О
x1
y1
vn
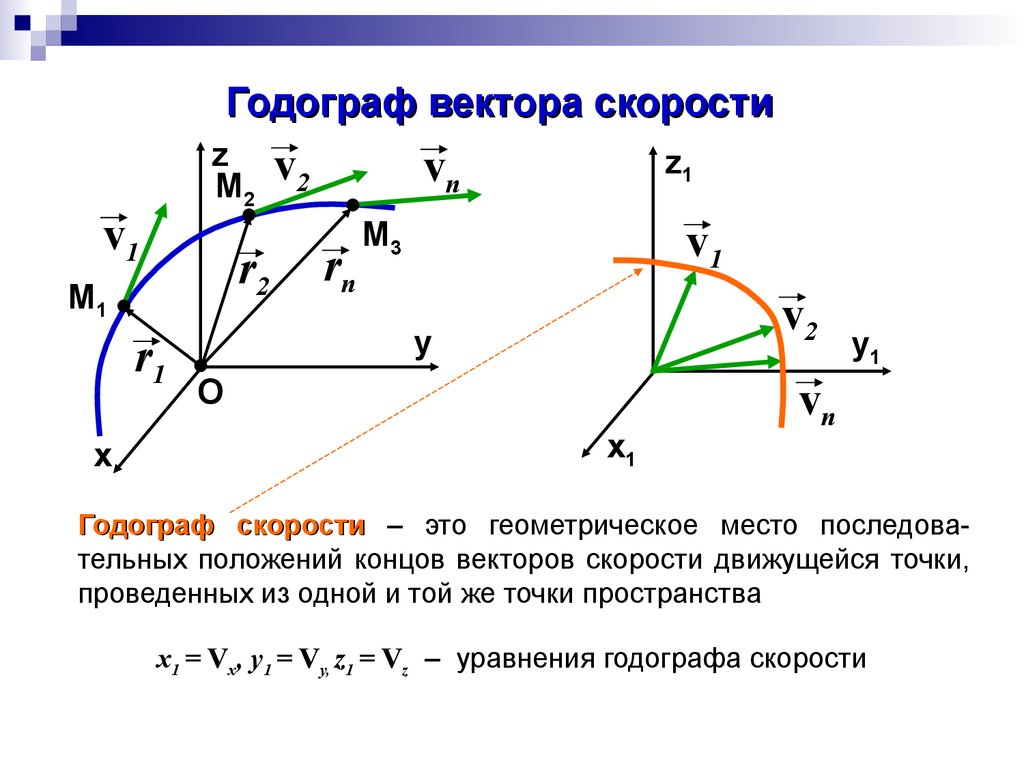
Годограф скорости – это геометрическое место последовательных положений концов векторов скорости движущейся точки,
проведенных из одной и той же точки пространства
x1 = Vx, y1 = Vy, z1 = Vz – уравнения годографа скорости

15.

Частные случаи движения
1. Равномерное прямолинейное движение
( v Const , ), a 0, an 0, a 0
2. Равномерное криволинейное движение
( v Const, 0), a 0, an 0, a an
3. Неравномерное прямолинейное движение
( v Const , ), a 0, an 0, a a
4. Равнопеременное движение
V V0 a t
a Const
1 2
s s0 Vt a t
2

16.

Пример оформления
расчетно - графической
работы

17.

Поступательное движение
Простейшие виды движения
твердого тела
1. Поступательное движение
2. Вращательное движение
Поступательное движение
Поступательным движением твердого тела называется такое
движение, при котором прямая соединяющая две любые точки
тела, перемещается, оставаясь параллельной самой себе.
A
O1
B
O2

18.

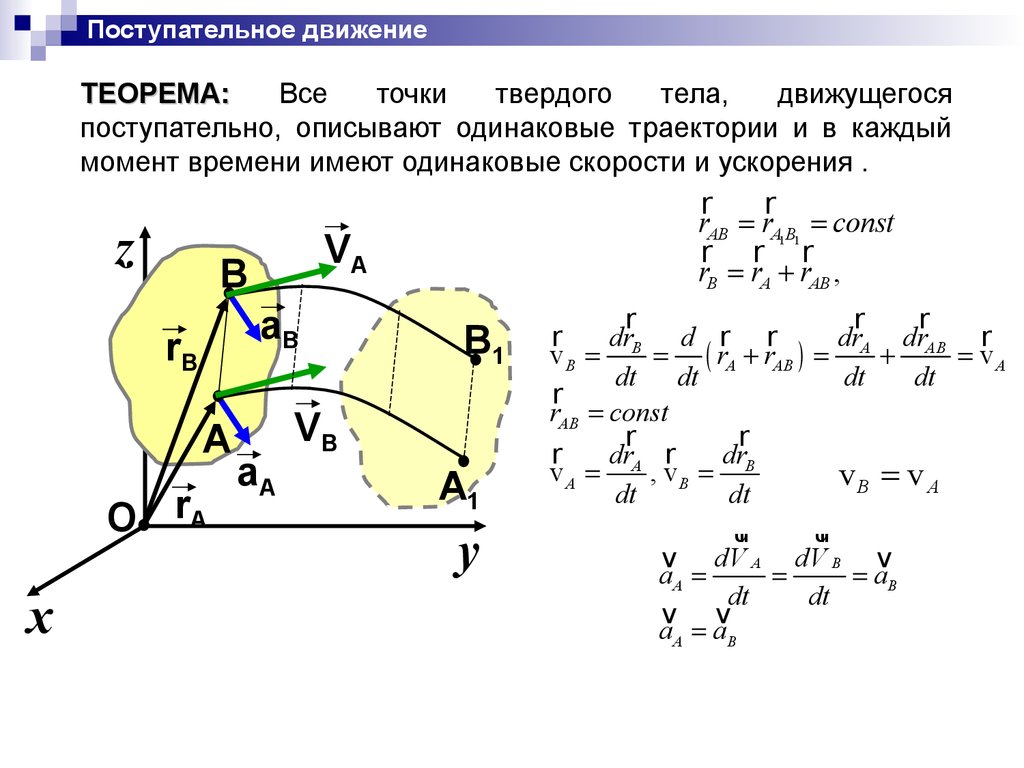
Поступательное движение
ТЕОРЕМА:
Все
точки
твердого
тела,
движущегося
поступательно, описывают одинаковые траектории и в каждый
момент времени имеют одинаковые скорости и ускорения .
r
r
rAB rA1B1 const
r r r
VA
r
B
B rA rAB ,
z
aB
rB
A
O rA
x
aA
B1
VB
A1
y
r
r
r
r
drB d r r
drA drAB r
vB
rA rAB
vA
dt dt
dt
dt
r
rAB const
r
r
r
drA r
drB
vA
, vB
vB v A
dt
dt
ur
ur
v dV A dV B v
aA
aB
dt
dt
v v
a A aB

19.

Вращательное движение
Вращательное движение
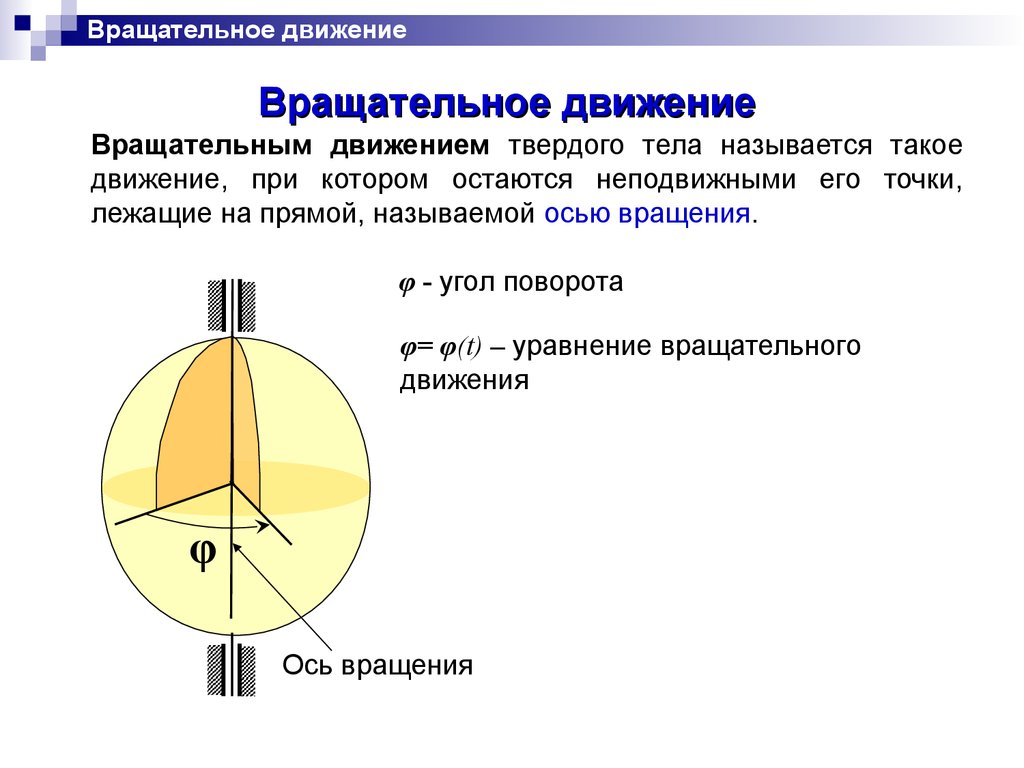
Вращательным движением твердого тела называется такое
движение, при котором остаются неподвижными его точки,
лежащие на прямой, называемой осью вращения.
φ - угол поворота
φ= φ(t) – уравнение вращательного
движения
φ
Ось вращения

20.

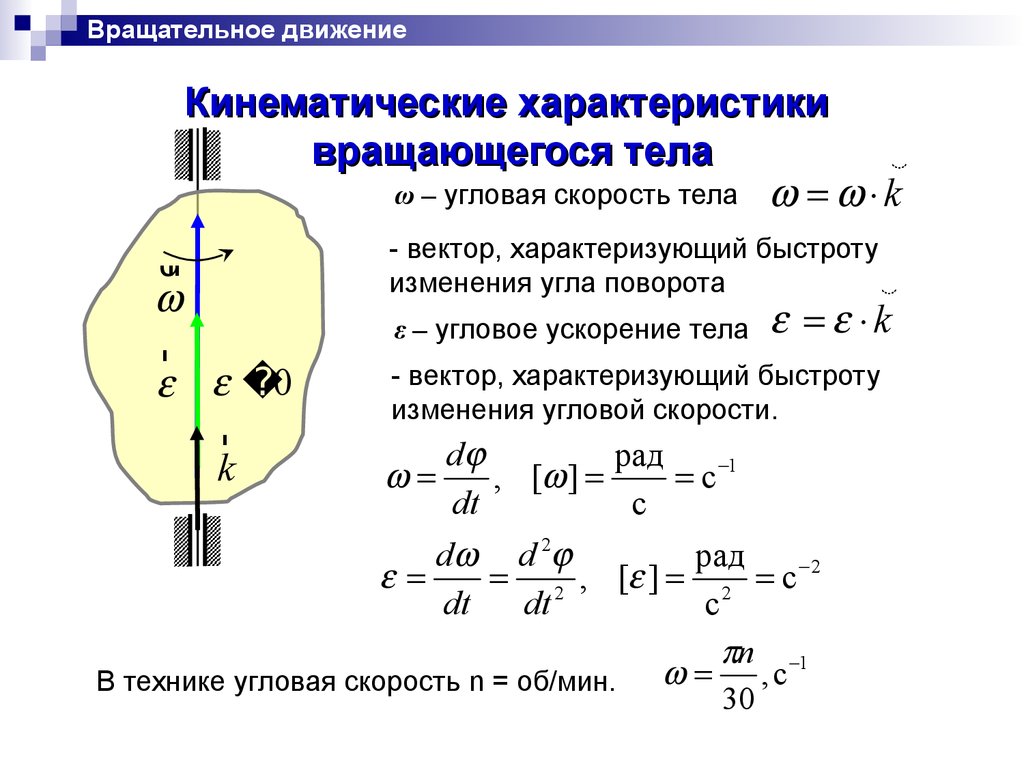
Вращательное движение
Кинематические характеристики
вращающегося тела
ω – угловая скорость тела k
ur
r
0
r
k
- вектор, характеризующий быстроту
изменения угла поворота
ε – угловое ускорение тела
k
- вектор, характеризующий быстроту
изменения угловой скорости.
d
рад
, [ ]
с 1
dt
с
d d 2
рад
2 , [ ] 2 с 2
dt
dt
с
n 1
,c
В технике угловая скорость n = об/мин.
30

21.

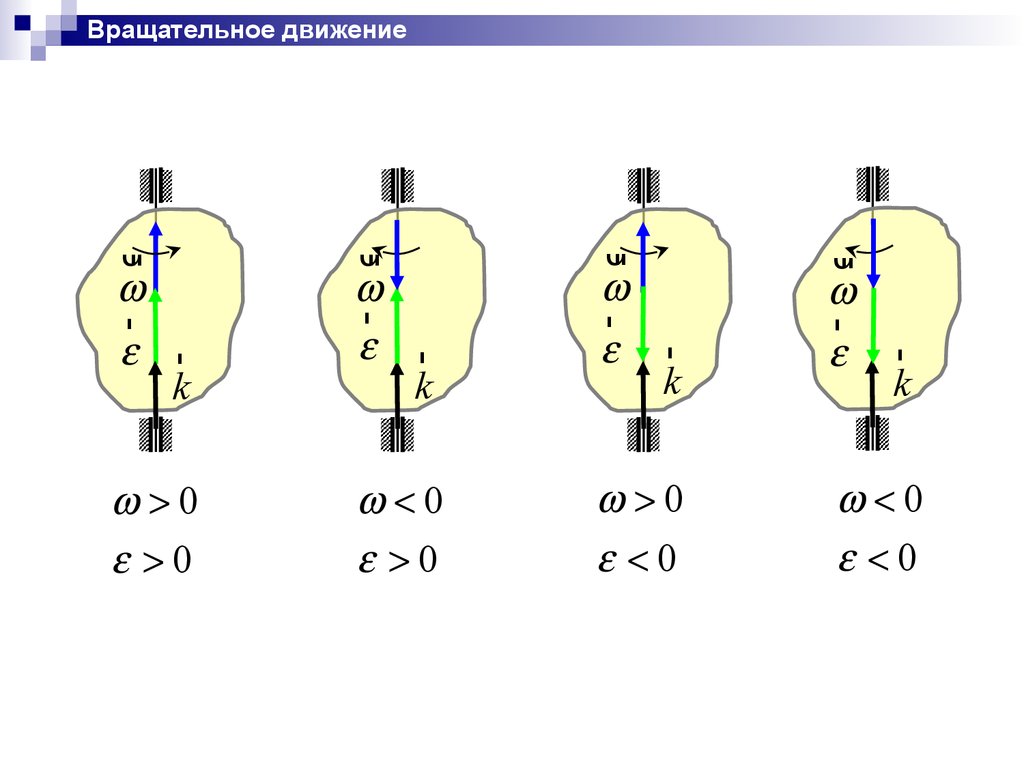
Вращательное движение
ur
r
r
k
ur
r
r
k
ur
r
r
k
ur
r
0
0
0
0
0
0
0
0
r
k

22.

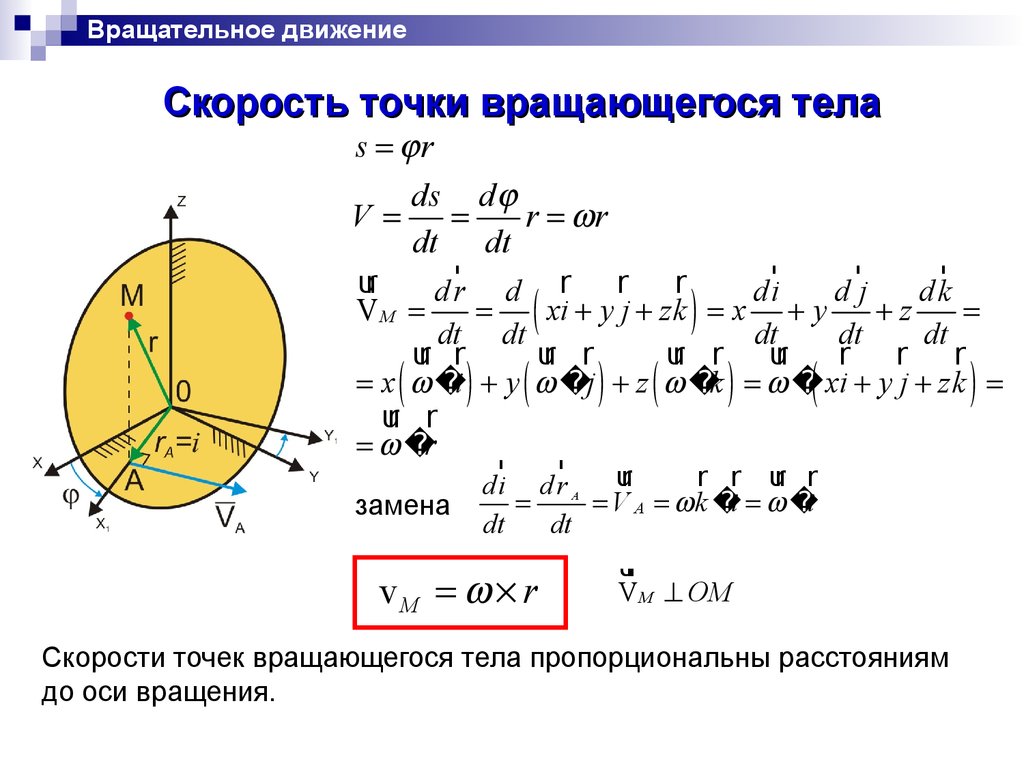
Вращательное движение
Скорость точки вращающегося тела
s r
ds d
V
r r
dt dt
r
r
r
r
ur
r
r
r
dr d
di
dj
dk
VM
xi y j zk x y
z
dt dt
dt
dt
dt
ur r
ur r
ur r ur
r r
r
x i y j z k xi y j zk
ur r
r
r
r
замена
r r ur r
di d r A ur
V A k i i
dt
dt
vM r
ur
V M OM
Скорости точек вращающегося тела пропорциональны расстояниям
до оси вращения.

23.

Вращательное движение
Ускорение точки вращающегося тела
τ
φ
aM
aMτ
a O
v
n
ε
aM
r
M
v
aM
ωO
O1
ε
α M
Oz
anМ
v
R, R const
dv d
a
R
R
dt
dt
M
2
2 2
v
R
aMn
2
R
R
aM - вращ.(касат.) ускорение
aM a M2 aMn 2 R 2 4
n
aM - центростр.(норм.) ускорение
r r rn
r r
r
aM r , aM v
n
aM aM

24.

Вращательное движение
Частные случаи вращательного
движения твердого тела
1. Равномерное вращение
2. Равнопеременное вращение
( const )
t
( const ) 1 0 t ,
1 2
0 0 t t
2
Передача вращательных движений
а) зубчатая (z- кол. зубцов)
r1
ω1
ω2
б) ременная
ω1
r2
ω2
r2
r1
1 z2
2 z1
1 r2
2 r1

25.

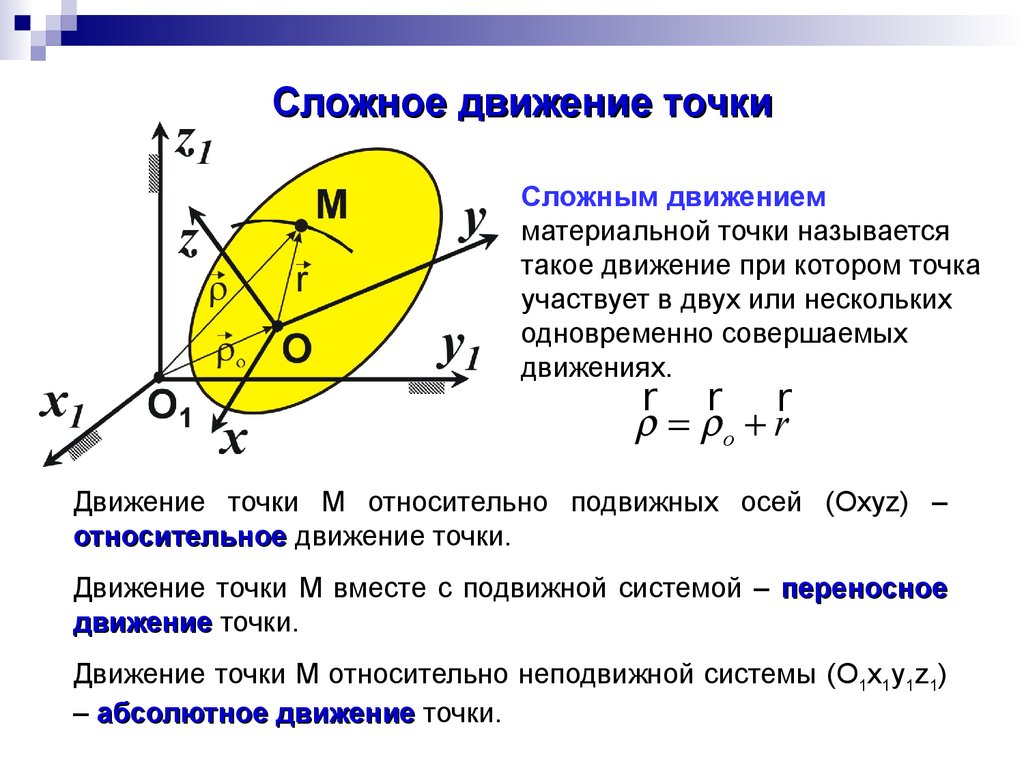
Сложное движение точки
Сложным движением
материальной точки называется
такое движение при котором точка
участвует в двух или нескольких
одновременно совершаемых
движениях.
r r r
o r
Движение точки M относительно подвижных осей (Oxyz) –
относительное движение точки.
Движение точки M вместе с подвижной системой – переносное
движение точки.
Движение точки M относительно неподвижной системы (O1x1y1z1)
– абсолютное движение точки.

26.

Сложное движение точки
Теорема сложения скоростей
Абсолютная скорость точки при сложном движении равна
геометрической сумме ее переносной и относительной
скоростей.
r r r r r r
r r r
o r
V & &o r& Vo r&
r r r r
r& r r r r& r& r&
& y&j zk
& xi yj zk
r xi y j zk
r xi
r& r r r r& r& r&
& y&j zk
& xi yj zk
r xi
r& r r
r& r r
r& r r
i e i
j e j
k e k
r
e угловая скорость вращения подвижной среды
r r
r r% r r
r& r r r r
& y&j zk
& e ( xi y j zk ) r& e r
r xi
(1)
r%
r& локальная производная
r r r r r r r
r& r r r
r Vr e r
Va Vo e r Vr Ve Vr
r
r r
|v a | v e2 v r2 2v e v r cos(v e v r )

27.

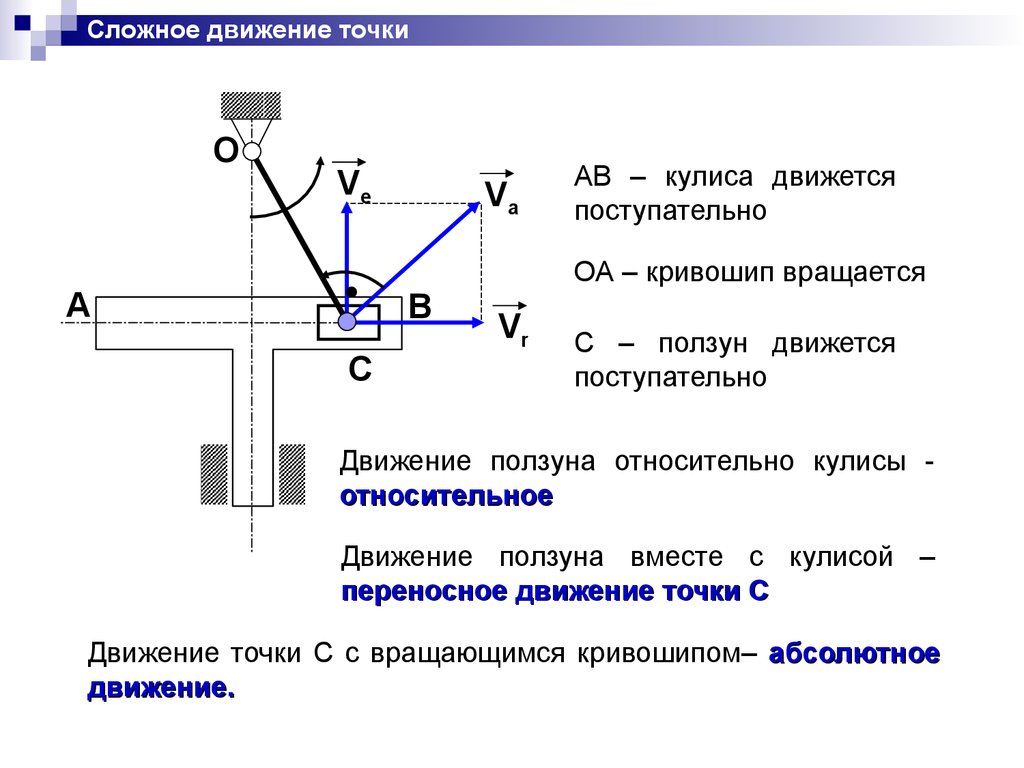
Сложное движение точки
O
Ve
Va
AB – кулиса движется
поступательно
ОА – кривошип вращается
A
B
C
Vr
С – ползун движется
поступательно
Движение ползуна относительно кулисы относительное
Движение ползуна вместе с кулисой –
переносное движение точки С
Движение точки С с вращающимся кривошипом– абсолютное
движение.

28.

Сложное движение точки
Теорема сложения ускорений
Абсолютное ускорение точки при сложном движении равно
геометрической сумме ее переносного, относительного
ускорений и кориолисова ускорения.
r& r& r r r r r& r r r r r r&
r
aa Va Vo &e r e r& Vr ao e r e r& Vr
r
r
r
r
Vr Vx i Vy j Vz k
r& r&
% r r r r r
Vr Vr e V ar e V
r r r
r
r r r r
r r r
aa ao e r e ( e r Vr ) ar e Vr
r r r
r
r r r r r r
aa ao e r e e r 2 e Vr ar
r
r r r
aa ae arк a

29.

Сложное движение точки
Ускорение Кориолиса
r r
r
aк 2 e v r
rr
r
| aк | 2 e v r sin( e v r )
Ускорение кориолиса характеризует совместный эффект вращательного
движения тела (подвижной среды) и относительного движения точки
r
aесли
к 0,
r r
V e // r
или
e 0
aк
aк
Vr
OZ
ω
Vr
OZ
ω
aк
ω
O
Z
Vr
aк
ω
O
Z
Vr

30.

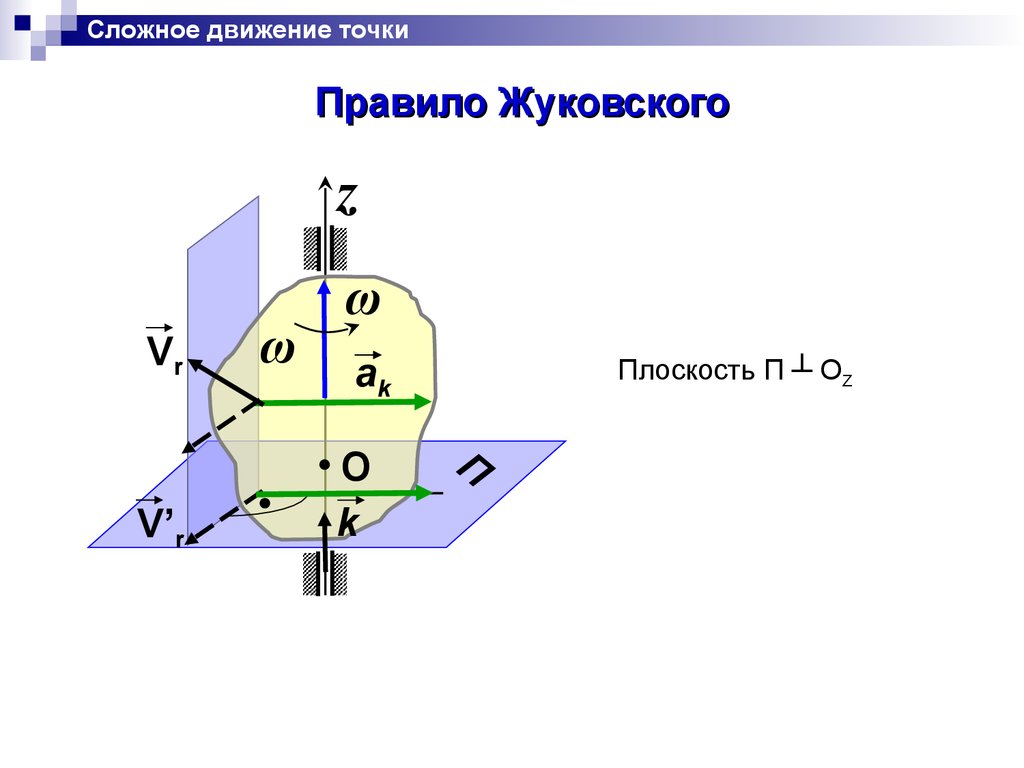
Сложное движение точки
Правило Жуковского
z
Vr
V’r
ω
ω
ak
O
k
Плоскость П ┴ OZ
П

31.

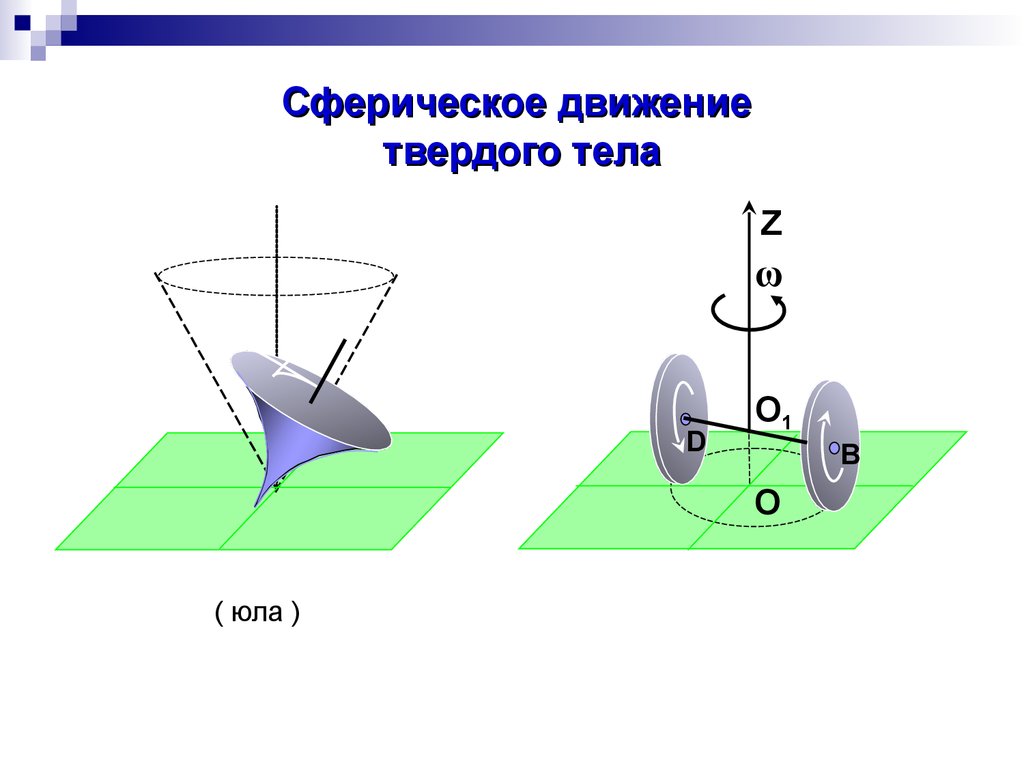
Сферическое движение
твердого тела
Z
ω
D
O1
B
O
( юла )

32.

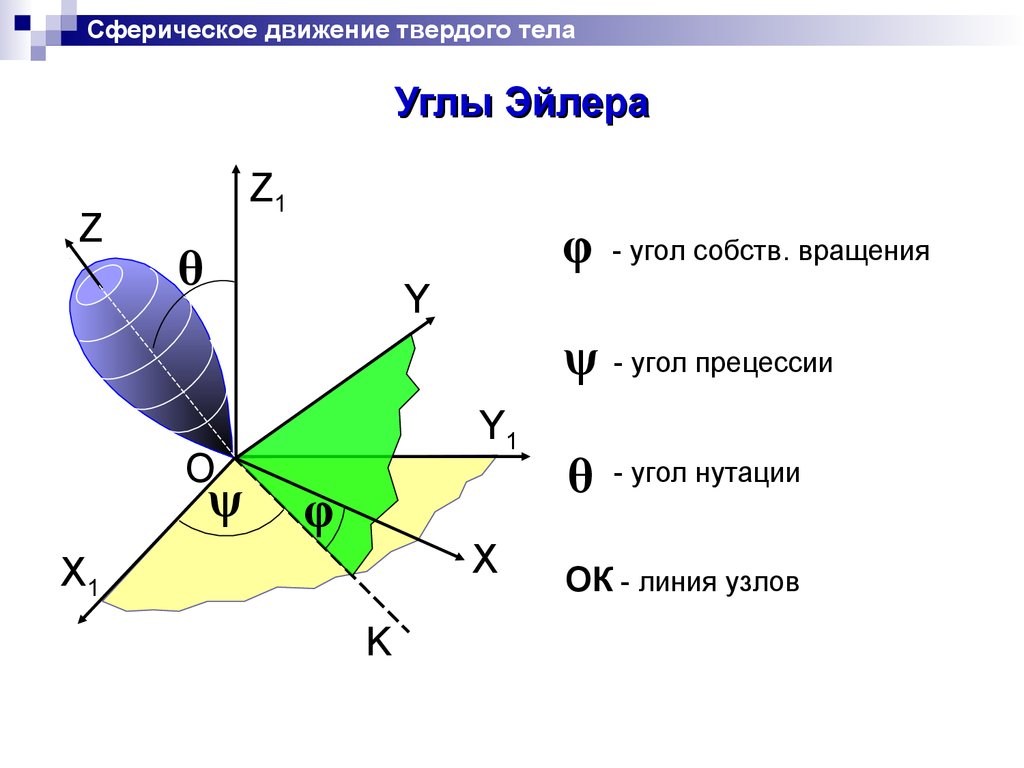
Сферическое движение твердого тела
Углы Эйлера
Z
Z1
φ
θ
- угол собств. вращения
Y
ψ - угол прецессии
O
ψ
Y1
φ
X
X1
K
θ
- угол нутации
ОК - линия узлов

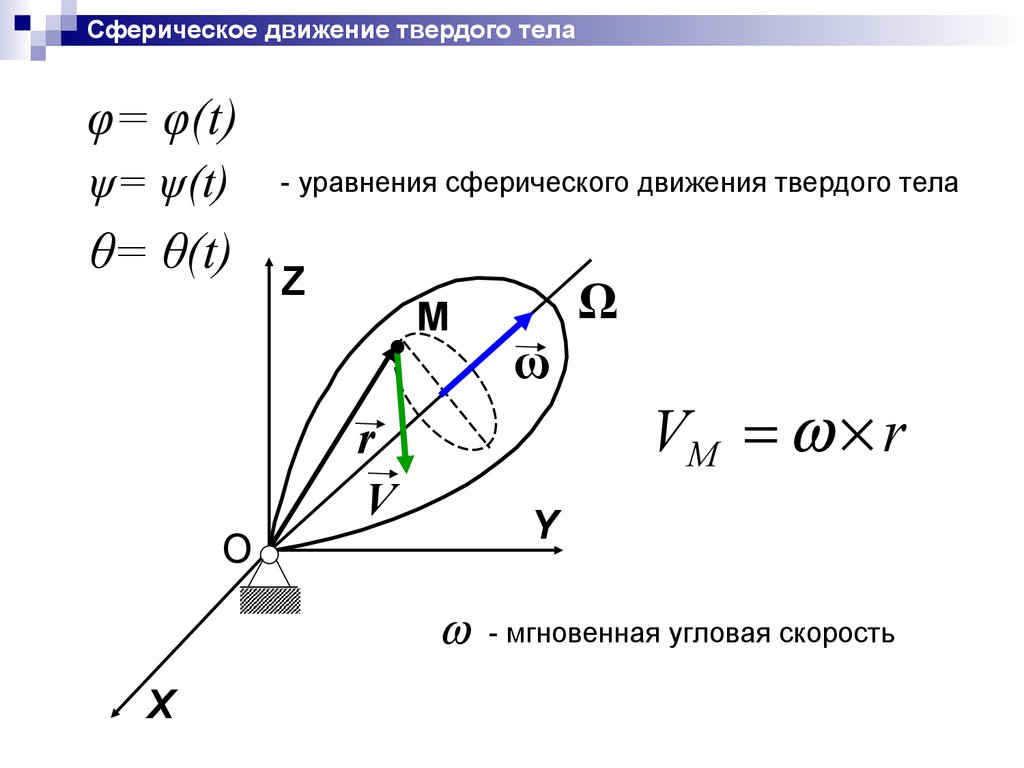
33.

Сферическое движение твердого тела
φ= φ(t)
ψ= ψ(t)
θ= θ(t)
- уравнения сферического движения твердого тела
Z
M
r
V
ω
VM r
Y
O
X
Ω
- мгновенная угловая скорость

34.

Сферическое движение твердого тела
ω1
P1
P3
P2
ε
ω3
ω2
O
ε
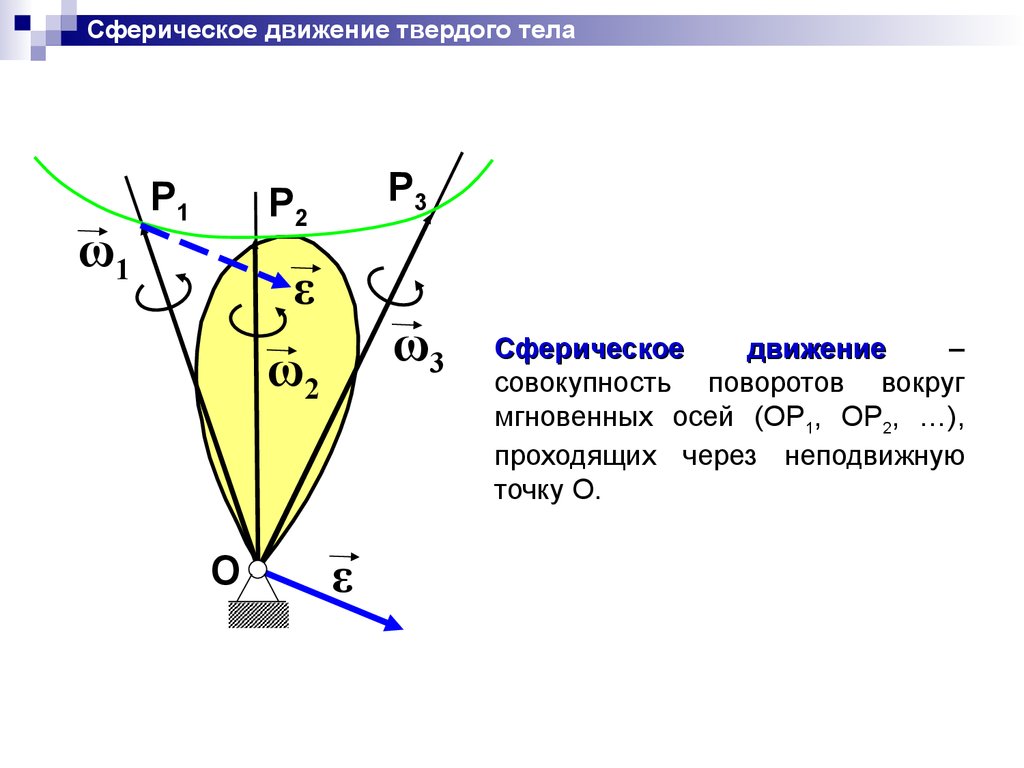
Сферическое
движение
–
совокупность поворотов вокруг
мгновенных осей (OP1, OP2, …),
проходящих через неподвижную
точку O.

35.

Плоскопараллельное движение
твердого тела
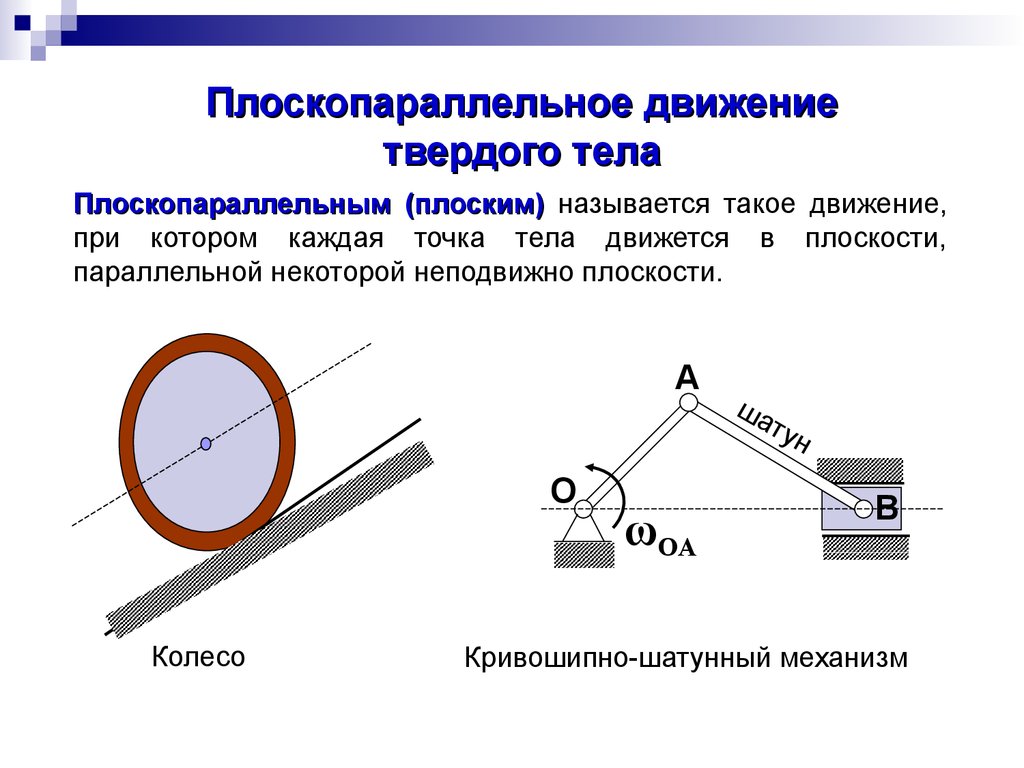
Плоскопараллельным (плоским) называется такое движение,
при котором каждая точка тела движется в плоскости,
параллельной некоторой неподвижно плоскости.
A
O
Колесо
ωOA
ша
ту н
B
Кривошипно-шатунный механизм

36.

Плоскопараллельное движение твердого тела
Уравнения плоского движения
II
M (S)
I
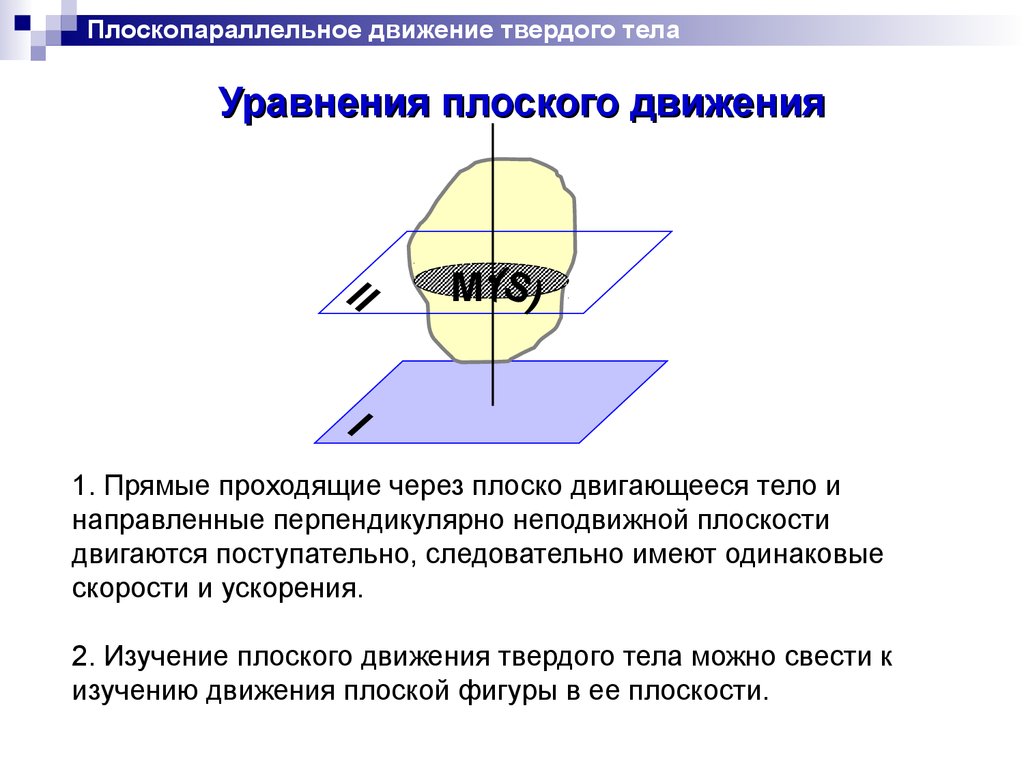
1. Прямые проходящие через плоско двигающееся тело и
направленные перпендикулярно неподвижной плоскости
двигаются поступательно, следовательно имеют одинаковые
скорости и ускорения.
2. Изучение плоского движения твердого тела можно свести к
изучению движения плоской фигуры в ее плоскости.

37.

Плоскопараллельное движение твердого тела
3. Так как положение плоской фигуры на ее
плоскости определяется положением двух
ее точек, то движение плоской фигуры можно
изучать как движение прямолинейного
отрезка в этой плоскости.
4. Движение плоской фигуры в ее плоскости
можно разложить на два простейших
движения: поступательное и вращательное.
(·) A (полюс) – произвольная точка тела
x A x A (t )
y A y A (t )
(t )

38.

Плоскопараллельное движение твердого тела
ε (ε>0)
A
ω
(S)
A
ω
ε
(S)
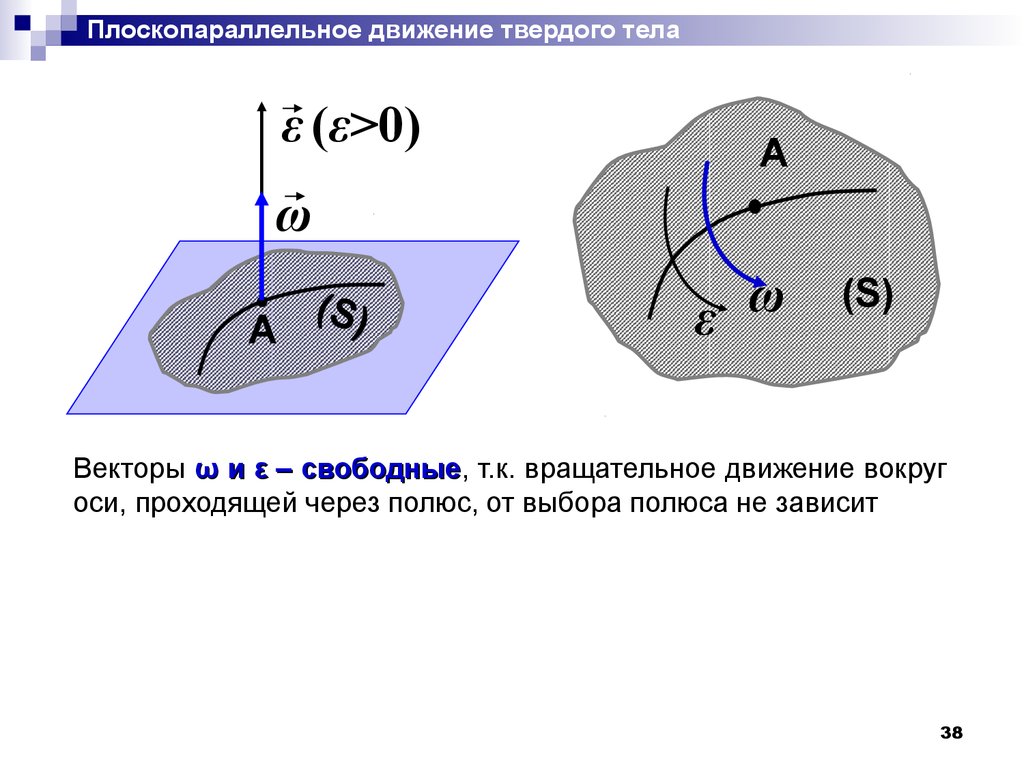
Векторы ω и ε – свободные,
свободные т.к. вращательное движение вокруг
оси, проходящей через полюс, от выбора полюса не зависит
38

39.

Плоскопараллельное движение твердого тела
Определение скоростей точек
при плоском движении
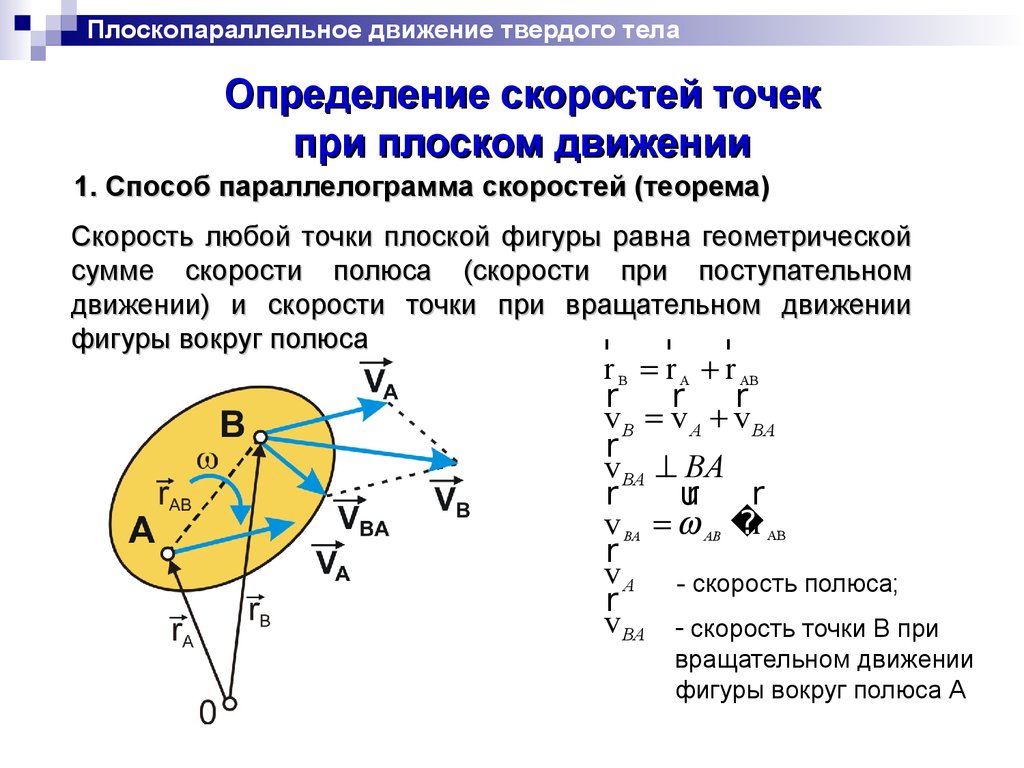
1. Способ параллелограмма скоростей (теорема)
Скорость любой точки плоской фигуры равна геометрической
сумме скорости полюса (скорости при поступательном
движении) и скорости точки при вращательном движении
фигуры вокруг полюса
r r r
r B r A r AB
r
r
r
v B v A v BA
r
v BA BA
r
ur
r
v BA AB r AB
r
v A - скорость полюса;
r
v BA - скорость точки В при
вращательном движении
фигуры вокруг полюса А

40.

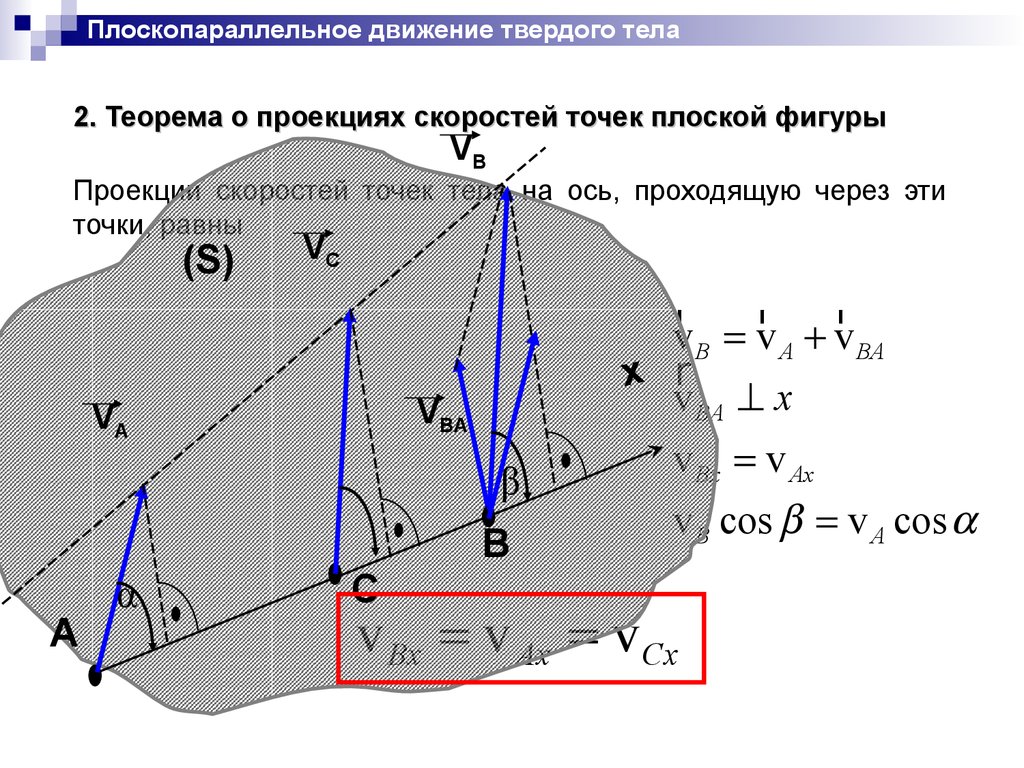
Плоскопараллельное движение твердого тела
2. Теорема о проекциях скоростей точек плоской фигуры
VB
Проекции скоростей точек тела на ось, проходящую через эти
точки, равны
(S)
VС
r
r
r
v B v A v BA
x r
v BA х
VBA
VA
β
B
A
α
С
v Bx v Ax
v B cos v A cos
v Bx v Ax v Cx

41.

Плоскопараллельное движение твердого тела
3. Мгновенный центр скоростей
Мгновенным центром скоростей (МЦС) называется точка плоской
фигуры, скорость которой в данный момент времени равна нулю (P)
A
P
VA
AP=
r
r
v PА v A
r
r
r
v P v A v PА 0
VA
ω
B
VB
(S)
r
vP 0
r
r
v A v AP , v A
AP,
r
r
v B v BP , v B
BP
vA
vB
...
AP BP

42.

Плоскопараллельное движение твердого тела
Частные случаи определения
мгновенного центра скоростей
Cкорости двух точек параллельны
a)
A
VA
VA
б)
A
в)
A
B
B
P
VB
VB
ω vA
VA
ω
P
B
vB
... .
AP BP
VB
P→∞
v A vB
0.

43.

Плоскопараллельное движение твердого тела
Качение тела по неподвижной
поверхности
O
ω
VO
vO
vM
OP MP
M
VM
P
vO
OP
или
vM
MP

44.

Плоскопараллельное движение твердого тела
Ускорение точки тела
при плоском движении
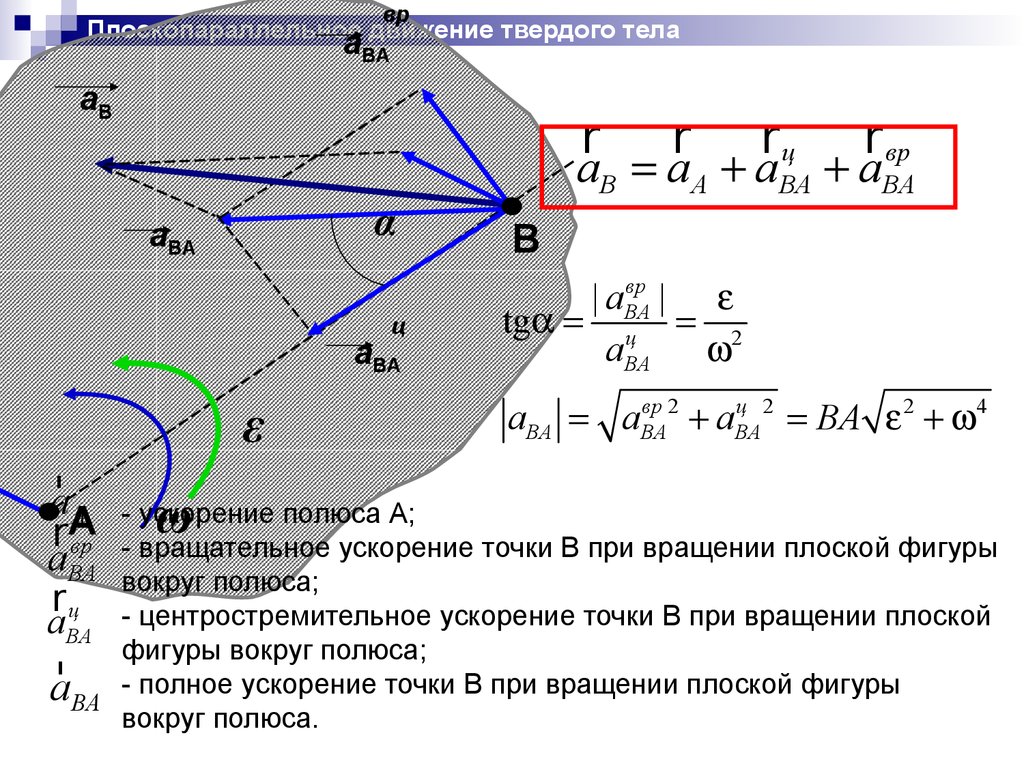
Теорема. Ускорение любой точки плоской фигуры равно
геометрической сумме ускорения полюса (ускорения при
поступательном движении) и ускорения точки при вращательном
движении фигуры вокруг полюса.
r
r
r
v B v A v BA
r r
r
r
v B v A rAB
r
r r&
r
dv B r& r& r
aB
v A rAB rAB
dt
r r
r r& r r
aB v A rAB v BA
r r r
r r& r r
a v r r
B
A
AB
AB
r
r
r вр r ц
aB a A a BA a BA
r
r вр r ц
aBA aBA aBA
r
r
r
aB a A aBA
ц
aBA
2
BA
вр
aBA
BA
rц
r вр
aBA aBA

45.

вр
Плоскопараллельное движение твердого тела
aBA
aB
r
r
r ц r вр
aB a A aBA aBA
α
aBA
ц
aBA
r
aA
rA
вр
aBA
ε
ω
B
вр
| aBA
|
tg ц 2
aBA
вр 2
ц 2
аBA aBA
aBA
ВА 2 4
- ускорение полюса А;
- вращательное ускорение точки В при вращении плоской фигуры
вокруг полюса;
r ц - центростремительное ускорение точки В при вращении плоской
aBA
вокруг полюса;
r фигуры
aBA - полное ускорение точки В при вращении плоской фигуры
вокруг полюса.

46.

Плоскопараллельное движение твердого тела
Мгновенный центр ускорений
Точка тела, ускорение которой в данный момент времени равно
нулю называется мгновенным центром ускорений (МЦУ) (Q).
ω
aA
α
B
Q
ε
Дано:
A
AQ
r r r
, , а А
Доказательство:
r
| aA |
2 4
arctg 2
ц
aAQ
aAQ
aA
aврB
aC
AQ
...
a
AQ BQ CQ
a AQ AQ 2 4
a AQ a A
aQ a A a AQ 0
r
| aA |
2 4
2 4

47.

Плоскопараллельное движение твердого тела
Частные случаи определения
ускорений
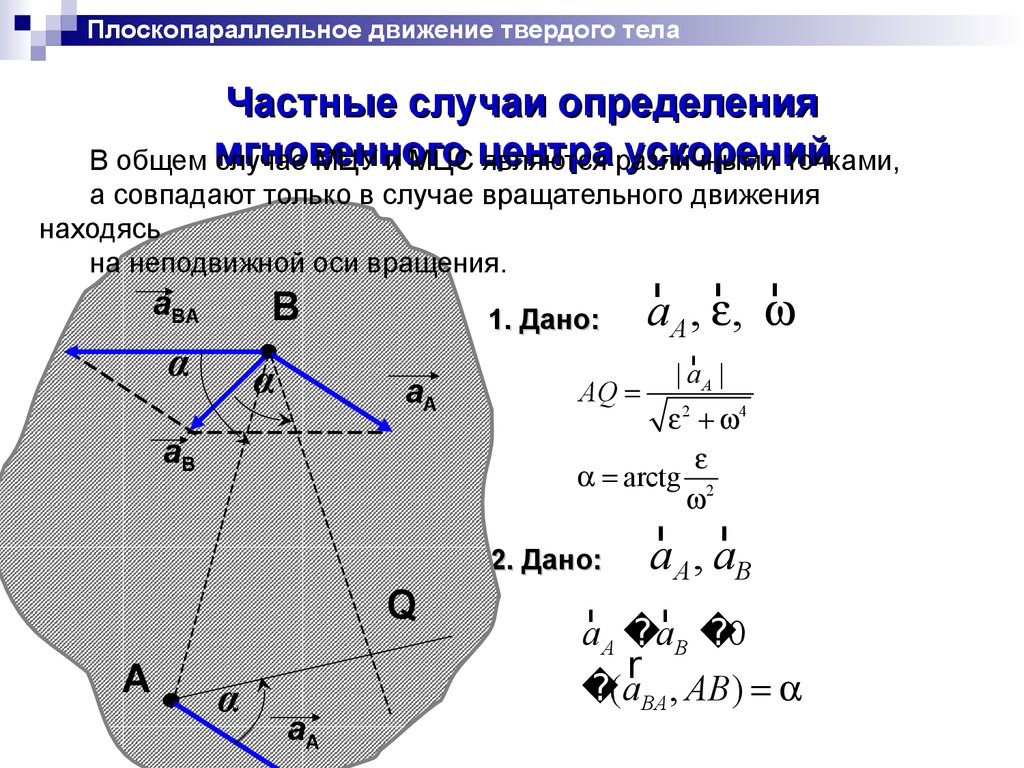
В общем мгновенного
случае МЦУ и МЦС центра
являются различными
точками,
а совпадают только в случае вращательного движения
находясь
на неподвижной оси вращения.
aBA
B
α
α
1. Дано:
aA
aB
AQ
A
α
aA
r
| aA |
2 4
arctg 2
2. Дано:
Q
r r r
a A , ,
r r
a A , aB
r
r
a A aB 0
r
(aBA , AB)

48.

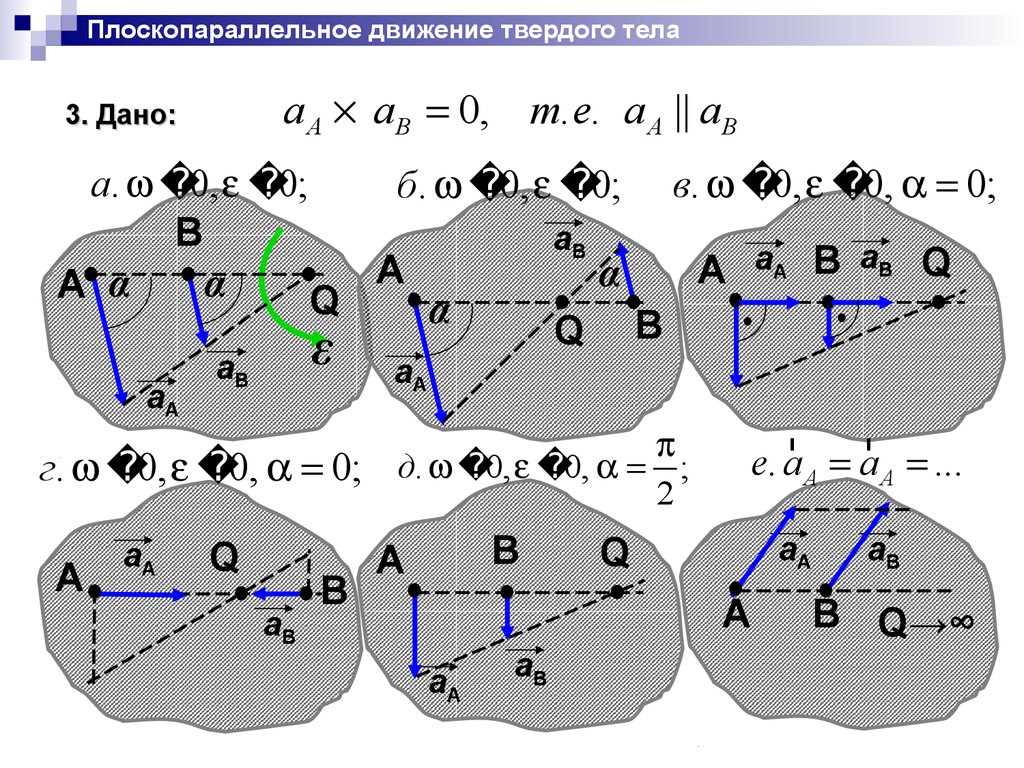
Плоскопараллельное движение твердого тела
a A aB 0, т. е. a A || aB
3. Дано:
а. 0, 0;
б. 0, 0; в. 0, 0, 0;
B
aB
aA B aB Q
A
A
α
α
A α
Q
α
B
Q
ε
aA
aB
aA
г. 0, 0, 0;
A
aA
Q
aB
B
r
r
е. a A a A ...
д. 0, 0, ;
2
B
A
aA
Q
A
aA
aB
aB
B Q→∞