Теоретическая механика. Кинематика

1.

ТЕОРЕТИЧЕСКА
Я МЕХАНИКА
КИНЕМАТИКА

2. Лекция 8

Сложное движение твердого тела.
Сложение поступательных движений.
Сложение вращательных движений.
Сложение поступательного и
вращательного движений.
Общий случай составного движения
тела.
Кинематические инварианты.

3.

Сложное
движение твердого тела –
такое движение, при котором тело
участвует одновременно в двух или
нескольких движениях.
Все
определения,
касающиеся
составляющих движения, данные для
сложного движения точки, остаются
справедливыми для твердых тел.

4.

Кинематика
сложного движения точки
используется здесь для получения новых
соотношений,
описывающих
сложное
движение твердого тела.
Сложение
поступательных движений
твердого тела – При поступательных
движениях все точки твердого тела имеют
одинаковые скорости, что позволяет
использовать
теорему
о
сложении
скоростей точки для сложного движения:
v v v .
a
r
e

5.

Таким
образом, абсолютная скорость
тела, равная скорости одной из точек этого
тела, равна геометрической сумме
переносной
и
относительной
скоростей этого тела.
Сложение
вращательных
движений
твердого тела – здесь рассмотрим два
случая
различного
положения
осей
вращения:
оси вращений параллельны
оси вращений пересекаются.

6.

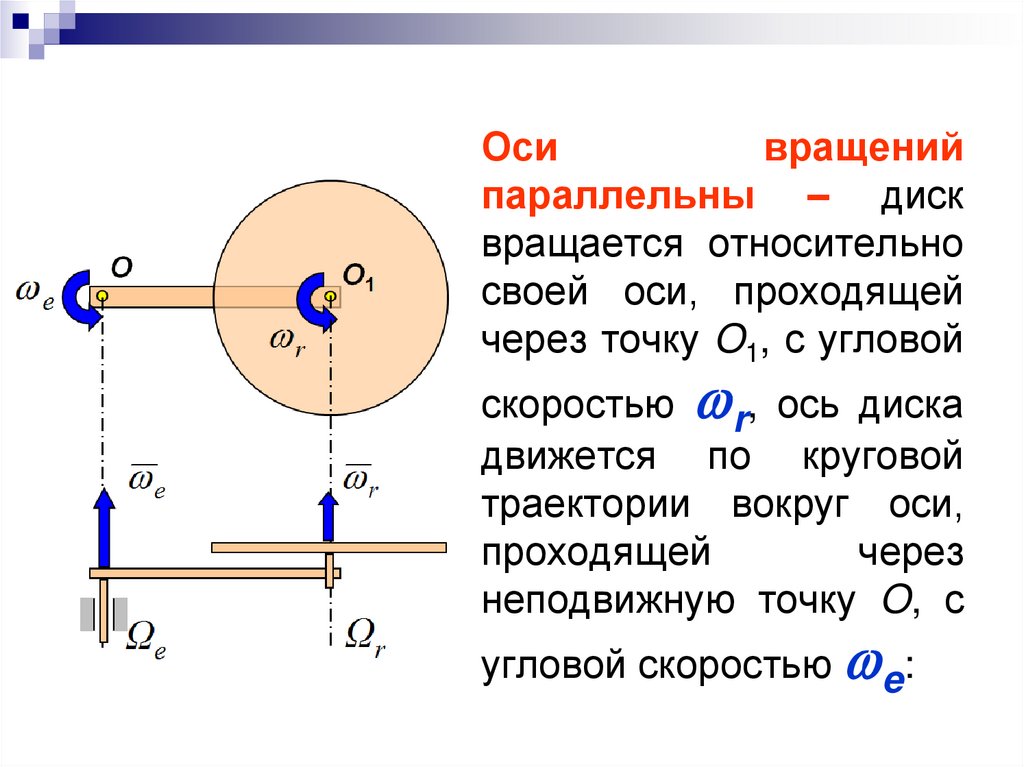
Оси
вращений
параллельны – диск
вращается относительно
своей оси, проходящей
через точку O1, с угловой
скоростью r, ось диска
движется по круговой
траектории вокруг оси,
проходящей
через
неподвижную точку O, с
угловой скоростью e:

7.

e O
e
Ωe
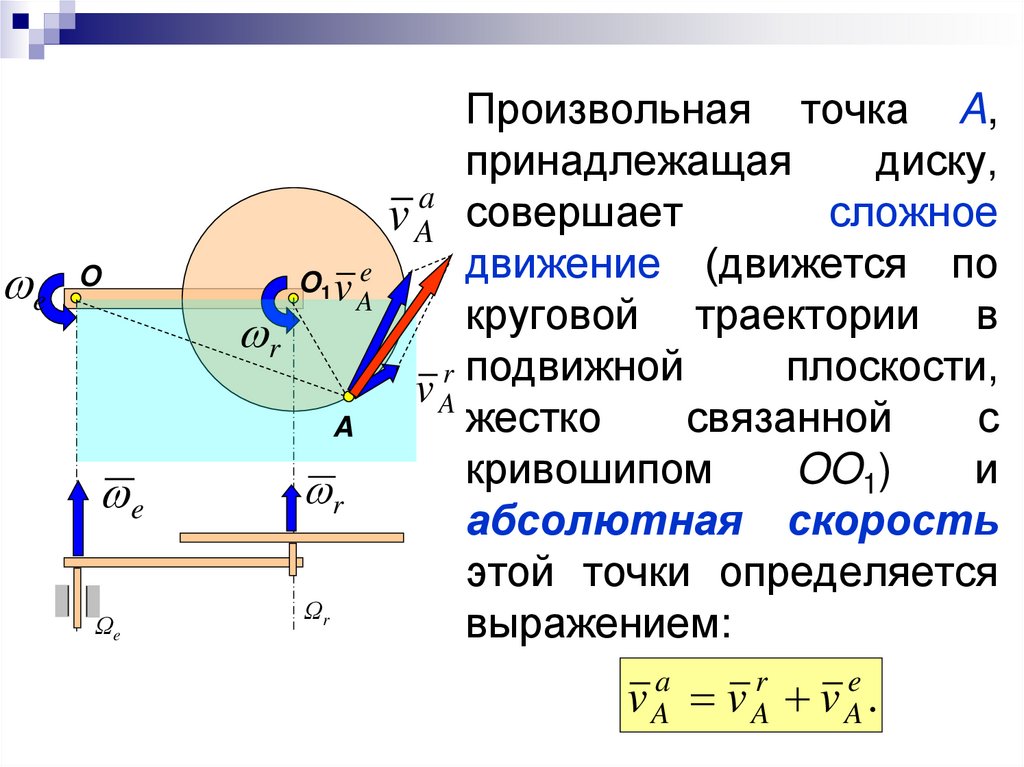
Произвольная точка A,
принадлежащая
диску,
a
сложное
v A совершает
движение (движется по
O1 v e
A
круговой
траектории
в
r
плоскости,
r подвижной
vA
жестко
связанной
с
A
кривошипом
OO
)
и
1
r
абсолютная скорость
этой точки определяется
Ω
выражением:
r
v Aa v Ar v Ae .

8.

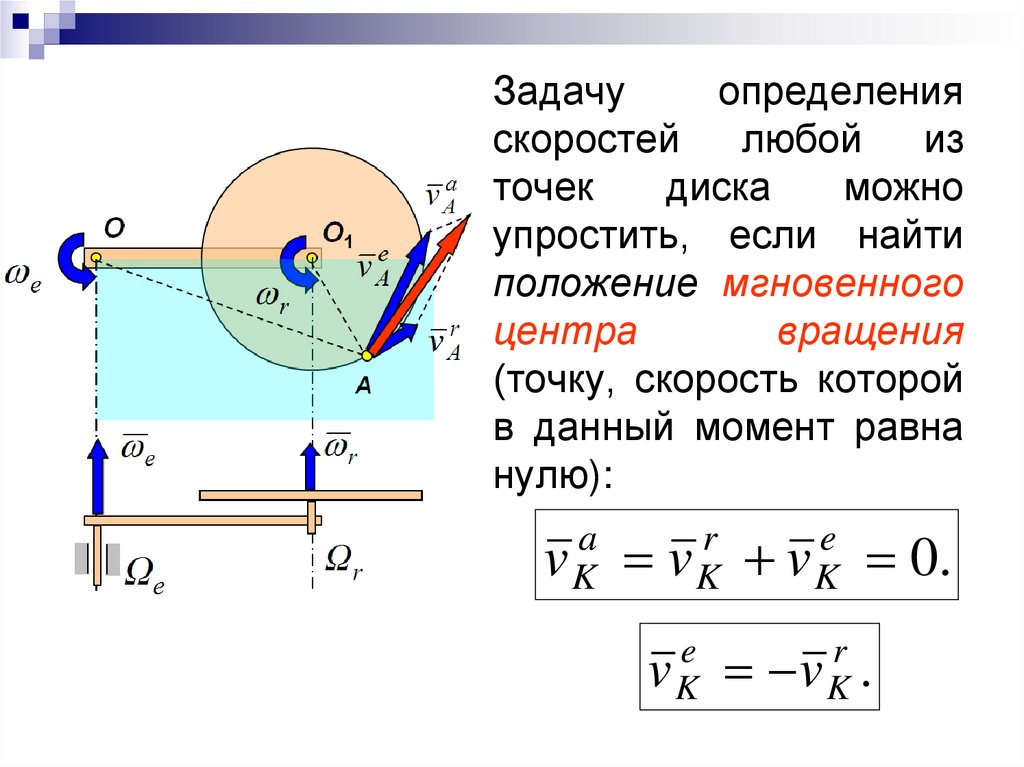
Задачу
определения
скоростей
любой
из
точек
диска
можно
упростить, если найти
положение мгновенного
центра
вращения
(точку, скорость которой
в данный момент равна
нулю):
a
vK
r
e
vK vK
e
vK
0.
r
v K .

9.

v Ke
e
O
a
vA
K
r
r
vK
e
Ωe
O1 v Ae
v Ar
A
r
Ωr
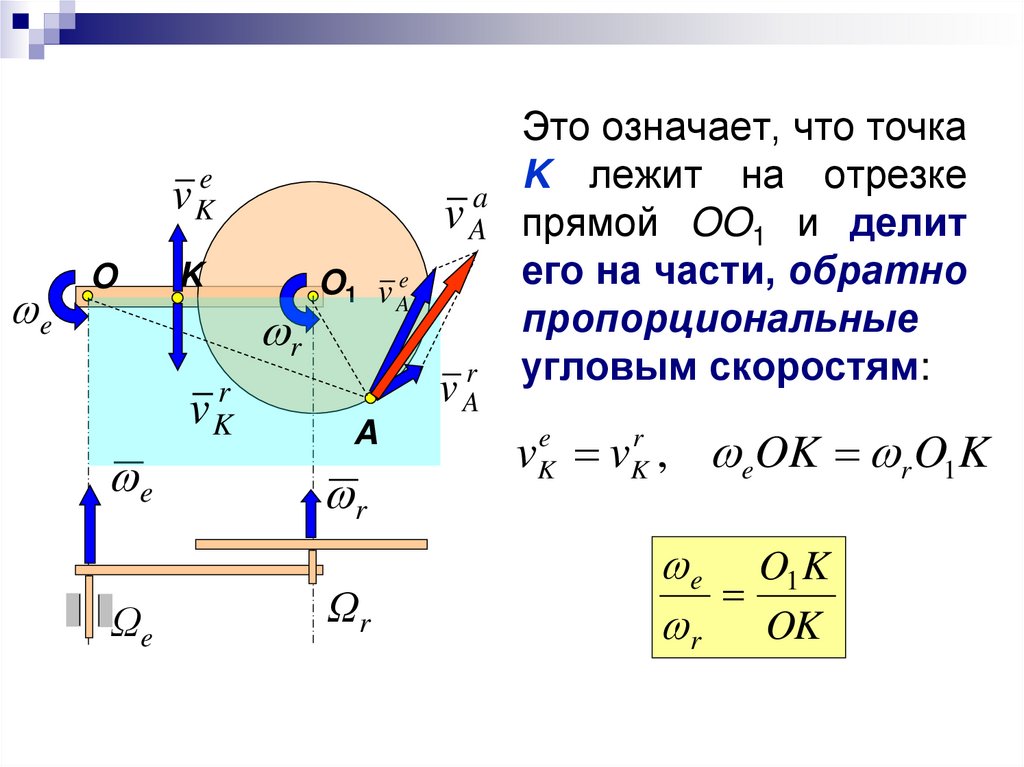
Это означает, что точка
K лежит на отрезке
прямой OO1 и делит
его на части, обратно
пропорциональные
угловым скоростям:
v v , eOK r O1 K
e
K
r
K
e O1 K
r OK

10.

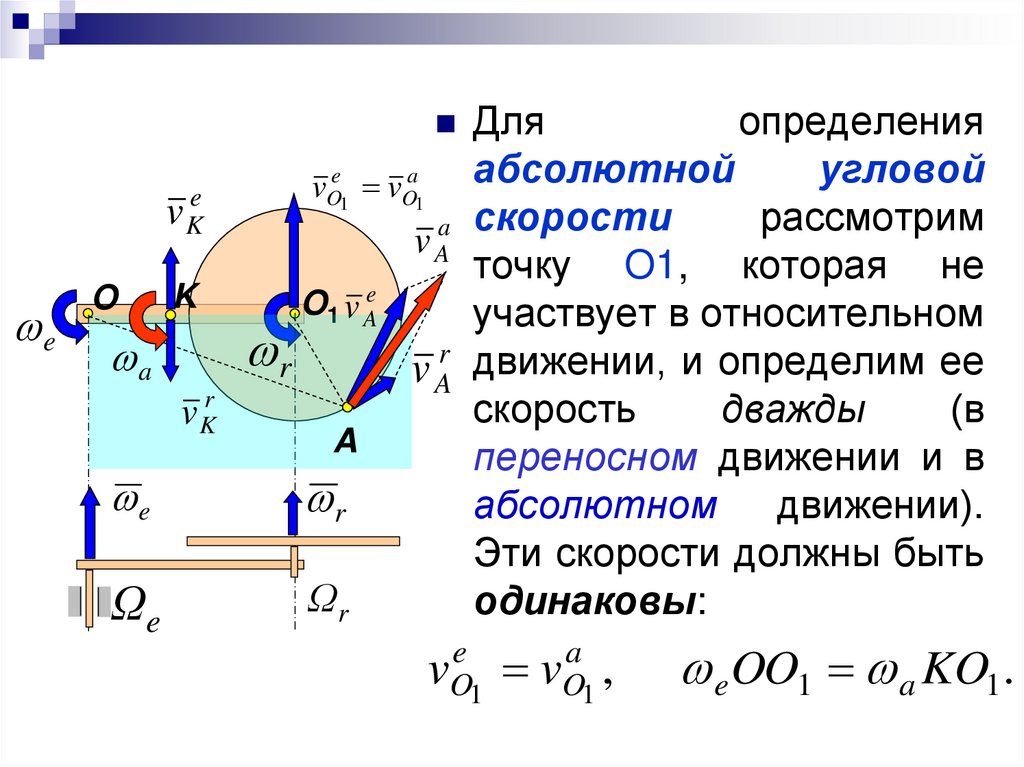
Для
v Ke
e
O
K
a
v Kr
e
Ωe
определения
абсолютной
угловой
vOe1 vOa1
рассмотрим
a скорости
vA
точку O1, которая не
O1 v Ae
участвует в относительном
r движении, и определим ее
r
vA
скорость
дважды
(в
A
переносном движении и в
r
абсолютном движении).
Эти скорости должны быть
Ωr
одинаковы:
vOe1 vOa1 ,
e OO1 a KO1.

11.

Представим
отрезок
OO1,
как
сумму
отрезков и отрезок OK
выразим через O1K:
e (OK KO1 )
r
e ( KO1 KO1 )
e
( r e ) KO1 a KO1.
Отсюда:
a e r .

12.

В случае противоположных
по направлению вращений
деление
отрезка
OO1
происходит так же обратно
пропорционально угловым
скоростям,
но
только
внешним образом (точка K
будет лежать на этой же
линии вне отрезка OO1 со
стороны большего вектора
угловой скорости)

13.

Тогда: OO1 KO1 KO
vOe1 vOa1
v Ke
e
O
a
v Aa
K
r
r
vK
e a
Ωe Ω a
O1 e
vA
v Ar
A
r
Ωr
и абсолютная
угловая скорость
будет равна разности
скоростей:
a e r .
Оба соотношения
можно объединить
одним векторным
соотношением:
a e r .

14.

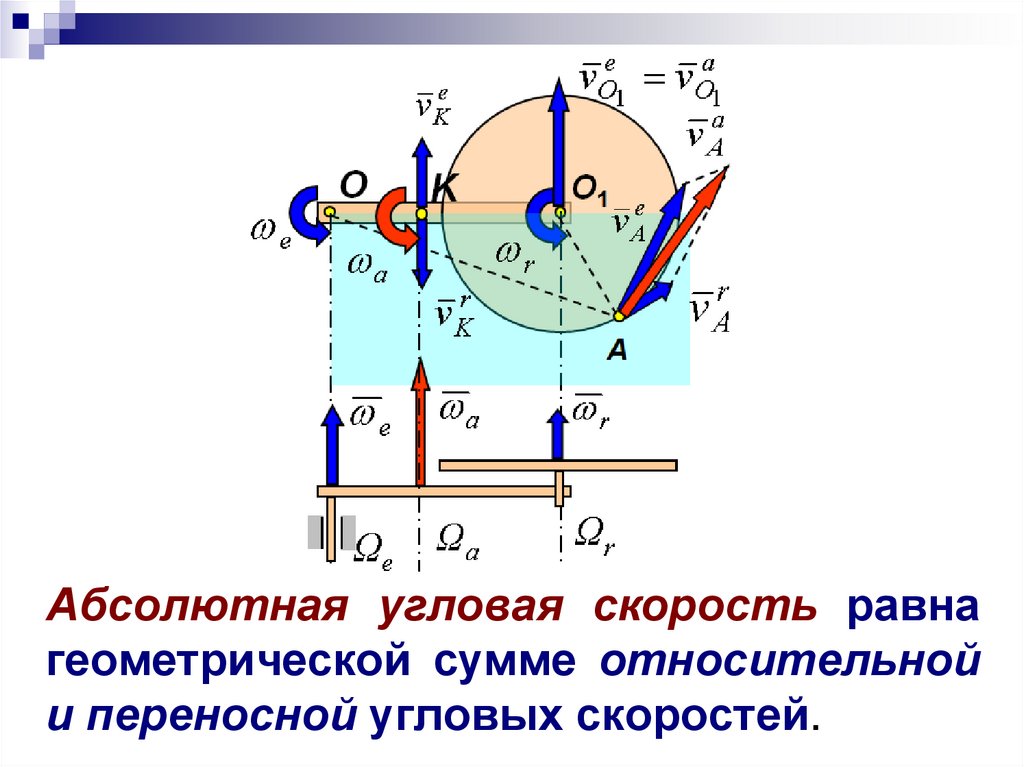
Абсолютная угловая скорость равна
геометрической сумме относительной
и переносной угловых скоростей.

15.

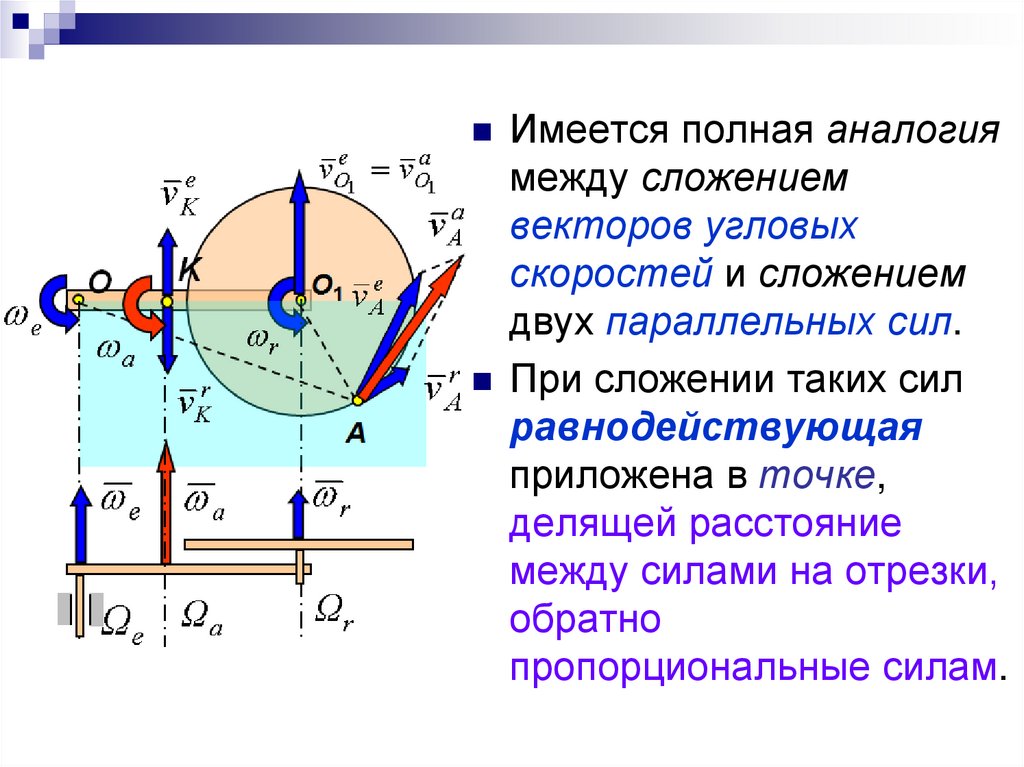
Имеется полная аналогия
между сложением
векторов угловых
скоростей и сложением
двух параллельных сил.
При сложении таких сил
равнодействующая
приложена в точке,
делящей расстояние
между силами на отрезки,
обратно
пропорциональные силам.

16.

Пара вращений – При сложении двух
параллельных сил, равных по величине и
противоположно направленных между собой
равнодействующая этих сил обращается в
ноль (система таких сил не приводится к
равнодействующей) и эти силы образуют
качественно новую простейшую систему,
называемой парой сил.
При этом действие пары сил характеризуется
моментом пары.

17.

Совершенно аналогично при сложении
двух параллельных векторов угловых
скоростей, равных по величине и
противоположно направленных между
собой, называемых парой вращений,
результирующая угловая скорость
обращается в ноль.

18.

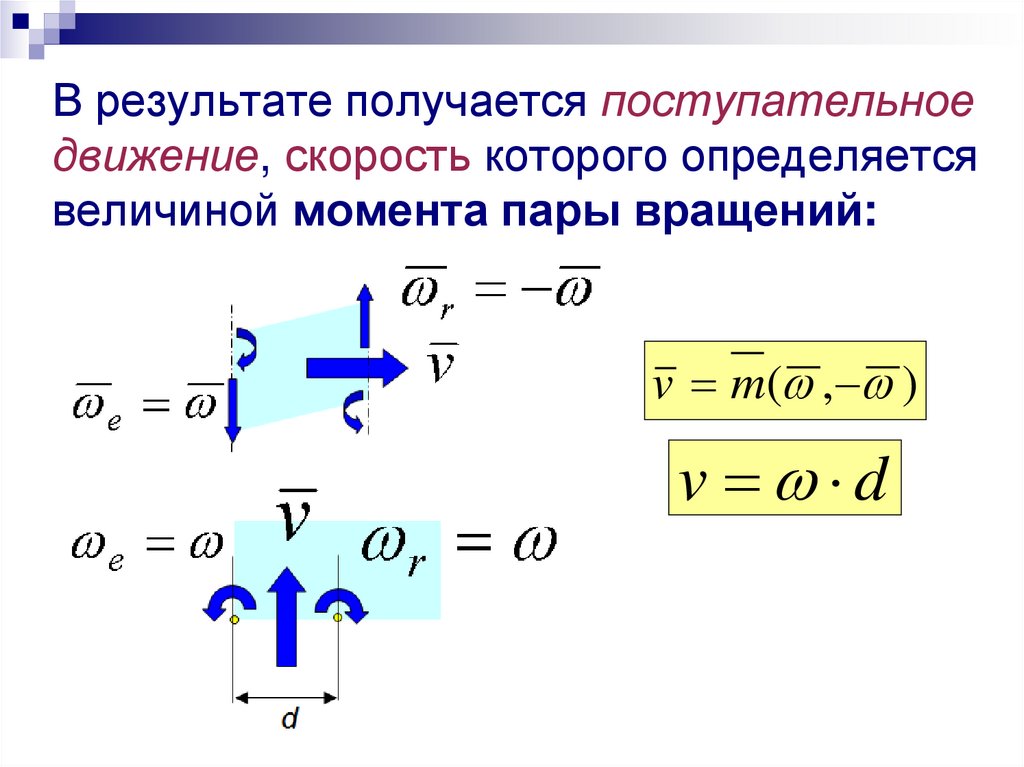
В результате получается поступательное
движение, скорость которого определяется
величиной момента пары вращений:
v m( , )
v d

19.

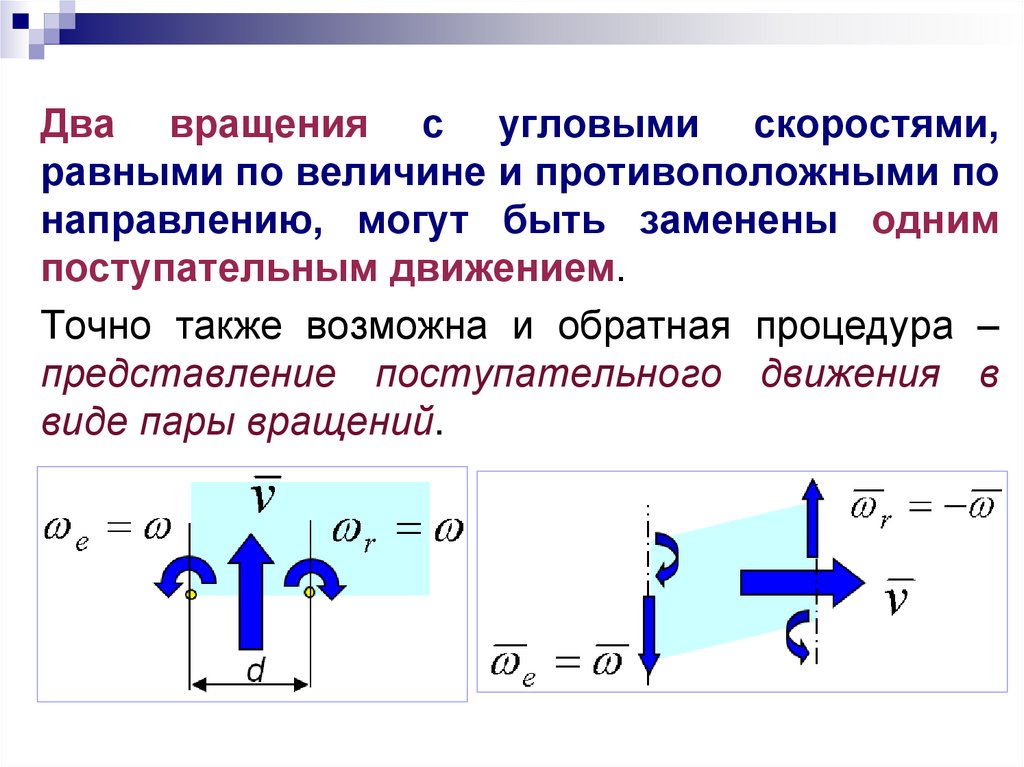
Два вращения с угловыми скоростями,
равными по величине и противоположными по
направлению, могут быть заменены одним
поступательным движением.
Точно также возможна и обратная процедура –
представление поступательного движения в
виде пары вращений.

20.

Вектор скорости поступательного движения
твердого
тела
является
свободным
вектором (может перемещаться параллельно
самому себе) в то время как векторы
угловой скорости являются скользящими
векторами, которые могут перемещаться
только по линии действия.

21. Сложение вращательных движений твердого тела в случае пересечения осей вращений

Тело
вращается
с
угловой
скоростью r относительно
своей оси, проходящей через
точку пересечения с другой
осью вращения O.
Относительно
второй
оси
первая ось вращается с
угловой скоростью e

22.

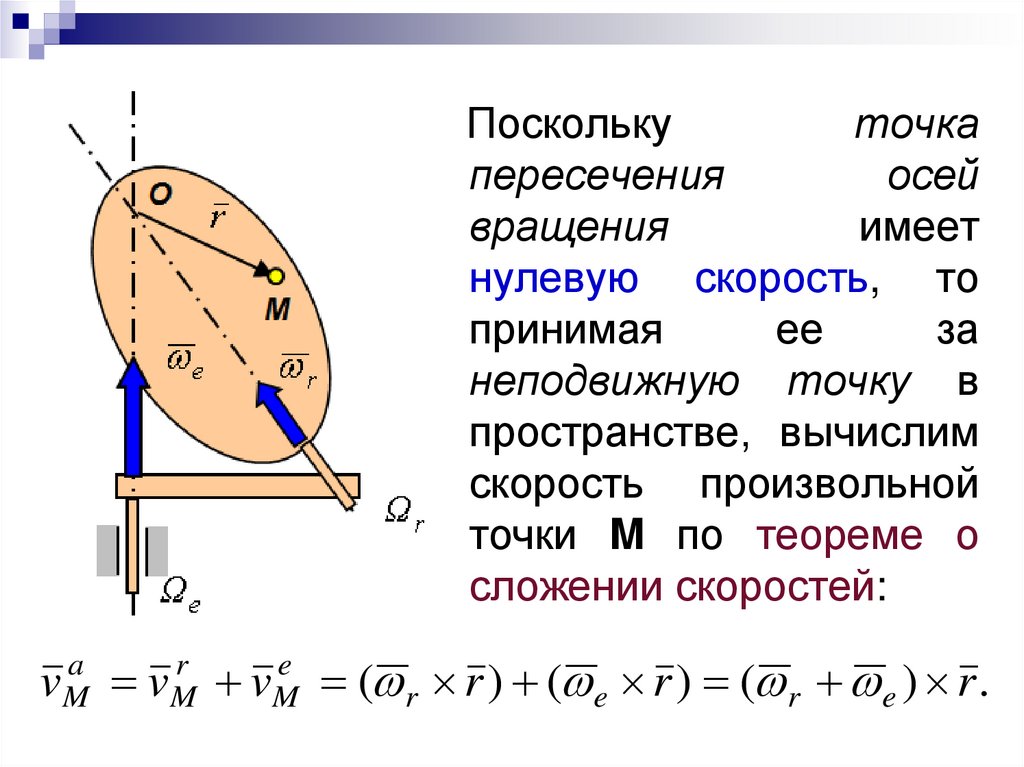
Поскольку
точка
пересечения
осей
вращения
имеет
нулевую скорость, то
принимая
ее
за
неподвижную точку в
пространстве, вычислим
скорость произвольной
точки M по теореме о
сложении скоростей:
a
r
e
vM vM vM
( r r ) ( e r ) ( r e ) r .

23.

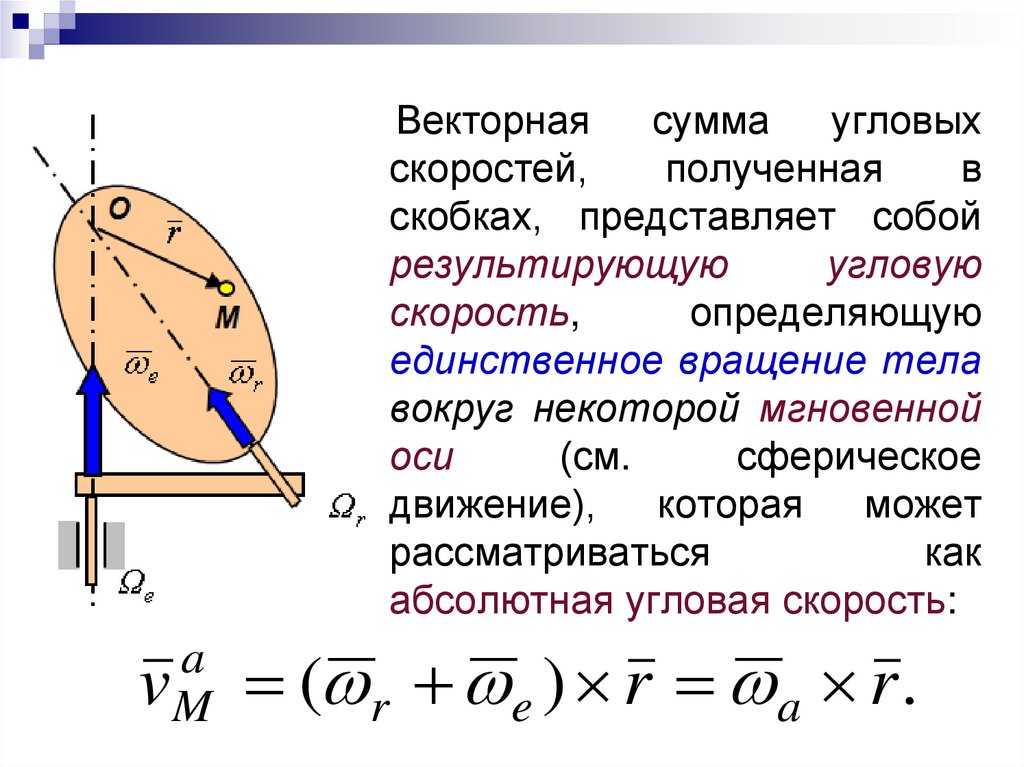
Векторная
сумма
угловых
скоростей,
полученная
в
скобках, представляет собой
результирующую
угловую
скорость,
определяющую
единственное вращение тела
вокруг некоторой мгновенной
оси
(см.
сферическое
движение),
которая
может
рассматриваться
как
абсолютная угловая скорость:
a
vM ( r e ) r a r .

24.

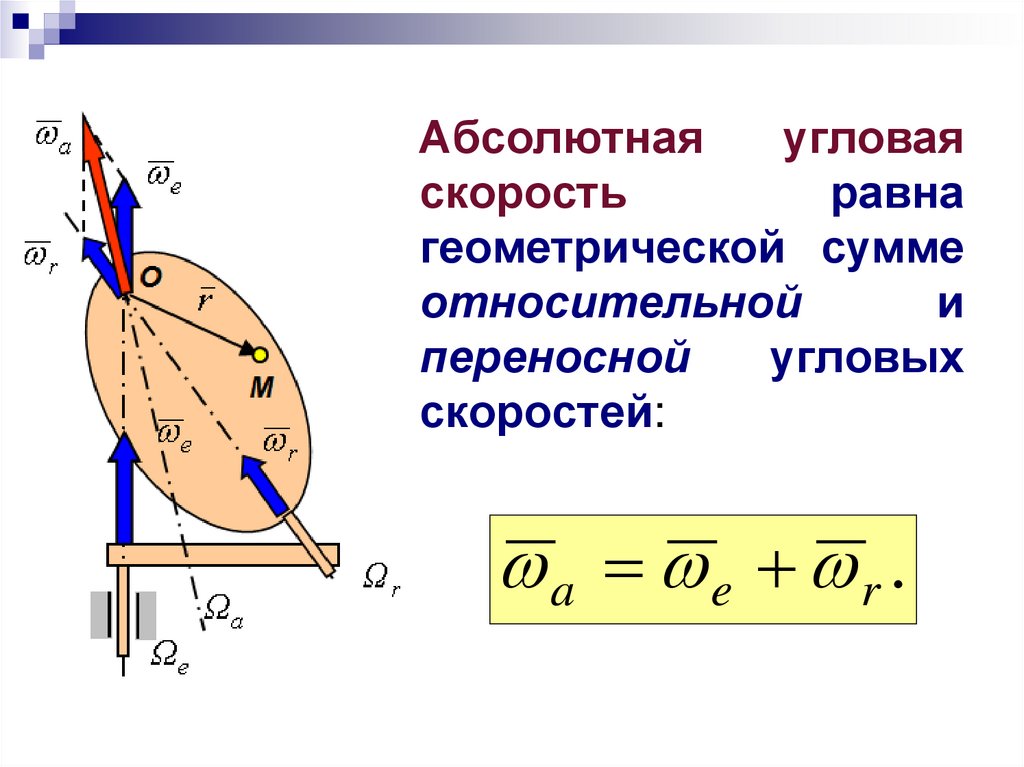
Абсолютная
угловая
скорость
равна
геометрической сумме
относительной
и
переносной
угловых
скоростей:
a e r .

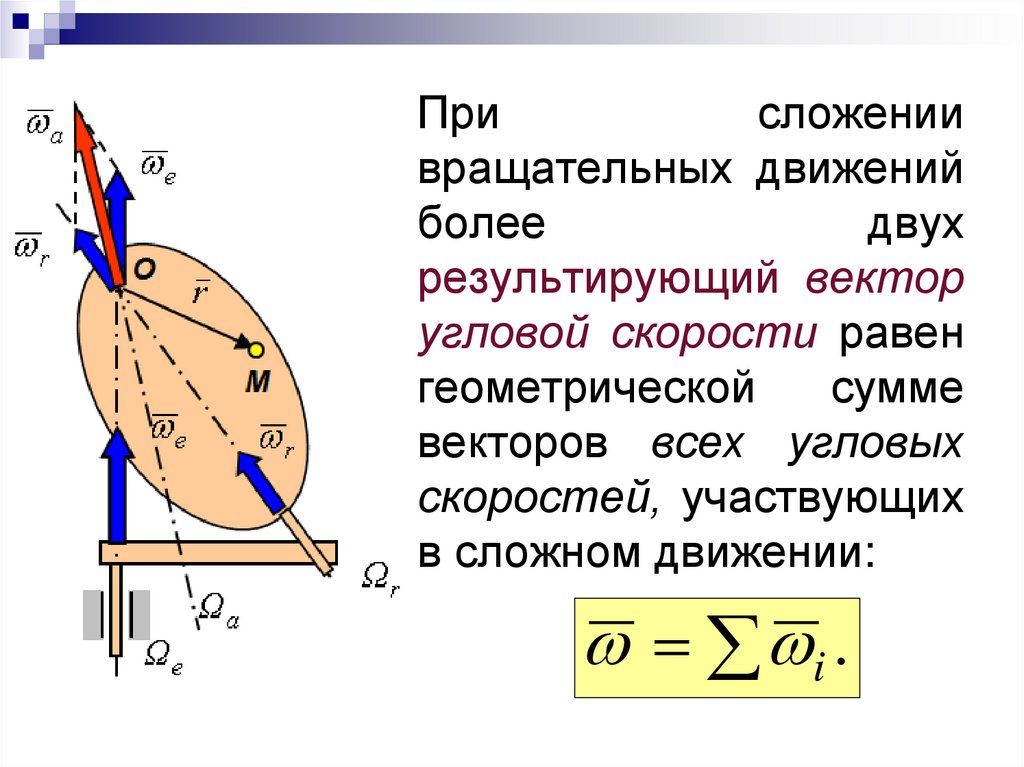
25.

При
сложении
вращательных движений
более
двух
результирующий вектор
угловой скорости равен
геометрической
сумме
векторов всех угловых
скоростей, участвующих
в сложном движении:
i .

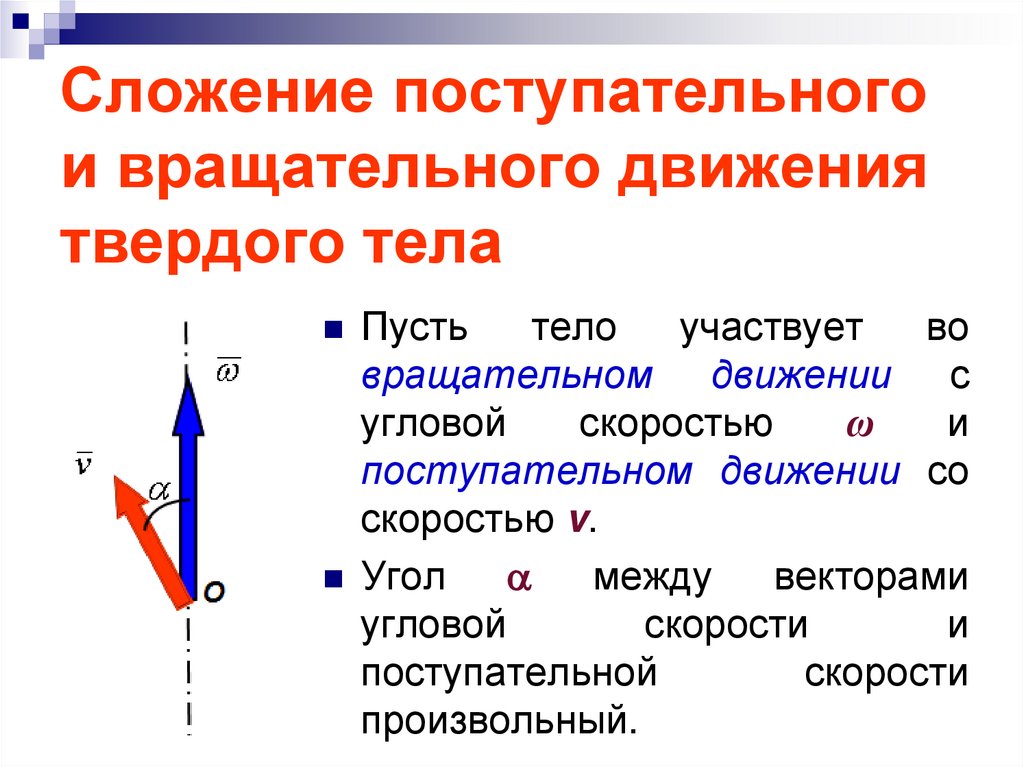
26. Сложение поступательного и вращательного движения твердого тела

Пусть
тело
участвует
во
вращательном движении с
угловой
скоростью
ω
и
поступательном движении со
скоростью v.
Угол
между
векторами
угловой
скорости
и
поступательной
скорости
произвольный.

27.

v
v*
O
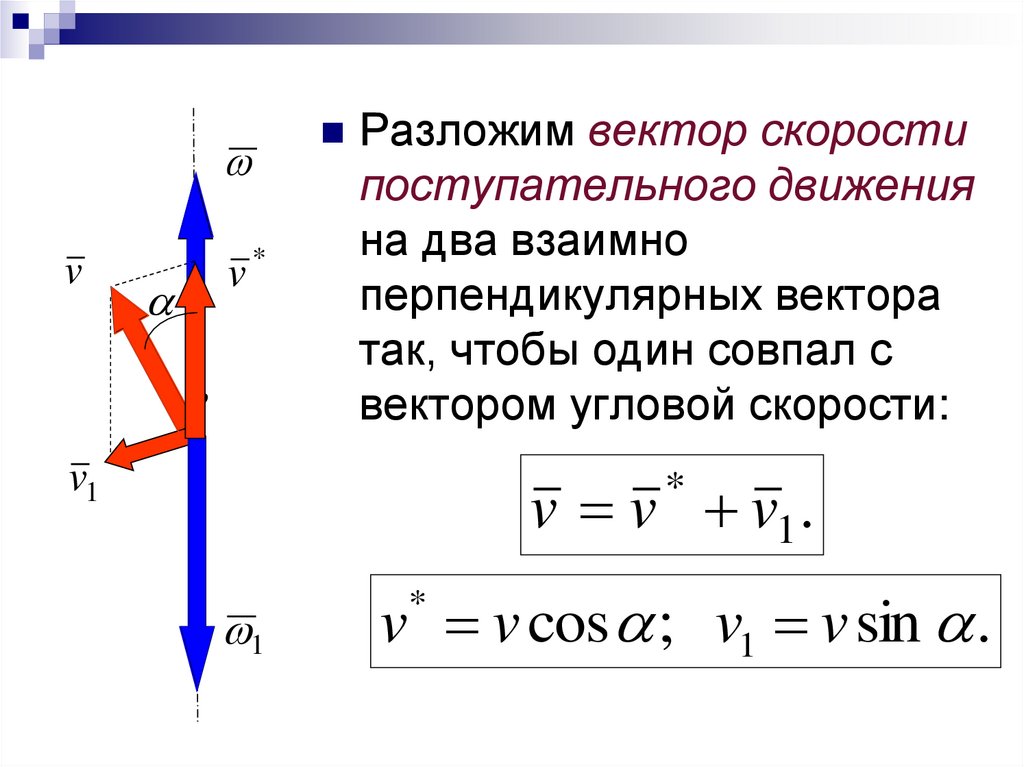
Разложим вектор скорости
поступательного движения
на два взаимно
перпендикулярных вектора
так, чтобы один совпал с
вектором угловой скорости:
v1
v v v1 .
*
1
v v cos ; v1 v sin .
*

28.

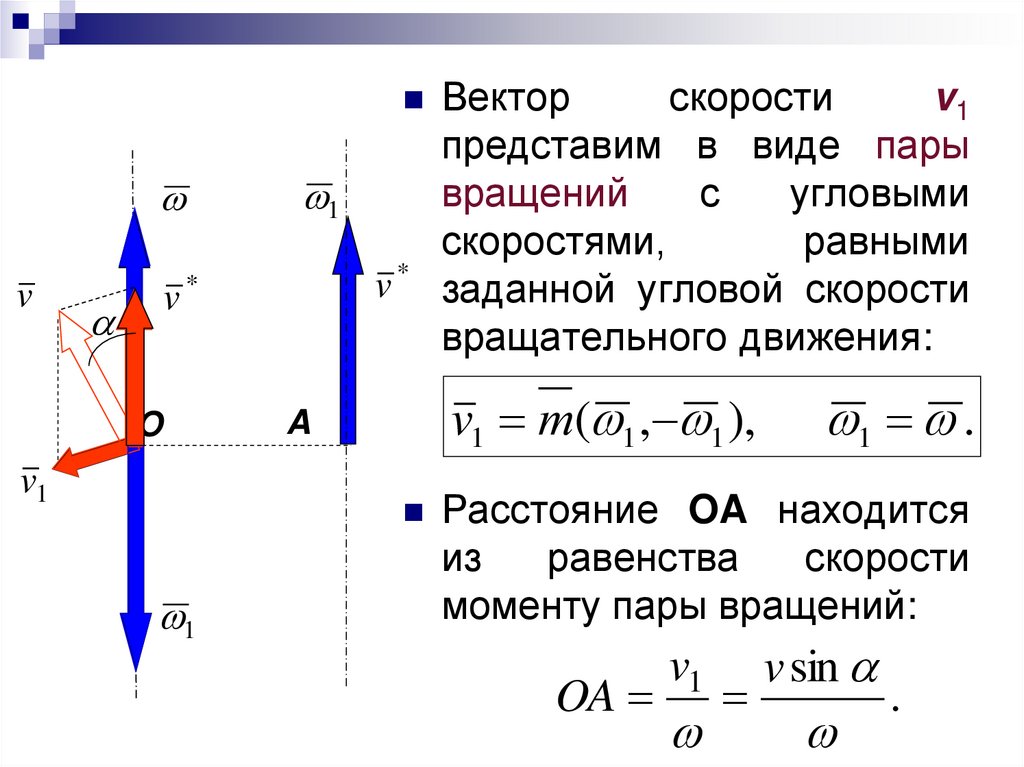
Вектор
1
v
v
v*
*
O
v1
A
скорости
v1
представим в виде пары
вращений
с
угловыми
скоростями,
равными
заданной угловой скорости
вращательного движения:
v1 т( 1 , 1 ),
1 .
Расстояние
1
OA находится
из
равенства
скорости
моменту пары вращений:
OA
v1
v sin
.

29.

Вектор
v
1
v*
O
v1
1
A
оставшейся
поступательной
скорости
v*, как свободный вектор
v * перенесем в точку A, а два
вектора угловых скоростей,
изображенные в точке O,
можно удалить, поскольку
они равны по величине,
направлены
по
одной
прямой в противоположные
стороны:
1 ( ) 0

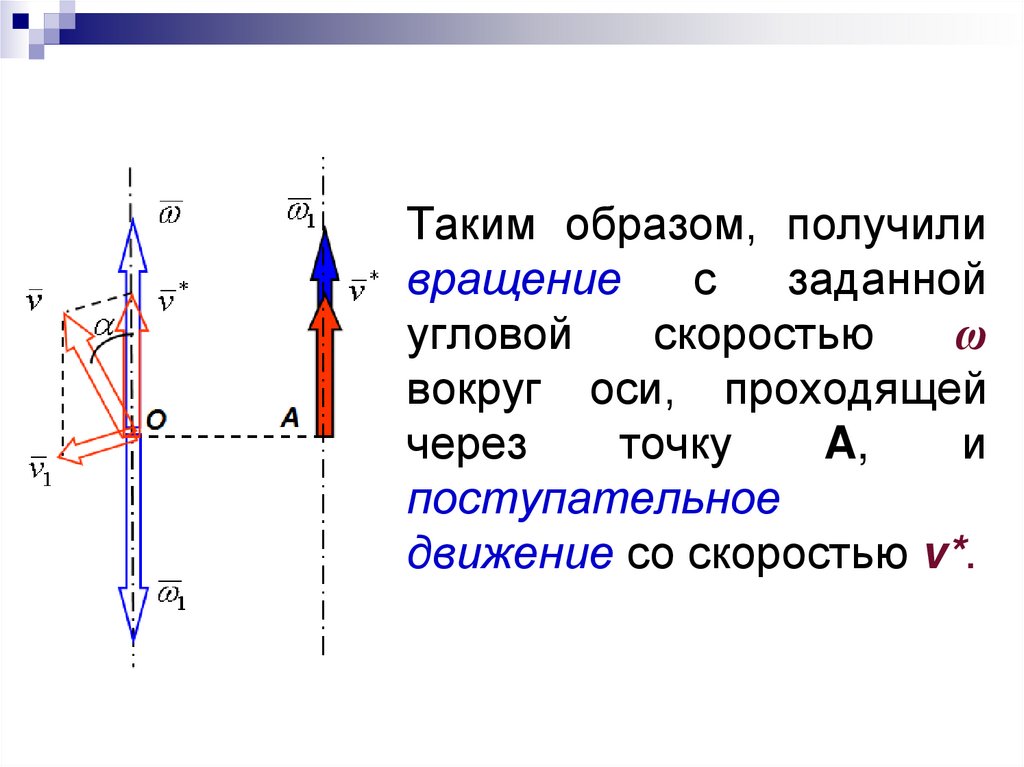
30.

Таким образом, получили
вращение
с
заданной
угловой
скоростью
ω
вокруг оси, проходящей
через
точку
A,
и
поступательное
движение со скоростью v*.

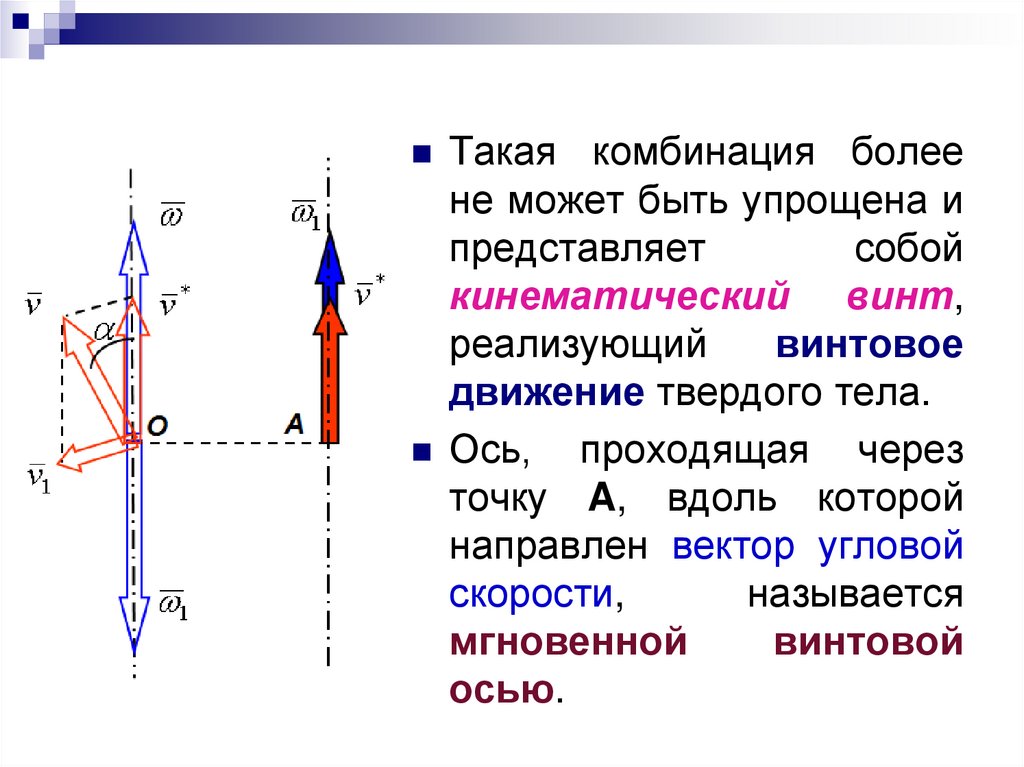
31.

Такая
комбинация более
не может быть упрощена и
представляет
собой
кинематический винт,
реализующий
винтовое
движение твердого тела.
Ось,
проходящая через
точку A, вдоль которой
направлен вектор угловой
скорости,
называется
мгновенной
винтовой
осью.

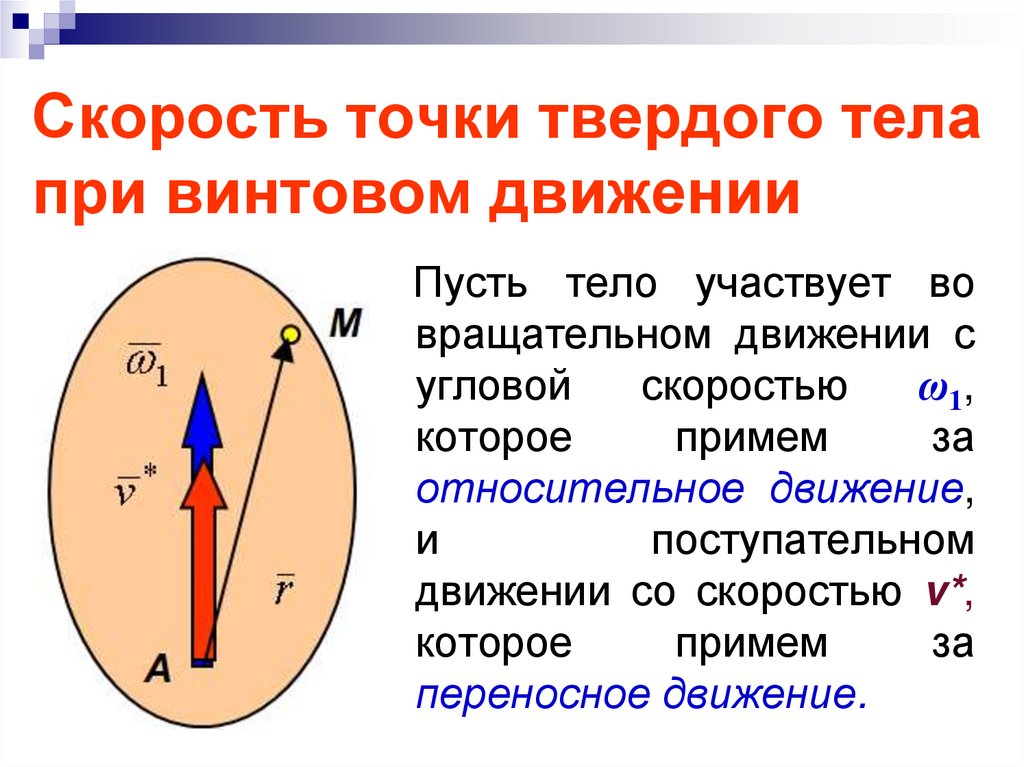
32. Скорость точки твердого тела при винтовом движении

Пусть тело участвует во
вращательном движении с
угловой
скоростью
ω1 ,
которое
примем
за
относительное движение,
и
поступательном
движении со скоростью v*,
которое
примем
за
переносное движение.

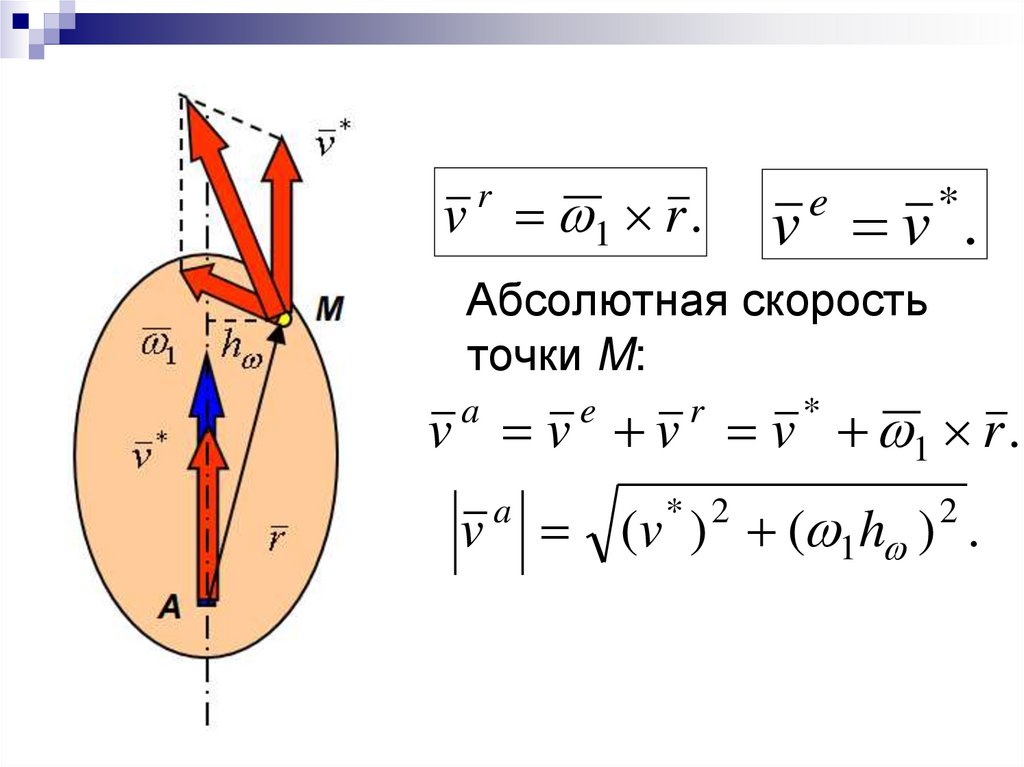
33.

v 1 r .
r
v v .
e
*
Абсолютная скорость
точки M:
v v v v 1 r .
a
v
e
a
r
*
(v ) ( 1h ) .
* 2
2

34.

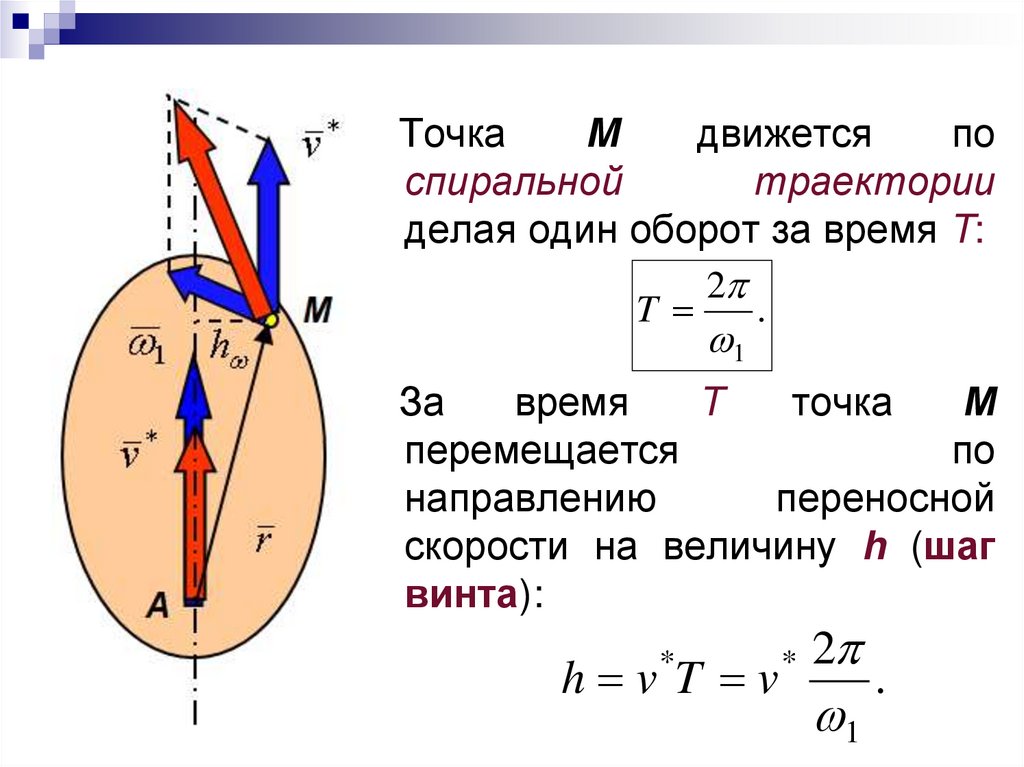
Точка
M
движется
по
спиральной
траектории
делая один оборот за время T:
2
T
.
1
За
время
T
точка
М
перемещается
по
направлению
переносной
скорости на величину h (шаг
винта):
h v T v
*
* 2
1
.

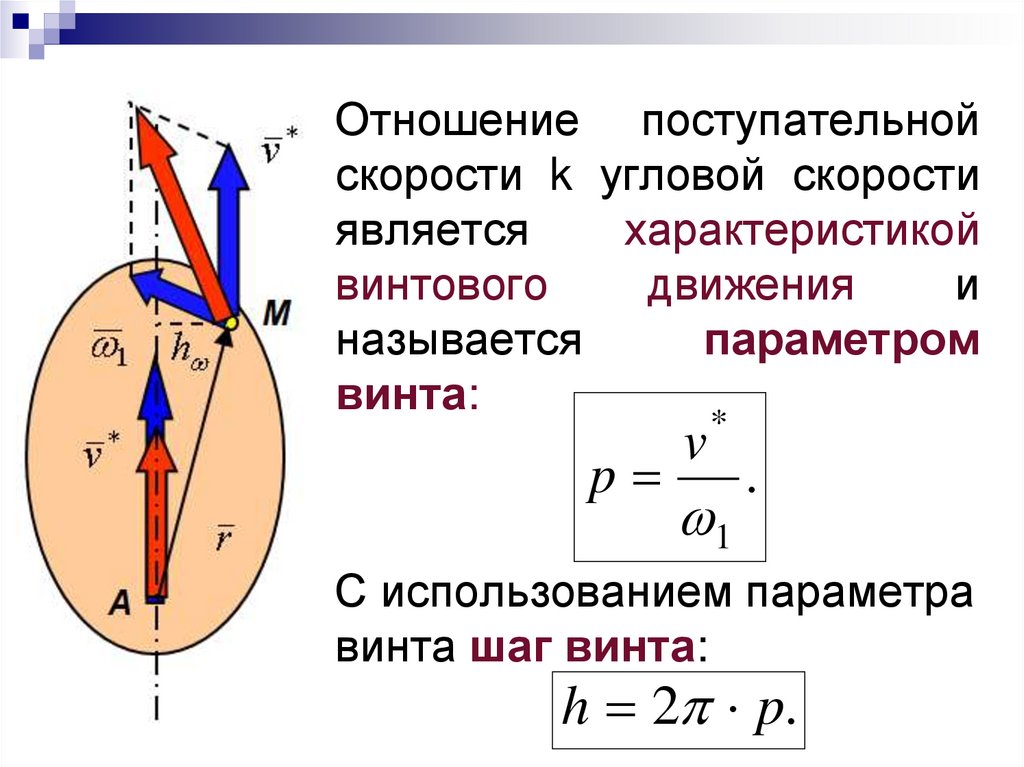
35.

Отношение поступательной
скорости k угловой скорости
является
характеристикой
винтового
движения
и
называется
параметром
винта:
p
v
*
1
.
С использованием параметра
винта шаг винта:
h 2 p.

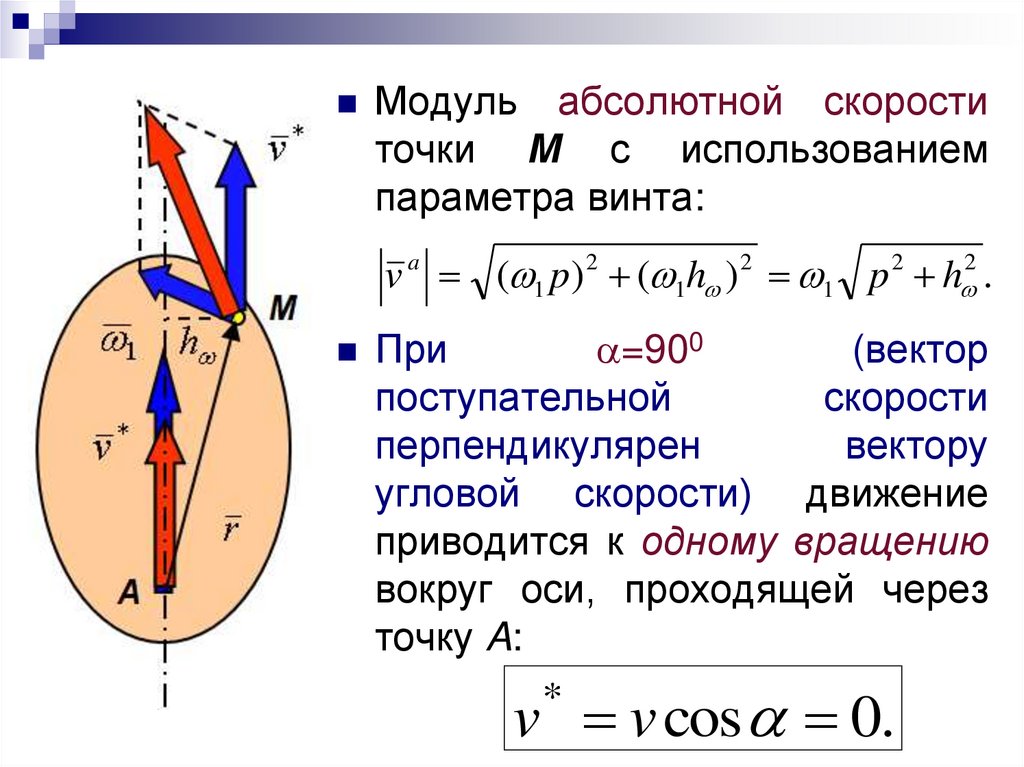
36.

Модуль
абсолютной скорости
точки M с использованием
параметра винта:
v a ( 1 p) 2 ( 1h ) 2 1 p 2 h 2 .
=900
(вектор
поступательной
скорости
перпендикулярен
вектору
угловой скорости) движение
приводится к одному вращению
вокруг оси, проходящей через
точку A:
*
При
v v cos 0.

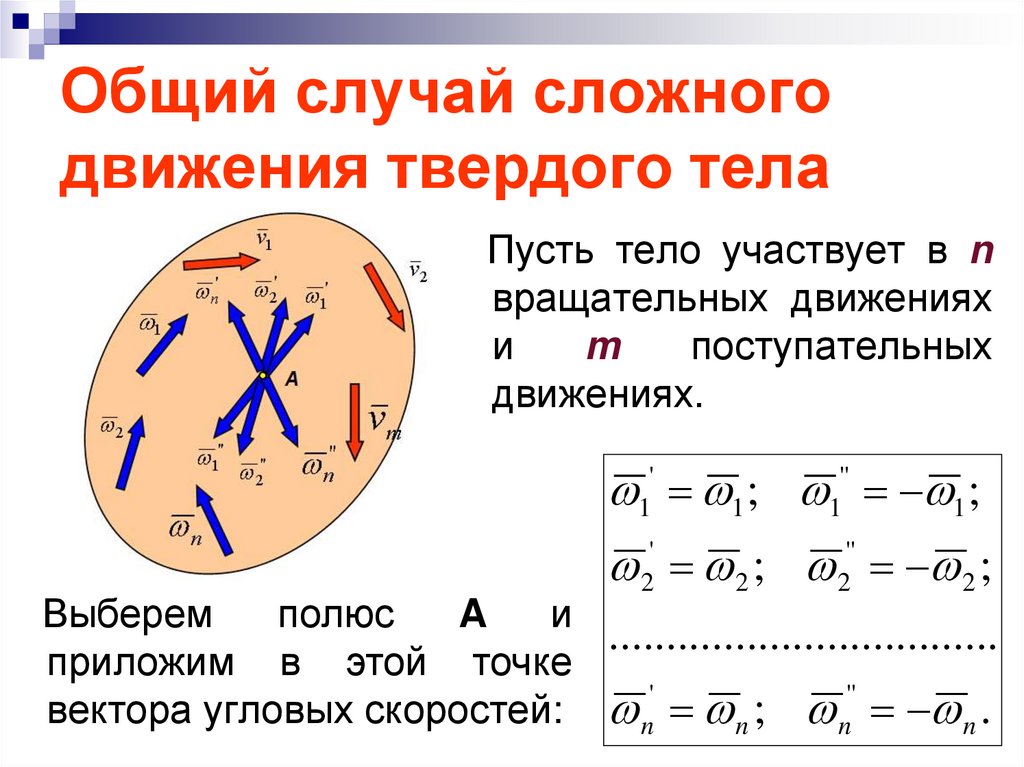
37. Общий случай сложного движения твердого тела

Пусть тело участвует в n
вращательных движениях
и
m
поступательных
движениях.
1' 1 ; 1'' 1 ;
2' 2 ; 2'' 2 ;
Выберем
полюс
A
и
..................................
приложим в этой точке
'
''
вектора угловых скоростей: n n ; n n .

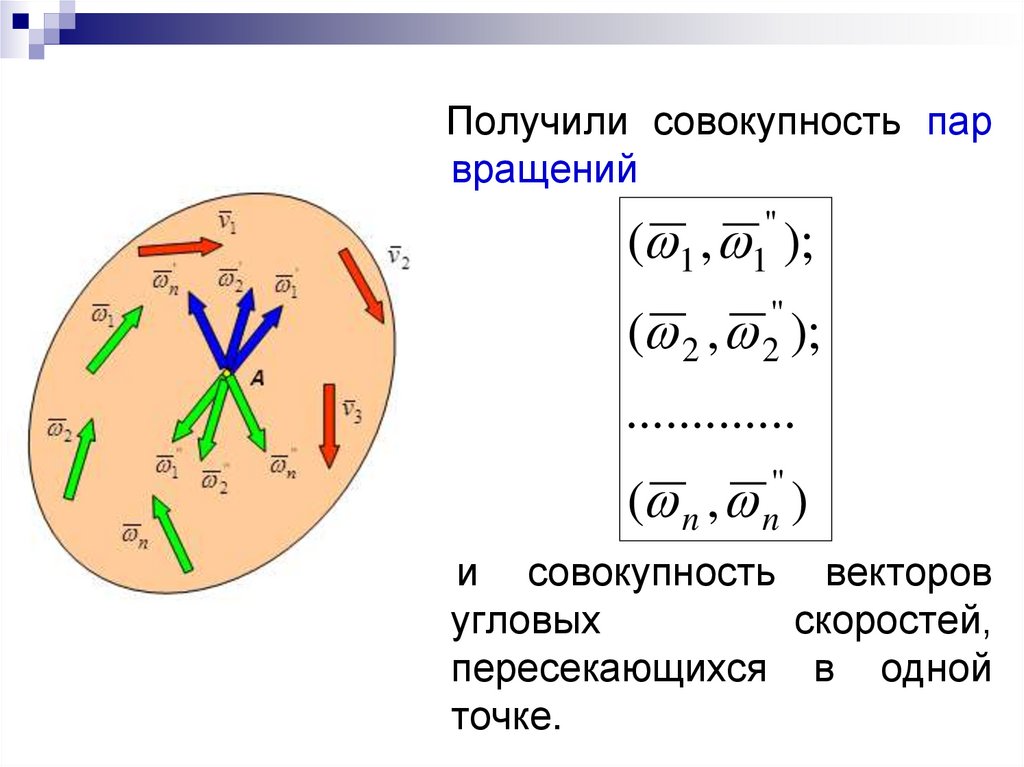
38.

Получили совокупность пар
вращений
''
( 1 , 1 );
''
( 2 , 2 );
.............
''
( n , n )
и совокупность векторов
угловых
скоростей,
пересекающихся в одной
точке.

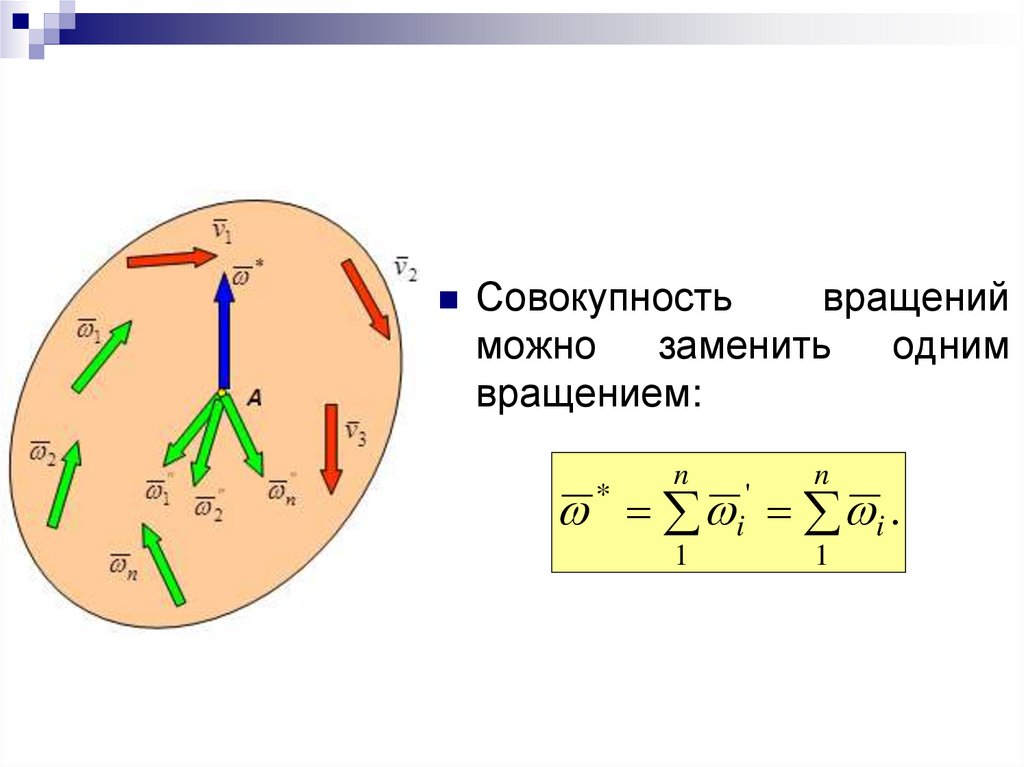
39.

Совокупность
вращений
можно
заменить
одним
вращением:
n
n
i i .
*
1
'
1

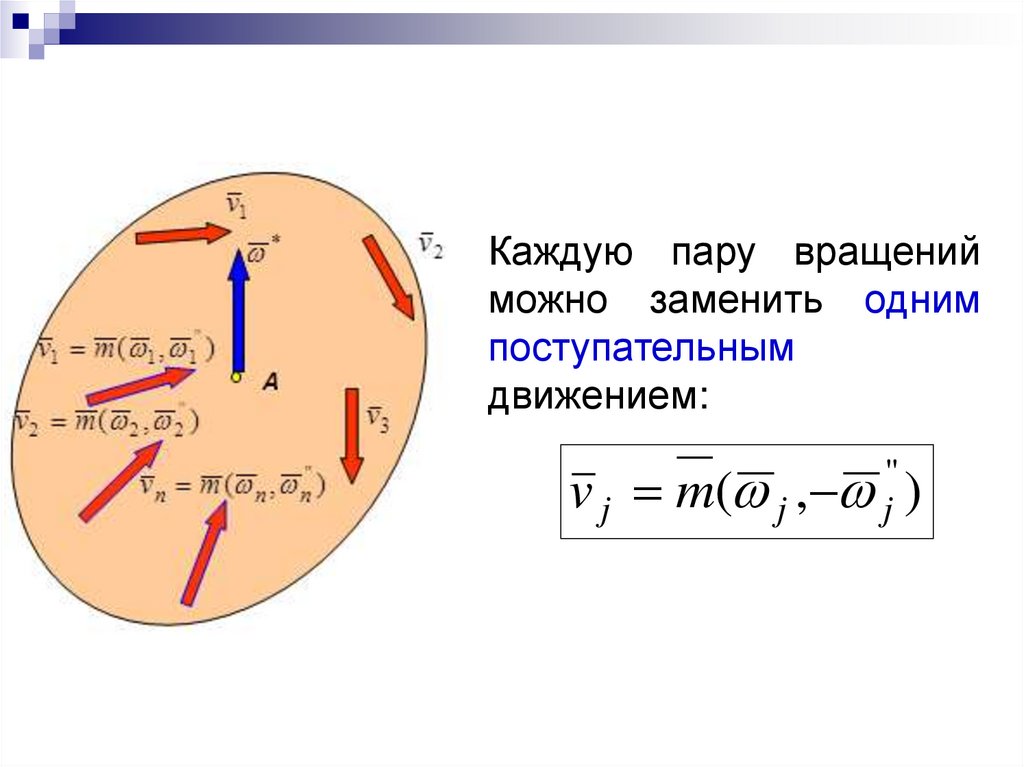
40.

Каждую пару вращений
можно заменить одним
поступательным
движением:
''
v j m( j , j )

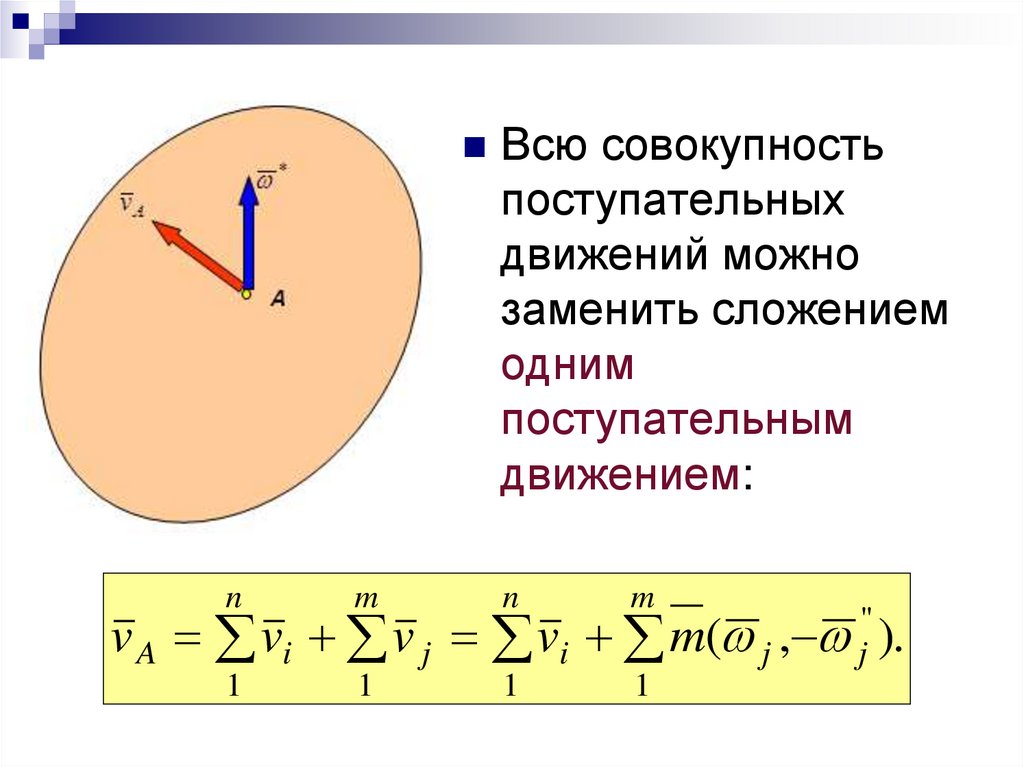
41.

Всю совокупность
поступательных
движений можно
заменить сложением
одним
поступательным
движением:
n
m
n
m
1
1
1
1
v A vi v j vi
''
m( j , j ).

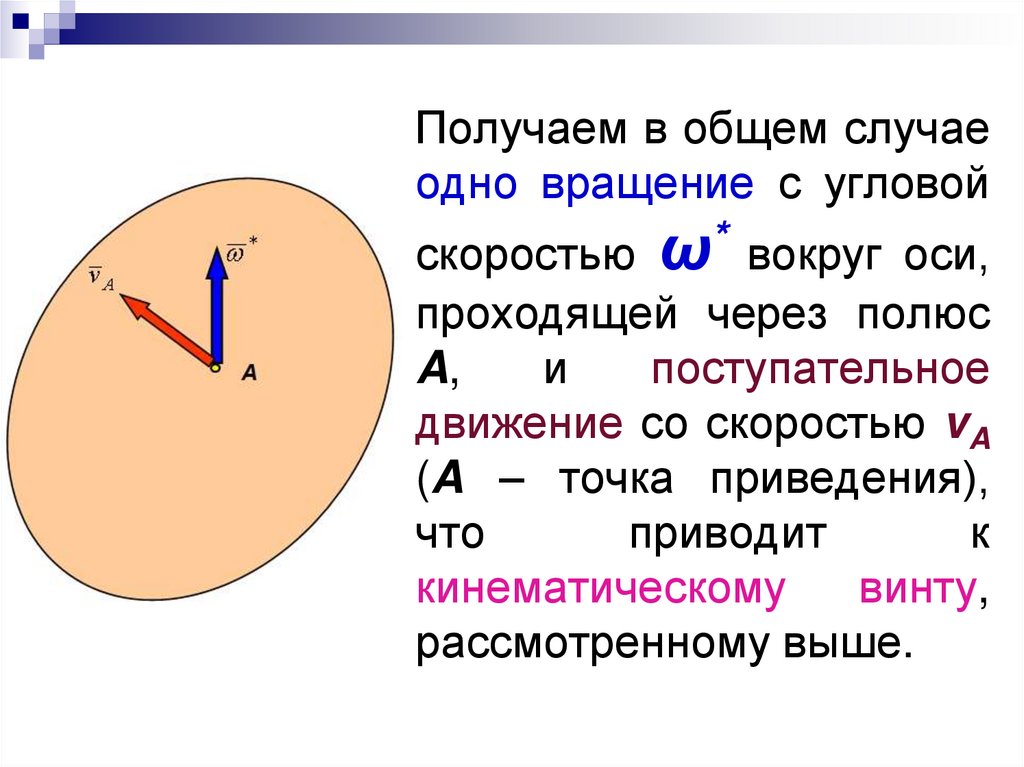
42.

Получаем в общем случае
одно вращение с угловой
скоростью ω* вокруг оси,
проходящей через полюс
A,
и
поступательное
движение со скоростью vA
(A – точка приведения),
что
приводит
к
кинематическому
винту,
рассмотренному выше.

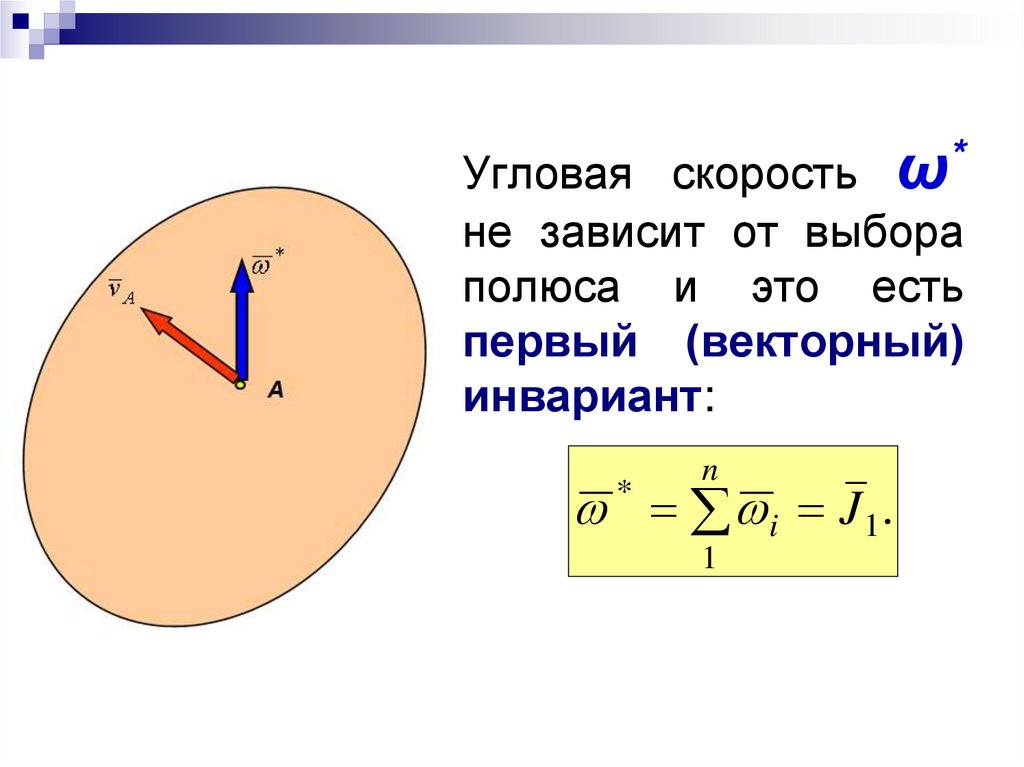
43.

Угловая скорость ω*
не зависит от выбора
полюса и это есть
первый (векторный)
инвариант:
n
i J 1 .
*
1

44.

Скорость поступательного
движения
зависит
от
выбора
полюса,
но
существует
скалярная
величина, связанная с
поступательной скоростью,
инвариантная к выбору
полюса.

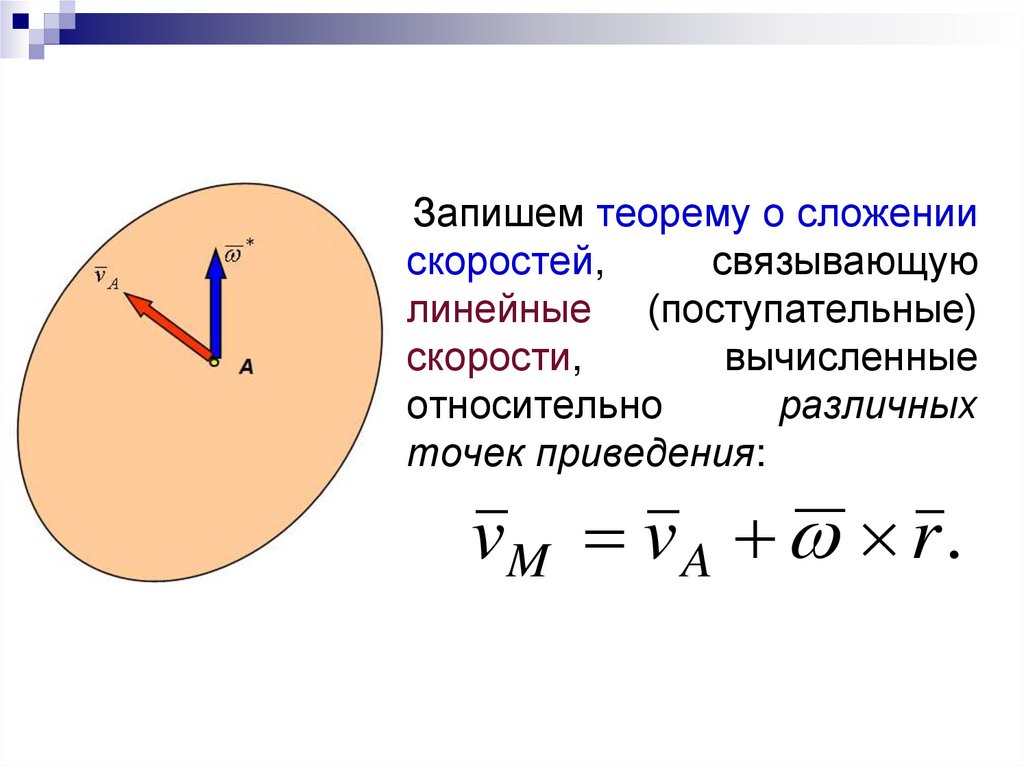
45.

Запишем теорему о сложении
скоростей,
связывающую
линейные (поступательные)
скорости,
вычисленные
относительно
различных
точек приведения:
vM v A r .

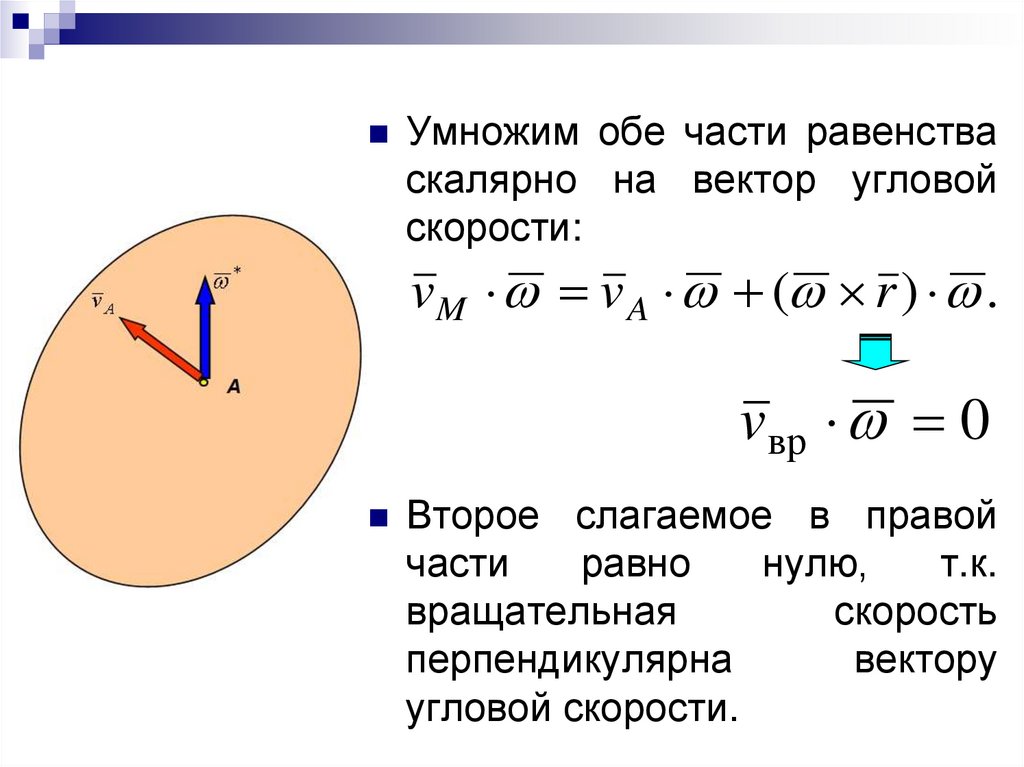
46.

Умножим обе части равенства
скалярно на вектор угловой
скорости:
vM v A ( r ) .
vвр 0
Второе
слагаемое в правой
части
равно
нулю,
т.к.
вращательная
скорость
перпендикулярна
вектору
угловой скорости.

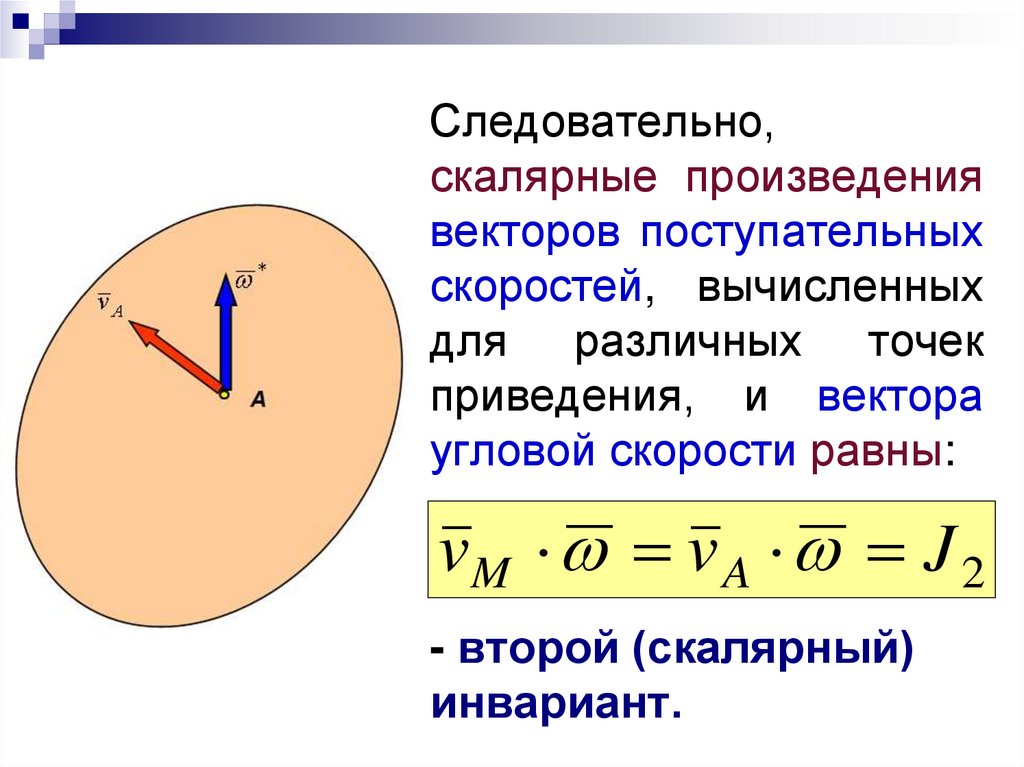
47.

Следовательно,
скалярные произведения
векторов поступательных
скоростей, вычисленных
для различных точек
приведения, и вектора
угловой скорости равны:
vM v A J 2
- второй (скалярный)
инвариант.

48.

Раскрывая скалярные произведения получаем:
vM cos(vM , ) v A cos(v A , ),
Откуда:
v M cos(v M , ) v A cos(v A , ) v
- минимальная поступательная скорость.
*

49.

Итак, угловые скорости в кинематике
складываются так же, как силы в статике
(эти векторы являются скользящими
векторами).
Поступательные
скорости
в
кинематике складываются так же, как
моменты пар в статике (эти векторы
являются свободными векторами).

50. Пример (кинематические инварианты движения твердого тела)

В
некоторый момент времени известны
координаты и скорости трех точек A, B, C
твердого тела, движущегося в пространстве:
A = (2, 1, 0), B = (1, 1, 3), C = (1, 0, 1);
V A (4, 4, 1), V B (16, 23, 5), V C (1, 15, 9).
Найти
кинематические
движения.
инварианты

51. Решение

Кинематические инварианты движения:
1. Первый инвариант – угловая скорость.
2. Второй инвариант – скалярное
произведение скорости точки тела на
его угловую скорость.
Определяем угловую скорость тела.
Пусть точка A – полюс.

52.

Кинематические
соотношения
скоростями точек твердого тела:
VB VA AB, VC VA AC,
где
AB ( 1,0,3), AC ( 1, 1,1)
Уравнение (*) принимает вид
j
k
16 4 i
23 4 x y z ;
5 1
1 0 3
между
(*)
j
k
1 4 i
15 4 x y z .
9 1
1 1 1
Получаем ωx = –4 c–1, ωy = 4 c–1 , ωz = –7 c–1

53.

Первый инвариант
J1 x2 y2 z2 9 c 1
Второй инвариант
м
J 2 VA xVAx yVAy zVAz 16 16 7 7 2
с
или
м
J 2 VB xVBx yVBy zVBz 64 92 35 7 2
с
м
J 2 VC xVCx yVCy zVCz 4 60 63 7 2
с

54.

Проверим теорему о равенстве проекций
векторов скоростей точек на ось их
соединяющую
VA AB 4 ( 1) 4 0 1 3 1,
VB AB 16 ( 1) 23 0 5 3 1.
Аналогично для других скоростей
VA AC VC AC 7,
VB BC VC BC 33.

55.

Данное
движение
тела
является
мгновенно-винтовым, т.к. J2 ≠ 0. Если бы
второй инвариант был бы равен нулю, то
движение было бы вращательным или
мгновенно-вращательным. Для плоского
движения, например, скорости всегда
перпендикулярны
вектору
угловой
скорости, и J 2 V 0.

56.

Для мгновенно-винтового движения тела
можно найти мгновенную винтовую ось,
все точки которой имеют скорость,
направленную вдоль вектора угловой
скорости.
Уравнение оси:
Vx y z z y
x
где
P
J2
2
V y z x x z
y
Vz x y y x
z
P,
– шаг кинематического винта.

57.

Все способы преобразования сил и
пар
сил
в
статике
подобны
преобразованиям
скоростей
твердого тела в кинематике.
И в статике, и в кинематике при
приведении системы в общем случае
получается статический винт (динама),
и соответственно кинематический винт.

58.

Как в статике, так и в кинематике
существуют
соответствующие
инвариантные величины (помечены
звездочками)
и
их
производные
(главный минимальный момент и
минимальная
поступательная
скорость).

59. Вопросы

Что понимается под плоским движением
АТТ?
Уравнение плоского движения АТТ.
Разложение плоского движения АТТ на
поступательное
и
вращательное
движение.
Угловая скорость и угловое ускорение
АТТ.

60. Вопросы

Скорость точки тела при плоском
движении.
Мгновенный центр вращения.
Ускорения точек АТТ при плоском
движении.
Мгновенный центр ускорений.
Кинематические инварианты.