Сферическое движение твердого тела

1.

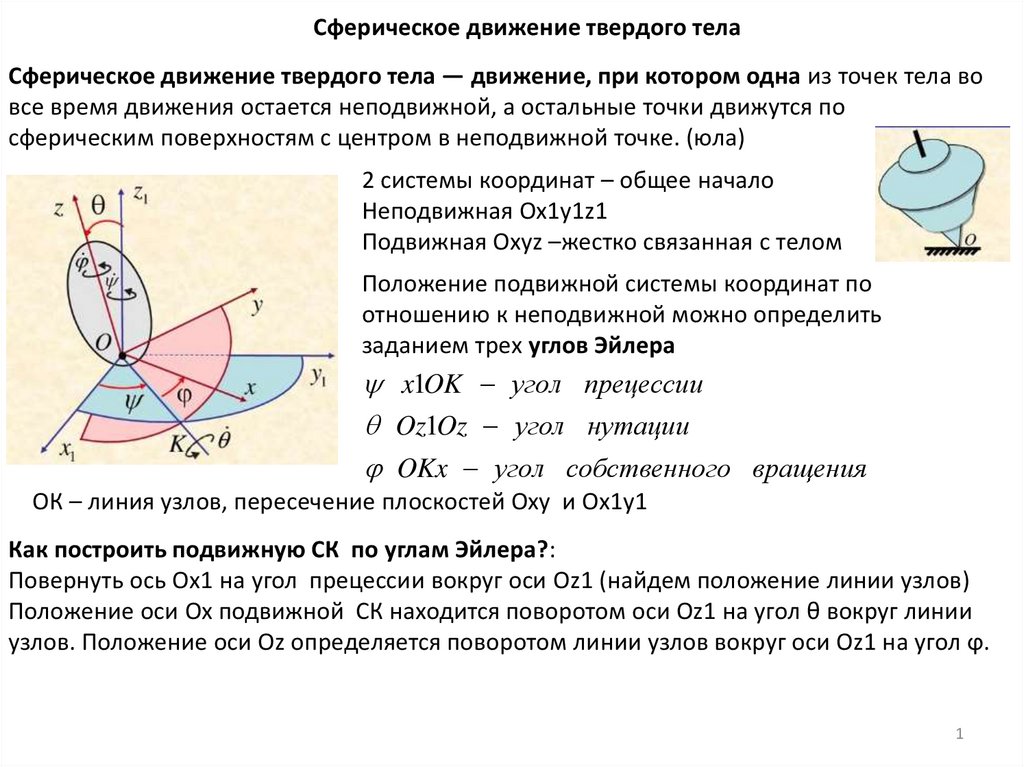
Сферическое движение твердого тела
Сферическое движение твердого тела — движение, при котором одна из точек тела во
все время движения остается неподвижной, а остальные точки движутся по
сферическим поверхностям с центром в неподвижной точке. (юла)
2 системы координат – общее начало
Неподвижная Ox1y1z1
Подвижная Oxyz –жестко связанная с телом
Положение подвижной системы координат по
отношению к неподвижной можно определить
заданием трех углов Эйлера
x1OK угол прецессии
Oz1Oz угол нутации
OKx угол собственного вращения
ОК – линия узлов, пересечение плоскостей Oxy и Ox1y1
Как построить подвижную СК по углам Эйлера?:
Повернуть ось Ох1 на угол прецессии вокруг оси Оz1 (найдем положение линии узлов)
Положение оси Oх подвижной СК находится поворотом оси Oz1 на угол θ вокруг линии
узлов. Положение оси Oz определяется поворотом линии узлов вокруг оси Oz1 на угол ϕ.
1

2.

Изменение углов Эйлера во времени – закон
сферического движения твердого тела
t , t , t
Сферическое движение можно рассматривать как три
одновременно происходящих вращения вокруг оси Oz1,
линии узлов ОК и оси Oz.
Мерами изменения углов Эйлера являются соответствующие угловые скорости:
1 t , 2 t , 3 t
Мгновенная ось вращения — геометрическое место точек
тела, скорости которых в данный момент времени равны
нулю. (Существование мгновенной оси можно
проиллюстрировать на примере качения без проскальзывания
подвижного конуса по неподвижному. Очевидно, что
мгновенной осью является линия контакта между конусами.)
Для определения положение мгновенной оси, достаточно найти
какую-либо точку C твердого тела, скорость которой в данный
момент равна нулю. Прямая, проходящая через точку C и
неподвижную точку O, будет мгновенной осью вращения тела.
2

3.

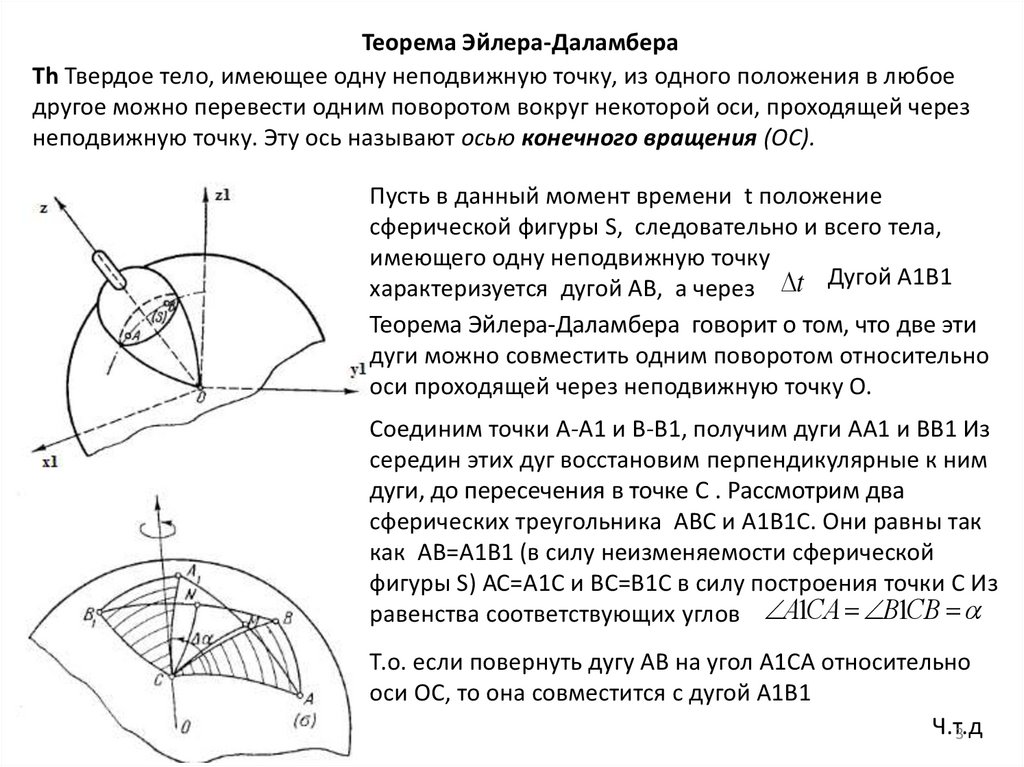
Теорема Эйлера-Даламбера
Th Твердое тело, имеющее одну неподвижную точку, из одного положения в любое
другое можно перевести одним поворотом вокруг некоторой оси, проходящей через
неподвижную точку. Эту ось называют осью конечного вращения (ОС).
Пусть в данный момент времени t положение
сферической фигуры S, следовательно и всего тела,
имеющего одну неподвижную точку
характеризуется дугой АВ, а через t Дугой А1В1
Теорема Эйлера-Даламбера говорит о том, что две эти
дуги можно совместить одним поворотом относительно
оси проходящей через неподвижную точку О.
Соединим точки А-А1 и В-В1, получим дуги АА1 и ВВ1 Из
середин этих дуг восстановим перпендикулярные к ним
дуги, до пересечения в точке С . Рассмотрим два
сферических треугольника АВС и А1В1С. Они равны так
как АВ=А1В1 (в силу неизменяемости сферической
фигуры S) АС=А1С и ВС=В1С в силу построения точки С Из
равенства соответствующих углов А1СА В1СВ
Т.о. если повернуть дугу АВ на угол А1СА относительно
оси ОС, то она совместится с дугой А1В1
Ч.т.д
3

4.

1. Перевод твердого тела, имеющего одну неподвижную точку, из одного
положения в другое за какой-то промежуток времени одним поворотом
относительно конечной оси вращения не соответствует действительном
перемещению тела.
2. Но если t 0 , то перемещение совершаемое поворотом относительно
конечной оси на угол будет приближаться к действительному
перемещению, а конечная ось вращения будет приближаться к своему
предельному положению – мгновенной оси вращения
4

5.

Скорость и ускорение точки тела, совершающего сферическое движение
Th (Эйлера) Скорость любой точки тела при его сферическом движении находится как
вращательная вокруг мгновенной оси вращения с угловой скоростью, равной
геометрической сумме угловых скоростей составляющих вращений:
v r
1 2 3 - Мгновенная угловая скорость
r
- Радиус вектор точки тела, проведенный через неподвижный центр
Рассмотрим сложение двух вращательных движений (угол θ зафиксируем).
По теореме сложения скоростей при сложном движении точки принимая вращение с
угловой скоростью ω1 за переносное, вращение с у.с. ω3 за относительное получим
v vr ve По формуле Эйлера vr 3 r v e 1 r v 3 1 r
3 1 - Абсолютная угловая скорость в случае сложения двух вращательных
движений
5

6.

Так как в общем случае сферического движения тело одновременно участвует в трех
вращениях, абсолютная угловая скорость определяется равенством 1 2 3
Принимаем результат предыдущего сложения двух вращательных движений за
переносное движение, а вращение с угловой скоростью ω2 за относительное.) Скорость
любой точки тела, совершающего сферическое движение, находится по формуле Эйлера:
v r
Из определения векторного произведения следует, что если векторы абсолютного
углового ускорения и радиус-вектор точки направлены по одной прямой, то v = 0. Это
доказывает существование мгновенной оси вращения, положение которой совпадает с
направлением вектора мгновенной угловой скорости. При известном положении
мгновенной оси вращения модули скоростей точек тела определяются формулой:
v = ωh.
6

7.

Кинематические уравнения Эйлера в подвижной системе координат
Аналитический способ задания скорости.
1. Найдем проекции радиус-вектора и мгновенной угловой скорости произвольной токи
тела на оси подвижной СК Oxyz
r rx , ry , rz
1 2 3
1 направлена по Оz1
2 направлена по ОK проекция на Оz 0
3 направлена по Оz (отлична от нуля только проекция на Оz )
1 1 Sin Sin , 1 Sin Cos , 1 Cos
2 2 Cos , 2 Sin , 0
3 0, 0, 3
1 Sin Sin 2 Cos , 1 Sin Cos 2 Sin , 1 Cos 3
7

8.

2. Записываем векторное произведение в координатной форме
1 t ,
i
j k
v r x y z
rx ry rz
учитывая
2 t ,
3 t
получим
vx rz Sin Cos Sin ry Cos
v y rx Cos rz Sin Sin Cos
Кинематические уравнения Эйлера
vz ry Sin Sin Cos rx Sin Cos Sin
8

9.

Угловая скорость / угловое ускорение твердого тела при сферическом движении
Мгновенная угловая скорость твердого тела, при
сферическом движении, - скорость поворота тела вокруг
мгновенной оси.
Вектор мгновенной угловой скорости направлен по оси
мгновенной оси вращения в сторону, откуда поворот тела
виден происходящим против часовой стрелки.
Т.к. положение мгновенной оси вращения изменяется, то
вектор угловой скорости будет менять не только модуль но
и направление.
Вектор мгновенного углового ускорения – производная по
времени от вектора мгновенной угловой скорости, направлен
по касательной к годографу вектора угловой скорости.
ОЕ – мгновенная ось углового ускорения
9

10.

Вычисление углового ускорения
Модуль и направление углового ускорения вычисляются на основании проекций
мгновенной угловой скорости на неподвижные или подвижные оси (в зависимости от
задачи)
d y
d x
d
x
, y
, z z ,
dt
dt
dt
x2 y2 z2
y
x
Cos , x , Cos , y , Cos , z z
10

11.

Ускорение точек твердого тела, совершающего сферическое движение
Th Ривальса Ускорение любой точки твердого тела, совершающего сферическое
движение равно векторной сумме его вращательного и осестремительного
ускорения
a a вр a ос
dv d r d
dr
a
r r v a вр a ос
dt
dt
dt
dt
aос v r
a вр hE , hE r Sin ;
a ос 2 h , h r Sin ,
a
a вр не ортогонален a ос
a a 2 a a Cos a , a
2
вр
2
ос
вр
ос
вр
ос
hE h 2hE h 2 Cos a вр , a ос
2
2 2
Если мгновенная ось вращения тела неподвижна, то
a вр a ос , hE h R, a R 2 4
11