Similar presentations:
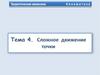
Сложные движения точки
1.
z1
z
o
1
x
1
y
1
o
x
y
Подвижная система координат
Неподвижная система координат
2.
Относительное движение:z
движение точки относительно
подвижной системы координат
1
Относительная траектория
Переносное движение:
z
движение подвижной системы
координат
относительно
неподвижной
o
1
x
1
y
1
o
y
Переносная траектория
x
Подвижная система координат
Неподвижная система координат
3.
Относительное движение:Абсолютная траектория
z
движение точки относительно
подвижной системы координат
1
Относительная траектория
Переносное движение:
z
движение подвижной системы
координат
относительно
неподвижной
o
Абсолютное движение:
1
x
1
движение точки относительно
неподвижной системы координат
y
1
o
y
Переносная траектория
x
Подвижная система координат
Неподвижная система координат
4.
zaa v
e
ae
ra
1
z
rr
o
1
x
r
e
y
1
1
o
x
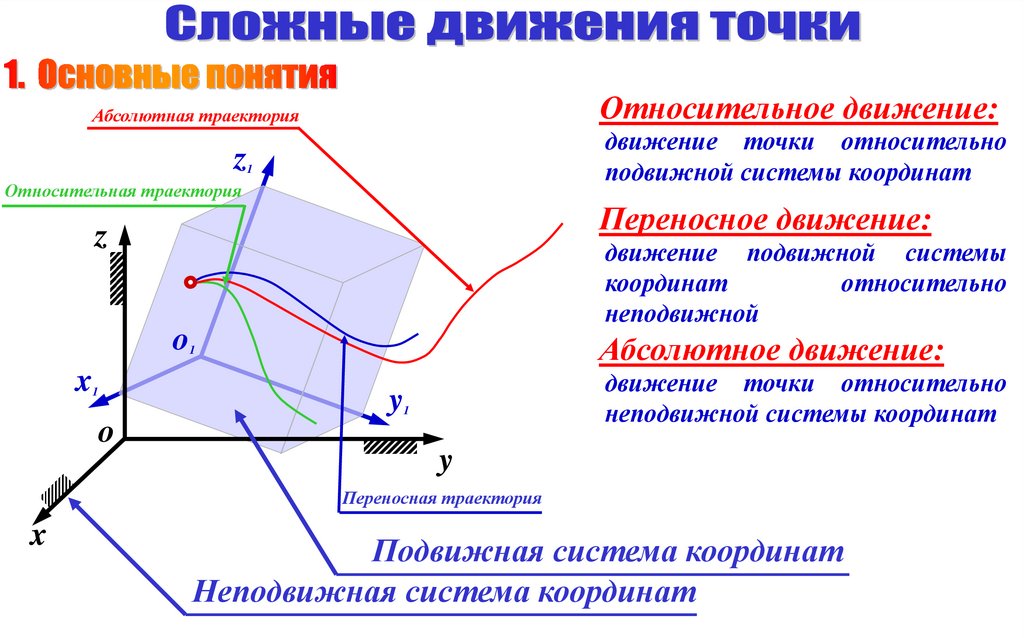
ra re rr
dra dre drr
;
dt
dt dt
y
va Относительное движение:
rr – радиус-вектор
относительного
движения;
vr – относительная скорость;
ar – относительное ускорение;
vr Переносное движение:
rе
a
–
радиус-вектор
движения;
r v – переносная скорость;
е
aе – переносное ускорение;
переносного
Абсолютное движение:
ra – радиус-вектор абсолютного
движения;
va – абсолютная скорость;
a – абсолютное ускорение;
va ve v r - Теорема о сложении скоростей
a
5.
Корабль идет курсом ЮВ со скоростью a узлов, при этом флюгер на мачте показывает ветер В.Корабль уменьшает скорость до a/2 узлов, флюгер на мачте показывает ветер СВ.
Определить направление и скорость ветра.
Решение: v v v ;
a
e
r
y
vк1
v a абсолютная скорость ( скорость ветра );
v e переносная скорость ( скорость корабля );
vr относительная скорость ( показания флюгера );
Положение 1: v v
в
к 1 vф 1 ;
vф1
vф2
vв
Положение 2: v v
в
к 2 vф 2 ;
vвx vк 1 cos 45 vф 1 ; vвx vк 2 cos 45 vф 2 cos 45 ;
vвy vк 1 sin 45 0 ;
vвy vк 2 sin 45 0 vф 2 sin 45 0 ;
vк2 vвx a 2 2 vф 1 ; vвx a 2 4 vф 2 2 2 ;
vк1 vвy a 2 2 ;
vвy a 2 4 vф 2 2 2 ;
vк2
a 2 2 a 2 4 vф 2 2 2 ; vф 2 a 2 ;
2
x
vвx 0 ; vв vвx
vвy2 a 2 2 узлов ;
0
Ответ:
0
0
vв a 2 2 узлов ; направление – с СЕВЕРА
6.
vevr
va
В кулисном механизме при качании кривошипа ОС вокруг оси О,
перпендикулярной плоскости рисунка, ползун А, перемещаясь вдоль кривошипа,
приводит в движение стержень ОВ, движущийся в вертикальных направляющих К.
Определить скорость движения ползуна А относительно кривошипа ОС в
функции от угловой скорости ω и угла поворота φ кривошипа. Расстояние ОК = l .
Решение: va ve vr ;
va абсолютная скорость ( скорость стержня ОВ );
ve переносная скорость ( скорость точки А кривошипа ОС );
vr относительная скорость ( скорость ползуна А относительно кривошипа ОС );
φ
ω
φ
O
ve OA;
vr ve tg ;
A
l
Ответ:
K
С
l
l
OA
;
ve
;
cos
cos
l
vr
tg ;
cos
l
vr
tg ;
cos
7.
z1z
~
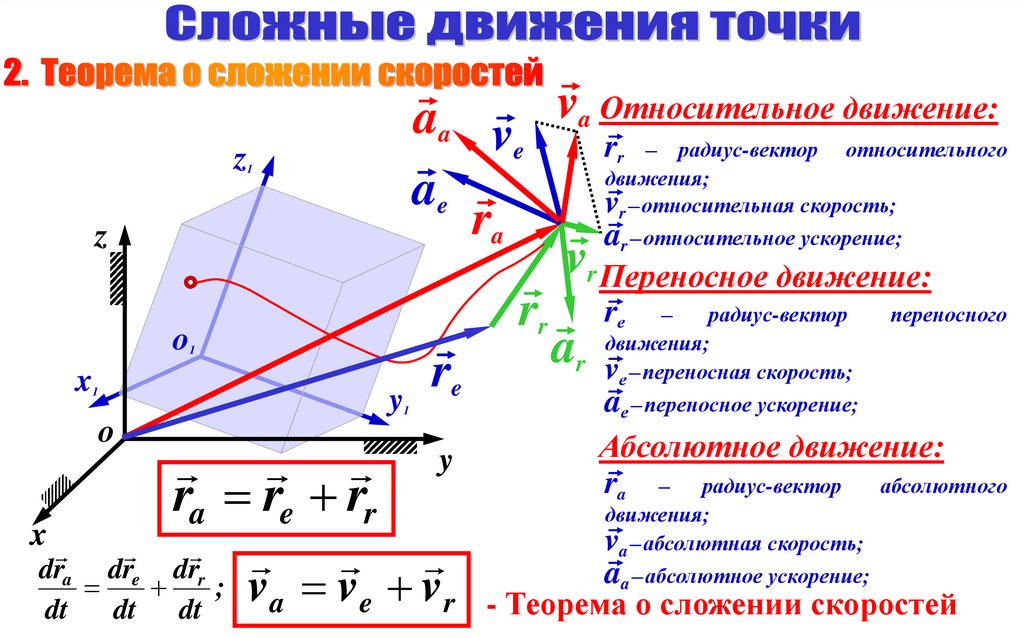
d R – локальная производная вектора
относительно
dt производная
подвижной системы координат;
dR – полная производная вектора
относительно
dt производная
неподвижной системы координат.
R
R
o1
y1
o
x1
x
y
В случае поступательного
переносного
движения
годографы вектора в подвижной
и
неподвижной
системе
координат
совпадают,
проекции
вектора
на
подвижные и неподвижные оси
совпадают, локальная и полная
производные вектора равны:
~
dR d R
dt
dt
8.
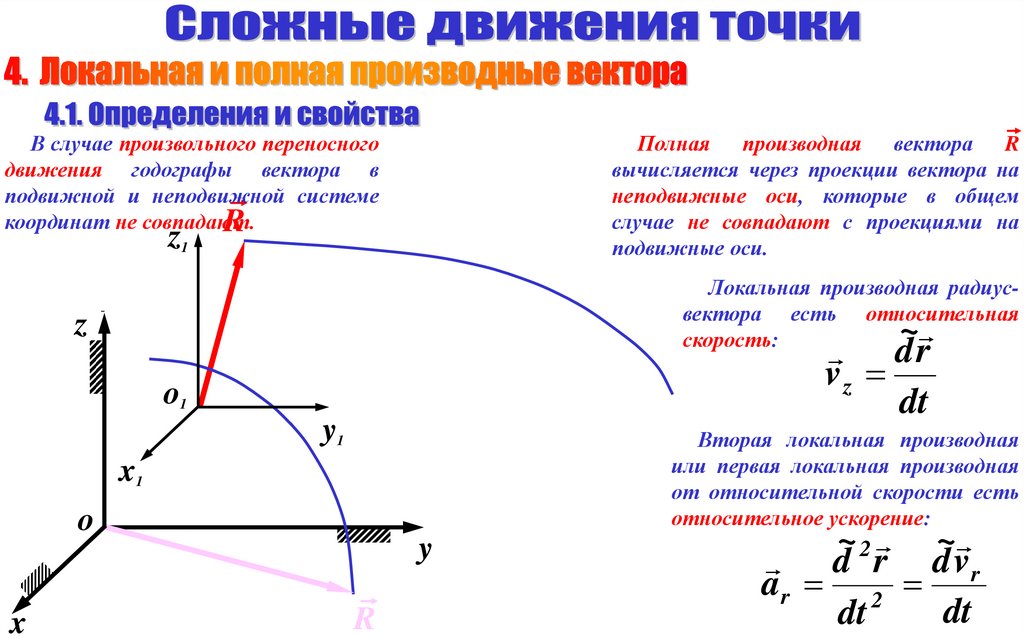
Полная производная вектора Rвычисляется через проекции вектора на
неподвижные оси, которые в общем
случае не совпадают с проекциями на
подвижные оси.
В случае произвольного переносного
движения годографы вектора в
подвижной и неподвижной системе
координат не совпадают.
R
z1
Локальная производная радиусвектора есть относительная
скорость:
~
dr
vz
dt
z
o1
y1
x1
o
x
y
R
Вторая локальная производная
или первая локальная производная
от относительной скорости есть
относительное ускорение:
2
r
r
2
~ ~
d r dv
a
dt
dt
9.
z1R
z
j1
o1
x1
o
x
k1
i1 y1
R x1 i1 y1 j1 z1 k1 ;
dR dx1
dy1
dz1
d i1
d j1
d k1
i1
j1
k 1 x1
y1
z1
;
dt
dt
dt
dt
dt
dt
dt
~
d R dx1
dy1
dz1
i1
j1
k1 ;
dt
dt
dt
dt
d i1
d j1
d k1
i1 ,
j1 ,
k1 ;
dt
dt
dt
~
dR d R
x1 i1 y1 j1 z1 k1 ;
dt
dt
~
y
dR d R
R – формула Бура
dt
dt
В моменты времени, когда вектор R коллинеарен (однонаправлен) вектору ω значение локальной
и полной производной совпадают.
10.
k1 Rz
i1
k x1
z1
aa
j1
ρ
o1
Ra
o
x
i
j
y
y1
R x1 i1 y1 j1 z1 k1 ; Ra xi yj zk ; Ra R ;
2
2
2
dRa d dR
d Ra d d R
;
;
a
a
a
2
2
2
r
e
a
dt
dt dt
dt
dt
dt
2
2
Абсолютное a d Ra ; Переносное a d ;
ae ускорение – a dt 2 ускорение – e dt 2
~
~
dR d R d R
R
, ω = 0, т.к. переносное
dt
dt движение –
dt
dR dx1 dy1 dz1
поступательное;
i1
j1 k1 ;
dt dt
dt
dt
~2
2
2
2
2
2
ar
d R d x 1 d y1 d z 1 d R d R
2 i1 2 j1 2 k1 ;
2 ar ;
2
2
dt
dt
dt
dt
dt
dt
vr
aa ae a r
11.
dvaaa
;
dt
d
va vr ve ; ve vO1 e R ; aa vr vO1 R ;
dt
dv
~
dvr
d
dvrr d vO1 d e dR
O1
e v r
R e
.
aa
e R
dt
dt
dt
dt
dt
dt
dt
~
~
dvr d vr dR d R
e vr ;
e R vr e R ;
dt
dt
dt
dt
~
d vr dvO1 d e
aa
R e e R 2 e vr
dt dt
dt
d R
vr e R .
dt
aK 2 e vr ̶ ускорение Кориолиса.
( ) ( )
ae aO1 ae ae ̶ переносное ускорение;
~
d vr
ar
̶ относительное ускорение;
dt
Кинематическая теорема Кориолиса ̶
Модуль ускорения Кориолиса:
ak 2 e Vr sin e ,Vr
aa ae ar aK
12.
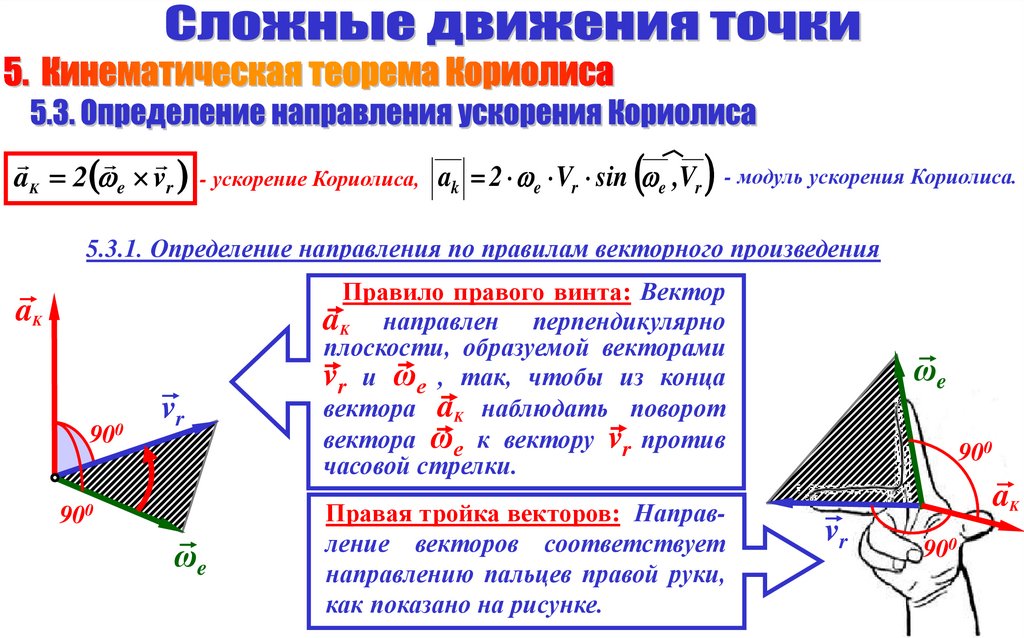
aK 2 e vr - ускорение Кориолиса, ak 2 e Vr sin e ,Vr- модуль ускорения Кориолиса.
5.3.1. Определение направления по правилам векторного произведения
aK
900
vr
900
ωe
Правило правого винта: Вектор
aK направлен перпендикулярно
плоскости, образуемой векторами
vr и ωе , так, чтобы из конца
вектора aK наблюдать поворот
вектора ωе к вектору vr против
часовой стрелки.
Правая тройка векторов: Направление векторов соответствует
направлению пальцев правой руки,
как показано на рисунке.
ωe
900
aK
vr
900
13.
aK 2 e vr - ускорение Кориолиса, ak 2 e Vr sin e ,Vr- модуль ускорения Кориолиса.
5.3.2. Определение направления по правилу Жуковского
ωe
aK
vr
900
900
900
Для определения направления
ускорения Кориолиса необходимо
спроектировать вектор vr на
плоскость,
перпендикулярную
вектору ωе , и повернуть на 900
в сторону вращения.
14.
5.3.3. Примеры определения направления ускорения Кориолисаω
С
Fна берег
Fна воду
З
vr
900
aK
Ю
В
15.
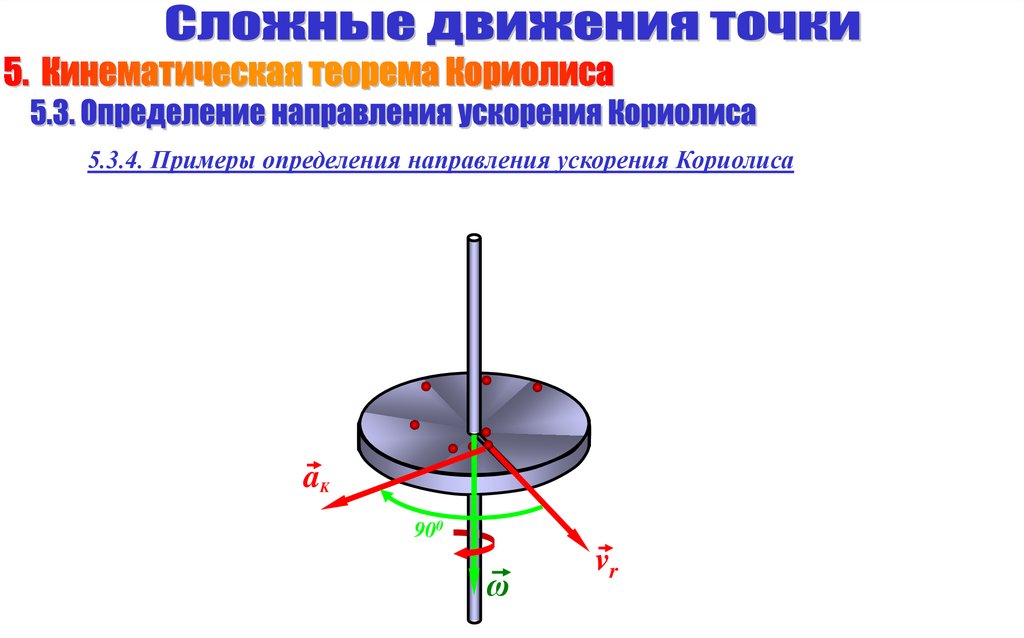
5.3.4. Примеры определения направления ускорения КориолисаaK
900
ω
vr
16.
5.3.5. Примеры определения направления ускорения Кориолисаvr
ωe
ωe
900
aK
17.
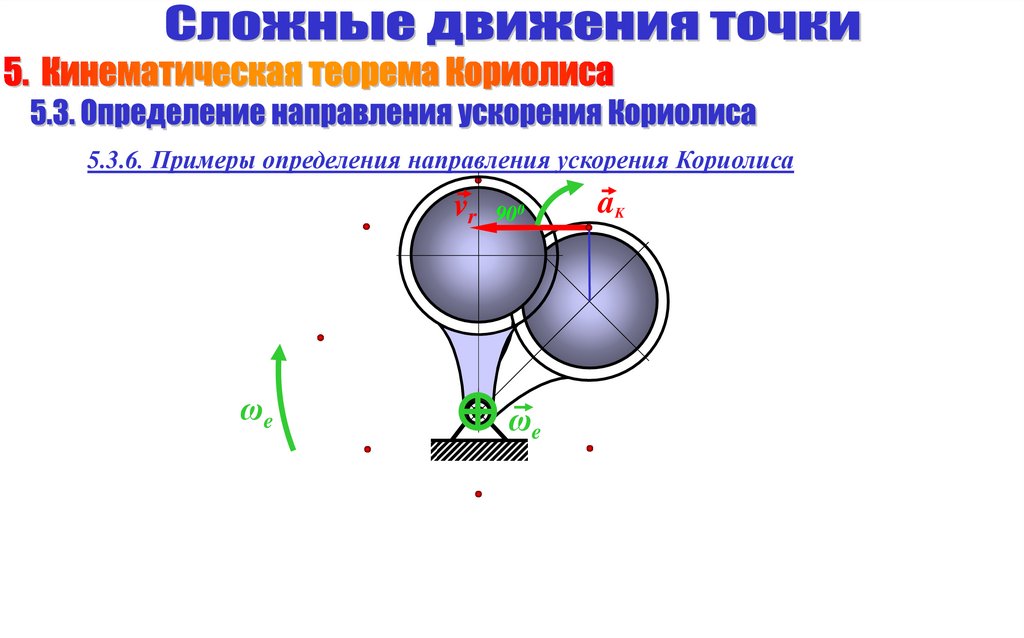
5.3.6. Примеры определения направления ускорения Кориолисаvr 900
ωe
ωe
aK
18.
На тележке, движущейся по горизонтали вправо с ускорением ae = 0.492 м/с2, установлен электрический мотор,ротор которого при пуске в ход вращается по закону φ = t2 [рад]. Радиус ротора R = 0.2 м.
Определить абсолютное ускорение точки А обода ротора при t = 1 с в положении, указанном на рисунке .
Решение: a a a e a r a к ;
ar arn ar ;
arn R r2 ; r 2 t t 1 c 2 рад с ;
y
ar
aa – абсолютное ускорение
(ускорение точки точки А относительно земли);
aа
ae – переносное ускорение
(ускорение тележки);
ar – относительное ускорение
(ускорение точки А во вращательном движении ротора);
aК = 0 – кориолисово ускорение
(переносное движение – поступательное);
arn 0.2 4 0.8 м с 2 ;
n
a
2
ar R r ;
r r 2 рад с ; r
a r 0.2 2 0.4 м с 2 ;
ar
a 0.894 м с ;
n 2
ar
O
2
arτ
2
r
aax ae ar cos 60
aax 0.492 0.4 0.5 0.8 0.866 0 ;
aay a r sin 60 0 arn sin 30 0 ;
aay 0.4 0.866 0.8 0.5 0.746 м с 2 ;
2
2
aa aax
aay
0.746 м с 2 ;
0
arn cos 30 0 ;
300
ωr
600
300
A
x
ae
Ответ:
aa 0.746 м с 2 ;
направление – ВЕРТИКАЛЬНО ВВЕРХ
19.
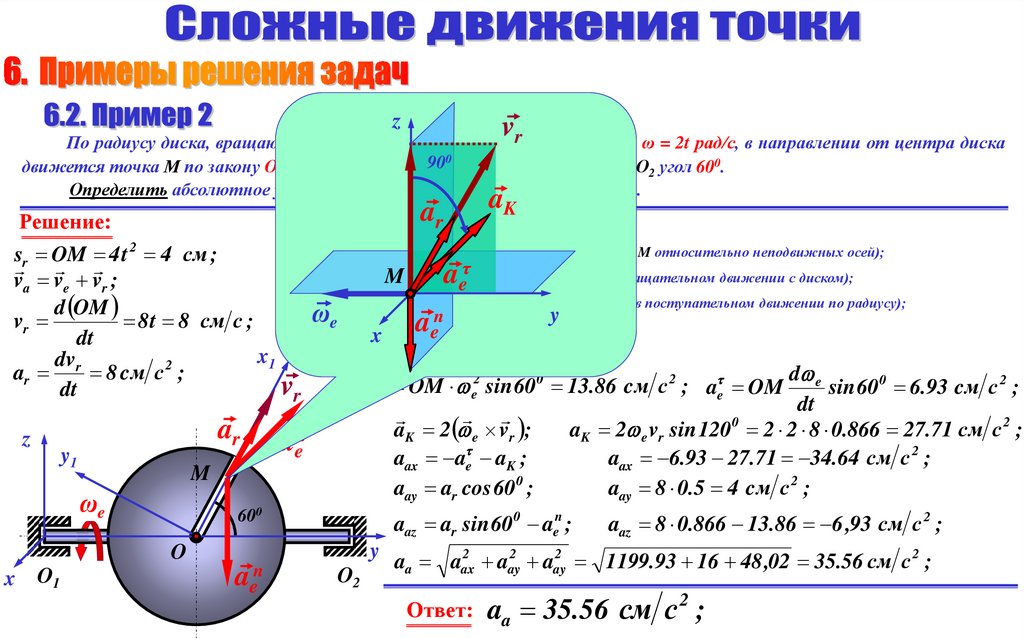
zv
r скоростью ω = 2t рад/с, в направлении от центра диска
По радиусу диска, вращающегося вокруг оси О О с угловой
1 2
900
движется точка М по закону ОМ = 4t2 см. Радиус ОМ составляет с осью О1О2 угол 600.
Определить абсолютное ускорение точки М в момент времени t = 1 c .
aK
a
Решение:
aa ae ar aк ;r
aa – абсолютное ускорение (ускорение точки точки M относительно неподвижных осей);
sr OM 4 t 2 4 см ;
ae – переносное
Mускорение
aeτ(ускорение точки М во вращательном движении с диском);
va ve vr ;
ar – относительное ускорение (ускорение точки М в поступательном движении по радиусу);
d OM
ωe
y
n
vr
8 t 8 см с ;
a
aК – кориолисово
ускорение;
e
x
dt
n
a
a
x1
e
e ae ;
dvr
2
ar
8 cм с ;
d e
n
2
0
2
ae OM e sin 60 13.86 cм с ; ae OM
sin 60 0 6.93 cм с 2 ;
vr
dt
dt
0
2
a
2
v
sin
120
2
2
8
0
.
866
27
.
71
см
с
;
a
2
v
;
a
τ
K
e r
K
e
r
r
z
a
e
y1
aax 6.93 27.71 34.64 см с 2 ;
aax a e aK ;
M
aay ar cos 60 0 ;
aay 8 0.5 4 cм с 2 ;
ωe
600
aaz ar sin 60 0 aen ;
O
x O1
aen
O2
aaz 8 0.866 13.86 6 ,93 см с 2 ;
y a a 2 a 2 a 2 1199.93 16 48 ,02 35.56 см с 2 ;
a
ax
ay
ay
Ответ: aa 35.56 см с
2
;












 physics
physics