Similar presentations:
Сложное движение точки
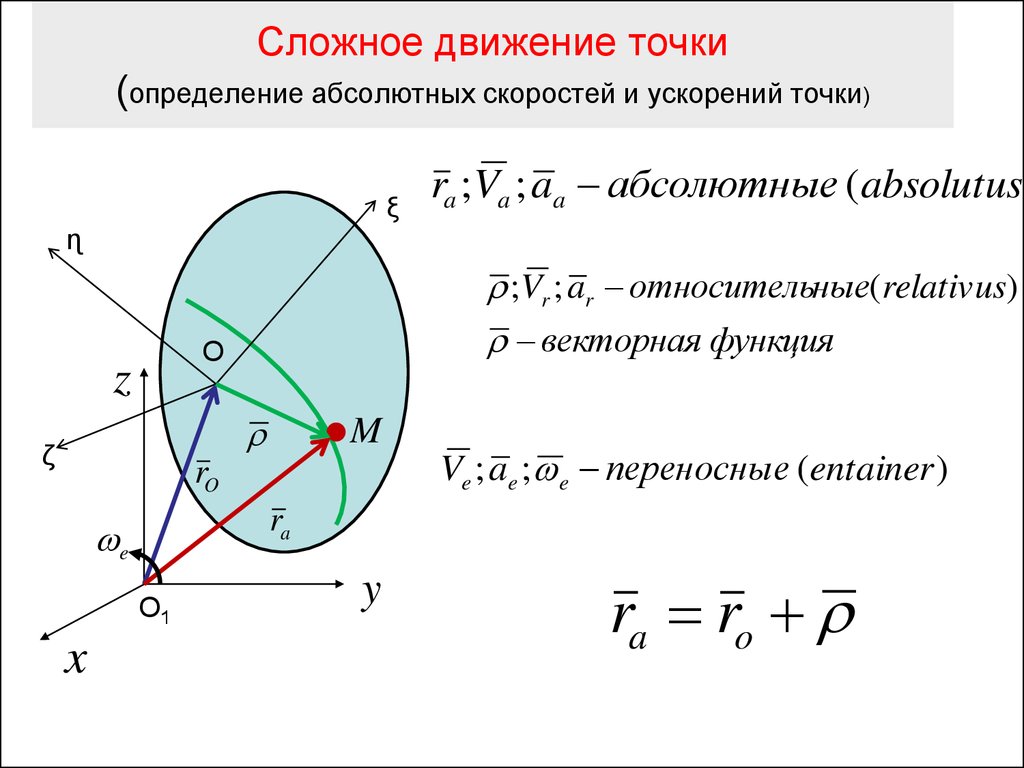
1. Сложное движение точки (определение абсолютных скоростей и ускорений точки)
ξra ;Va ; aa абсолютные (absolutus
ɳ
;Vr ; ar относительные(relativus)
векторная функция
O
z
ζ
M
rO
ra
e
O1
x
Ve ; ae ; e переносные (entainer )
y
ra ro
2. Теорема о сложении скоростей при сложном движении точки
Абсолютная скорость точки равна геометрической суммеотносительной и переносной скоростей.
Va Vr Ve
Геометрическая интерпретация
Va Vr Ve 2Vr Ve cos(180 )
2
Ve
Va
Vr
2
Va Vr2 Ve2 2VrVe cos
3. Теорема Кориолиса (Теорема о сложении ускорений при сложном движении точки)
aa ar ae akТеорема. Абсолютное ускорение точки
при сложном движении равно
геометрической сумме относительного,
переносного ускорений и ускорения
Кориолиса .
Относительное ускорение характеризует изменение
относительной скорости в относительном движении точки.
Переносное ускорение характеризует изменение
переносной скорости в переносном движении точки.
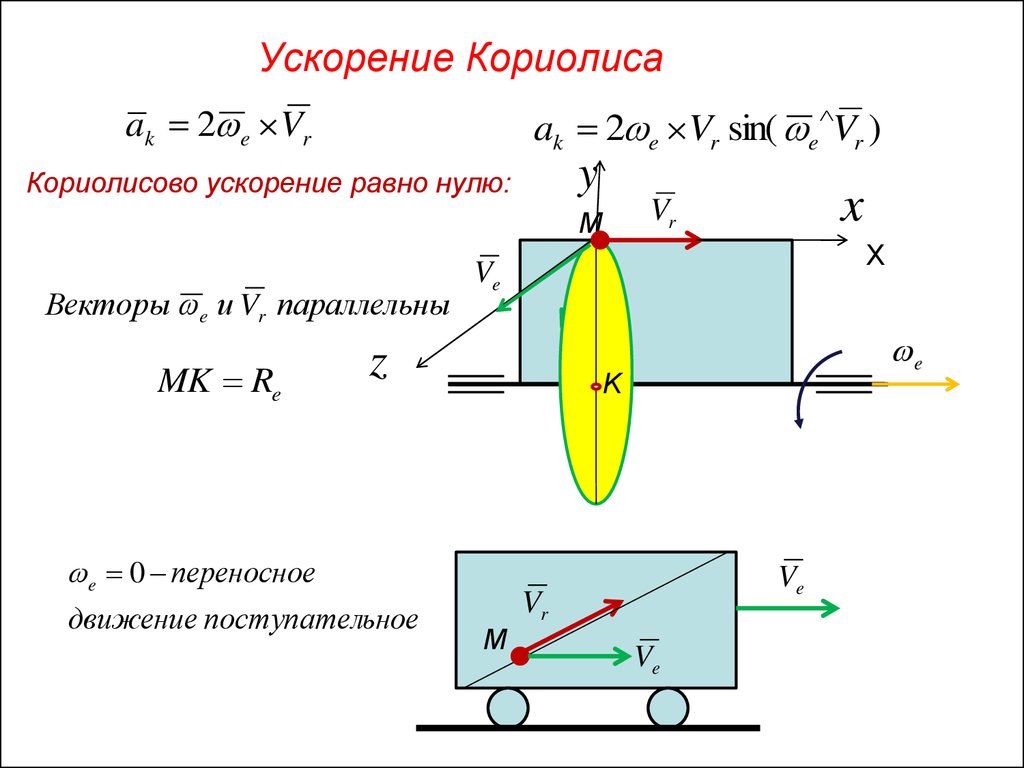
4. Ускорение Кориолиса
ak 2 e Vrak 2 e Vr sin( e Vr )
y
Кориолисово ускорение равно нулю:
Векторы e и Vr параллельны
MK Re
X
Ve
z
e
K
e 0 переносное
движение поступательное
x
Vr
M
Ve
Vr
M
Ve
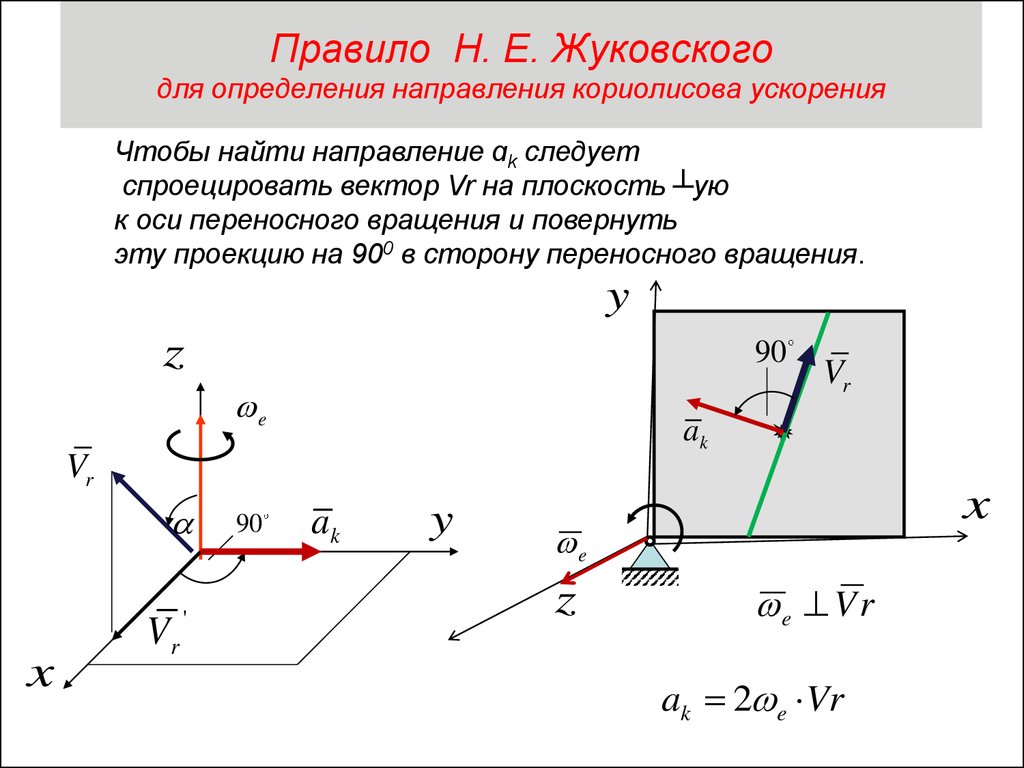
5. Правило Н. Е. Жуковского для определения направления кориолисова ускорения
Чтобы найти направление ɑk следуетспроецировать вектор Vr на плоскость ┴ую
к оси переносного вращения и повернуть
эту проекцию на 900 в сторону переносного вращения.
y
z
90
e
Vr
ak
Vr
x
Vr
'
90
ak
y
x
e
z
e V r
ak 2 e Vr
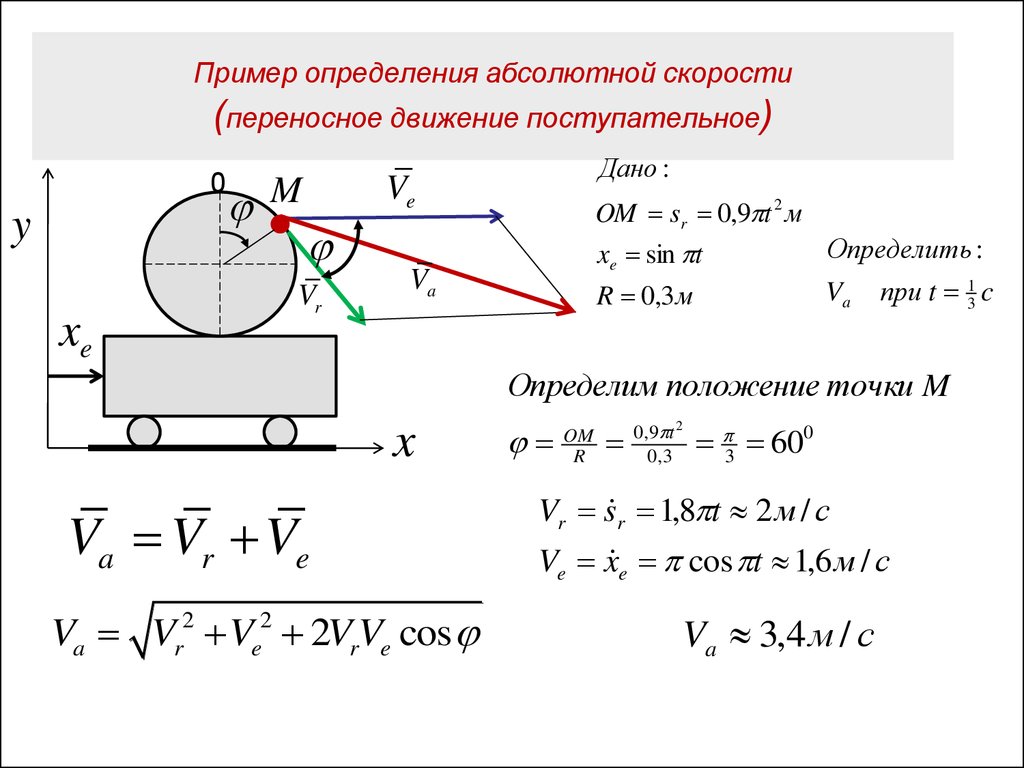
6. Пример определения абсолютной скорости (переносное движение поступательное)
0y
xe
M
Дано :
Ve
Vr
OM sr 0,9 t 2 м
Va
xe sin t
Определить :
R 0,3 м
Va
при t 13 c
Определим положение точки M
x
Va Vr Ve
Va Vr2 Ve2 2VrVe cos
OM
R
0, 9 t 2
0,3
3 600
Vr s r 1,8 t 2 м / с
Ve x e cos t 1,6 м / с
Va 3,4 м / с
7. Пример определения абсолютного ускорения (переносное движение поступательное)
y0
Vr s r 1,8 t
Ve x e cos t
ae
M
α
α
a nr
a r
xe
y1
x1
x
aa ar ae ak
ak 0
ae V e 2 sin t 8,5 м / с 2
ar a n r a r
a
n
r
V 2r
R
(1,8 t ) 2
R
0,1м / с 2
a r V r 1,8 6 м / с 2
aax1 a n r ae sin 7,2
aay1 a r ae cos 1,8
2
2
aa a 2 ax1 aay
7
,
4
м
/
с
1
8. Пример определения абсолютной скорости (переносное движение вращательное)
Дано :Треугольник вращается по закону
e 0,9 t 2 .
Vr
Va
S r 1,2 sin tм
М
Sr
e
Точка M движется по закону
Определить в момент времени t 16 c
Ve
Va; aa
Определим положение точки M
t 16 c; OM S r 1,2 sin
0
Va Vr Ve
6
Vr S 1,2 cos t 3,3м / с
Ve e OM
Va V 2 r V 2 e 3,34 м / с
0,6 м
e 1,8 t 0,9c 1
Ve 0,54 м / с
9. Пример определения абсолютного ускорения (переносное движение вращательное)
t 16 c; OM Sr 1,2 sinVr
6
0,6 м
e e 1,8 t 0,9c 1
e e 1,8 5,6c 2
a
e
0
n
a e
e
ar
aa ar ae ak
ar V r 1,2 2 sin t 5,9 м / с 2
М
Sr
Vr S 1,2 cos t
ae a e a n e
ak
y
a n e 2 e OM 0,5 м / с 2
a e e OM 0,3 м / с 2
ak 2 e Vr sin 900 4 м / с 2
x
aax ar a n e 6,4
aay ak a e 4,3
aa a 2 ax a 2 ay 7,7 м / с 2
10. Пример распределения скоростей (переносное движение вращательное)
Траект. перенос. дв-яТраект. относ. дв-я.
Z
MK Re
O
M
Ve
Va
K
x
Vr
e
y
x
Ve e Re
11. Пример распределения ускорений (переносное движение вращательное)
Zω
O
L
α
ɑk
ɑτe
ɑne
900
M
ar
Vr
e
x
y







 physics
physics mechanics
mechanics








