Кинематика сложного движения твёрдого тела

1.

А.И. Родионов
Теоретическая механика.
Ч.1. КИНЕМАТИКА

2.

Лекция 10.
Кинематика сложного движения твёрдого тела.
§10.1.Плоское движение Т.Т. как сложение вращений
вокруг параллельных и антипараллельных осей.
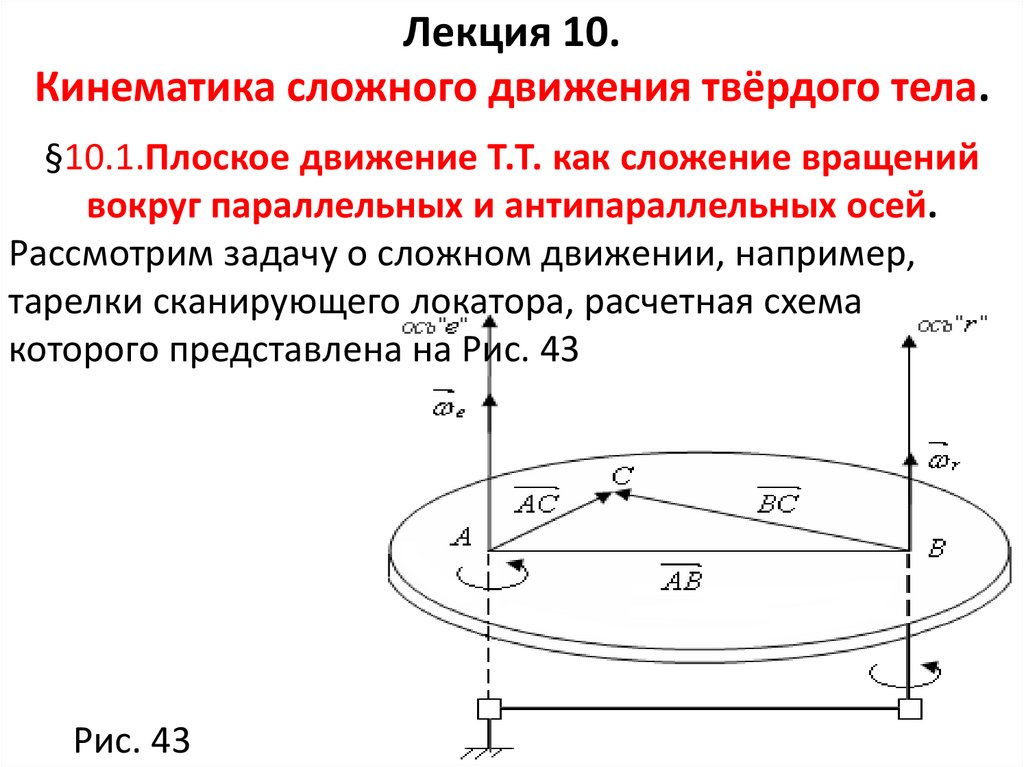
Рассмотрим задачу о сложном движении, например,
тарелки сканирующего локатора, расчетная схема
которого представлена на Рис. 43
Рис. 43

3.

Анализ Рис. 43 однозначно показывает, что объект
движется в плоскости ( X Y ), то есть совершает плоское
движение. Найдём скорость точки С, взяв за полюс
сначала точку , а потом точку . Тогда
V A [ AC ] V C V B [ BC ]
Точка
лежит
на
оси
переносного
движения,
поэтому
VA r BA участвует только в относительном
движении, поэтому . Точка лежит на оси относительного
движения, поэтому
участвует только в переносном
движении VB e AB . Тогда
[ AC BC ] [ e AB r BA]
[ AB e r AB]
и
Из этого следует

4.

§10.2. Теорема о сложении угловых скоростей при
плоском движении:
Угловая скорость плоского движения Т.Т как целого
равна геометрической сумме переносной и
относительной угловых скоростей.
e r
(63)
Т.к e и r могут быть при плоском движении
параллельны или антипараллельны, то e r
Рис. 44

5.

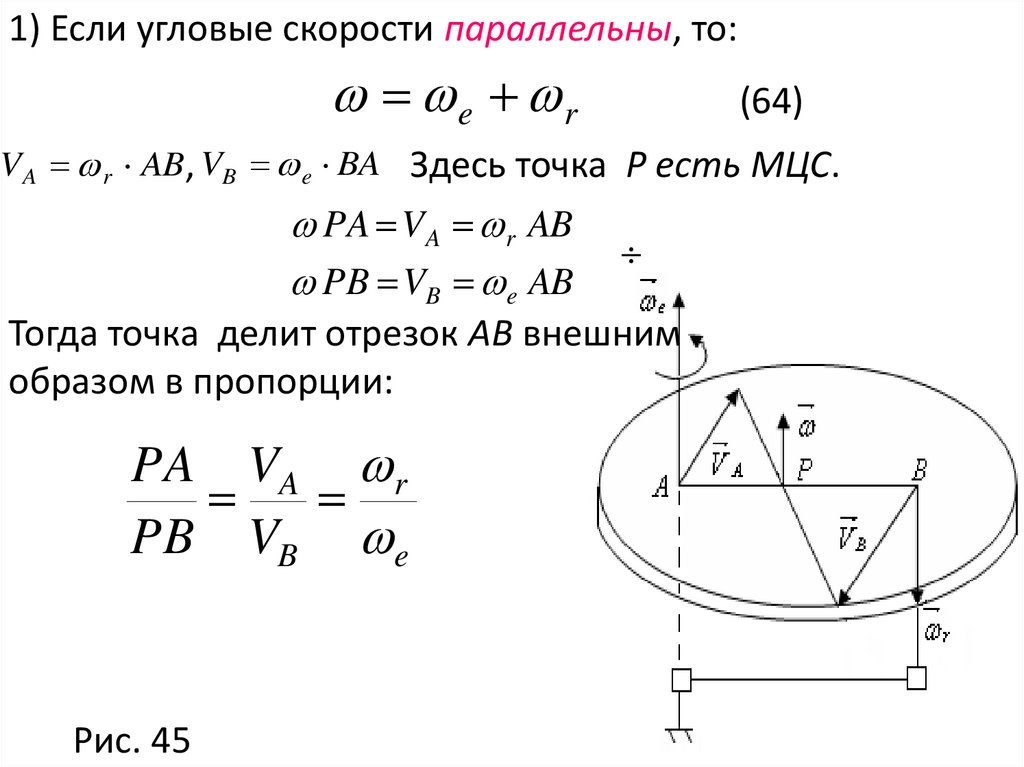
1) Если угловые скорости параллельны, то:
e r
(64)
V A r AB, VB e BA Здесь точка P есть МЦС.
PA VA r AB
PB VB e AB
Тогда точка делит отрезок AB внешним
образом в пропорции:
PA VA r
PB VB e
Рис. 45

6.

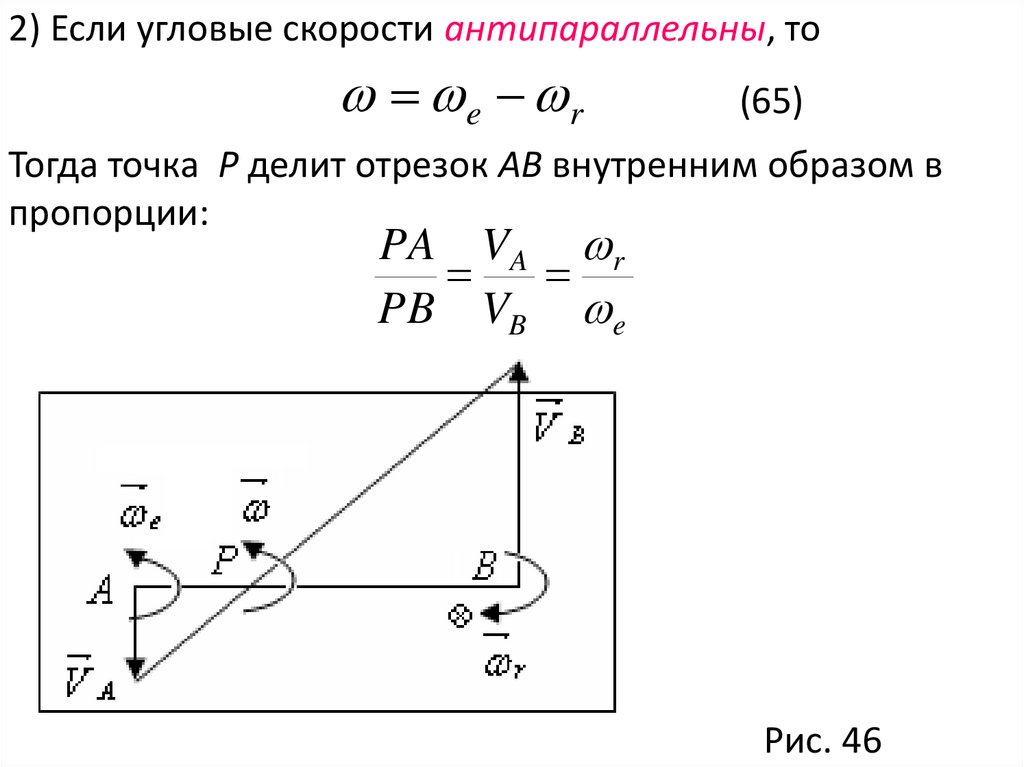
2) Если угловые скорости антипараллельны, то
e r
(65)
Тогда точка P делит отрезок AB внутренним образом в
пропорции:
PA VA r
PB VB e
Рис. 46

7.

§10.2. Четыре Представления плоского
движения:
1. Как поступательное с полюсом и вращения
относительно полюса (как сложное, составное
движение).
2. Как мгновенный поворот вокруг МЦП. (в этом случае
плоское движение не представляется как сложное).
3. Как качение подвижной центроиды без
проскальзывания по неподвижной. (в этом случае
плоское движение не представляется как сложное).
4. Как сложение вращений Т.Т вокруг параллельных и
антипараллельных осей (как сложное движение).

8.

§10.3. Метод Виллиса расчёта планетарных и
дифференциальных редукторов.
Суть метода Виллиса расчёта планетарных и
дифференциальных редукторов заключается в
том, что переходя в систему координат, связанную
с водилом, получаем в относительном движении
(относительно водила) рядовую передачу с
кратным зацеплением колёс или с паразитными
колесами, к которой применима теория
передаточного отношения для расчёта угловых
скоростей колес.

9.

Записав формулу Виллиса получим практически
мгновенный расчёт угловых скоростей:
1r 1 вод
m ri ведомых
1
ir i вод
rk ведущих
Где m - число внешних зацеплений.
n1 nвод
m z i ведомые
1
ni nвод
z k ведущие
Где z - число зубьев, n - шаг n
30
(66)

10.

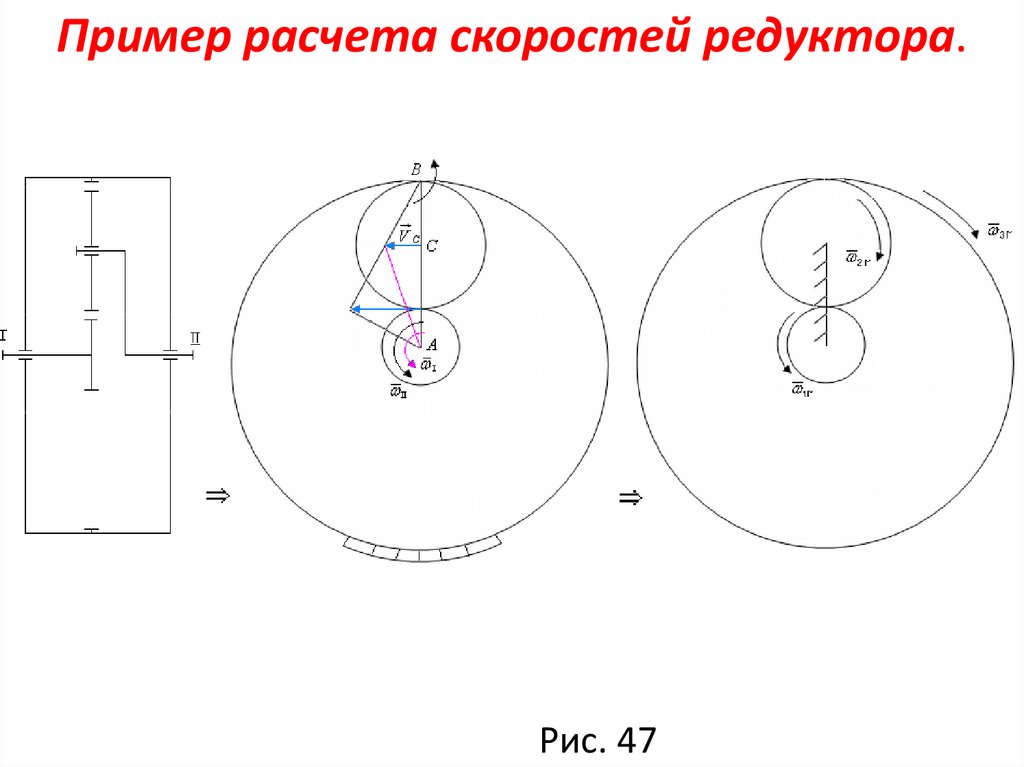
Пример расчета скоростей редуктора.
Рис. 47

11.

Дано: r1 20 см
r2 25 см
r3 70 см
4500 рад с
______________
2 , ?
Используем метод Виллиса, переходим в систему отсчёта,
связанную с водилом. Получаем рядовое зацепление.
1r 1 вод
1 r2 r3
1
3r 3 вод 3
r1 r2
4500
70
20
4500
70
20
1000 рад с