Численное интегрирование

1.

ЧИСЛЕННОЕ
ИНТЕГРИРОВАНИЕ
Click to add Text

2.

Пусть требуется вычислить интеграл
(1)
b
I f ( x)dx
a

3.

Если функция
f ( x) является
непрерывной на отрезке a, b , то
интеграл (1) существует и может быть
вычислен по формуле НьютонаЛейбница
b
I f ( x)dx F (b) F (a)
a

4.

Задача численного интегрирования:
найти определенный интеграл на
отрезке, если подынтегральная
функция на отрезке задана таблично.
Формулы приближенного
интегрирования называются
квадратурными формулами

5.

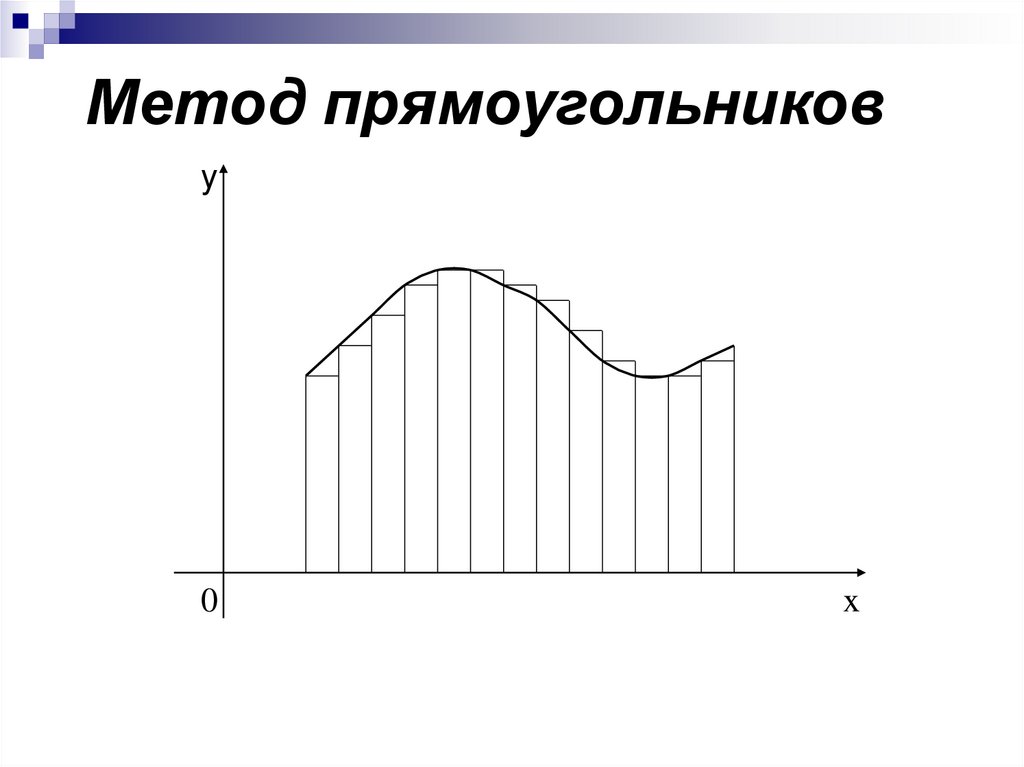
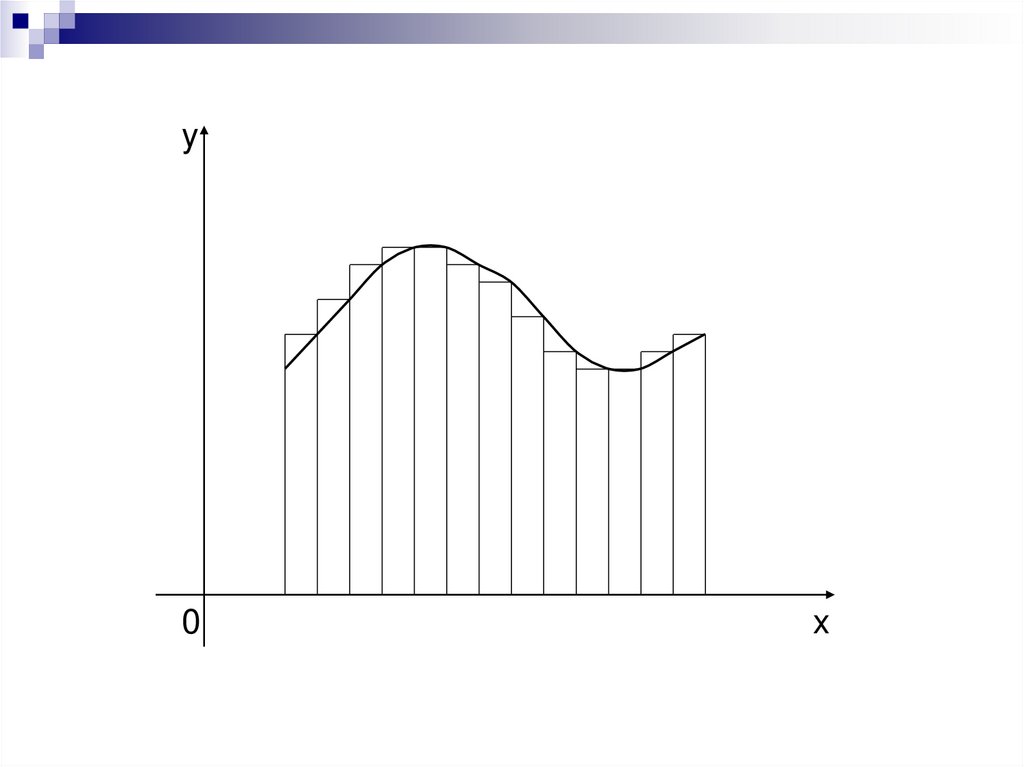
Метод прямоугольников
y
0
x

6.

формула
левых прямоугольников:
n 1
b a
I л f x dx
y0 y1 y n 1 h y i
n
i 0
a
b
b a
h
n

7.

y
0
x

8.

формула
правых прямоугольников:
n
b a
I П f x dx
y1 y2 yn h yi
n
i 1
a
b

9.

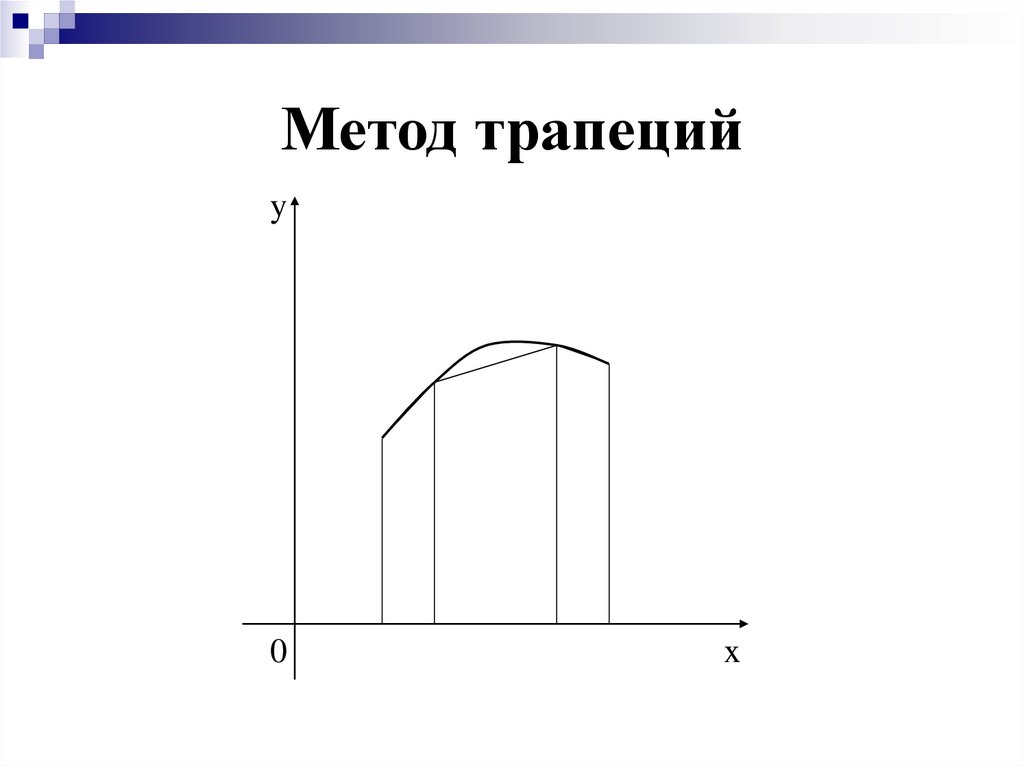
Метод трапеций
y
0
x

10.

формула трапеции
b
h
f x dx 2 y0 2 y1 2 y2 2 yn 1 yn
a
b a
h
n

11.

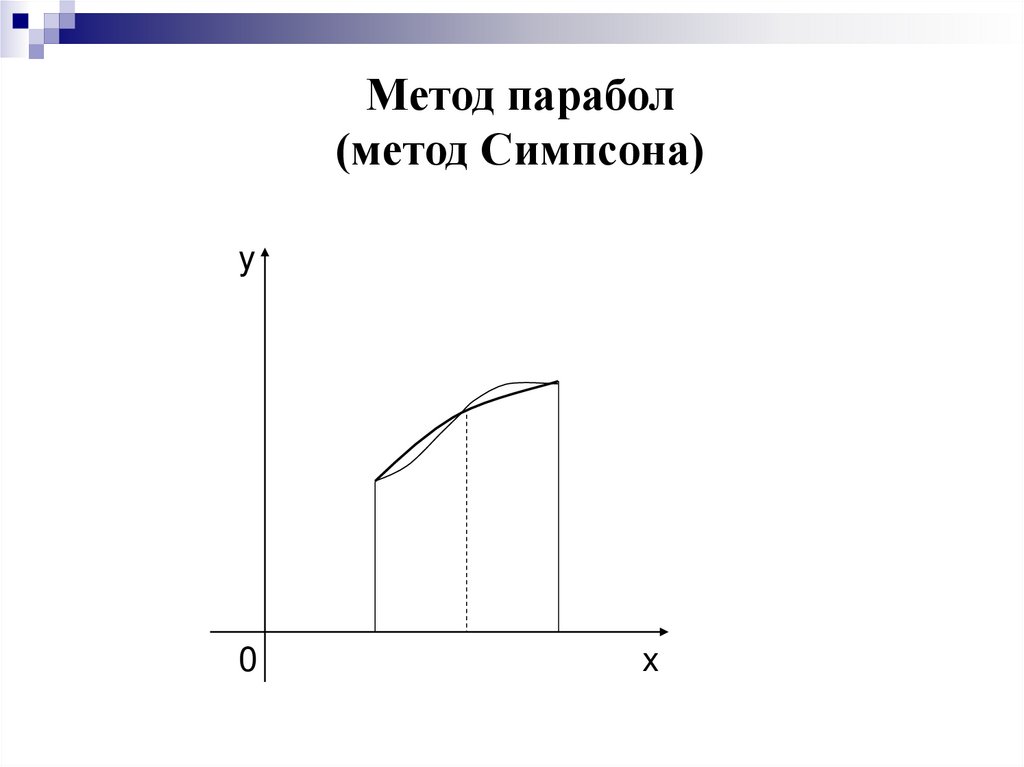
Метод парабол
(метод Симпсона)
y
0
x

12.

квадратурная формула Симпсона
b
f x dx
a
b a
y0 y2 n 4 y1.
6n
y2 n 1 2 y2
b a
h
2n
y2 n 2

13.

Метод трапеций
double trapezoidalIntegral(double a, double b, int n, const std::function<double (double)> &f) {
const double width = (b-a)/n;
double trapezoidal_integral = 0;
for(int step = 0; step < n; step++) {
const double x1 = a + step*width;
const double x2 = a + (step+1)*width;
trapezoidal_integral += 0.5*(x2-x1)*(f(x1) + f(x2));
}
return trapezoidal_integral;
}

14.

Метод Симпсона
double simpsonIntegral(double a, double b, int n, const std::function<double (double)> &f) {
const double width = (b-a)/n;
double simpson_integral = 0;
for(int step = 0; step < n; step++) {
const double x1 = a + step*width;
const double x2 = a + (step+1)*width;
simpson_integral += (x2-x1)/6.0*(f(x1) + 4.0*f(0.5*(x1+x2)) + f(x2));
}
return simpson_integral;
}