Численное интегрирование. Формула трапеций и Симпсона

1. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Формула трапеций и
Симпсона

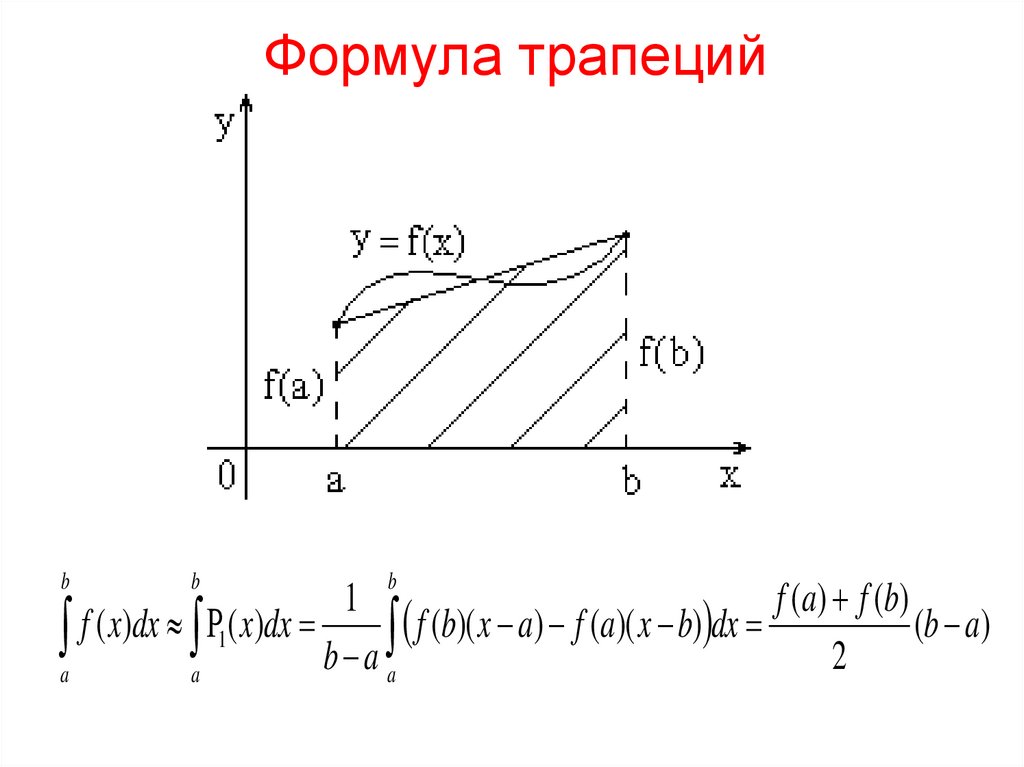
2. Формула трапеций

При n=1 , f ( x) 1 ( x)
Для построения Р1(х) требуется две
x
y
точки
X0=a
Y0=f(a)
X1=b
Y1=f(b)
x x1
x x0
1 ( x ) y0
y1
x0 x1
x1 x0
Подставив значения x0,x1,y0 и y1
получим окончательно формулу
трапеций

3.

Формула трапеций
1
f (a) f (b)
a f ( x)dx a 1( x)dx b a a f (b)( x a) f (a)( x b) dx 2 (b a)
b
b
b

4. Формула Симпсона

При n=2 , f ( x) 2 ( x)
Для построения Р2(х) требуется три точки
x
y
X0=a
Y0=f(a)
a b
x1
2
X2=b
a b
y1 f
2
2
2
i 0
j 0
j i
2 ( x ) yi
x xj
xi x j
Y2=f(b)
Подставив значения x0,x1,x2,y0 ,y1и y2
получим окончательно формулу
Симпсона

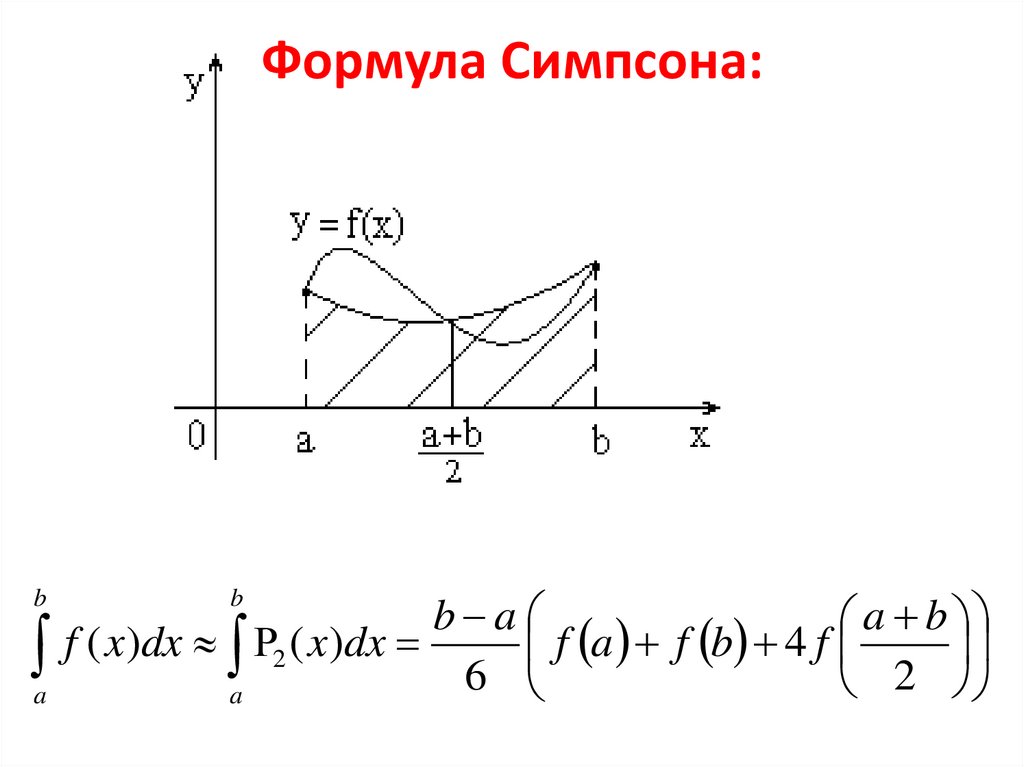
5. Формула Симпсона:

b
a
b a
a b
f ( x )dx 2 ( x)dx
f a f b 4 f
6
2
a
b

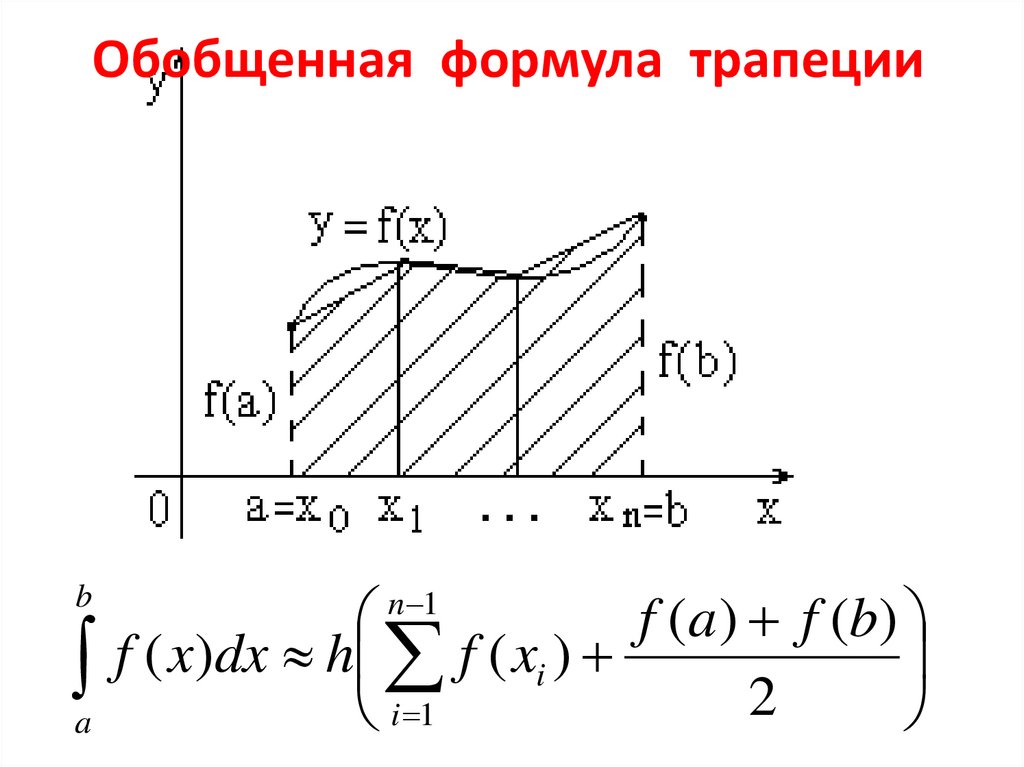
6. Обобщенная формула трапеции

b
a
f ( a ) f ( b)
f ( x )dx h f ( xi )
2
i 1
n 1

7. Обобщенная формула Симпсона

b
a
h y0 y2m 2 y2 y4 ... y2m 2
f ( x)dx
3 4 y1 y3 ... y2m 1
b a b a
где h
n
2m

8. Вычислить приближенно по формуле трапеций интеграл , полагая n=10

1
e
x2
dx
0
При n=10 разобьем отрезок
интегрирования на 10 частей с шагом
b a 1 0
h
0,1
n
10

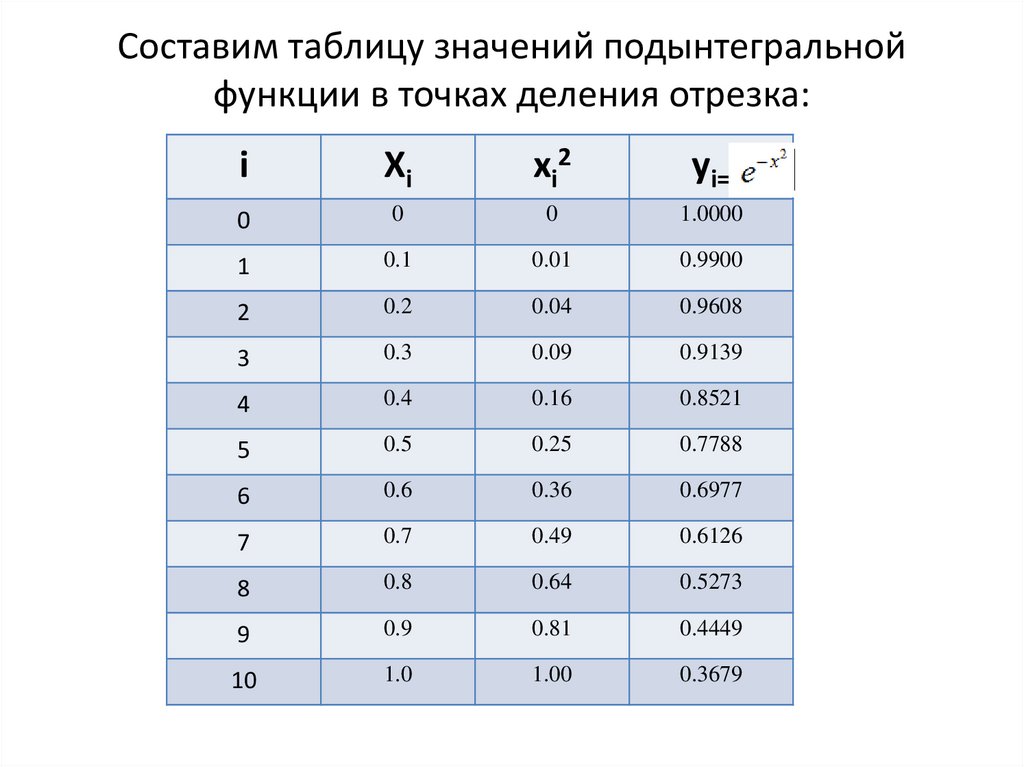
9. Составим таблицу значений подынтегральной функции в точках деления отрезка:

i
Xi
xi2
yi=
0
0
0
1.0000
1
0.1
0.01
0.9900
2
0.2
0.04
0.9608
3
0.3
0.09
0.9139
4
0.4
0.16
0.8521
5
0.5
0.25
0.7788
6
0.6
0.36
0.6977
7
0.7
0.49
0.6126
8
0.8
0.64
0.5273
9
0.9
0.81
0.4449
10
1.0
1.00
0.3679

10. По формуле трапеций получим значение интеграла

Произведем вычисления:
По формуле трапеций получим
значение интеграла

11. Вычислить приближенно интеграл по формуле Симпсона при n=10

b a 1 0
h
0,1
n
10
1
e
x2
dx
0
Составим таблицу значений
подынтегральной функции, в точках
деления отрезка, записывая ординаты с
четными и нечетными номерами в разные
столбцы:

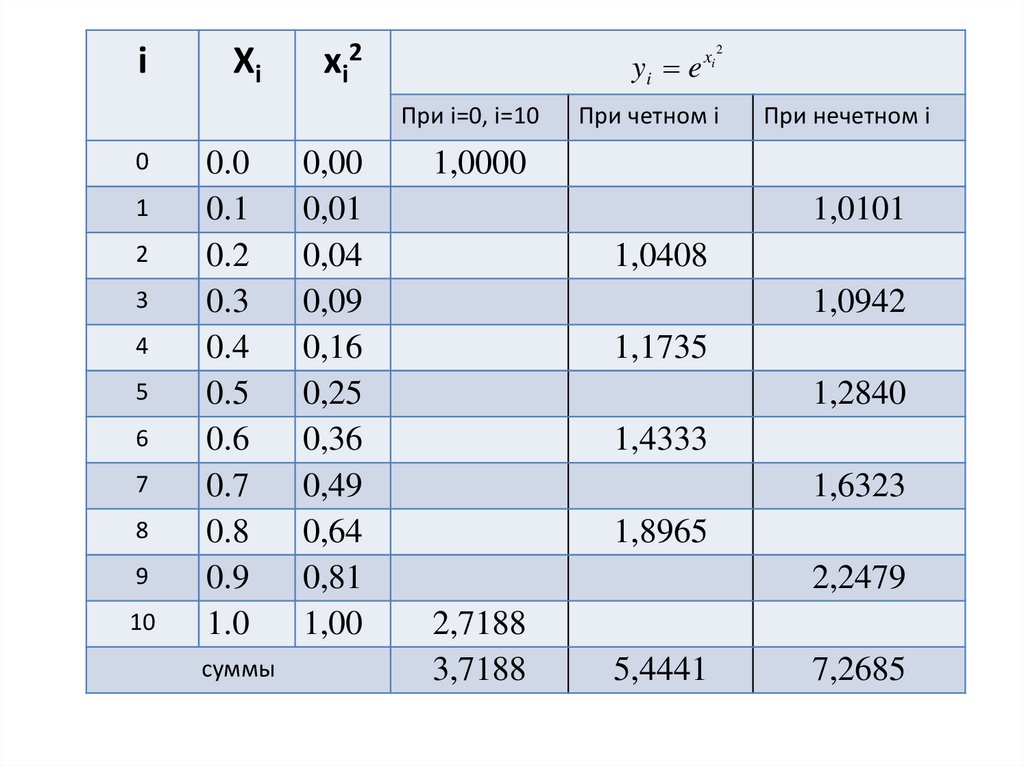
12.

i
Xi
xi2
yi e
При i=0, i=10
0
1
2
3
4
5
6
7
8
9
10
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
суммы
0,00
0,01
0,04
0,09
0,16
0,25
0,36
0,49
0,64
0,81
1,00
xi 2
При четном i
При нечетном i
1,0000
1,0101
1,0408
1,0942
1,1735
1,2840
1,4333
1,6323
1,8965
2,2479
2,7188
3,7188
5,4441
7,2685

13. Затем по формуле Симпсона находим