Similar presentations:
Методы численного интегрирования (нахождение определенных интегралов)
1. Методы численного интегрирования (нахождение определенных интегралов)
2. 1. Аналитический метод
bf ( x)dx F ( x) a F (b) F (a)
b
a
Где F(x) – первообразная функции f(x)
3.
Аналитический метод интегрирования невсегда может быть применен на
практике.
Пример «неберущегося» интеграла:
b
e
dx
x
a
2
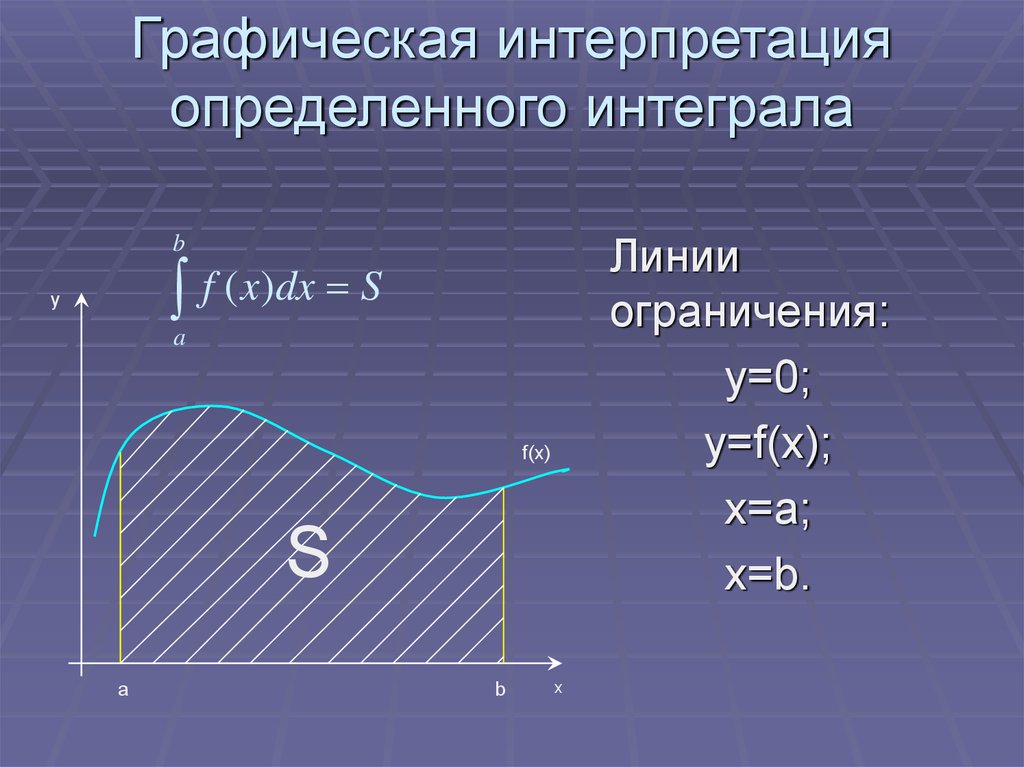
4. Графическая интерпретация определенного интеграла
Линииограничения:
y=0;
y=f(x);
x=a;
x=b.
b
f ( x)dx S
y
a
f(x)
S
a
b
x
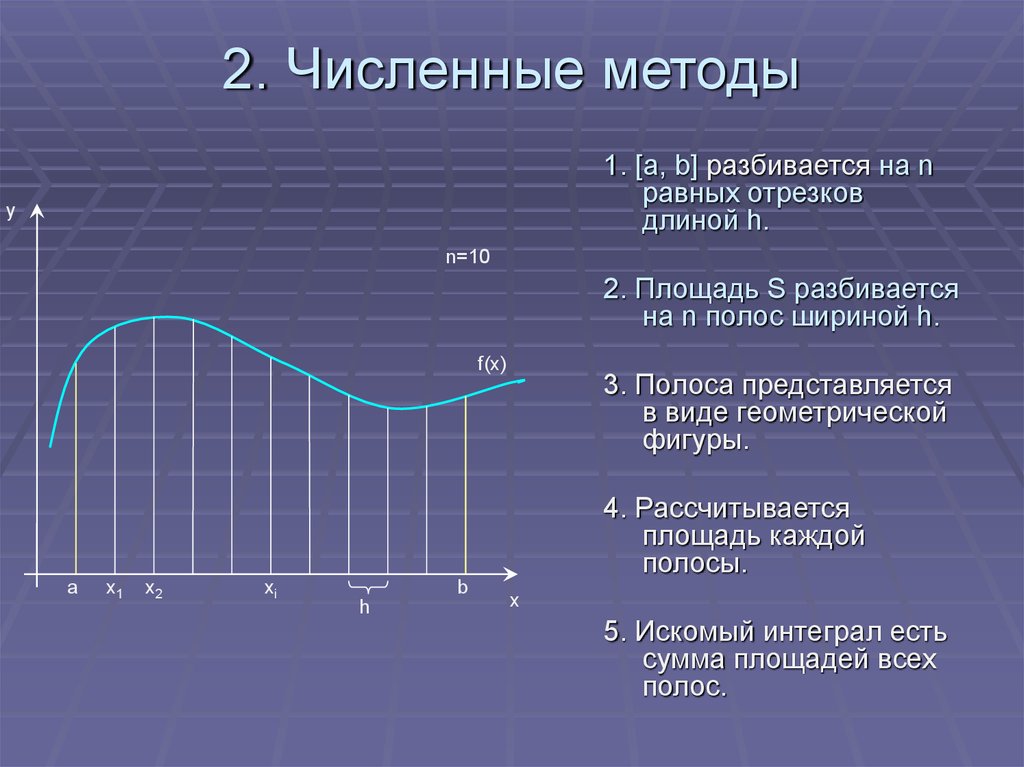
5. 2. Численные методы
1. [a, b] разбивается на nравных отрезков
длиной h.
y
n=10
2. Площадь S разбивается
на n полос шириной h.
f(x)
3. Полоса представляется
в виде геометрической
фигуры.
4. Рассчитывается
площадь каждой
полосы.
a
x1
x2
xi
b
h
x
5. Искомый интеграл есть
сумма площадей всех
полос.
6. 1. Метод прямоугольников
Отдельно взятая полоса представляетсяв виде прямоугольника шириной h.
ВОПРОС: Какая величина принимается за
высоту прямоугольника?
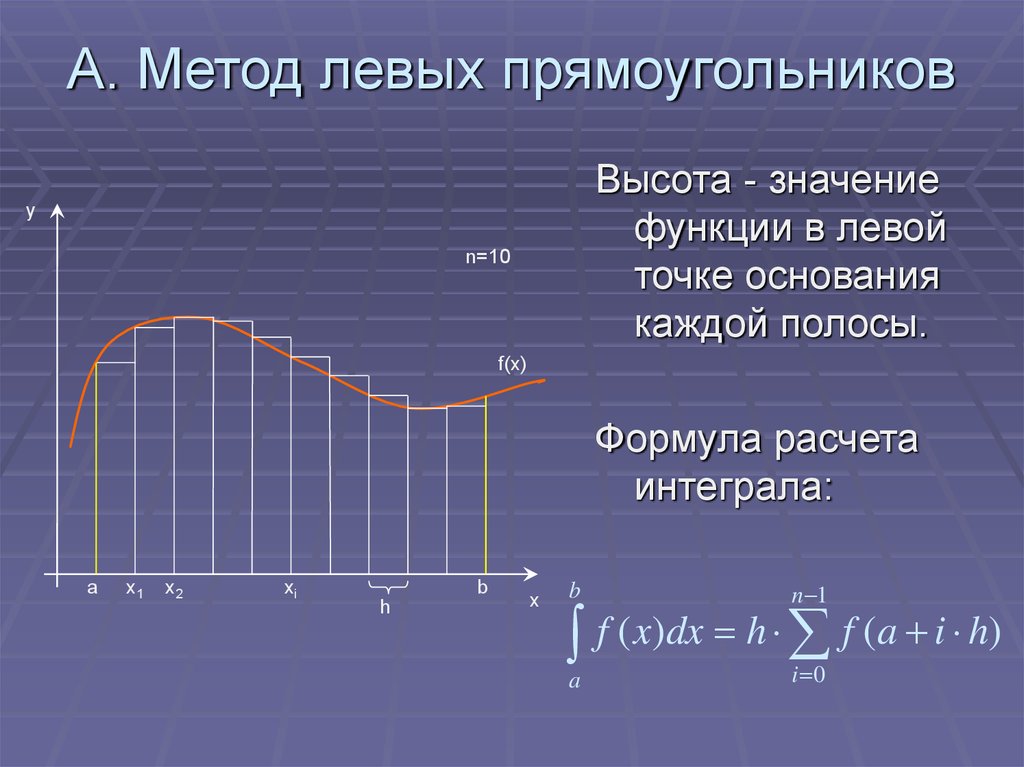
7. А. Метод левых прямоугольников
Высота - значениефункции в левой
точке основания
каждой полосы.
y
n=10
f(x)
Формула расчета
интеграла:
a
x1
x2
xi
b
h
x
b
n 1
a
i 0
f ( x)dx h f (a i h)
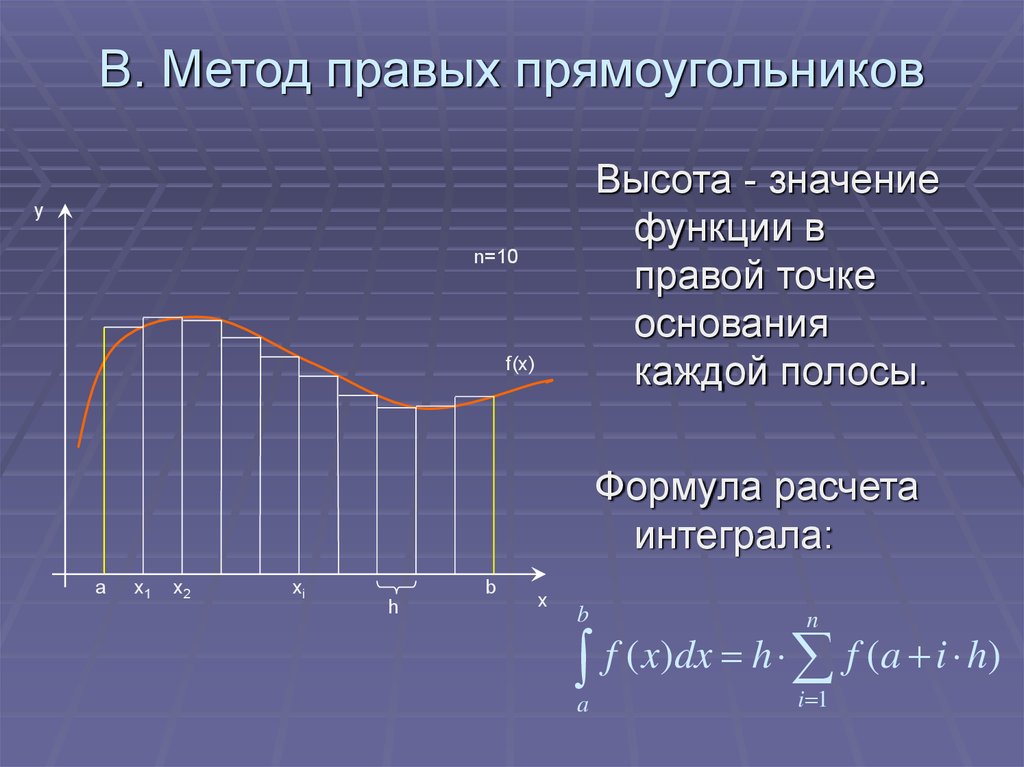
8. B. Метод правых прямоугольников
Высота - значениефункции в
правой точке
основания
каждой полосы.
y
n=10
f(x)
Формула расчета
интеграла:
a
x1
x2
xi
b
h
x
b
n
a
i 1
f ( x)dx h f (a i h)
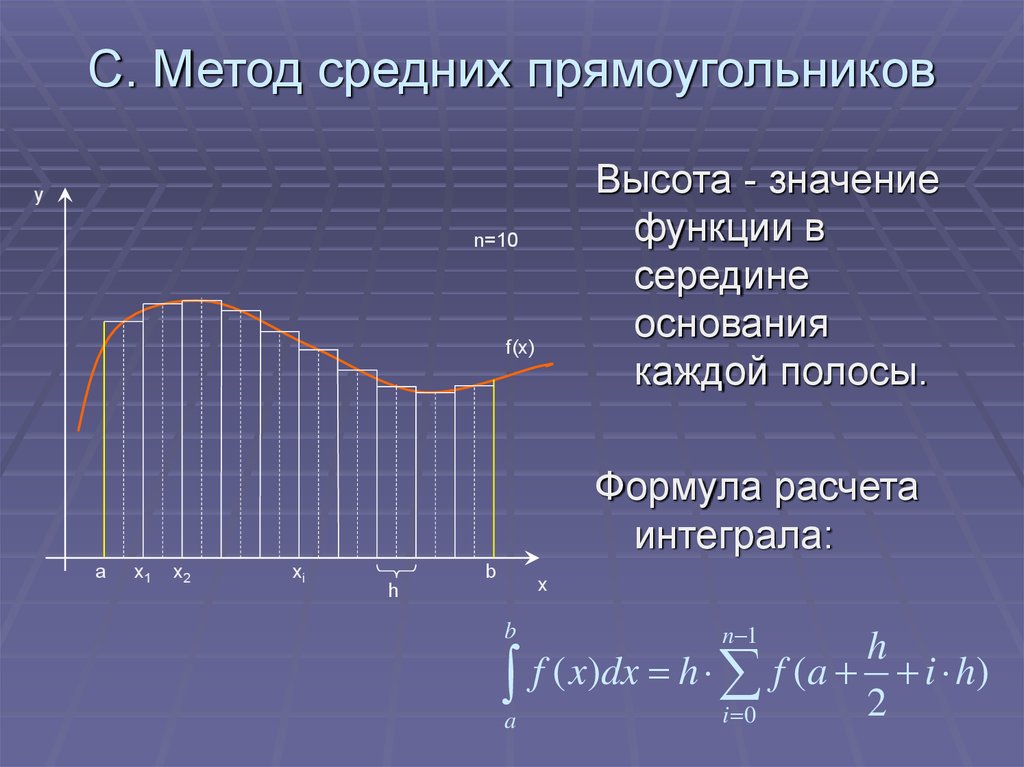
9. С. Метод средних прямоугольников
Высота - значениефункции в
середине
основания
каждой полосы.
y
n=10
f(x)
Формула расчета
интеграла:
a
x1
x2
xi
b
x
h
b
a
n 1
h
f ( x)dx h f (a i h)
2
i 0
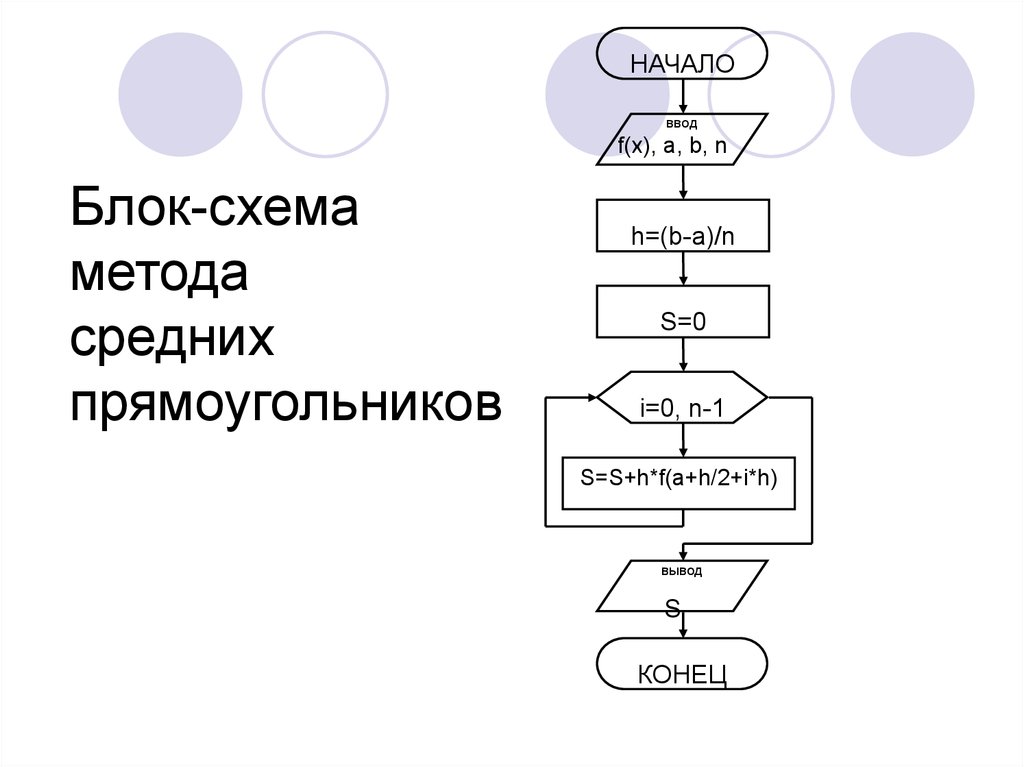
10. Блок-схема метода средних прямоугольников
НАЧАЛОввод
f(x), a, b, n
Блок-схема
метода
средних
прямоугольников
h=(b-a)/n
S=0
i=0, n-1
S=S+h*f(a+h/2+i*h)
вывод
S
КОНЕЦ
11. 2. Метод трапеций
Отдельно взятая полоса представляется в видеперевернутой трапеции высотой h.
Основания трапеции будут равны значениям
функции в левой и правой точке высоты
трапеции.
c1 c 2
Площадь трапеции:
S h
;
2
где
h высота;
c1и c 2 основания
12.
yГладкая кривая
заменяется
ломаной линией
n=5
f(x)
a
x1
x2
h
xi
b
x
Интеграл рассчитывается по следующей формуле:
b
a
f ( x)dx h
f ( xi 1 ) f ( xi )
f (a) f ( x1 )
f ( x1 ) f ( x2 )
h
... h
...
2
2
2
n 1
f ( xn 1 ) f (b)
f (a) f (b)
h
h
h f ( a i h)
2
2
i 1
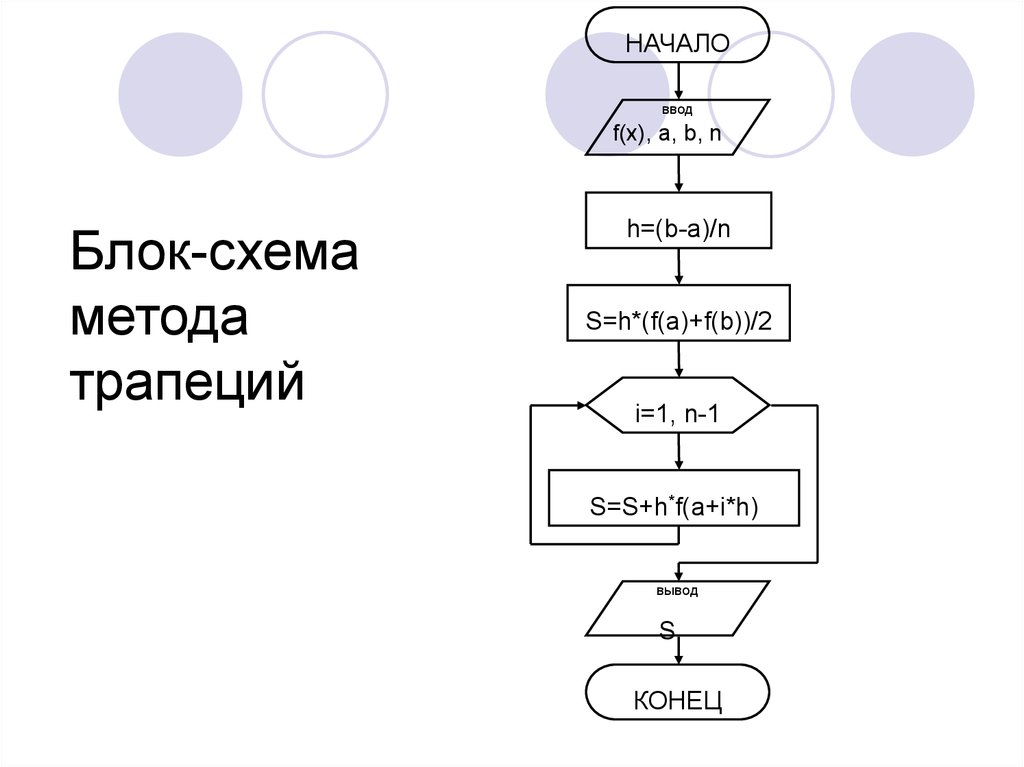
13. Блок-схема метода трапеций
НАЧАЛОввод
f(x), a, b, n
Блок-схема
метода
трапеций
h=(b-a)/n
S=h*(f(a)+f(b))/2
i=1, n-1
S=S+h*f(a+i*h)
вывод
S
КОНЕЦ
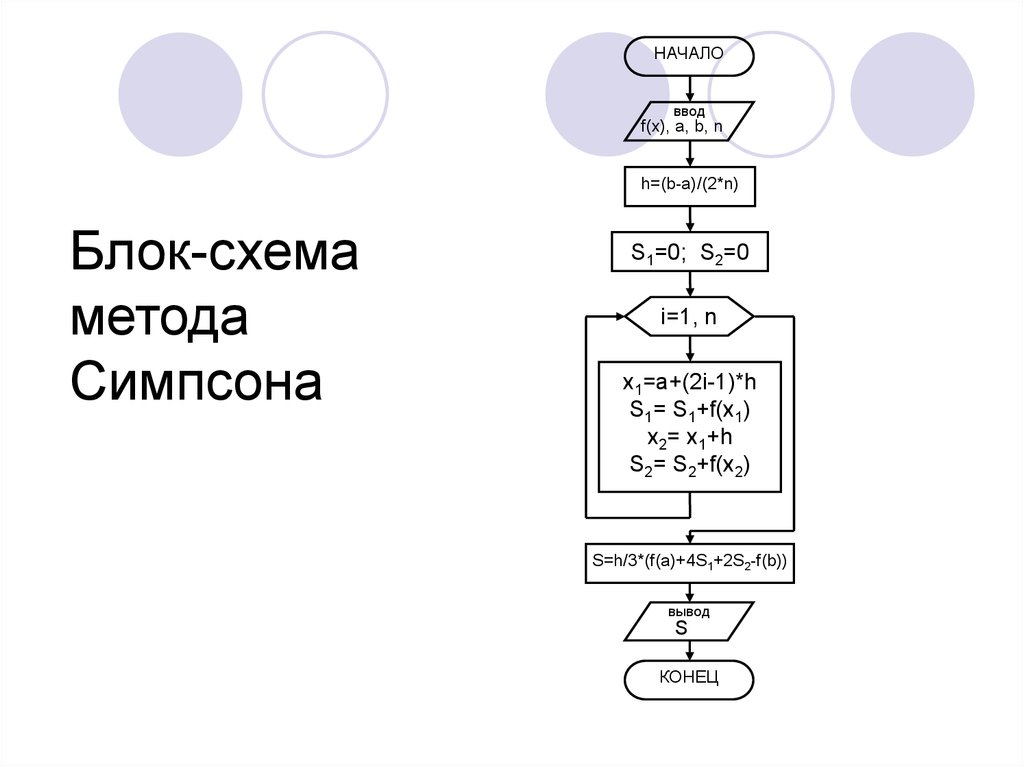
14. 3. Метод Симпсона
Гладкая функция заменяется участкамипарабол.
Через любые 3 точки на плоскости можно
провести одну и только одну параболу.
Парабола проводится через точки
пересечения границ 2-х соседних полос
с графиком подынтегральной функции.
15.
yГладкая
кривая
заменяется
участками
парабол
n=6
f(x)
a
x1
x2
h
xi
b
x
Каждая парабола заменяет исходную подынтегральную
функцию сразу над двумя полосами. Следовательно,
число разбиений должно быть четным !!!
Рассмотрим ситуацию с одной параболой (2-мя полосами)
и выведем формулу для расчета интеграла.
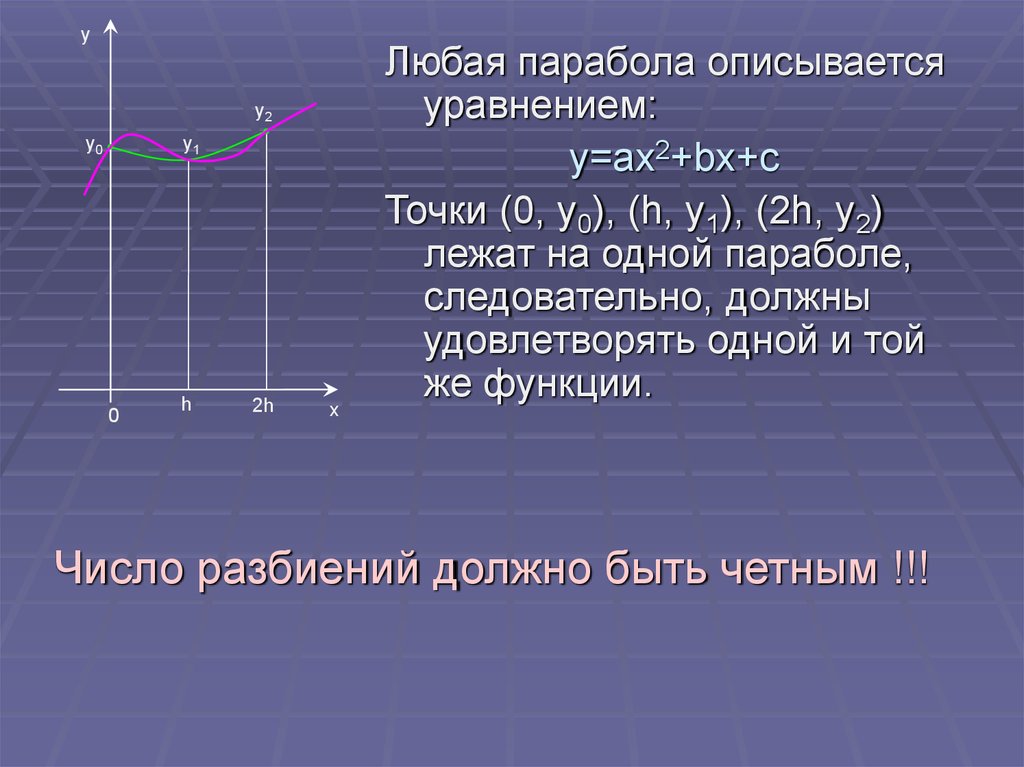
16.
yy2
y0
y1
0
h
2h
x
Любая парабола описывается
уравнением:
y=ax2+bx+c
Точки (0, y0), (h, y1), (2h, y2)
лежат на одной параболе,
следовательно, должны
удовлетворять одной и той
же функции.
Число разбиений должно быть четным !!!
17.
Подставляем координаты 3-х точек в уравнение дляпараболы, получаем систему линейных
алгебраических уравнений.
a 0 2 b 0 c y 0
2
a h b h c y1
2
a
(
2
h
)
b 2h c y 2
Здесь неизвестные - параметры параболы: a, b, c.
Из 1-го уравнения: y0=c.
Произведя замену, получим новую систему уравнений:
a h 2 b h y1 y0
a (2h) 2 b 2h y2 y0
Решаем полученную СЛАУ методом Крамера:
18.
ay1 y0
y1 y0
h
h2
y 2 y0
2h
( 2 h ) 2 y 2 y0
h
2
h
; b
( 2h) 2 2h
h2
h
( 2h) 2 2h
Выведем формулу для расчета коэффициентов a и b:
a
y1 y0
h
y 2 y0
2h
h2
h
2h( y1 y0 ) h( y2 y0 ) y2 y0 2 y1
3
3
2h 4h
2h 2
( 2h) 2 2h
y1 y0
h2
b
( 2 h ) 2 y 2 y0
h2
h
( 2h) 2 2h
h 2 ( y2 y0 ) 4h 2 ( y1 y0 ) 4 y1 y2 3 y0
3
3
2h 4h
2h
19.
Площадь под фигурыможно вычислить,
проинтегрировав
полученную
параболическую
зависимость:
y=ax2+bx+c
y
y2
y0
y1
h
0
2h
x
2h
ax bx
8 3
S (ax bx c)dx
cx ah 2bh 2 2ch
2
3
0 3
0
2h
3
2
2
Подставим в полученную формулу значения
для коэффициентов параболы a, b и c:
20.
Получим:4 y1 y2 3 y0 2
8 y2 y0 2 y1 3
S
h 2
h 2 y0 h
2
3
2h
2h
4
h( y2 y0 2 y1 ) h(4 y1 y2 3 y0 ) 2 y0 h
3
h
( y0 4 y1 y2 )
3
Если число разбиений будет не 2, а 4, то формула для
вычисления интеграла будет иметь следующий вид:
h
h
h
S ( y0 4 y1 y2 ) ( y2 4 y3 y4 ) ( y0 4 y1 2 y2 4 y3 y4 )
3
3
3
21.
В общем виде:h
S ( y0 4 y1 2 y2 4 y3 2 y4 ... 2 yn 2 4 yn 1 yn )
3
h
S ( y0 4 yнечетн. 2 yчетн . yn )
3
Формула Симпсона
22. Блок-схема метода Симпсона
НАЧАЛОввод
f(x), a, b, n
h=(b-a)/(2*n)
Блок-схема
метода
Симпсона
S1=0; S2=0
i=1, n
x1=a+(2i-1)*h
S1= S1+f(x1)
x2= x1+h
S2= S2+f(x2)
S=h/3*(f(a)+4S1+2S2-f(b))
вывод
S
КОНЕЦ
23. Замечания о погрешности численного интегрирования
24.
Для оценки погрешности численногоинтегрирования сравним значения интеграла,
рассчитанные различными численными
методами с истинным значением интеграла,
рассчитанным аналитически.
Пример:
/4
10
sin
2
xdx
0
Истинное значение: S=5
25.
Методn=4
n=10
n=50
Значение,
S
Погрешность, %
Значение,
S
Погрешность, %
Значение,
S
Погрешность, %
Левых
прямоугольников
3,953831
20,9234
4,597016
8,0597
4,921049
1,5790
Средних
прямоугольников
5,032273
0,6454
5,005144
0,1029
5,000206
0,0041
Трапеций
4,935579
1,2884
4,989714
0,2057
4,999589
0,0082
Симпсона
5,000041
0,0008
5,000001
0,00002
5,000000
~10-7
Истинное значение
5
26.
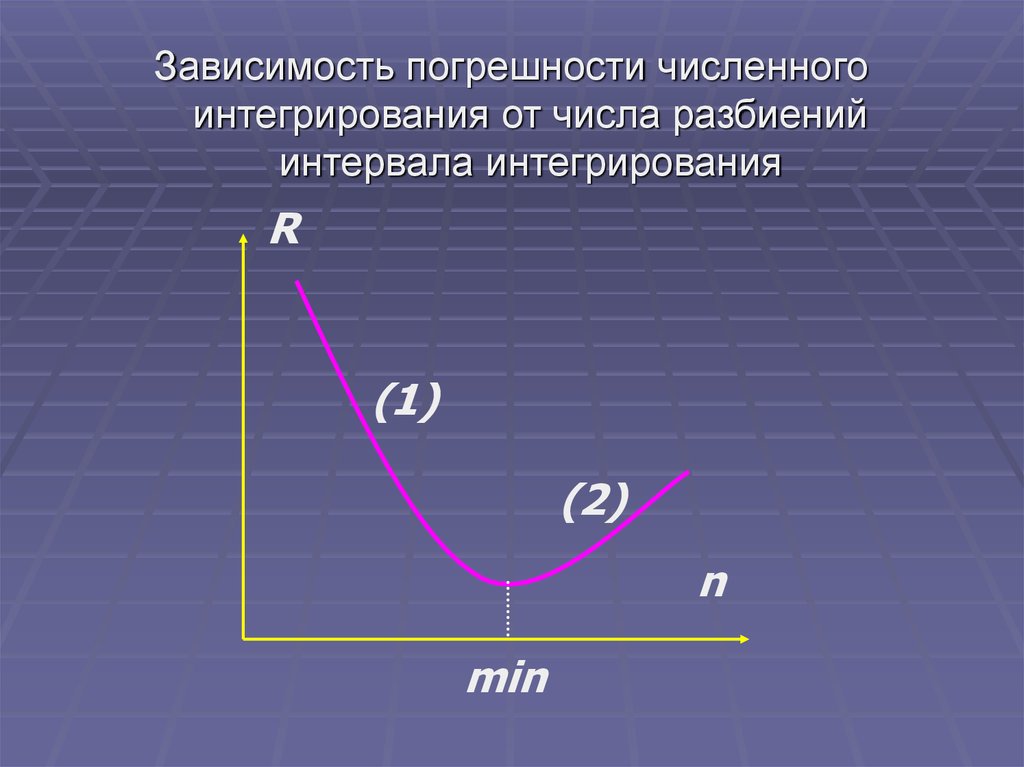
Из таблицы видно, что погрешность зависит отметода интегрирования и от количества
разбиений интервала интегрирования.
Метод левых (правых) прямоугольников
Метод трапеций
Погрешность
уменьшается
Метод средних прямоугольников
Метод Симпсона
27.
Зависимость погрешности численногоинтегрирования от числа разбиений
интервала интегрирования
R
(1)
(2)
n
min

















 mathematics
mathematics








