Численное интегрирование функции с одной переменной

1.

Численное интегрирование
функции с одной переменной

2.

Постановка задачи численного
интегрирования
• Численными методами можно вычислить
только определенные интегралы
b
Заданы пределы
интегрирования
I f ( x)dx
a
a b

3.

Геометрический смысл
определенного интеграла
y f (x)
Вычисление
определенного
интеграла – это
вычисление площади
криволинейной
трапеции.
Трапеция это …
a
b

4.

Формула Ньютона-Лейбница
b
I f ( x)dx F (b) F (a )
a
Первообразная функции f(x)

5.

Метод прямоугольников
Шаг
интегрирования
b a
h
n
n частей
одинаковой
длины

6.

Метод прямоугольников
b a
h
n
xi 1 xi h
=х0
х1
х2
х3
a=x 0<x 1<x 2<…<x n=b
i 0,1, 2, ..., n 1

7.

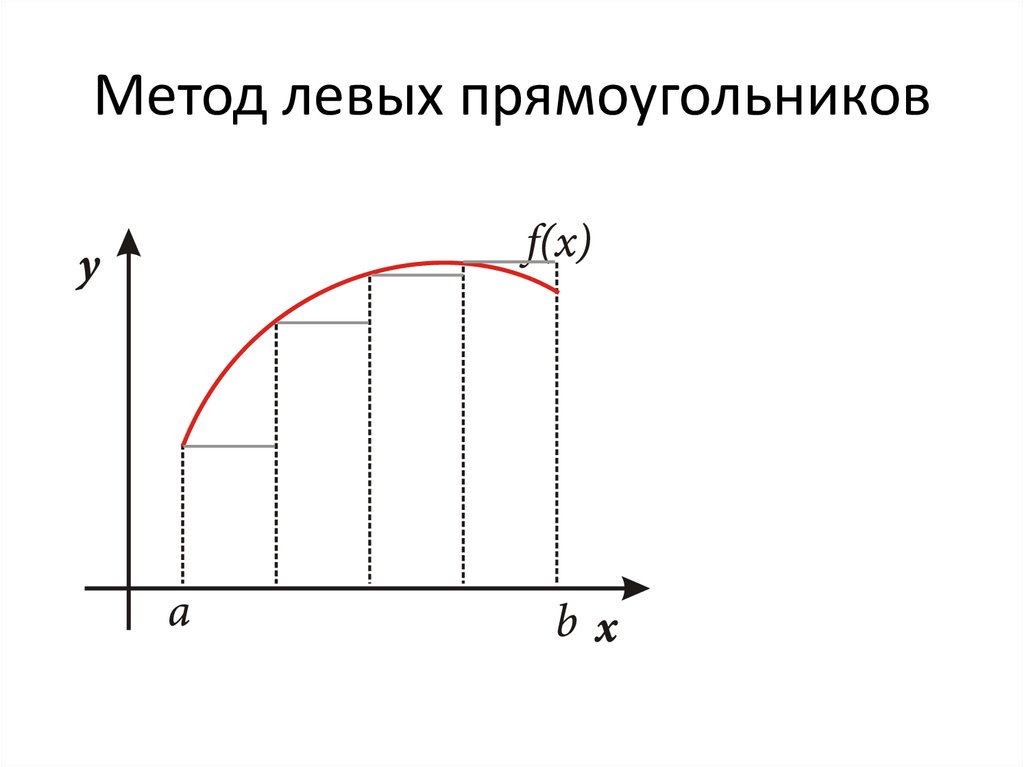
Метод левых прямоугольников

8.

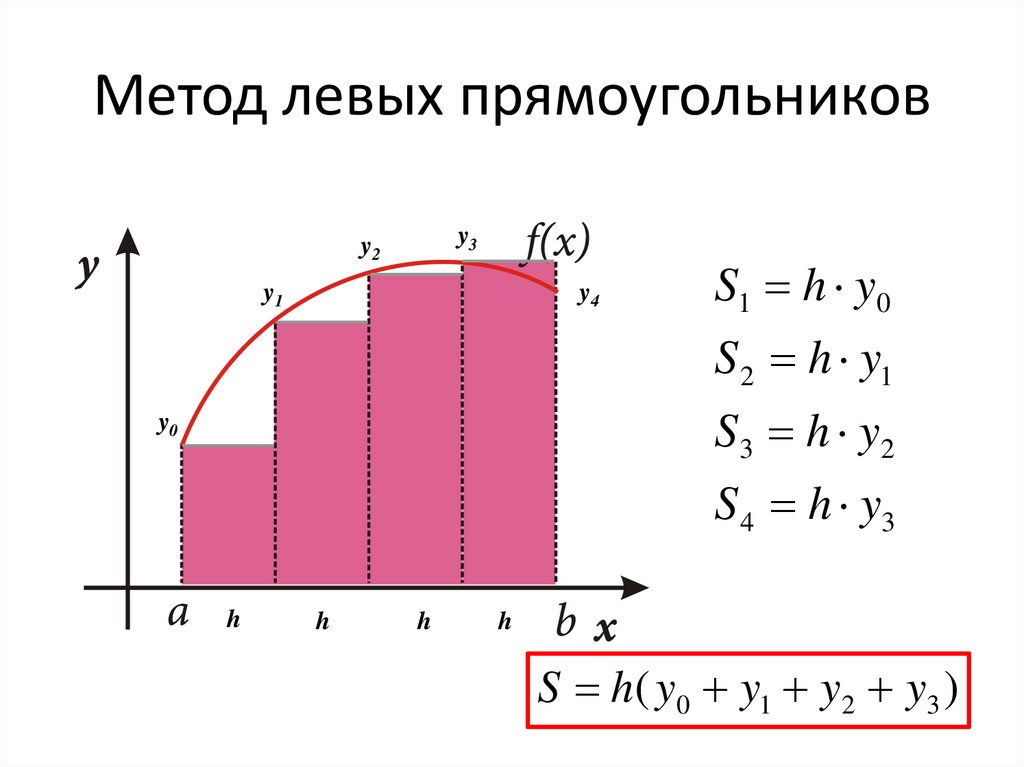
Метод левых прямоугольников
y3
y2
y1
y4
S1 h y0
S 2 h y1
S3 h y2
y0
S 4 h y3
h
h
h
h
S h( y0 y1 y2 y3 )

9.

Метод левых прямоугольников
b
f ( x)dx h( y0 y1 ... y n 1 )
a
b a
I I
f ( xi )
n i 0
л
n 1

10.

Метод правых прямоугольников

11.

Метод правых прямоугольников
y3
y2
y1
y4
S1 h y1
S 2 h y2
S 3 h y3
y0
S 4 h y4
h
h
h
h
S h( y1 y2 y3 y4 )

12.

Метод правых прямоугольников
b
f ( x)dx h( y1 y 2 ... y n )
a
I I
пр
b a
f ( xi )
n i 1
n

13.

Пример: вычислить значение
интеграла e dx по формуле левых
прямоугольников с шагом h=0,1
1
x2
0
n 1
b
a
I Iл
f ( xi )
n i 0
Составим таблицу значений функции

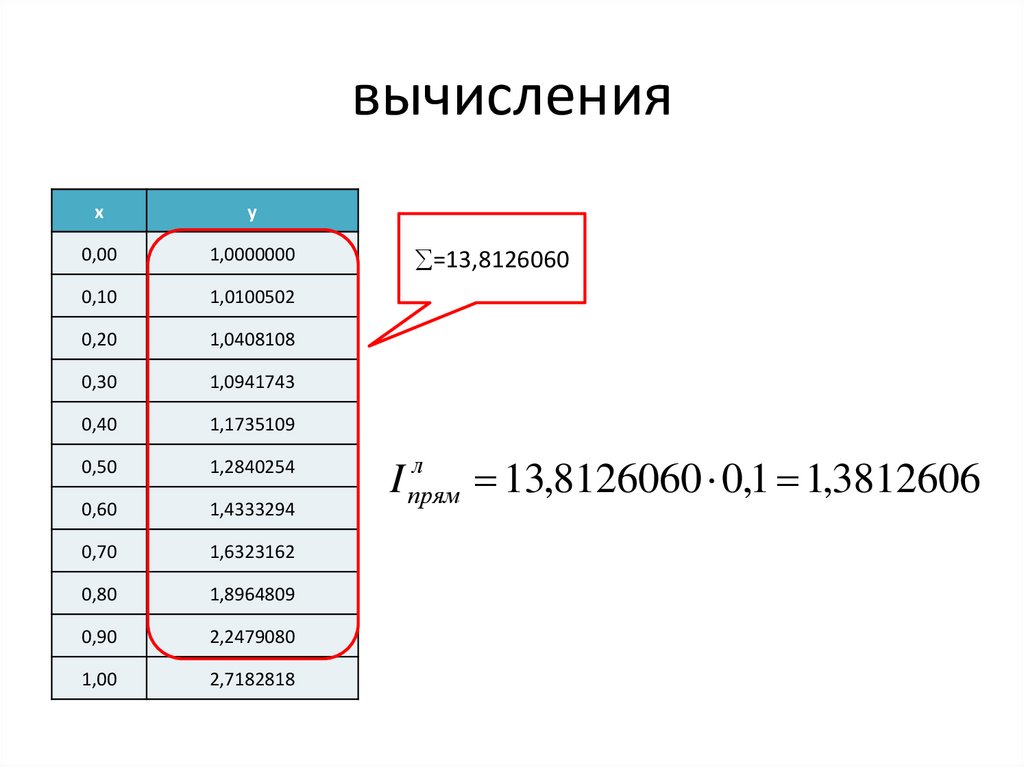
14.

вычисления
x
y
0,00
1,0000000
0,10
1,0100502
0,20
1,0408108
0,30
1,0941743
0,40
1,1735109
0,50
1,2840254
0,60
1,4333294
0,70
1,6323162
0,80
1,8964809
0,90
2,2479080
1,00
2,7182818
=13,8126060
л
I прям
13,8126060 0,1 1,3812606

15.

Метод трапеций
• Трапеция это…
• Площадь трапеции…

16.

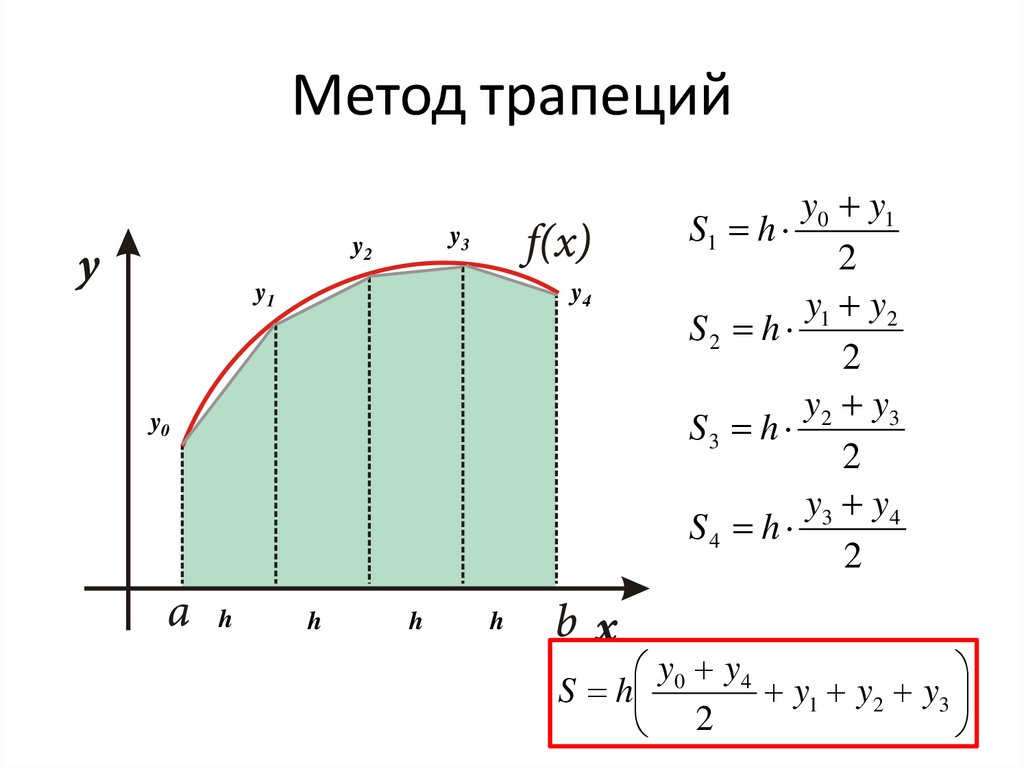
Метод трапеций

17.

Метод трапеций
y3
y2
y1
y4
y0
h
h
h
y0 y1
S1 h
2
y1 y2
S2 h
2
y 2 y3
S3 h
2
y3 y 4
S4 h
2
h
y0 y 4
S h
y1 y2 y3
2

18.

Метод трапеций
b
a
y0 y n
f ( x)dx h(
y1 ... y n 1 )
2
I I трап
b a f ( x0 ) f ( xn )
f ( xi )
n
2
i 1
n 1

19.

1
Пример: e
x2
dx
0
x
y
0,00
1,0000000
0,10
1,0100502
0,20
1,0408108
0,30
1,0941743
0,40
1,1735109
0,50
1,2840254
0,60
1,4333294
0,70
1,6323162
0,80
1,8964809
0,90
2,2479080
1,00
2,7182818
y0 y10 9
S 0,1
yi
i 1
2
I трап 1,467175

20.

Метод Симпсона
=х0
х1
х2
х3

21.

Метод Симпсона
f ( xi 1 ) f ( xi )
y L2 ( x) f ( xi )
( x xi )
h
f ( xi 1 ) 2 f ( xi ) f ( xi )
2
(
x
x
)
i
2
h
2

22.

Метод Симпсона
Ii
xi 1
xi
h
L2 ( x)dx ( f ( xi ) 4 f ( xi ) f ( xi 1 ))
6
n 1
n 1
h
I I c 6 f ( x0 ) f ( xn ) 4 f ( xi ) 2 f ( xi )
i 0
i 1

23.

Правило Рунге практической
оценки погрешности
• Оценки погрешности зависят по h
• Чем меньше h, тем выше точность
I I Ch
h
h
2
k
1 k 1
h
I I Ch k ( I I )
2
2

24.

Правило Рунге практической оценки
погрешности
h
2
I I
I I k
2 1
h
2
h
Для формул прямоугольников и трапеций
k=2
Для формулы Симпсона k=4

25.

Правило Рунге практической оценки
погрешности
I I пр
1
h
I I пр
3
I I тр
1
I
3
h
2
пр
h
2
тр
I
h
тр
1
h
I I С I I С
15
h
2
С

26.

Вычисление интеграла с заданной
точностью
Определить точность и начальную величину
шага h
Вычислить значение интеграла Ih
Уменьшить значение h в 2 раза и вычислить Ih/2
Сравнить Ih и Ih/2 по формуле Рунге
Процедура прекращается когда результаты
двух вычислений отличаются меньше чем на

27.

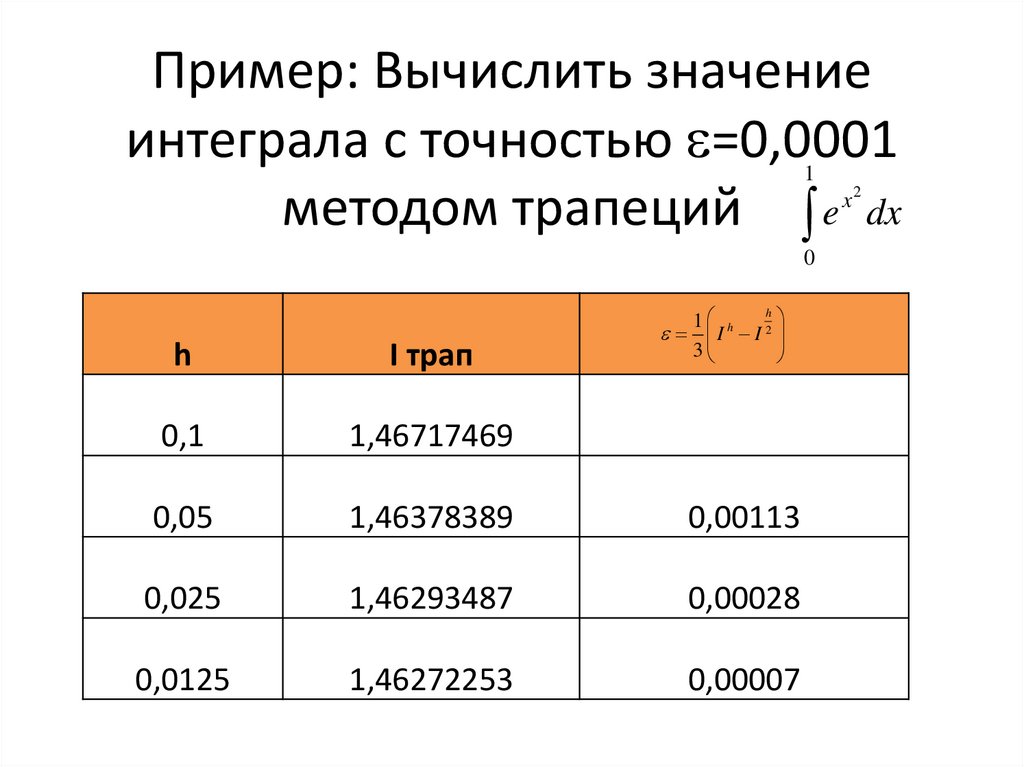
Пример: Вычислить значение
интеграла с точностью =0,0001
методом трапеций e dx
1
x2
0
h
1 h
I I 2
3
h
I трап
0,1
1,46717469
0,05
1,46378389
0,00113
0,025
1,46293487
0,00028
0,0125
1,46272253
0,00007