Similar presentations:
Угол между прямыми. Угол между прямой и плоскостью
1.
Угол между прямыми. Угол междупрямой и плоскостью.
Геометрия, 10 класс.
2.
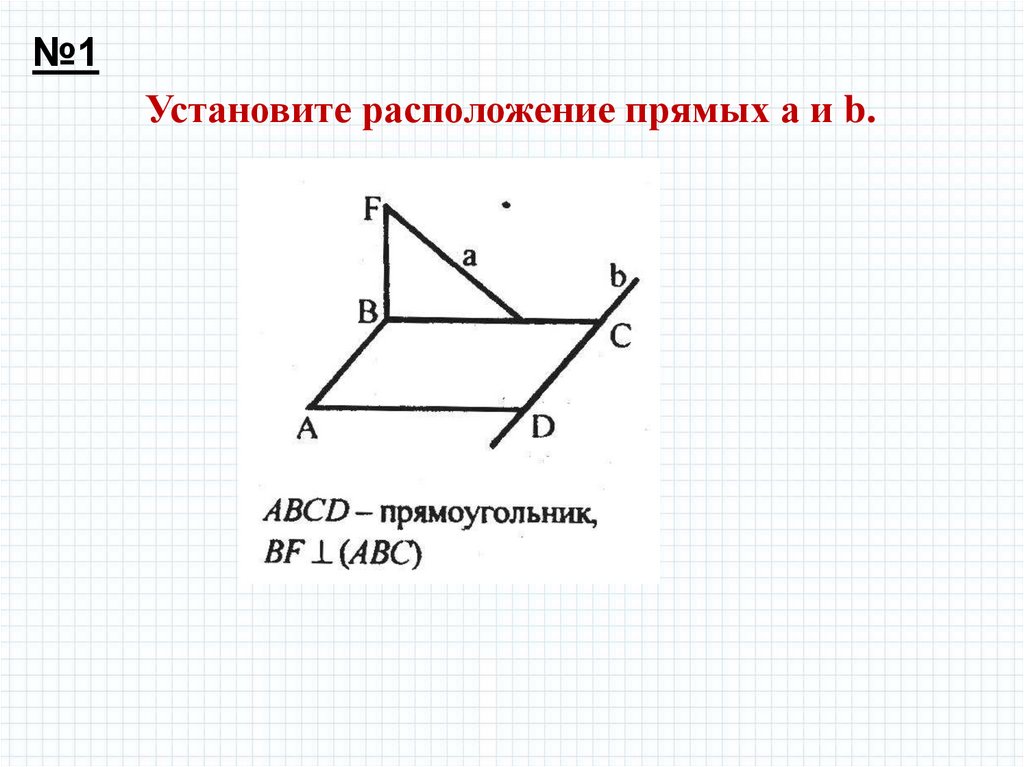
№1Установите расположение прямых а и b.
3.
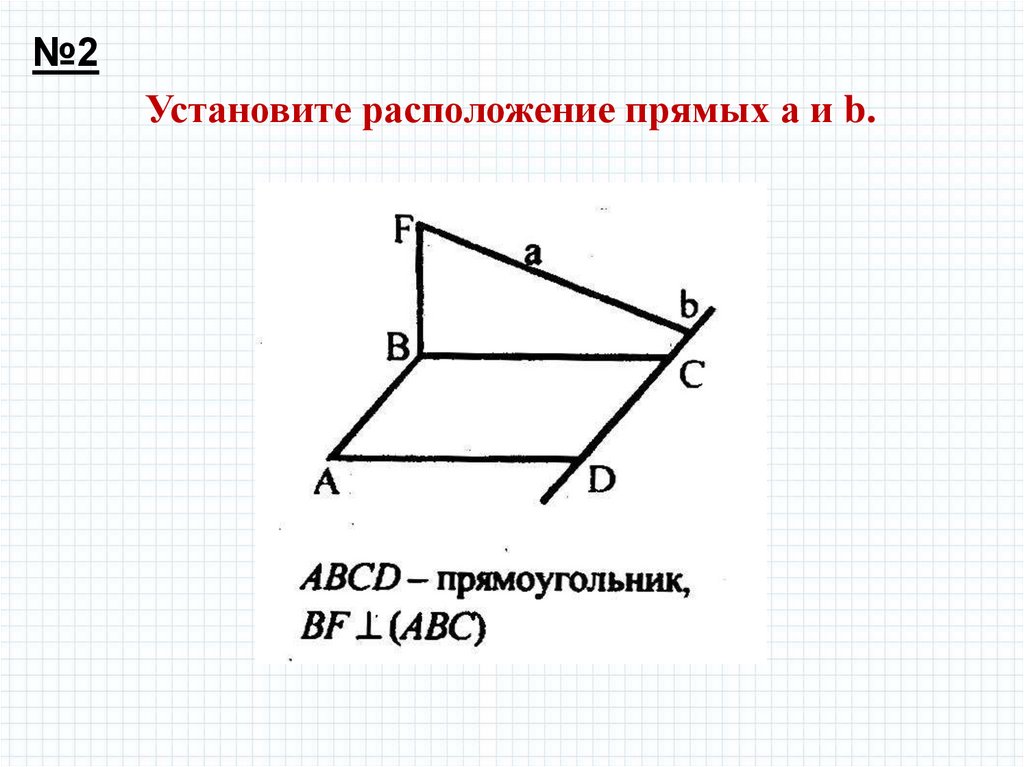
№2Установите расположение прямых а и b.
4.
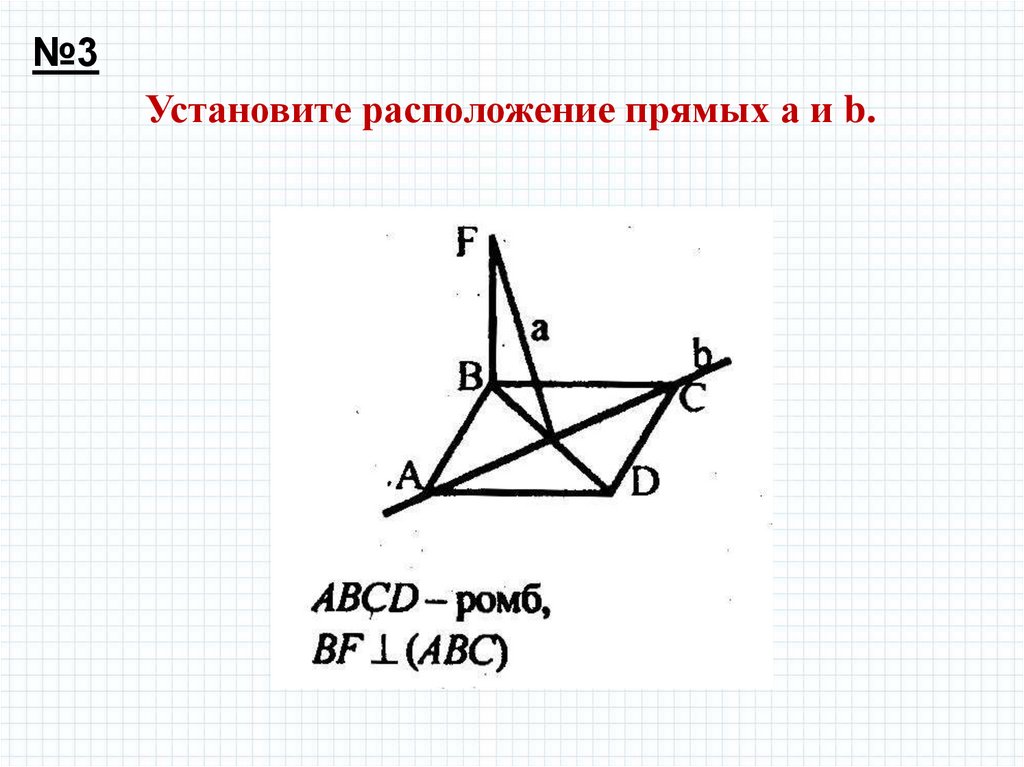
№3Установите расположение прямых а и b.
5.
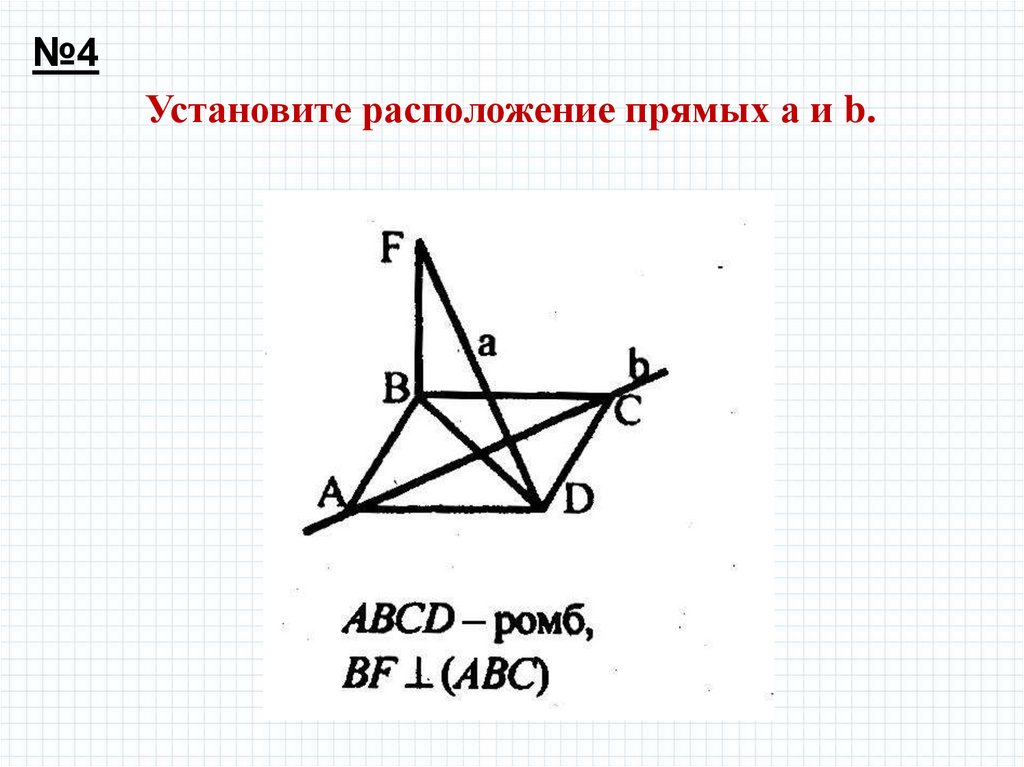
№4Установите расположение прямых а и b.
6.
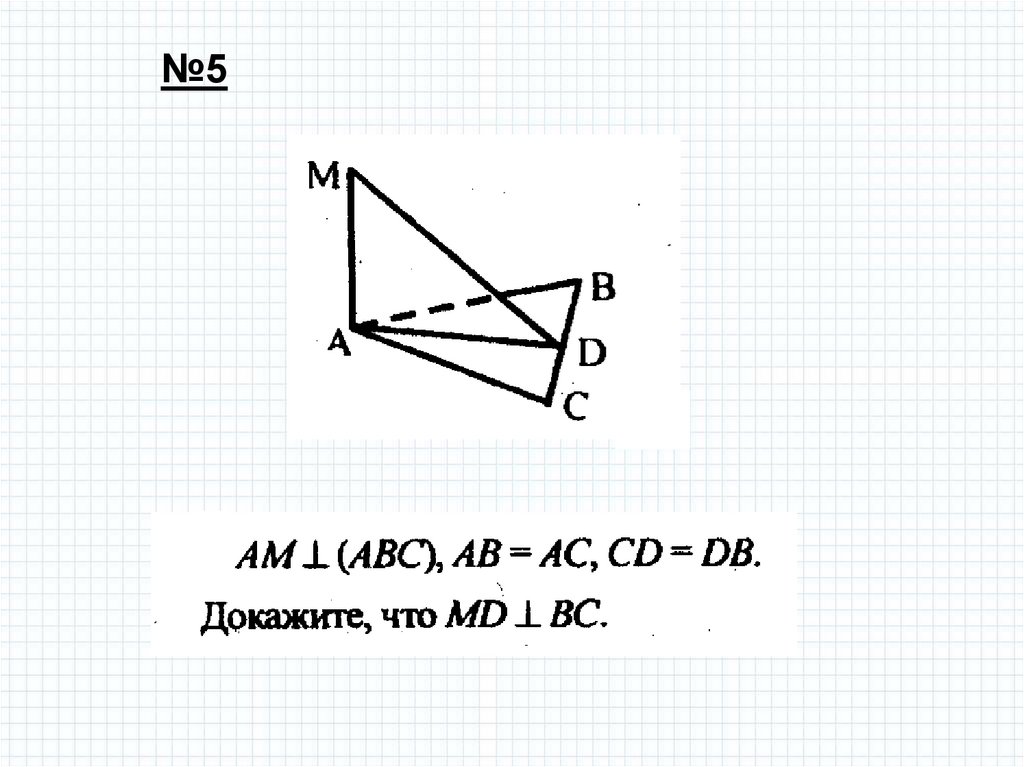
№57.
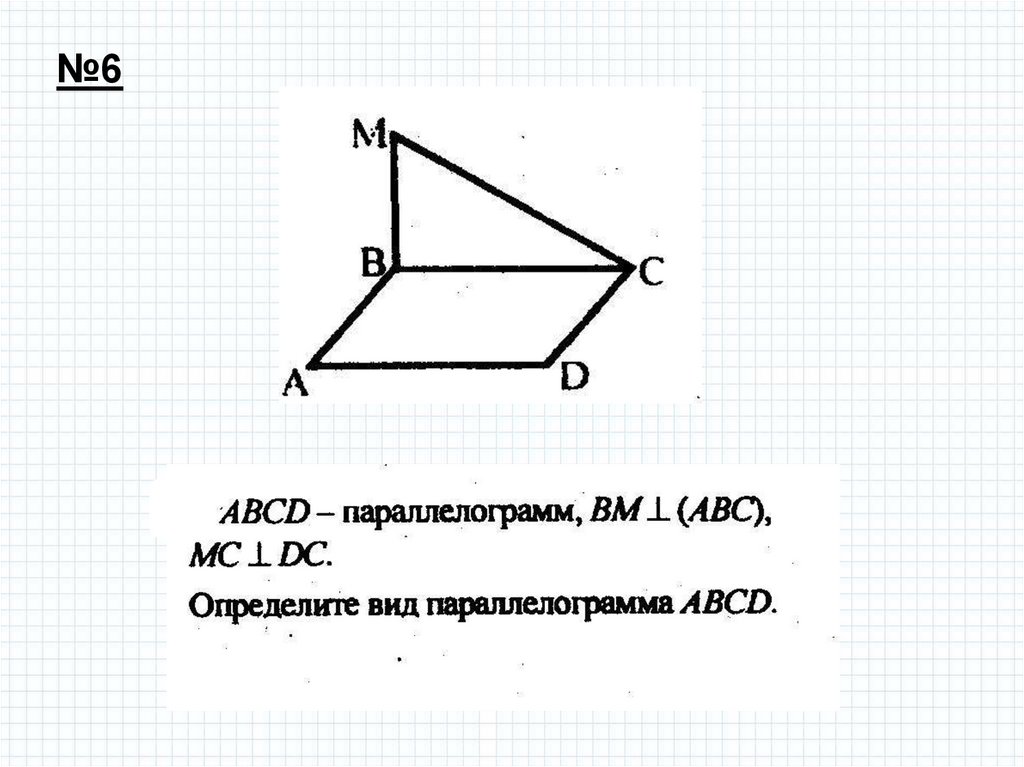
№68.
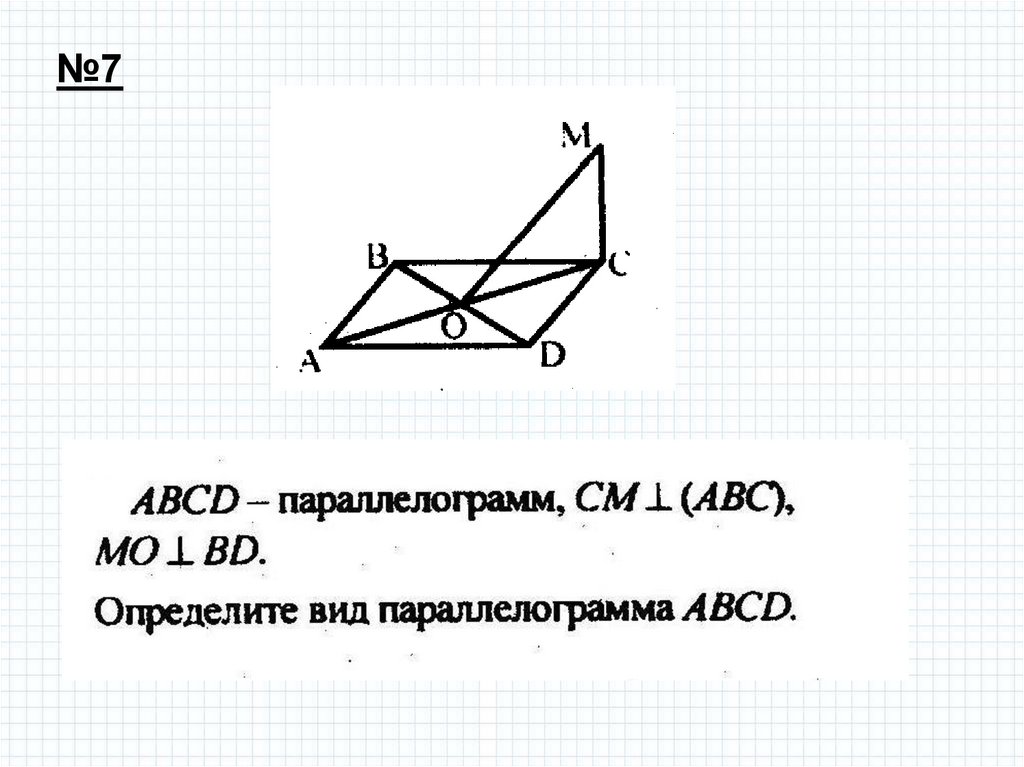
№79.
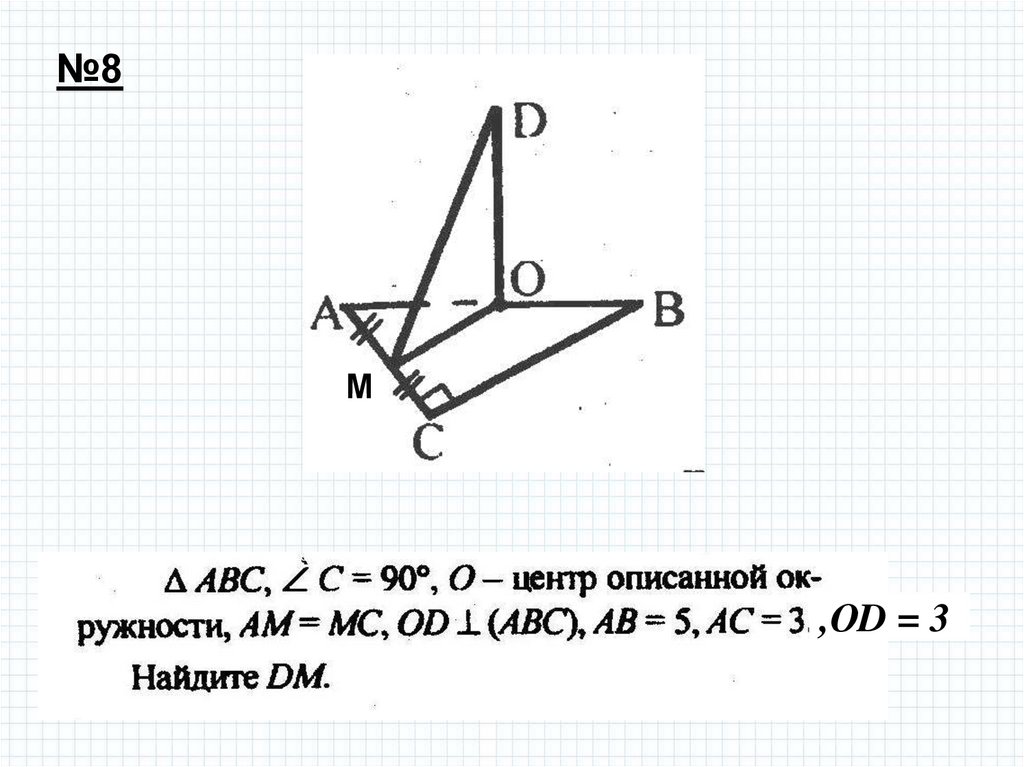
№8М
,ОD = 3
10.
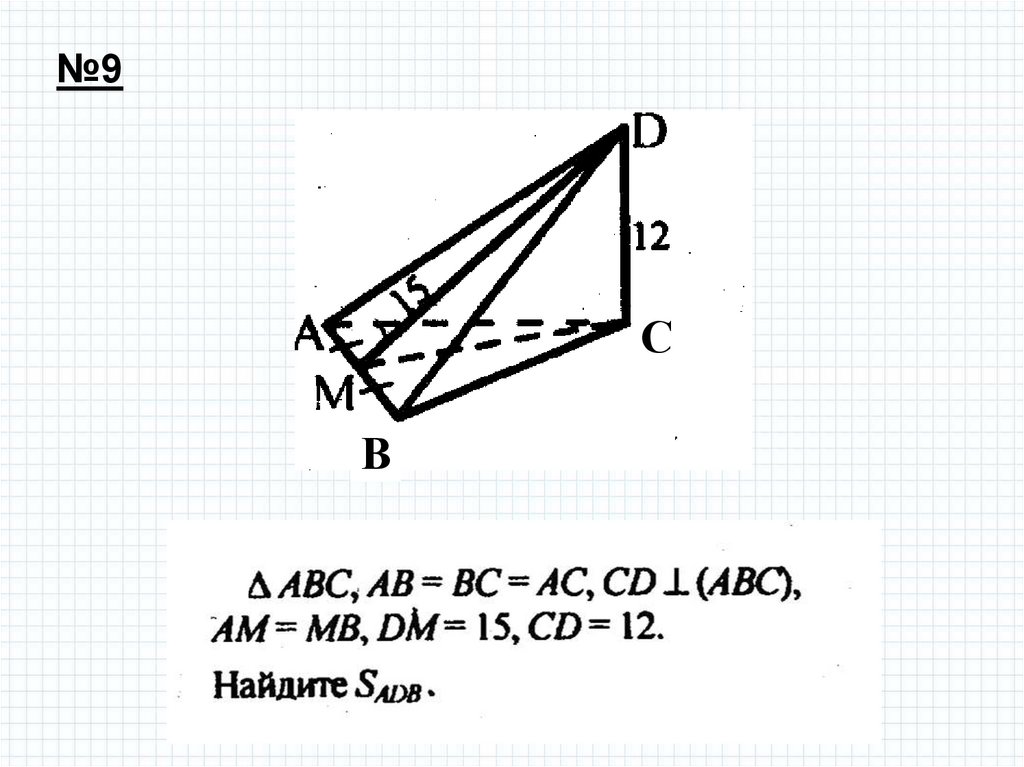
№9С
В
11.
Проекция точки на плоскостьПроекцией точки на
плоскость называется основание
перпендикуляра, проведенного из
этой точки к плоскости, если
точка не лежит в плоскости, и сама
точка, если она лежит в
плоскости.
На рисунке 54
точка М1 — проекция точки М на плоскость ,
a N — проекция самой точки N на ту же плоскость
(N a).
12.
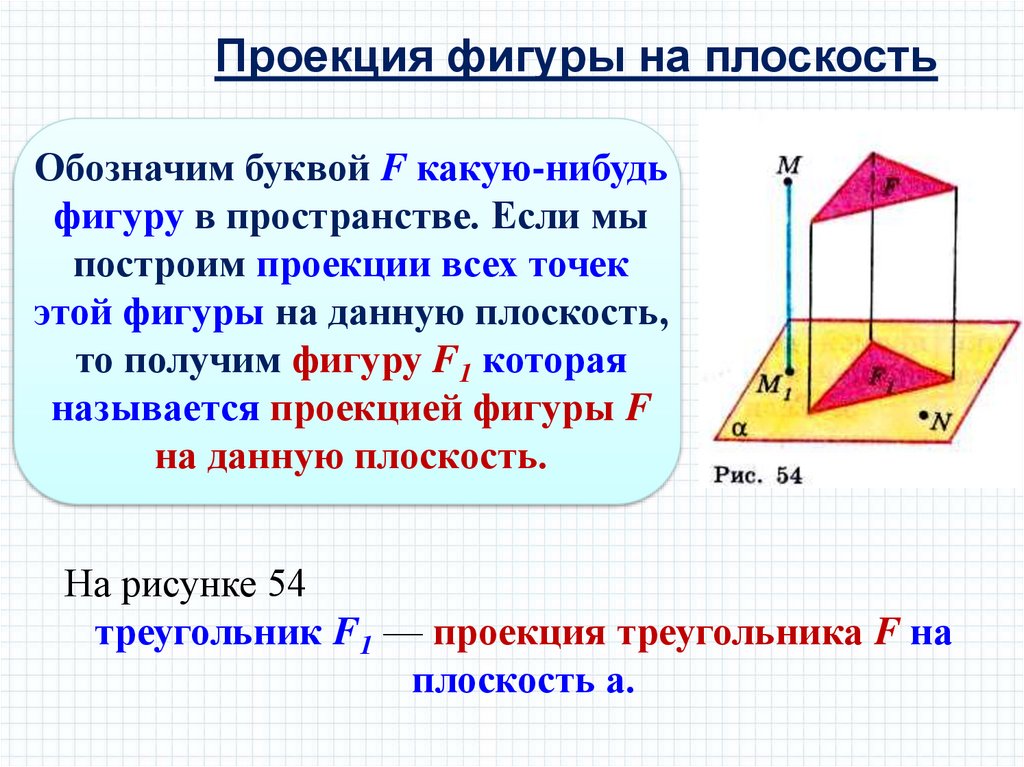
Проекция фигуры на плоскостьОбозначим буквой F какую-нибудь
фигуру в пространстве. Если мы
построим проекции всех точек
этой фигуры на данную плоскость,
то получим фигуру F1 которая
называется проекцией фигуры F
на данную плоскость.
На рисунке 54
треугольник F1 — проекция треугольника F на
плоскость а.
13.
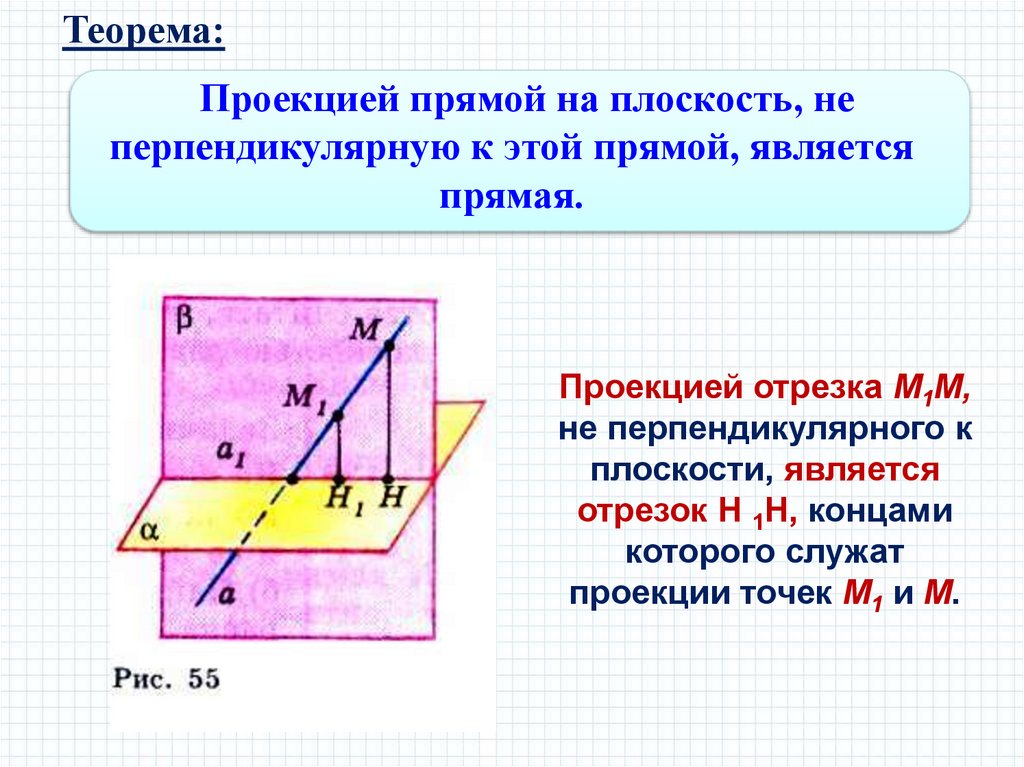
Теорема:Проекцией прямой на плоскость, не
перпендикулярную к этой прямой, является
прямая.
Проекцией отрезка М1М,
не перпендикулярного к
плоскости, является
отрезок Н 1Н, концами
которого служат
проекции точек М1 и М.
14.
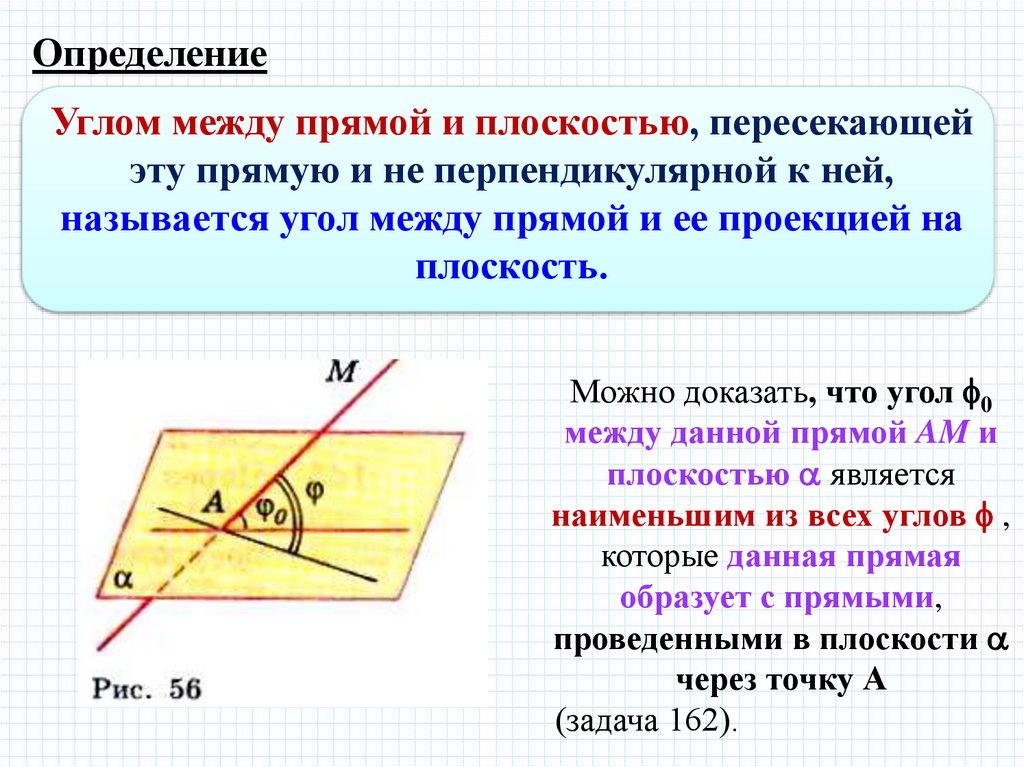
ОпределениеУглом между прямой и плоскостью, пересекающей
эту прямую и не перпендикулярной к ней,
называется угол между прямой и ее проекцией на
плоскость.
Можно доказать, что угол 0
между данной прямой AM и
плоскостью является
наименьшим из всех углов ,
которые данная прямая
образует с прямыми,
проведенными в плоскости
через точку А
(задача 162).
15.
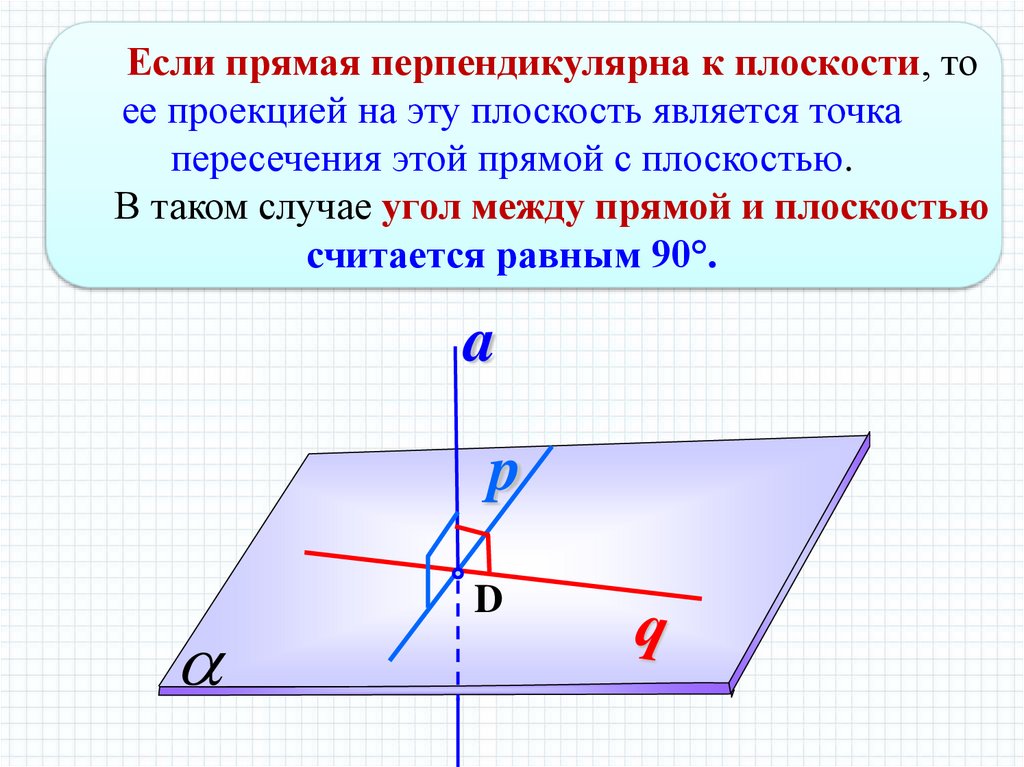
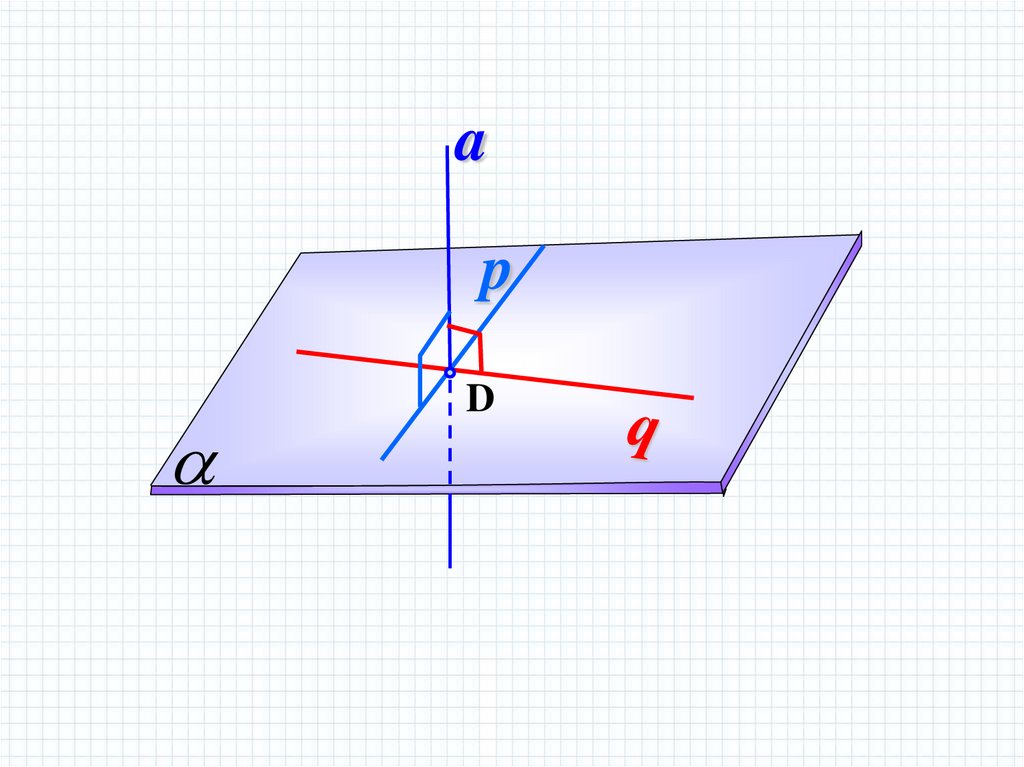
Если прямая перпендикулярна к плоскости, тоее проекцией на эту плоскость является точка
пересечения этой прямой с плоскостью.
В таком случае угол между прямой и плоскостью
считается равным 90°.
a
p
D
16.
ap
D
17.
сa
18.
Если прямая параллельна плоскости, то еепроекцией на эту плоскость является прямая
параллельная данной.
В таком случае угол между прямой и
плоскостью считается равным 0°.
с
a
19.
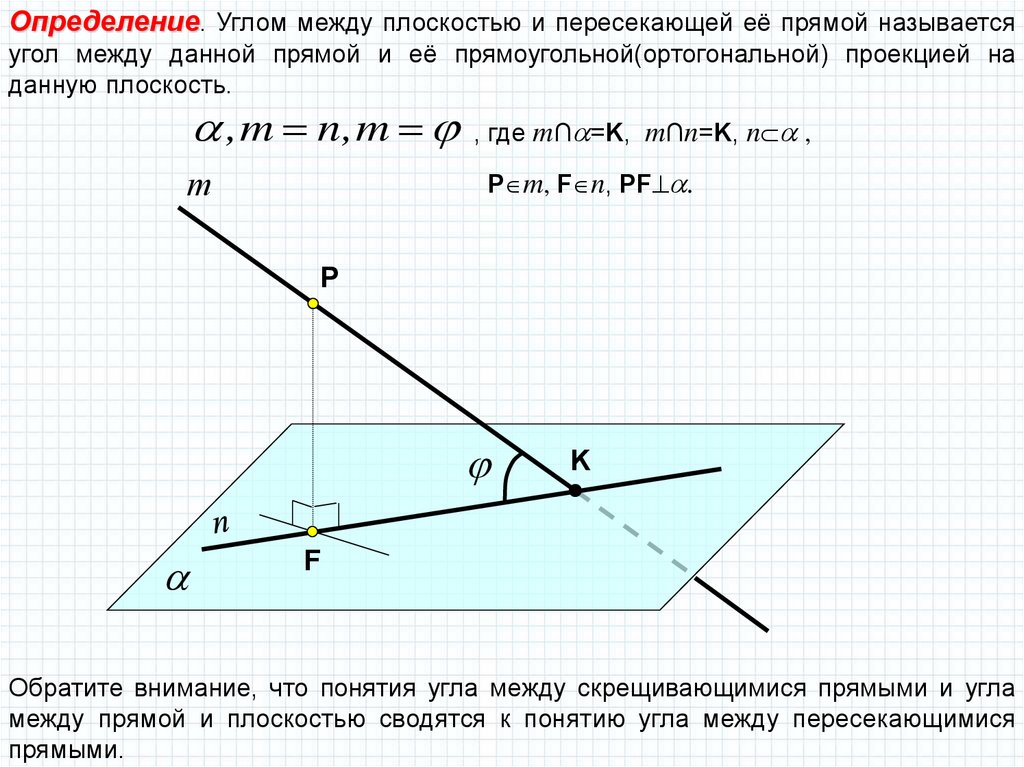
Определение. Углом между плоскостью и пересекающей её прямой называетсяугол между данной прямой и её прямоугольной(ортогональной) проекцией на
данную плоскость.
,m n,m , где m∩ =K, m∩n=K, n ,
P m, F n, PF .
т
P
K
F
Обратите внимание, что понятия угла между скрещивающимися прямыми и угла
между прямой и плоскостью сводятся к понятию угла между пересекающимися
прямыми.
20.
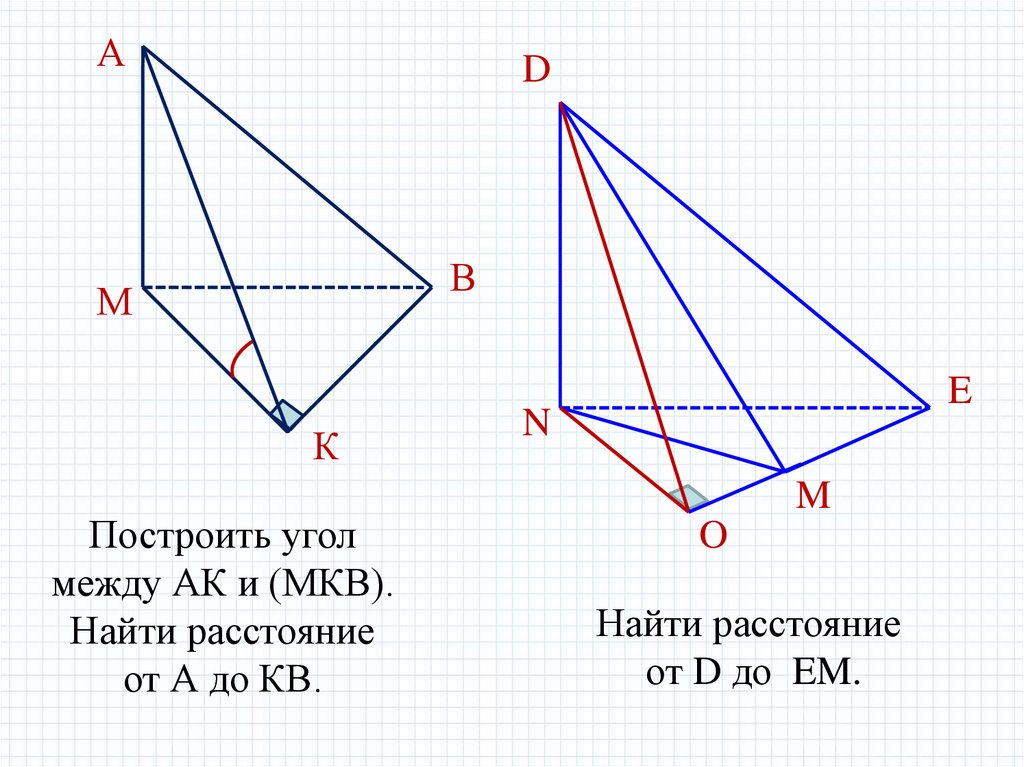
АD
В
М
К
Построить угол
между АК и (МКВ).
Найти расстояние
от А до КВ.
E
N
M
O
Найти расстояние
от D до EM.
21.
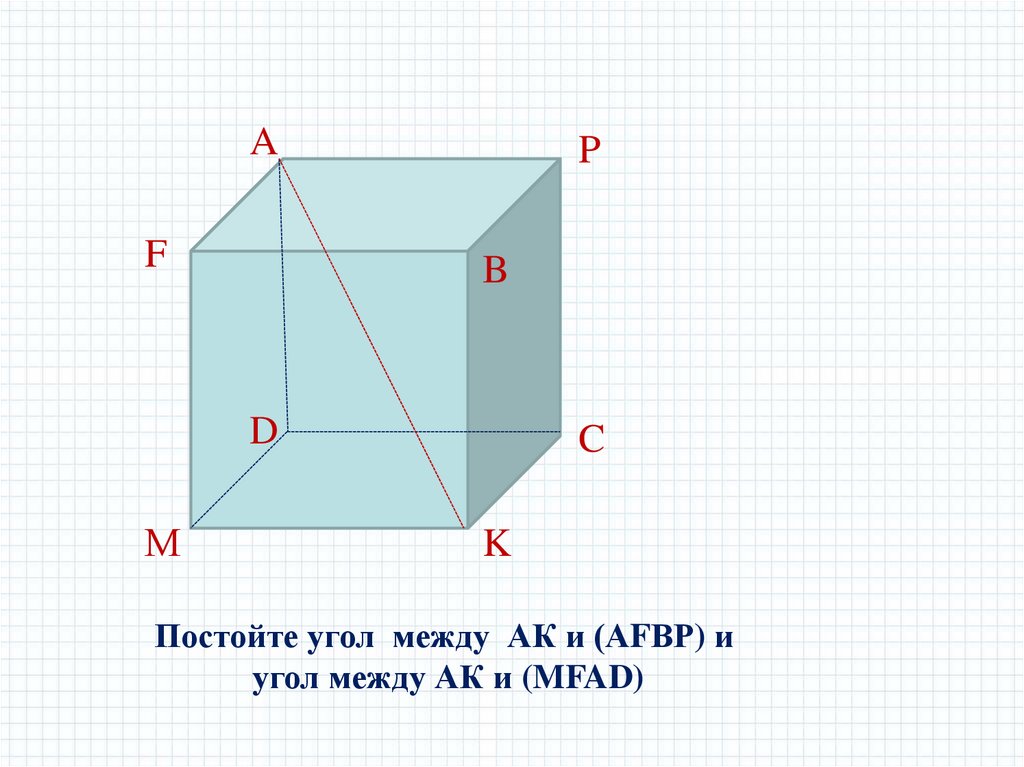
AF
P
B
D
М
C
K
Постойте угол между АК и (АFВР) и
угол между АК и (MFAD)
22.
ААМ (МВК)
В
М
К
Найти угол между АК и (АМВ)
23.
ААМ (МВК)
В
М
К
Найти угол между АК и (АМВ)







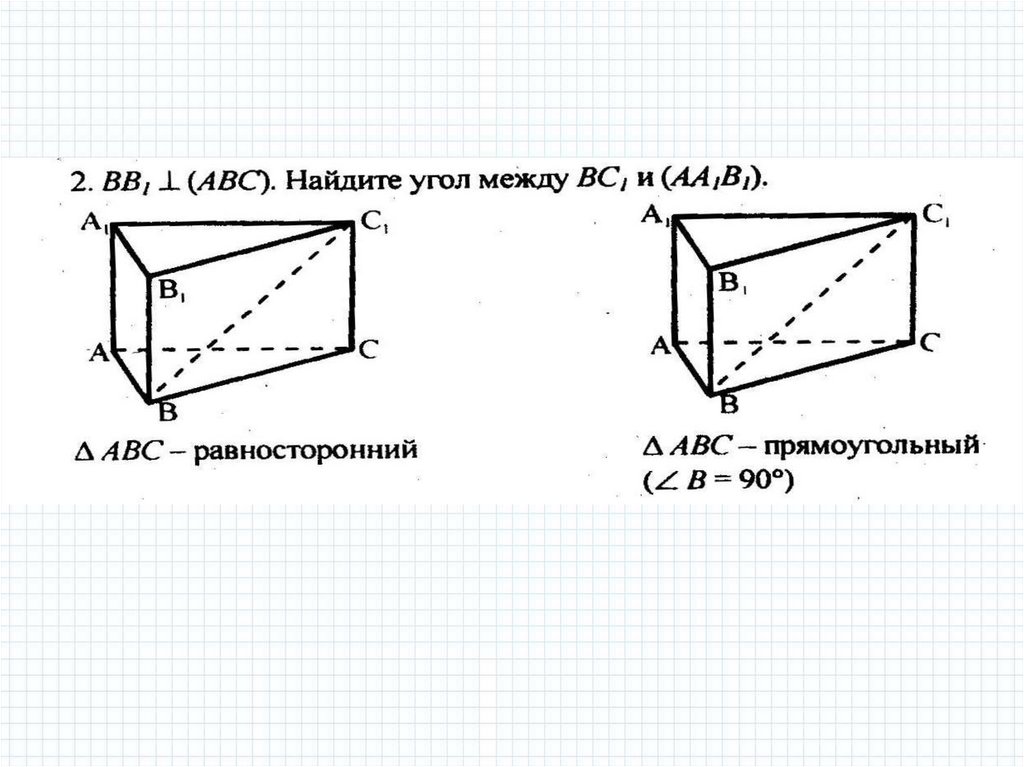
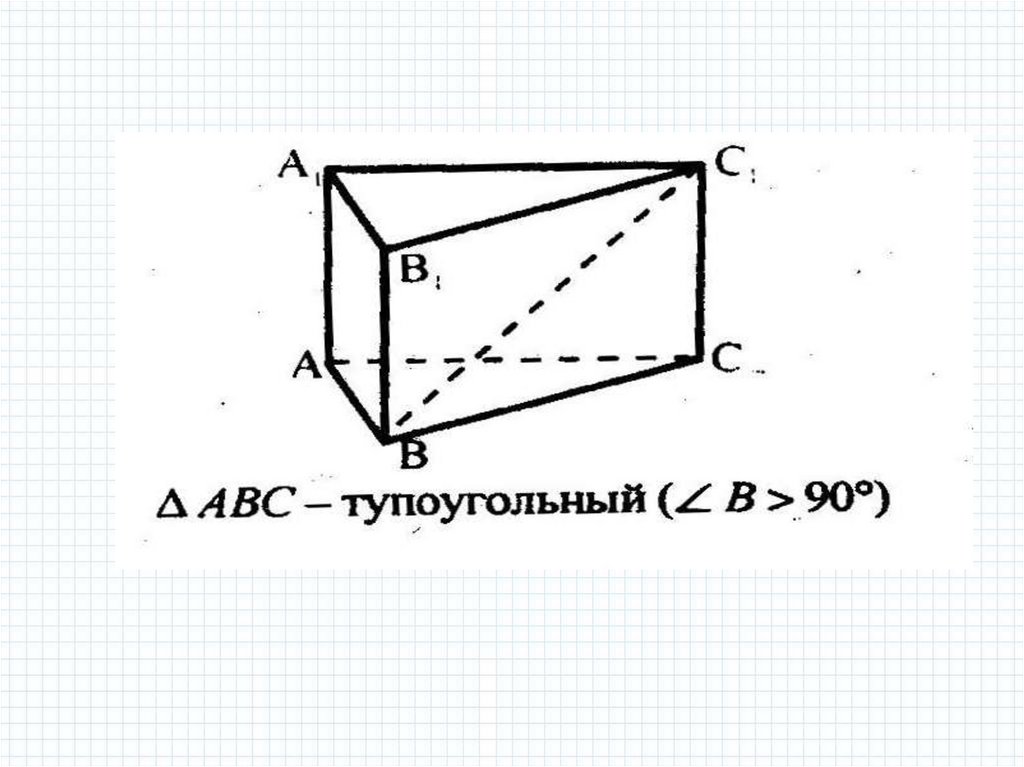
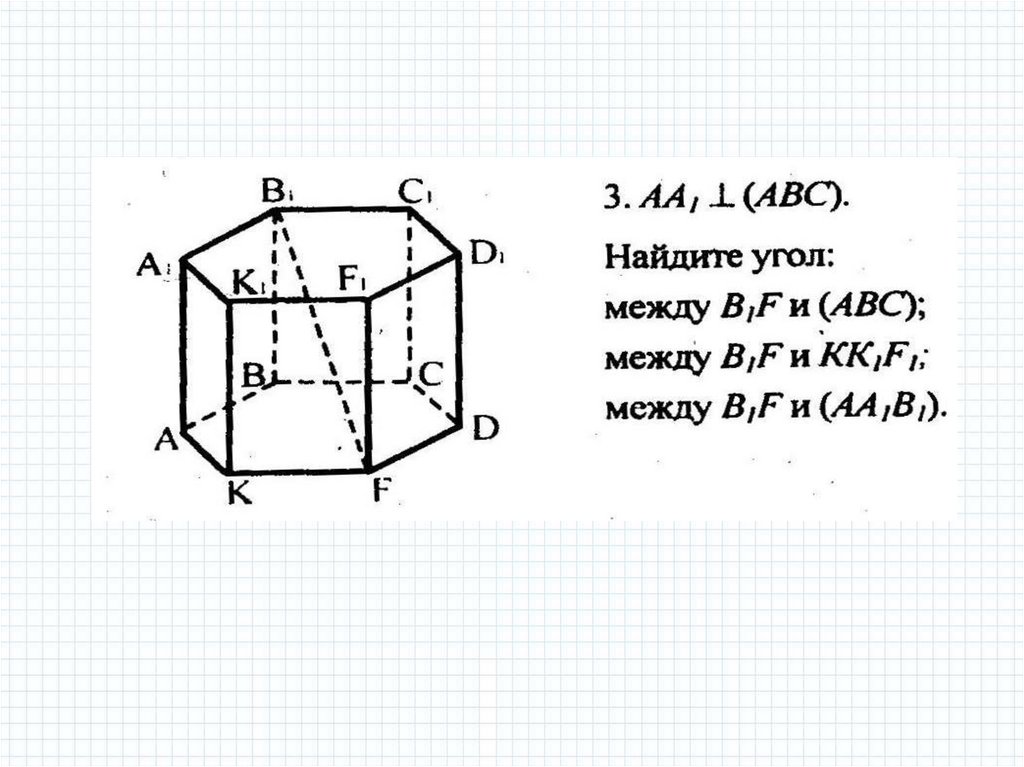
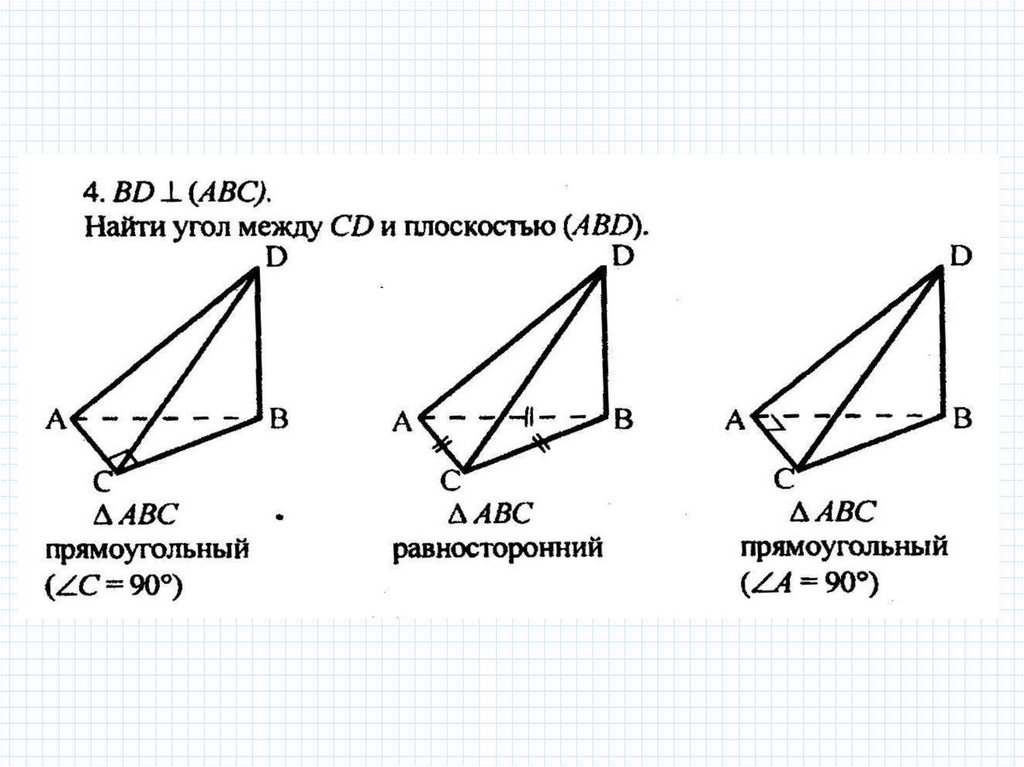
 mathematics
mathematics