Similar presentations:
Угол между прямой и плоскостью
1.
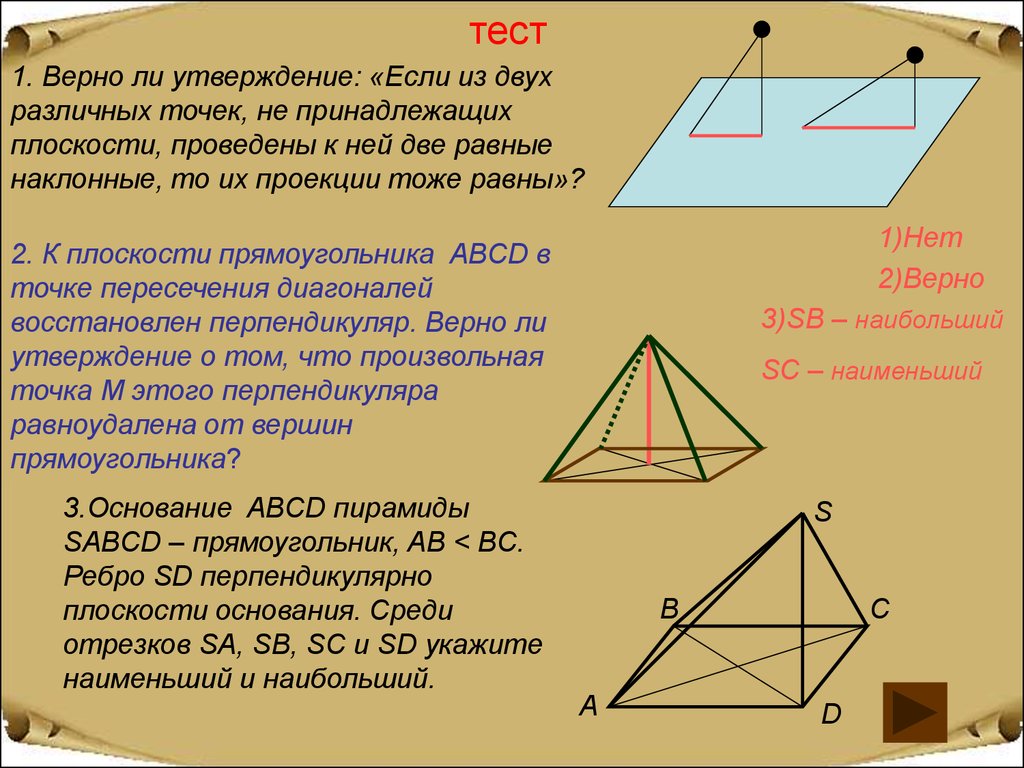
тест1. Верно ли утверждение: «Если из двух
различных точек, не принадлежащих
плоскости, проведены к ней две равные
наклонные, то их проекции тоже равны»?
1)Нет
2)Верно
2. К плоскости прямоугольника ABCD в
точке пересечения диагоналей
восстановлен перпендикуляр. Верно ли
утверждение о том, что произвольная
точка M этого перпендикуляра
равноудалена от вершин
прямоугольника?
3)SB – наибольший
SC – наименьший
3.Основание ABCD пирамиды
SABCD – прямоугольник, AB < BC.
Ребро SD перпендикулярно
плоскости основания. Среди
отрезков SA, SB, SC и SD укажите
наименьший и наибольший.
S
B
A
C
D
2.
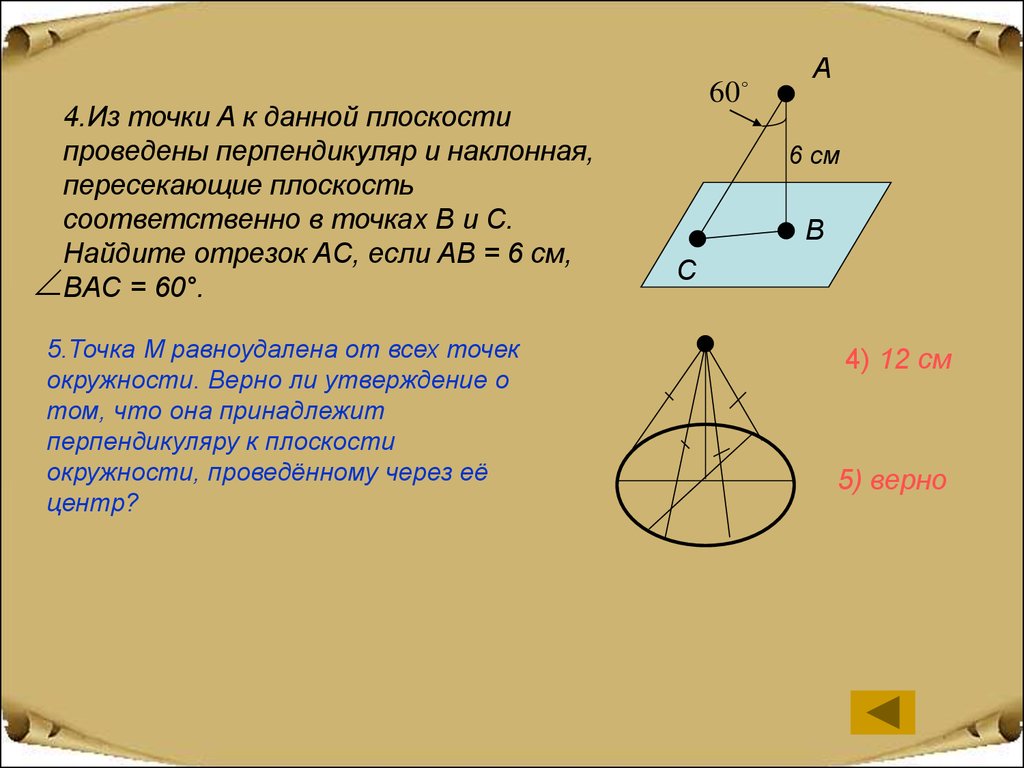
4.Из точки A к данной плоскостипроведены перпендикуляр и наклонная,
пересекающие плоскость
соответственно в точках B и C.
Найдите отрезок AC, если AB = 6 см,
BAC = 60°.
5.Точка M равноудалена от всех точек
окружности. Верно ли утверждение о
том, что она принадлежит
перпендикуляру к плоскости
окружности, проведённому через её
центр?
60
А
6 см
В
С
4) 12 см
5) верно
3. Угол между прямой и плоскостью
План урока:1. Проекция точки, прямой.
2. Угол между прямой и
плоскостью.
3. Задачи на нахождение
угла между прямой и
плоскостью.
4.
Проекция точки на плоскость.1. А ;
А
В
С
АВ
Точка B – проекция точки
A на плоскость
2.
С
Точка С – проекция точки
С на плоскость
5.
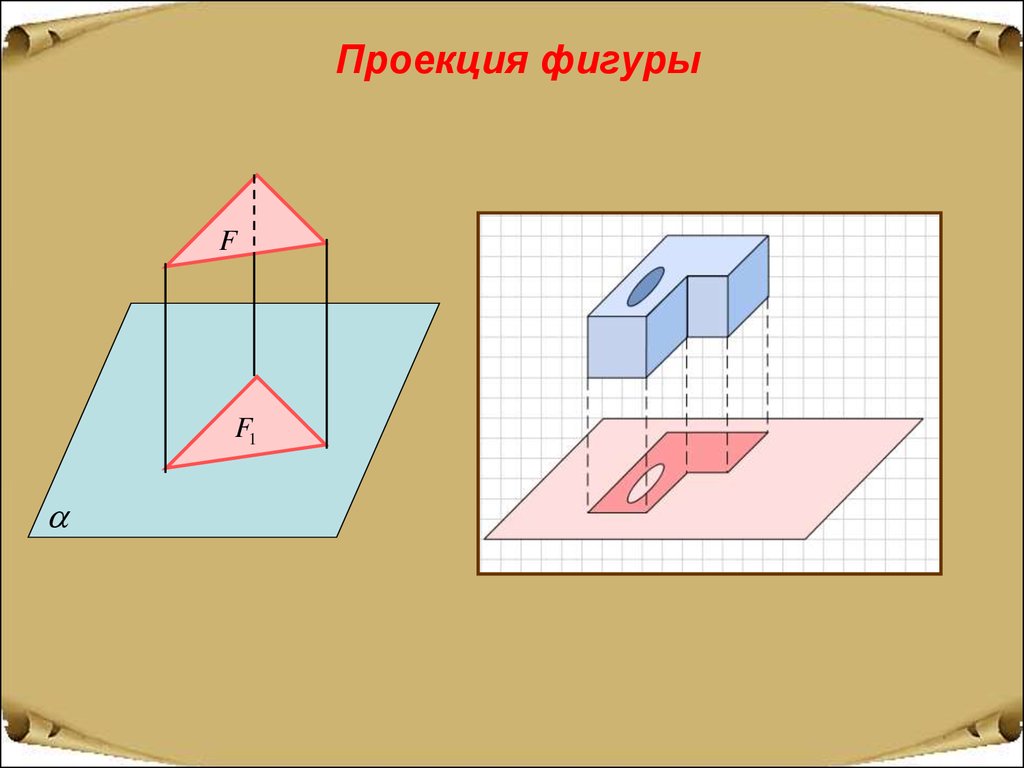
Проекция фигурыF
F1
6.
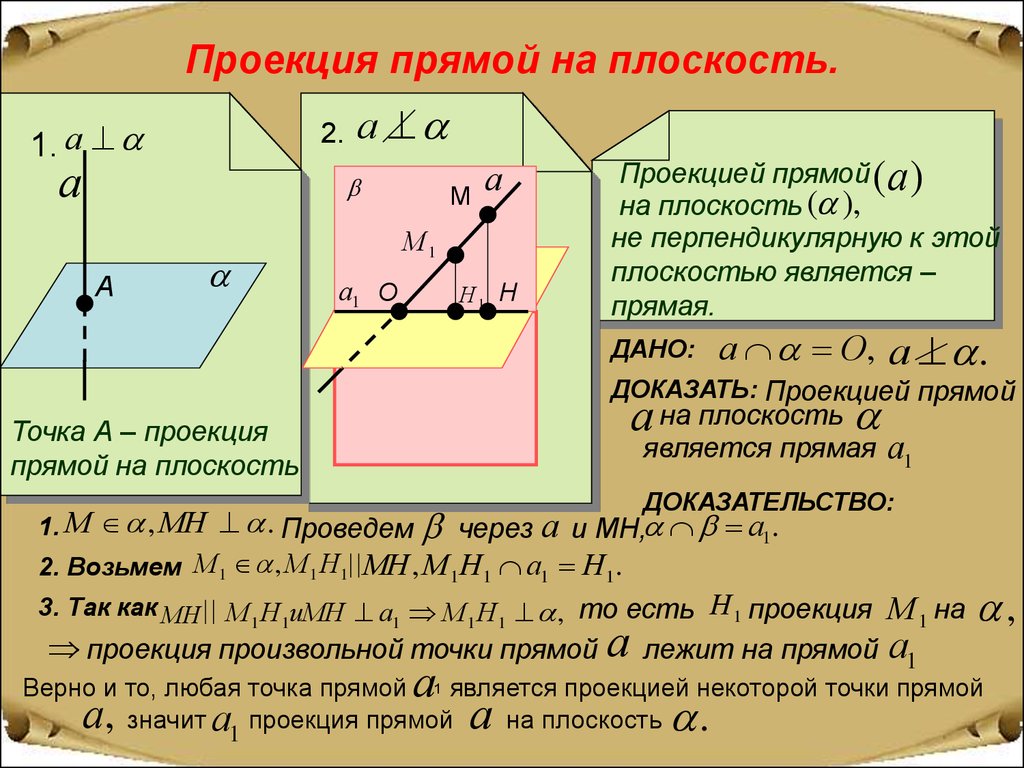
Проекция прямой на плоскость.1. а
2.
а
а
А
М
а
М1
а1 О
Н1 Н
Проекцией прямой (а )
на плоскость ( ),
не перпендикулярную к этой
плоскостью является –
прямая.
ДАНО:
а О, а .
ДОКАЗАТЬ: Проекцией прямой
а на плоскость
Точка А – проекция
прямой на плоскость
1. М , МН . Проведем
является прямая
а1
ДОКАЗАТЕЛЬСТВО:
через а и МН, а1.
2. Возьмем М 1 , М 1 Н1 МН , М 1 Н1 а1 Н1 .
3. Так как МН М1 Н1иМН а1 М1 Н1 , то есть Н 1 проекция М 1 на
проекция произвольной точки прямой а лежит на прямой а1
а
,
Верно и то, любая точка прямой 1 является проекцией некоторой точки прямой
значит а1 проекция прямой
на плоскость
а,
а
.
7.
Угол между прямой и плоскостью.Углом между прямой и плоскостью, пересекающей
эту прямую и не перпендикулярную к ней, называется
угол между прямой и ее проекцией на плоскость.
а
а1 А
Если
а на плоскость
а , а а1– проекция прямой
а, то (а, ) (а1 , а)
8.
А что, еслиа ?
а или
9.
аа
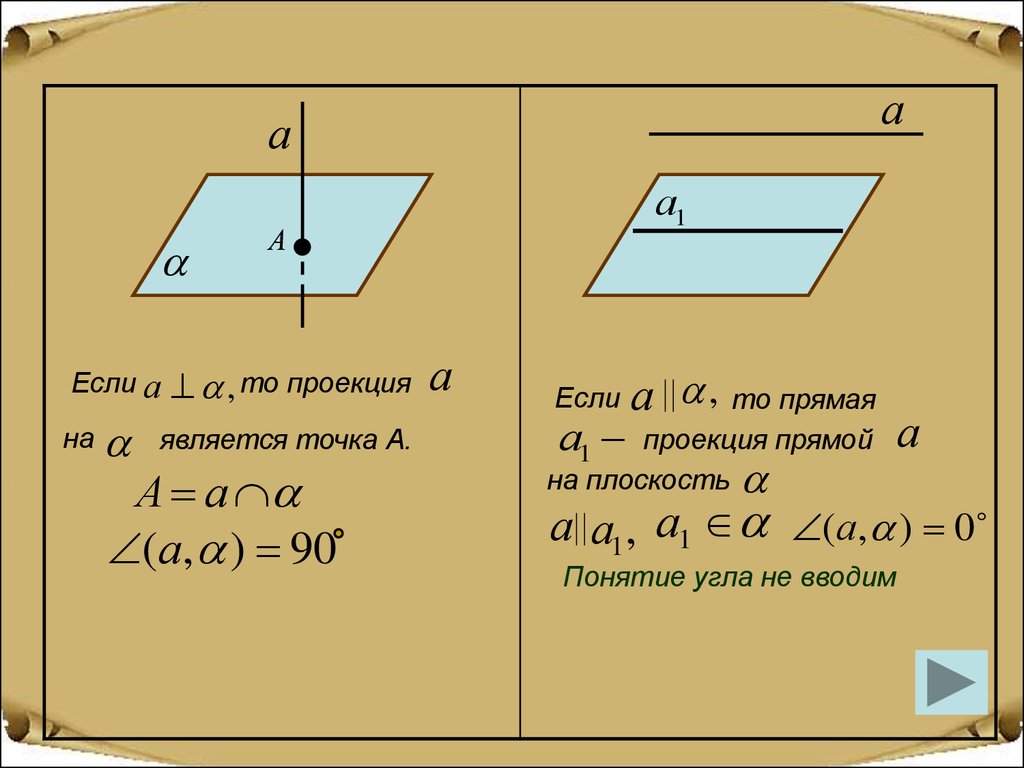
Если а
на
а1
А
, то проекция
является точка А.
А а
(а, ) 90
а
Если
а1
а , то прямая
проекция прямой
на плоскость
а
а а1 , а1 (а, ) 0
Понятие угла не вводим
10.
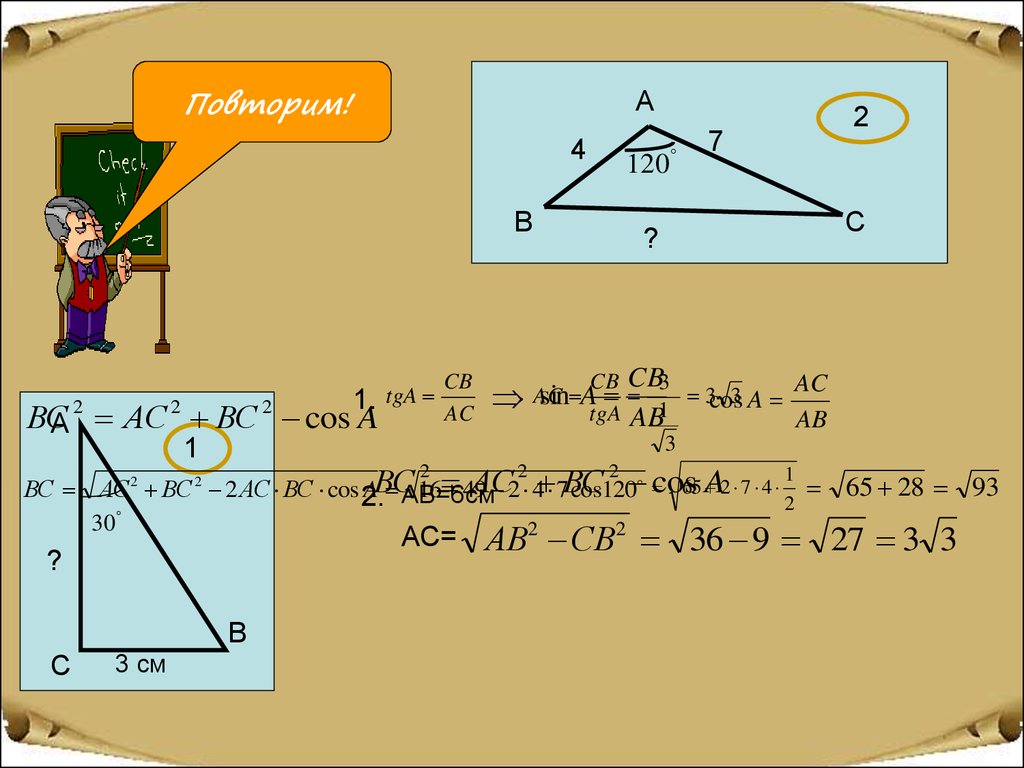
Повторим!А
4
В
1.
ВС
А АС ВС cos A
2
2
2
1
ВС АС ВС
30
2
2
АС=
В
3 см
CB
AC
7
?
С
CB CB3
AC
sin A 1 3cos3 A AC
tgA AB
AB
3
2
2
2
1
ВС
АС
ВС
65 A
2 7 4 65 28 93
2 АС ВС cos 2.
A АВ=6см
16 49 2 4 7 cos120 cos
2
?
С
tgA
120
2
АВ2 СВ2 36 9 27 3 3
11.
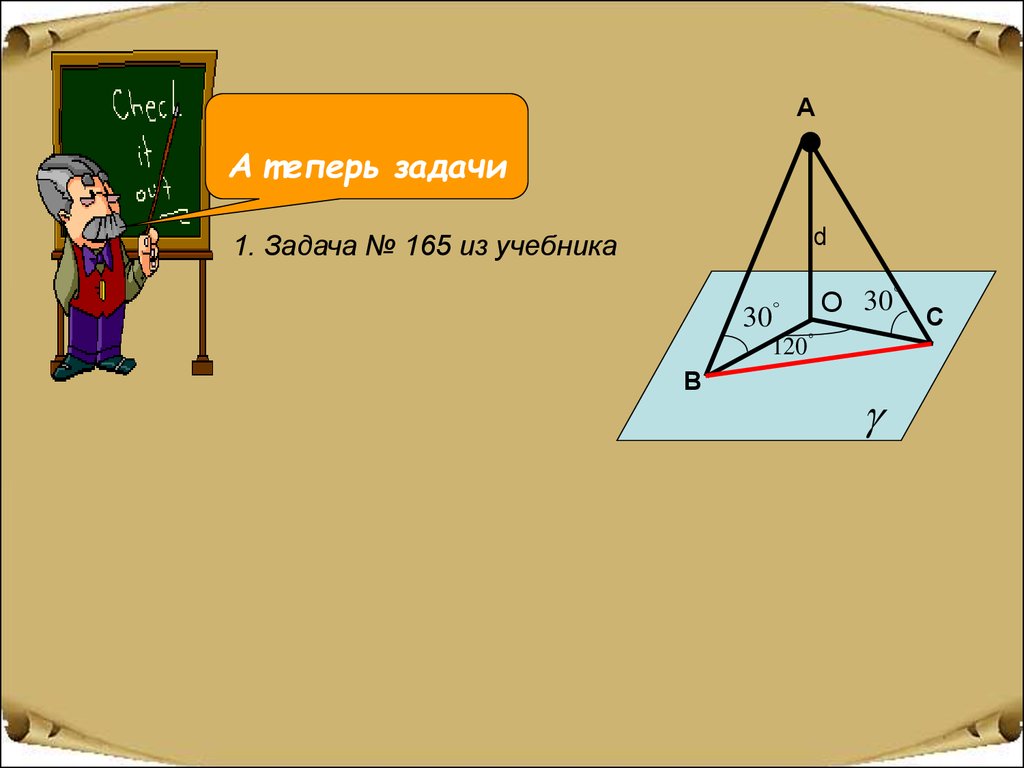
А т еперь задачи1. Задача № 165 из учебника
12.
АА т еперь задачи
d
1. Задача № 165 из учебника
30
120
В
О 30 С





 mathematics
mathematics