Similar presentations:
Угол между прямой и плоскостью
1.
2.
АВ
С
α
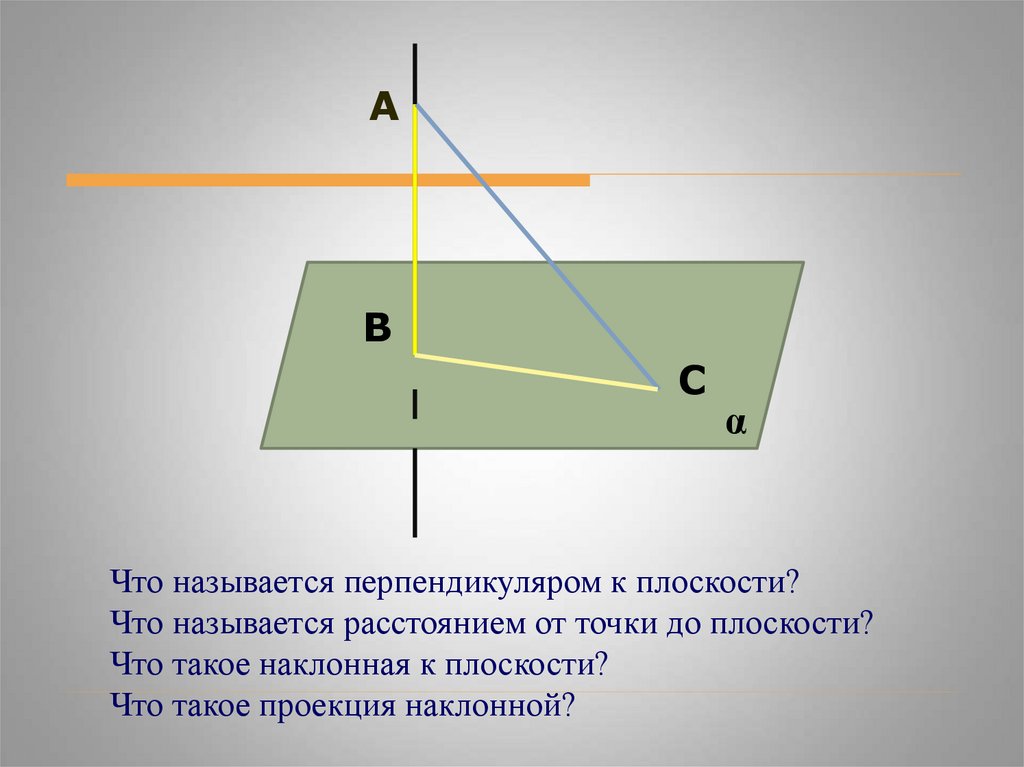
Что называется перпендикуляром к плоскости?
Что называется расстоянием от точки до плоскости?
Что такое наклонная к плоскости?
Что такое проекция наклонной?
3.
Ас
В
С
α
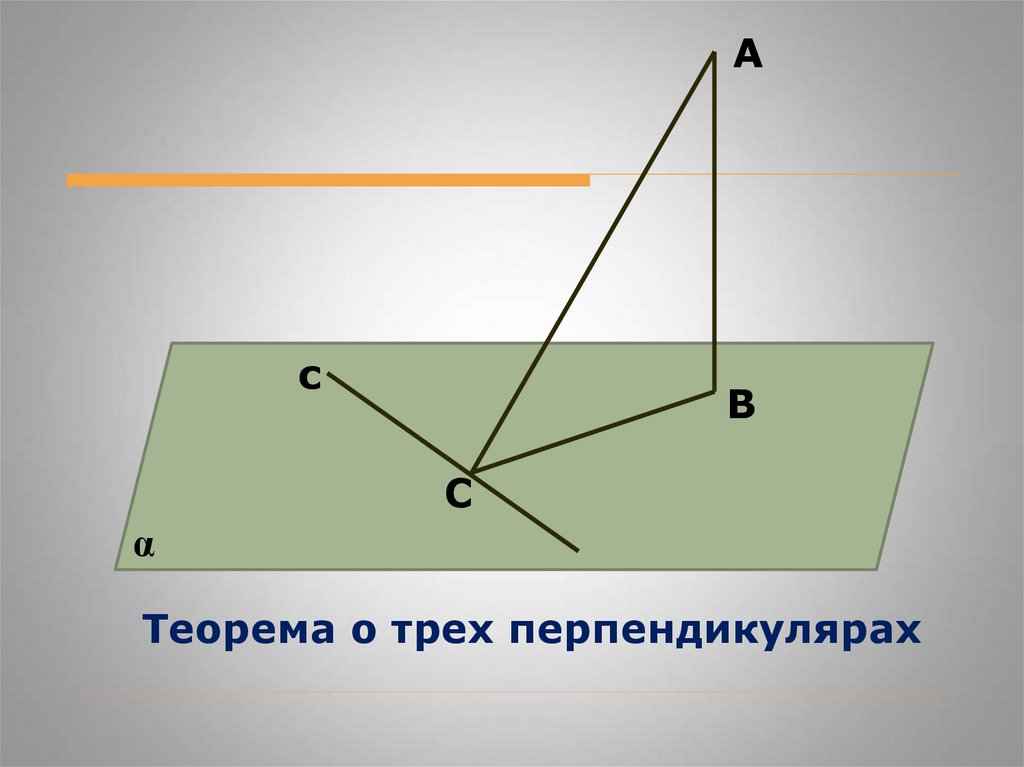
Теорема о трех перпендикулярах
4.
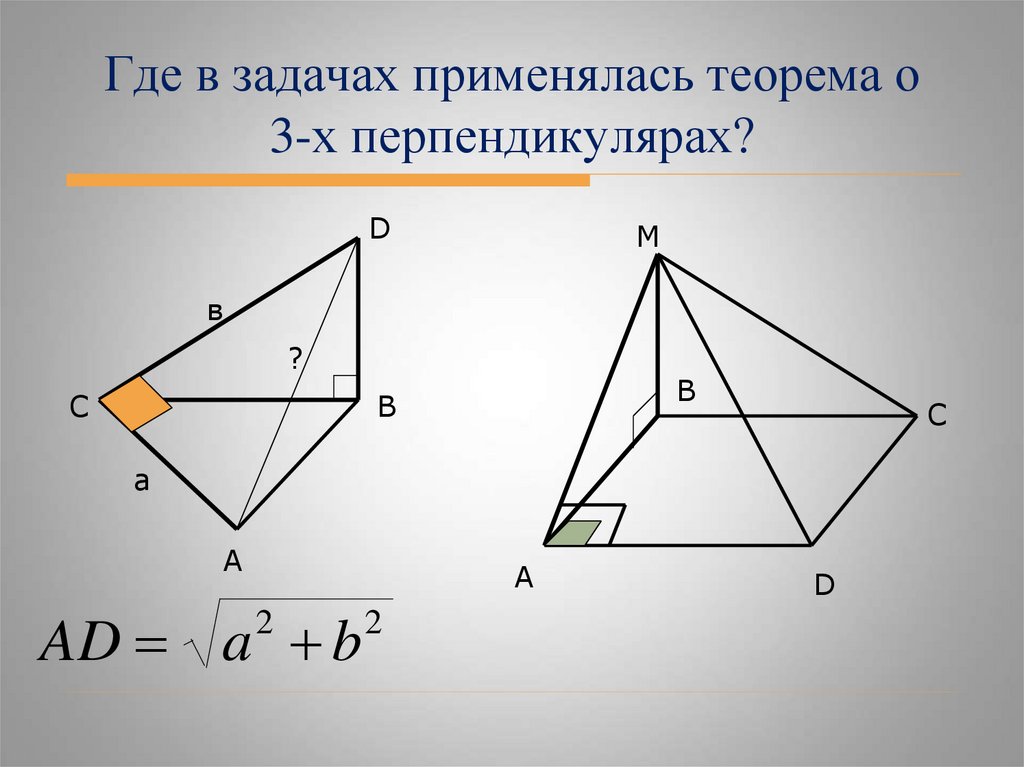
Где в задачах применялась теорема о3-х перпендикулярах?
D
M
в
?
С
B
В
C
а
А
А
AD a b
2
2
D
5.
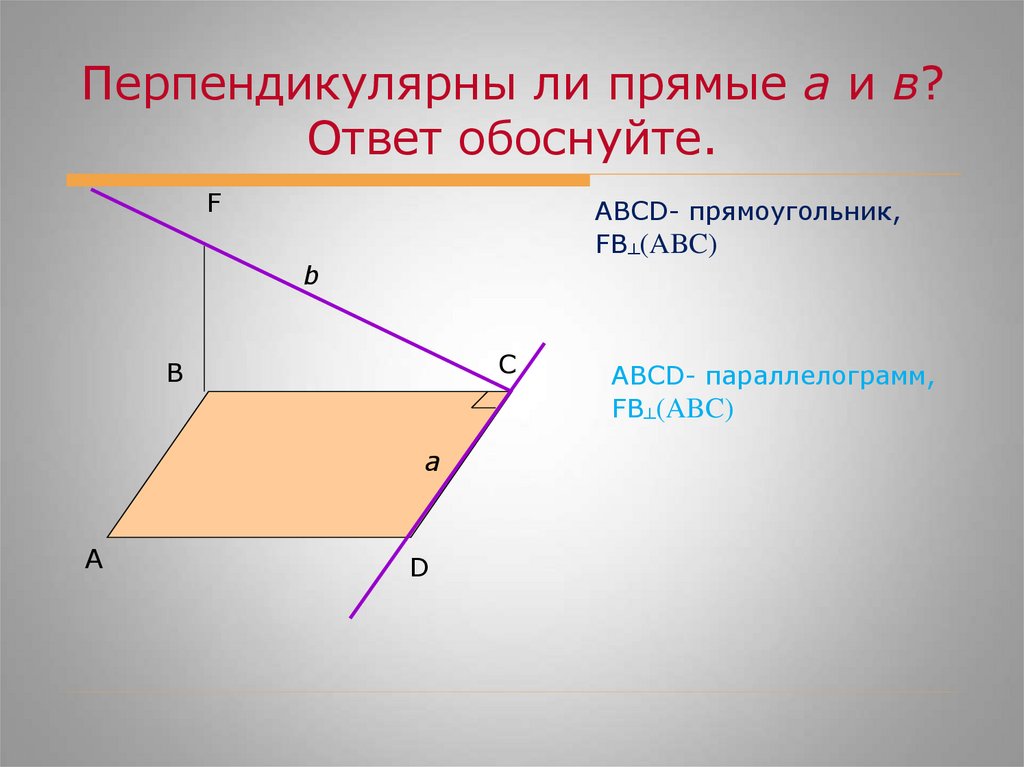
Перпендикулярны ли прямые а и в?Ответ обоснуйте.
F
ABCD- прямоугольник,
FB┴(ABC)
b
С
В
a
А
D
ABCD- параллелограмм,
FB┴(ABC)
6.
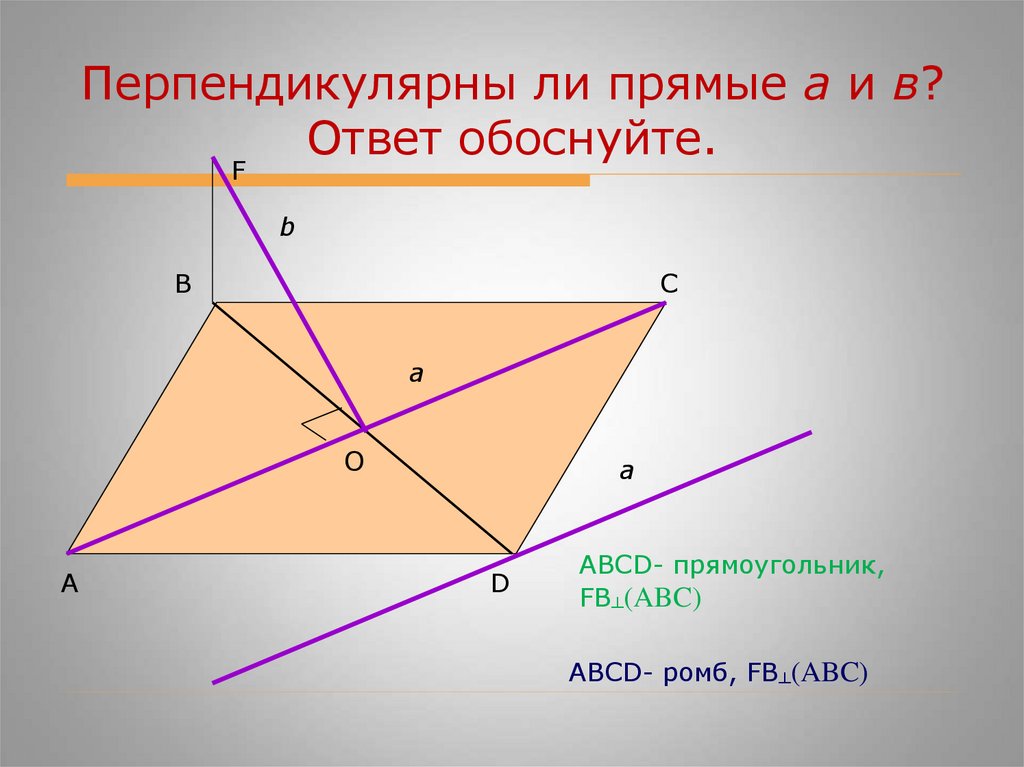
Перпендикулярны ли прямые а и в?Ответ обоснуйте.
F
b
B
C
a
O
А
a
D
ABCD- прямоугольник,
FB┴(ABC)
ABCD- ромб, FB┴(ABC)
7.
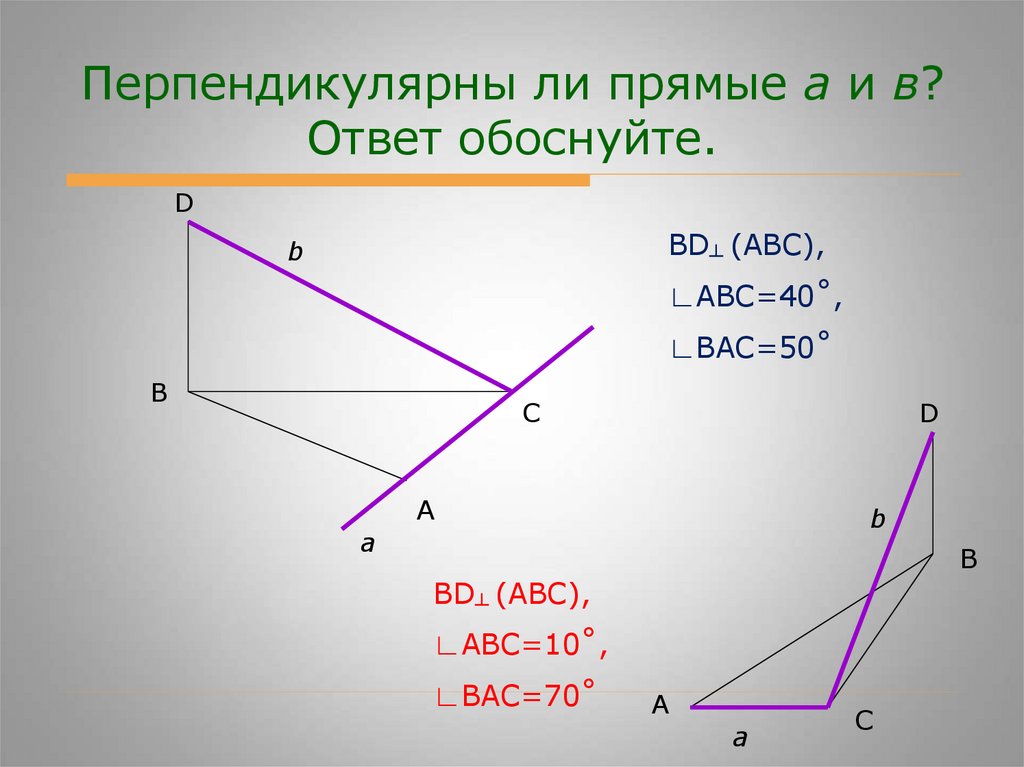
Перпендикулярны ли прямые а и в?Ответ обоснуйте.
D
BD┴ (ABC),
b
∟ABC=40˚,
∟BAC=50˚
B
C
D
A
b
a
B
BD┴ (ABC),
∟ABC=10˚,
∟BAC=70˚
A
a
C
8.
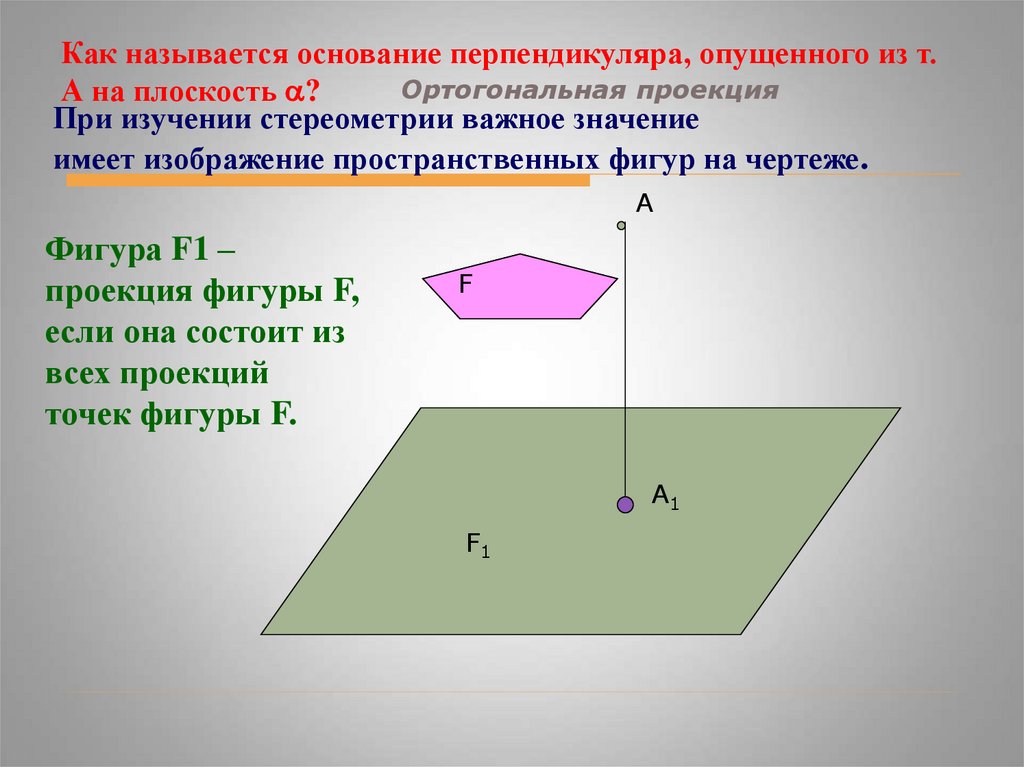
Как называется основание перпендикуляра, опущенного из т.Ортогональная проекция
А на плоскость ?
При изучении стереометрии важное значение
имеет изображение пространственных фигур на чертеже.
А
Фигура F1 –
проекция фигуры F,
если она состоит из
всех проекций
точек фигуры F.
F
А1
F1
9.
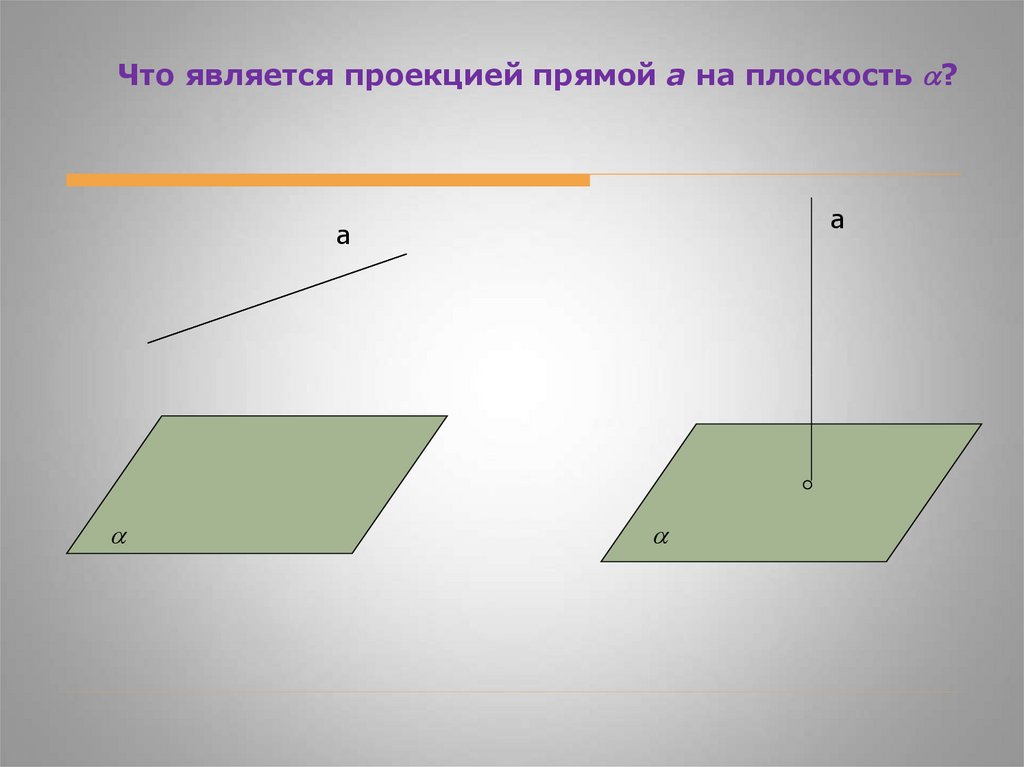
Что является проекцией прямой а на плоскость ?a
a
10.
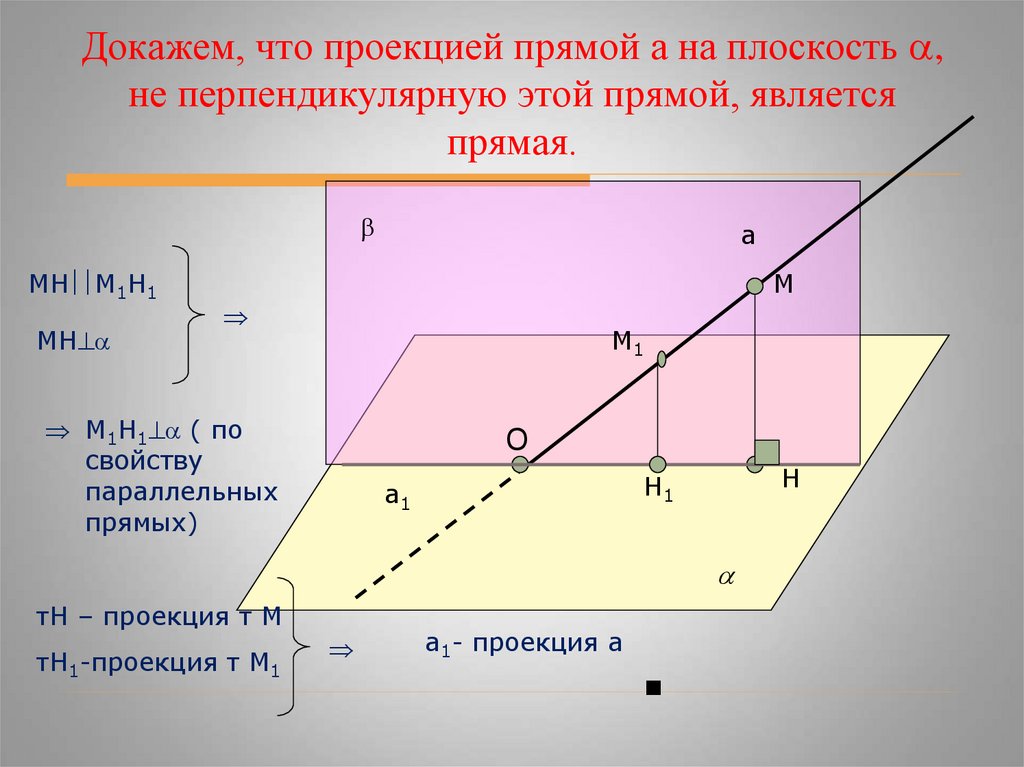
Докажем, что проекцией прямой а на плоскость ,не перпендикулярную этой прямой, является
прямая.
МН М1Н1
МН
а
М
М1
М1Н1 ( по
свойству
параллельных
прямых)
О
Н
Н1
а1
тН – проекция т М
тН1-проекция т М1
а1- проекция а
11.
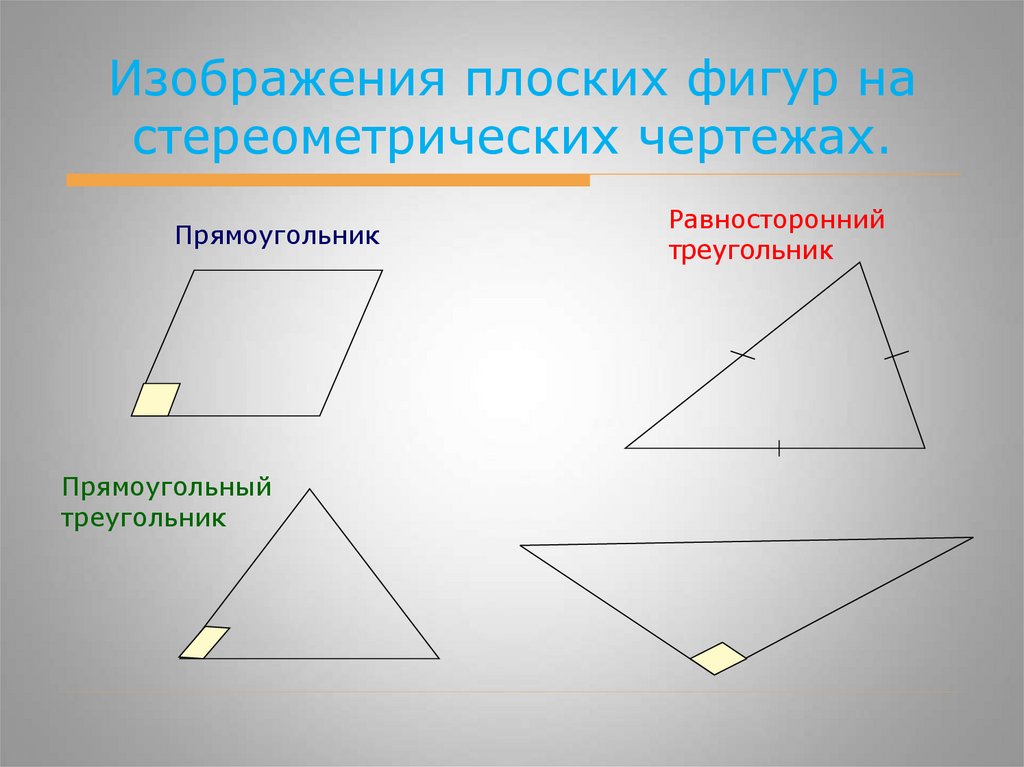
Изображения плоских фигур настереометрических чертежах.
Прямоугольник
Прямоугольный
треугольник
Равносторонний
треугольник
12.
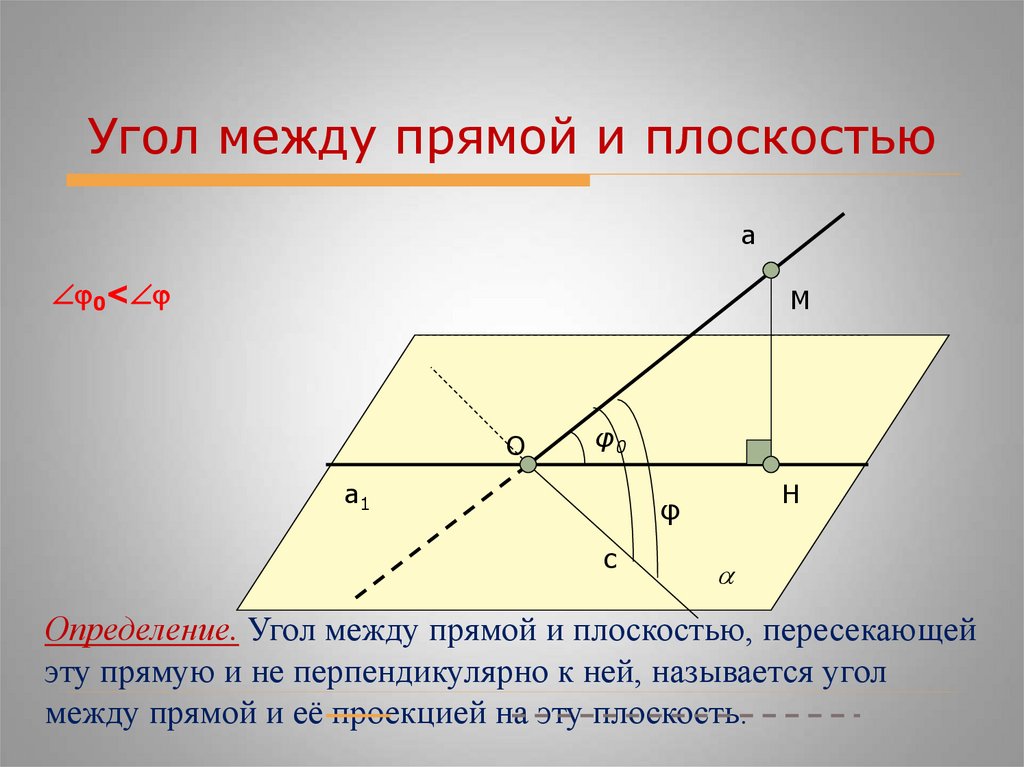
Угол между прямой и плоскостьюа
0<
M
O
φ0
а1
H
φ
с
Определение. Угол между прямой и плоскостью, пересекающей
эту прямую и не перпендикулярно к ней, называется угол
между прямой и её проекцией на эту плоскость.
13.
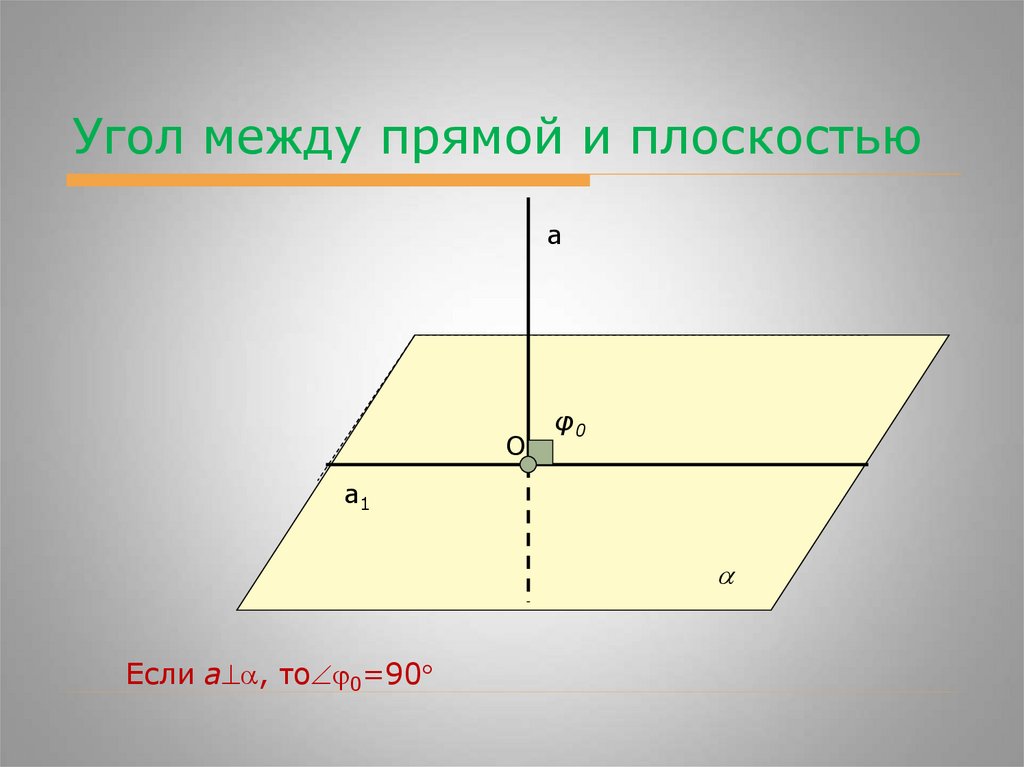
Угол между прямой и плоскостьюа
O
φ0
а1
Если а , то 0=90
14.
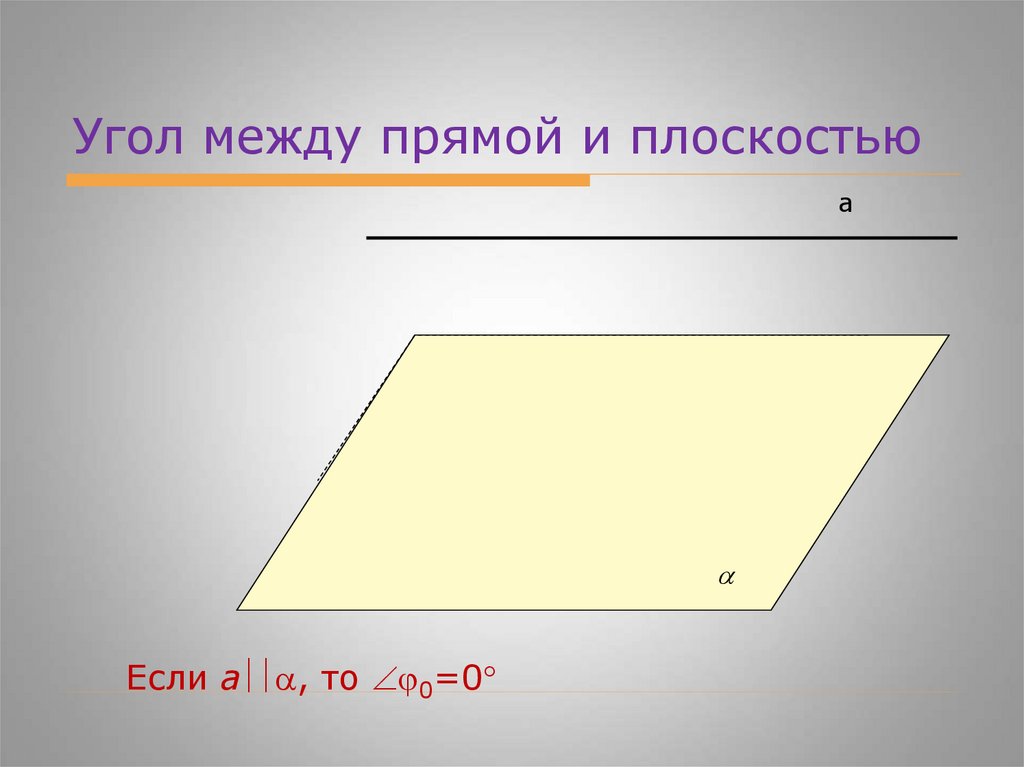
Угол между прямой и плоскостьюа
Если а , то 0=0
15.
С каким новым понятием познакомились?Угол между прямой и плоскостью
Что называется углом между прямой и плоскостью?
Углом между прямой и плоскостью, пересекающей эту прямую и не
перпендикулярно к ней, называется угол между прямой и её
проекцией на эту плоскость.
Как построить угол между прямой а и плоскостью ?
План
1. Выбрать т. М на прямой а
2. Опустить МН
3. Построить ОН=а1проекция прямой а
4. = (а, )- искомый.
а
М
О
Н
а1
16.
Работа в группах.Задание 1.
Алгоритм
1. Найдите точку пересечения прямой и плоскости.
2. Найдите (выберите) точку прямой не лежащую в
плоскости.
3. Опустите перпендикуляр из точки к плоскости или
найдите проекцию данной точки на плоскость.
4. Соедините эти точки. Полученная прямая - проекция
прямой на плоскость.
5. Выделите дугой полученный угол.
а
О
17.
Задание 2.ОПРЕДЕЛЕНИЕ. Углом между прямой и
плоскостью, пересекающей эту прямую и
не перпендикулярной к ней, называется
_____________________________________
18.
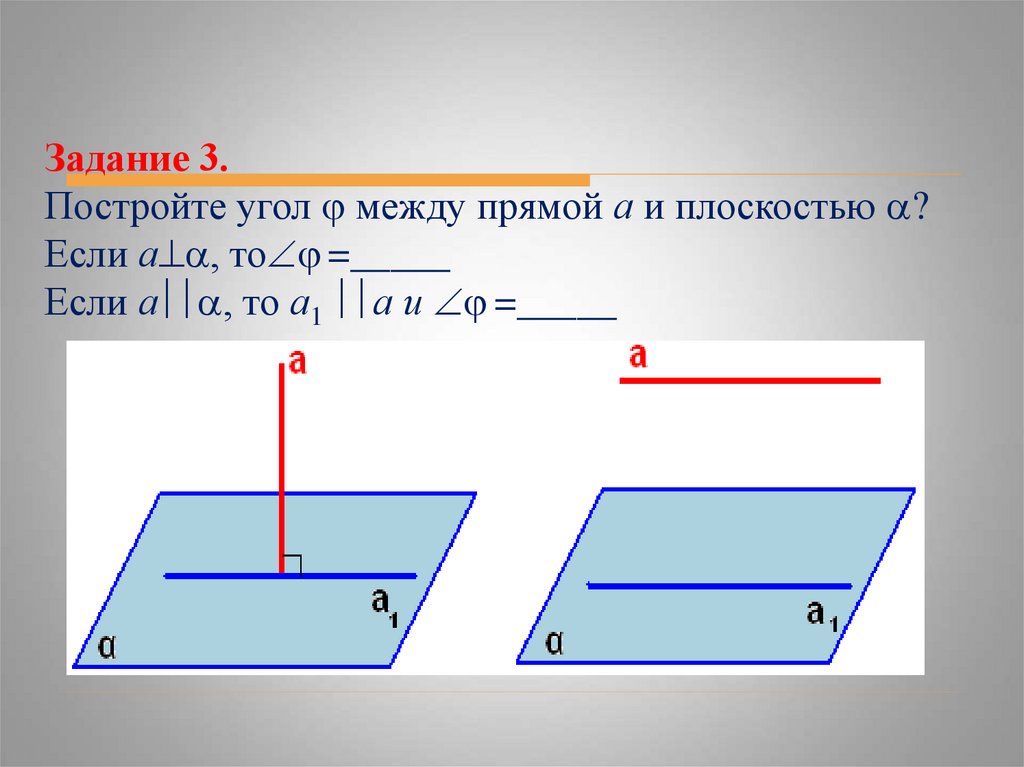
Задание 3.Постройте угол между прямой а и плоскостью ?
Если а , то =_____
Если а , то а1 а и =_____
19.
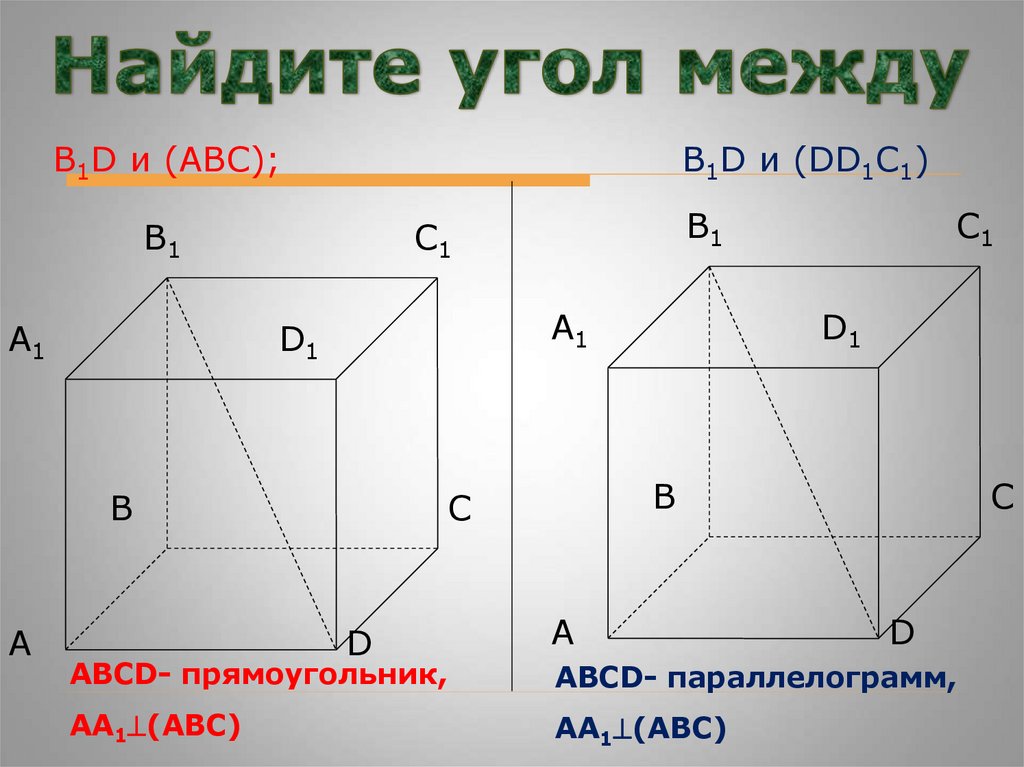
В1D и (ABC);В1D и (DD1C1)
В1
А1
А1
D1
В
А
В1
С1
D1
В
С
D
С1
А
С
D
АВСD- прямоугольник,
АВСD- параллелограмм,
АА1 (АВС)
АА1 (АВС)
20.
А1А1
С1
В1
В1
С
А
С1
В
В
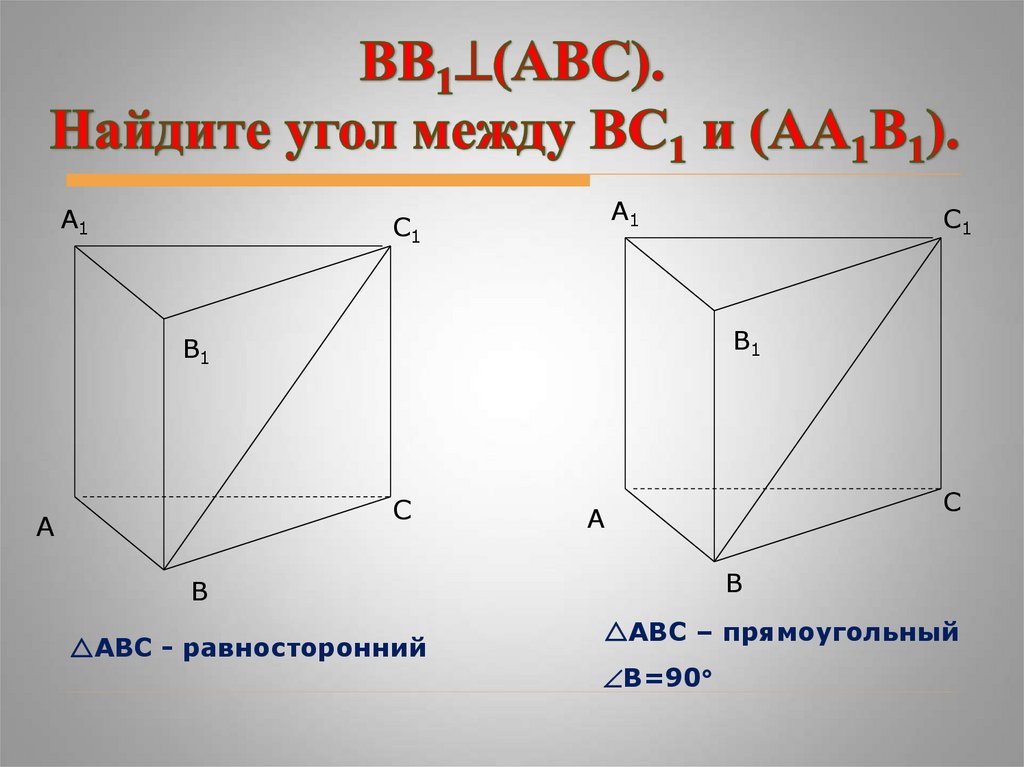
АВС - равносторонний
С
А
АВС – прямоугольный
В=90
21.
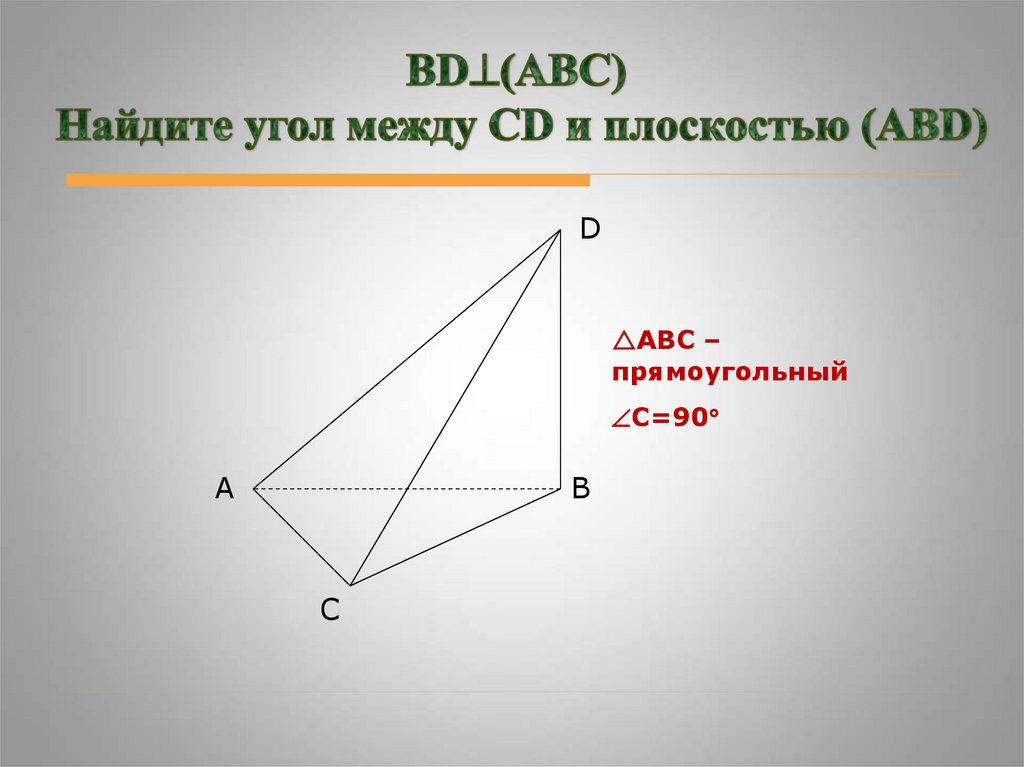
DАВС –
прямоугольный
C=90
А
B
C
22.
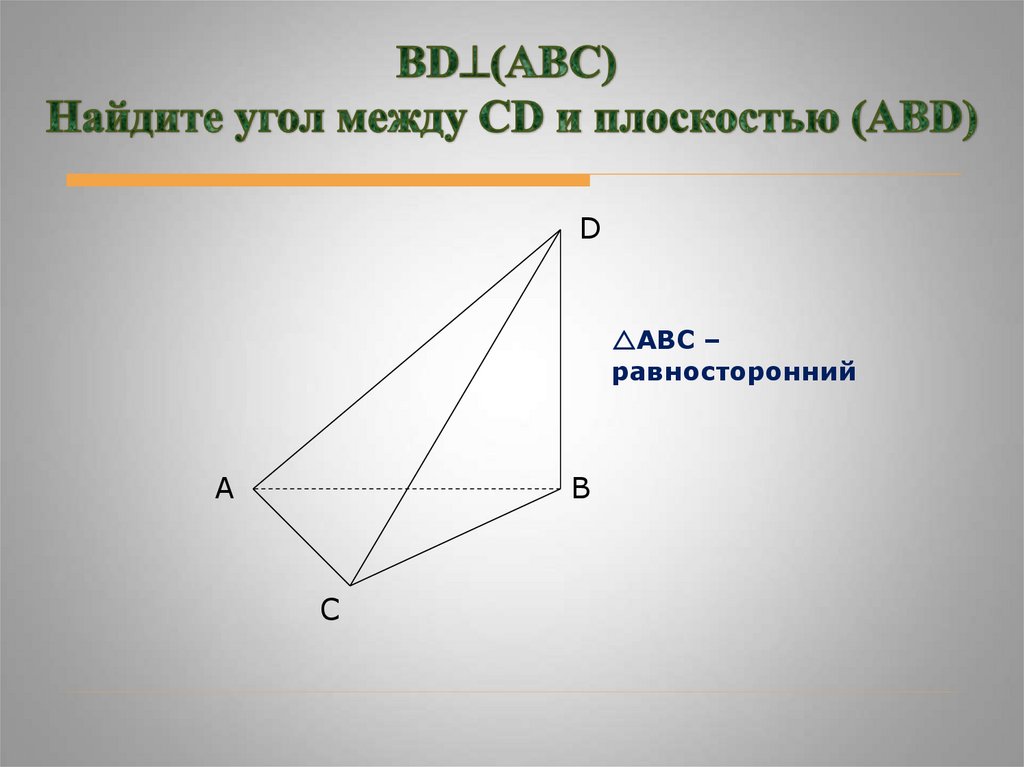
DАВС –
равносторонний
А
B
C
23.
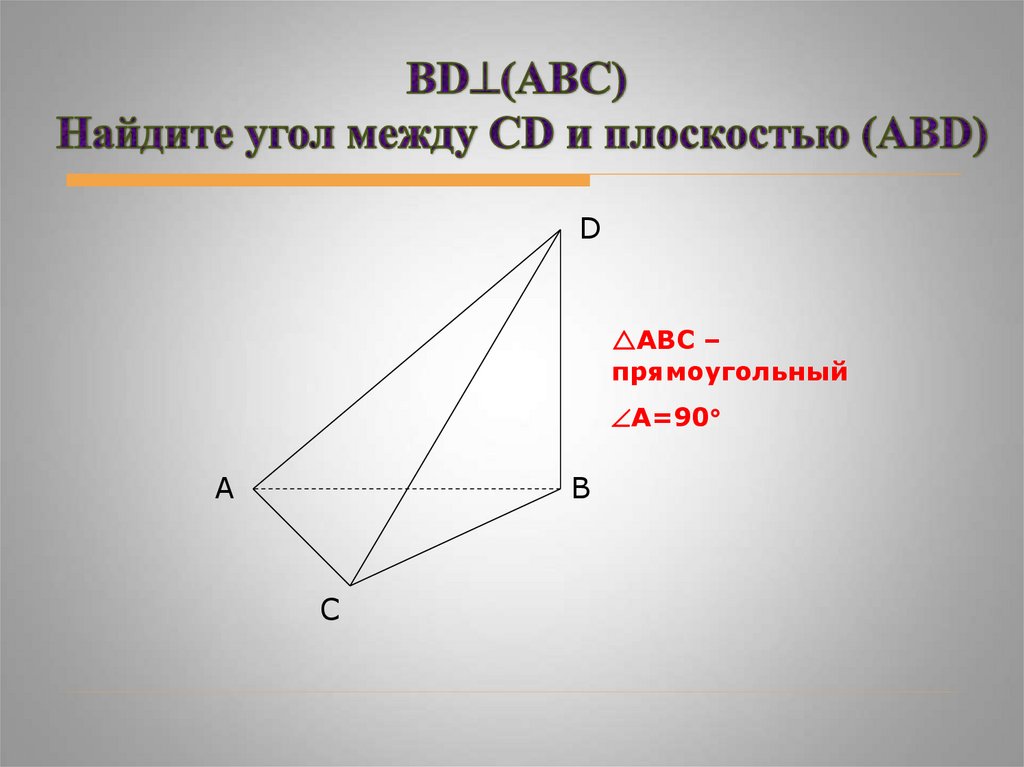
DАВС –
прямоугольный
А=90
А
B
C





 mathematics
mathematics