Similar presentations:
Угол между прямой и плоскостью
1. Урок геометрии в 10 классе на тему «Угол между прямой и плоскостью»
Дороги не те знания, которыеотлагаются в мозгу, как жир, дороги те,
которые превращаются в умственные
мышцы.
Герберт Спенсер (1820-1903) английский
философ и социолог
2. Перпендикулярны ли прямые а и b? Ответ обоснуйте.
FABCD- прямоугольник,
FB┴(ABC)
b
С
В
a
А
D
ABCD- параллелограмм,
FB┴(ABC)
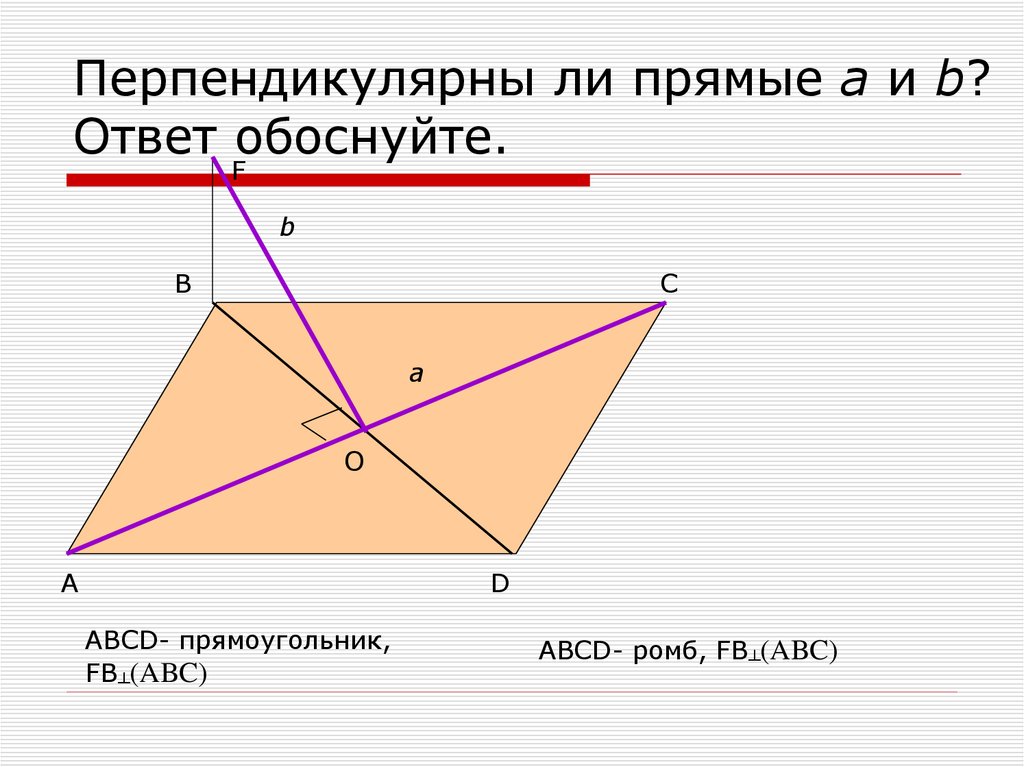
3. Перпендикулярны ли прямые а и b? Ответ обоснуйте.
Fb
B
C
a
O
А
D
ABCD- прямоугольник,
FB┴(ABC)
ABCD- ромб, FB┴(ABC)
4. Перпендикулярны ли прямые а и b? Ответ обоснуйте.
DBD┴ (ABC),
b
∟ABC=40˚,
∟BAC=50˚
B
C
D
A
b
a
B
BD┴ (ABC),
∟ABC=10˚,
∟BAC=70˚
A
a
C
5.
Основание перпендикуляра, опущенного из т.А наплоскость называется ортогональная проекция
Фигура F1 –проекция фигуры F ,если она состоит из
всех проекций точек фигуры F.
А
F
А1
F1
6. Докажем, что проекцией прямой а на плоскость , не перпендикулярную этой прямой, является прямая.
Докажем, что проекцией прямой а наплоскость , не перпендикулярную этой
прямой, является прямая.
МН М1Н1
МН
а
М
М1Н1 ( по
свойству
параллельных
прямых)
М1
О
Н
Н1
а1
т.Н – проекция т.М
т.Н1-проекция т.М1
а1- проекция а
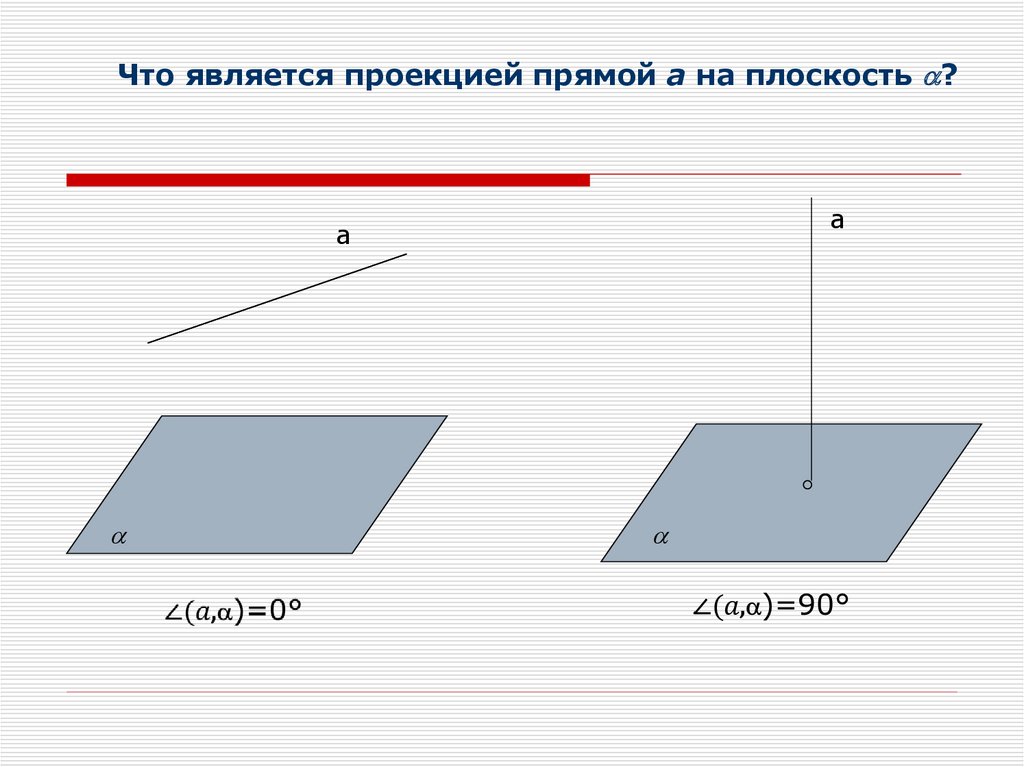
7.
Что является проекцией прямой а на плоскость ?a
a
8.
Определение. Угол между прямой и плоскостью,пересекающей эту прямую и не перпендикулярной к
ней, называется угол между прямой и её проекцией
на эту плоскость.
а
0<
M
O
φ0
а1
H
φ
с
9.
Вопросы:1. Что называется углом между прямой и
плоскостью?
2. Как построить угол между прямой а и
плоскостью ?
План
1. Выбрать т. М на прямой а
2. Опустить МН
3. Построить ОН=а1проекция прямой а
4. = (а, )- искомый.
а
М
а1
О
Н
10. Помните!
Недостаточно лишь понять задачу,необходимо желание решить её. Без
сильного желания решить трудную
задачу невозможно, но при наличии
такового – возможно. Где есть
желание, найдется путь!
Пойя. Д.
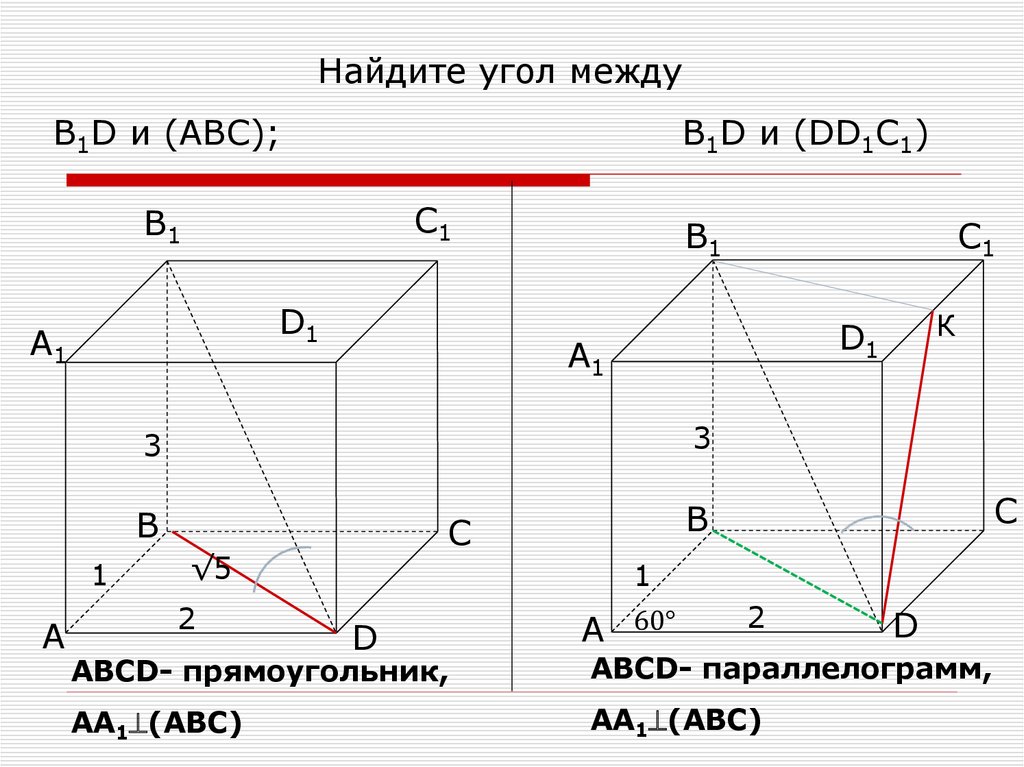
11.
Найдите угол междуВ1D и (ABC);
В1D и (DD1C1)
С1
В1
D1
А1
1
А
А1
3
В
В
С
√5
К
D1
3
2
С1
В1
С
1
D
А
2
D
АВСD- прямоугольник,
АВСD- параллелограмм,
АА1 (АВС)
АА1 (АВС)
12.
Образец оформления записи:13. ВВ1(АВС).Найдите угол между ВС1 и (АА1В1).
ВВ1 (АВС).Найдите угол междуВС1 и (АА1В1).
А1
С1
В1
А1
С1
В1
3
А
С
2
А
С
1
2
В
В
АВС - равносторонний
3
АВС – прямоугольный
В=90
14. ВВ1(АВС).Найдите угол между ВС1 и (АА1В1).
ВВ1 (АВС).Найдите угол междуВС1 и (АА1В1).
А1
С1
В1
А
3
С
150°
В
4
АВС – тупоугольный,
В>90
15. АА1(АВС)
АА1 (АВС)B1
C1
А1
D1
K1
F1
В
С
D
А
K
Найдите угол:
Между В1F и (АВС);
Между В1F и (КК1F);
Между В1F и (АА1В1);
F
В основании лежит
правильный шестиугольник,
АВ=3, АА1=5
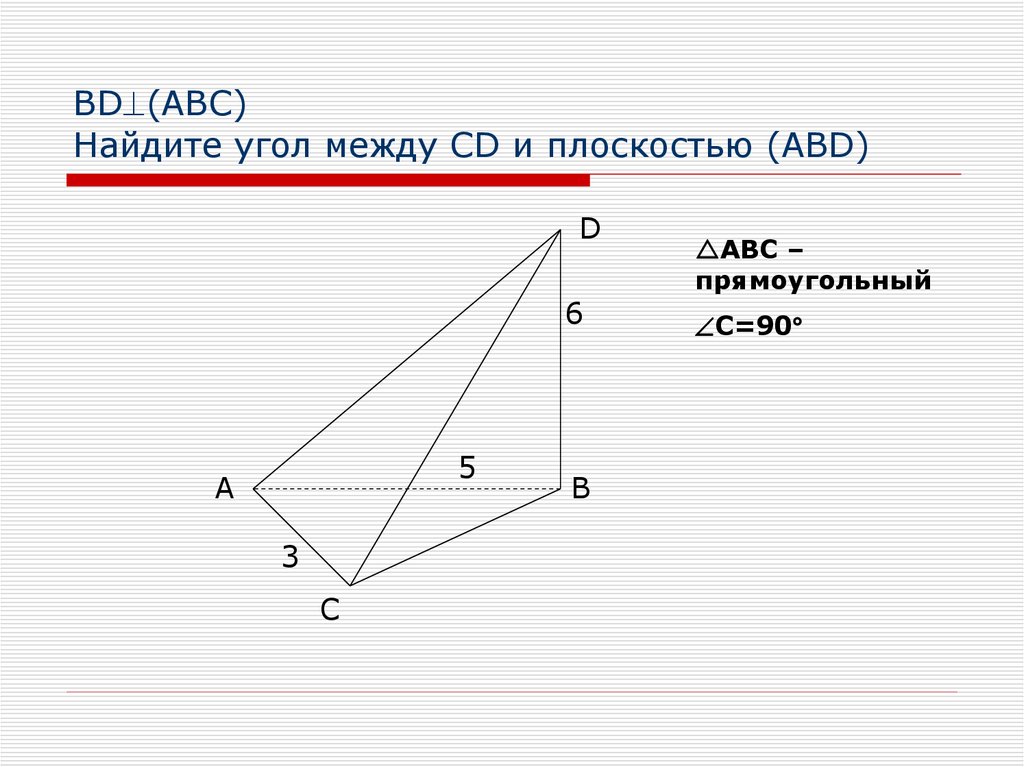
16. BD(АВС) Найдите угол между CD и плоскостью (ABD)
BD (АВС)Найдите угол между CD и плоскостью (ABD)
D
6
5
А
3
C
B
АВС –
прямоугольный
C=90
17. BD(АВС) Найдите угол между CD и плоскостью (ABD)
BD (АВС)Найдите угол между CD и плоскостью (ABD)
D
6
АВС –
равносторонний
А
B
4
C
18. BD(АВС) Найдите угол между CD и плоскостью (ABD)
BD (АВС)Найдите угол между CD и плоскостью (ABD)
D
2
5
3
А
C
B
АВС –
прямоугольный
А=90
19. Задание:
1.Учебник п.14.3 знать формулировки основных утверждений2.Решить задачи на вычисление угла между прямой и
плоскостью (презентация-слайд 13 закончить обоснование
и расчет в задаче №2, слайды 15-20 решение для 3 различных
видов многогранников на выбор, у шестиугольного можно
сделать один пункт)















 mathematics
mathematics