Similar presentations:
Угол между прямой и плоскостью
1. Угол между прямой и плоскостью
2.
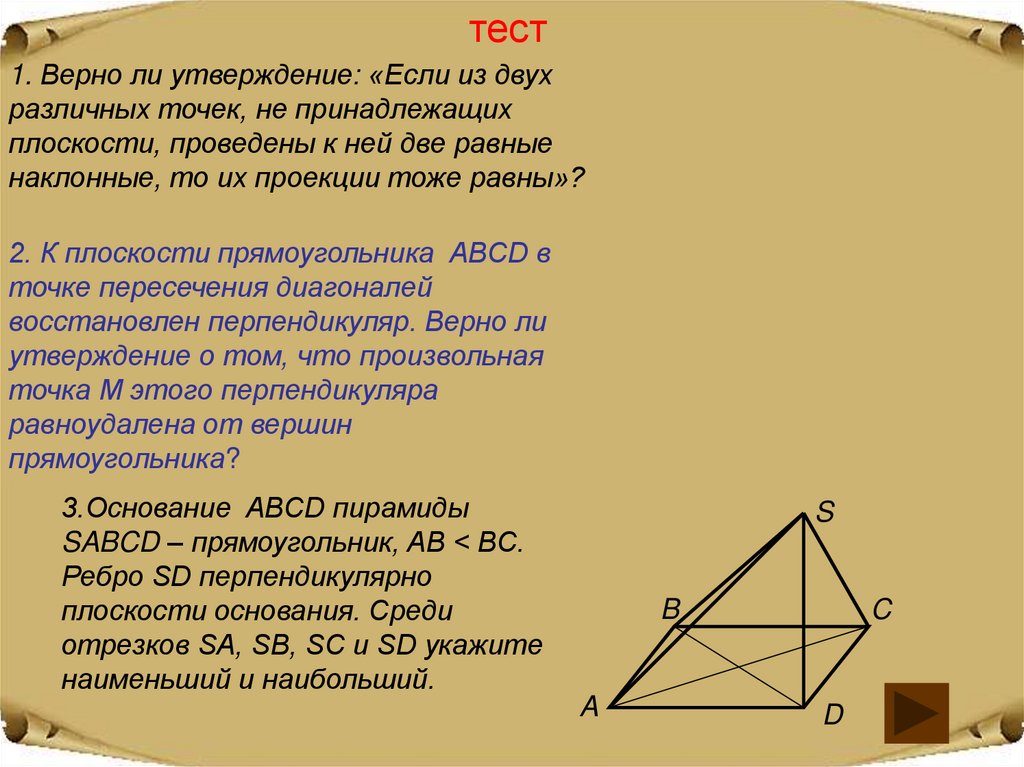
тест1. Верно ли утверждение: «Если из двух
различных точек, не принадлежащих
плоскости, проведены к ней две равные
наклонные, то их проекции тоже равны»?
2. К плоскости прямоугольника ABCD в
точке пересечения диагоналей
восстановлен перпендикуляр. Верно ли
утверждение о том, что произвольная
точка M этого перпендикуляра
равноудалена от вершин
прямоугольника?
3.Основание ABCD пирамиды
SABCD – прямоугольник, AB < BC.
Ребро SD перпендикулярно
плоскости основания. Среди
отрезков SA, SB, SC и SD укажите
наименьший и наибольший.
S
B
A
C
D
3.
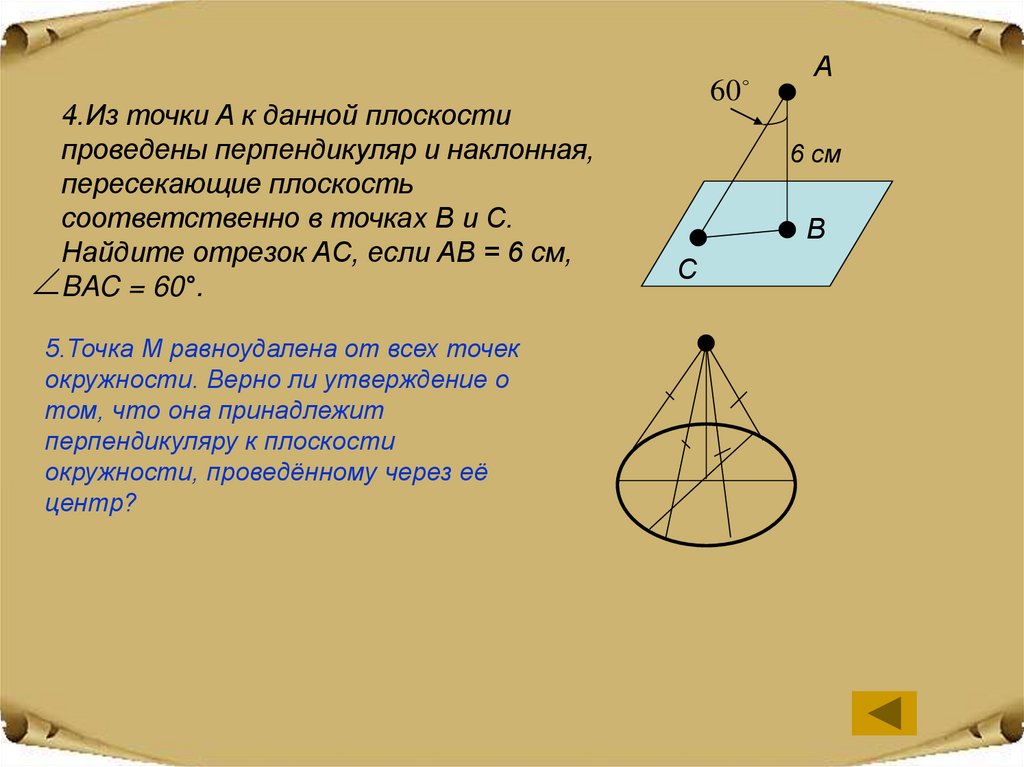
4.Из точки A к данной плоскостипроведены перпендикуляр и наклонная,
пересекающие плоскость
соответственно в точках B и C.
Найдите отрезок AC, если AB = 6 см,
BAC = 60°.
5.Точка M равноудалена от всех точек
окружности. Верно ли утверждение о
том, что она принадлежит
перпендикуляру к плоскости
окружности, проведённому через её
центр?
60
А
6 см
В
С
4.
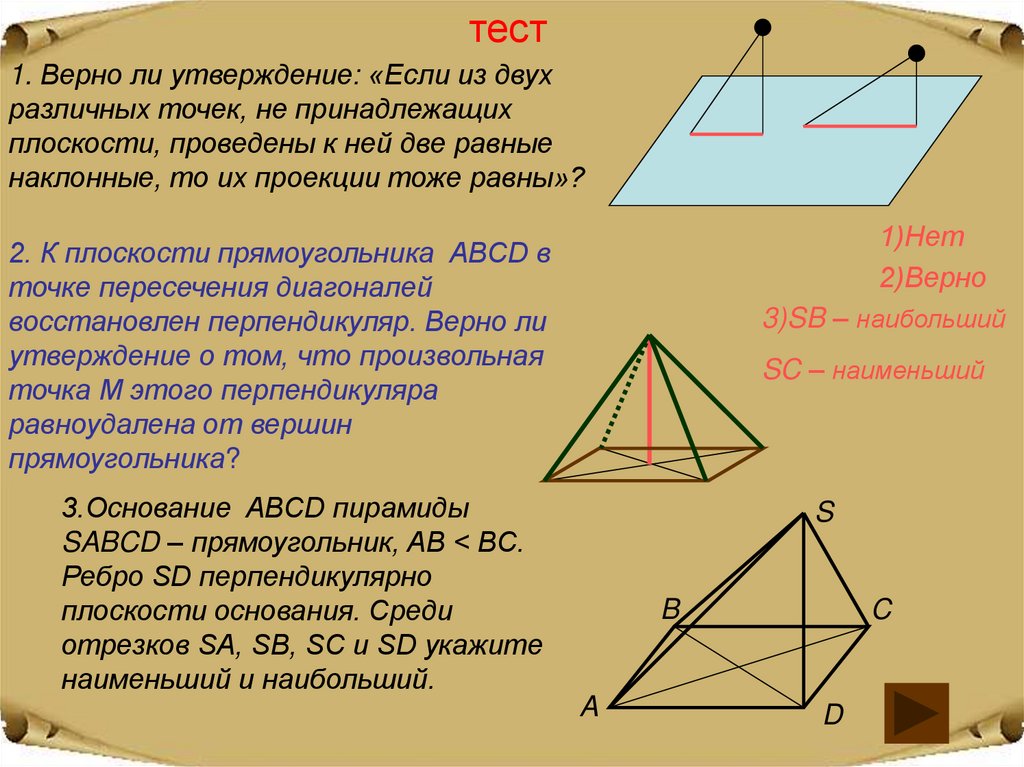
тест1. Верно ли утверждение: «Если из двух
различных точек, не принадлежащих
плоскости, проведены к ней две равные
наклонные, то их проекции тоже равны»?
1)Нет
2)Верно
2. К плоскости прямоугольника ABCD в
точке пересечения диагоналей
восстановлен перпендикуляр. Верно ли
утверждение о том, что произвольная
точка M этого перпендикуляра
равноудалена от вершин
прямоугольника?
3)SB – наибольший
SC – наименьший
3.Основание ABCD пирамиды
SABCD – прямоугольник, AB < BC.
Ребро SD перпендикулярно
плоскости основания. Среди
отрезков SA, SB, SC и SD укажите
наименьший и наибольший.
S
B
A
C
D
5.
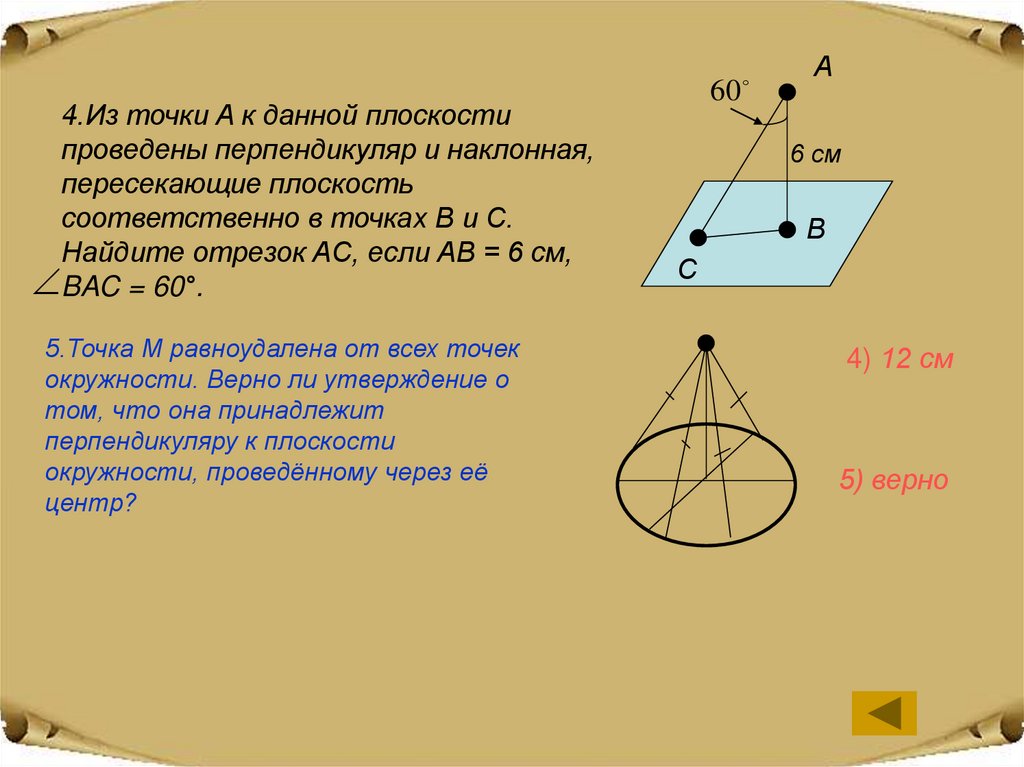
4.Из точки A к данной плоскостипроведены перпендикуляр и наклонная,
пересекающие плоскость
соответственно в точках B и C.
Найдите отрезок AC, если AB = 6 см,
BAC = 60°.
5.Точка M равноудалена от всех точек
окружности. Верно ли утверждение о
том, что она принадлежит
перпендикуляру к плоскости
окружности, проведённому через её
центр?
60
А
6 см
В
С
4) 12 см
5) верно
6.
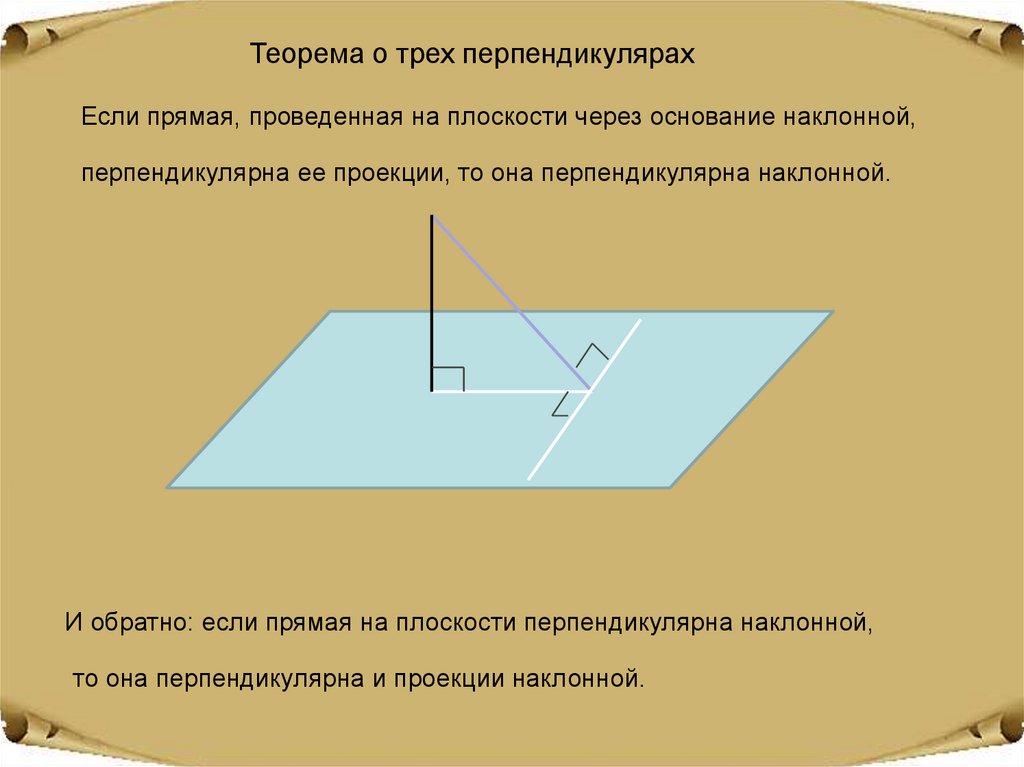
Теорема о трех перпендикулярахЕсли прямая, проведенная на плоскости через основание наклонной,
перпендикулярна ее проекции, то она перпендикулярна наклонной.
И обратно: если прямая на плоскости перпендикулярна наклонной,
то она перпендикулярна и проекции наклонной.
7. Перпендикулярны ли прямые а и в? Ответ обоснуйте.
FABCD- прямоугольник,
FB┴(ABC)
b
С
В
a
А
D
ABCD- параллелограмм,
FB┴(ABC)
8. Перпендикулярны ли прямые а и в? Ответ обоснуйте.
Fb
B
C
a
O
А
a
D
ABCD- прямоугольник,
FB┴(ABC)
ABCD- ромб, FB┴(ABC)
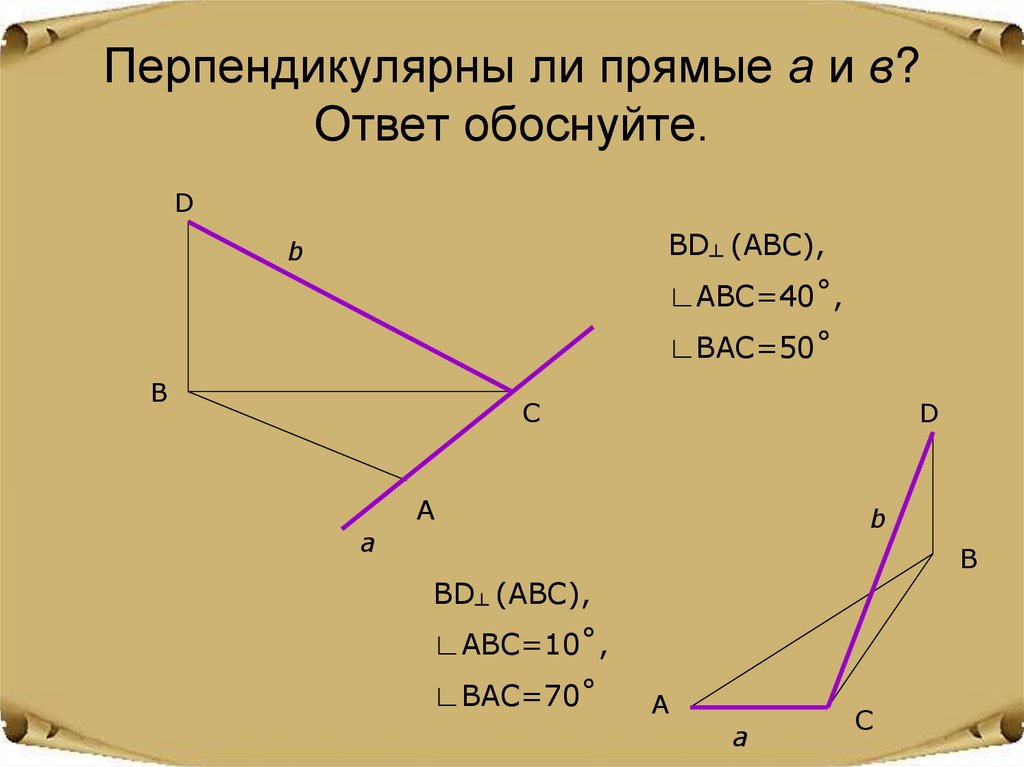
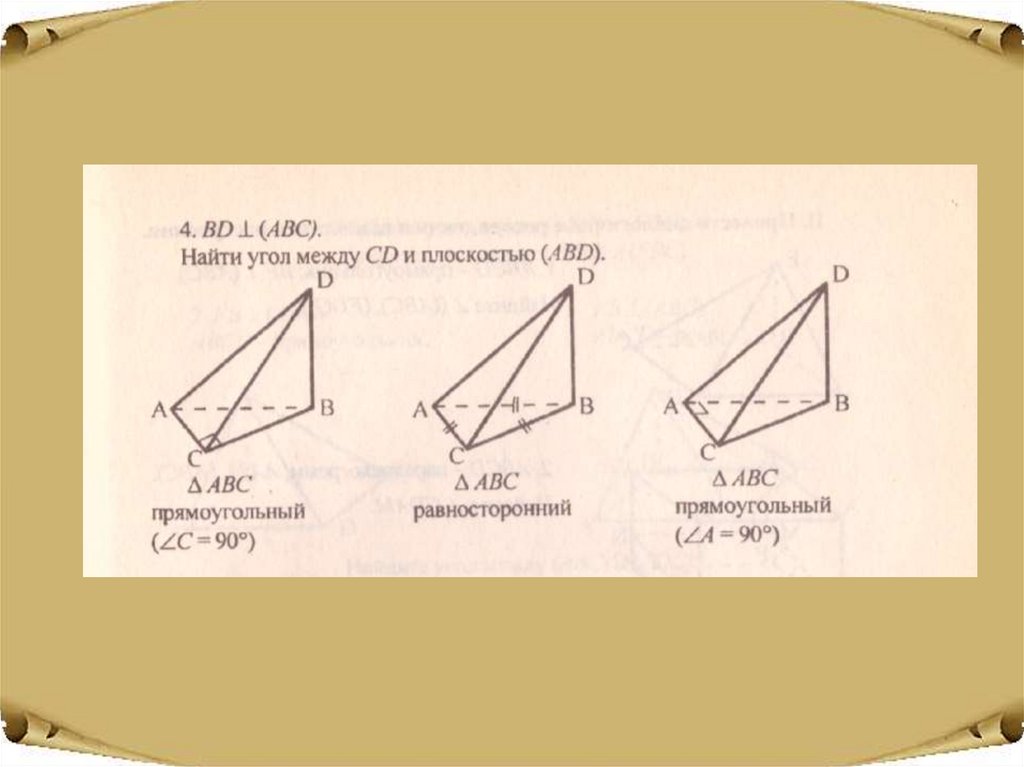
9. Перпендикулярны ли прямые а и в? Ответ обоснуйте.
DBD┴ (ABC),
b
∟ABC=40˚,
∟BAC=50˚
B
C
D
A
b
a
B
BD┴ (ABC),
∟ABC=10˚,
∟BAC=70˚
A
a
C
10.
Угол между прямой и плоскостью.Углом между прямой и плоскостью, пересекающей
эту прямую и не перпендикулярную к ней, называется
угол между прямой и ее проекцией на плоскость.
а
а1 А
Если а , а а1– проекция прямой
а на плоскость а, то (а, ) (а1 , а)
11.
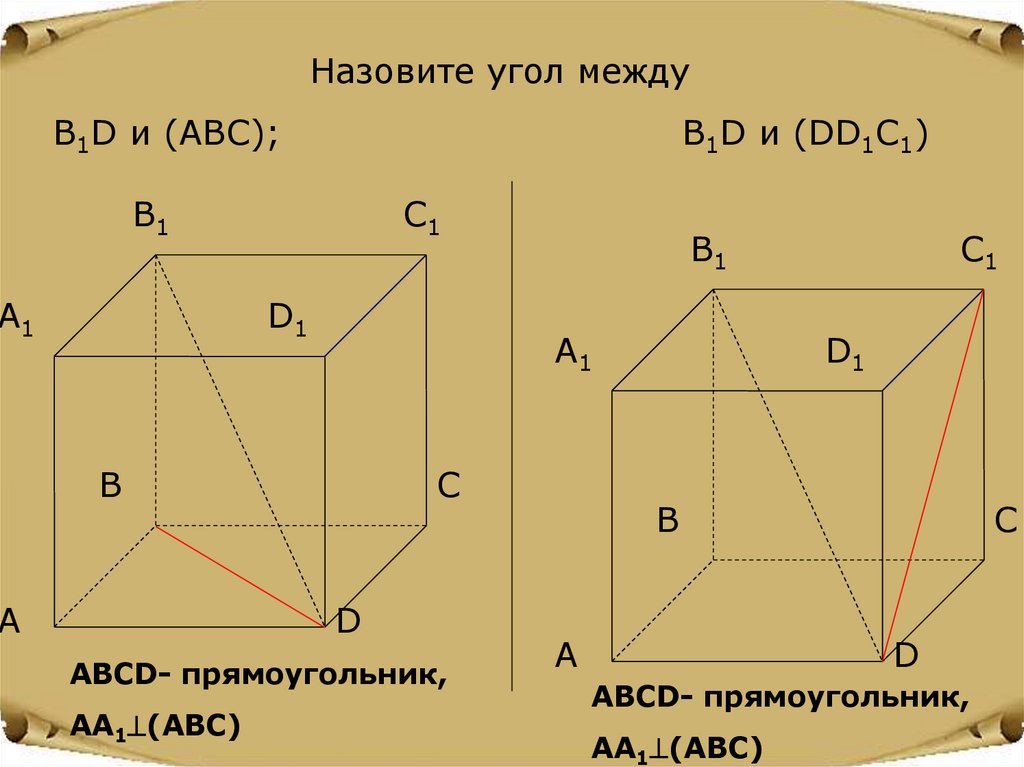
Назовите угол междуВ1D и (ABC);
В1D и (DD1C1)
В1
А1
С1
D1
А1
В
А
С
D
АВСD- прямоугольник,
АА1 (АВС)
В1
С1
D1
В
А
С
D
АВСD- прямоугольник,
АА1 (АВС)
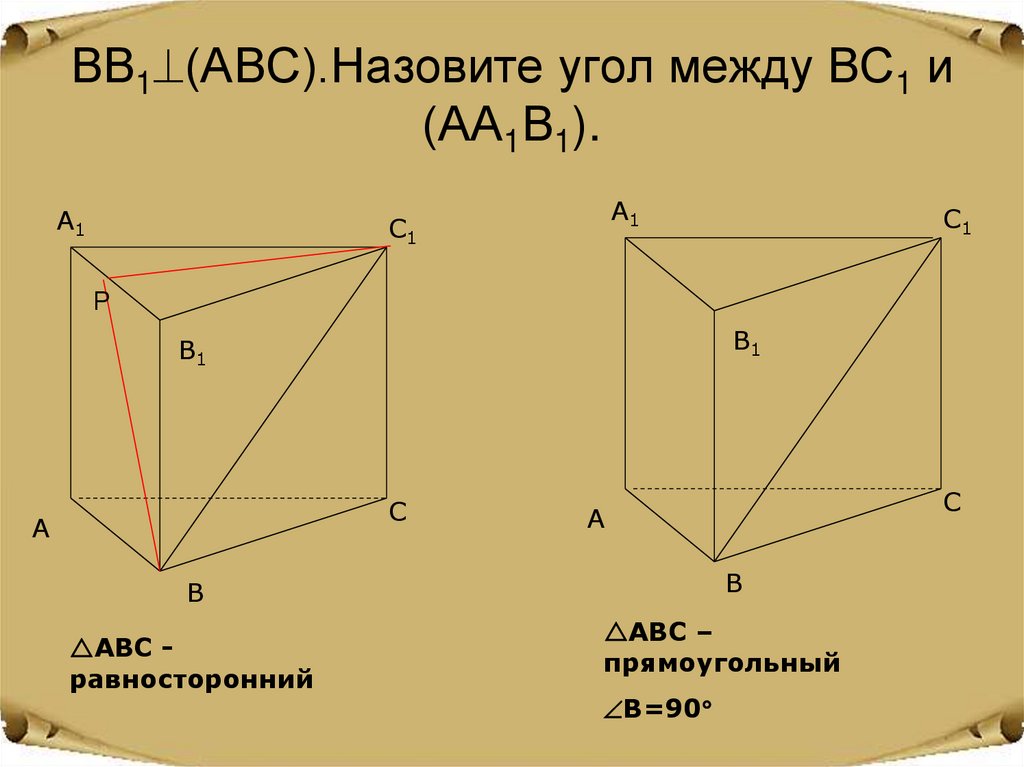
12. ВВ1(АВС).Назовите угол между ВС1 и (АА1В1).
ВВ1 (АВС).Назовите угол между ВС1 и(АА1В1).
А1
А1
С1
С1
Р
В1
В1
С
А
В
В
АВС равносторонний
С
А
АВС –
прямоугольный
В=90
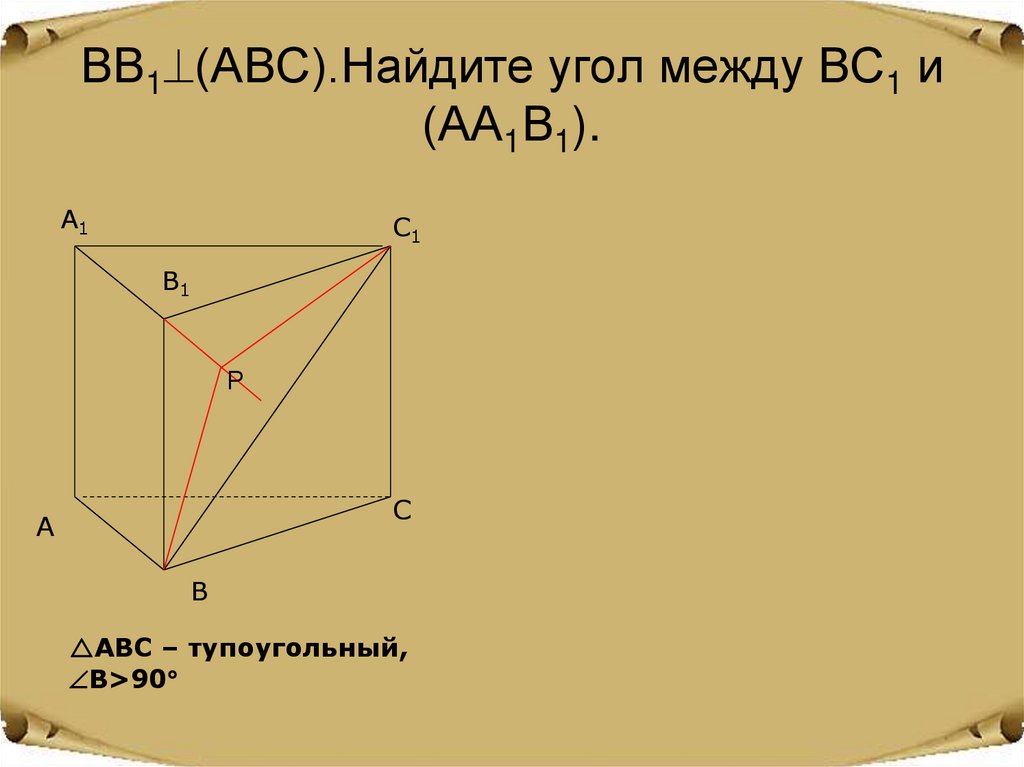
13. ВВ1(АВС).Найдите угол между ВС1 и (АА1В1).
ВВ1 (АВС).Найдите угол между ВС1 и(АА1В1).
А1
С1
В1
Р
С
А
В
АВС – тупоугольный,
В>90
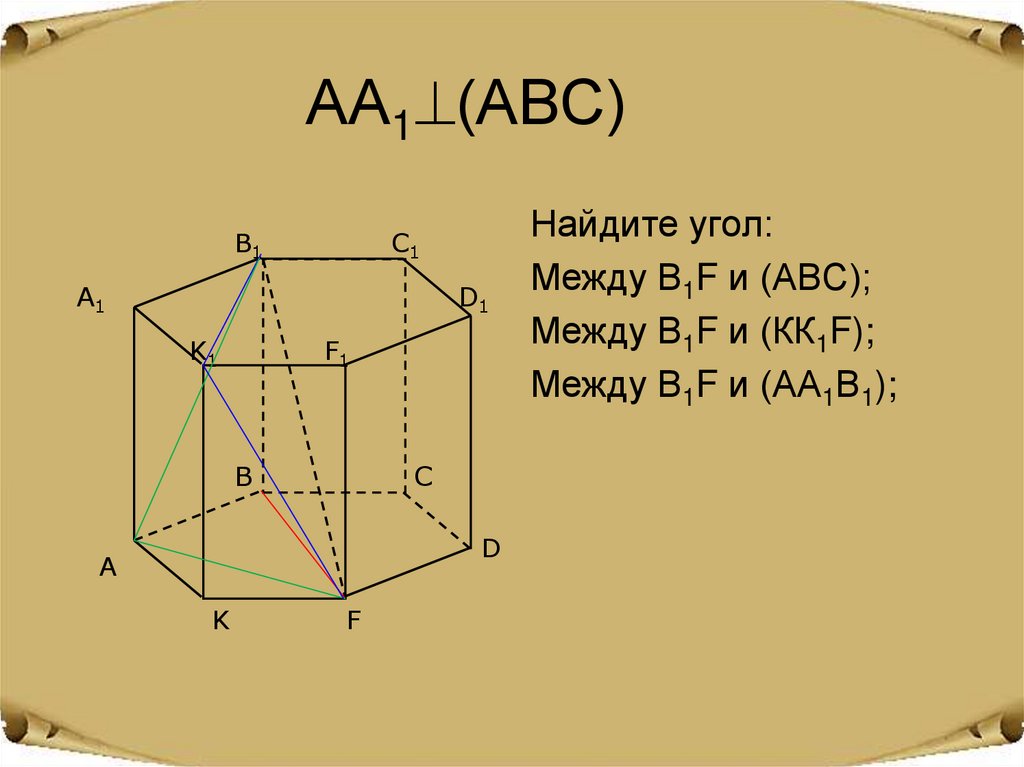
14. АА1(АВС)
АА1 (АВС)B1
C1
А1
D1
K1
F1
В
С
D
А
K
F
Найдите угол:
Между В1F и (АВС);
Между В1F и (КК1F);
Между В1F и (АА1В1);
15.
Схема построения линейного угла между плоскостями1. Выделить линию пересечения плоскостей и определить,
есть ли плоскость ей перпендикулярная
да
нет
(использовать определение
(использовать теорему
(использовать определение)
линейного угла)
о трех перпендикулярах)
2. Выделить или
2. Выделить или построить
2. Выделить или построить
построить прямые
в одной из данных плоскостей
первый
перпендикуляр
пересечения этой
перпендикуляр к линии
плоскости с данными
3. Определить второй
пересечения плоскостей
плоскостями.
перпендикуляр
3. Выделить или построить
3. Сделать вывод, что
перпендикуляр к линии
4. Построить третий
угол между этими
пересечения плоскостей,
перпендикуляр
прямыми является
лежащий в другой плоскости
5. Сделать вывод, что
линейным углом.
и проходящий через основание
угол между построенными
перпендикуляра из п. 2
наклонной и ее проекцией
является линейным углом 4. Сделать вывод, что
угол между построенными
перпендикулярами является
линейным углом между
двумя плоскостями
16.
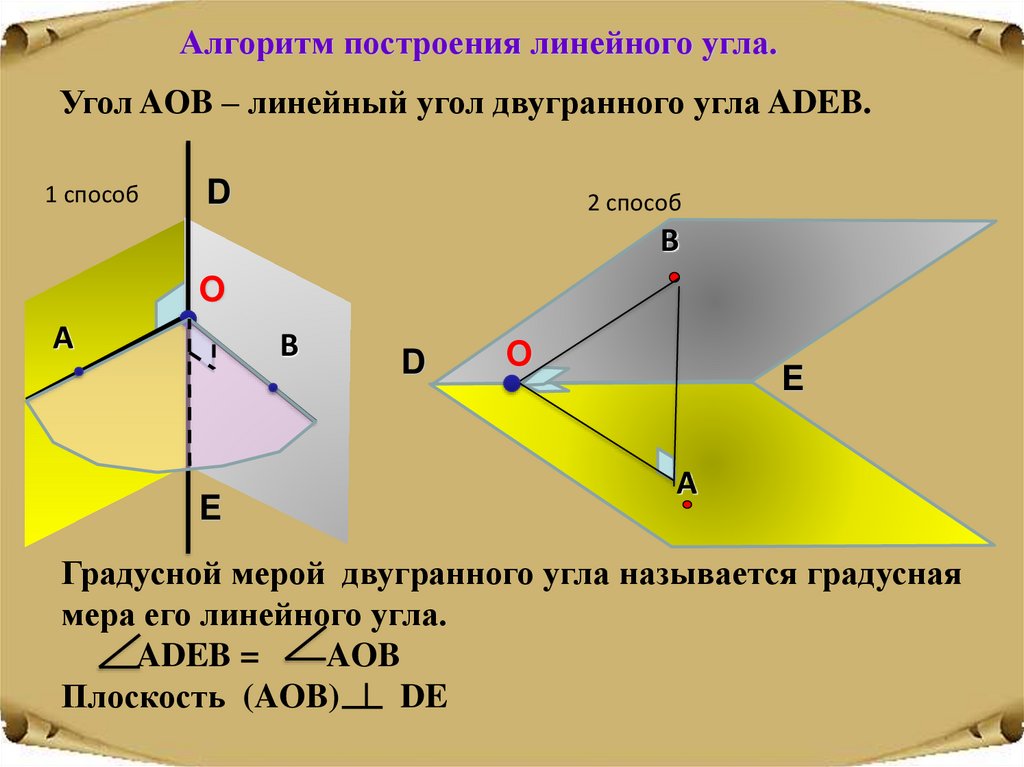
Алгоритм построения линейного угла.Угол AОB – линейный угол двугранного угла ADEB.
1 способ
D
2 способ
B
O
A
B
E
D
O
E
A
Градусной мерой двугранного угла называется градусная
мера его линейного угла.
ADEB =
AOB
Плоскость (AOB)
DE
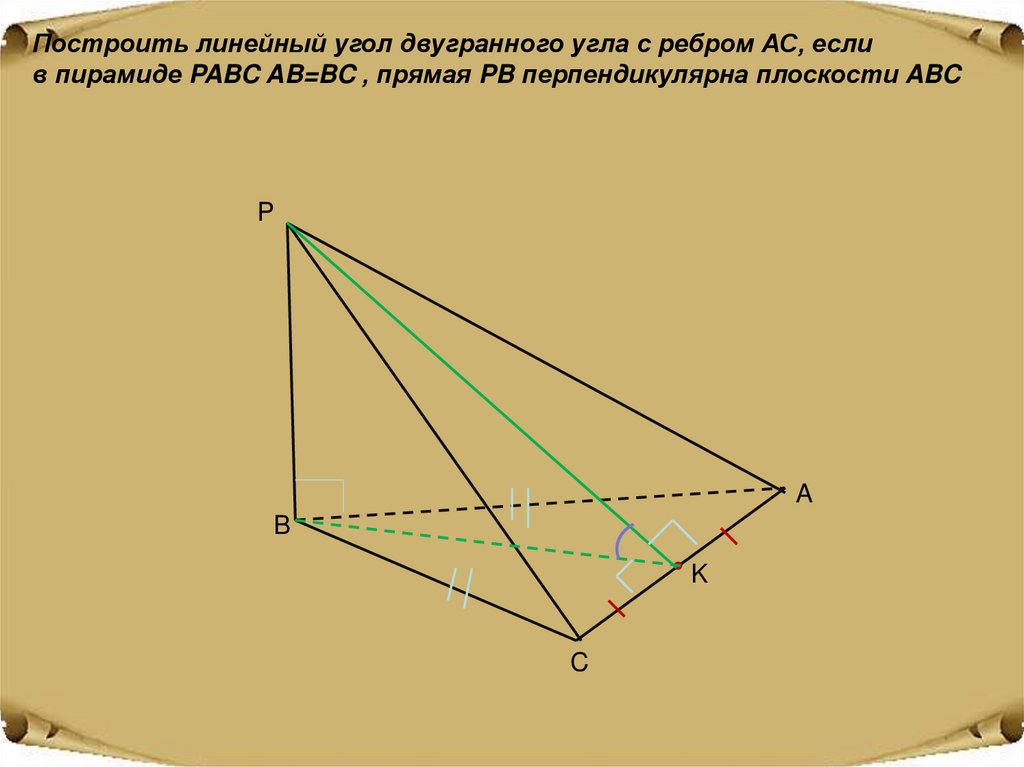
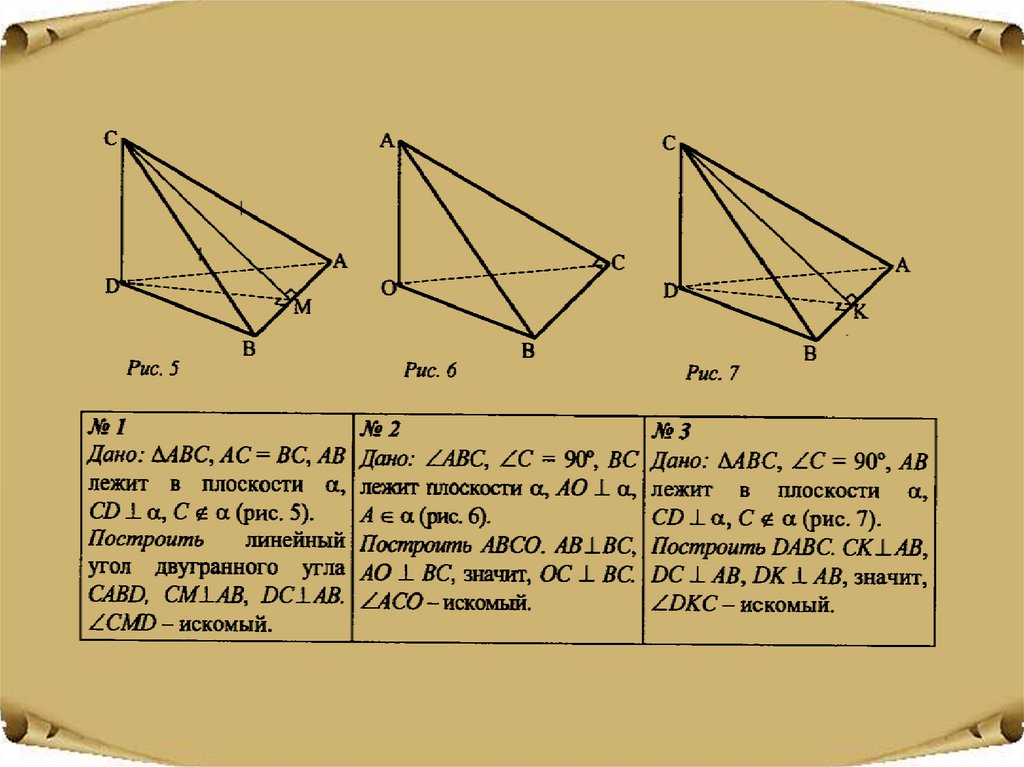
17.
Построить линейный угол двугранного угла с ребром АС, еслив пирамиде PABC AB=BC , прямая PB перпендикулярна плоскости ABC
P
A
B
K
C
18.
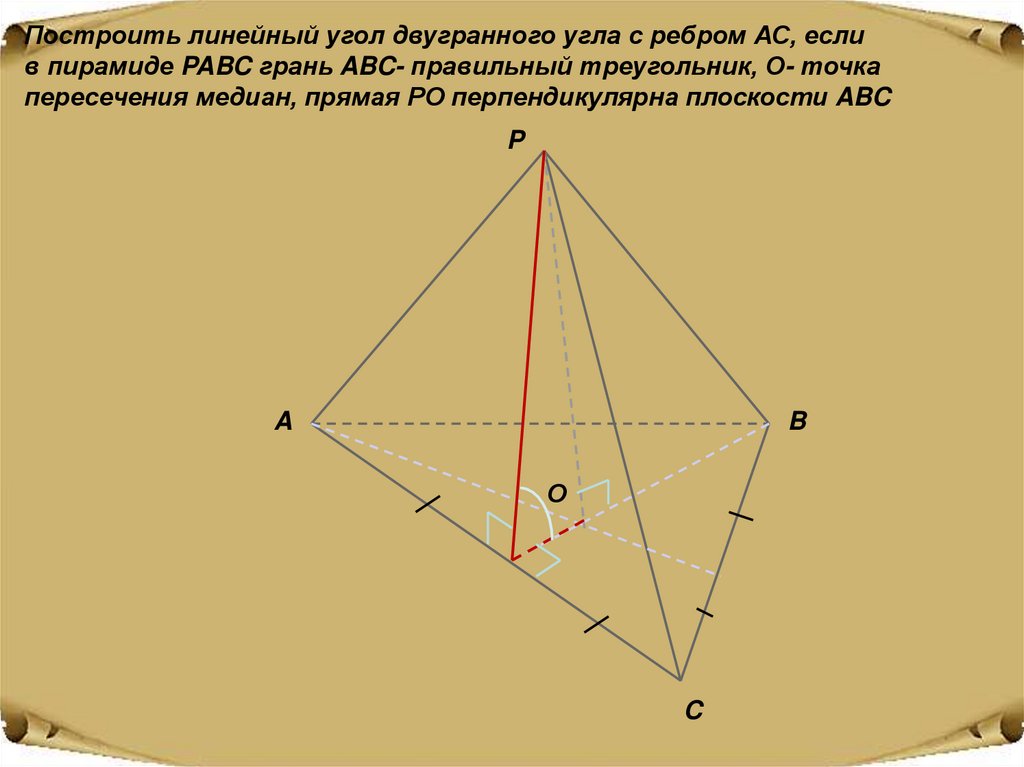
Построить линейный угол двугранного угла с ребром АС, еслив пирамиде PABC грань ABC- правильный треугольник, О- точка
пересечения медиан, прямая РО перпендикулярна плоскости ABC
P
A
B
О
C
19.
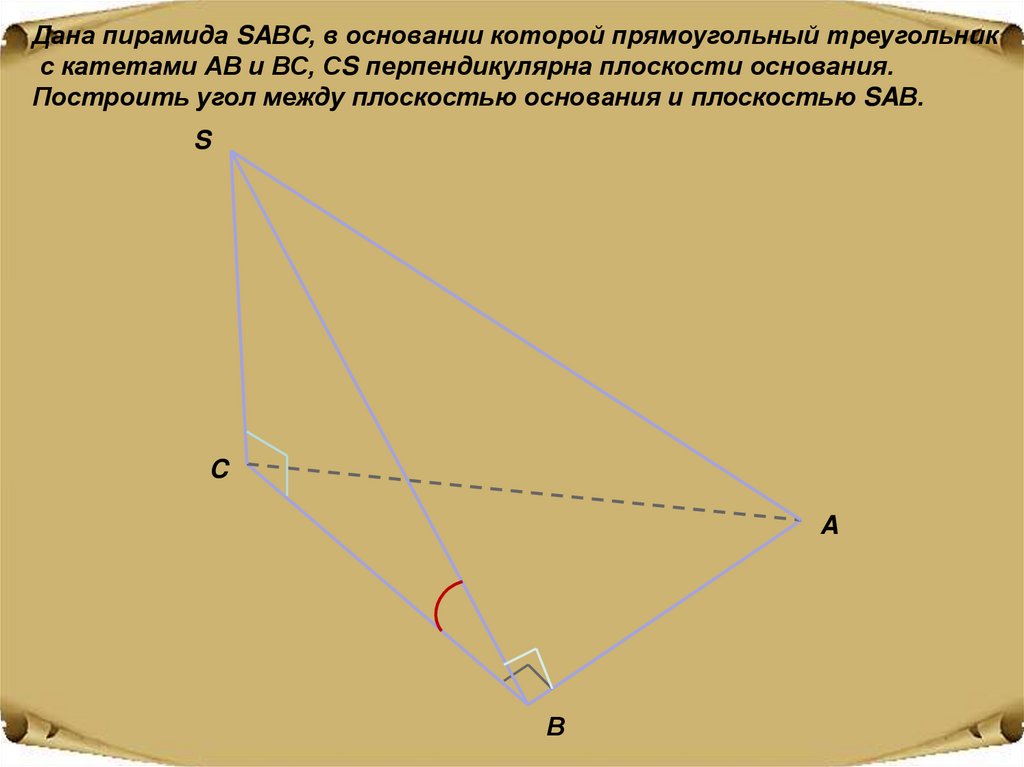
Дана пирамида SAВC, в основании которой прямоугольный треугольникс катетами АВ и ВС, СS перпендикулярна плоскости основания.
Построить угол между плоскостью основания и плоскостью SAВ.
S
C
A
В
20.
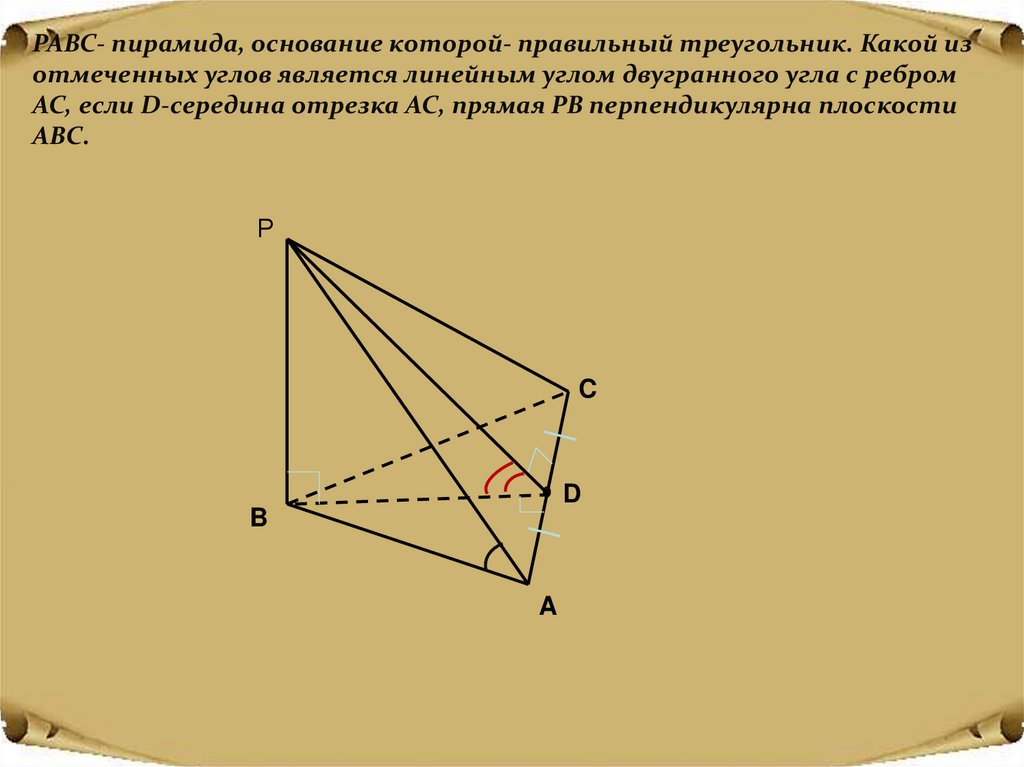
PABC- пирамида, основание которой- правильный треугольник. Какой изотмеченных углов является линейным углом двугранного угла с ребром
AC, если D-середина отрезка AC, прямая PB перпендикулярна плоскости
ABC.
Р
C
D
B
A
21.
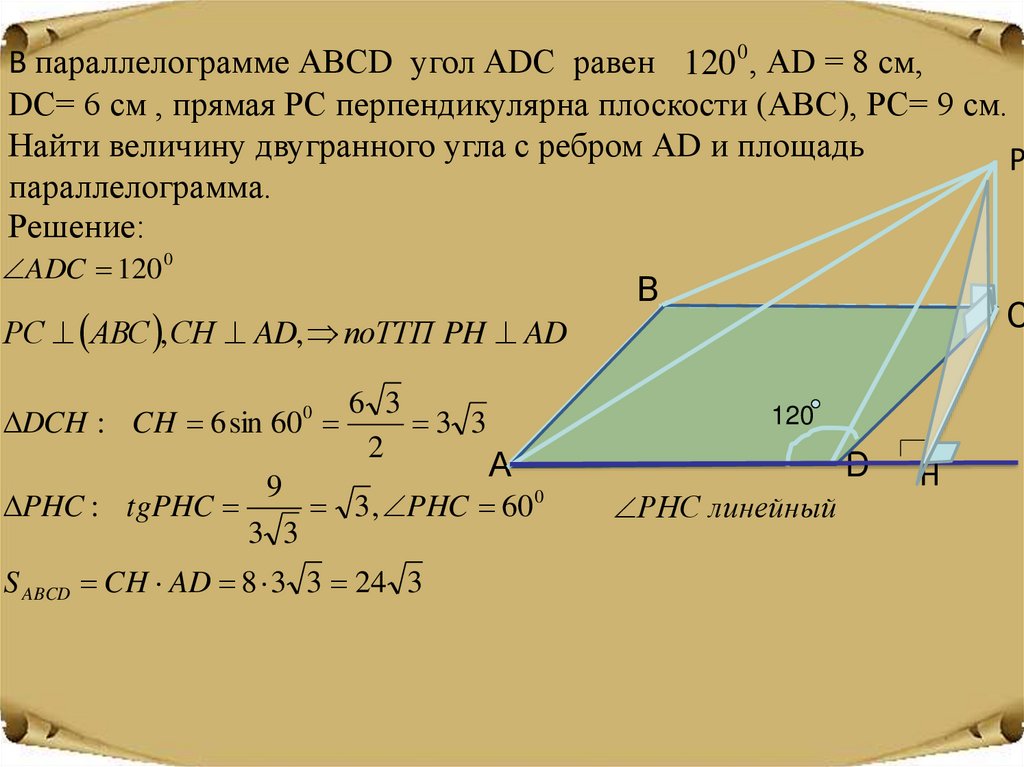
В параллелограмме АВСD угол АDС равен 120 0 , АD = 8 см,DС= 6 см , прямая РС перпендикулярна плоскости (АВС), РС= 9 см.
Найти величину двугранного угла с ребром АD и площадь
P
параллелограмма.
Решение:
ADC 120 0
РС АВС , СH AD, поТТП PH AD
6 3
DCH : CH 6 sin 60
3 3
2
А
9
PHC : tgPHC
3 , PHC 600
3 3
0
S ABCD CH AD 8 3 3 24 3
В
С
120
D
РНС линейный
H






 mathematics
mathematics