Similar presentations:
Угол между прямой и плоскостью. Проекция точки на плоскость
1. Угол между прямой и плоскостью
2.
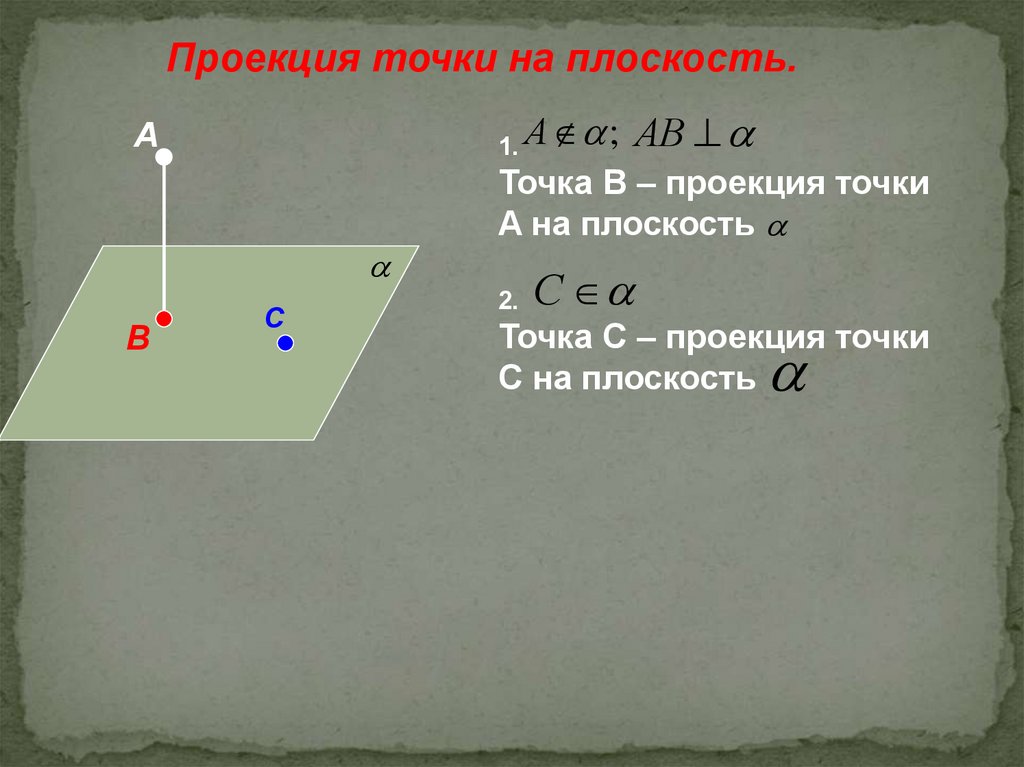
Проекция точки на плоскость.1. А ;
А
В
С
АВ
Точка B – проекция точки
A на плоскость
2.
С
Точка С – проекция точки
С на плоскость
3.
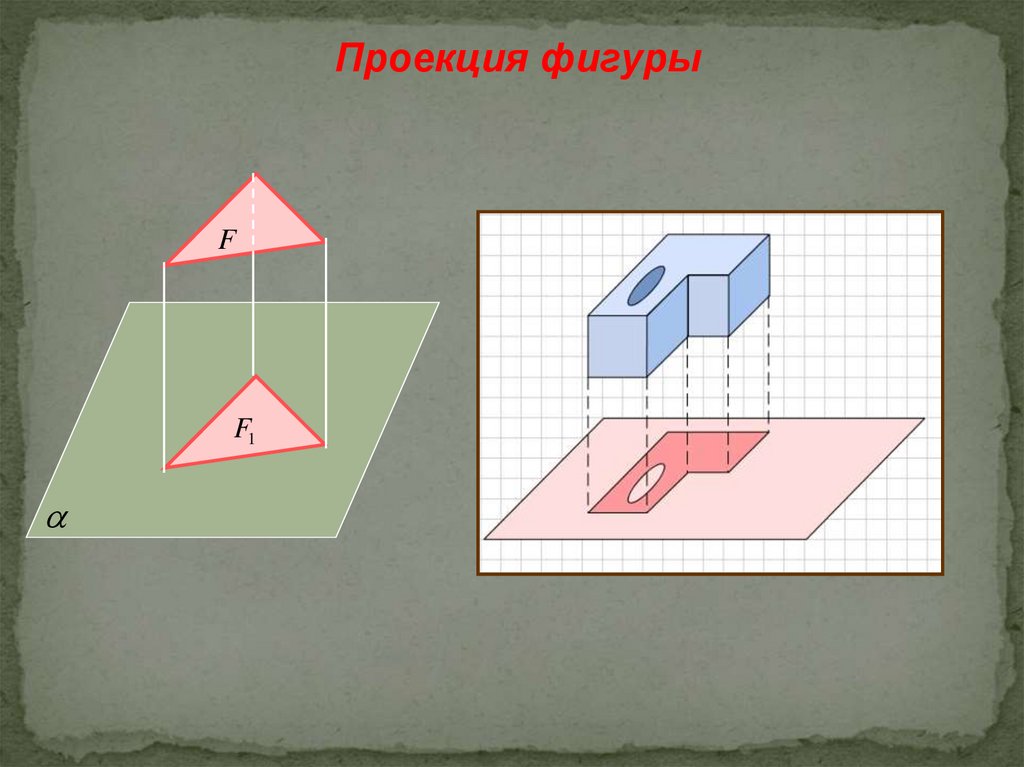
Проекция фигурыF
F1
4.
Проекция прямой на плоскость.1. а
2.
а
а
А
М
а
М1
а1 О
Н1 Н
Проекцией прямой (а )
на плоскость ( ),
не перпендикулярную к этой
плоскостью является –
прямая.
ДАНО:
а О, а .
ДОКАЗАТЬ: Проекцией прямой
а на плоскость
Точка А – проекция
прямой на плоскость
1. М , МН . Проведем
является прямая
а1
ДОКАЗАТЕЛЬСТВО:
через а и МН, а1.
2. Возьмем М 1 , М 1 Н1 МН , М1 Н1 а1 Н1 .
3. Так как МН М 1 Н1иМН а1 М1 Н1 , то есть Н 1 проекция М 1 на
проекция произвольной точки прямой а лежит на прямой а1
а
,
Верно и то, любая точка прямой 1 является проекцией некоторой точки прямой
значит а1 проекция прямой
на плоскость
а,
а
.
5.
Угол между прямой и плоскостью.Углом между прямой и плоскостью, пересекающей
эту прямую и не перпендикулярную к ней, называется
угол между прямой и ее проекцией на плоскость.
а
а1 А
Если
а на плоскость
а , а а1– проекция прямой
а, то (а, ) (а1 , а)
6.
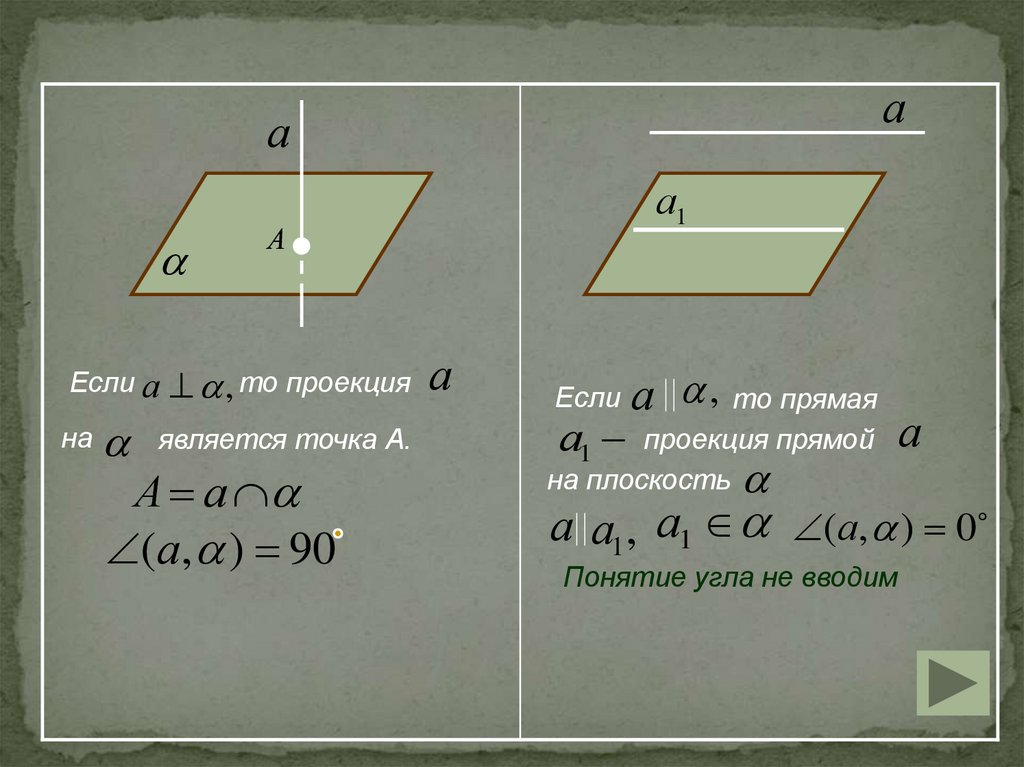
А что, еслиа ?
а или
7.
аа
Если а
на
а1
А
, то проекция
является точка А.
А а
(а, ) 90
а
Если
а1
а , то прямая
проекция прямой
на плоскость
а
а а1 , а1 (а, ) 0
Понятие угла не вводим




 mathematics
mathematics