Similar presentations:
Угол между прямой и плоскостью
1.
ТЕМА:«Угол между прямой и плоскостью»
Записать полностью конспект!
ЧИСЛО, ТЕМА, ФАМИЛИЯ
ВЫПОЛНЕННЫЕ РАБОТЫ
В ЛИЧНЫЕ СООБЩЕНИЯ!
2.
а — наклоннаяВМ — перпендикуляр из М на α
В — основание перпендикуляра
В — проекция М на α
АВ — проекция наклонной
A
a
M
B
α
3.
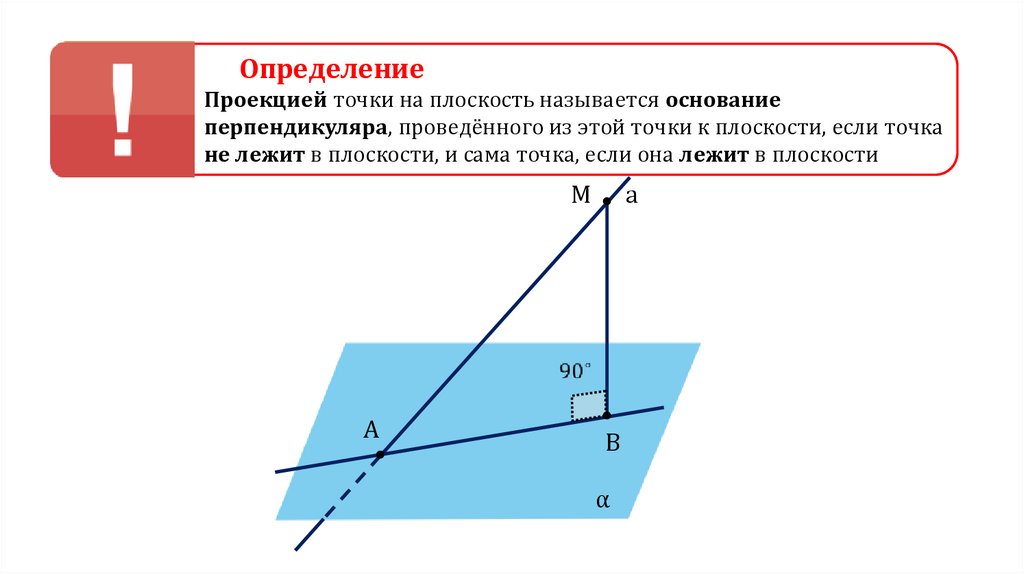
ОпределениеПроекцией точки на плоскость называется основание
перпендикуляра, проведённого из этой точки к плоскости, если точка
не лежит в плоскости, и сама точка, если она лежит в плоскости
M
A
a
B
α
4.
ТеоремаПроекцией прямой на плоскость,
не перпендикулярную к этой
прямой, является прямая
5.
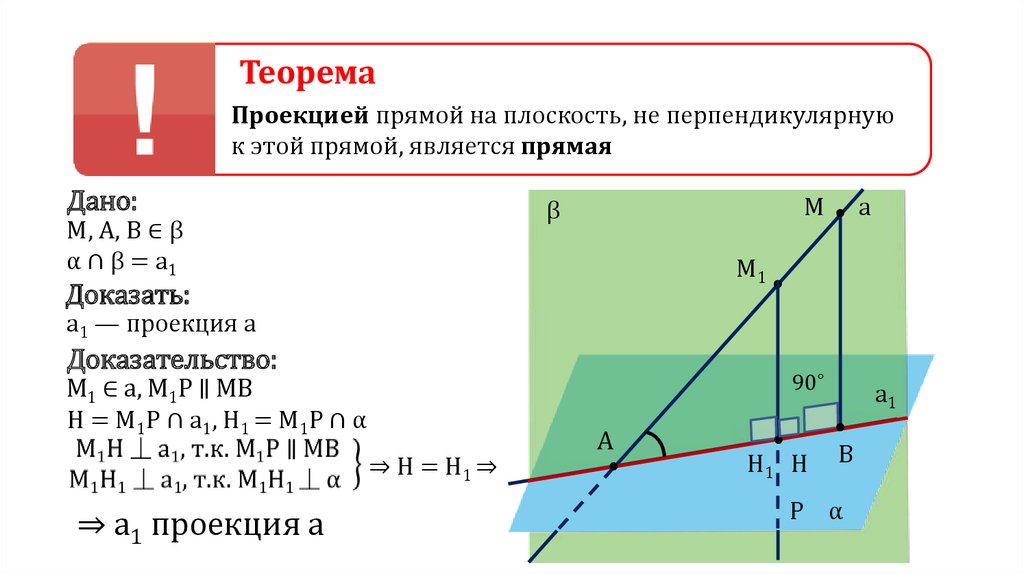
ТеоремаПроекцией прямой на плоскость, не перпендикулярную
к этой прямой, является прямая
Дано:
M
β
M, A, B ∈ β
α ∩ β = a1
a
M1
Доказать:
a1 — проекция a
Доказательство:
М1 ∈ а, М1Р ∥ МВ
Н = М1Р ∩ а1, Н1 = М1Р ∩ α
a1
⇒ H = H1 ⇒
⇒ а1 проекция а
A
H1 H
B
P α
6.
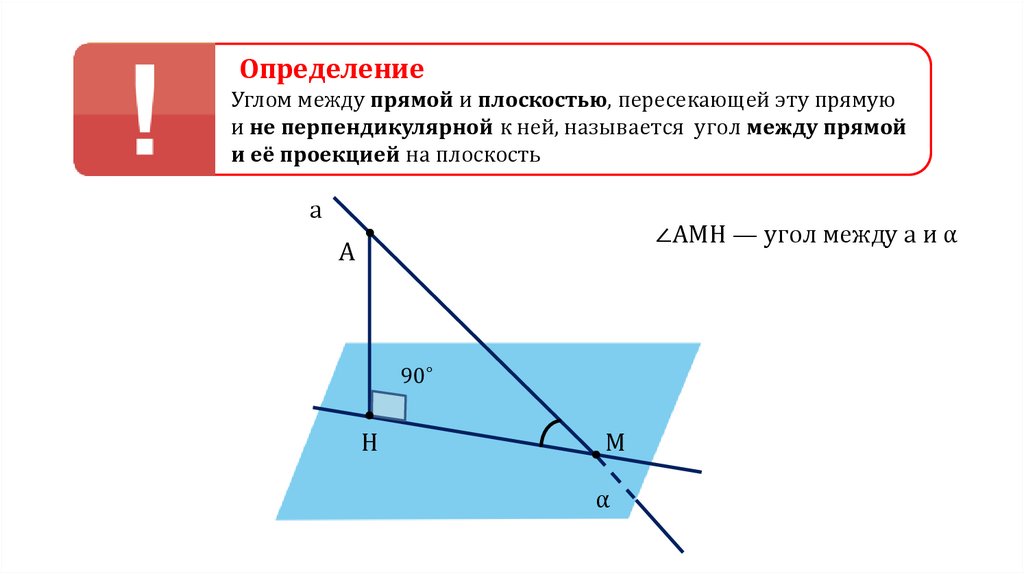
ОпределениеУглом между прямой и плоскостью, пересекающей эту прямую
и не перпендикулярной к ней, называется угол между прямой
и её проекцией на плоскость
a
∠АМH — угол между а и α
A
H
M
α
7.
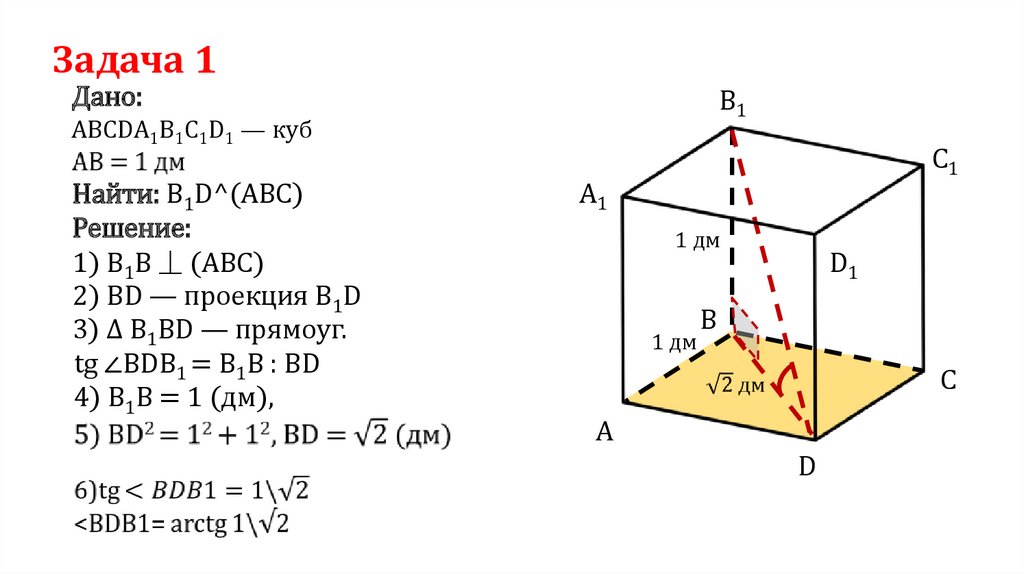
Задача 1B1
Дано:
ABCDA1B1C1D1 — куб
Найти: B1D^(ABC)
Решение:
1) B1B ⏊ (ABC)
2) BD — проекция B1D
3) ∆ B1BD — прямоуг.
tg ∠BDB1 = B1B : BD
4) B1B = 1 (дм),
C1
A1
1 дм
1 дм
D1
B
C
A
D



 mathematics
mathematics








