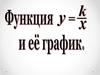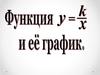Графики прямой и обратной пропорциональности

1. Проект урока по теме «Графики прямой и обратной пропорциональности»

2. Китайская пословица гласит:

«Я слушаю, - я забываю;
Я вижу, - я запоминаю;
Я делаю, - я усваиваю.»

3. Прямая пропорциональность.

• Функция вида y = kx + b называется
линейной функцией, где k, b - числа
(параметры), x - переменная
(аргумент)
• Линейная функция вида y = kx
называется прямой
пропорциональностью.

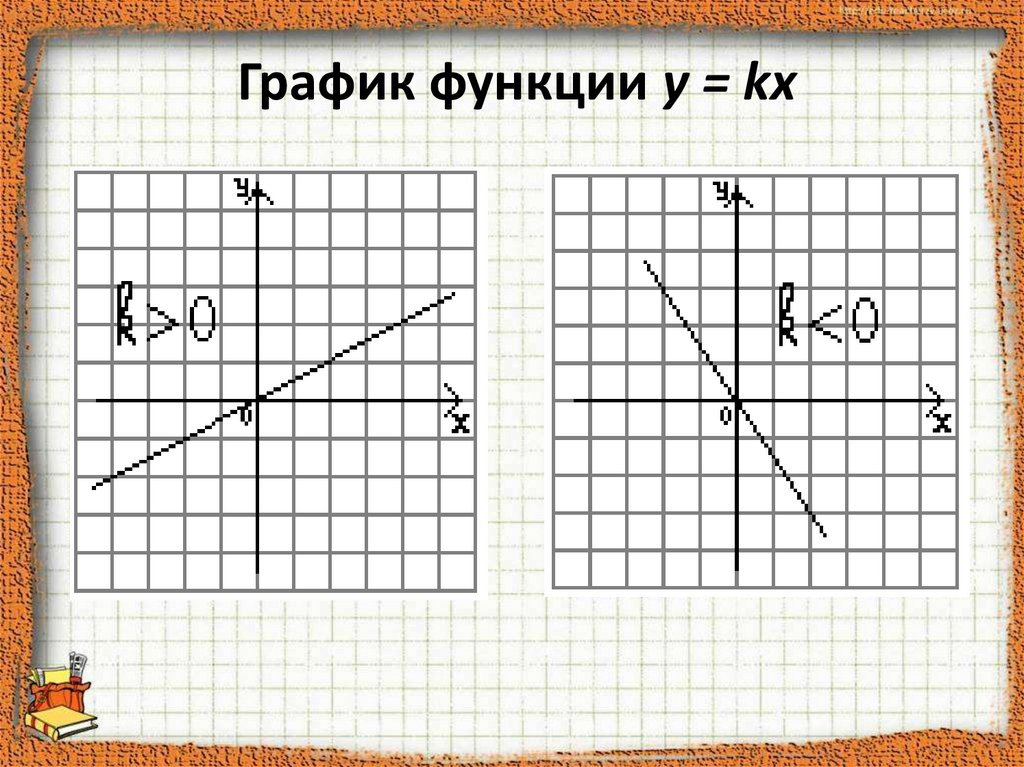
4. Свойства функции y = kx

1. Dy = R
2. Корни: x = 0
3. При k > 0 y > 0 при x (0; )
y < 0 при x (- ; 0)
При k < 0 y > 0 при x (- ; 0)
y < 0 при x (0; )
4. При k > 0 функция возрастает
При k < 0 функция убывает
5. Экстремумов нет.
6. Наибольшего и наименьшего значения нет.
7. Ey = R
8. Нечётная, непериодическая.
График - прямая, строим по двум точкам.
Замечание: График функции y = kx + b получаем
перемещением графика функции y = kx по вертикали:
если b > 0 , то вверх на b
если b < 0 , то вниз на b

5. График функции y = kx

6. Обратная пропорциональность.

Функция вида y = k / x называется
обратной пропорциональностью.

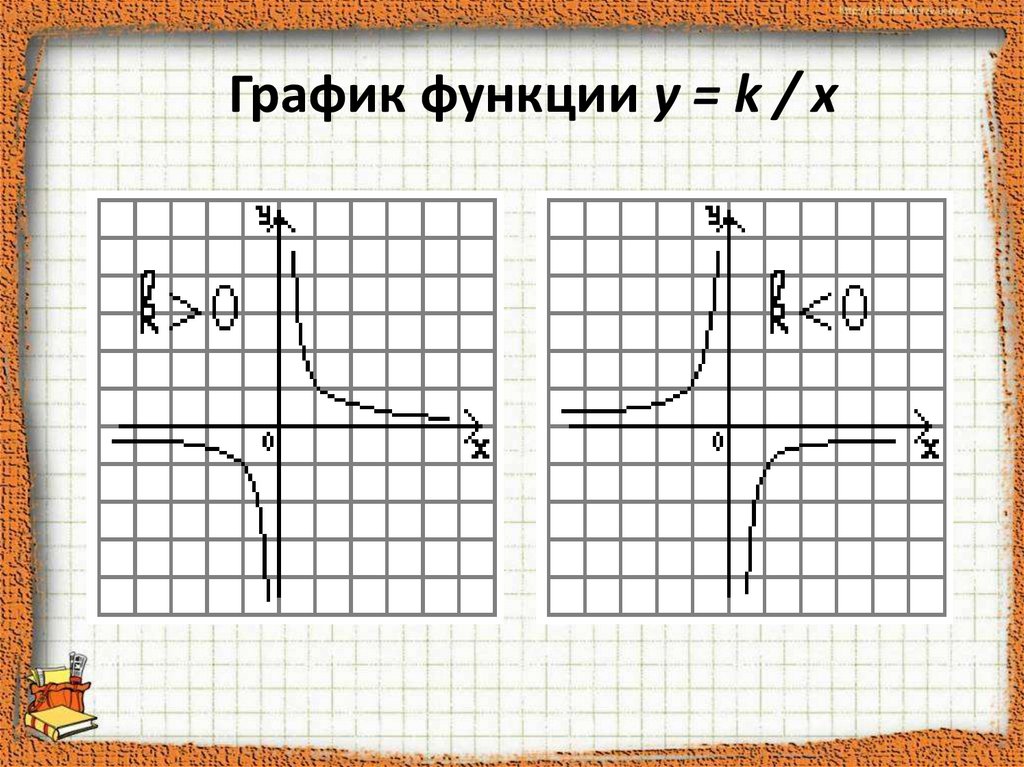
7. Свойства функции y = k / x

1. Dy = (- ; 0) (0; )
2. Корней нет
3. При k > 0 y > 0 при x (0; )
y < 0 при x (- ; 0)
При k < 0 y > 0 при x (- ; 0)
y < 0 при x (0; )
4. При k > 0 функция убывает
При k < 0 функция возрастает
5. Экстремумов нет.
6. Наибольшего и наименьшего значения нет.
7. Ey = (- ; 0) (0; )
8. Нечётная, непериодическая.
График - гипербола, строим заполняя таблицу.

8. График функции y = k / x

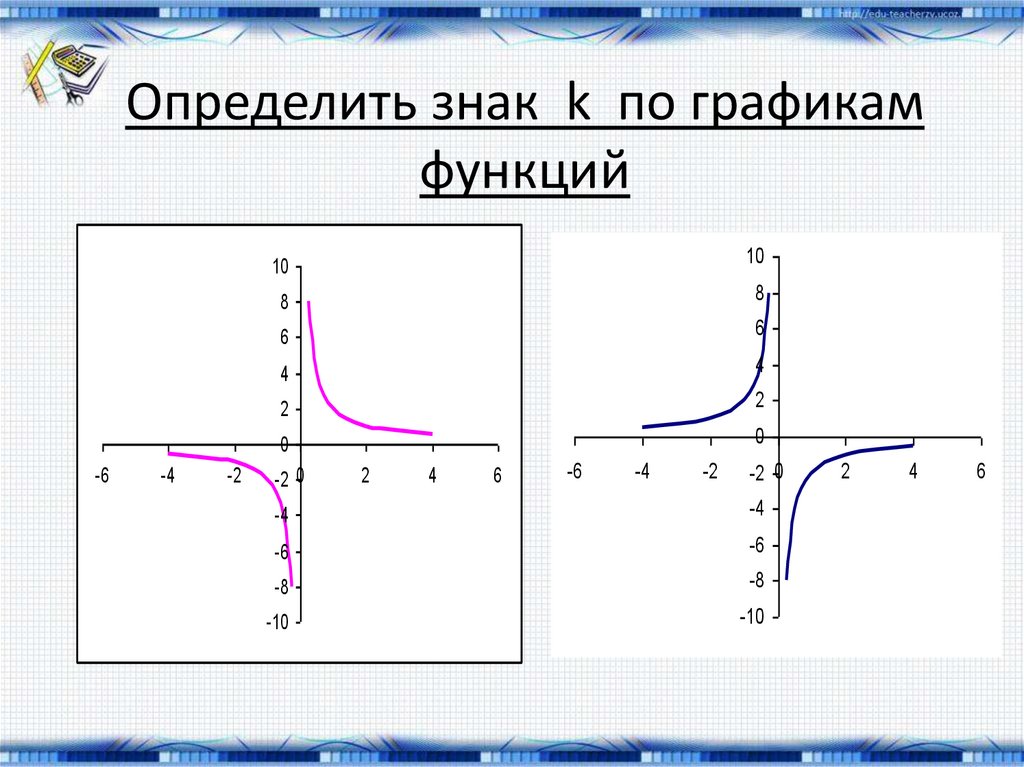
9. Определить знак k по графикам функций

-6
-4
-2
10
10
8
8
6
6
4
4
2
2
0
0
-2 0
2
4
6
-6
-4
-2
-2 0
-4
-4
-6
-6
-8
-8
-10
-10
2
4
6