По графику функции определите промежуток, в котором функция возрастает.

Задачи, приводящие к понятию обратной пропорциональности.

ИСТОРИЯ ПРОИСХОЖДЕНИЯ ТЕРМИНА "ГИПЕРБОЛА"

2.86M

Category: $mathematics$ mathematics

Обратная пропорциональность. 9 класс

1.

Открытый урок
По алгебре 9 класс
Коровашкова Алла Дмитриевна
гимназия№205
2011г.

2.

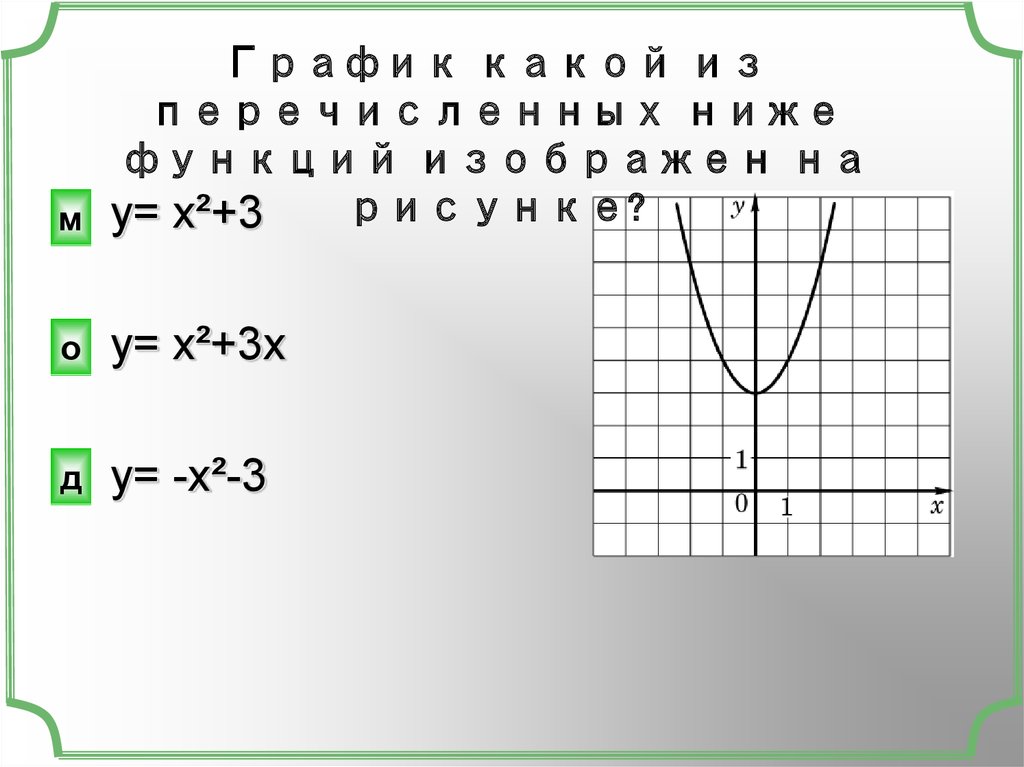
График какой из
перечисленных ниже
функций изображен на
рисунке?
мм y= x²+3
о
y= x²+3x
д
y= -x²-3

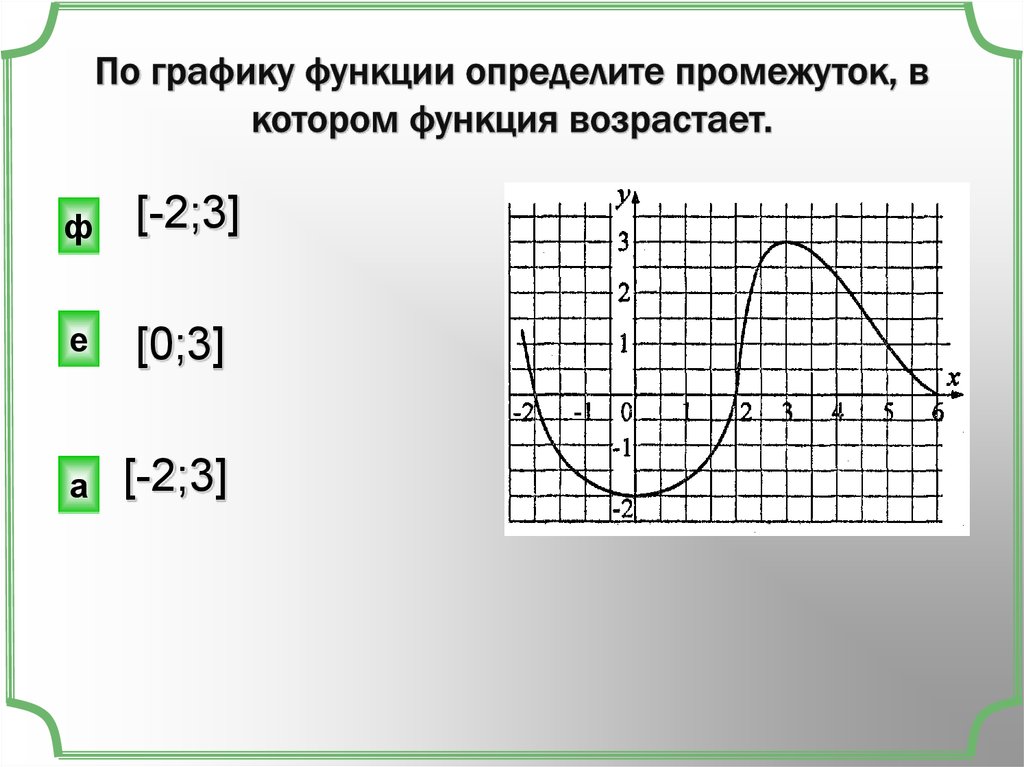
3. По графику функции определите промежуток, в котором функция возрастает.

ф
[-2;3]
е
[0;3]
а[
[-2;3]

4.

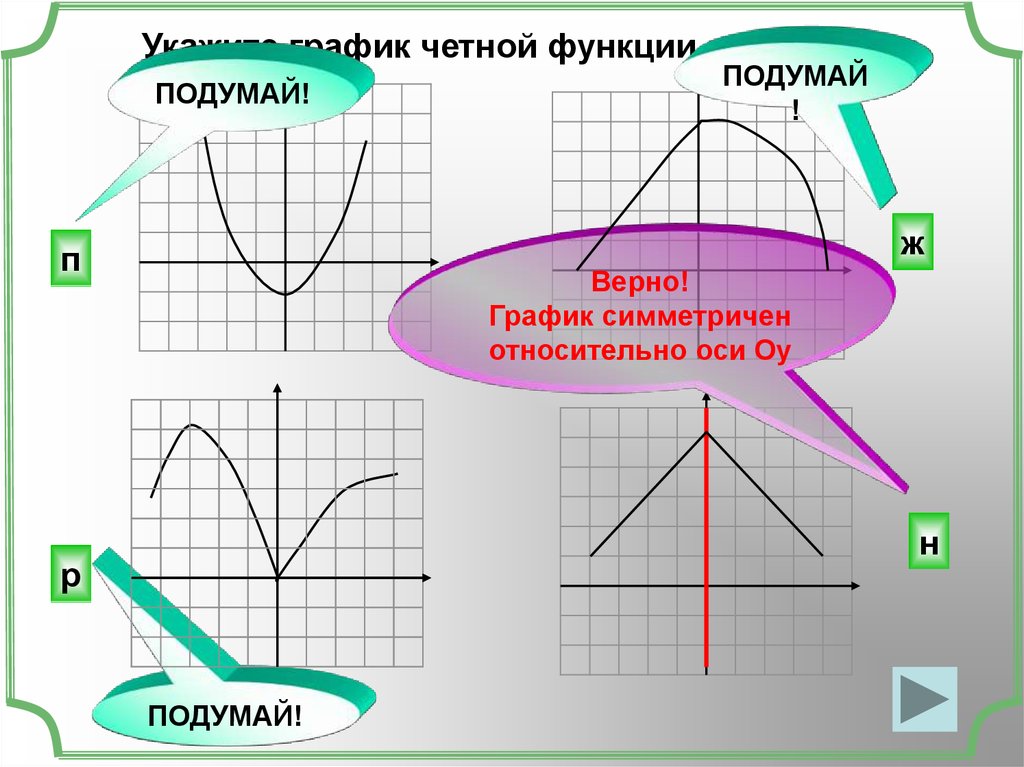
Укажите график четной функции.
ПОДУМАЙ!
ПОДУМАЙ
!
ж
п
Верно!
График симметричен
относительно оси Оу
н
р
ПОДУМАЙ!

5.

Укажите график возрастающей функции.
ПОДУМАЙ!
е
ы
Верно!
о
я
Подумай!
ПОДУМАЙ!

6.

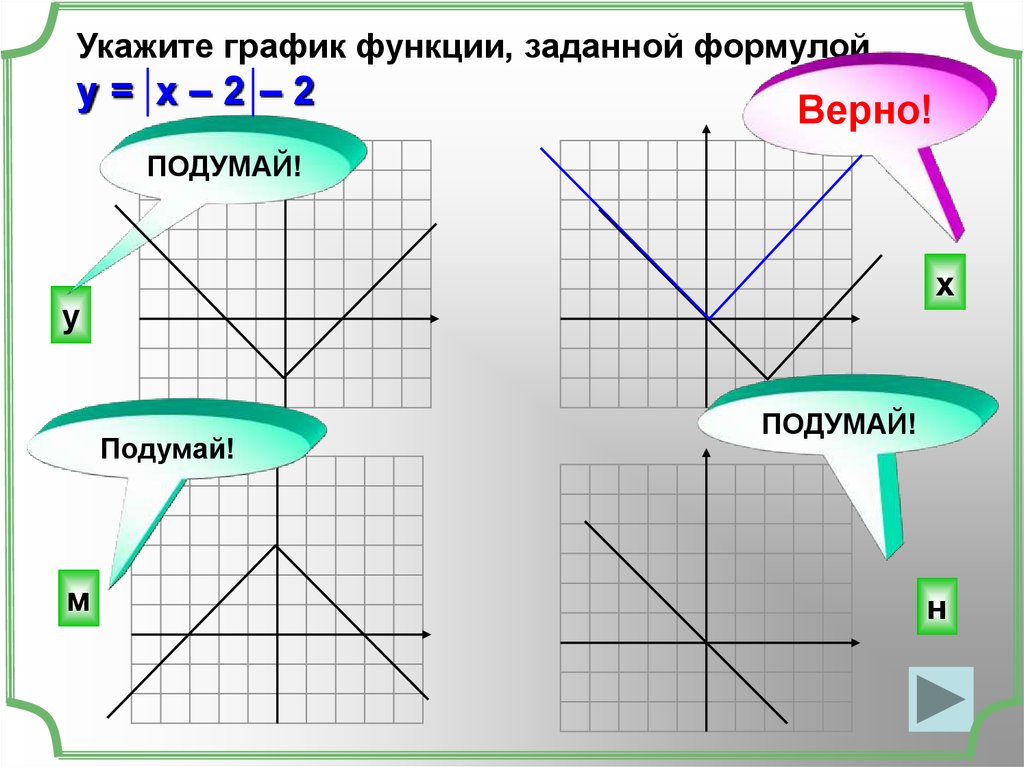
Укажите график функции, заданной формулой
у= х–2 –2
Верно!
ПОДУМАЙ!
х
у
Подумай!
м
ПОДУМАЙ!
н

7.

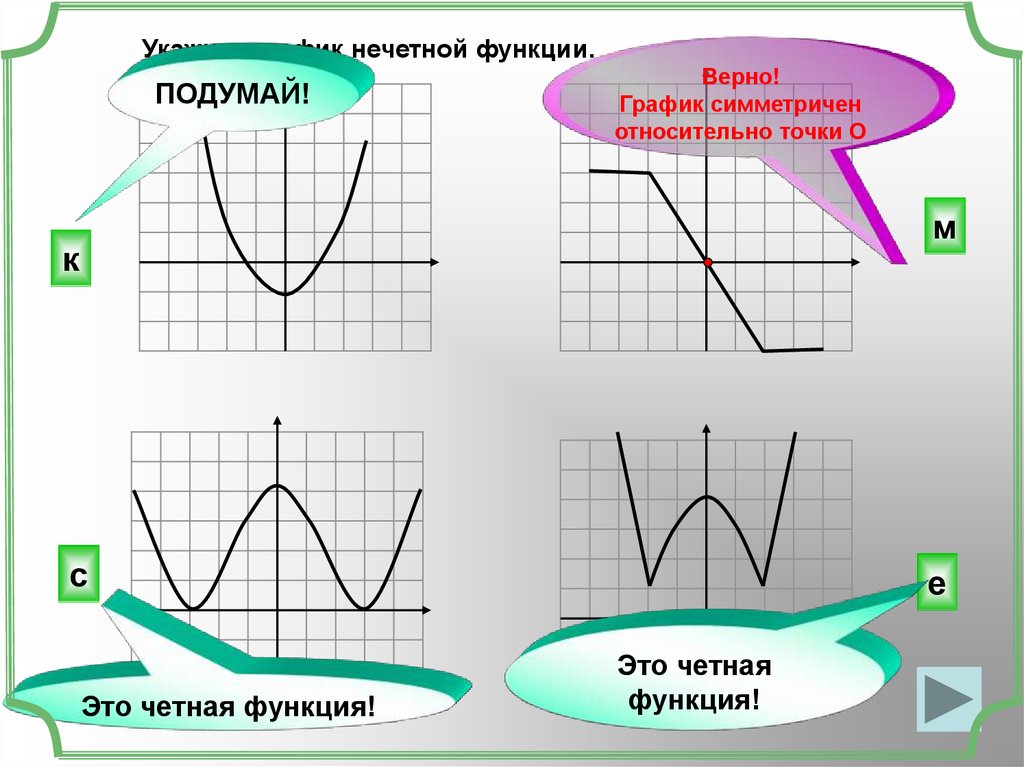
Укажите график нечетной функции.
ПОДУМАЙ!
Верно!
График симметричен
относительно точки О
м
к
с
Это четная функция!
е
Это четная
функция!

Менехм
(греч. Μέναιχμος, лат. Menaechmus, ок.
380 до н. э. — ок. 320 до н. э.) —
древнегреческий математик, ученик
Евдокса, член Афинской Академии
Платона. Упоминается у античных
авторов как первый исследователь
конических сечений и в связи с
попытками решить проблему удвоения
куба
Есть упоминание, что Менехм участвовал
в обучении Александра Македонского,
и при этом произнёс знаменитую фразу
«В геометрии нет царского пути».
Впрочем, за честь быть автором этой
фразы с ним соперничает Евклид, а за
честь её выслушать — Птолемей I.
Умер Менехм, предположительно, в
городе Кизик.

9.

10.

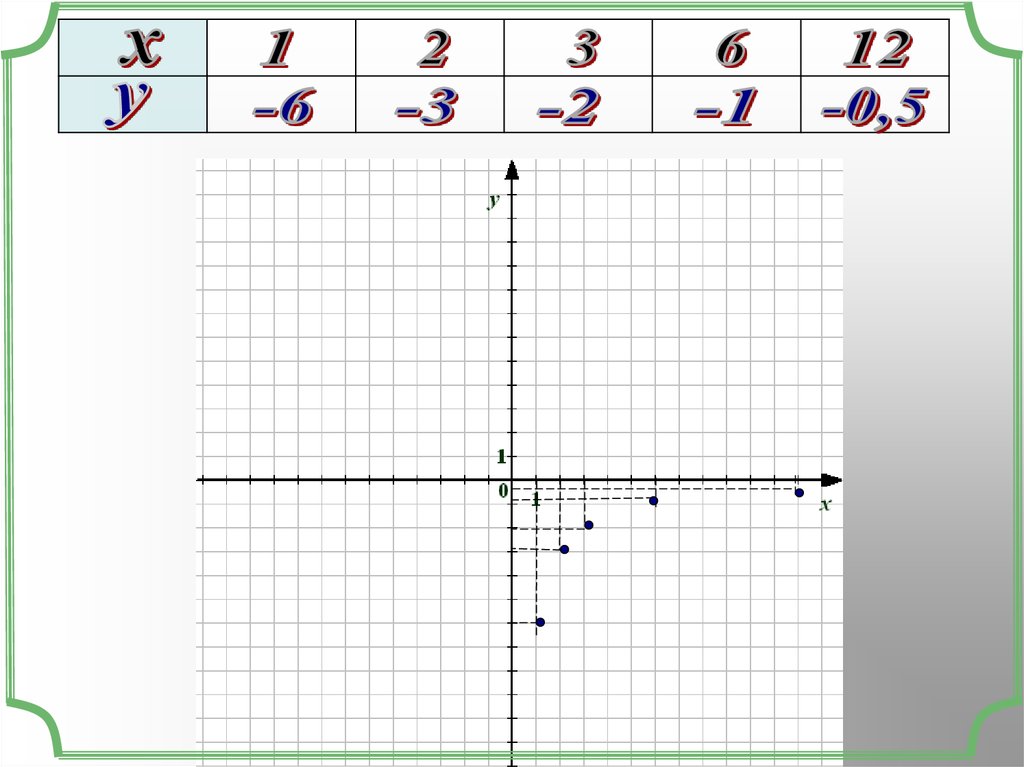
12
y
x
Мы видим, что если х
уменьшать в несколько раз, то
у будет увеличиваться во
столько же раз.
Наоборот, если значение х
увеличить в несколько раз, то
значение у во столько же раз
уменьшается.
Поэтому функцию такого вида
называют обратной
пропорциональностью.

11. Задачи, приводящие к понятию обратной пропорциональности.

1
еход путь S проходит со скоростью v
t часов. Выразите время пешехода
через путь и скорость.
1) Если
S
60
60
, tто
v

12. Задачи, приводящие к понятию обратной пропорциональности.

1
еход путь S проходит со скоростью v
t часов. Выразите время пешехода
через путь и скорость.
2) ЕслиS
3
3
t
, то
v
Как связаны между собой
скорость и время?

13. О п р е д е л е н и е.

Обратной пропорциональностью
называется функция, которую
можно задавать формулой вида
где х – независимая переменная
k – не равное нулю число.

14.

1.Много будешь знать, скоро
состаришься.
2.Чем скорее проедешь, тем скорее
приедешь.
3. Тише едешь, дальше будешь.
4. Чем дальше в лес, тем больше дров.
5. Чем больше раз проверю, тем меньше
вероятность ошибиться.

15. Свойства функции

1
х 0
бластью определения функции явля
множество всех чисел, отличных от н
2
k 0 у 0
Областью значений функции являет
множество всех чисел, отличных от н

16. График функции

строим по точкам график функции

17.

18.

гипербола

19. ИСТОРИЯ ПРОИСХОЖДЕНИЯ ТЕРМИНА "ГИПЕРБОЛА"

ИСТОРИЯ ПРОИСХОЖДЕНИЯ ТЕРМИНА
"ГИПЕРБОЛА"
Одним из первых, кто начал изучать
конические сечения — эллипс,
парабола, гипербола, был ученик
знаменитого Платона,
древнегреческий математик Менехм
(IV в. до н.э.). Решая задачу об
удвоении куба, Менехм задумался: «А
что случится, если разрезать конус
плоскостью, перпендикулярной его
образующей?». Так, изменяя угол при
вершине прямого кругового конуса,
Менехм получил три вида кривых:
эллипс — если угол при вершине
конуса острый; парабола — если угол
прямой; одну ветвь гиперболы — если
угол тупой.

20. График функции

строим по точкам график функции

21.

22.

гипербола

23. Особенности графиков.

Симметричность
ветвей графика
относительно (0; 0)
k>0
I, III четверти

24. Особенности графиков.

Симметричность
ветвей графика
относительно (0; 0)
k<0
II, IV четверти

25. План исследования функции

1.ООФ
2.МЗФ
3.Нули функции
4.Знакопостоянство
5.Монотонность
6.Четная или нечетная
7.Наибольшее и наименьшее значение функции

26.

Свойства функции У=
1.
1.Область
D ( у ) ;0
к
х
0 ;
, где к>0 :
у
E ( у ) ;0 0;
определения
2.
2.Область
значений
3. у>0, если х 0 ;
у<0, если х ; 0
1
4. Функция
-3 -2 -1 0 1 2 3
убывает при
-1
х ; 0 0;
5. Нечетная, симметрична
относительно т.О
6. унаим.= НЕТ
унаиб.= НЕТ
7. Нулей нет,график оси координат не
пересекает.
х

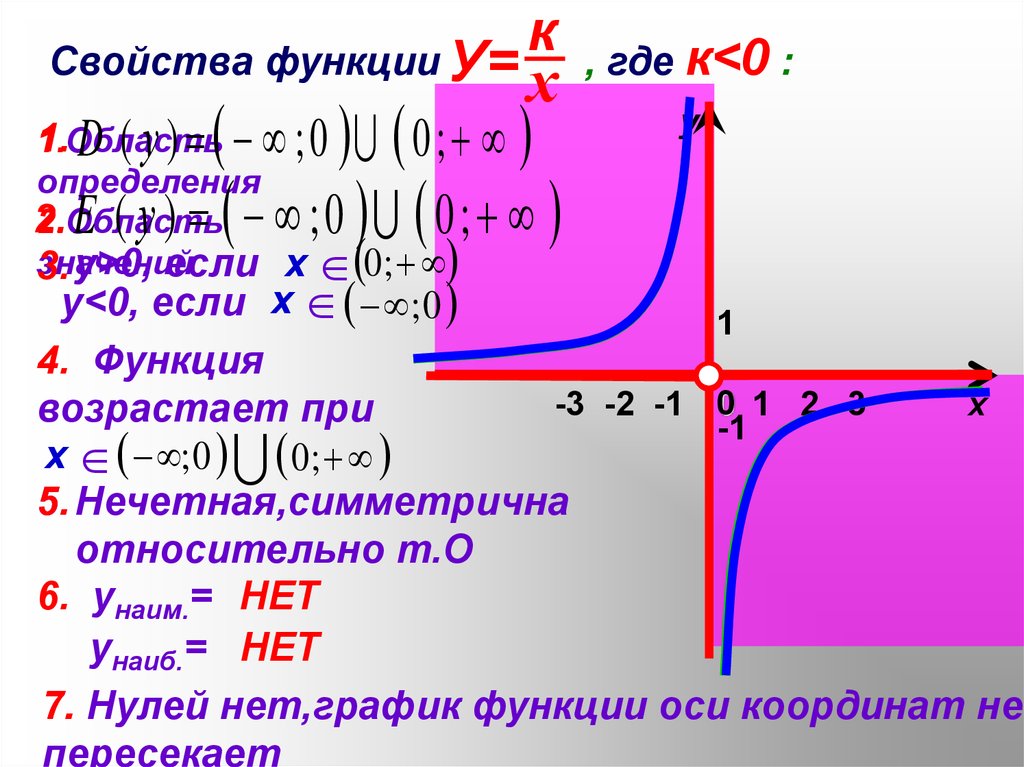
27.

Свойства функции У=
1.
1.Область
D ( у ) ;0
к
х
0 ;
, где к<0 :
у
E ( у ) ;0 0;
определения
2.
2.Область
значений
3. у>0, если х 0 ;
у<0, если х ; 0
1
4. Функция
х
-3 -2 -1 0 1 2 3
возрастает при
-1
х ; 0 0;
5. Нечетная,симметрична
относительно т.О
6. унаим.= НЕТ
унаиб.= НЕТ
7. Нулей нет,график функции оси координат не
пересекает

28.

Задание №1
Укажите, какую из функций
можно назвать
обратной пропорциональностью:
х
у
3
3
у
х
у 3х
у х 3
у х
3
1
у
3х

29.

Задание №2
Укажите среди графиков
гиперболу
Не верно
1
Подумай
Молодец!
2
3

30.

Задание №3
Задайте функцию обратной
пропорциональности, если ее графи
проходит через точку:
( 1; 3 )
х
у
k
3
1
k 3

31.

Задание №3
Задайте функцию обратной
пропорциональности, если ее графи
проходит через точку:
( 2; -6 )
( -12; 4 )
( 5; 0,5 )

32.

Задание №4
Постройте график функции
Проверка

33.

I, III четверти
Симметрично
Относительно
О (0; 0)

34.

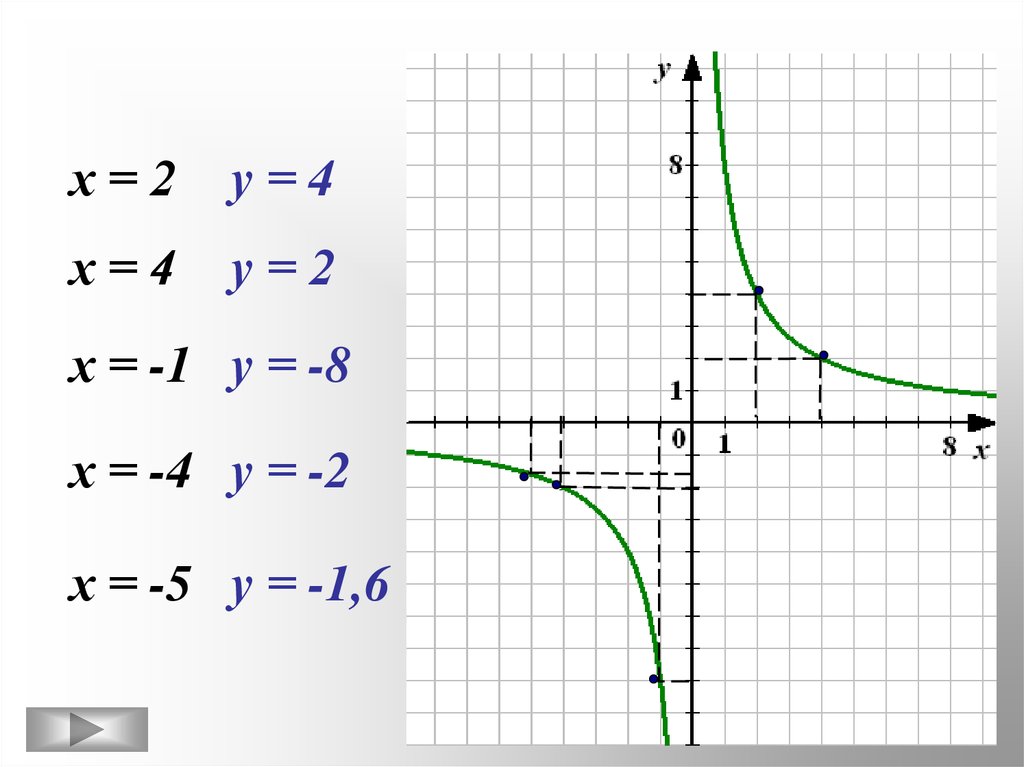
Задание №4
Постройте график функции
Найдите по графику:
1) Значение у, соответствующее
значению х, равному 2; 4; -1; -4; -5
Проверка

35.

х=2
у=4
х=4
у=2
х = -1 у = -8
х = -4 у = -2
х = -5 у = -1,6

36.

Задание №5
Постройте график функции
Найдите по графику
значение у, соответствующее
значению х, равному 2; 4; -1; -4; -5
Найдите по графику:
значение х, которому соответствуе
значение у, равное -4; -2; 8
Проверка

37.

у = -4 х = -2
у = -2 х = -4
у=8
х=1

38.

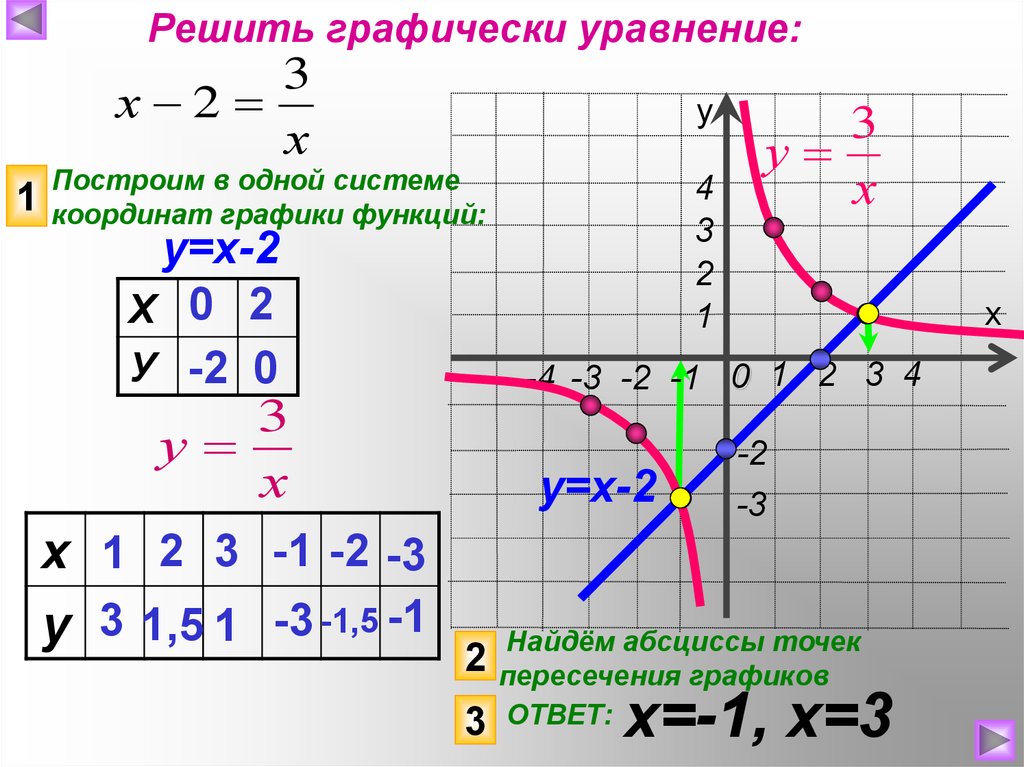
Решить графически уравнение:
3
х 2
х
1
у
Построим в одной системе
координат графики функций:
у=х-2
Х 0 2
У -2 0
3
у
х
х 1 2 3 -1 -2 -3
у 3 1,5 1 -3 -1,5 -1
4
3
2
1
3
у
х
х
-4 -3 -2 -1 0 1 2 3 4
у=х-2
-2
-3
Найдём абсциссы точек
2 пересечения
графиков
3
ОТВЕТ:
х=-1, х=3

39.

Решить графически систему уравнений:
3
у
У= х
у=3х²
1
Построим в одной с. к.
графики функций:
3
У= х
х 1 2 3 -1
у 3 1,5 1 -3
у=3х²
Х 0 ±1
У 0 3
5
4
3
2
1
у=3х²
(1;3)
3
y
х
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
-1
-2 -3
-2
-1,5 -1
-3
-4
-5
Найдём координаты точек
2 пересечения
графиков
3 ОТВЕТ (1;3)
х