Similar presentations:
Понятие функции, способы её задания, график функции. Преобразование графиков
1. Понятие функции, способы её задания, график функции. Преобразование графиков.
2. Числовая функция
Определение. Числовой функцией с областьюопределения D называется соответствие при
котором каждому числу x из множества D
сопоставляется по некоторому правилу число y,
зависящее от x.
x – аргумент функции (независимая переменная)
Число у, соответствующее числу х, называют
значением функции f в точке х и обозначают f(x)
3.
Область определения функции f обозначаютD(f).
Множество, состоящее из всех чисел f(x), таких, что
х принадлежит области определения функции f,
называют областью значений функции f и
обозначают E(f).
4.
Объединением множеств А и В называетсямножество, состоящее из всех элементов, которые
принадлежат хотя бы одному из множеств А или В.
Объединение множеств А и В обозначается так:
А В
5.
Функции вида f(x)=p(x), где p(x) – многочлен,называют целыми рациональными функциями,
а функции видаf x p x
q x
где p(x) и q(x) – многочлены, называют
дробно-рациональными функциями.
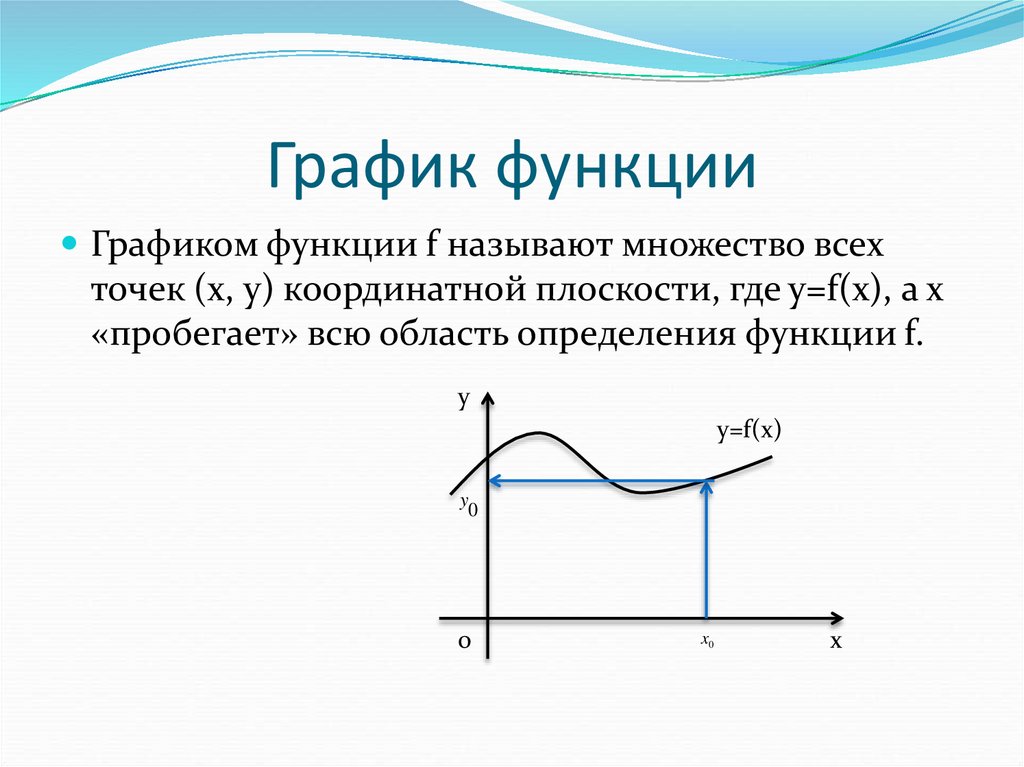
6. График функции
Графиком функции f называют множество всехточек (х, у) координатной плоскости, где y=f(x), а х
«пробегает» всю область определения функции f.
y
y=f(x)
y
0
0
x0
x
7. Линейная функция
y = kx + by
b – свободный
коэффициент
k – угловой
коэффициент
k = tg α
b
b
k
α
0
x
8.
Свойства линейной функцииy = kx + b
1о D(y) = (−∞; +∞); E(y) = (−∞; +∞).
2о Если b = 0, то функция нечетная.
Если b ≠ 0, то функция ни четная, ни нечетная.
b
о
3 Если х = 0, то у = b, если у = 0, то х = − .
k
4о Если k > 0, то функция возрастает при х (−∞; +∞).
Если k < 0, то функция убывает при х (−∞; +∞).
9.
Степенная функцияn
y=x
y
y = xn, где n = 2k, k Z
y = xn, где n = 2k +1, k Z
1
01
x
10.
Свойства степенной функцииn
y=x
Если n = 2k, где k
Если n = 2k +1, где k
Z
Z
1о D(y)=(−∞; +∞).
1о D(y)=(−∞; +∞).
2о E(y)=[0 ; +∞).
2о E(y)=(−∞; +∞).
3о Функция четная.
3о Функция нечетная.
4о Если х = 0, то у = 0.
4о Если х = 0, то у = 0.
5о Функция возрастает
5о Функция
при х [0 ; +∞);
убывает при х (−∞; 0].
возрастает
при х (−∞; +∞).
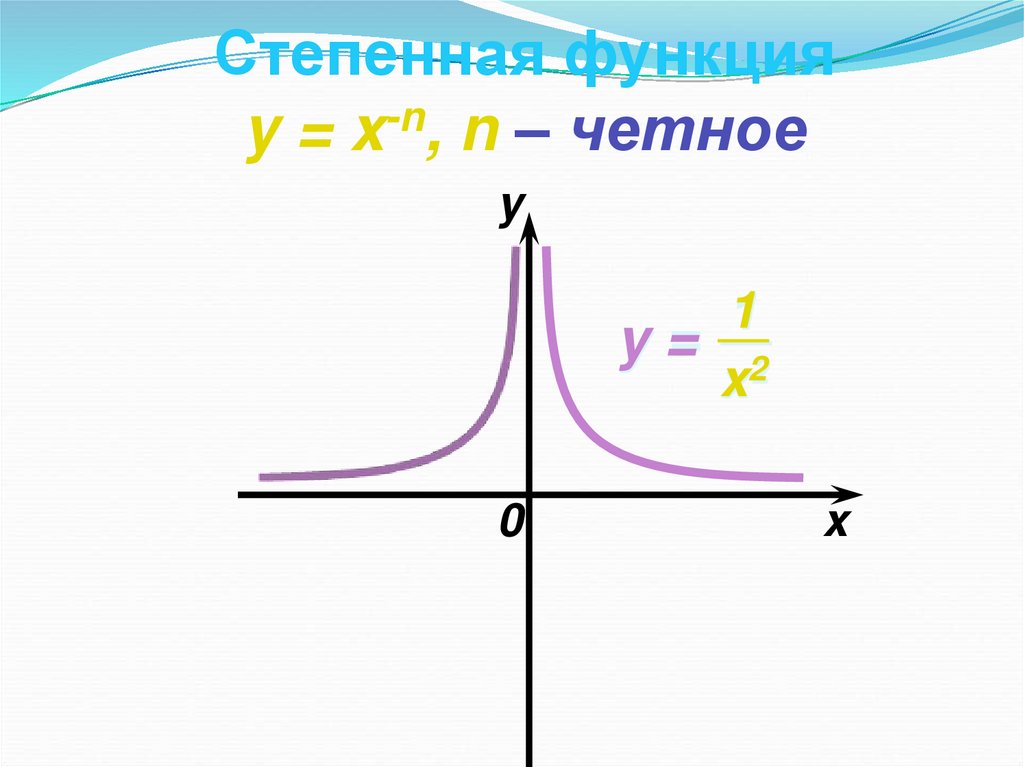
11.
Степенная функцияy = x-n, n – четное
y
1
y= 2
x
0
x
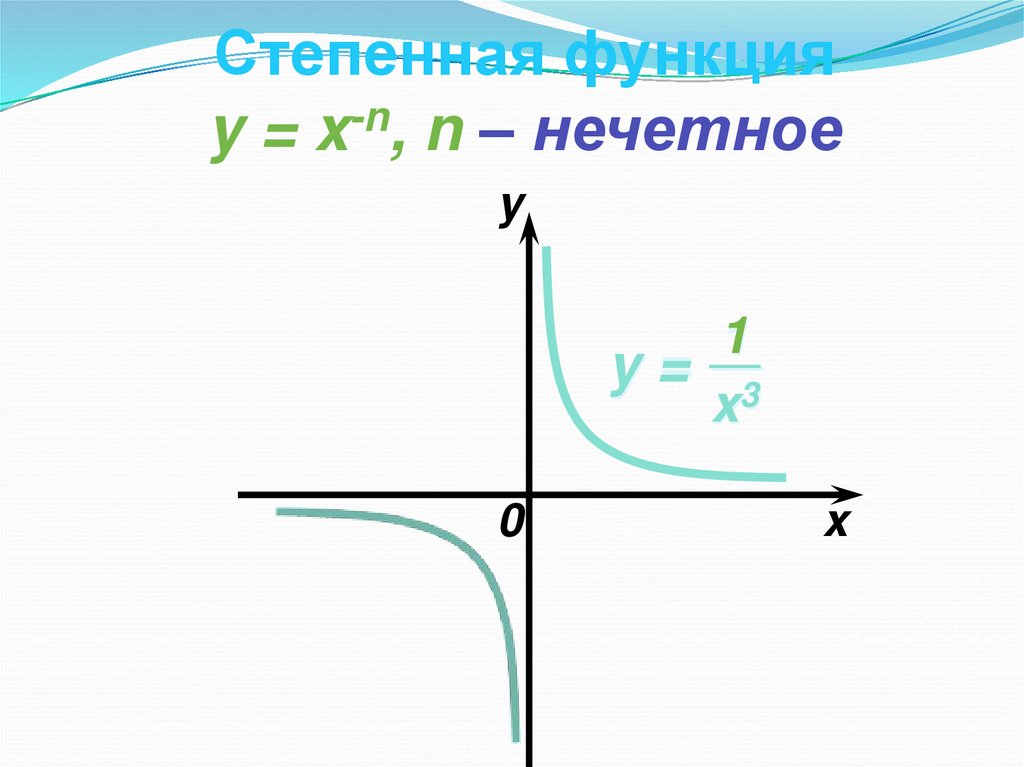
12.
Степенная функцияy = x-n, n – нечетное
y
1
y= 3
x
0
x
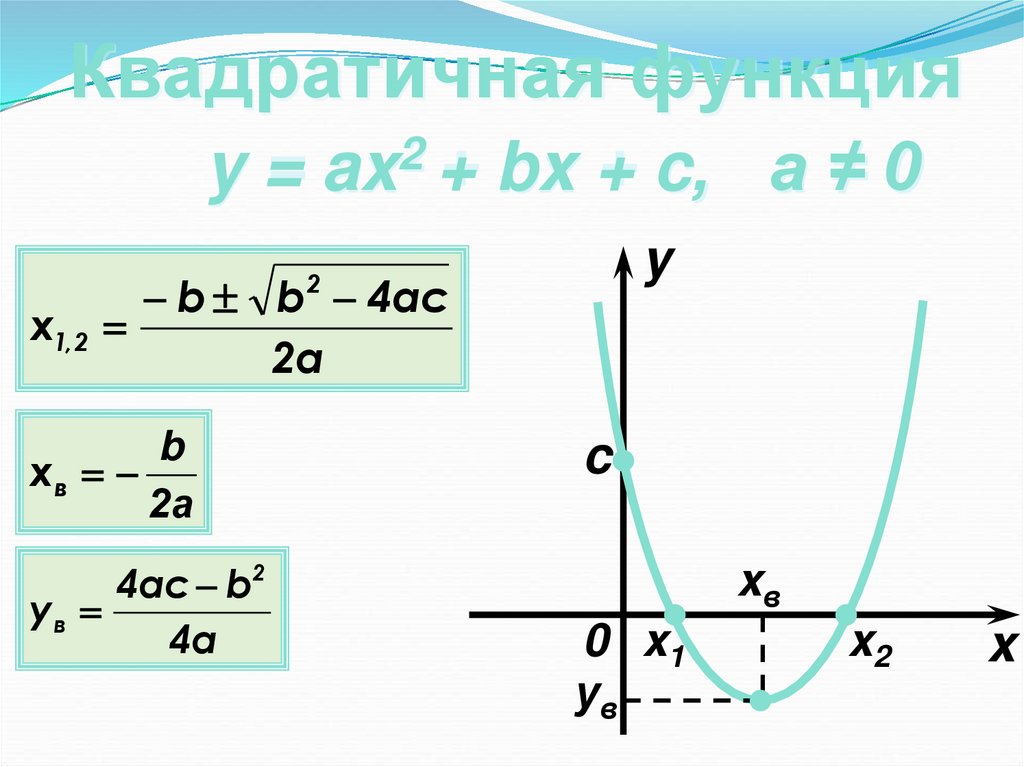
13.
Квадратичная функция2
y = ax + bx + c,
y
2
b b 4ac
x1,2
2a
b
xв
2а
4ac b
yв
4a
а≠0
c
2
xв
0 x1
ув
x2
x
14.
Свойства квадратичной функции2
y = ax + bx + c,
а≠0
1о D(y) = (−∞; +∞).
2о Если a > 0, то E(y) = [ув ; +∞);
Если a < 0, то E(y) = (−∞; ув ].
3о Если b = 0, то функция четная.
Если b ≠ 0, то функция ни четная, ни нечетная.
2-4ac
b
±
√
b
о
4 Если х = 0, то у = c, если у = 0, то х1,2 =
2a
5о Если a > 0, то функция возрастает при х [xв ;
+∞);
функция убывает при х (−∞; хв ].
Если a < 0, то функция возрастает при х (−∞; хв ];
функция убывает при х [xв ; +∞).
15.
Обратнаяпропорциональность
y
k
y=
,k>0
x
k
y=
,k<0
x
0
x
16.
Свойства обратнойпропорциональности
k
у=
x
1о D(y) = (−∞; 0)u(0; +∞)
2о E(y) = (−∞; 0)u(0 ; +∞)
3о Функция нечетная.
4о х ≠ 0, у ≠ 0.
5о Если k > 0, то функция убывает
при х (−∞; 0)u(0; +∞).
Если k < 0, то функция возрастает
при х (−∞; 0)u(0; +∞).
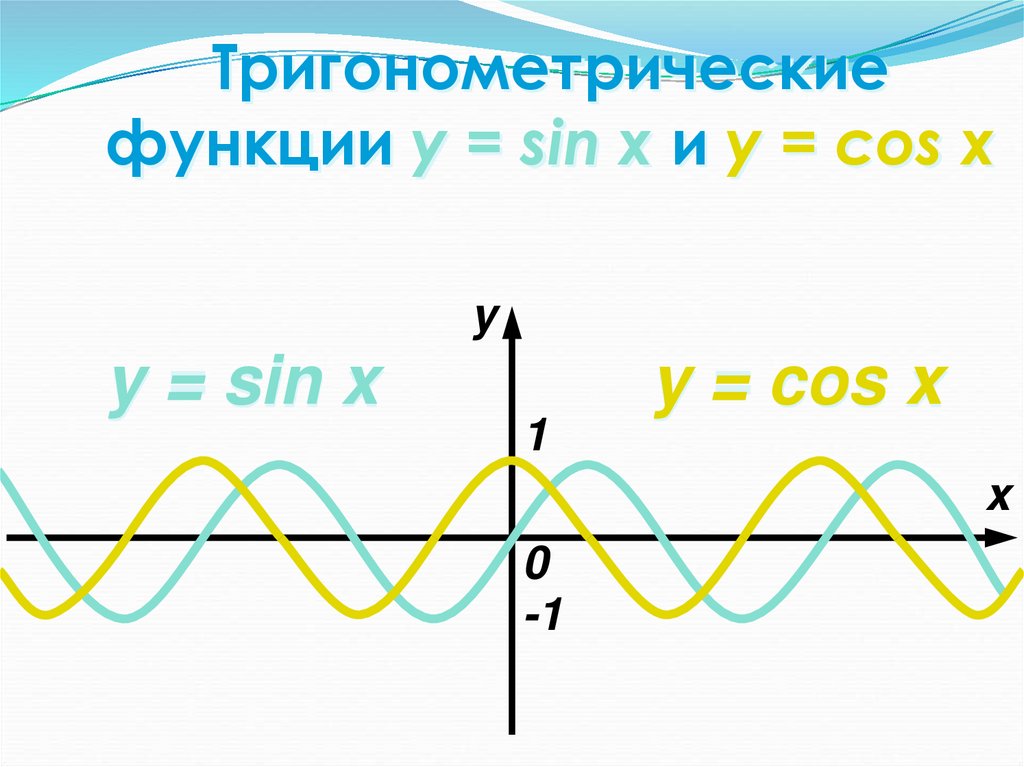
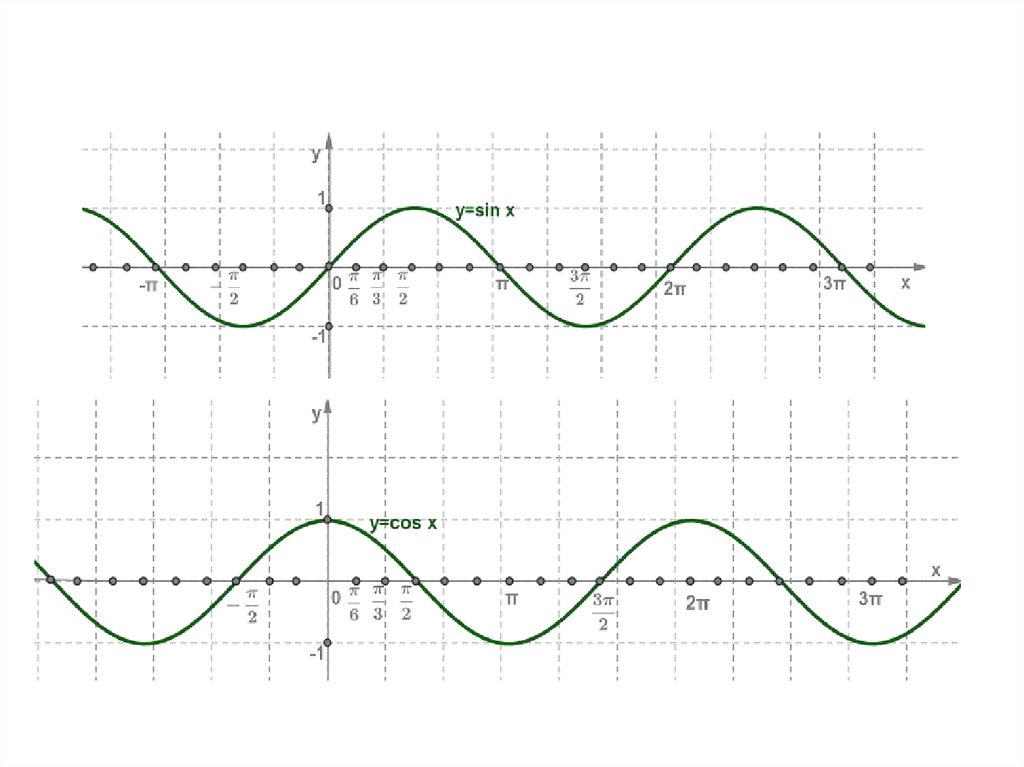
17. Тригонометрические функции y = sin x и y = cos x
yy = sin x
1
y = cos x
x
0
-1
18.
Свойства функцииy = sin x
1о D(y)=(−∞; +∞).
2о E(y)=[−1; 1].
3о Функция нечетная.
4о Если х = 0, то у = 0.
π
π
о
5 Функция возрастает при х [− +2πn; +2πn].
2
2
π
Функция убывает прих [ +2πn;3π +2πn].
2
2
π
π
6о xmax = +2πn; xmin = − +2πn, где
2
2
n Z.
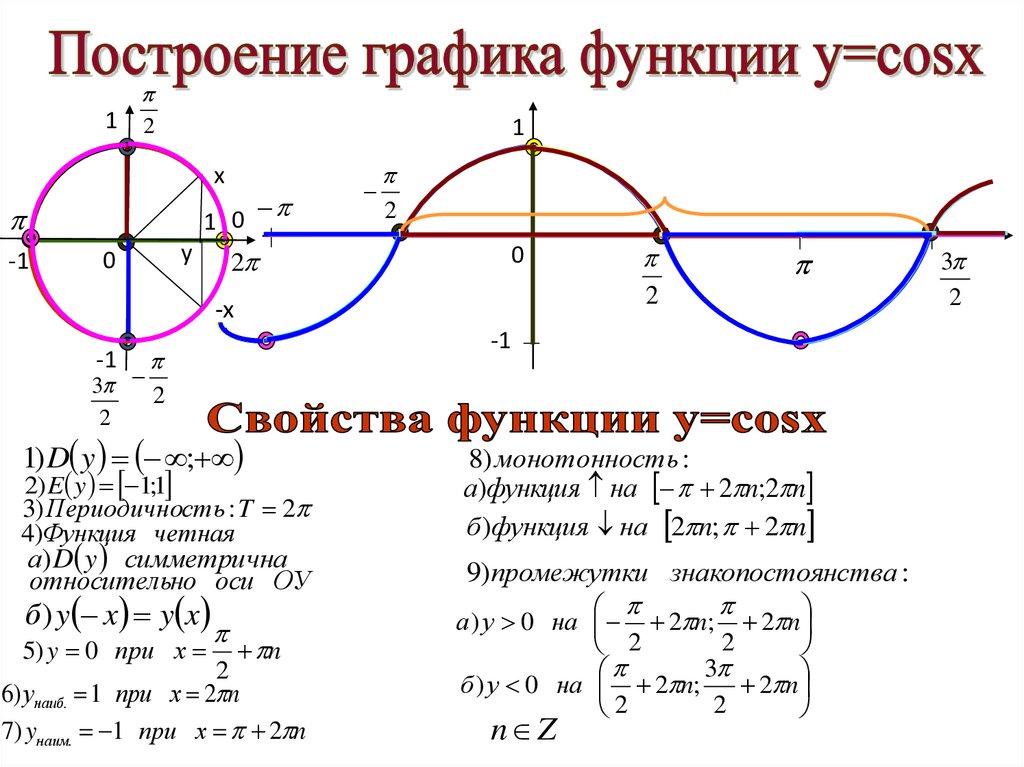
19.
Свойства функцииy = cos x
1о D(y)=(−∞; +∞).
2о E(y)=[−1; 1].
3о Функция четная.
4о Если х = 0, то у = 1.
5о Функция возрастает при х [−π+2πn;2πn],
n Z.
Функция убывает при х [2πn; Π+2πn], где
n Z.
6o xmax = 2πn; xmin = π+2πn, где n Z.
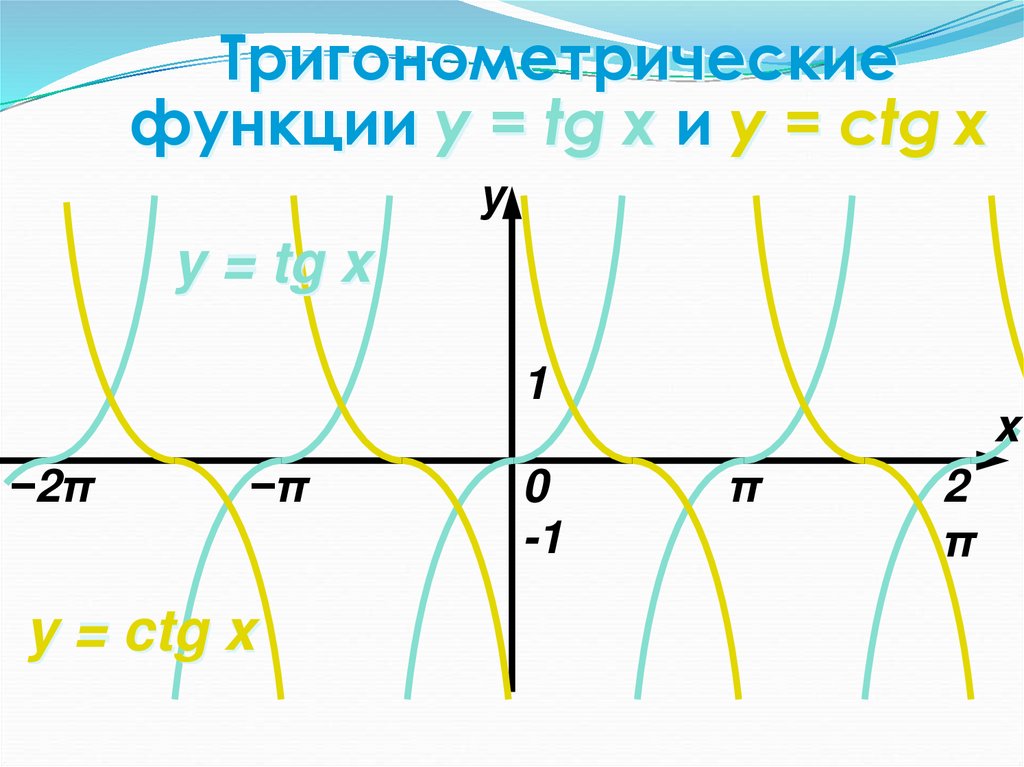
20. Тригонометрические функции y = tg x и y = ctg x
уy = tg x
1
x
−2π
−π
y = ctg x
0
-1
π
2
π
21.
Свойства функцииy = tg x
π
π
о
1 D(y)= (− +πn; +πn),где n
2
2
2о E(y)=(−∞; +∞).
Z.
3о Функция нечетная.
4о Если х = 0, то у = 0.
5о Функция возрастает при х (−
где n Z.
6o Экстремумов нет.
π
2
+πn;
π
2
+πn),
22.
Свойства функцииy = ctg x
1о D(y)=(πn; π+πn), где n Z
2о E(y)=(−∞; +∞).
3о Функция нечетная.
π
о
4 х ≠ 0; у = 0 если х = +πn, где n Z.
2
о
5 Функция убывает при х (πn; π+πn), где
n Z.
6o Экстремумов нет.
23. Преобразование графиков
Параллельный перенос на вектор (0;b) вдольоси ординат.
x x
y y b
Для построения графика функции f(x)+b, где b –
постоянное число, надо перенести график f на
вектор (0;b) вдоль оси ординат.
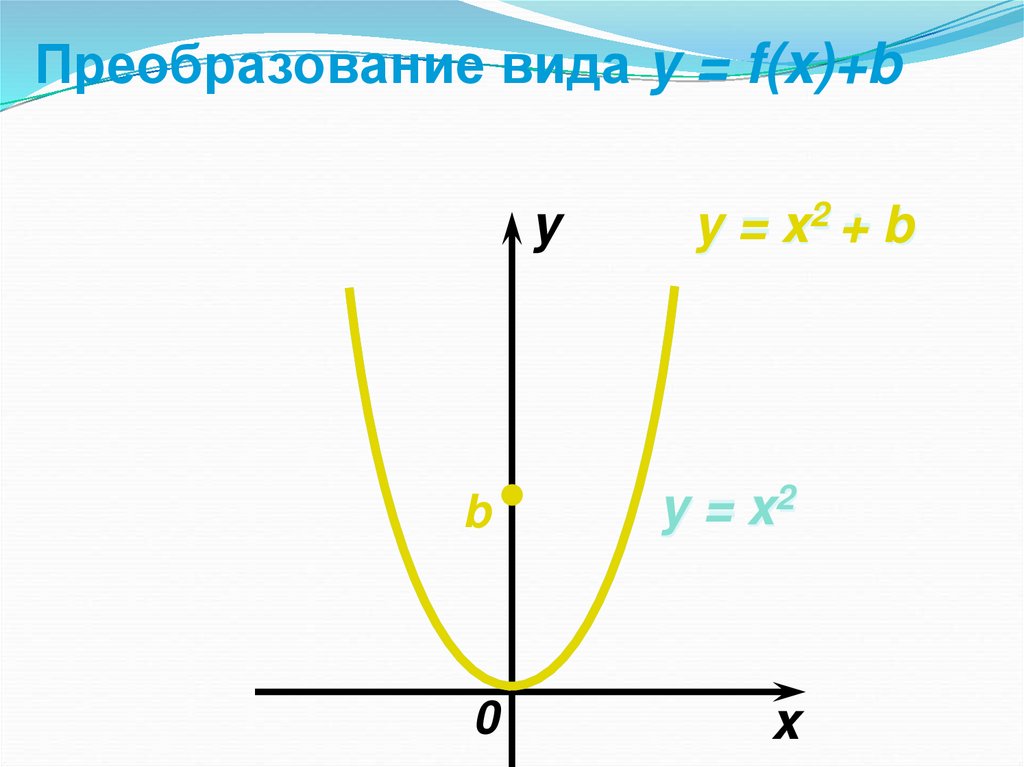
24. Преобразование вида y = f(x)+b
— Это параллельный переносграфика функции y = f(x) на b
единиц вдоль оси ординат
Если b > 0, то
происходит
смещение
Если b < 0,
то
происходит
смещение
25.
Преобразование вида y = f(x)+by
y = x2 + b
b
y = x2
0
x
26.
Растяжение вдоль оси Оу с коэффициентом kx x
y ky
Для построения графика функции y=kf(x) надо
растянуть график функции y=f(x) в k раз вдоль оси
ординат.
27.
Замечание. Если 0<|k|<1, то растяжение скоэффициентом k часто называют сжатием.
28. Преобразование вида y = kf(x)
— Это растяжение (сжатие) в k разграфика функции y = f(x)
вдоль оси ординат
Если , |k| > 1, то
происходит
Если , |k| < 1,
то
происходит
Растяжение
Сжатие
29. Преобразование вида y = kf(x)
yk
1
0
1
x
30.
Параллельный перенос вдоль оси абсцисс навектор (а;0)
x x a
y y
График функции y=f(x-a) получается из графика f
переносом (вдоль оси абсцисс) на вектор (а;0).
Если а>0, то вектор (а;0) направлен в
положительном направлении оси абсцисс, а при
a<0 – в отрицательном.
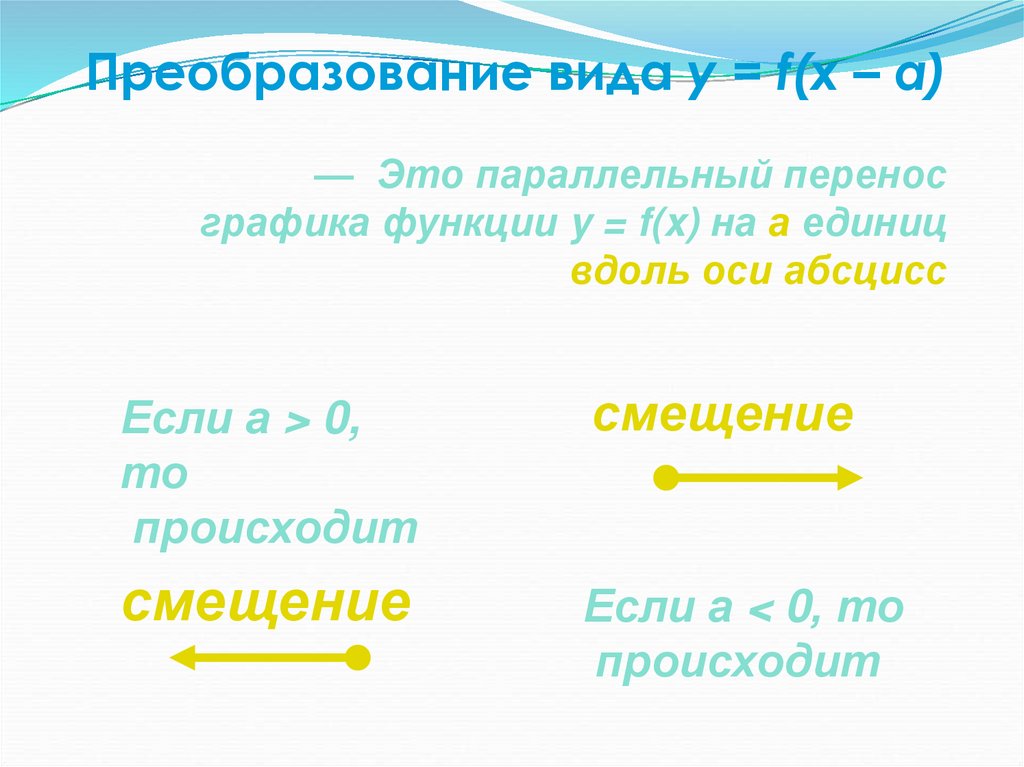
31. Преобразование вида y = f(x – a)
— Это параллельный переносграфика функции y = f(x) на а единиц
вдоль оси абсцисс
Если а > 0,
то
происходит
смещение
смещение
Если а < 0, то
происходит
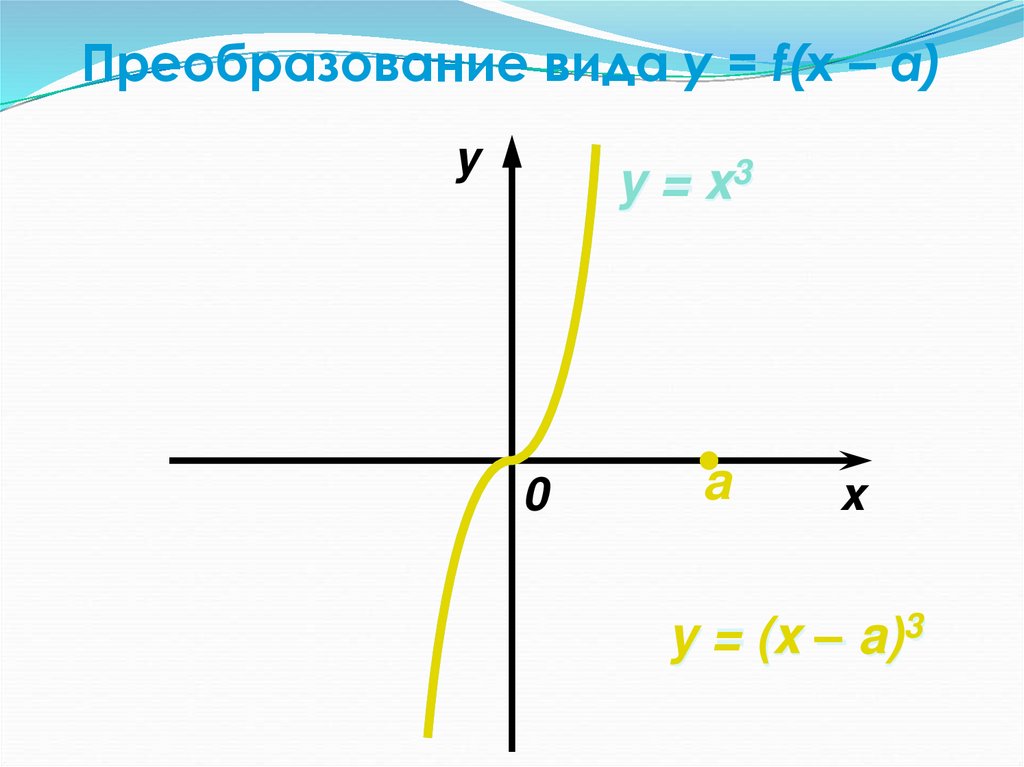
32. Преобразование вида y = f(x – a)
yy = x3
0
a
x
y = (x – a)3
33.
Растяжение вдоль оси Ох с коэффициентом kx kx
y y
Для построения графика функции
x
y f
k
надо подвергнуть график функции f растяжению с
коэффициентом k вдоль оси абсцисс.
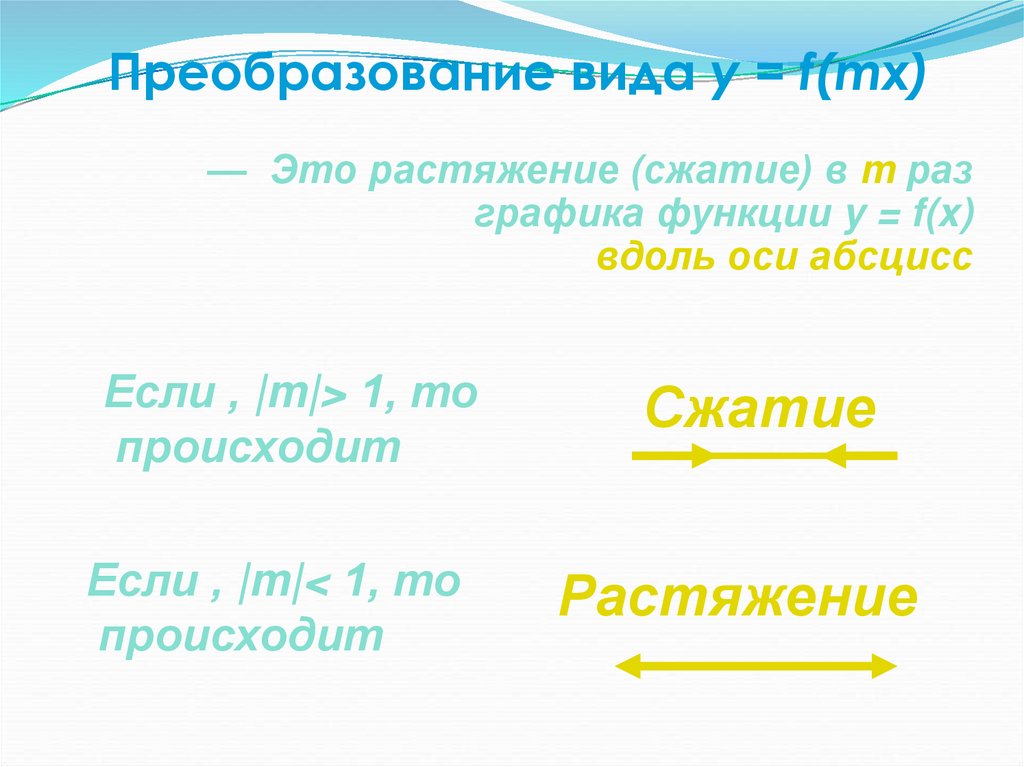
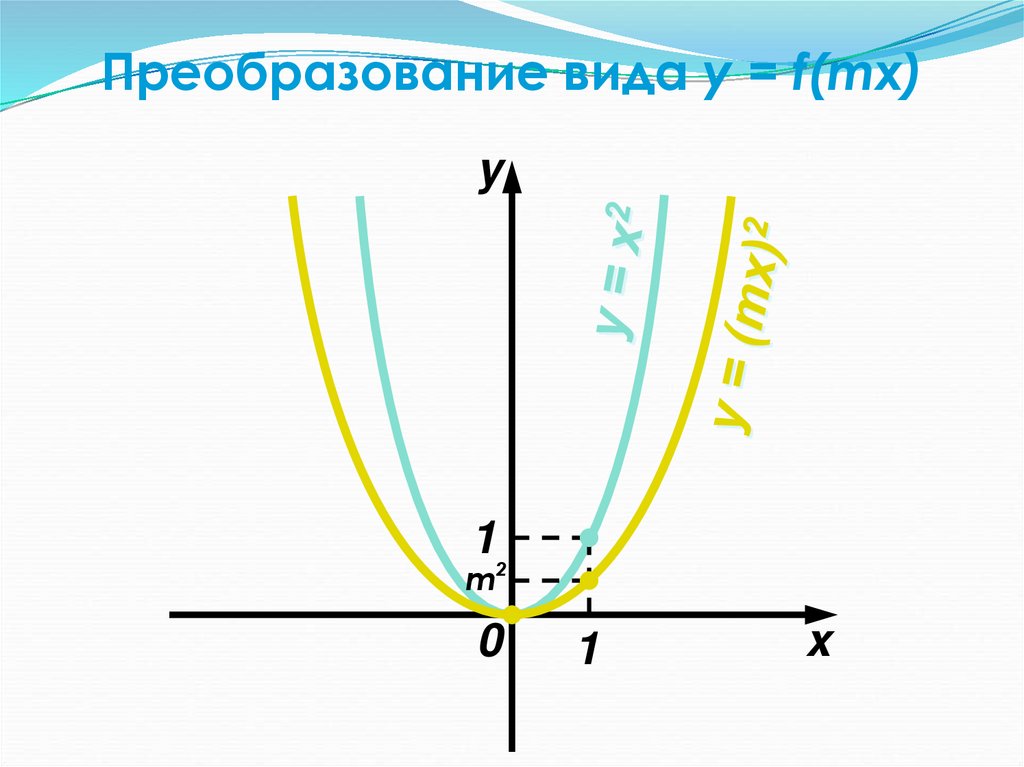
34. Преобразование вида y = f(mx)
— Это растяжение (сжатие) в m разграфика функции y = f(x)
вдоль оси абсцисс
Если , |m|> 1, то
происходит
Сжатие
Если , |m|< 1, то
происходит
Растяжение
35. Преобразование вида y = f(mx)
y12
m
0
1
x
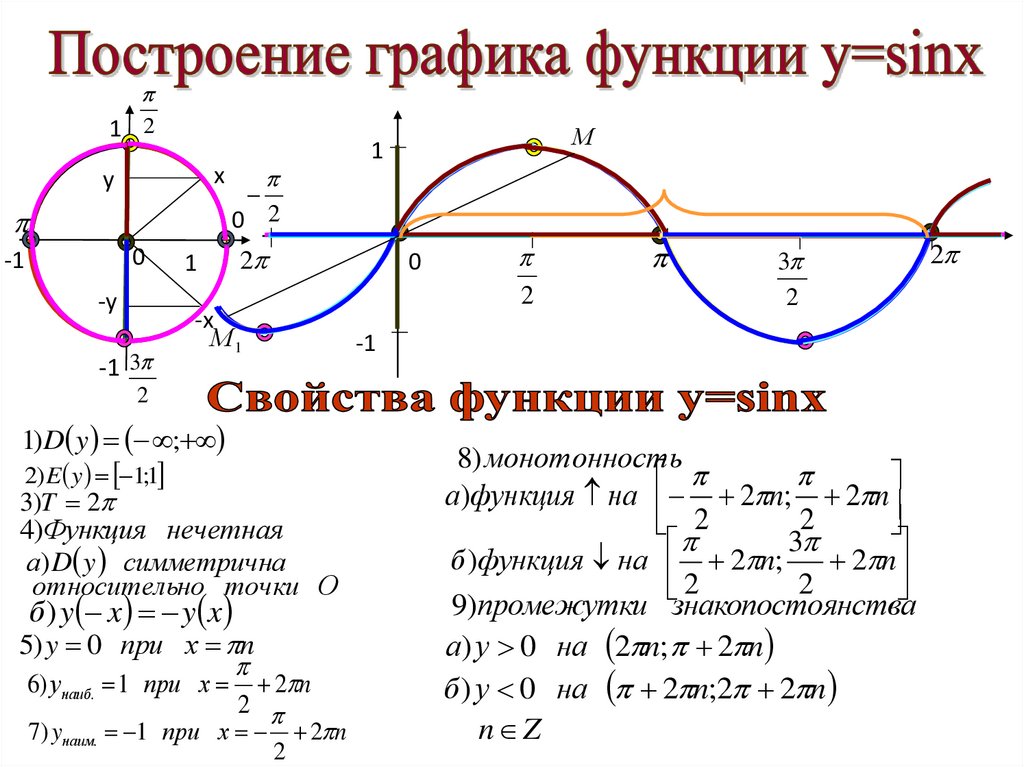
36. Тригонометрические функции, их свойства и графики
37.
1 2x
y
М
1
0 2
0
-1
-y
-1 3
1
2
0
-x
М1
2
3
2
-1
2
1) D y ;
2) E y 1;1
3)T 2
4)Функция нечетная
а) D y симметрична
относительно точки О
б ) y x y x
5) y 0 при х n
6) унаиб. 1 при х
2 n
2
7) yнаим. 1 при х
2
2 n
8) монотонность
а)функция на 2 n; 2 n
2
2
3
б )функция на 2 n;
2 n
2
2
9)промежутки знакопостоянства
а) у 0 на 2 n; 2 n
б ) у 0 на 2 n;2 2 n
n Z
2
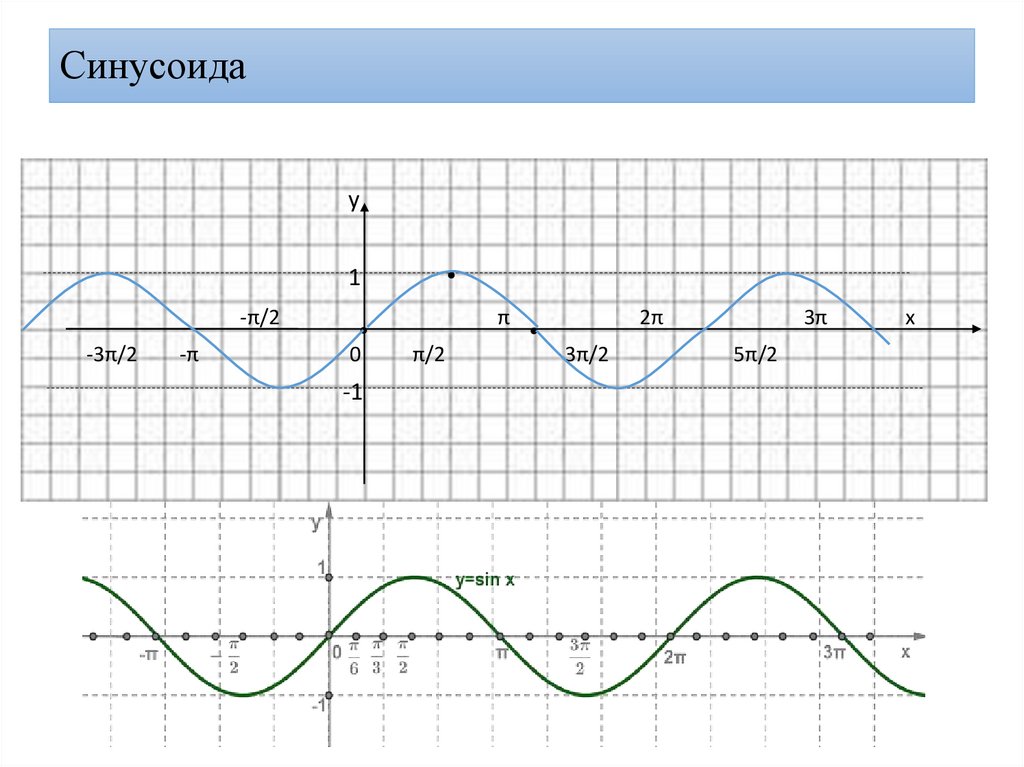
38. Синусоида
у1
-π/2
-3π/2
-π
π
0
-1
π/2
2π
3π/2
3π
5π/2
х
39.
1 21
x
1 0
-1
y
0
2
2
0
-x
-1
2
-1
3 2
2
1) D y ;
2) E y 1;1
3) Периодичность : T 2
4)Функция четная
8) монотонность :
а)функция на 2 n;2 n
б )функция на 2 n; 2 n
б) y x y x
9)промежутки знакопостоянства :
а ) у 0 на 2 n; 2 n
а) D y симметрична
относительно оси ОУ
5) y 0 при х
n
2
6) унаиб. 1 при х 2 n
7) yнаим. 1 при х 2 n
2
2
3
б ) у 0 на 2 n;
2 n
2
2
n Z
3
2
40.
41. Преобразование графиков функций y=sin x и y=cos x
Параллельный перенос вдоль оси OYПараллельный перенос вдоль оси OX
Растяжение (сжатие) в k раз вдоль оси OY
Растяжение (сжатие) в k раз вдоль оси OX
Симметрия относительно оси абсцисс
Пример построения графика сложной функции
41
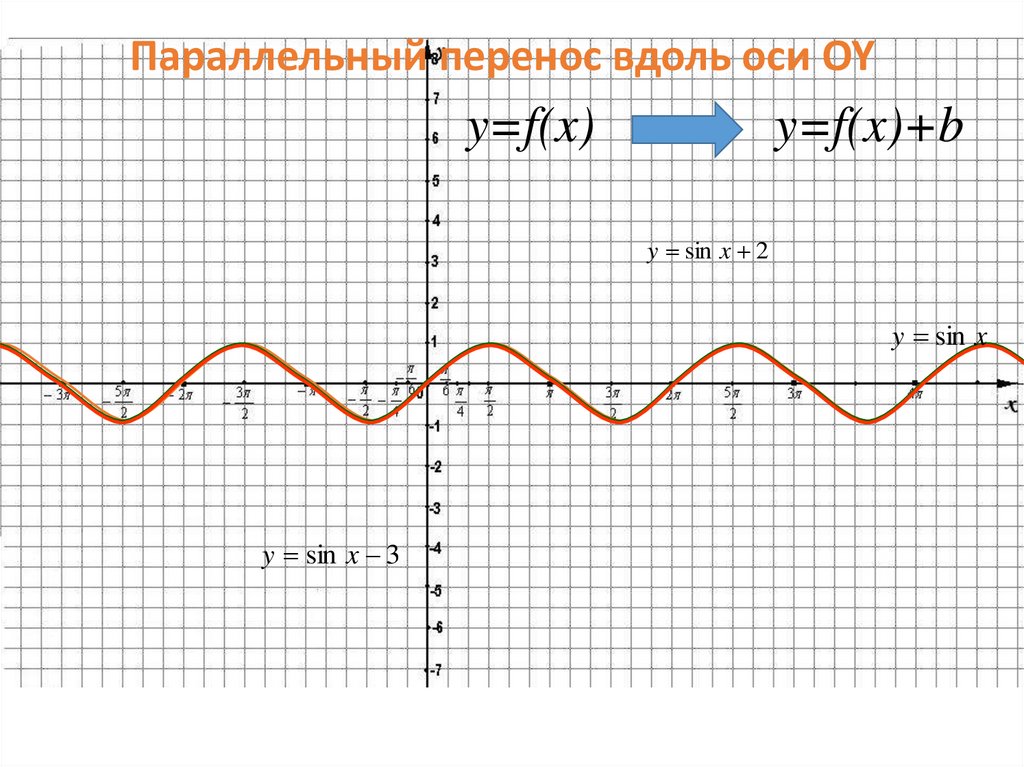
42.
Параллельный перенос вдоль оси OYy=f(x)
y=f(x)+b
y sin x 2
y sin x
y sin x 3
43.
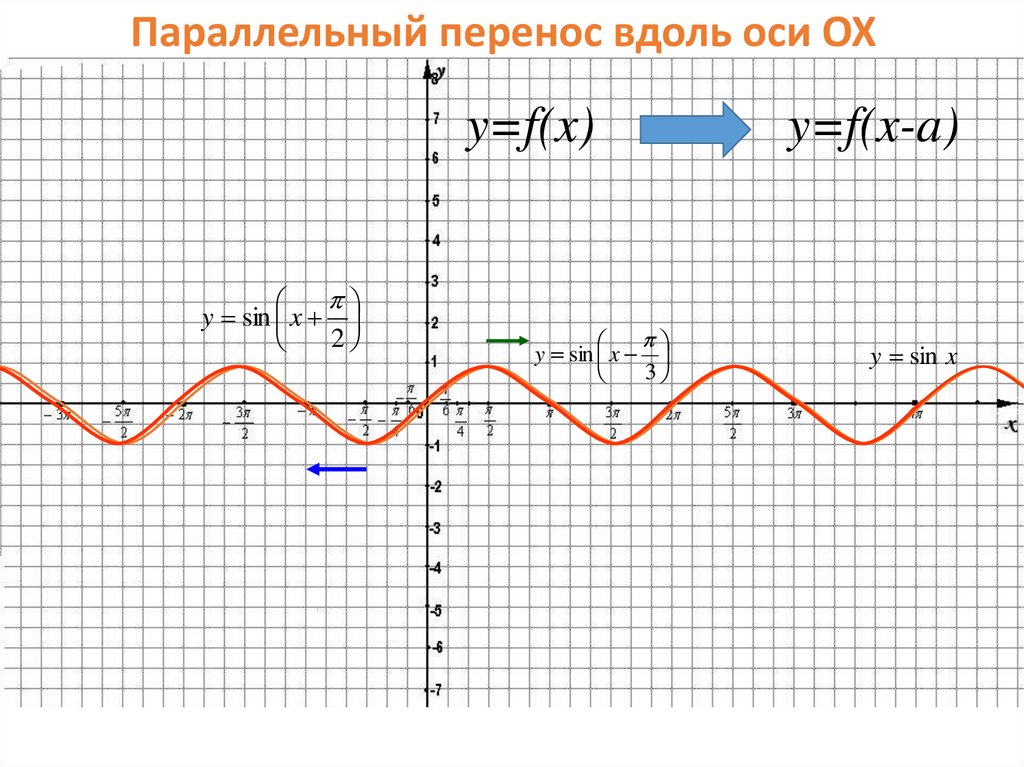
Параллельный перенос вдоль оси OXy=f(x)
y sin x
2
y sin x
3
y=f(x-a)
y sin x
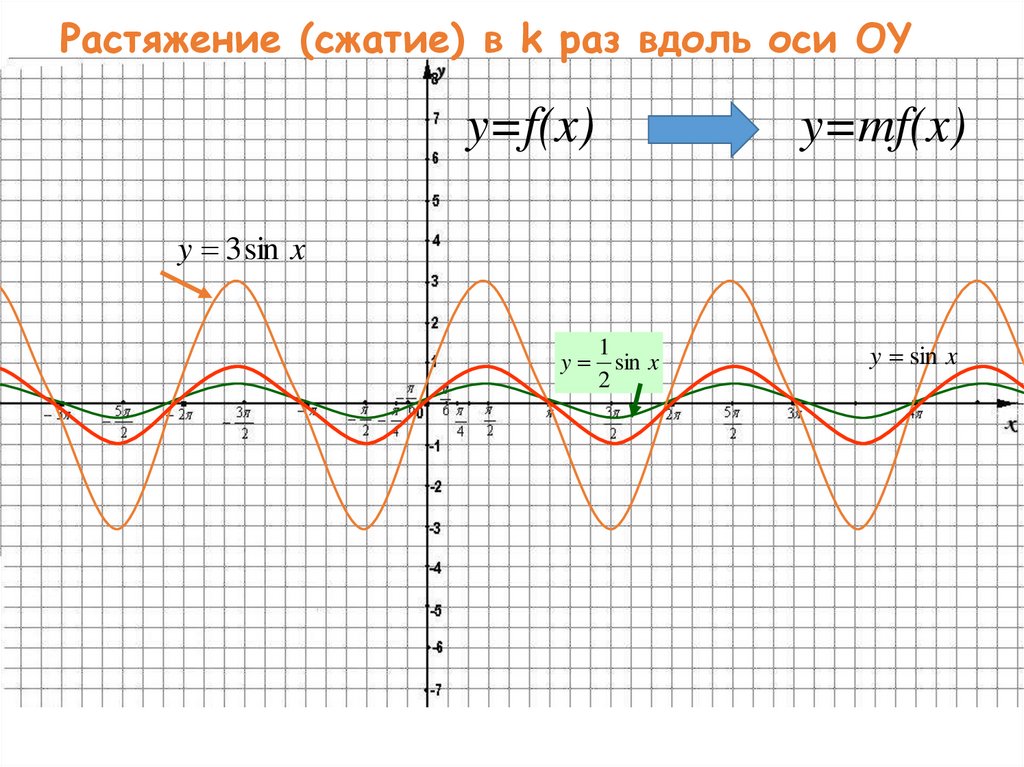
44. Растяжение (сжатие) в k раз вдоль оси OY
y=f(x)y=mf(x)
y 3 sin x
y
1
sin x
2
y sin x
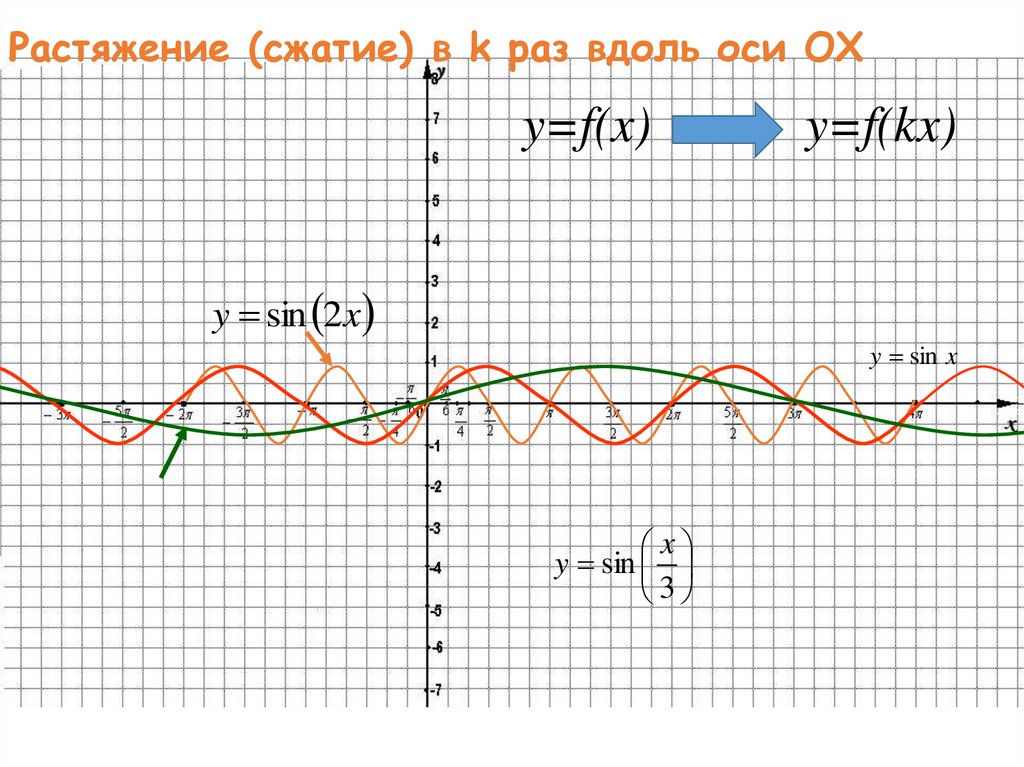
45. Растяжение (сжатие) в k раз вдоль оси OX
y=f(x)y=f(kx)
y sin 2 x
y sin x
x
y sin
3
46.
Симметрия относительно оси абсциссy=f(x)
y=-f(x)
y cos x
y cos x
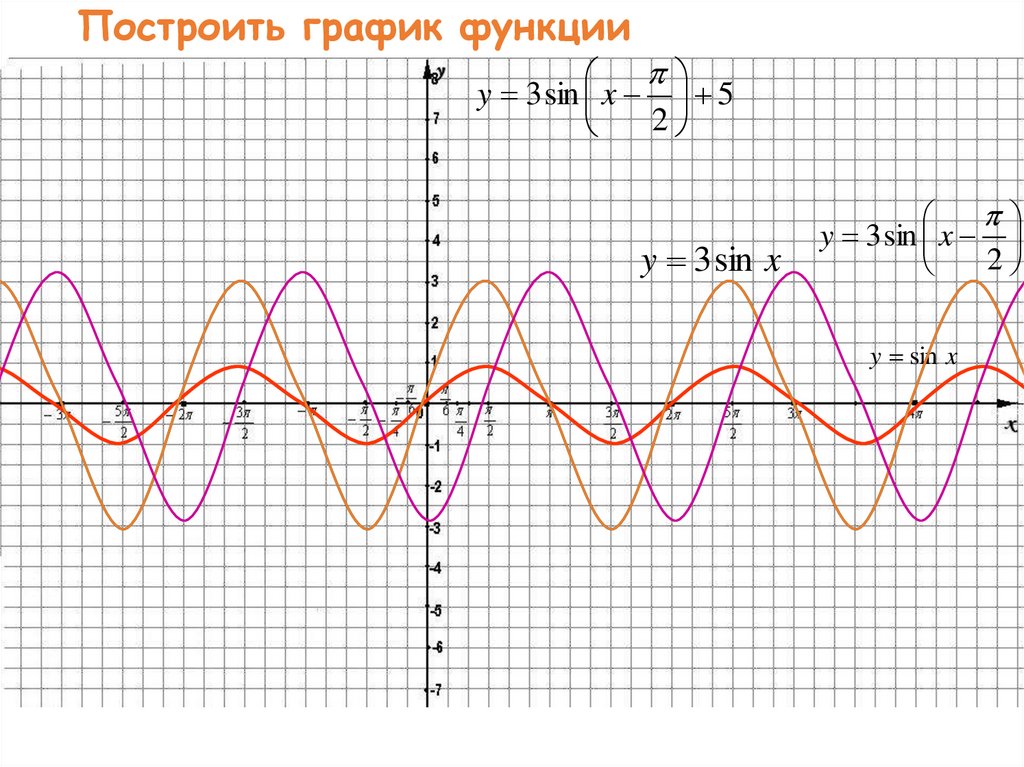
47. Построить график функции
y 3 sin x 52
y 3 sin x
y 3 sin x
2
y sin x
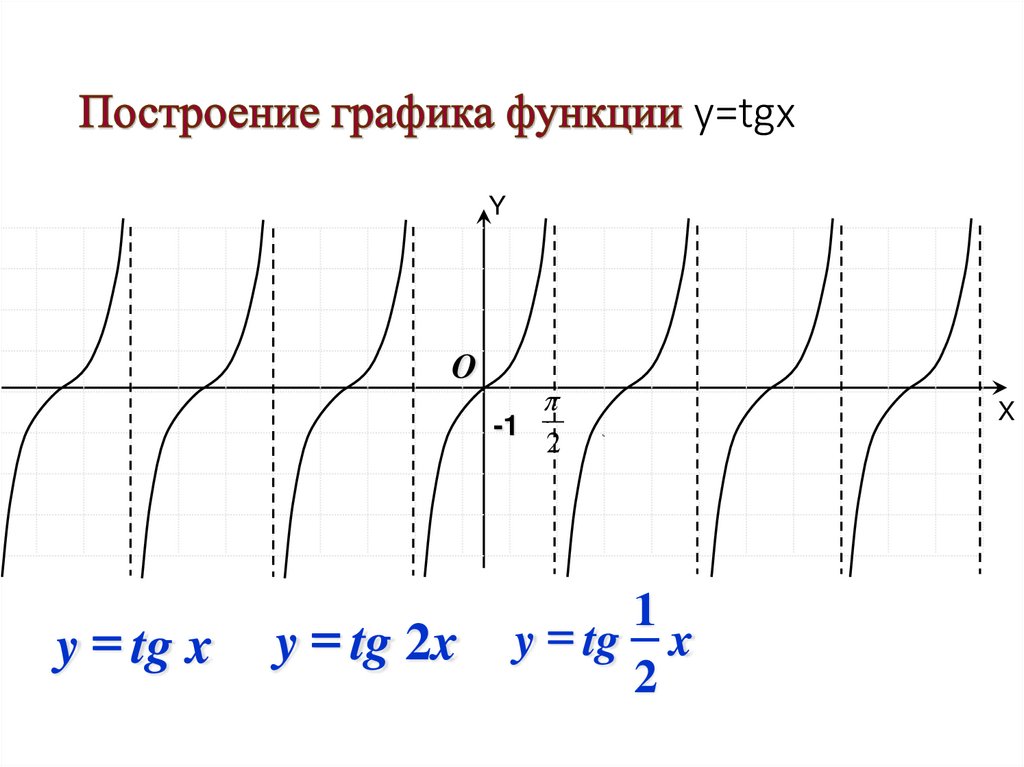
48. Построение графика функции y=tgx
y=tgxY
O
y tg x
y tg 2x
-1
2
1
y tg x
2
X
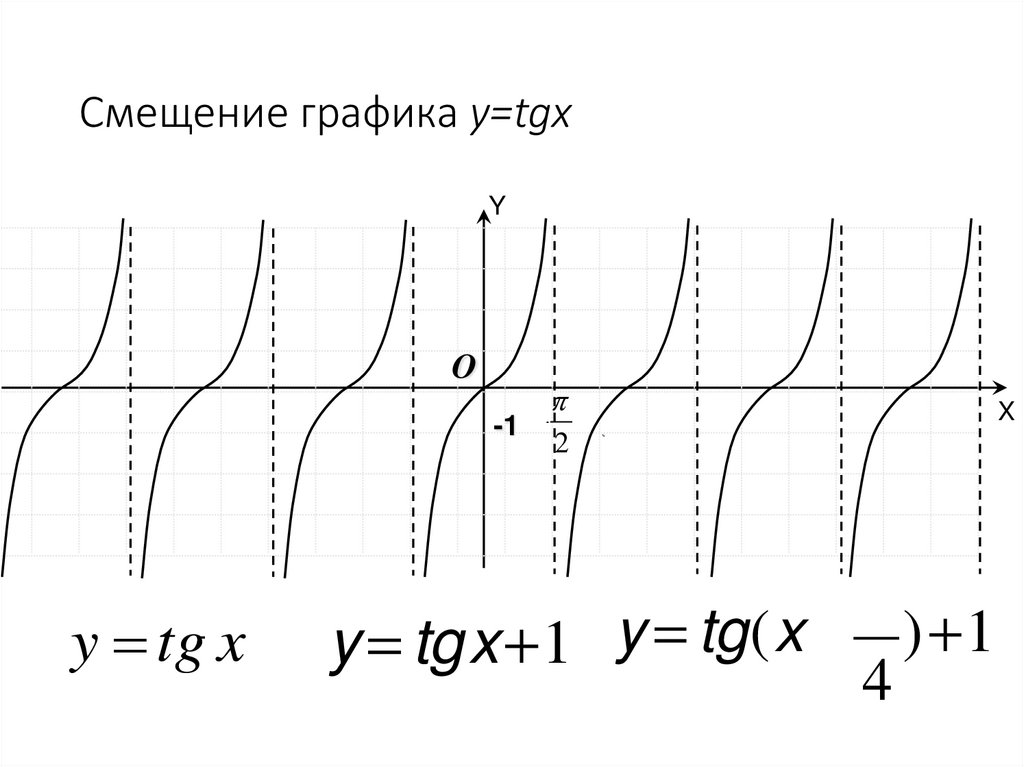
49. Смещение графика y=tgx
YO
-1
y tg x
2
X
p
y = tgx+1 y = tg(x - ) +1
4
50. Свойства графика функции y=tg x
1.2.
3.
4.
5.
6.
7.
8.
Область определения: x≠π/2+πn, n∈Z
Множество значений: y∈(-∞;∞)
Функция периодическая Т=π
Функция нечетная
y=0, при x=πn, n∈Z
y>0, при x∈(πn; π/2+πn), n∈Z
y<0, при x∈(-π/2+πn; πn), n∈Z
Функция возрастает на интервалах: (-π/2+πn; π/2+πn), n∈Z
51. Решение уравнений при помощи графика функции y=tg x
Найти корни уравнения tg x=-1 на промежутке [- π; 3π/2]y=tg x
y=-1
Y
-
-p
p
3p
;
Ответ
4 4
:
p
4O
-1
2
3p
4
3p
2
X
y=-1
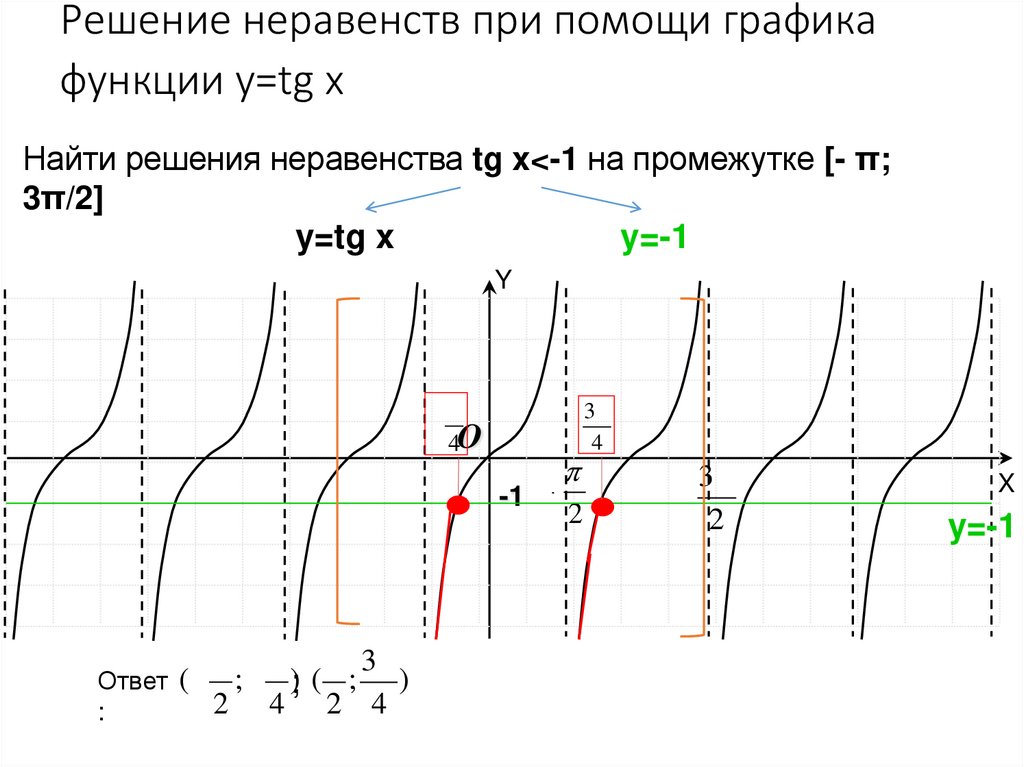
52. Решение неравенств при помощи графика функции y=tg x
Найти решения неравенства tg x<-1 на промежутке [- π;3π/2]
y=tg x
y=-1
Y
-
-p
p p p 3p
(;- ); ( ; )
Ответ
2 4 2 4
:
p
4O
-1
2
3p
4
3p
2
X
y=-1
53. Построение графика функции y=ctg x
y=ctg xY
O
-1
y ctg x y ctg 2x
2
1
y ctg x
2
X
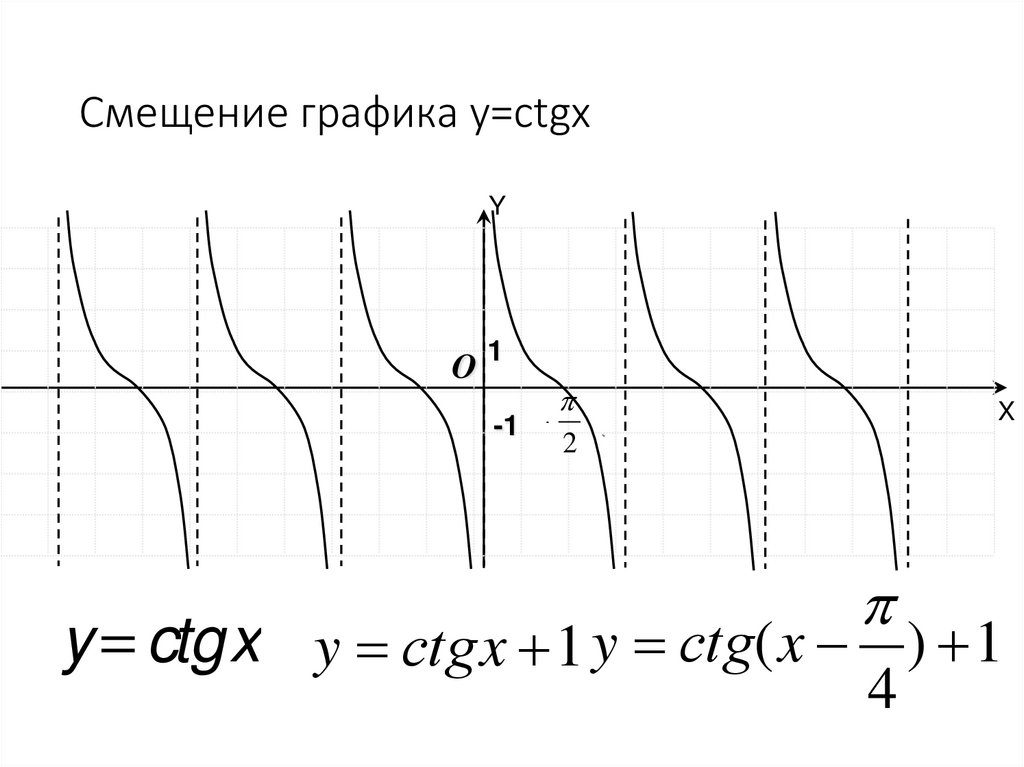
54. Смещение графика y=ctgx
YO1
-1
2
X
y = ctgx y сtg x 1 y сtg( x ) 1
4
55. Свойства графика функции y=ctg x
1.2.
3.
4.
5.
6.
7.
8.
Область определения: x≠πn, n∈Z
Множество значений: y∈(-∞;∞)
Функция периодическая T=π
Функция нечетная
y=0, при x=π/2+πn, n∈Z
y>0, при x∈(0+πn; π/2+πn), n∈Z
y<0, при x∈(-π/2+πn; 0+πn), n∈Z
Функция убывает на интервалах (πn; π+πn), n∈Z
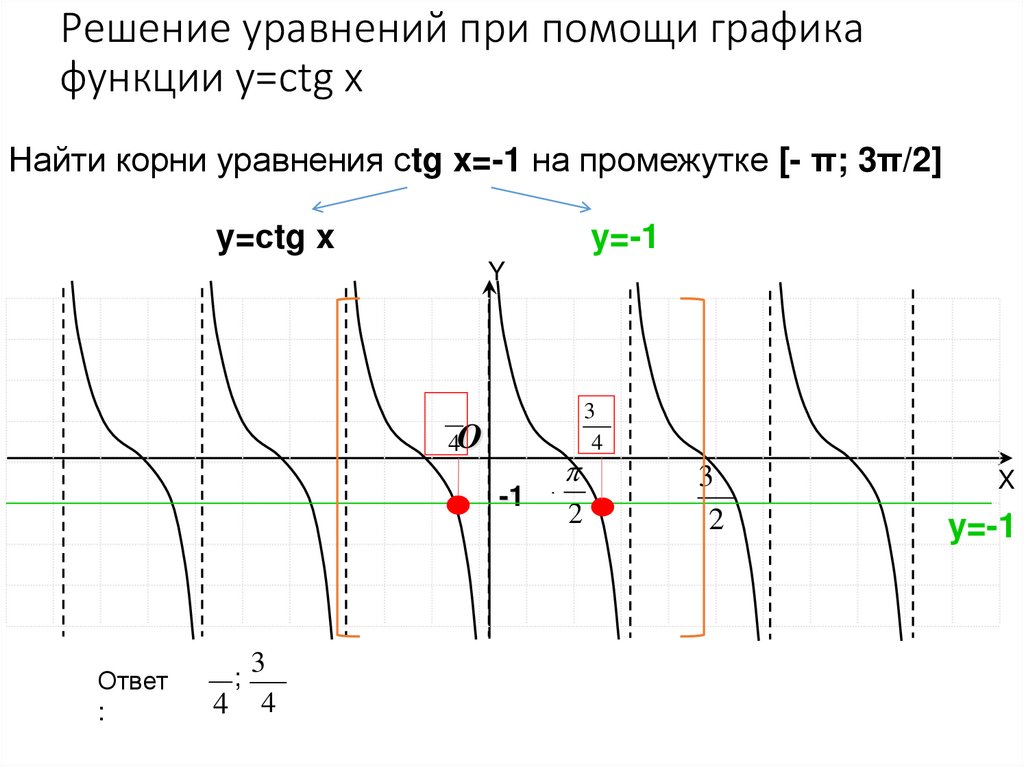
56. Решение уравнений при помощи графика функции y=сtg x
Найти корни уравнения сtg x=-1 на промежутке [- π; 3π/2]y=сtg x
y=-1
Y
-
-p
p
3p
;
Ответ
4 4
:
p
4O
-1
2
3p
4
3p
2
X
y=-1
57. Решение неравенств при помощи графика функции y=ctg x
Найти решения неравенства ctg x<-1 на промежутке [- π;3π/2]
y=сtg x
-
-p
3p
p
(
;p )
(;0)
Ответ
;
4
4
:
y=-1
Y
p
4O
-1
2
3p
4
3p
2
X
y=-1
y=сtg x
































 mathematics
mathematics








