Тригонометрические функции y = sin x и y = cos x

Тригонометрические функции y = tg x и y = ctg x

1.06M

Category: $mathematics$ mathematics

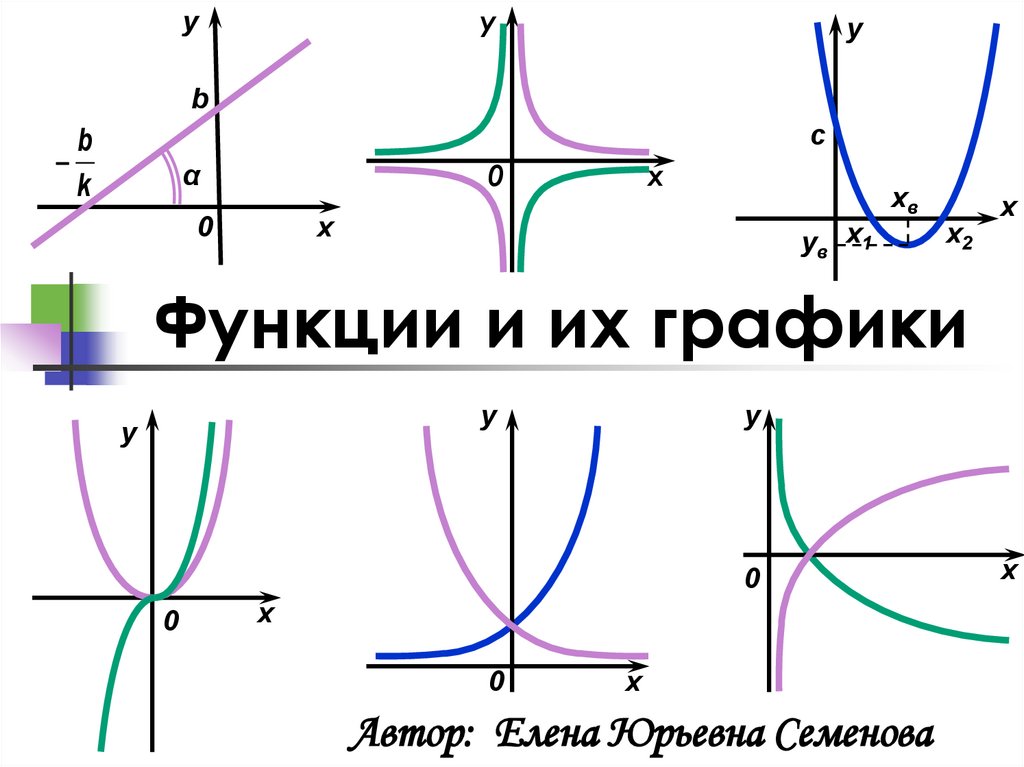
Функции и их графики

1. Функции и их графики

y
y
y
b
c
b
k
0
α
0
x
xв
x
ув x1
x
x2
Функции и их графики
y
y
y
0
0
x
0
x
Автор: Елена Юрьевна Семенова
x

2. Содержание

Функции и их графики.
Преобразование графиков функций.
Свойства функций.

3. Функции.

Линейная функция
Квадратичная функция
Степенная функция
Обратная пропорциональность
Показательная функция
Логарифмическая функция
Тригонометрические функции

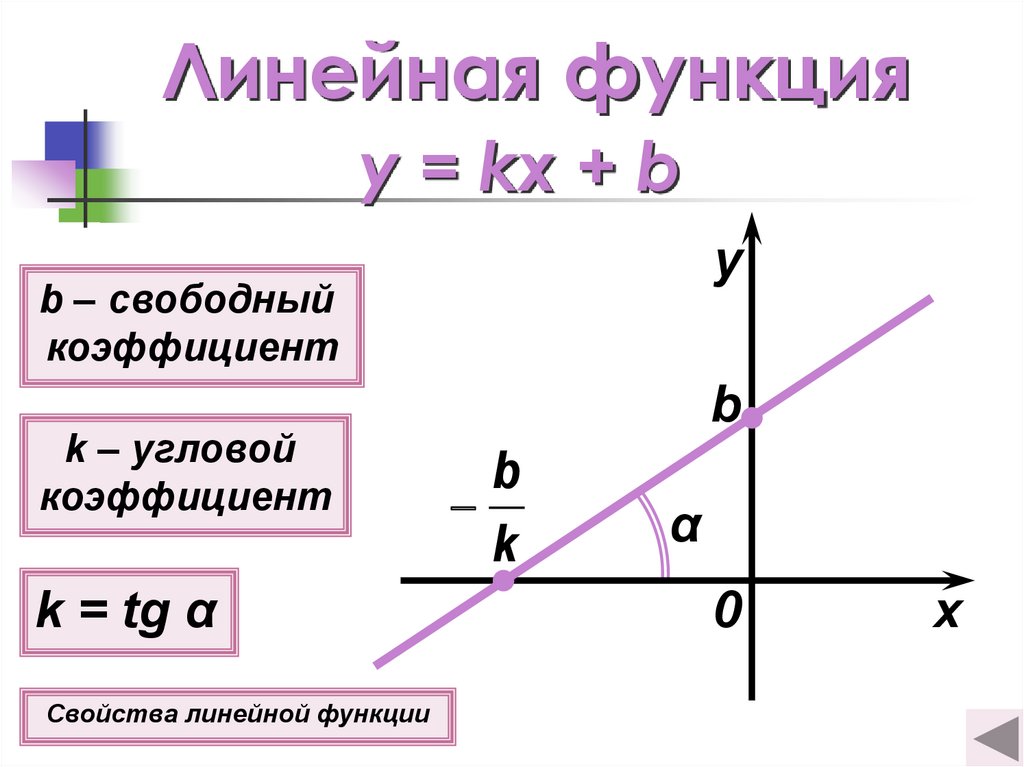
4. Линейная функция

y = kx + b
y
b – свободный
коэффициент
k – угловой
коэффициент
k = tg α
Свойства линейной функции
b
b
k
α
0
x

5.

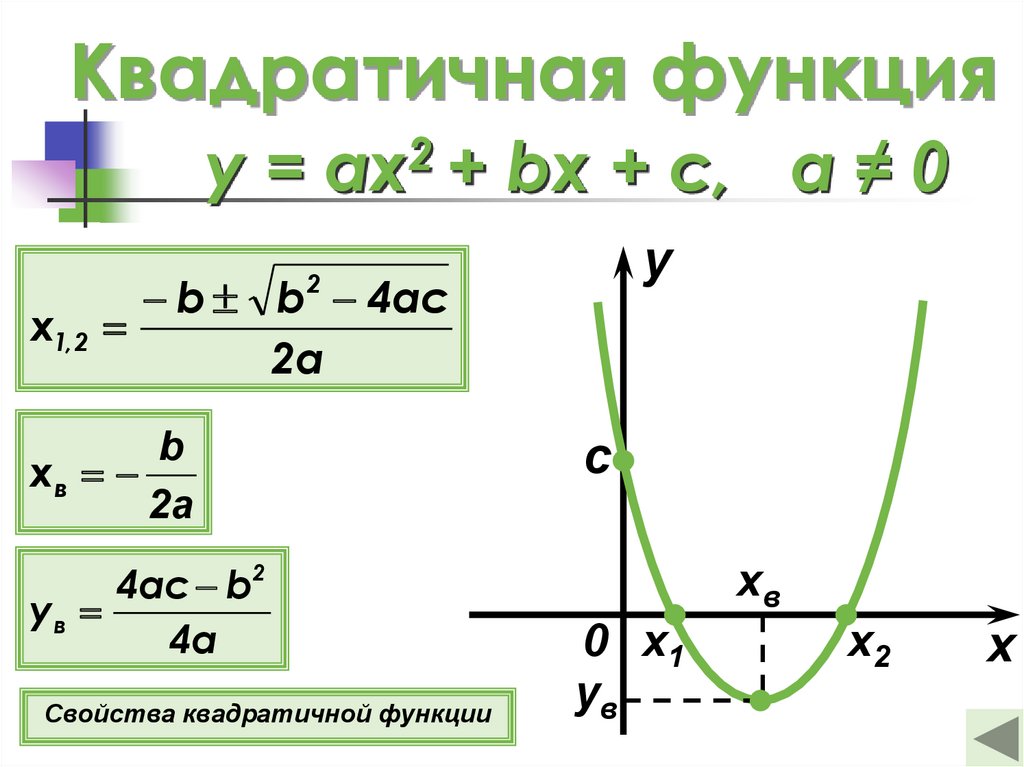
Квадратичная функция
y = ax2 + bx + c, а ≠ 0
x1,2
y
2
b b 4ac
2a
b
xв
2а
4ac b2
yв
4a
Свойства квадратичной функции
c
xв
0 x1
ув
x2
x

6.

Степенная функция
y = xn
y = xn, где n = 2k, k
y
Z
y = xn, где n = 2k +1, k
Z
1
01
Свойства степенной функции
x

7.

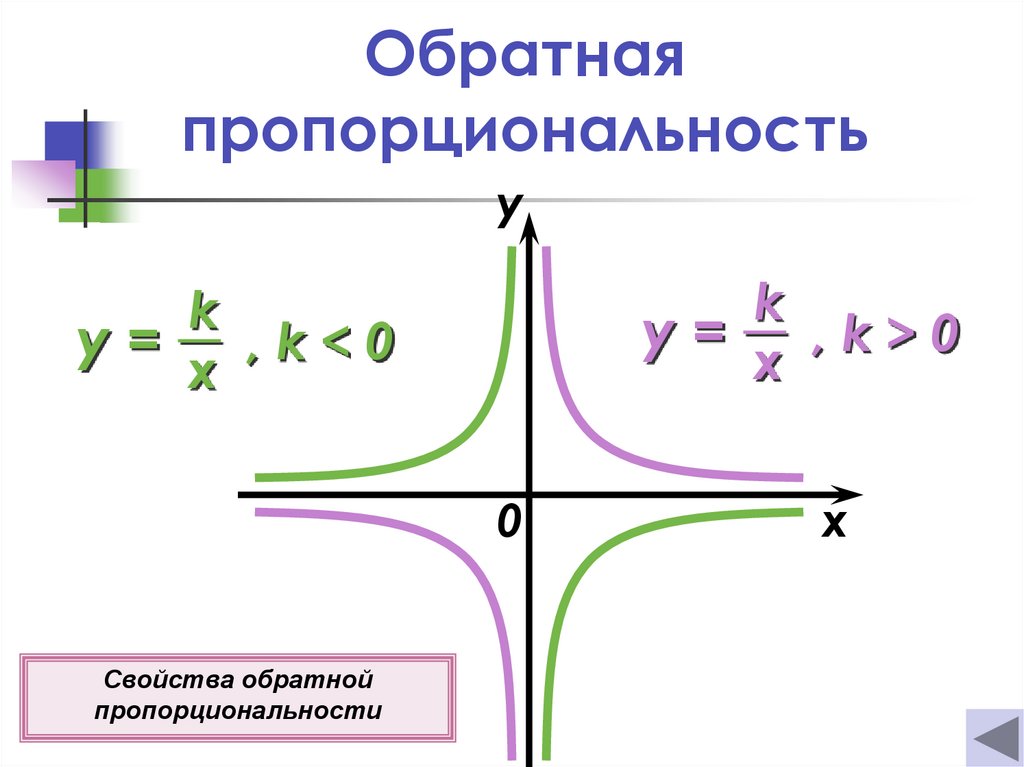
Обратная
пропорциональность
y
k
y=
,k>0
x
k
y=
,k<0
x
0
Свойства обратной
пропорциональности
x

8.

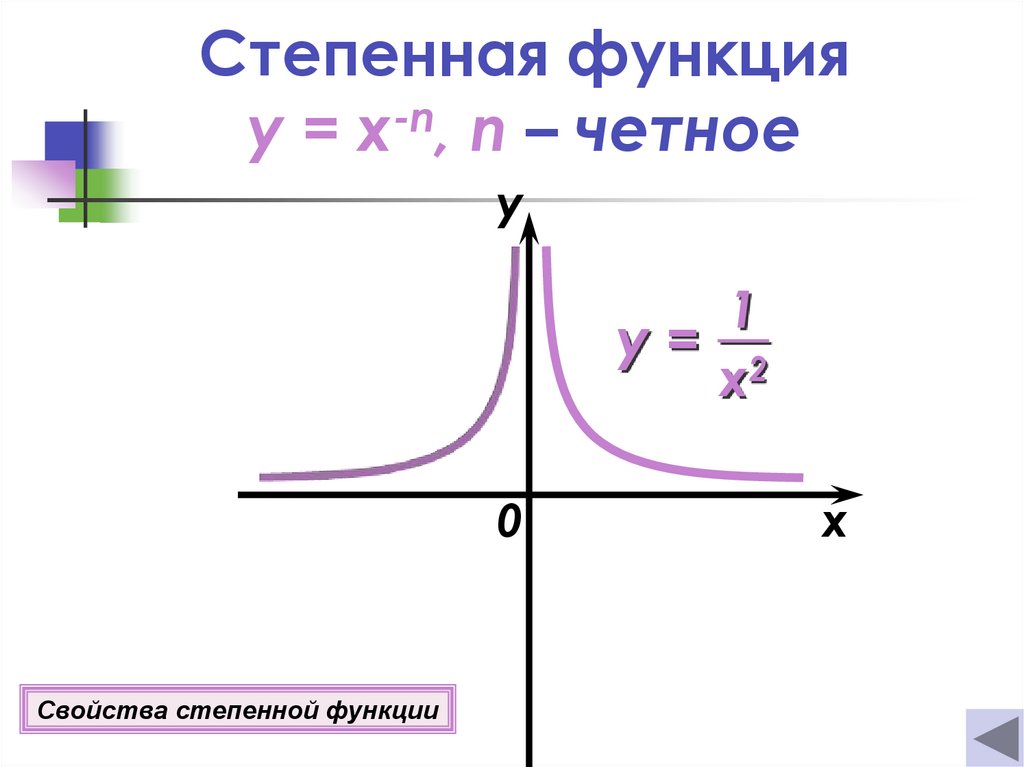
Степенная функция
y = x-n, n – четное
y
1
y= 2
x
0
Свойства степенной функции
x

9.

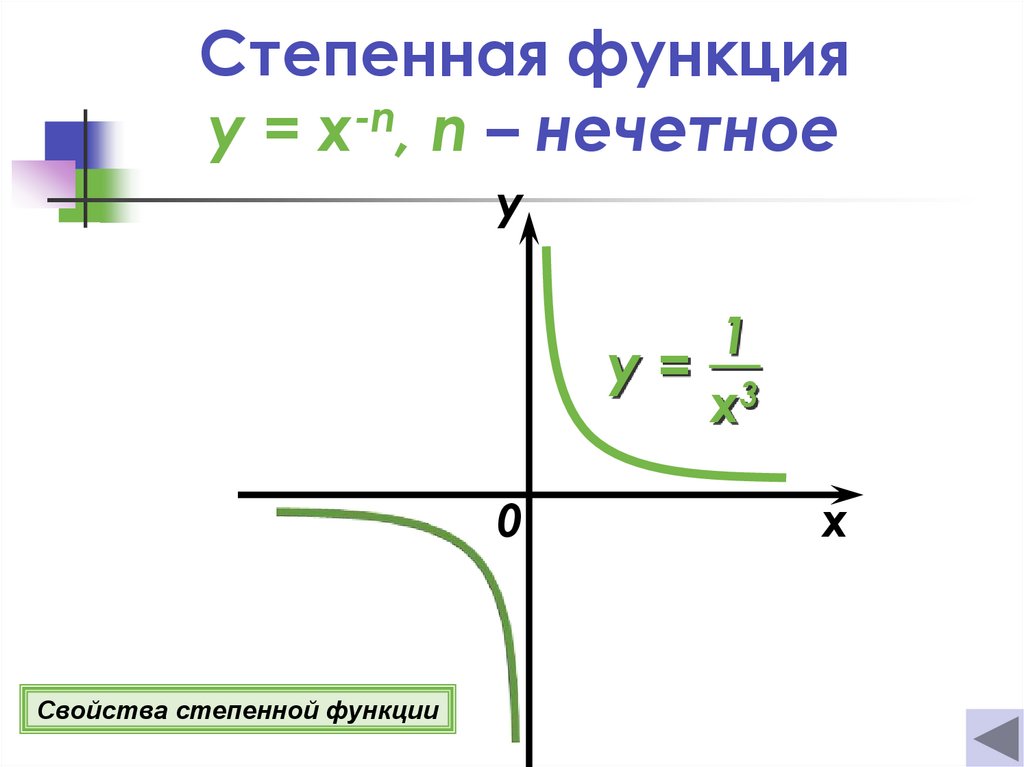
Степенная функция
y = x-n, n – нечетное
y
1
y= 3
x
0
Свойства степенной функции
x

10.

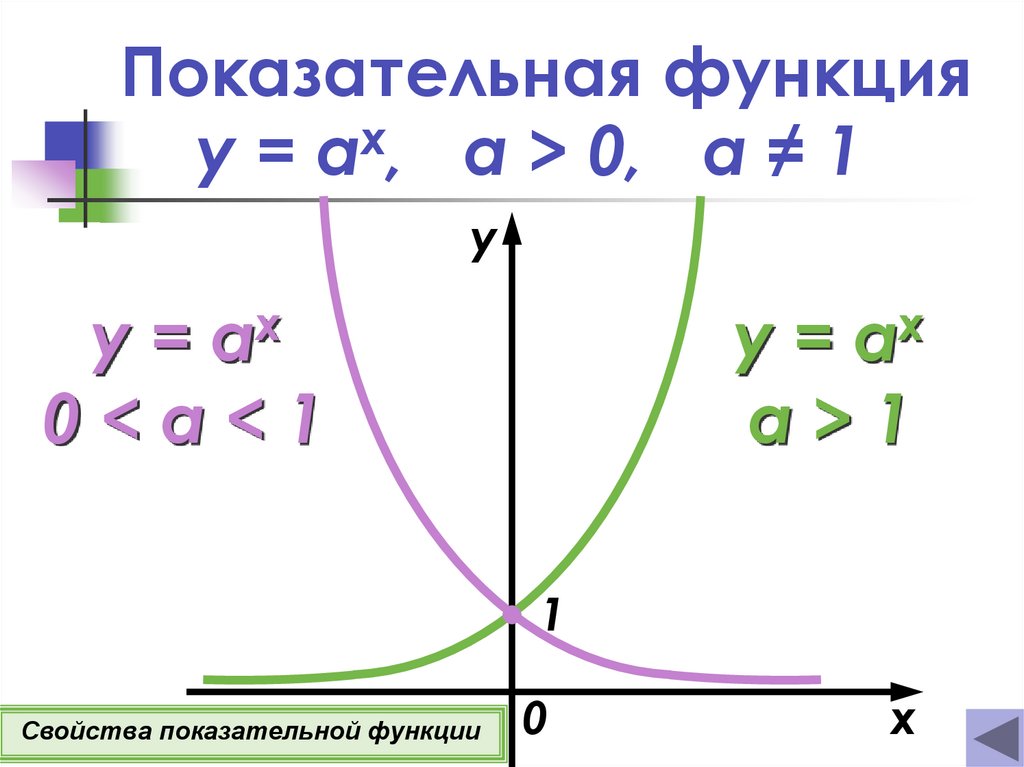
Показательная функция
y = ax, а > 0, a ≠ 1
y
x
a
x
a
y=
0<a<1
y=
a>1
1
Свойства показательной функции
0
x

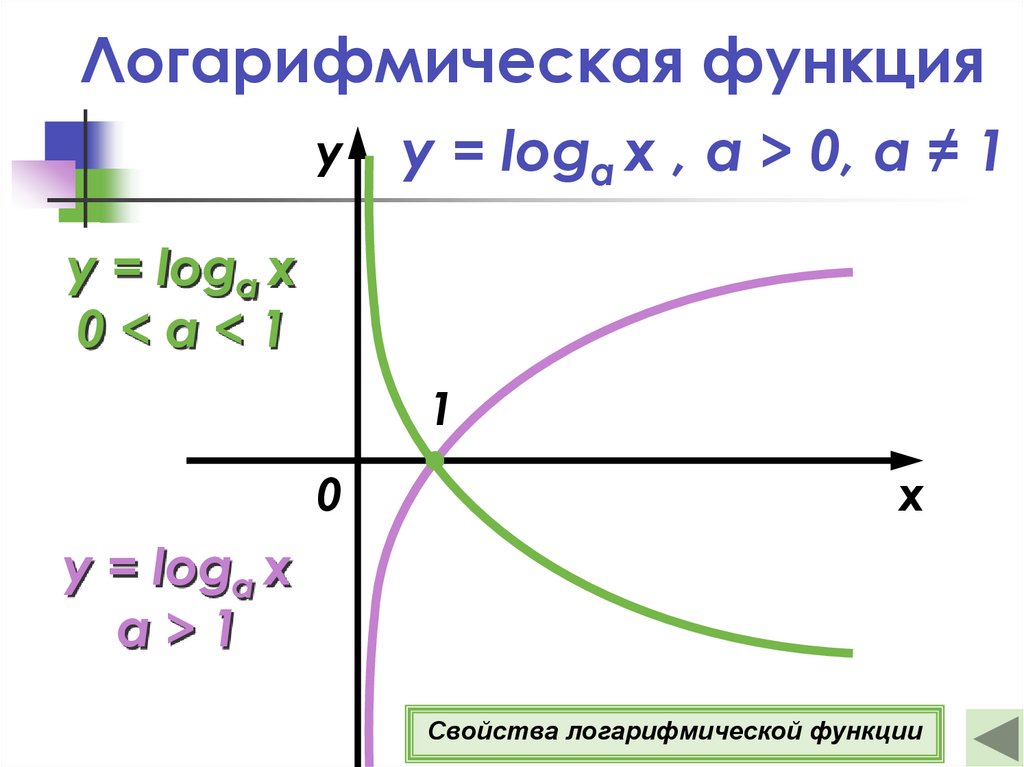
11. Логарифмическая функция

y
y = loga x , а > 0, a ≠ 1
y = loga x
0<a<1
1
0
x
y = loga x
a>1
Свойства логарифмической функции

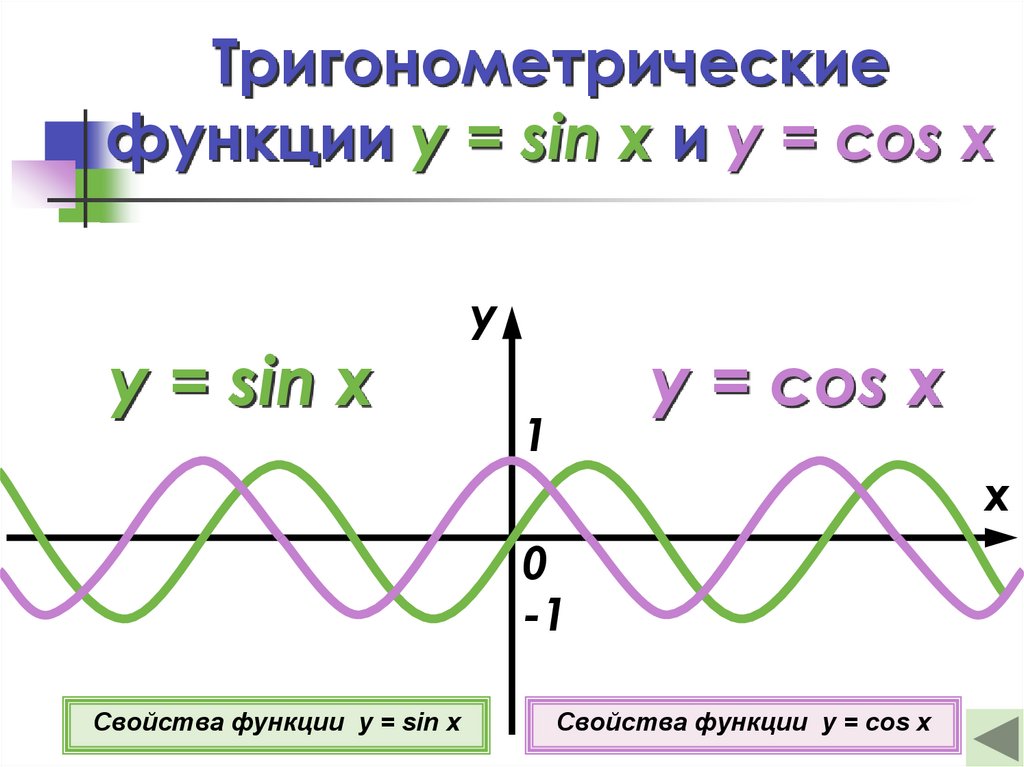
12. Тригонометрические функции y = sin x и y = cos x

y = sin x
y
y = cos x
1
x
0
-1
Свойства функции y = sin x
Свойства функции y = cos x

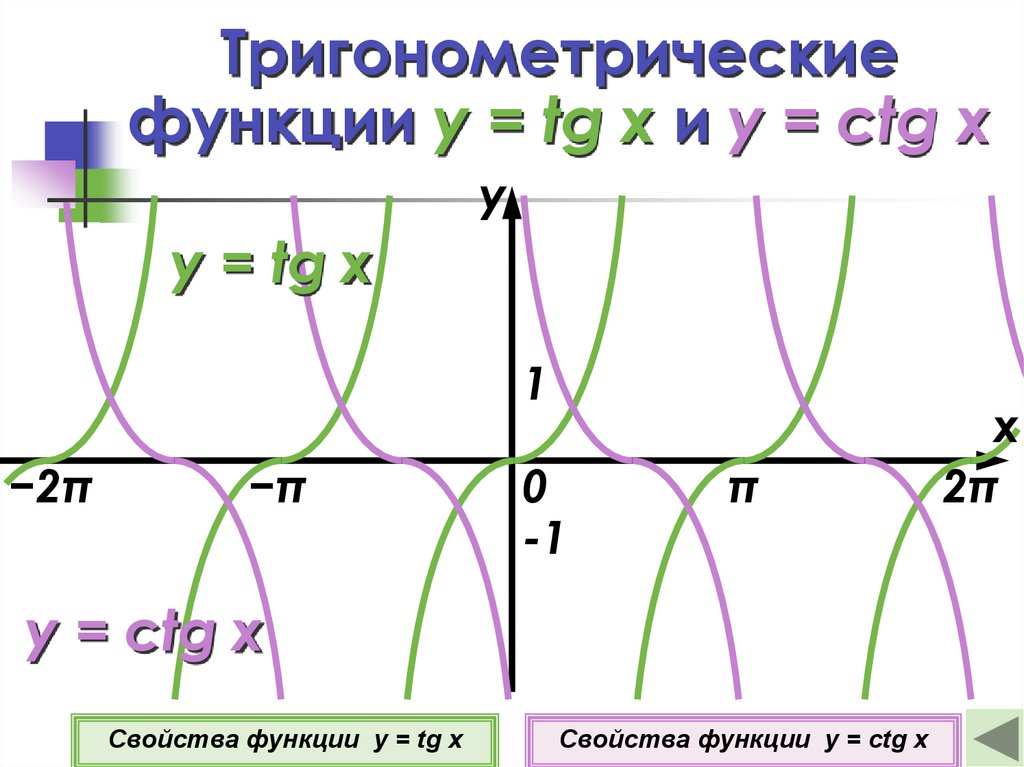
13. Тригонометрические функции y = tg x и y = ctg x

у
y = tg x
1
−2π
−π
0
-1
π
y = ctg x
Свойства функции y = tg x
Свойства функции y = ctg x
x
2π

14. Геометрические преобразования графиков

Преобразование вида y = f(x)+ b
Преобразование вида y = f(x – a)
Преобразование вида y = kf(x)
Преобразование вида y = f(mx)
Преобразование вида y = |f(x)|
Преобразование вида y = f(|x|)
Преобразование вида |y|= f(x)

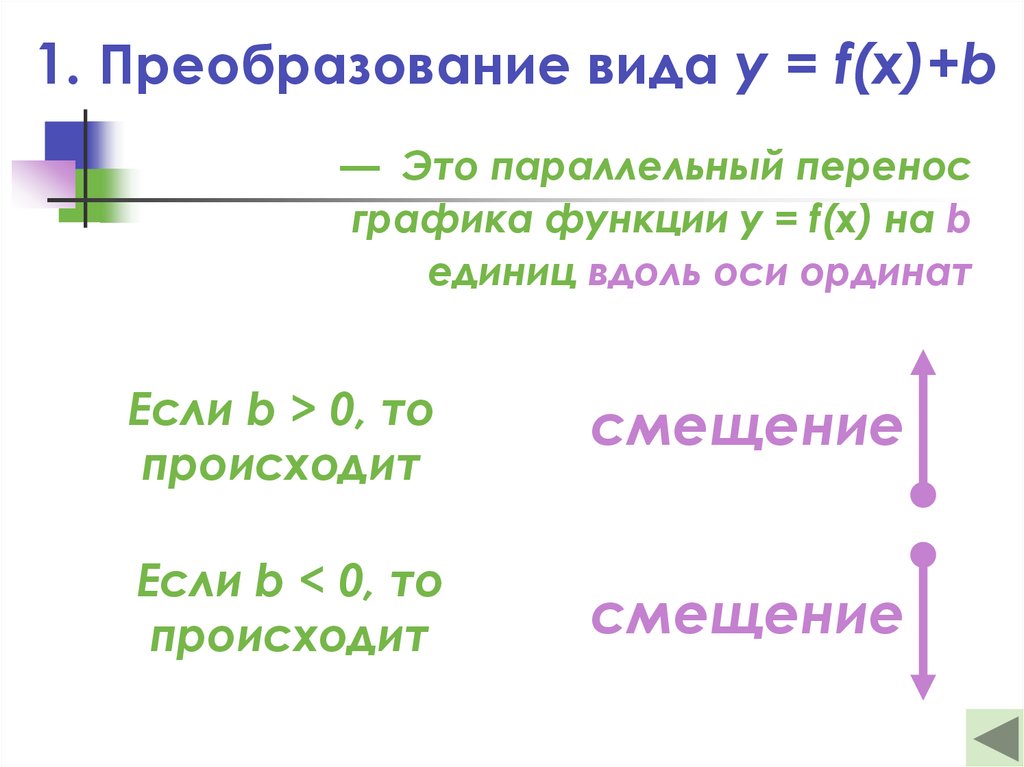
15. 1. Преобразование вида y = f(x)+b

— Это параллельный перенос
графика функции y = f(x) на b
единиц вдоль оси ординат
Если b > 0, то
происходит
смещение
Если b < 0, то
происходит
смещение

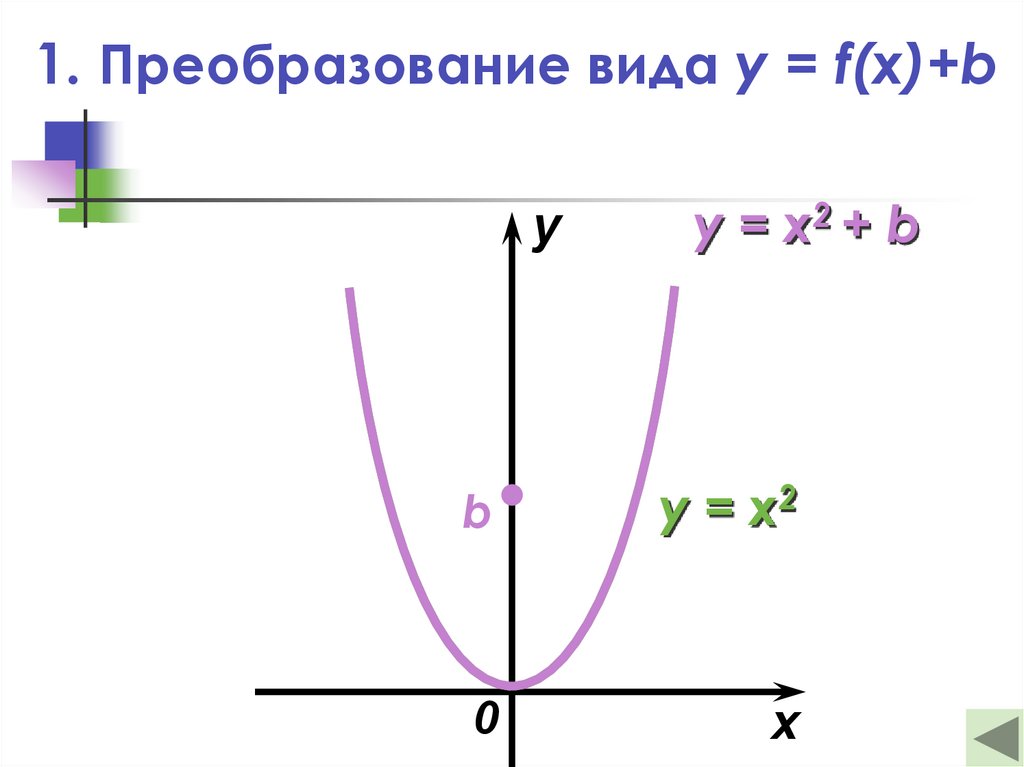
16.

1. Преобразование вида y = f(x)+b
y
y = x2 + b
b
y = x2
0
x

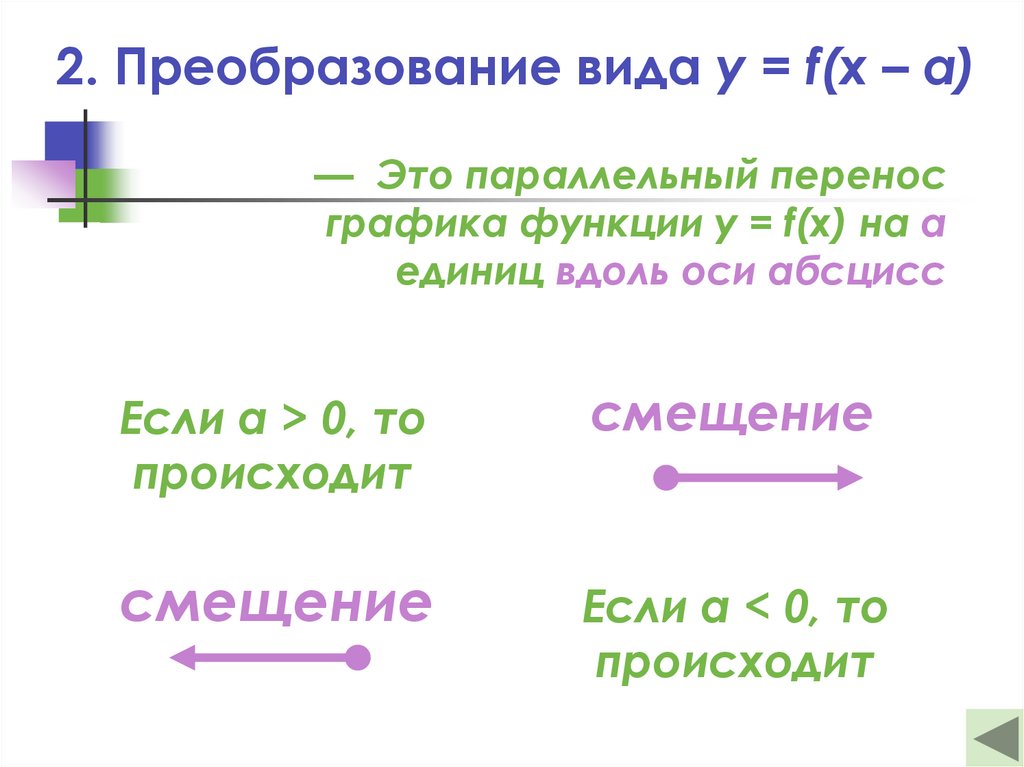
17. 2. Преобразование вида y = f(x – a)

— Это параллельный перенос
графика функции y = f(x) на а
единиц вдоль оси абсцисс
Если а > 0, то
происходит
смещение
смещение
Если а < 0, то
происходит

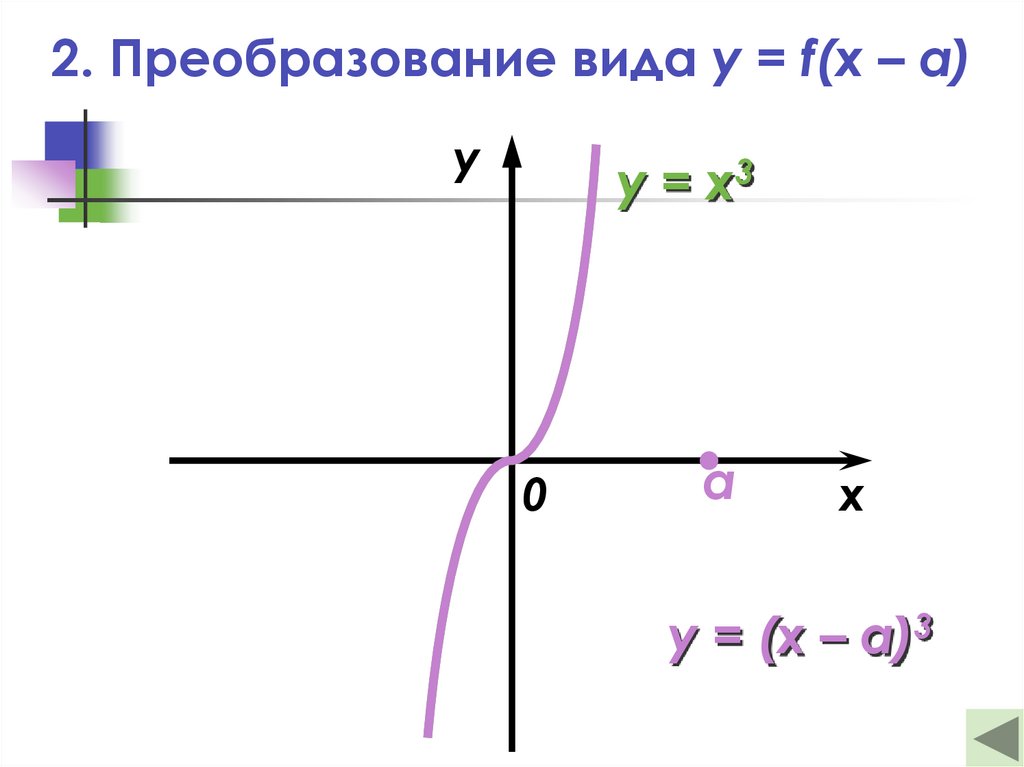
18. 2. Преобразование вида y = f(x – a)

y
y = x3
0
a
x
y = (x – a)3

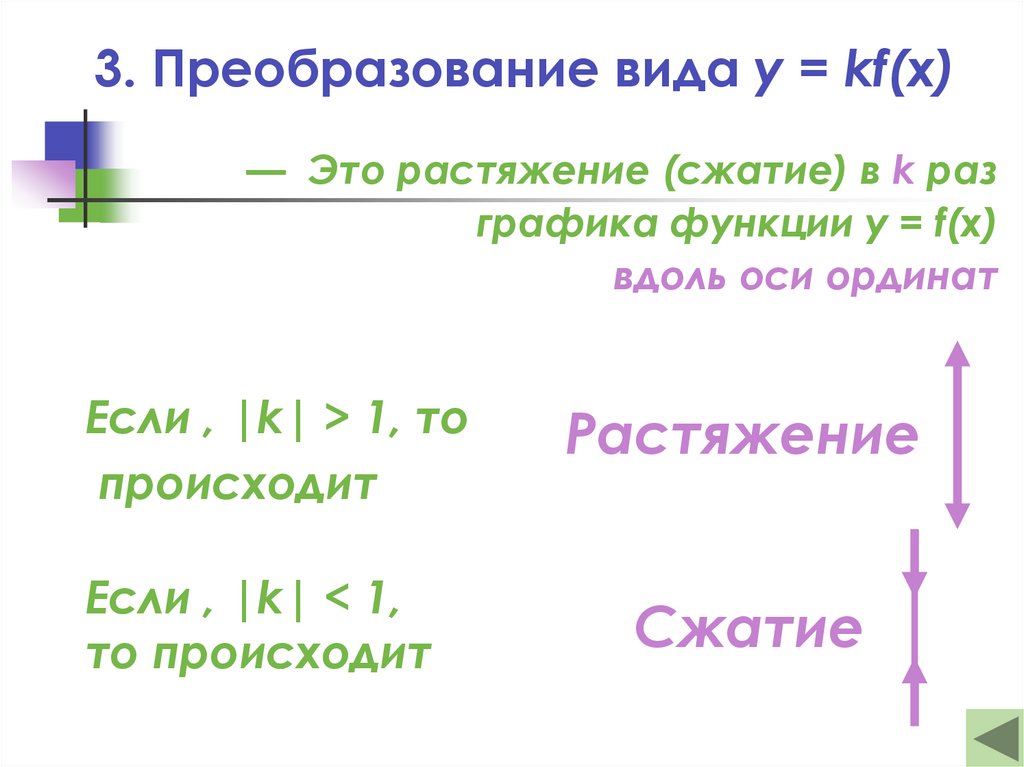
19. 3. Преобразование вида y = kf(x)

— Это растяжение (сжатие) в k раз
графика функции y = f(x)
вдоль оси ординат
Если , |k| > 1, то
происходит
Если , |k| < 1,
то происходит
Растяжение
Сжатие

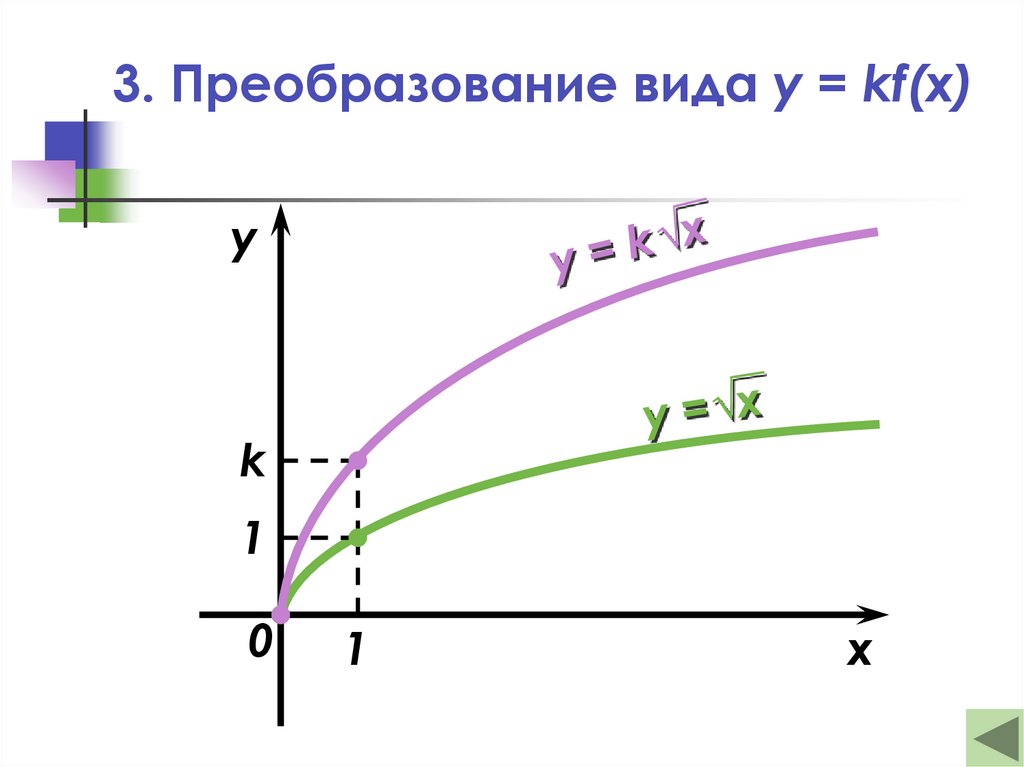
20. 3. Преобразование вида y = kf(x)

y
k
1
0
1
x

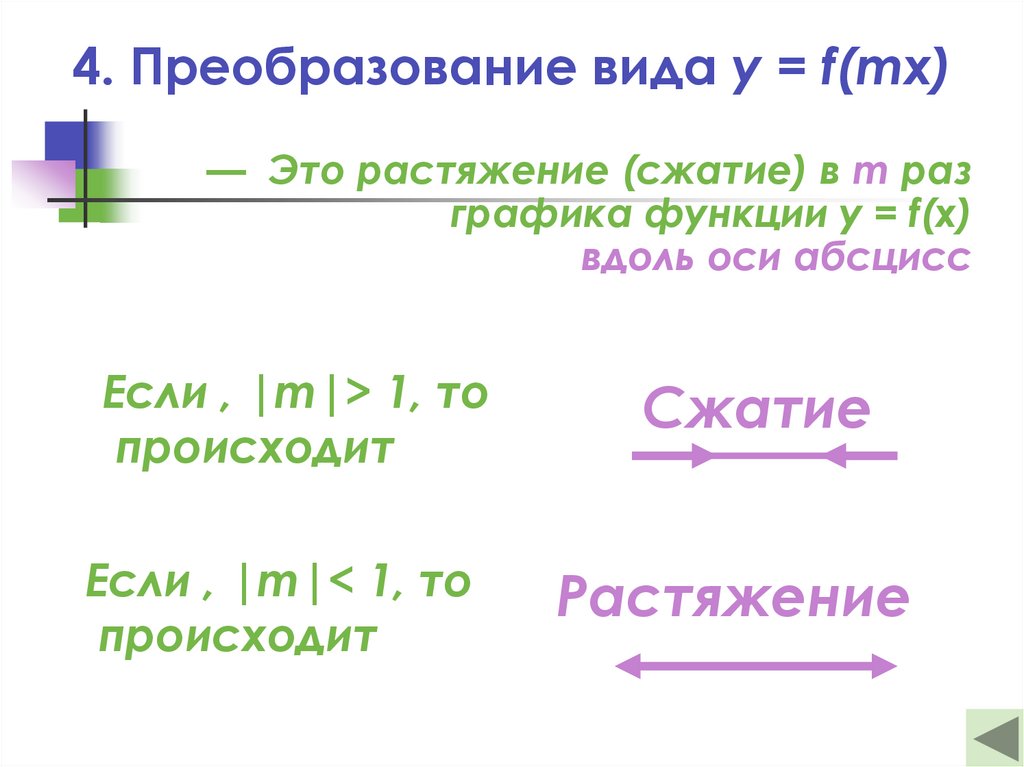
21. 4. Преобразование вида y = f(mx)

— Это растяжение (сжатие) в m раз
графика функции y = f(x)
вдоль оси абсцисс
Если , |m|> 1, то
происходит
Если , |m|< 1, то
происходит
Сжатие
Растяжение

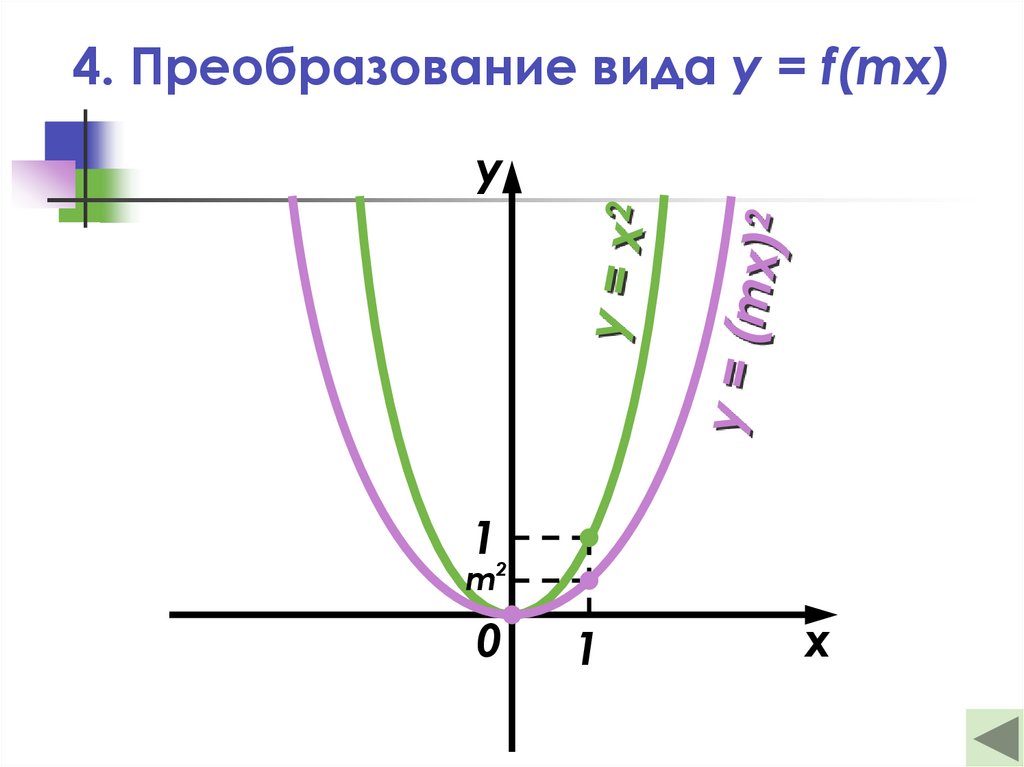
22. 4. Преобразование вида y = f(mx)

y
12
m
0
1
x

23. 5. Преобразование вида y = |f(x)|

— Это отображение нижней части
графика функции y = f(x) в верхнюю
полуплоскость относительно оси абсцисс
с сохранением верхней части графика
у
y = |f(x)|
y = f(x)
х
0

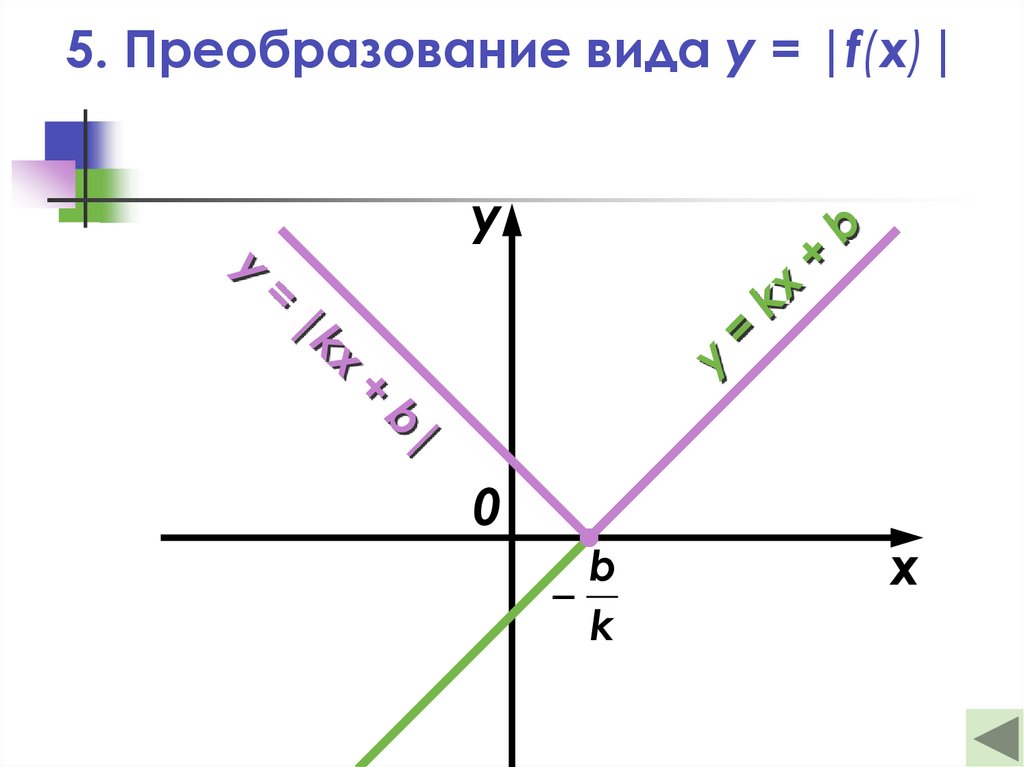
24.

5. Преобразование вида y = |f(x)|
y
0
b
k
x

25. 6. Преобразование вида y = f (|x|)

— Это отображение правой части графика
функции y = f(x) в левую полуплоскость
относительно оси ординат
с сохранением правой части графика
y = f(|x|)
у
0
y = f(x)
х

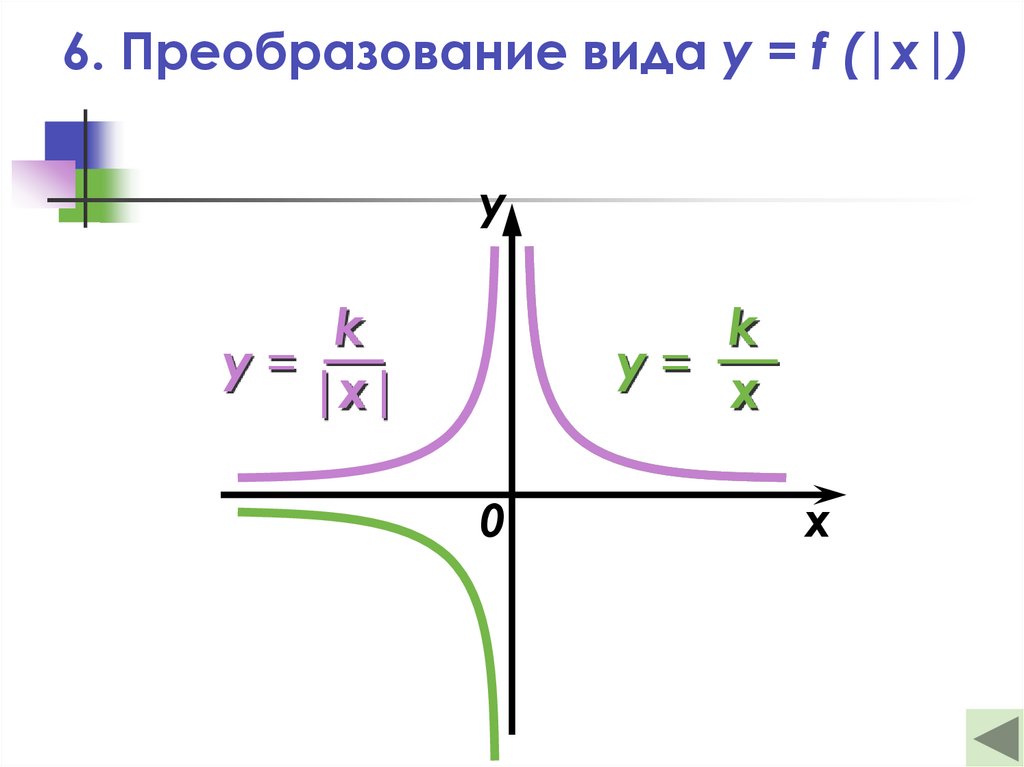
26.

6. Преобразование вида y = f (|x|)
y
k
у=
|x|
k
у=
x
0
x

27.

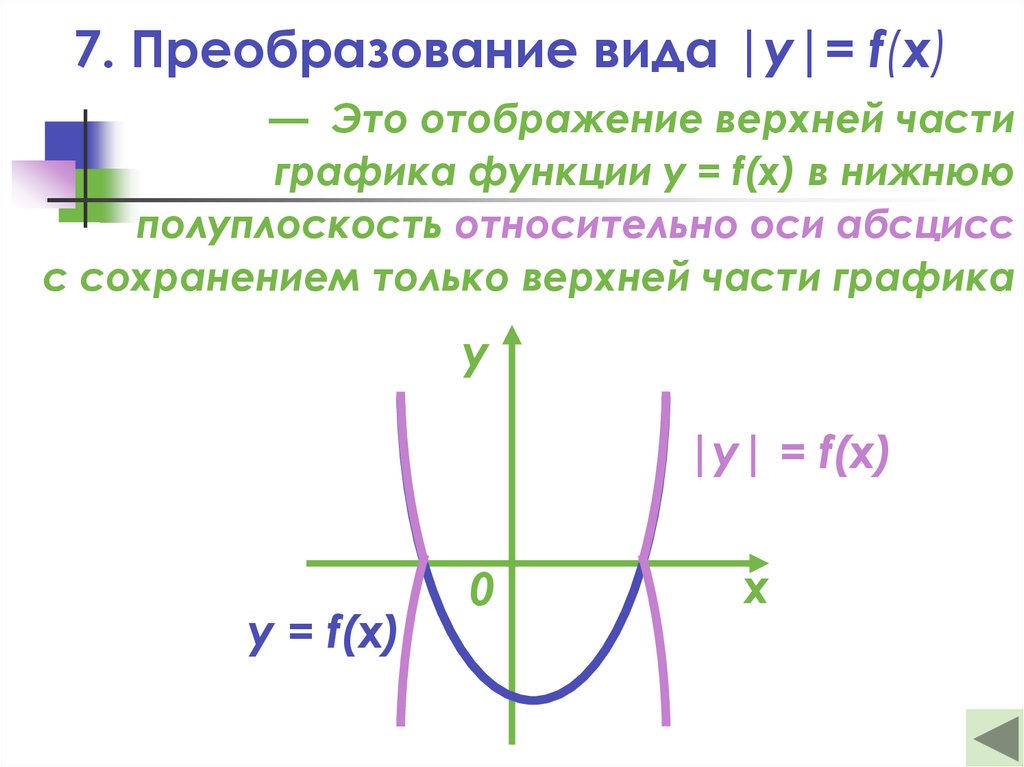
7. Преобразование вида |y|= f(x)
— Это отображение верхней части
графика функции y = f(x) в нижнюю
полуплоскость относительно оси абсцисс
с сохранением только верхней части графика
у
|y| = f(x)
х
y = f(x)
0

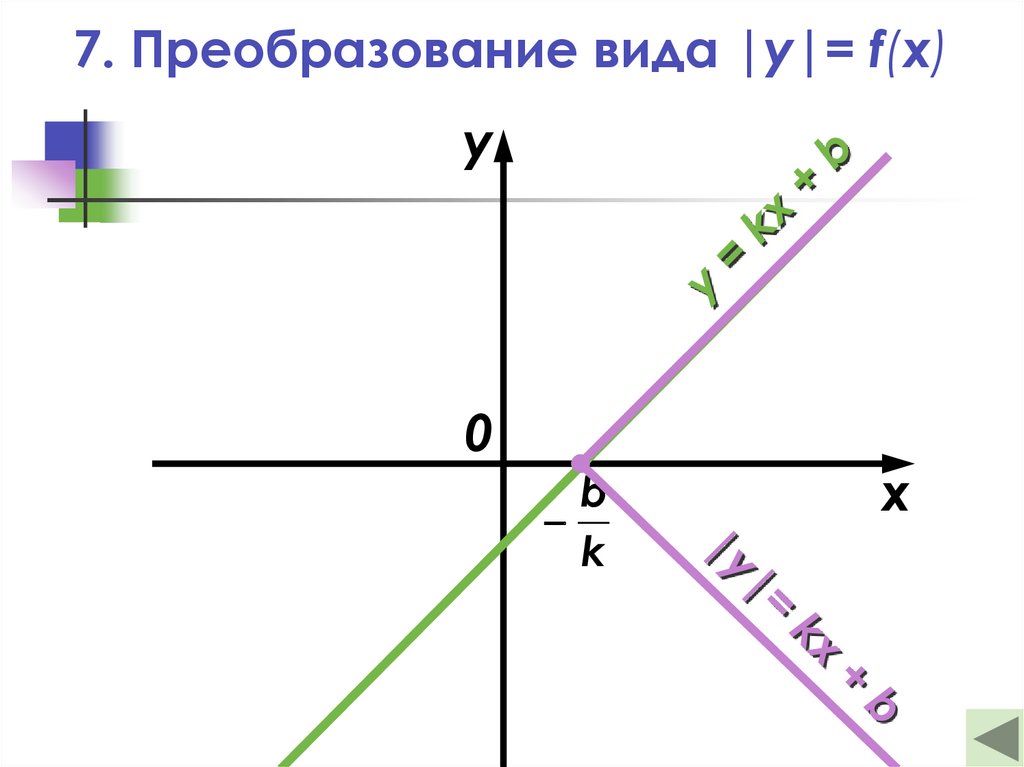
28.

7. Преобразование вида |y|= f(x)
y
0
b
k
x

29.

Свойства функций
• Свойства линейной функции
• Свойства квадратичной функции
• Свойства степенной функции
• Свойства обратной пропорциональности
• Свойства показательной функции
• Свойства логарифмической функции
• Свойства тригонометрических функций:
y = sin x
y = tg x
y = cos x
y = ctg x

30.

Свойства линейной функции
y = kx + b
1о D(y) = (−∞; +∞); E(y) = (−∞; +∞).
2о Если b = 0, то функция нечетная.
Если b ≠ 0, то функция ни четная, ни нечетная.
b
о
3 Если х = 0, то у = b, если у = 0, то х = − .
k
4о Если k > 0, то функция возрастает при х (−∞; +∞).
Если k < 0, то функция убывает при х (−∞; +∞).

31.

Свойства квадратичной функции
y=
2
ax +
bx + c, а ≠ 0
1о D(y) = (−∞; +∞).
2о Если a > 0, то E(y) = [ув ; +∞);
Если a < 0, то E(y) = (−∞; ув ].
3о Если b = 0, то функция четная.
Если b ≠ 0, то функция ни четная, ни нечетная.
2-4ac
b
±
√
b
о
4 Если х = 0, то у = c, если у = 0, то х1,2 =
2a
5о Если a > 0, то функция возрастает при х [xв ; +∞);
функция убывает при х (−∞; хв ].
Если a < 0, то функция возрастает при х (−∞; хв ];
функция убывает при х [xв ; +∞).
Подробнее

32.

Свойства степенной функции
y=
Если n = 2k, где k
Z
n
x
Если n = 2k +1, где k
Z
1о D(y)=(−∞; +∞).
1о D(y)=(−∞; +∞).
2о E(y)=[0 ; +∞).
2о E(y)=(−∞; +∞).
3о Функция четная.
3о Функция нечетная.
4о Если х = 0, то у = 0.
4о Если х = 0, то у = 0.
5о Функция возрастает
5о Функция возрастает
при х [0 ; +∞);
убывает при х (−∞; 0].
при х (−∞; +∞).

33.

Свойства обратной
пропорциональности
k
у=
x
1о D(y) = (−∞; 0)u(0; +∞)
2о E(y) = (−∞; 0)u(0 ; +∞)
3о Функция нечетная.
4о х ≠ 0, у ≠ 0.
5о Если k > 0, то функция убывает
при х (−∞; 0)u(0; +∞).
Если k < 0, то функция возрастает
при х (−∞; 0)u(0; +∞).

34.

Свойства степенной функции
y=
Если n = 2k, где k
Z
-n
x
Если n = 2k +1, где k
Z
1о D(y)=(−∞; 0)U(0; +∞).
1о D(y)=(−∞; 0)U(0; +∞).
2о E(y)=(0 ; +∞).
2о E(y)=(−∞; 0)U(0; +∞).
3о Функция четная.
4о Если х = 1, то у = 1.
5о Функция возрастает
при х (−∞; 0);
убывает при х (0 ; +∞).
6º функция ограничена
снизу прямой у = 0.
3о Функция нечетная.
4о Если х = 1, то у = 1;
если х = -1, то у = -1.
5о Функция убывает
при х (−∞; 0);(0; +∞).
6º Функция не
ограничена

35.

Свойства показательной функции
y=
x
a,
а > 0, a ≠ 1
1о D(y)=(−∞; +∞).
2о E(y)=(0 ; +∞).
3о Функция ни четная, ни нечетная.
4о Если х = 0, то у = 1.
5о Если а > 1, то функция возрастает
при х (−∞; +∞).
Если 0 < а < 1, то функция убывает
при х (−∞; +∞).
Подробнее

36.

Свойства логарифмической
функции y = loga x , а > 0, a ≠ 1
1о D(y)= (0 ; +∞).
2о E(y)= (−∞; +∞).
3о Функция ни четная, ни нечетная.
4о Если х = 1 , то у = 0.
5о Если а > 1, то функция возрастает
при х (0; +∞).
Если 0 < а < 1, то функция убывает
при х (0; +∞).
Подробнее

37.

Свойства функции
y = sin x
1о D(y)=(−∞; +∞).
2о E(y)=[−1; 1].
3о Функция нечетная.
4о Если х = 0, то у = 0.
π
π
о
5 Функция возрастает при х [− +2πn; +2πn].
2
2
π
Функция убывает при х [ +2πn; 3π +2πn].
2
2
π
π
6о xmax = +2πn; xmin = − +2πn, где n Z.
2
2
Подробнее