Similar presentations:
График функции y = f(x)
1.
2. Пусть задан график функции y = f(x)
Преобразование вида y = kf(x)Преобразование вида y = f(x) + b
Преобразование вида y = f(x – a)
Преобразование вида y = f(mx)
Преобразование вида y = |f(x)|
Преобразование вида y = f(|x|)
3. 1. Преобразование вида y = kf(x)
— Это растяжение (сжатие) в k разграфика функции y = f(x)
вдоль оси ординат
Если , |k| > 1, то
происходит
Растяжение
Сжатие
Если , |k| < 1,
то происходит
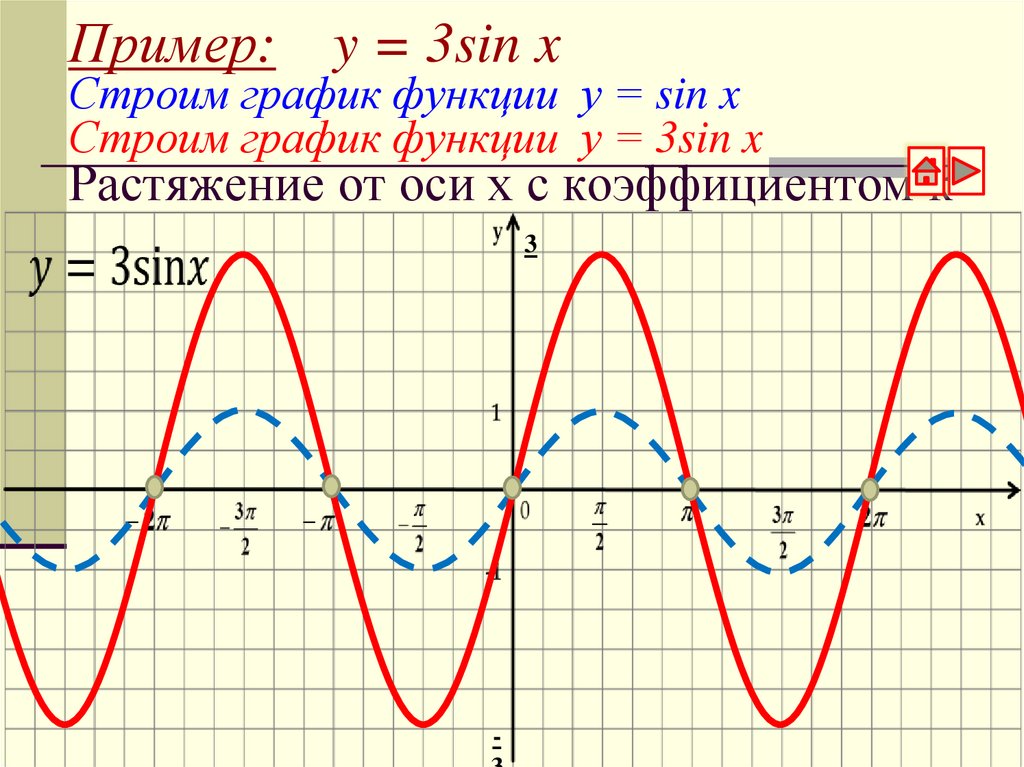
4. Пример: y = 3sin x Строим график функции у = sin x Строим график функции у = 3sin x Растяжение от оси х с коэффициентом к
3-
5.
6.
2.Для построенияграфика функции y=-f(x)
необходимо график
функции
y=f(x)симметрично
отобразить
относительно оси ОХ
7.
y3
2
2
0
1
-1
2
3
2
2
5
2
x
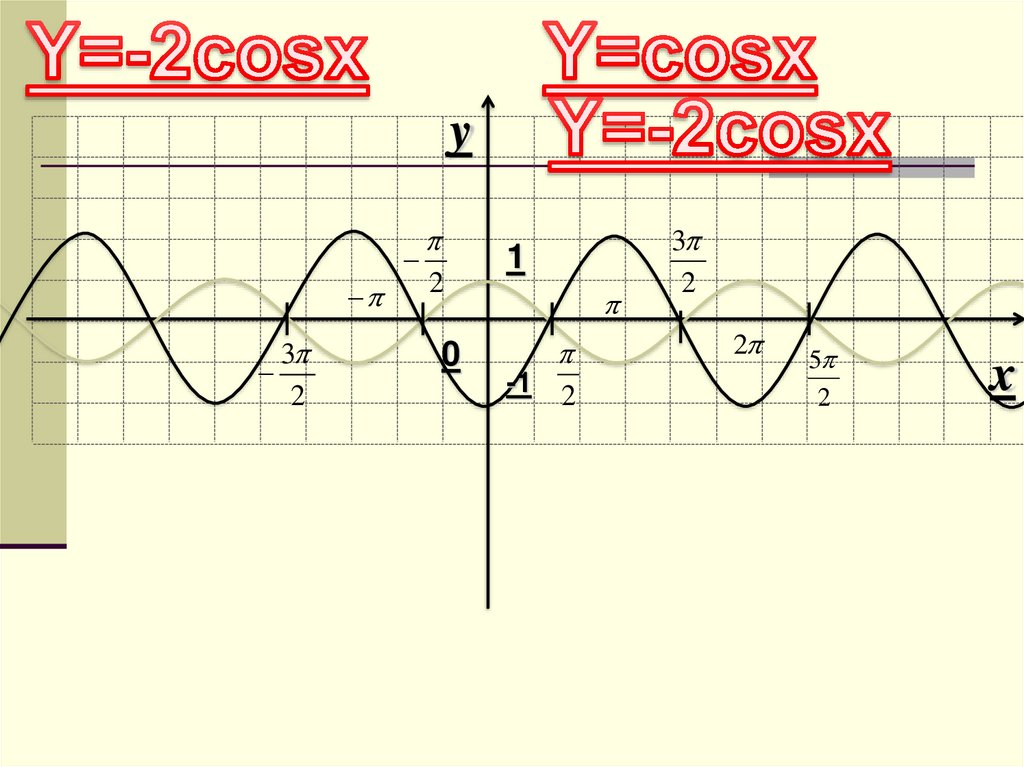
8. y = mf(x), где m=-1 Преобразование симметрии относительно оси х
9. y = mf(x), где m<0
y = mf(x), где m<010. 3. Преобразование вида y = f(x) + b
— Это параллельный переносграфика функции y = f(x) на b единиц
вдоль оси ординат
Если b > 0, то
происходит
смещение
Если b < 0, то
происходит
смещение
11. 3. Преобразование вида y = f(x) + b
Пример:y = sin x – 2
Строим график функции у = sin x
Строим график функции у = sin x – 2
12. 4. Преобразование вида y = f(x + a)
— Это параллельный переносграфика функции y = f(x) на а единиц
вдоль оси абсцисс
Если а < 0, то
происходит
смещение
смещение
Если а > 0, то
происходит
13. 4. Преобразование вида y = f(x – a)
Пример:y = tg (x – Π
)
3
Строим график функции у = tg x
Строим график функции у = tg (x – Π )
3
14.
44
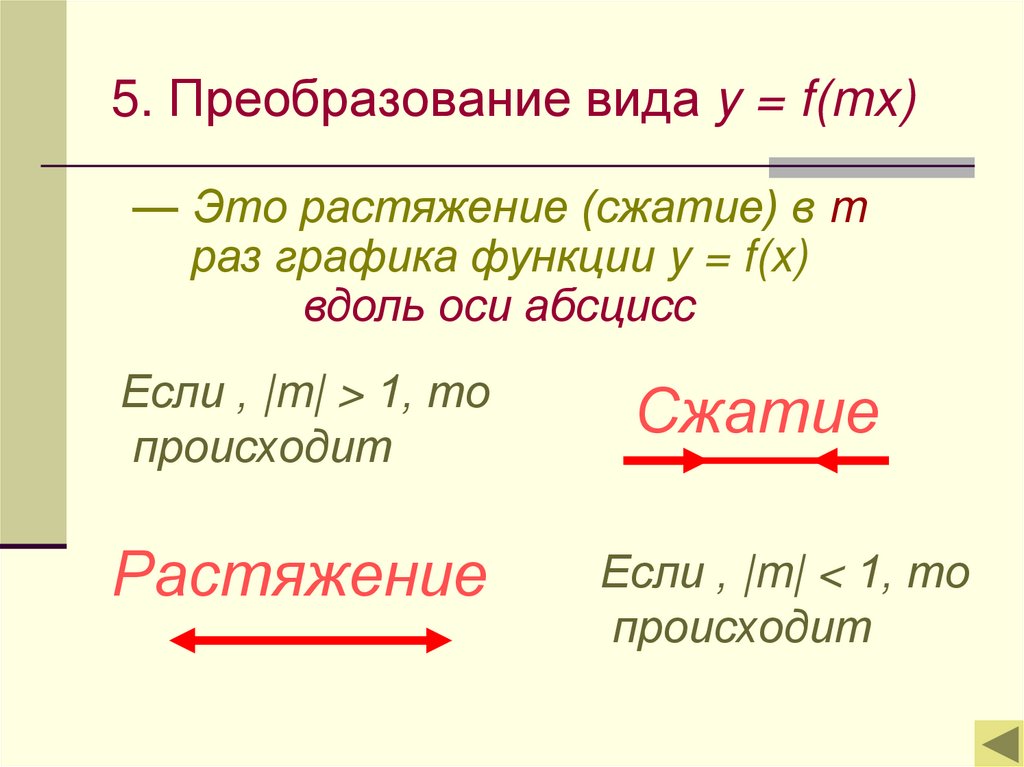
15. 5. Преобразование вида y = f(mx)
— Это растяжение (сжатие) в mраз графика функции y = f(x)
вдоль оси абсцисс
Если , |m| > 1, то
происходит
Сжатие
Растяжение
Если , |m| < 1, то
происходит
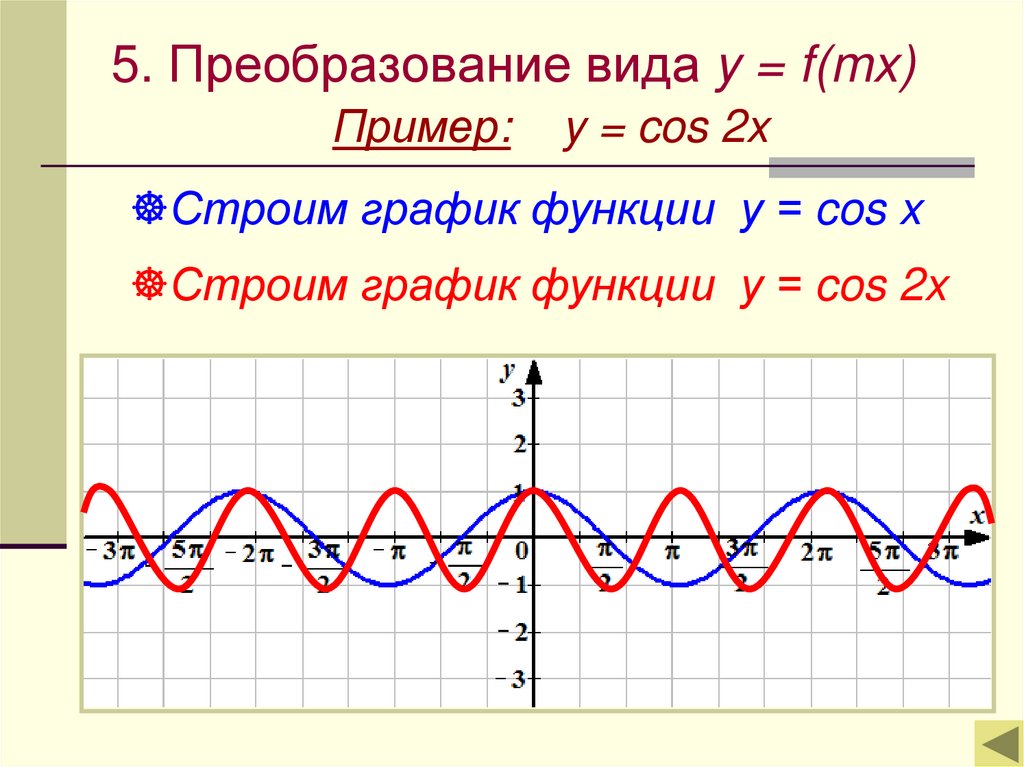
16. 5. Преобразование вида y = f(mx)
Пример:y = cos 2x
Строим график функции у = cos x
Строим график функции у = cos 2x
17. 6. Преобразование вида y = |f(x)|
— Это отображение нижней части графикафункции y = f(x) в верхнюю полуплоскость
относительно оси абсцисс
с сохранением верхней части графика
у
y = |f(x)|
y = f(x)
х
0
18. 6. Преобразование вида y = |f(x)|
Пример:y = |cos x|
Строим график функции у = cos x
Строим график функции у = |cos x|
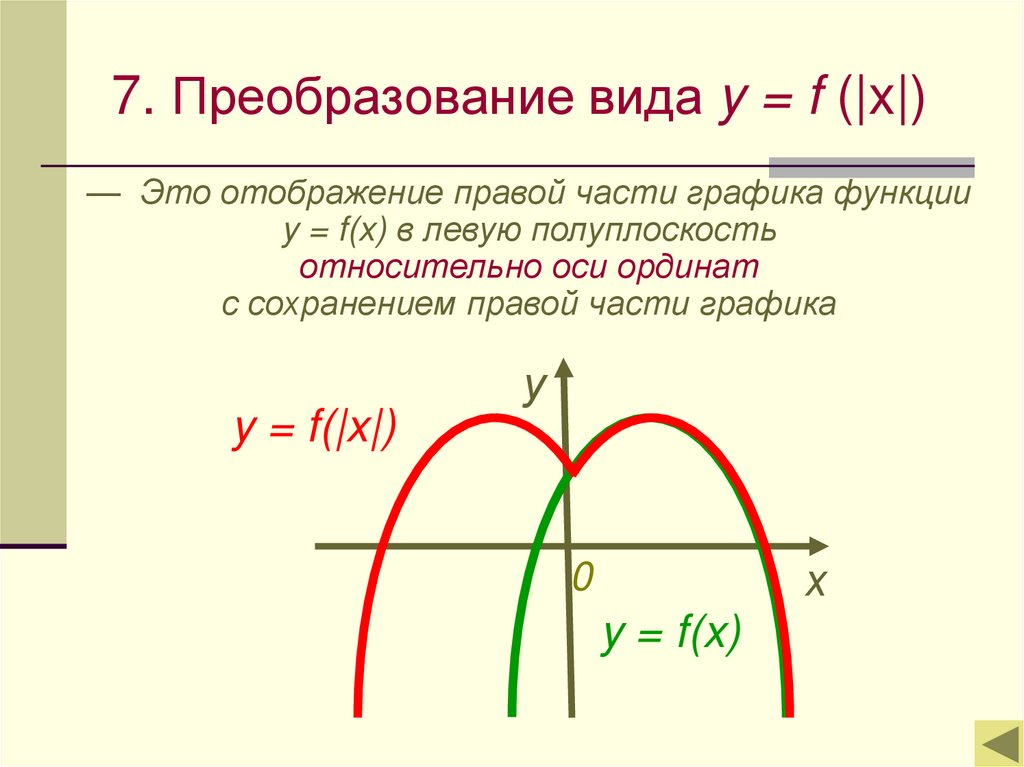
19. 7. Преобразование вида y = f (|x|)
— Это отображение правой части графика функцииy = f(x) в левую полуплоскость
относительно оси ординат
с сохранением правой части графика
у
y = f(|x|)
х
0
y = f(x)
20. 7. Преобразование вида y = f (|x|)
Пример:y = ctg |x|
Строим график функции у = ctg x
Строим график функции у = ctg |x|
21. Составь алгоритм построения графиков
22.
2y sin( x )
3
23.
y2
y sin( x )
3
2 3
2
x
1
2
-1
2
3
2
2
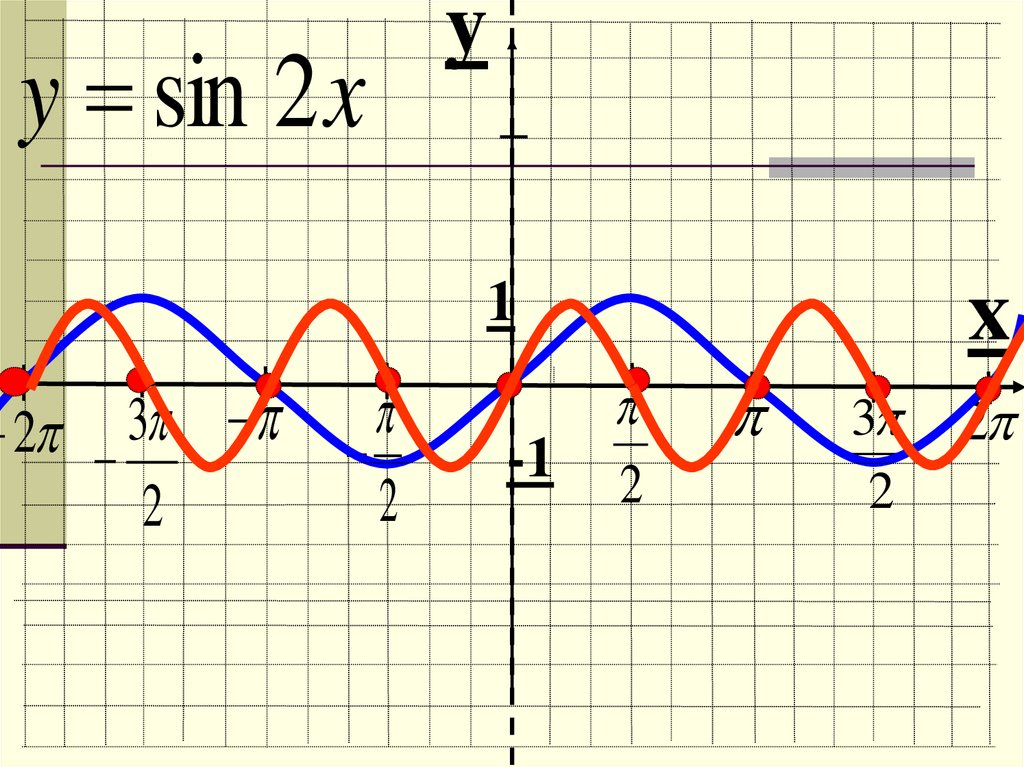
24.
y sin 2 x25.
y sin 2 x2 3
2
y
x
1
2
-1
2
3
2
2
26.
y 3 sin x27.
y 3 sin x2 3
2
y
x
1
2
-1
2
3
2
2
28.
y sin x 229.
yy sin x 2
2 3
2
x
1
2
-1
2
3
2
2
30.
1y sin x
2
31.
1y sin x
2
2 3
2
y
x
1
2
-1
2
3
2
2
32.
хy sin
2
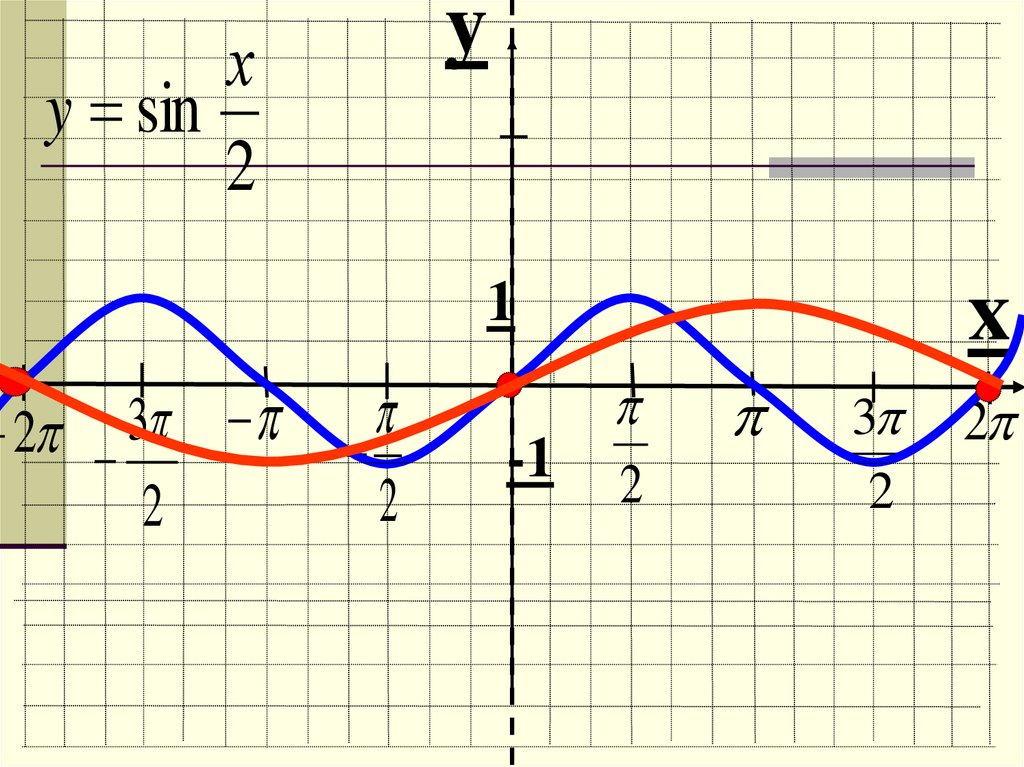
33.
yх
y sin
2
2 3
2
x
1
2
-1
2
3
2
2



















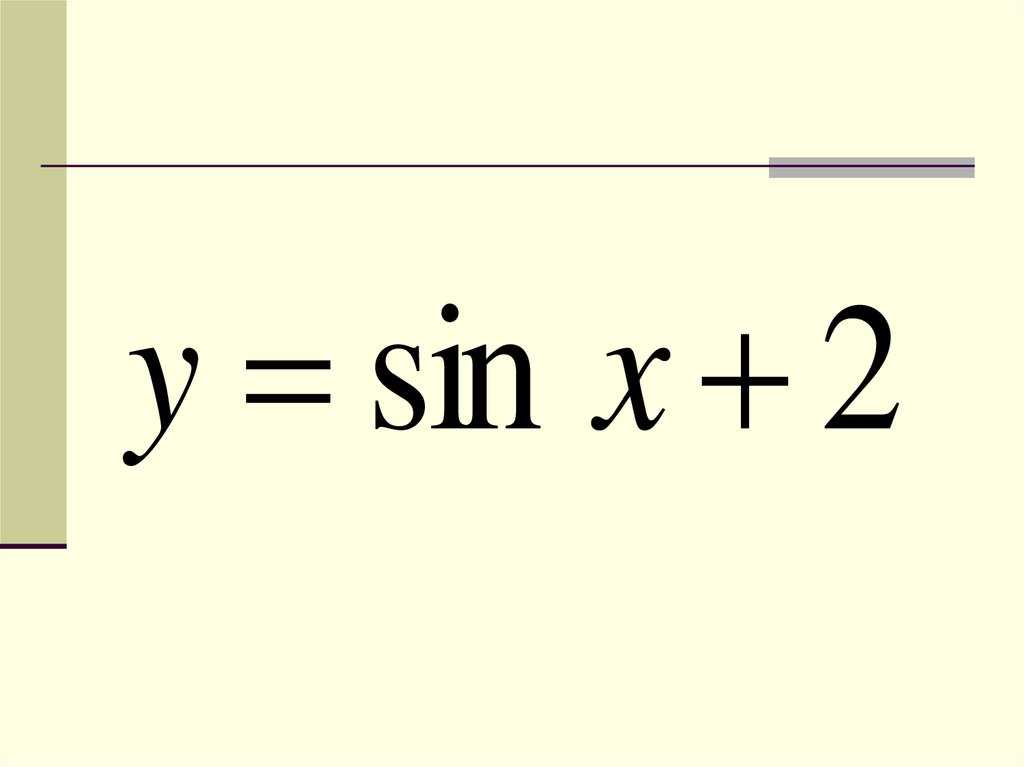

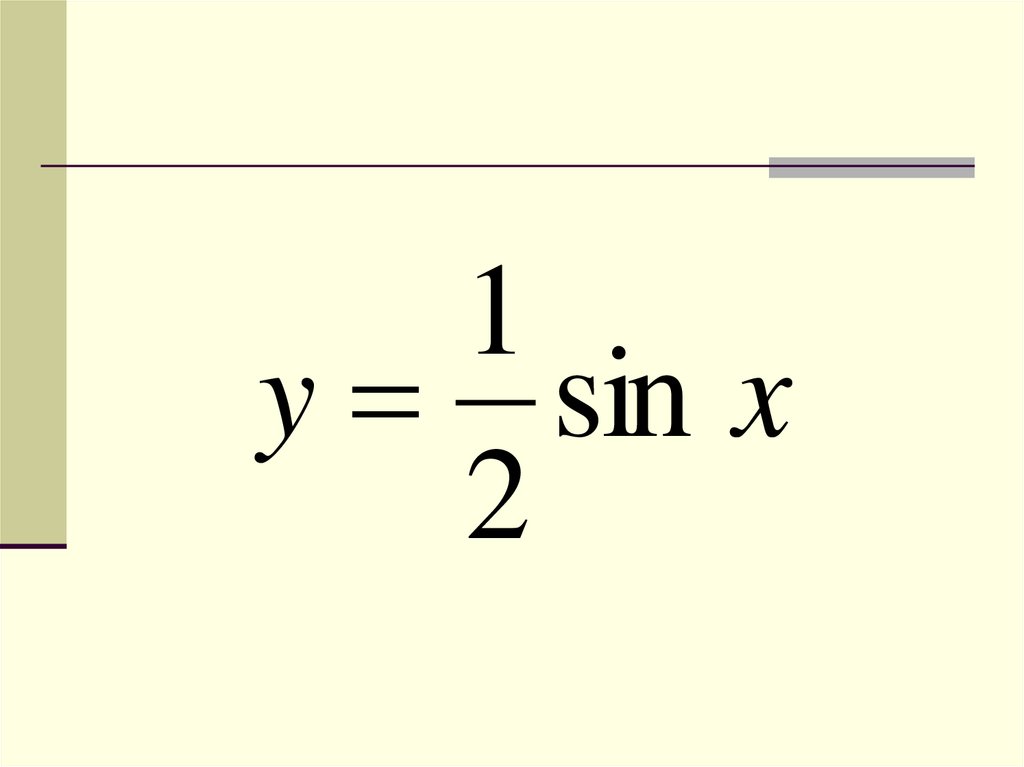

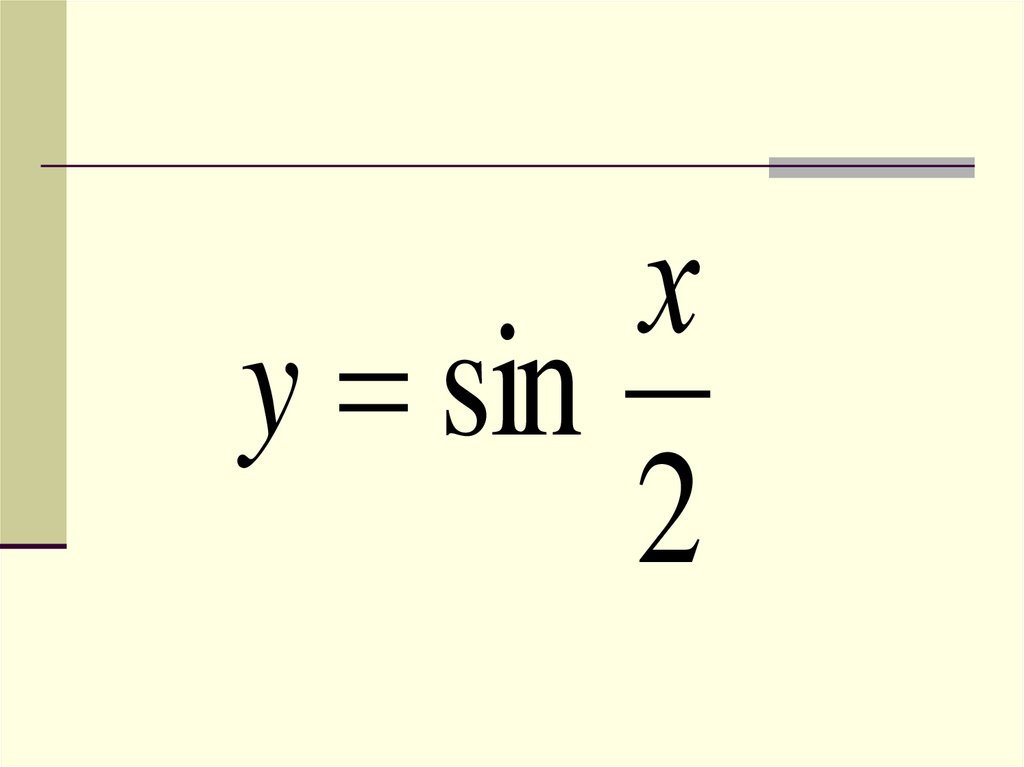
 mathematics
mathematics








