Similar presentations:
Определение подобных треугольников. 8 класс
1.
2.
Девизом к сегодняшнему уроку будут словадревнегреческого математика Фалеса:
- Что есть больше всего на свете? – Пространство.
- Что быстрее всего? – Ум.
- Что мудрее всего? – Время.
- Что приятнее всего? – Достичь желаемого.
3.
Бермудские острова,владение
Великобритании в
северо-западной части
Атлантического
океана, близ берегов
Северной Америки.
4.
Пуэрто-Рико,содружество ПуэртоРико, владение США в
Вест-Индии, на острове
Пуэрто-Рико и близ
лежащих островах
Флорида, полуостров
на юго-востоке
Северной Америки,
часть штата Флорида
(США).
5.
6. Треугольник
В∆АВС – треугольник
А,В,С – вершины
АВ, ВС, АС – стороны
А, В, C углы
А
А
С
7. Равнобедренный треугольник
• Две стороны равны• Углы при основании
равны
• Биссектриса, проведённая
к основанию, является
медианой и высотой
8. Равносторонний треугольник
• Все стороны равны• Углы все равны
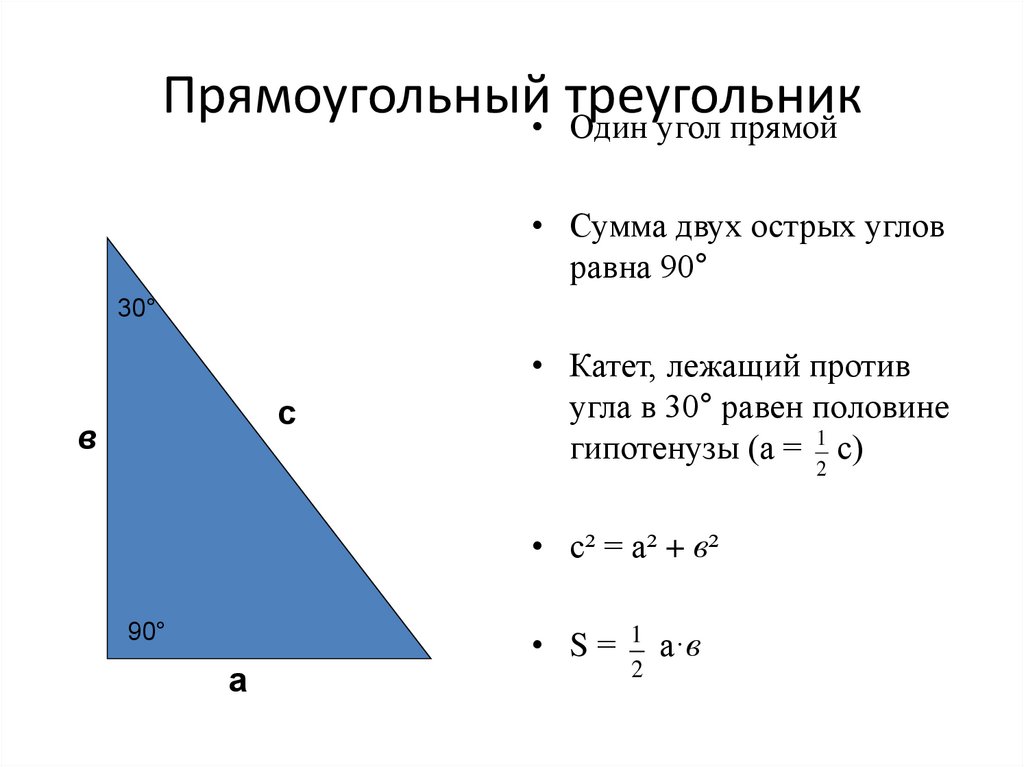
9. Прямоугольный треугольник
Прямоугольный• треугольникОдин угол прямой
• Сумма двух острых углов
равна 90°
30°
с
в
• Катет, лежащий против
угла в 30° равен половине
гипотенузы (а = 12 с)
• с² = а² + в²
90°
а
• S=
1
2
а·в
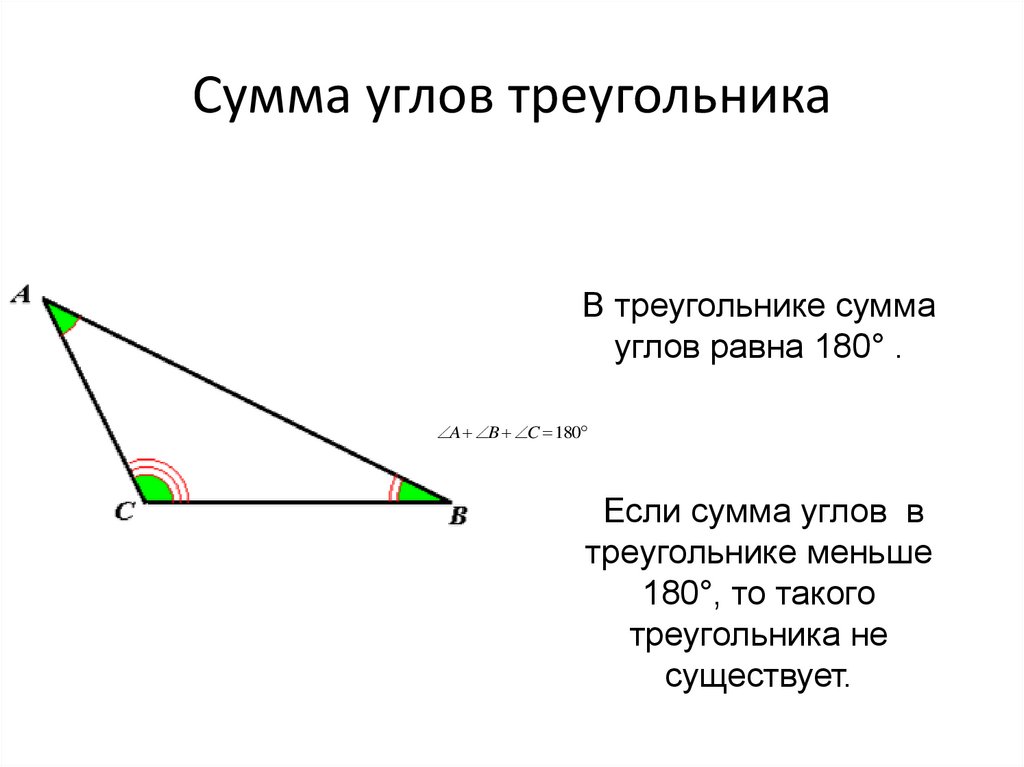
10. Сумма углов треугольника
В треугольнике суммауглов равна 180° .
A B C 180
Если сумма углов в
треугольнике меньше
180°, то такого
треугольника не
существует.
11.
12. Цели урока:
Сформулировать определение подобныхтреугольников;
Изучить
характеристики
подобных
треугольников и их свойства;
Узнать,
где
применяется
подобие
треугольников.
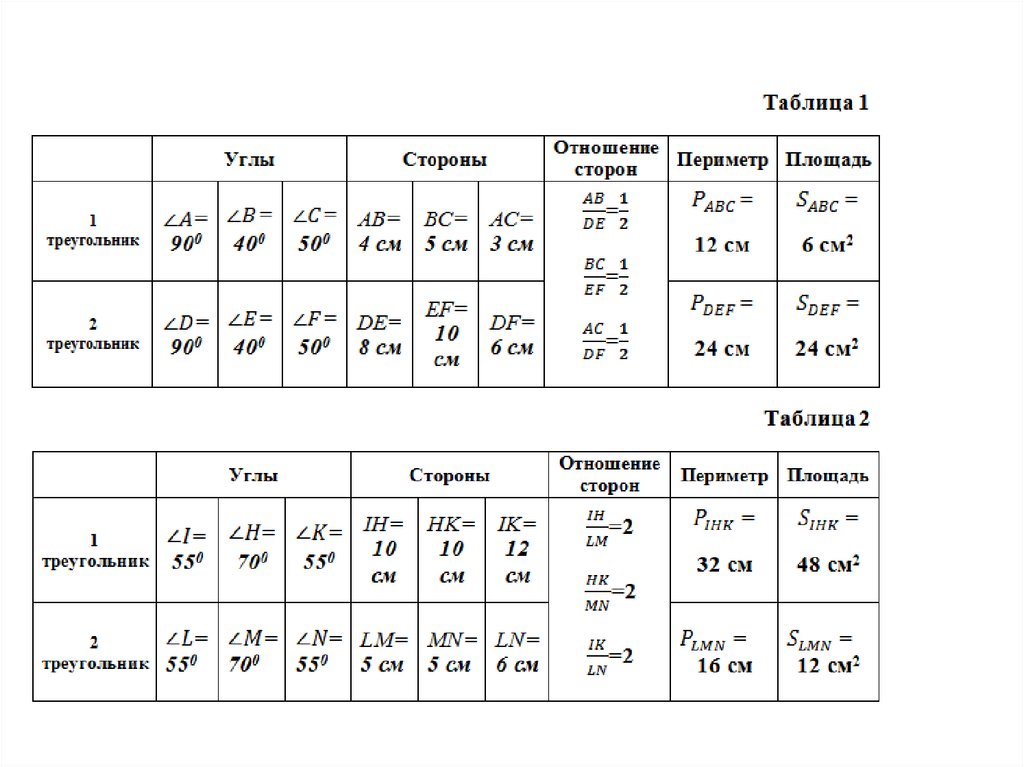
13. 1 этап исследования
14.
15. 2 этап исследования
Ответьте на вопросы:• Что можно сказать про углы каждой пары треугольников?
• Что можно сказать про стороны каждой пары
треугольников?
Заполните пропуски, используя ответы на предыдущие
этапы исследования:
Если углы двух треугольников __________и стороны
одного треугольника ___________ сходственным
сторонам
другого
треугольника,
то
такие
треугольники называются ПОДОБНЫМИ.
16. 3 этап исследования
Найдите коэффициенты подобиякаждой пары треугольников из 1
этапа исследования:
17.
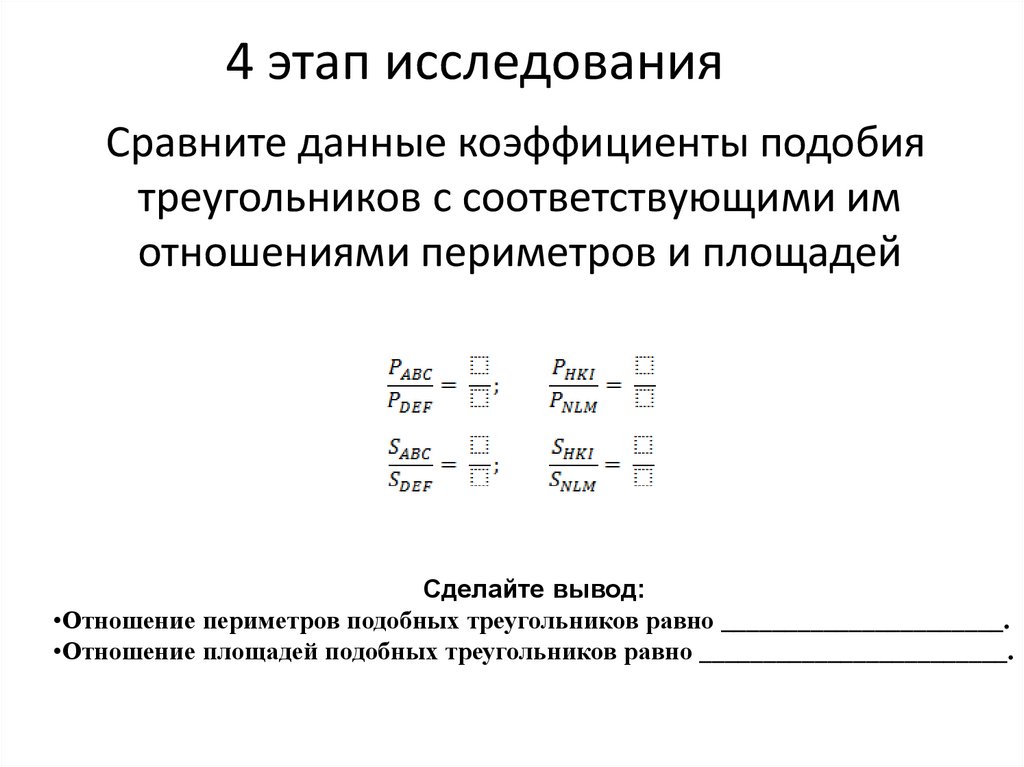
18. 4 этап исследования
Сравните данные коэффициенты подобиятреугольников с соответствующими им
отношениями периметров и площадей
Сделайте вывод:
•Отношение периметров подобных треугольников равно ______________________.
•Отношение площадей подобных треугольников равно ________________________.
19.
Вывод:• Отношение
периметров подобных треугольников равно
коэффициенту подобия.
• Отношение площадей подобных треугольников равно
квадрату коэффициента подобия.
20. Решение задач
21. Итоги урока
Сформулировать определение подобныхтреугольников;
Изучить характеристики подобных
треугольников и их свойства;
Узнать, где применяется подобие
треугольников.









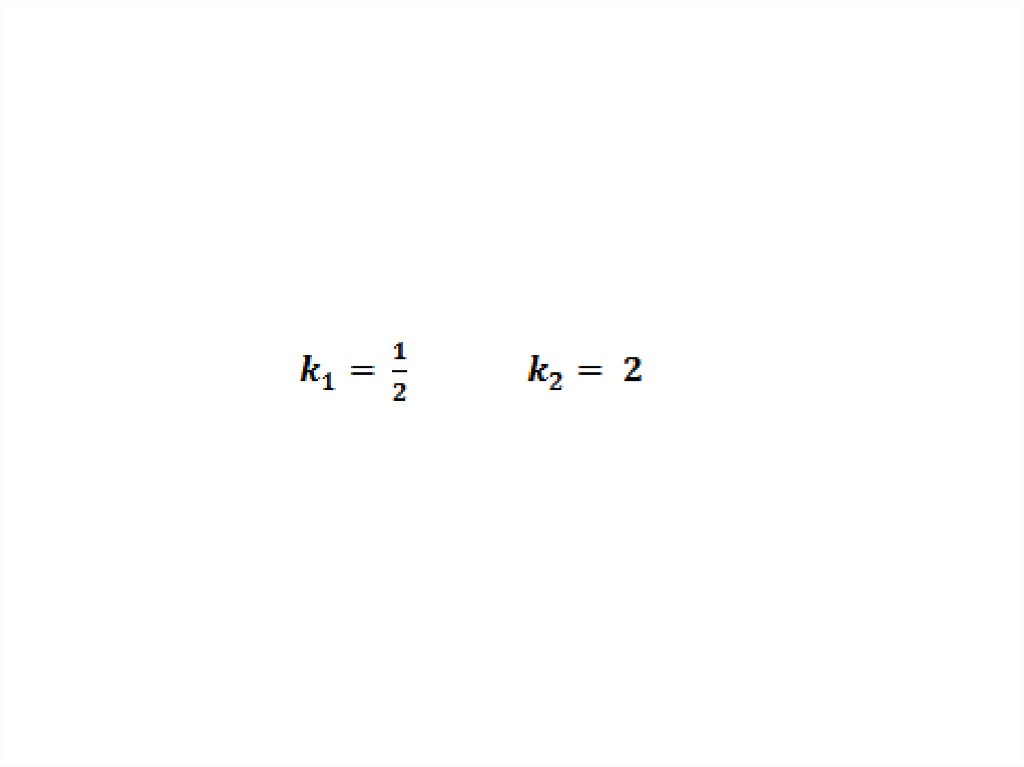





 mathematics
mathematics








