Similar presentations:
Определение подобных треугольников
1.
«Если за день ничемуне научился, зря
прожил день».
Китайская
пословица
2.
Повторим.• Дайте определение подобных
треугольников.
• Как читается первый признак подобия
треугольников?
• Как читается второй признак подобия
треугольников?
• Как читается третий признак подобия
треугольников?
• Что такое коэффициент подобия?
• Как называются стороны
прямоугольного треугольника?
3.
Тест («да» или «нет»)1.
Два треугольника подобны, если их углы соответственно равны и сходственные
стороны пропорциональны.
2.
Два равносторонних треугольника всегда подобны.
3.
Если три стороны одного треугольника соответственно пропорциональны трем
сторонам другого треугольника, то такие треугольники подобны.
4.
Стороны одного треугольника имеют длины 3, 4, 6 см, стороны другого
треугольника равны 9, 14, 18 см. Подобны ли эти треугольники?
5.
Периметры подобных треугольников равны.
6.
Если два угла одного треугольника равны 60° и 50°, а два угла другого
треугольника равны 50° и 80°, то такие треугольники подобны.
7.
Два прямоугольных треугольника подобны, если имеют по равному острому углу.
8.
Два равнобедренных треугольника подобны.
9.
Если два угла одного треугольника соответственно равны двум углам другого
треугольника, то такие треугольники подобны.
10.
Если две стороны одного треугольника соответственно пропорциональны двум
сторонам другого треугольника, то такие треугольники подобны.
4.
Проверка теста1
Два треугольника подобны, если их углы соответственно
равны и сходственные стороны пропорциональны.
да
2
Два равносторонних треугольника всегда подобны.
да
3
Если три стороны одного треугольника соответственно
пропорциональны трем сторонам другого треугольника, то
такие треугольники подобны.
да
4
Стороны одного треугольника имеют длины 3, 4, 6 см,
стороны другого треугольника равны 9, 14, 18 см. Подобны
ли эти треугольники?
нет
5
Периметры подобных треугольников равны.
нет
5.
Проверка теста6
Если два угла одного треугольника равны 60° и 50°, а два
угла другого треугольника равны 50° и 80°, то такие
треугольники подобны.
нет
7
Два прямоугольных треугольника подобны, если имеют по
равному острому углу.
да
8
Два равнобедренных треугольника подобны.
нет
9
Если два угла одного треугольника соответственно равны
двум углам другого треугольника, то такие треугольники
подобны.
да
10 Если две стороны одного треугольника соответственно
пропорциональны двум сторонам другого треугольника, то
такие треугольники подобны.
нет
6.
«Кто малое не познал,великое не познает».
Узбекская
пословица
7.
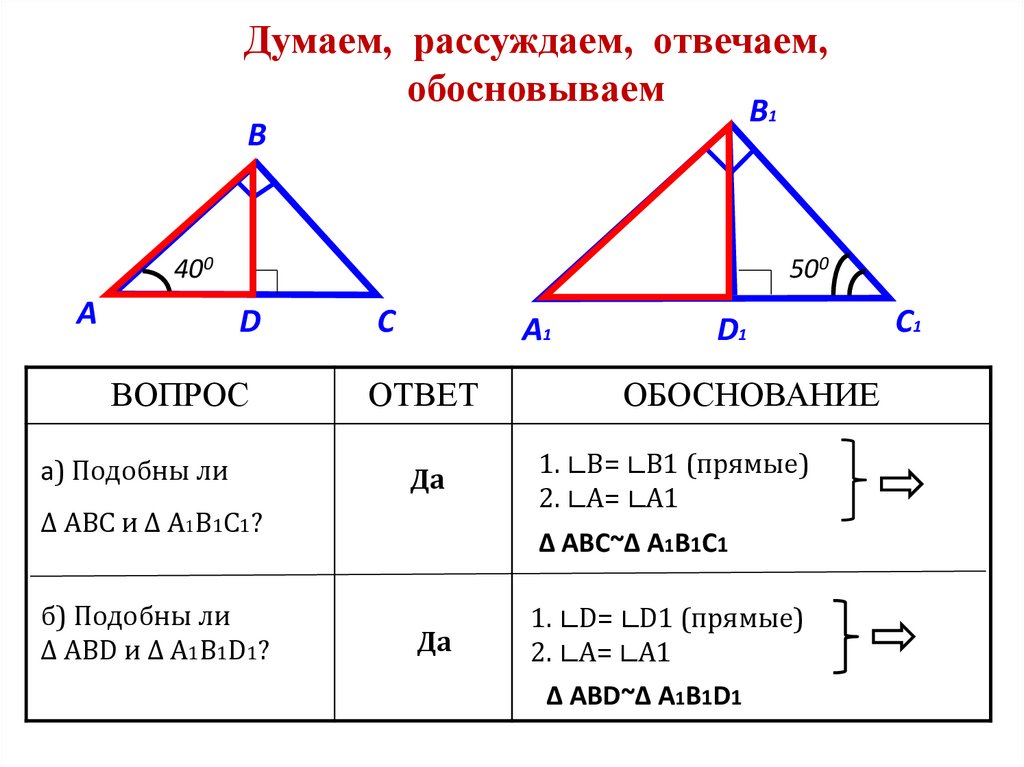
Думаем, рассуждаем, отвечаем,обосновываем
B1
B
400
A
500
D
ВОПРОС
a) Подобны ли
C
A1
ОТВЕТ
Да
Δ ABC и Δ A1B1C1?
б) Подобны ли
Δ ABD и Δ A1B1D1?
D1
ОБОСНОВАНИЕ
1. ∟В= ∟В1 (прямые)
2. ∟A= ∟A1
Δ ABC~Δ A1B1C1
Да
1. ∟D= ∟D1 (прямые)
2. ∟A= ∟A1
Δ ABD~Δ A1B1D1
C1
8.
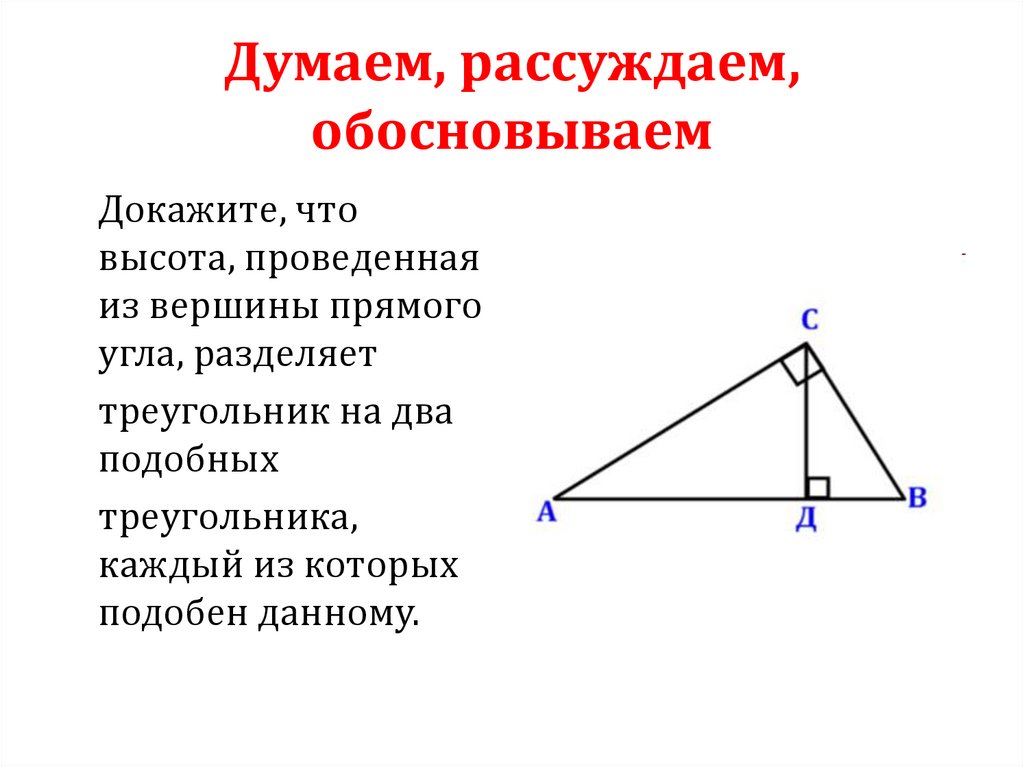
Думаем, рассуждаем,обосновываем
Докажите, что
высота, проведенная
из вершины прямого
угла, разделяет
треугольник на два
подобных
треугольника,
каждый из которых
подобен данному.
9.
CA
D
B
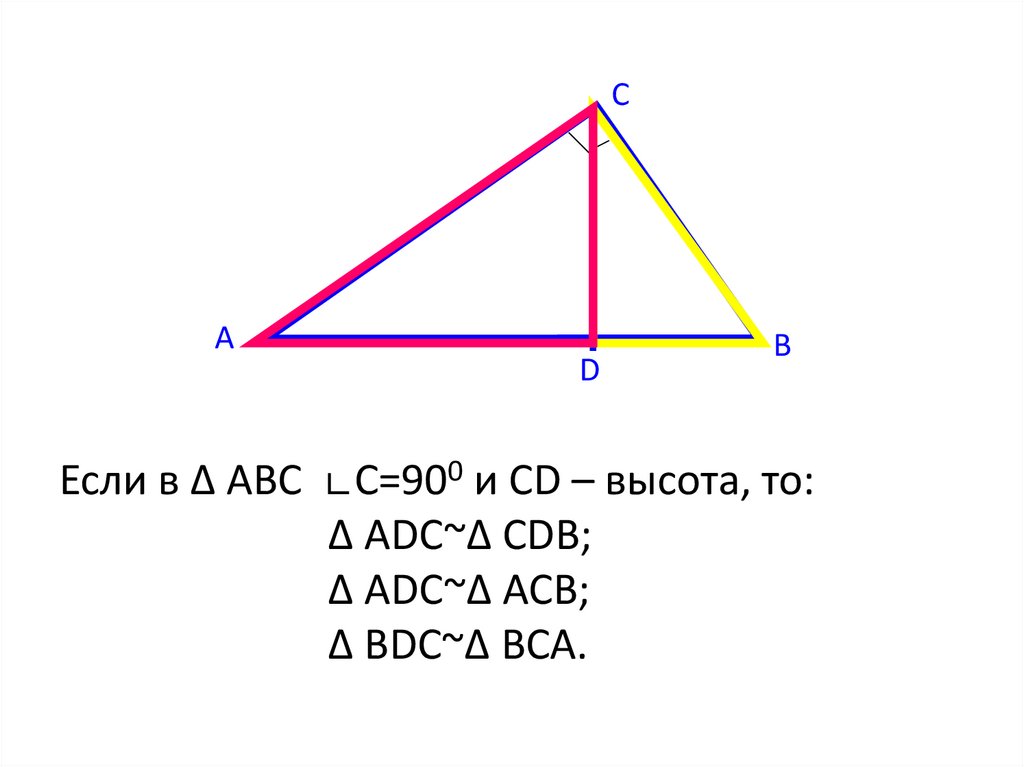
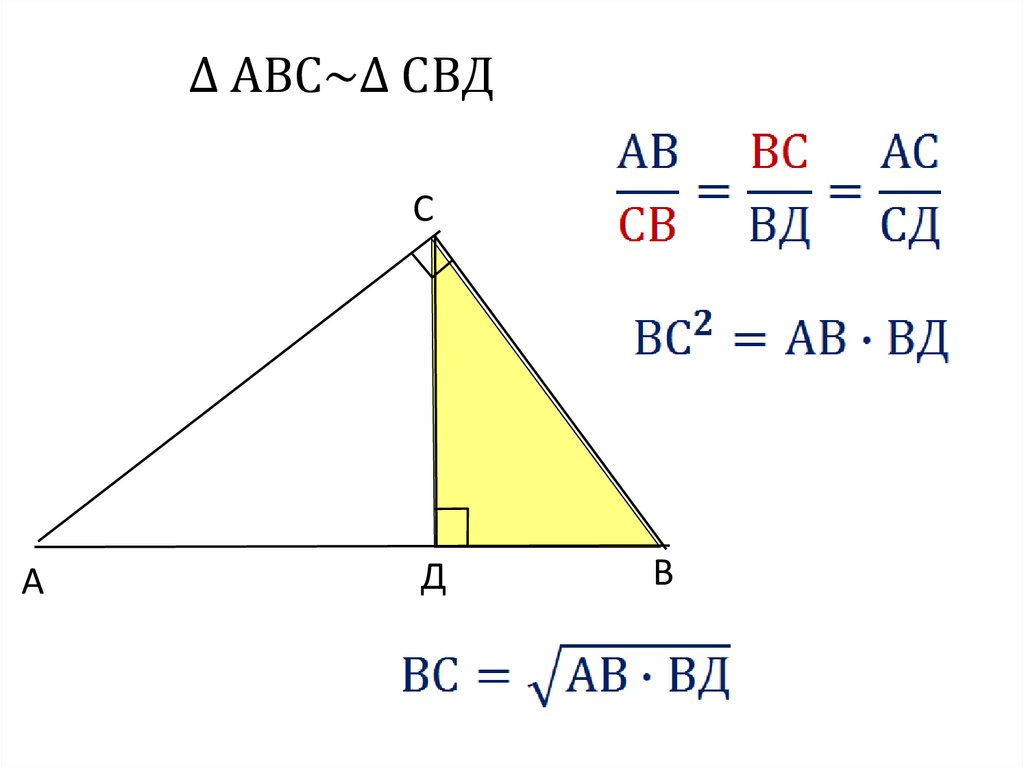
Если в Δ ABC ∟С=900 и CD – высота, то:
Δ АDC~Δ СDВ;
Δ АDC~Δ AСВ;
Δ BDC~Δ ВСА.
10.
«Труд при ученьескучен, да плод от
ученья вкусен».
Русская
пословица
11.
Работа по группам.1. Записать с помощью знака подобия
подобие двух прямоугольных
треугольников.
2. Записать пропорциональность
сходственных сторон.
3. Выразить из пропорции нужный отрезок.
12.
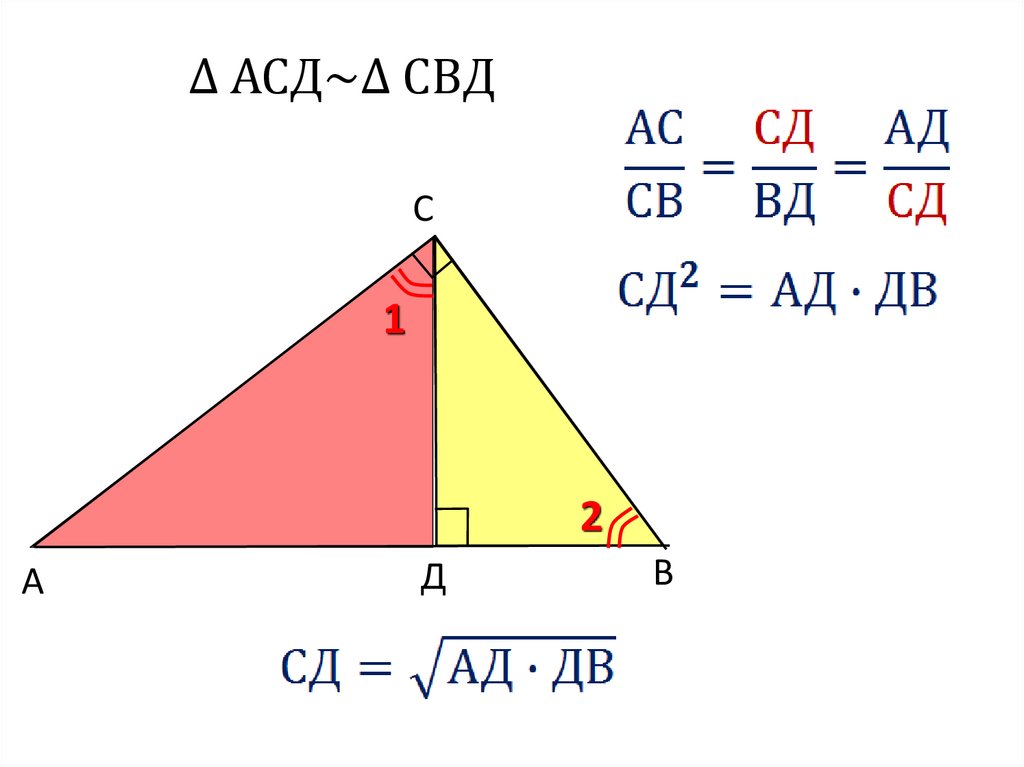
Δ АСД~Δ СВДC
1
2
A
Д
B
13.
Δ АВC~Δ АСDC
A
D
B
14.
Δ АBC~Δ СBДC
A
Д
B
15.
Выводы:1. В ходе работы мы составили равенства
некоторых отношений. Как можно назвать
элементы этих отношений?
Пропорциональные отрезки
Точнее, пропорциональные
отрезки в прямоугольном
треугольнике.
16.
Тема нашего урока«Пропорциональные
отрезки в прямоугольном
треугольнике».
17.
CA
D
B
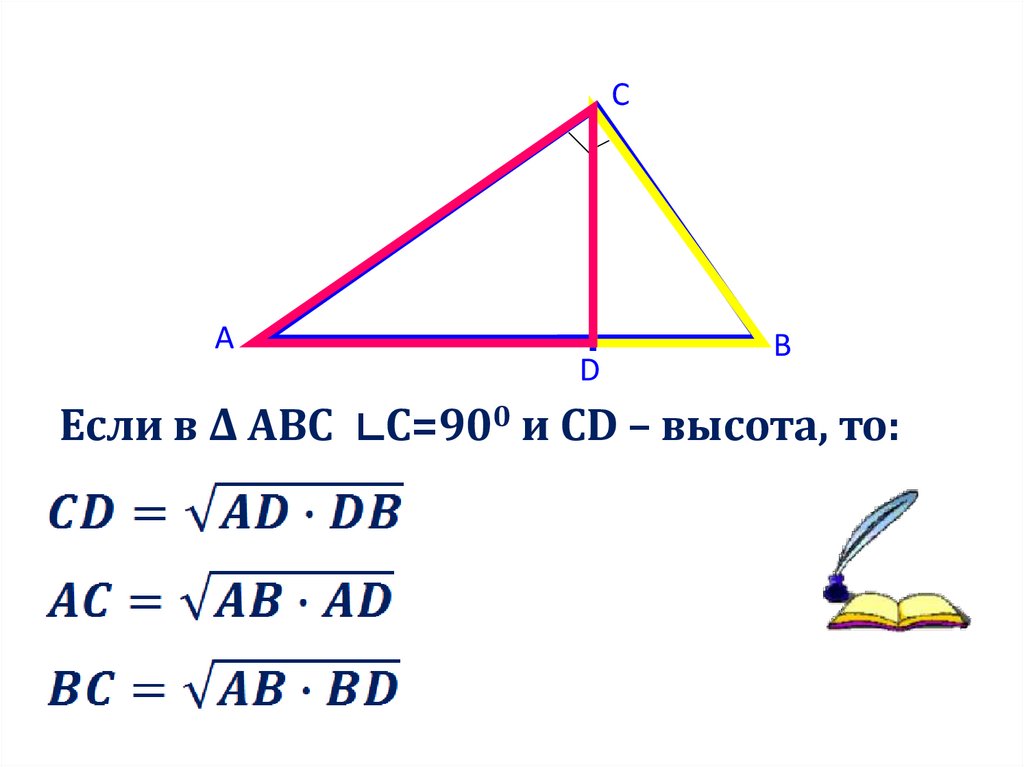
Если в Δ ABC ∟С=900 и CD – высота, то:
18.
Новое понятиеСреднее арифметическое
Средним
арифметическим чисел
m и n называется число
а, равное полусумме
чисел m и n.
Среднее пропорциональное
Средним геометрическим
(пропорциональным)
чисел m и n называется
число а, равное
квадратному корню из
произведения чисел чисел
m и n.
19.
Закрепим понятие.1.
Найдите среднее
арифметическое и
среднее геометрическое
чисел 3 и 12.
2.
Найти длину среднего
пропорционального
(среднего
геометрического)
отрезков MN и KP, если
MN = 9 см, KP = 27 см
20.
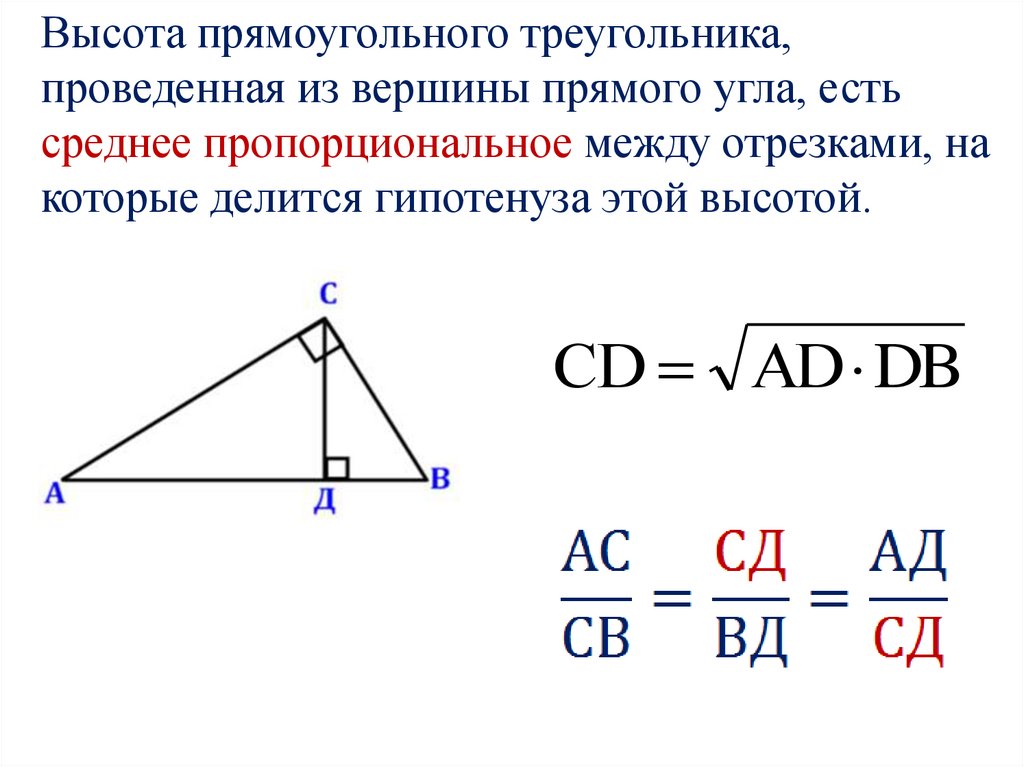
Высота прямоугольного треугольника,проведенная из вершины прямого угла, есть
среднее пропорциональное между отрезками, на
которые делится гипотенуза этой высотой.
СD АD DB
21.
22.
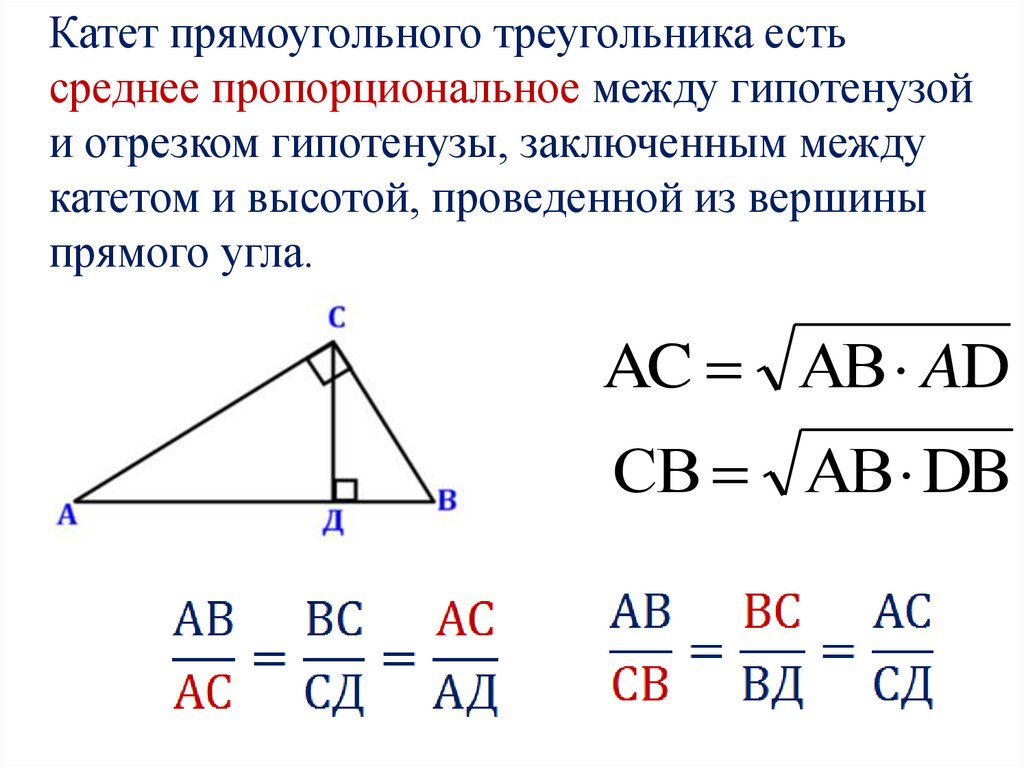
Катет прямоугольного треугольника естьсреднее пропорциональное между гипотенузой
и отрезком гипотенузы, заключенным между
катетом и высотой, проведенной из вершины
прямого угла.
AC АB AD
СB АB DB
23.
24.
«Ученье- семеназнаний,
а знания - семена
счастья».
Грузинская
пословица
25.
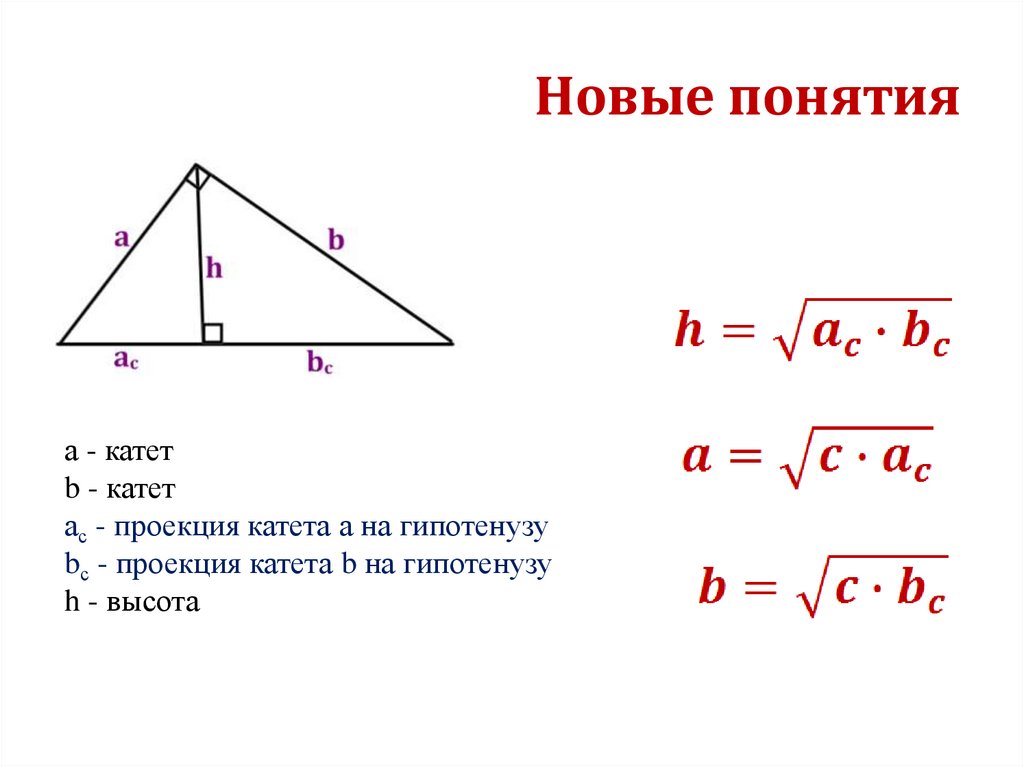
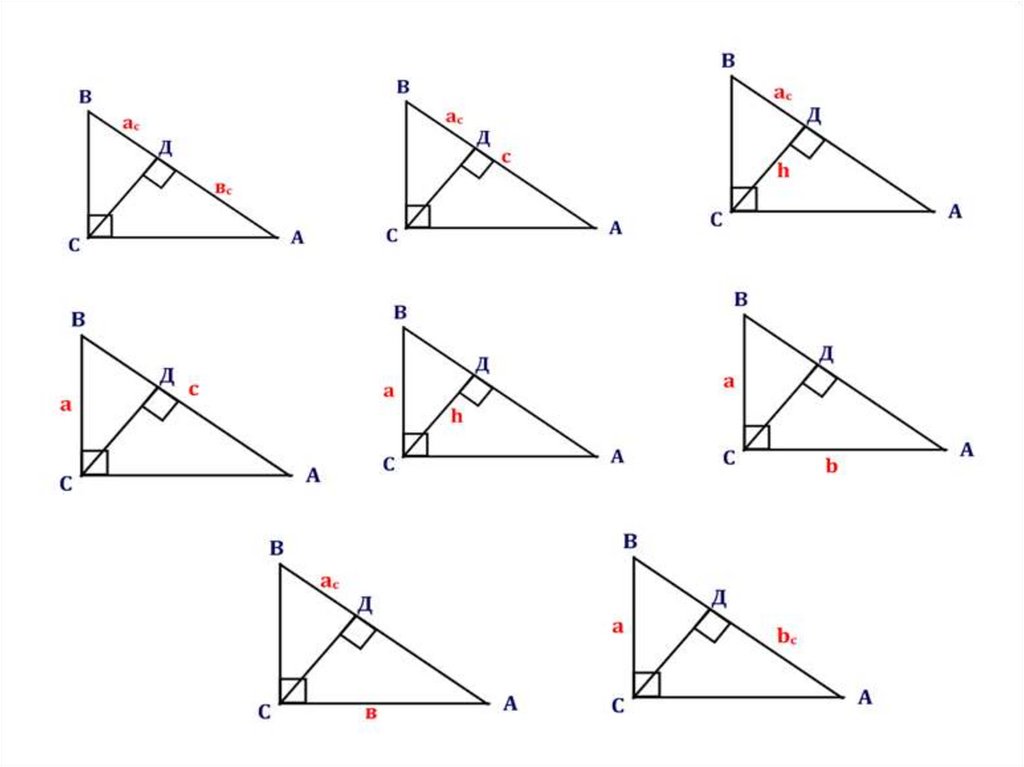
Новые понятияа - катет
b - катет
ас - проекция катета а на гипотенузу
bс - проекция катета b на гипотенузу
h - высота
26.
Физкультминутка.27.
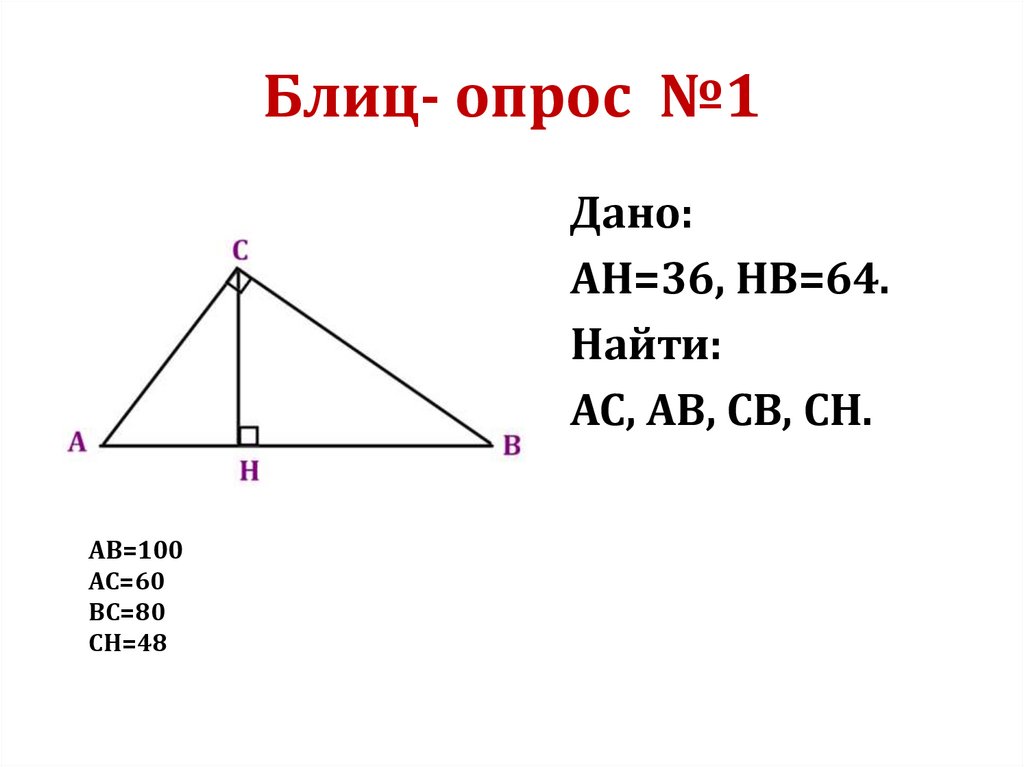
Блиц- опрос №1Дано:
АН=36, НВ=64.
Найти:
АС, АВ, СВ, СН.
АВ=100
АС=60
ВС=80
СН=48
28.
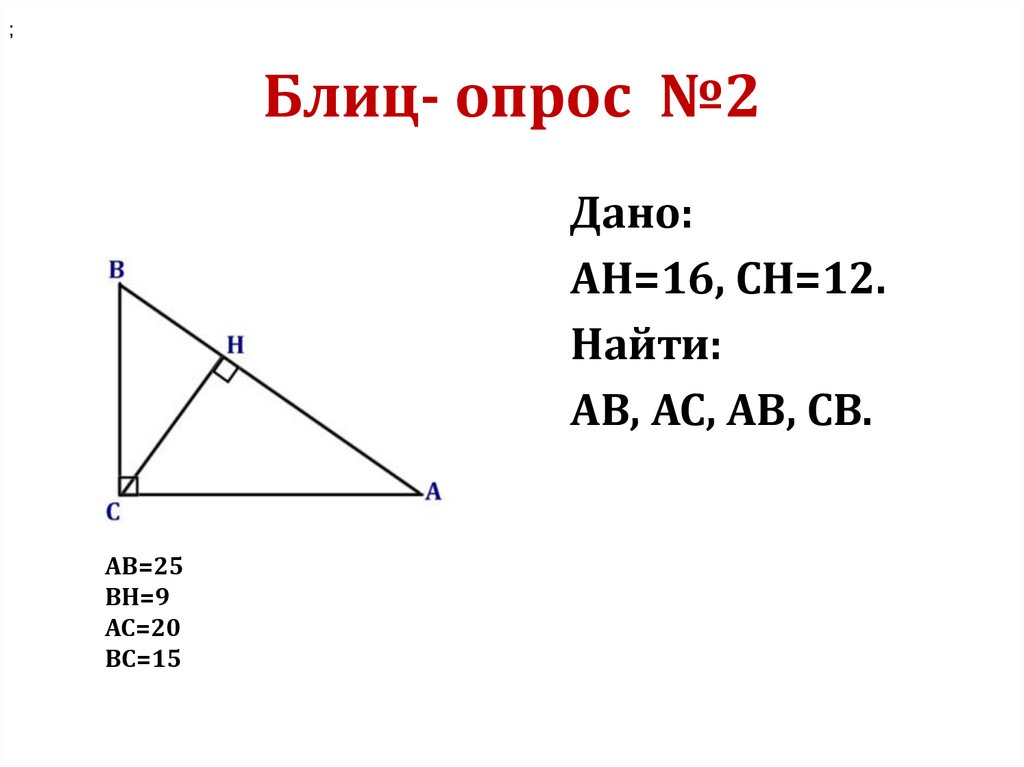
;Блиц- опрос №2
Дано:
АН=16, СН=12.
Найти:
АВ, АС, АВ, СВ.
АВ=25
ВН=9
АС=20
ВС=15
29.
Задание на дом.п.65. на стр. 146
Вопросы 10,11 на стр. 159
№№572, 573 на стр. 152
30.
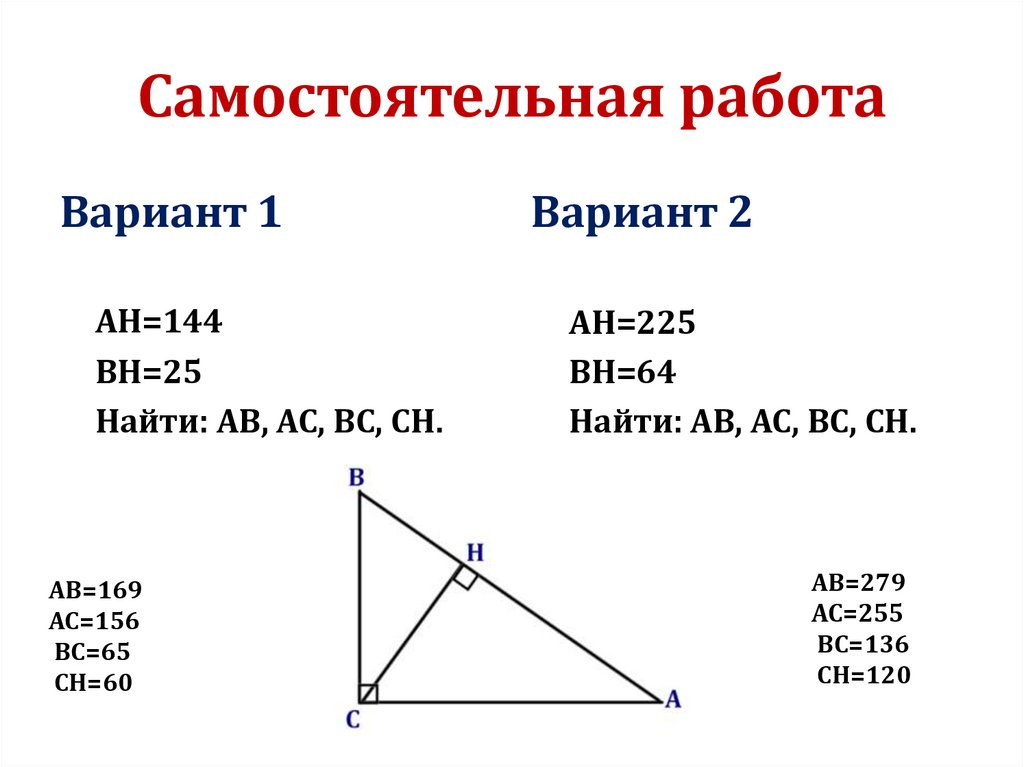
Самостоятельная работаВариант 1
АН=144
ВН=25
Найти: АВ, АС, ВС, СН.
АВ=169
АС=156
ВС=65
СН=60
Вариант 2
АН=225
ВН=64
Найти: АВ, АС, ВС, СН.
АВ=279
АС=255
ВС=136
СН=120
31.
Оцените свою работу на урокеКритерии оценивания:
"3"- 8-10 баллов
"4"- 11-13 баллов
"5"- 14 и более баллов
32.
33.
34.
35.
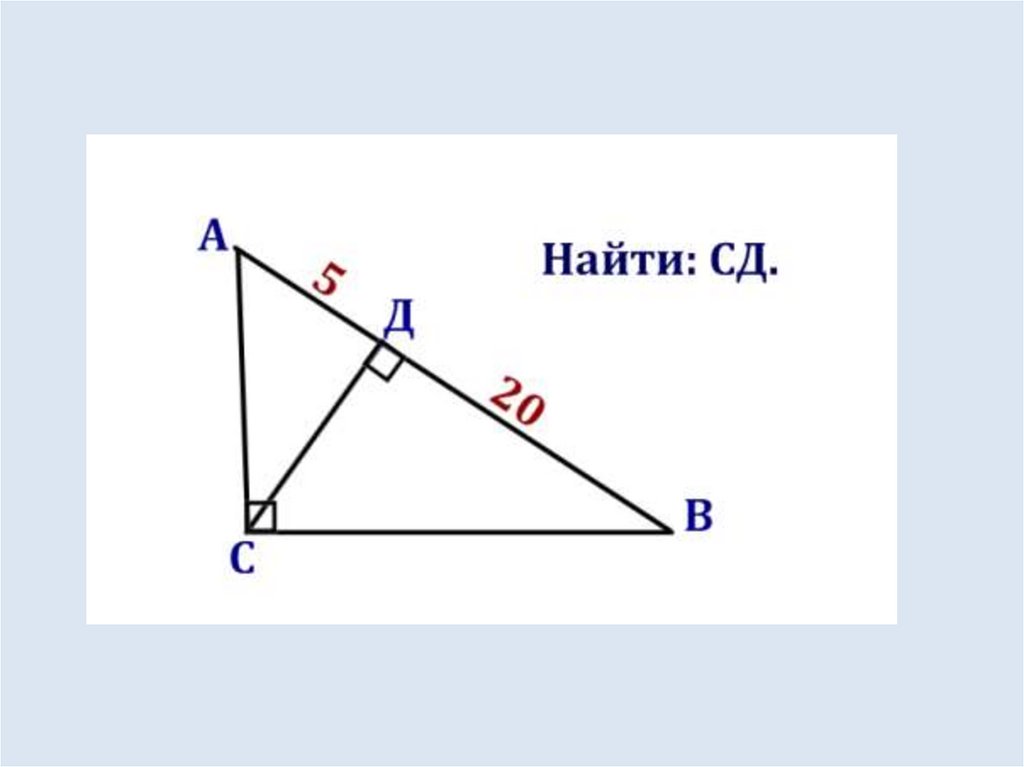
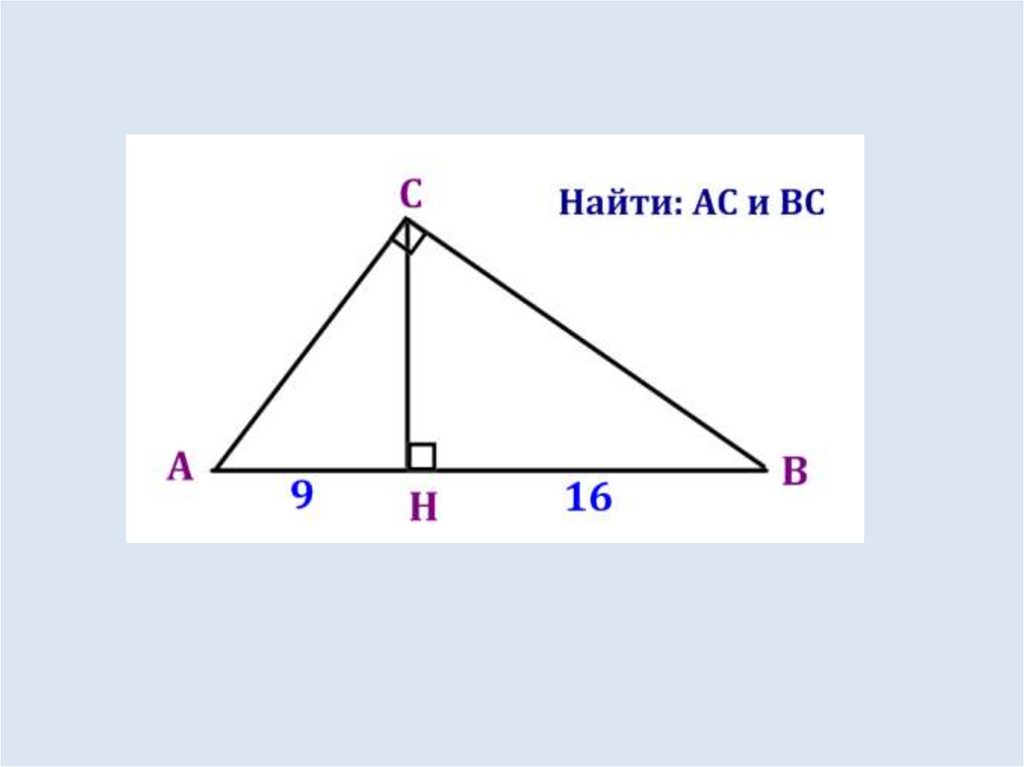
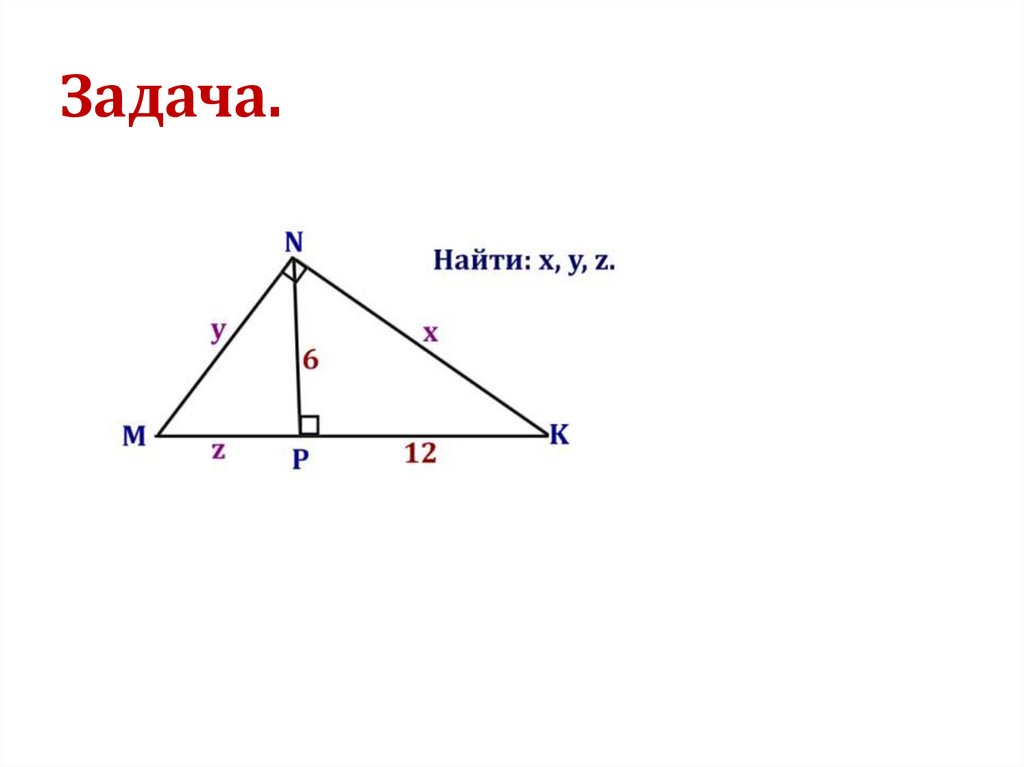
Задача.36.
Пропорциональныеотрезки в
прямоугольном
треугольнике.
Г-8
У-41




















 mathematics
mathematics








