Механическая работа и энергия

1.

МЕХАНИЧЕСКАЯ РАБОТА И ЭНЕРГИЯ
МЕХАНИЧЕСКАЯ РАБОТА
Работа - физическая величина, характеризующая процесс
превращения одной формы движения в другую.
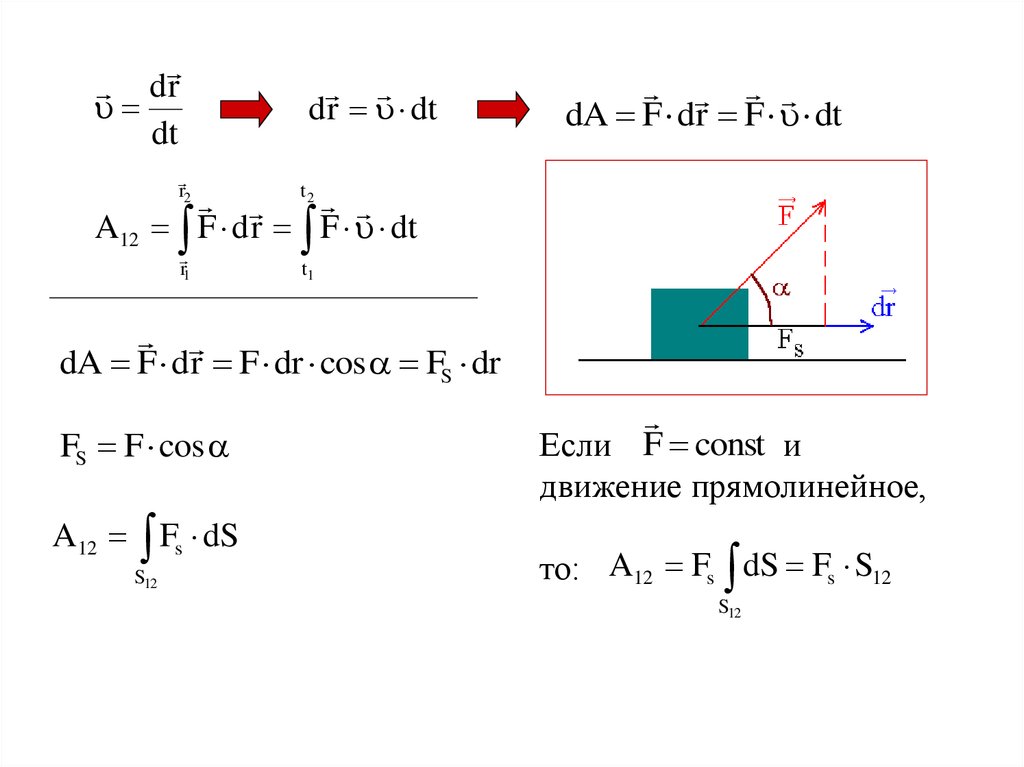
dA F dr
r2
A12 F d r
r1
[A] 1Н м 1Дж
Элементарная работа dA , совершаемая силой, равна скалярному
произведению силы F на элементарное перемещение точки
приложения силы
dr

2.

dr
dt
d r dt
dA F dr F dt
r2
t2
A12 F d r F dt
r1
t1
dA F dr F dr cos FS dr
FS F cos
A12 Fs dS
S12
Если F const и
движение прямолинейное,
то: A12 Fs dS Fs S12
S12

3.

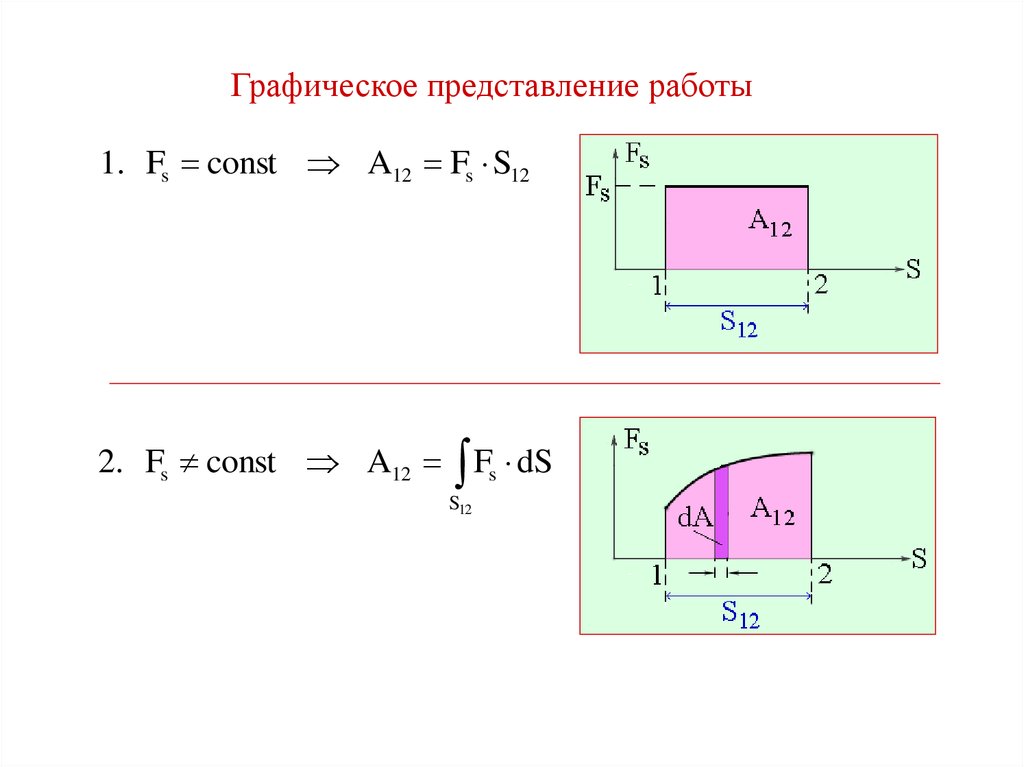
Графическое представление работы
1. Fs const A12 Fs S12
2. Fs const A12 Fs dS
S12

4.

Быстроту совершения работы характеризует мощность:
Мощность равна работе, совершаемой за единицу
времени.
A
N
Средняя мощность:
t
Мгновенная мощность:
1Дж
[ N]
1Вт
1с
dA
N
dt
dA F d r
N
F
dt
dt

5.

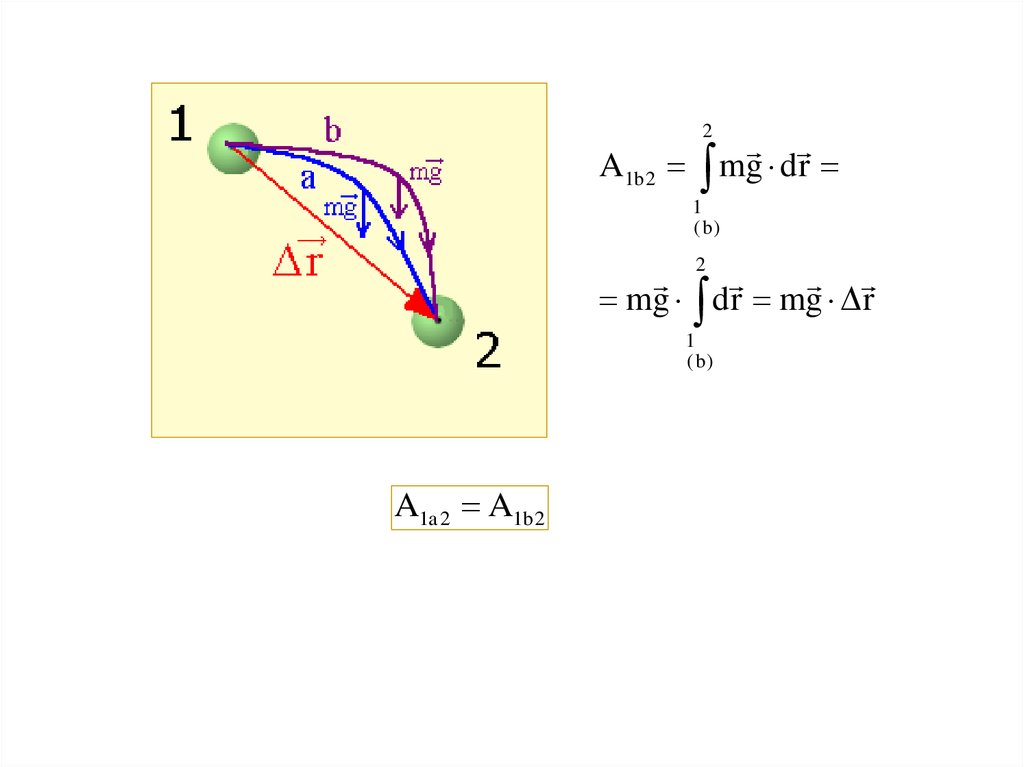
КОНСЕРВАТИВНЫЕ И НЕКОНСЕРВАТИВНЫЕ СИЛЫ
1. КОНСЕРВАТИВНЫЕ СИЛЫ (на примере силы тяжести)
Силы, работа которых не зависит
от формы пути, по которому
материальная точка переходит из
некоторого начального положения в
конечное,
называются
консервативными.
2
A1a 2 mg d r
1
(a )
2
mg d r mg r
1
(a )

6.

2
A1b 2
mg d r
1
(b)
2
mg d r mg r
1
(b)
A1a 2 A1b 2

7.

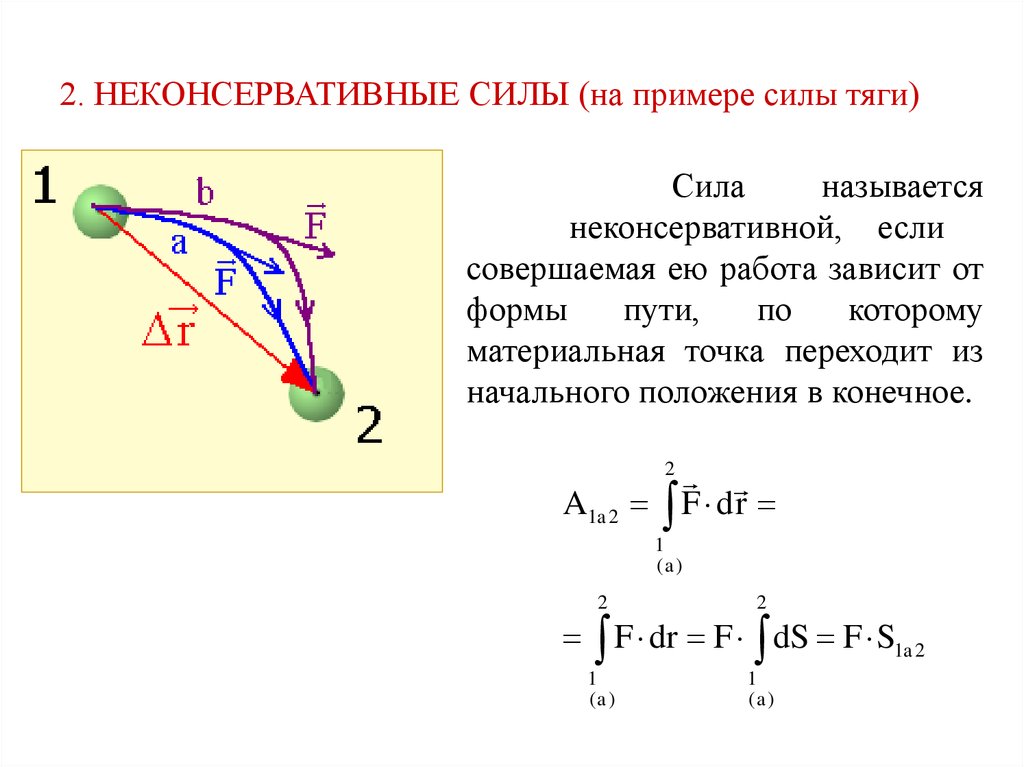
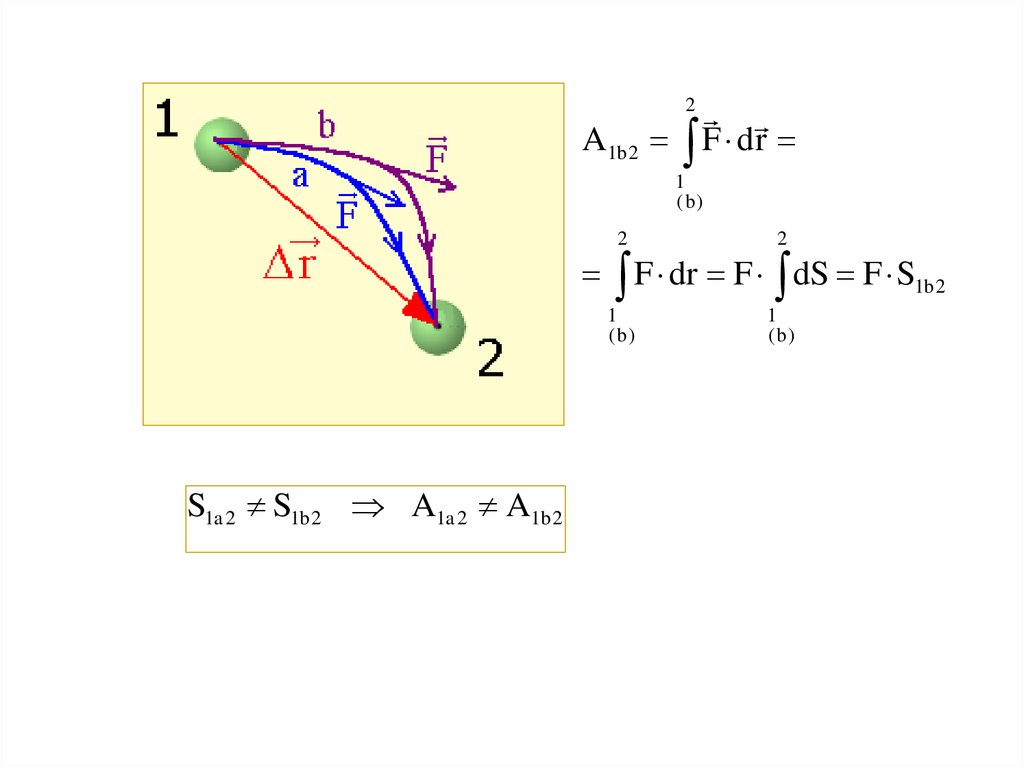
2. НЕКОНСЕРВАТИВНЫЕ СИЛЫ (на примере силы тяги)
Сила
называется
неконсервативной, если
совершаемая ею работа зависит от
формы
пути,
по
которому
материальная точка переходит из
начального положения в конечное.
F dr
2
A1a 2
1
(a )
2
2
1
(a )
1
(a )
F dr F dS F S1a 2

8.

F dr
2
A1b 2
1
(b)
2
2
1
(b)
1
(b)
F dr F dS F S1b 2
S1a 2 S1b 2 A1a 2 A1b 2

9.

ПОЛНАЯ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
Энергия - мера различных форм движения материи и типов
взаимодействия материальных объектов, являющаяся
однозначной, непрерывной, конечной, дифференцируемой
функцией состояния объекта (измеряется в Джоулях).
Функция состояния - это физическая характеристика
объекта, изменение которой при переходе объекта из одного
состояния в другое не зависит от траектории перехода, а
определяется параметрами начального и конечного
состояний.
Полная механическая энергия объекта является функцией
его скорости и координат :
E Eк Eп

10.

РАБОТА И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ПРИ
ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
Найдем работу силы F , под действием которой тело массой
m изменило свою скорость от 1 до 2 за время t.
d
dA F d r ; F m a; a
dt
d d r
dA m
m d m d
dt

11.

2
2 2
A dA m d m
2
1
1
m 22 m 12
2
2
m 2
Eк
кинетическая энергия
2
A E к 2 E к1 E к
Функция механического состояния, которая зависит от
массы материальной точки и квадрата её скорости и
приращение которой равно работе всех действующих на
точку сил, называется кинетической энергией точки

12.

РАБОТА И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ПРИ
ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
Представим твердое тело, имеющее ось вращения
Z, как систему материальных точек.
Для i-й точки (элемента): E к ,i
m R
i i i
2
2
E к ,i
n
Для тела:
E к E к ,i
i 1
2
mi i2 mi ( i R i ) 2
2
2
r r
1
2
1
2
2
1 2 n
I
m i R i2
2 i 1
2
I 2
Eк
2
... n
r
n

13.

Элементарная работа силы, действующей на твердое
тело при вращении его вокруг неподвижной оси равна
произведению момента этой силы относительно оси вращения
на элементарное угловое перемещение тела.
dA M
внешн.
d
При повороте на конечный угол:
2
.
A M внешн
d
1

14.

M z внеш. I ε z
d
εz
dt
dω
dA I
d I ω dω
dt
2
Jω 22 Jω12
A J ω dω
2
2
1
Это следует и из выражения: А =

15.

Качение тела.
Движение может быть представлено в виде суммы двух
движений: поступательного движения центра масс и
вращательного вокруг оси, проходящей через центр масс и
сохраняющей неизменную ориентацию в пространстве, тогда
кинетическая энергия такого движения равна сумме энергий
поступательного и вращательного движений:
m 2 I 2
Полная кинетическая энергия: E к
2
2

16.

СВОЙСТВА КИНЕТИЧЕСКОЙ ЭНЕРГИИ:
1. Это однозначная, конечная, непрерывная, дифференцируемая функция механического состояния объекта.
2. Она не может быть отрицательной.
3. Кинетическая энергия системы равна сумме кинетических
энергий отдельных тел.

17.

РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
A mg r

18.

A mg r cos
A mg (h1 h 2 ) mgh 1 mgh 2
E п mgh
A E п1 Е п 2 E п
Аналогично для силы упругости: A E п1 Е п 2 E п
k x
Eп
2
Функция механического состояния взаимодействующих тел
или их частей, зависящая от их координат, убыль которой равна
работе
консервативных
сил,
называется
взаимной
потенциальной энергией этих тел или их частей.
2

19.

СВОЙСТВА ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ:
1. Это однозначная, конечная, непрерывная, дифференцируемая функция механического состояния объекта.
2. Она может быть как положительной, так и отрицательной.
3. Потенциальная энергия характеризует оба взаимодействующих тела.
4. Числовое значение потенциальной энергии определяется с точностью до произвольной постоянной, зависящей от выбора нулевого уровня.

20.

СВЯЗЬ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ
С КОНСЕРВАТИВНОЙ СИЛОЙ
Если в каждой точке пространства на материальную точку
действует консервативная сила, то говорят, что точка находится в
потенциальном поле сил.
dA F d r F dr cos Fr dr
A E п1 Е п 2 E п
dA dE п
Fr dr dE п
dE п
Fr
dr
( 2)
(1)

21.

E п
Fx
x
F Fx i Fy j Fz k
Fy
E п
y
E п
Fz
z
E п E п E п
F
i
j
k
y
z
x
E п E п E п
grad E п
i
j
k
x
y
z
Градиент потенциальной энергии – вектор, указывающий
направление быстрейшего возрастания потенциальной энергии и
численно равный приращению энергии, приходящейся на
единицу длины этого направления.
F grad E п

22.

ЗАКОН СОХРАНЕНИЯ
ПОЛНОЙ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Механическая система называется замкнутой или
изолированной, если на нее не действуют внешние силы
(система не обменивается с внешними телами энергией).
Система называется незамкнутой, если на неё действуют
нескомпенсированные внешние силы.
Механическая система называется консервативной, если
на тела системы действуют только консервативные силы.
Рассмотрим механическую систему, тела которой
взаимодействуют как между собой, так и с внешними телами.
.
внешн.
внутр.
внешн.
dE к dAвнутр
dA
dA
dA
к
к
нк
нк
.
внешн.
dAвнутр
dA
dE п
к
к
.
внешн.
dAвнутр
dA
dAнк
нк
нк

23.

dE к dAнк dE п
dE к dE п dAнк
Приращение полной механической
энергии системы: dE dA нк
dE dA
нк
E Aнк
Приращение механической энергии системы материальных
точек равно алгебраической сумме работ всех внутренних и
внешних неконсервативных сил, действующих на точки
системы.

24.

Если Анк = 0, то Е = const
Полная механическая энергия системы сохраняется, если силы,
действующие на тела системы, являются консервативными –
закон сохранения механической энергии.

25.

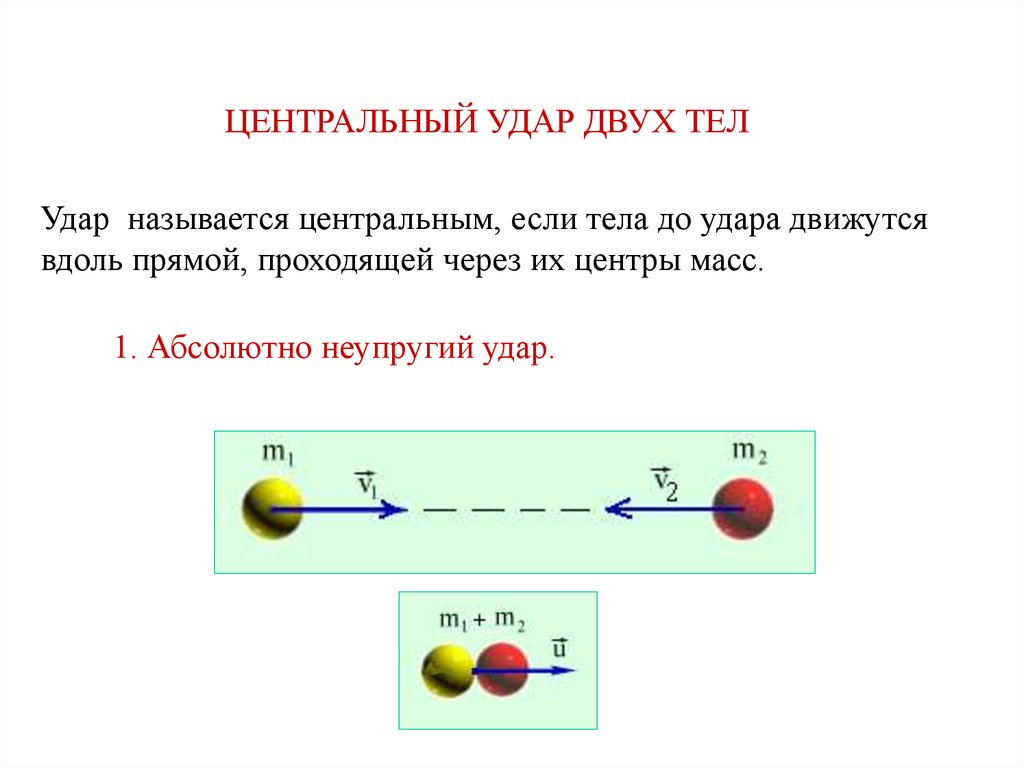
ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ
Удар называется центральным, если тела до удара движутся
вдоль прямой, проходящей через их центры масс.
1. Абсолютно неупругий удар.

26.

Кинетическая энергия относительного движения тел на
короткое время преобразуется в энергию упругой деформации.
Абсолютно неупругий удар – столкновение тел, в результате
которого тела объединяются, двигаясь дальше как единое
целое.

27.

m1 1 m2 2 m1 m2 u
m
m
2 2
u 1 1
m1 m 2
m1 12 m 2 22 (m1 m 2 ) u
Q
2
2
2
2
Кинетическая энергия переходит в тепловую или другие формы
энергии.

28.

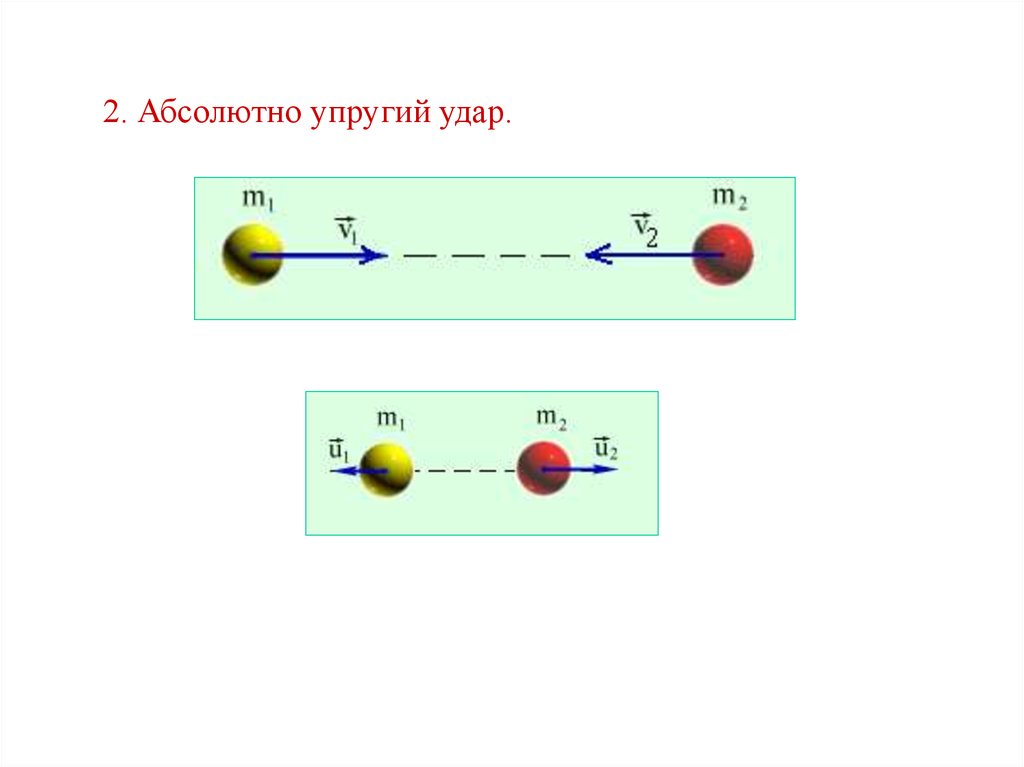
2. Абсолютно упругий удар.

29.

Абсолютно упругий удар – столкновение тел, в результате
которого в обоих взаимодействующих телах не остается
никаких деформаций и вся кинетическая энергия , которой
обладали тела до удара, после удара снова превращается в
кинетическую энергию.

30.

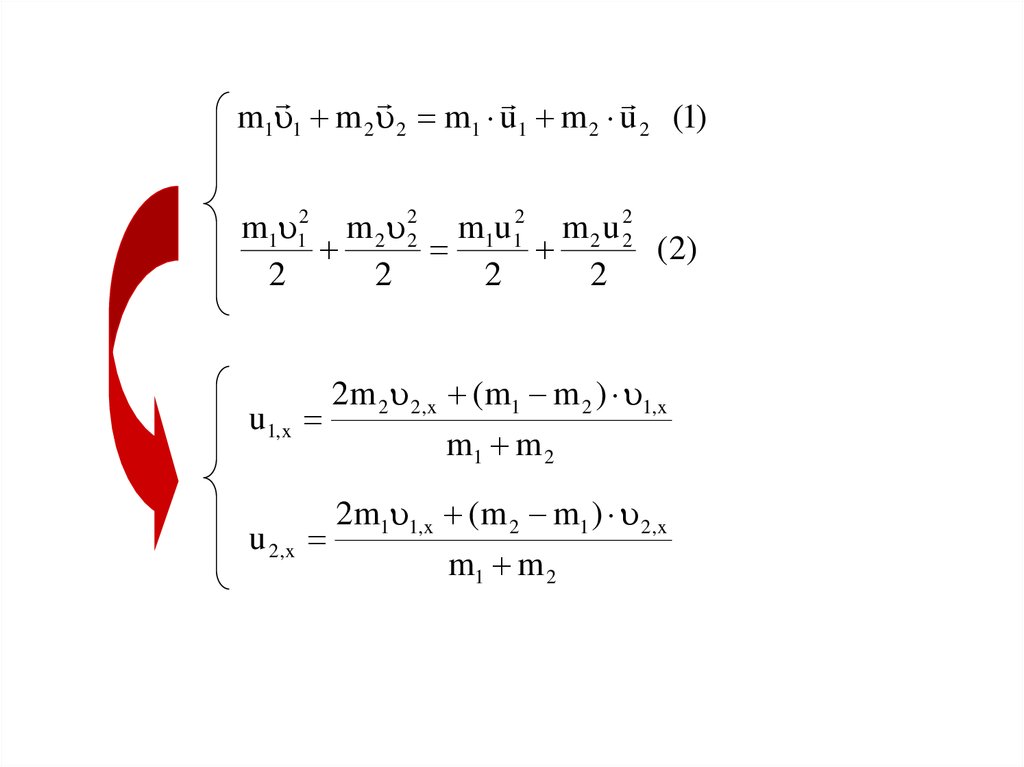
m1 1 m 2 2 m1 u1 m 2 u 2 (1)
m1 12 m 2 22 m1u12 m 2 u 22
( 2)
2
2
2
2
u1,x
2m 2 2,x (m1 m 2 ) 1,x
m1 m 2
u 2,x
2m1 1,x (m 2 m1 ) 2,x
m1 m 2