Similar presentations:
Механическая работа и энергия
1.
2. План лекции 4.1. Механическая работа и мощность. 4.2. Консервативные и неконсервативные силы. 4.3. Полная механическая энергия.
Тема 4. МЕХАНИЧЕСКАЯРАБОТА И ЭНЕРГИЯ
План лекции
4.1. Механическая работа и мощность.
4.2. Консервативные и неконсервативные силы.
4.3. Полная механическая энергия.
4.4. Кинетическая энергия и её связь с работой.
4.5. Потенциальная энергия и её связь с работой.
4.6. Связь потенциальной энергии с консервативной
силой.
3. 4.1. Механическая работа
Опыт показывает, что различные формы движенияматерии способны к взаимным превращениям.
В тепловой машине хаотическое молекулярное
движение превращается (частично) в упорядоченное
механическое.
При движении с трением механическое движение
превращается в хаотическое молекулярное.
4.
Установлено, что все взаимные превращенияразличных форм движения материи происходят в
строго определенных количественных соотношениях.
«Исчезновение» одной формы движения всегда
сопровождается «возникновением» эквивалентного
количества движения другой формы.
Работа – это физическая величина,
характеризующая процесс превращения одной
формы движения в другую.
5.
В механике принято говорить, что работасовершается силой, поскольку наличие силы,
наличие взаимодействия тел является необходимым
признаком работы.
Работа – скалярная величина, измеряемая в
джоулях (Дж).
Существуют понятия: элементарная работа силы и
полная работа силы.
6.
Элементарная работа силы равна скалярномупроизведению силы
на элементарное
F
перемещение dr точки приложения силы
dA F d r
Полная работа при конечном перемещении равна
алгебраической сумме элементарных работ и
определяется интегралом
r
2
A12
r1
r1
F dr
r2 – радиус-векторы начального и
и
конечного положения точки приложения силы.
7.
Выразим элементарное перемещение черезмгновенную скорость :
d r v dt
Тогда
dA (F v) dt
Интегрируя по времени, получим работу силы за
конечный промежуток времени
:
Δt t 2 t1
(F v) dt
t2
A 12
t1
8.
Распишем скалярное произведение(Fd r ) F d r cosα
И учтём, что
dr dS
.
Тогда элементарная работа силы запишется как
dA F dS cosα
α – угол между направлением силы и направлением
движения в каждой точке.
9.
Обозначим проекцию силы на направление движения:F cosα FS
В ряде случаев приведенные интегралы вычисляются
просто.
Так, если в процессе перемещения сила не
изменяется и движение является
прямолинейным, то
A12 FS dS FS S12 FS cos
S12
10.
1. Работа силы тяжести:Amg mg s cos 90O 0
2. Работа силы реакции опоры: A N N s cos 90O 0
O
A
F
s
cos
180
FТР s
3. Работа силы трения: ТР
ТР
4. Работа силы F:
AF FScos
11.
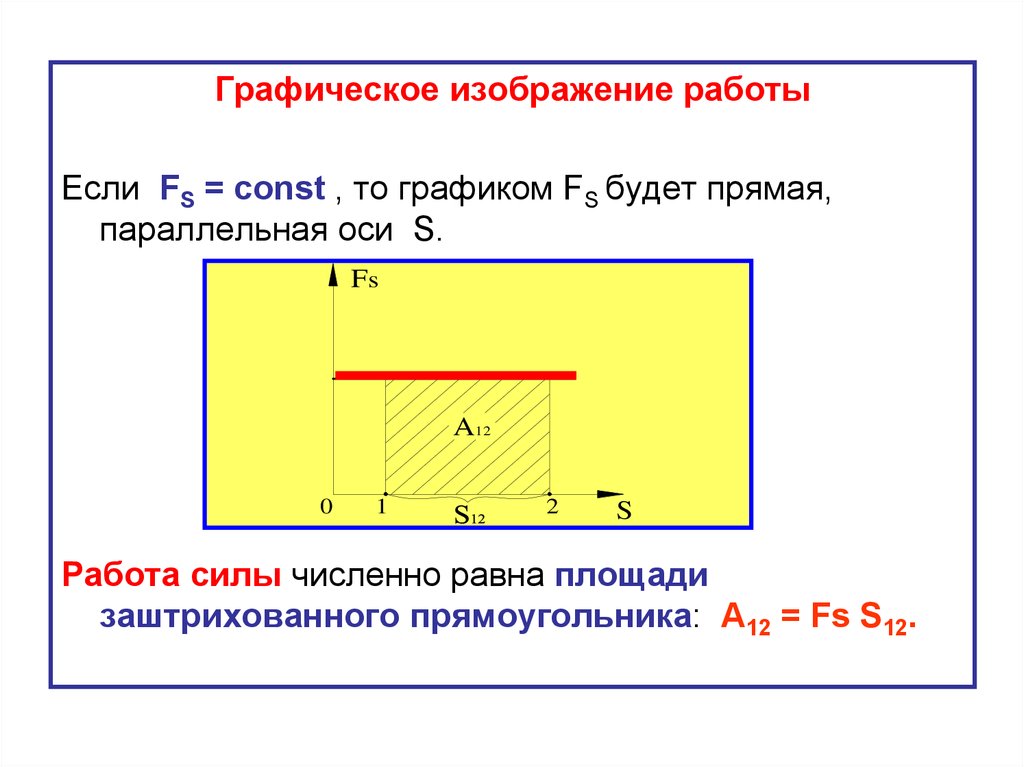
Графическое изображение работыЕсли FS = const , то графиком FS будет прямая,
параллельная оси S.
Fs
A12
0
1
2
S
Работа силы численно равна площади
заштрихованного прямоугольника: A12 = Fs S12.
12.
Если FS ≠ const, то графиком FS будет некотораякривая.
Fs
dA
A12
0
S
Элементарная работа dA равна площади узкой
полоски.
Полная работа силы на пути в этом случае равна
заштрихованной под графиком F(S) площади
криволинейной трапеции:
A 12
F
S
S1 2
dS
13.
14.
Работа силы тяжестиПусть материальная точка с массой m переместилась
по произвольной траектории из точки 1 в точку 2,
отстоящих от поверхности Земли соответственно на
расстояниях h1 и h2
15.
Вычислимработу силы тяжести mg на перемещении
Δr
r2
r2
A (mg d r ) mg d r (mg Δ r )
r1
r1
Сделаем дальнейшие преобразования:
A (mg Δ r ) mg Δ r cosα
mg Δ r mg
16.
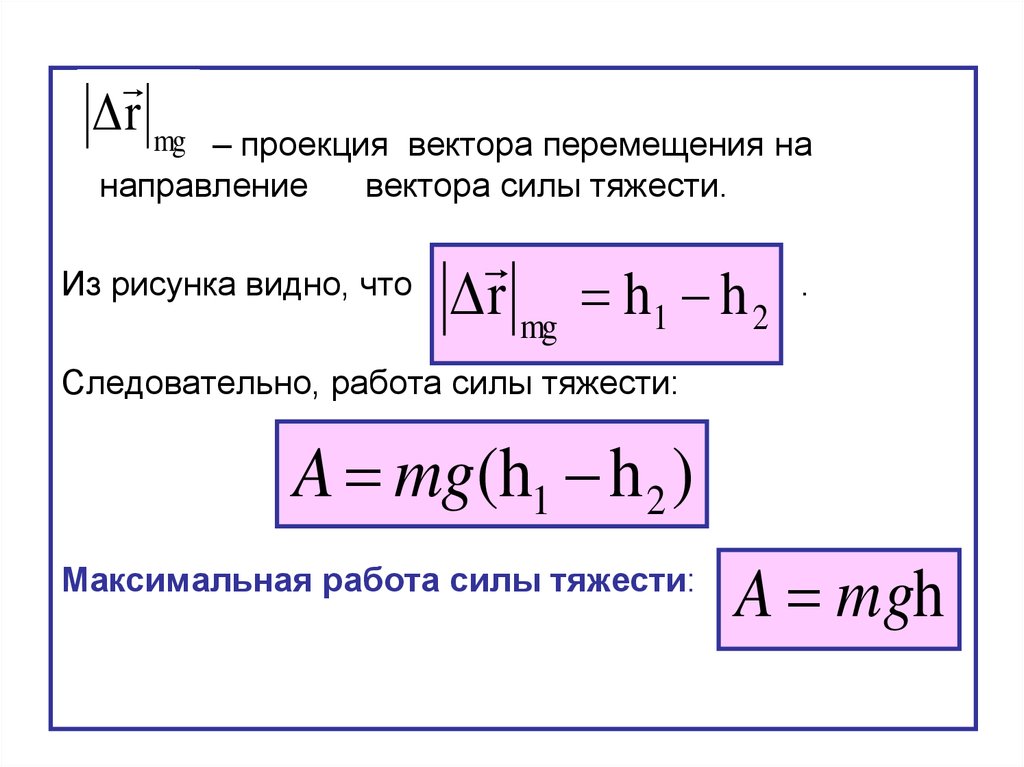
Δ r mg– проекция вектора перемещения на
направление
вектора силы тяжести.
Из рисунка видно, что
Δ r mg h1 h 2
.
Следовательно, работа силы тяжести:
A mg(h1 h 2 )
Максимальная работа силы тяжести:
A mgh
17.
Работа гравитационной силыРабота гравитационной силы вычисляется при
r2
вычислении интеграла
A (Fãð d r )
r1
при подстановки формулы гравитационной силы
GmM
F
2
r
r - расстояние между центрами тяжести тел.
Максимальная работа гравитационной силы:
G mM
A
r
18.
Работа силы упругостиПусть пружина деформирована.
х – абсолютное удлинение, k – жесткость пружины
По закону Гука:
Fóïð k x
19.
Вычислим интеграл.x2
x2
2
1
2
2
x x
A (k x dx) k (x dx) k ( )
2 2
x1
x1
Работа упругой силы не зависит от того как произошло
изменение длины пружины: быстро или медленно,
равномерно или с остановками. Она определяется
только начальной и конечной деформацией
пружины.
Максимальная работа упругой силы:
A
k x2
2
20.
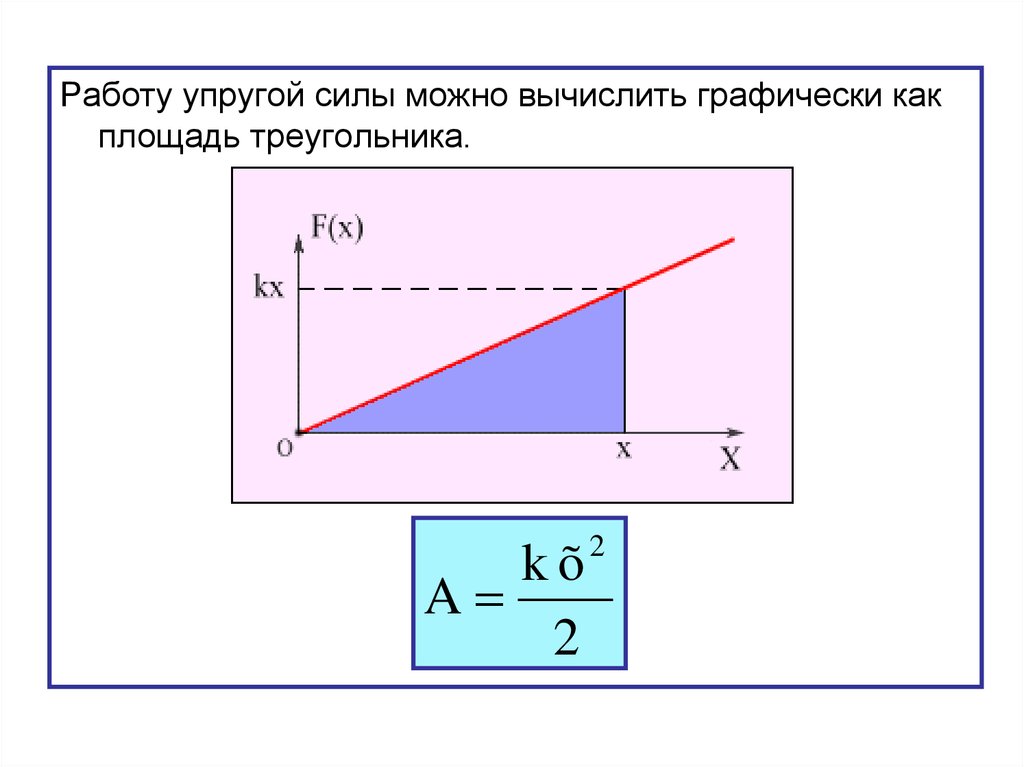
Работу упругой силы можно вычислить графически какплощадь треугольника.
kõ
A
2
2
21.
Мощность:- характеризует быстроту совершения работы;
- равна работе, совершаемой за единицу времени;
- величина скалярная, измеряемая в Вт (ваттах).
Различают среднюю и мгновенную мощность,если
совершаемая силой работа зависит от времени.
22.
Средняя мощность за промежуток времени Δtравна работе силы, совершённой за единицу
времени.
A
N
Δt
Мгновенная мощность – это мощность в данный
момент времени.
Она равна первой производной от работы по
времени.
dA
N
dt
23.
Учитывая, чтополучим
dA (F d r )
dr
v
dt
N (F v)
Мгновенная мощность равна скалярному
произведению силы на скорость.
24. 4.2. Консервативные и неконсервативные силы
Консервативными называются силы,работа которых:
- не зависит от формы пути, по которому
материальная точка переходит из некоторого
начального положения в конечное.
- по замкнутой траектории равна нулю.
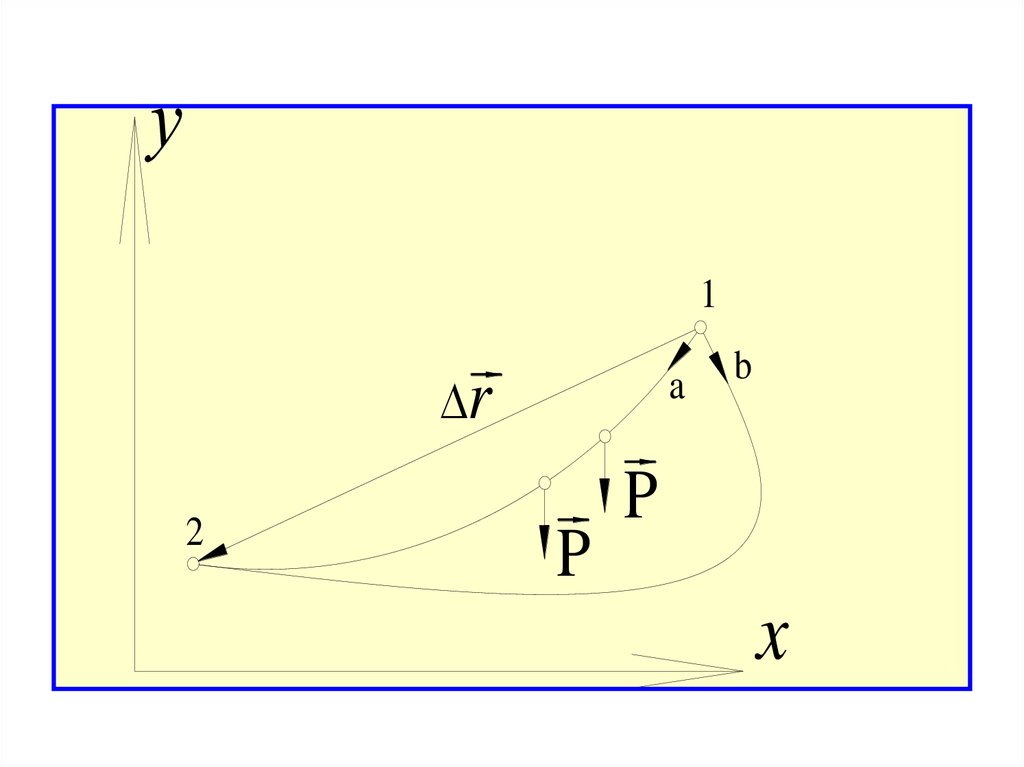
Найдём работу силы тяжести при перемещении
материальной точки из положения 1 в положение 2
по двум разным траекториям S1а2 и
S1б2
25.
1r
2
a
P
b
P
x
26.
Искомые работы соответственно равны2
2
A1a2
(mg d r )
и
A1b2
(mg d r )
1
1
b
(a)
Будем считать, что сила mg
одинакова во всех
точках рассматриваемой области пространства.
Вынесем mg за знаки интегралов.
A1a2
2
mg d r
1
и
A1b2
1
(a)
A1a2 mg Δr
2
mg d r
(b)
A1b2
mg Δ r
27.
Получили, что , двигаясь из положения 1 в положение 2по разным траектории 1а2 и 1б2, точка совершает
одно и то же перемещение Δ r
,
следовательно, работы одинаковы:
А1a2 = А1b2.
Таким образом, сила тяжести – консервативная сила.
Консервативными являются:
- гравитационная сила
- сила упругости
- электрическая сила
28.
Неконсервативной называется сила, работа которой зависитот формы пути, по которому материальная точка переходит
из начального положения в конечное.
Найдем работу силы трения, действующей на тело
при перемещении его из точки 1 в точку 2 по
горизонтальной поверхности по двум разным путям
S1a2 и S1b2 .
2тр
r
a
S1a2
тр
S1b2
Fòð
Fòð
b
29.
Искомые значения работ соответственно равны:2
2
A1b2 (Fтр d r )
A1a2 (Fтр d r )
1
(a)
1
(b)
Направление силы трения в процессе перемещения
тела изменяется, поэтому F выносить за знак
тр
интеграла нельзя.
Но проекцию силы трения на перемещение можно
вынести за знак интеграла, так как её значение
одинаково во всех точках траектории.
30.
2À1a2 Fòð
d r cos π
1
a
2
Fòð
dr
1
a
2
Fòð
dS
F
S
òð
1a2
1
a
31.
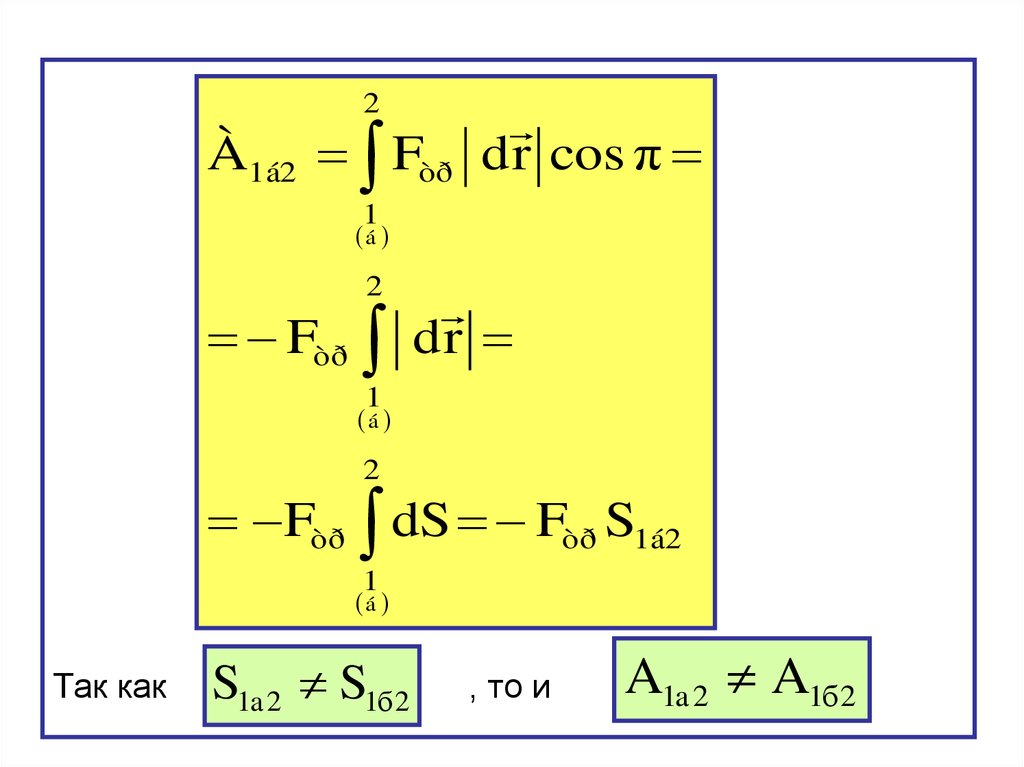
2À1á2 Fòð
d r cos π
1
á
2
Fòð
dr
1
á
2
Fòð dS Fòð S1á2
1
á
Так как
S1a 2 S1б 2
, то и
A1a 2 A1б 2
32.
Неконсервативными являются:- сила трения
- магнитные силы Ампера и Лоренца
- сила давления
Потенциальным называется силовое поле, в
котором действуют консервативные силы.
К потенциальным полям относится гравитационное и
электростатическое поле.
Вихревым называется силовое поле, в котором
действуют неконсервативные силы.
К вихревым полям относится магнитное поле.
33. 4.3. Полная механическая энергия
Способность различных форм движения к взаимнымпревращениям привели к мысли о том, что должна
существовать единая мера различных форм
движения.
Эта мера характеризует любое движение с точки
зрения возможностей превращения его в другие
формы.
Полная механическая энергия – единая мера
различных форм движения материи и типов
взаимодействия материальных объектов.
34.
Полная механическая энергия являетсяоднозначной, непрерывной, конечной,
дифференцируемой функцией механического
состояния объекта.
Функция состояния – такая физическая
характеристика объекта, изменение которой при
переходе объекта из одного состояния в другое
не зависит от пути перехода и целиком
определяется параметрами начального и
конечного состояний.
35.
Материальные объекты:- могут участвовать в разных взаимодействиях;
- могут участвовать в различных формах движения;
- могут перемещаться в пространстве;
- в них могут происходить различные процессы
(молекулярные, электромагнитные, ядерные и др.).
Обычно изменения, обусловленные участием объекта в
различных типах взаимодействий и формах
движения, рассматривают отдельно.
В связи с этим энергию определяют как сумму
нескольких слагаемых, каждое из которых зависит
только от одного или двух параметров.
36.
Полная механическая энергияМеханическое состояние объекта характеризуется
двумя параметрами – радиус-векторами
материальных точек, из которых он состоит, и их
скоростями (импульсами).
Поэтому полная механическая энергия объекта
является функцией координат и скоростей
материальных точек.
Кинетическая энергия определяется скоростями
точек объекта.
Потенциальная энергия зависит от их координат.
37.
Полная механическая энергия равна суммекинетической энергии взаимодействия частей
тела и потенциальной энергии взаимодействия
тела с внешними телами.
E EK En
38. 4.4. Кинетическая энергия и её связь с работой
Пусть на материальную точку с массой m действуетсила
F .
Найдем работу этой силы за время, в течение которого
модуль скорости точки изменяется от v1 до v2.
Элементарная работа силы
F
равна
A F dr
39.
Преобразуем это выражение:dA F d r m (a d r )
dv
m d r m (v dv)
dt
v
Найдем скалярное произведение вектора скорости v
на его приращение dv
.
40.
v dv v dv cos αгде α – угол между векторами
v и dv
Поскольку угол между векторами
то
.
v и dv
v dv v dv
,
.
Тогда элементарная работа запишется как
dA m v dv
равен 00,
41.
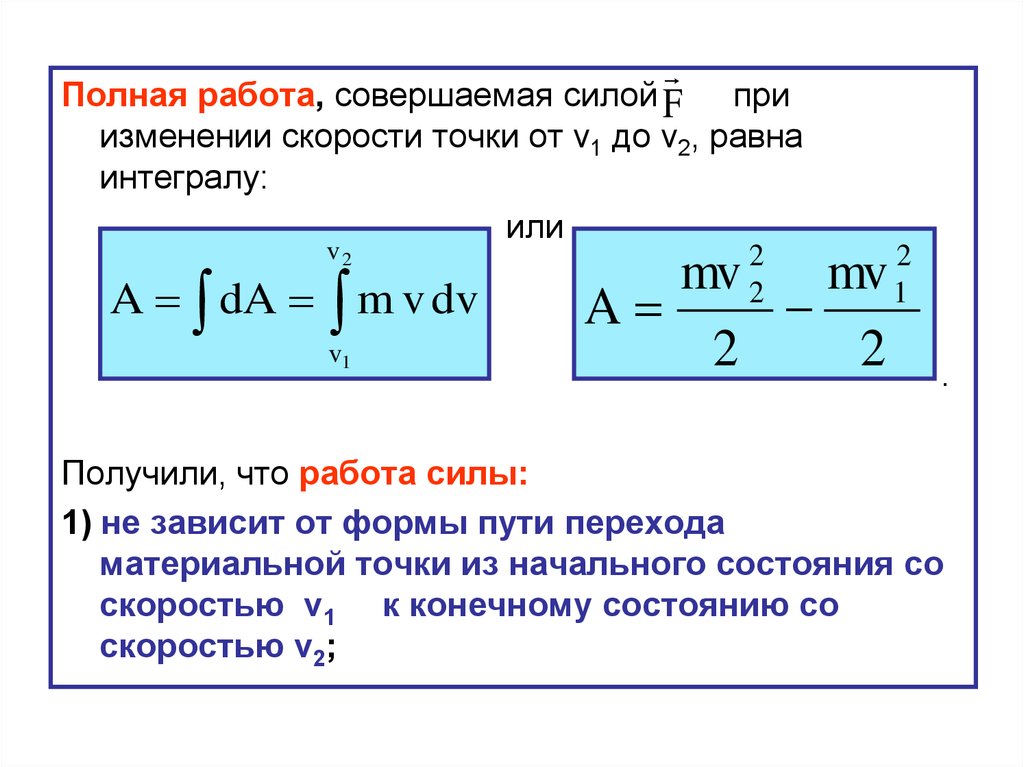
Полная работа, совершаемая силой Fпри
изменении скорости точки от v1 до v2, равна
интегралу:
или
v2
A dA m v dv
v1
2
2
mv
mv
A
2
2
2
1
.
Получили, что работа силы:
1) не зависит от формы пути перехода
материальной точки из начального состояния со
скоростью v1 к конечному состоянию со
скоростью v2;
42.
2) не зависит от способов, посредством которыхбыло достигнуто данное изменение скорости;
3) не зависит от того, каковы были промежуточные
состояния:
а) быстро или медленно изменялась скорость,
б) постоянная или переменная сила действовала на
точку,
в) по прямолинейной или криволинейной траектории она
перемещалась.
mv 22 mv 12
Величина
есть приращение
2
2
некоторой функции ЕК механического состояния
точки, зависящей от скорости.
43.
22
2
1
mv
mv
A
E K (v 2 ) E K (v1 )
2
2
Кинетическая энергия определяется формулой:
EK
mv
2
2
Изменение кинетической энергии равно работе
силы:
ΔΕ K A
44.
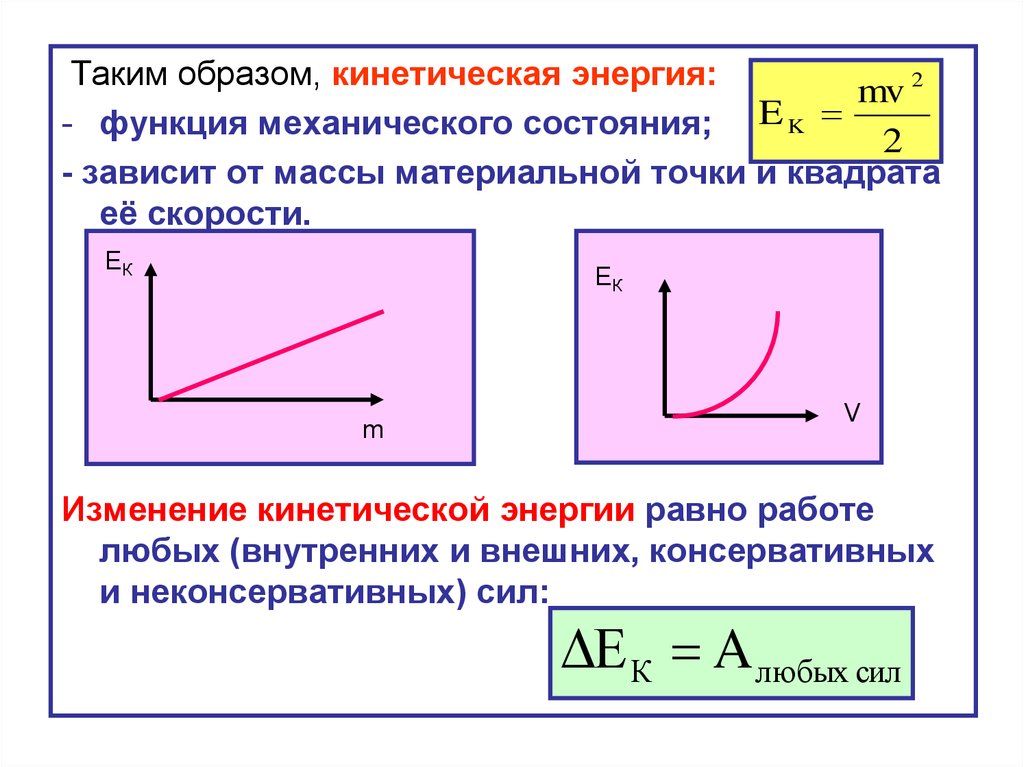
Таким образом, кинетическая энергия:mv 2
- функция механического состояния; E K
2
- зависит от массы материальной точки и квадрата
её скорости.
ЕК
ЕК
m
V
Изменение кинетической энергии равно работе
любых (внутренних и внешних, консервативных
и неконсервативных) сил:
ΔΕ К A любых сил
45.
Кинетическая энергия при вращательном движенииНайдем работу, совершаемую внешней силой при
повороте твердого тела на некоторый угол вокруг
неподвижной оси.
d
F
d
r +dr
r
dr
46.
Элементарная работа силытело, равна
F
, действующей на
dA F d r F d r cosα
Fτ d r
F
α – угол между векторами
и dr .
Fτ проекция вектора силы F на направление
вектора dr .
dr dS r d
47.
ТогдаdA Fτ r d
или
dA M z d
Mz – момент силы
относительно оси Z, совпадающей
с направлением углового перемещения.
Если угол – острый:
cos
Если угол – тупой:
cos
F 0, то и Мz 0,
F , то и Mz .
48.
dA Mz dЭлементарная работа силы при вращательном
движении равна скалярному произведению
момента этой силы относительно оси вращения
на элементарное угловое перемещение тела.
Полная работа силы при повороте тела на конечный
угол:
2
A M z d
1
49.
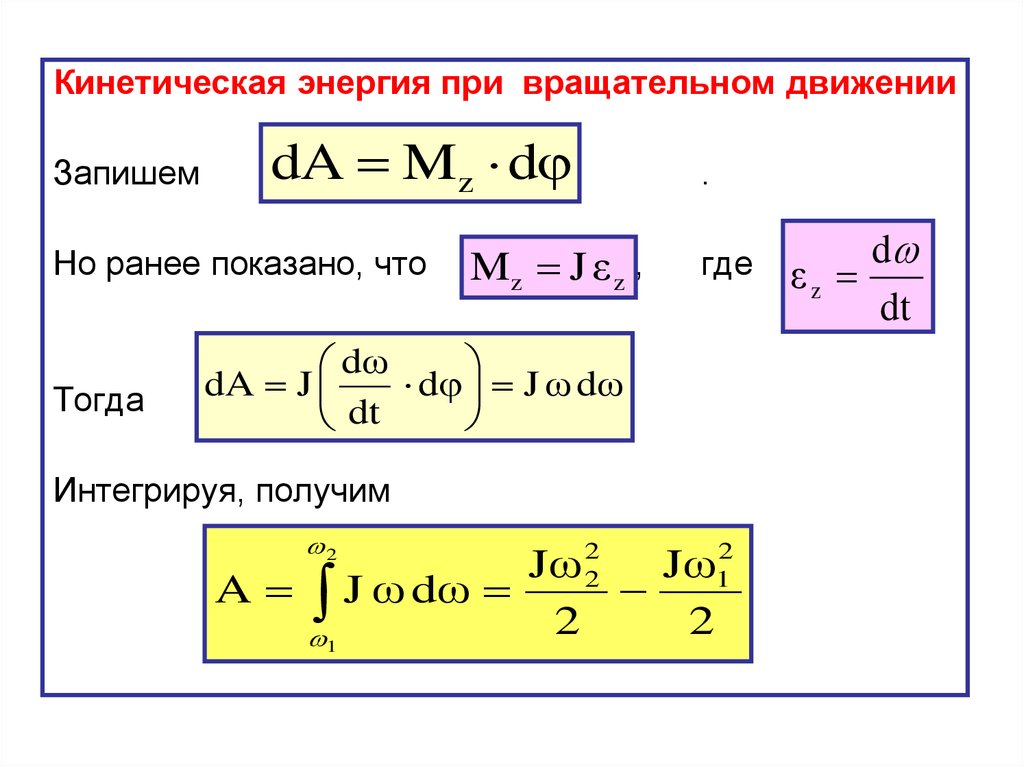
Кинетическая энергия при вращательном движенииЗапишем
dA Mz d
Но ранее показано, что
Тогда
Mz J ε z ,
.
где
dω
dA J
d J ω dω
dt
Интегрируя, получим
2
Jω 22
Jω12
A J ω dω
2
2
1
d
εz
dt
50.
Как показано ранее, работа всех действующих натело сил, равна изменению кинетической энергии
этого тела: А = .
Поэтому выражение
Jω
EK
2
2
представляет
собой
кинетическую
энергию
вращательного движения твердого тела.
Эту формулу можно получить иначе.
51.
Кинетическая энергия, которой обладает тело,складывается из кинетических энергий отдельных
его точек.
Разобьем вращающееся тело на элементы массой
dm, отстоящие на расстоянии r от оси вращения.
Тогда кинетическая энергия каждого элемента равна
dE K(âð)
dm v
2
2
52.
Так както
v = ω r,
dm ω r
2
2 2
dE K(вр)
.
Кинетическая энергия всего тела найдется
интегральным суммированием:
ω
ω
2
2
E K(âð) dE K(âð) dm r dm r
2
2
2
2
53.
выражениетела
J dm r
2
– есть момент инерции
Тогда для кинетической энергии вращательного
движения получаем выражение:
ЕК
E K(вр)
Jω
2
2
J
ЕК
.
w
54.
Если тело одновременно движется поступательно ивращается вокруг оси, проходящей через центр масс
и сохраняющей неизменную ориентацию в
пространстве, то кинетическая энергия такого
движения равна сумме энергий поступательного и
вращательного движений:
mv
Jω
EK
2
2
2
2
55.
Свойства кинетической энергии1. Кинетическая энергия – однозначная, конечная,
непрерывная, дифференцируемая функция
механического состояния объекта.
2. Кинетическая энергия не может быть
отрицательной.
3. Кинетическая энергия – величина аддитивная:
кинетическая энергия системы тел равна сумме
кинетических энергий отдельных тел.
56.
.4 Изменение кинетической энергии равно работе
всех действующих на тело сил – и
консервативных и неконсервативных.
Если работа сил положительна, то кинетическая
энергия тела возрастает, если отрицательна –
уменьшается.
5. Тело, обладающее кинетической энергией,
способно совершить работу.
57. 4.6. Потенциальная энергия и её связь с работой
Потенциальная энергия – это энергиявзаимодействия тел.
Взаимодействие может быть разным: гравитационным,
электромагнитным и т. д.
Потенциальная энергия равна максимальной
работе соответствующих сил в данных
конкретных условиях.
Потенциальная энергия тела, поднятого над
землёй) определяется формулой:
EП mqh
58.
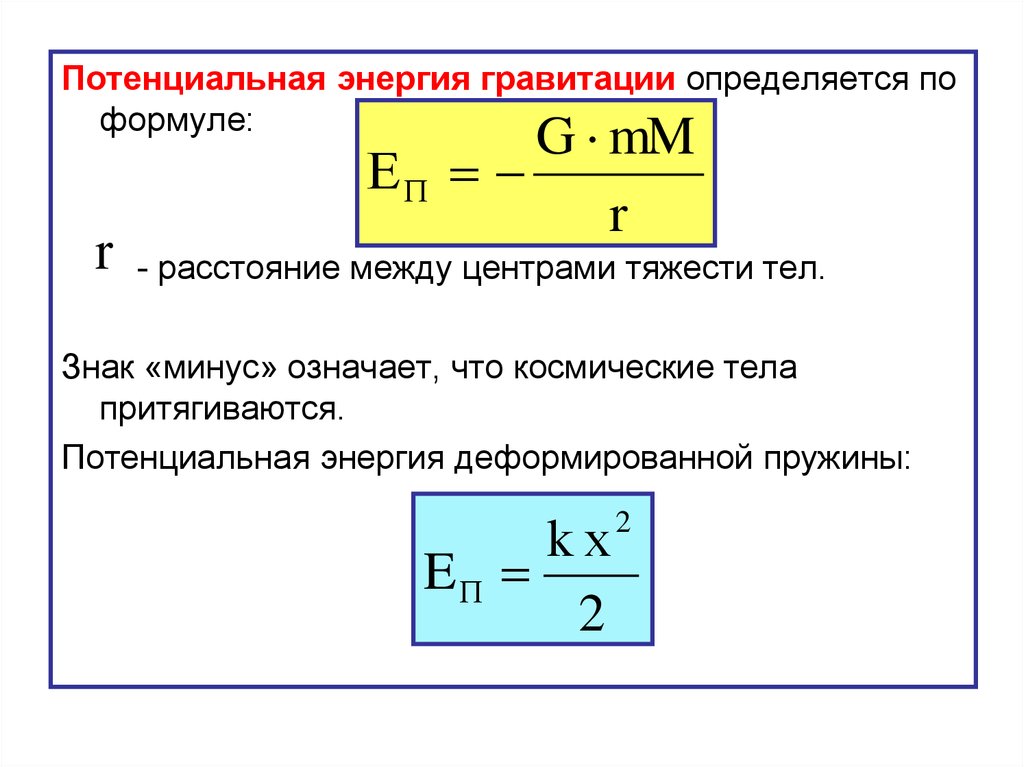
Потенциальная энергия гравитации определяется поформуле:
r
G mM
ЕП
r
- расстояние между центрами тяжести тел.
Знак «минус» означает, что космические тела
притягиваются.
Потенциальная энергия деформированной пружины:
kх
EП
2
2
59.
Свойства потенциальной энергии1. Потенциальная энергия – однозначная, конечная,
непрерывная, дифференцируемая функция
состояния механического объекта.
2. Потенциальная энергия может быть только
взаимной. Она в одинаковой степени
характеризует оба взаимодействующих тела.
3. Числовое значение потенциальной энергии
определяется с точностью до произвольной
постоянной, значение которой зависит от
выбора нулевого уровня (начала отсчета)
потенциальной энергии.
Нулевой уровень можно выбирается на бесконечном
расстоянии между телами, т.е. там, где сила их
взаимодействия равна нулю.
60.
4. Потенциальная энергия может иметь какположительное, так и отрицательное значение.
5. Состояние взаимодействующих тел можно
охарактеризовать потенциальной энергией
только в том случае, если между телами
действуют консервативные силы.
6. Изменение потенциальной энергии, взятое с
обратным знаком равно работе консервативной
силы.
ΔE Ï Aê
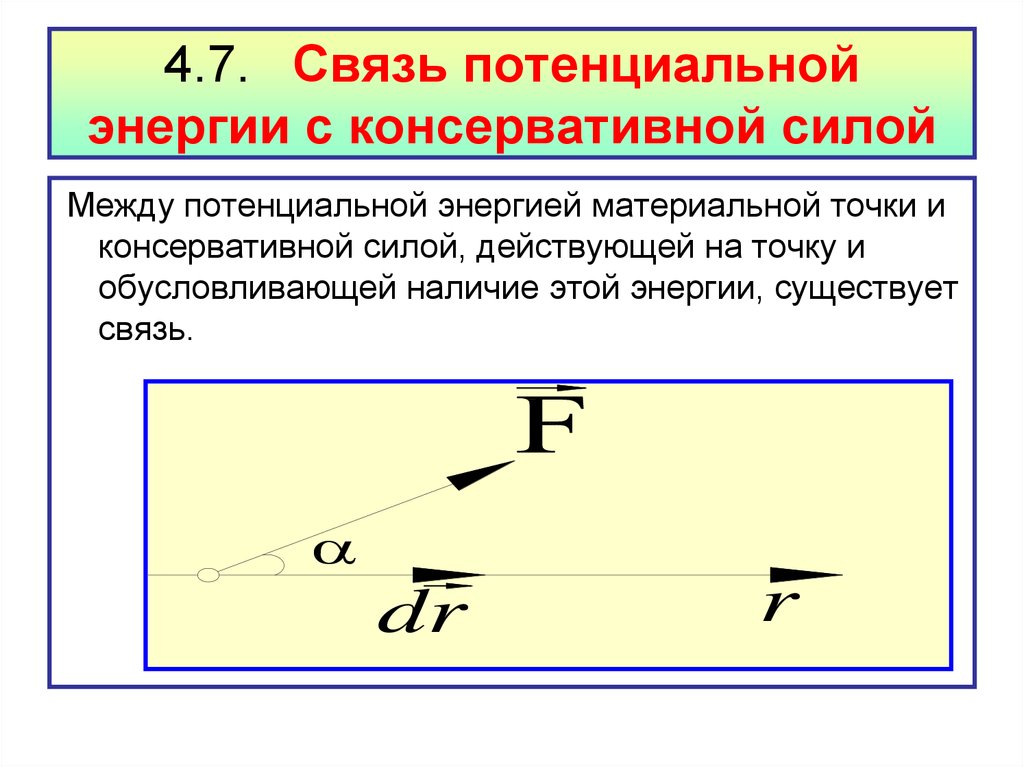
61. 4.7. Связь потенциальной энергии с консервативной силой
Между потенциальной энергией материальной точки иконсервативной силой, действующей на точку и
обусловливающей наличие этой энергии, существует
связь.
dr
r
62.
Если материальная точка переместилась впотенциальном поле в произвольном направлении
r, то консервативная сила совершит при этом
работу:
dA Fê dr Fê, r dr
где
Fr – проекция силы на направление dr
.
С другой стороны работа консервативной силы
равна убыли потенциальной энергии:
dA dE П
63.
Приравнивая правые части, получимdE Ï
Fê, r
dr
Проекция консервативной силы на произвольное
направление r равна по абсолютной величине и
противоположна по знаку производной от
потенциальной энергии по этому направлению.
64.
Полученное соотношение справедливо для любогонаправления в пространстве, в частности, для осей
Х, У, Z декартовой системы координат.
dE П
Fx
dx
dE П
Fy
dy
dE П
Fz
dz
65.
Учтём, что вектор силы можно записать как:F Fx i Fy j Fz k
i , j , k – орты координатных осей X, Y, Z.
Тогда
dE П dE П dE П
F
i
j
k
dy
dz
dx
66.
Вектор, стоящий в правой части этого выражения,называется градиентом функции потенциальной
энергии и обозначается как qrad Eп.
Понятие градиента вводится для любых векторных
величин, значение модуля которых зависит от
направления в пространстве.
Градиент любой функции – это вектор,
направленный в сторону возрастания функции и
численно равный изменению функции на
единичном расстоянии.
df df df
gradf
i
j
k
dx
dу
dk
67.
gradE ПdЕ П dЕ П dЕ П
i
j
k
dx
dу
dk
Градиент потенциальной энергии:
- вектор, направленный в сторону возрастания
потенциальной энергии;
- численно равен приращению потенциальной
энергии, приходящейся на единицу длины этого
направления.
Мы получили, что
FK qrad E П
Консервативная сила, действующая на материальную
точку, равна по модулю и противоположна по
направлению градиенту потенциальной энергии.
68.
Две формулы в равной мере выражают связьконсервативной силы с потенциальной энергией
и наоборот.
dE П
Fr
dr
r2
E п FK d r
r1
Величина консервативной силы равна изменению
потенциальной энергии тела на единичном
расстоянии.
Изменение потенциальной энергии, взятое с
обратным знаком равна работе консервативной
силы.
69.
Рисунок отражает указанные выше соотношения длясилы тяжести и потенциальной энергией в
гравитационном силовом поле.
EП = mgh
mg



























































 physics
physics








