Работа и энергия

1. РАБОТА И ЭНЕРГИЯ

Работа и мощность
Кинетическая и потенциальная
энергия
Закон сохранения энергии в механике

2. Работа постоянной силы

Элементарная работа – физическая величина,
равная скалярному произведению вектора силы
на вектор бесконечно малого перемещения под
действием данной силы
A Fdr
A Fdr cos
– угол между векторами F и dr
Механическая работа равна нулю, если:
•сила, действующая на тело, равна нулю
•перемещение равно нулю
•сила, действует на тело перпендикулярно перемещению

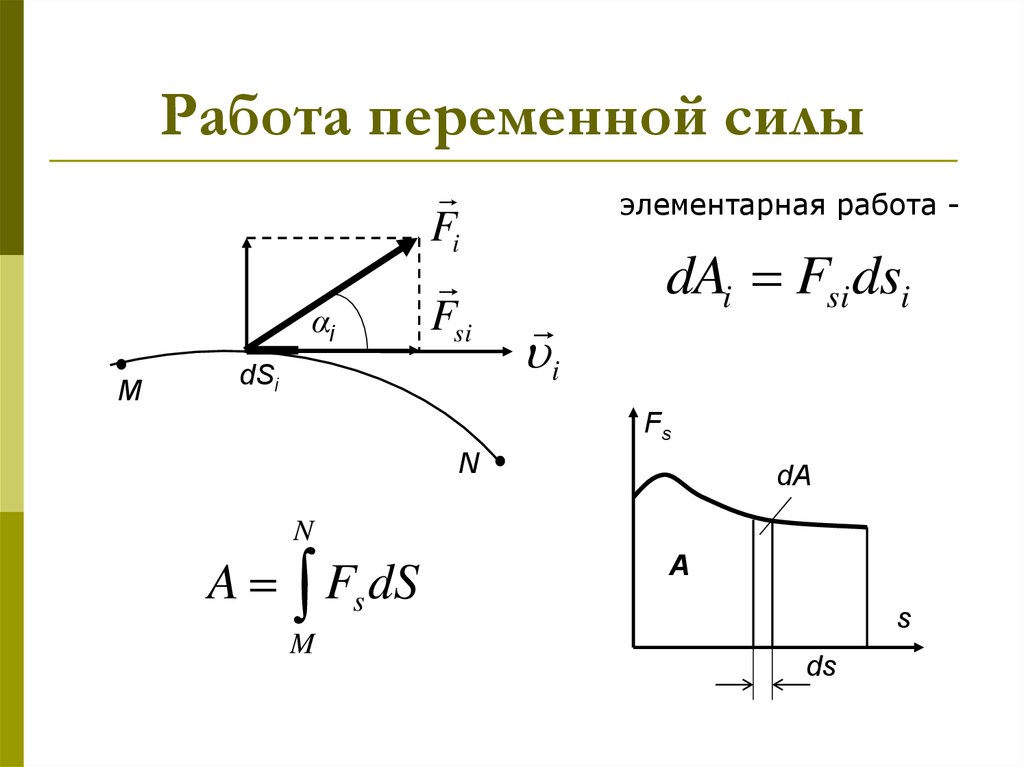
3. Работа переменной силы

αi
M
Fi
Fsi
dSi
элементарная работа -
dAi Fsi dsi
i
Fs
N
dA
N
A Fs dS
M
A
s
ds

4. Силы консервативные и диссипативные

Силы с точки зрения
совершаемой
работы
Потенциальные
(консервативные)
Непотенциальные
(диссипативные)

5. Консервативные силы

Силы, работа которых не зависит от формы
траектории или работа которых по замкнутой
траектории равна нулю называются
консервативными
A
0
L
Поле, работа сил которого не зависит от формы
траектории движения тела в данном поле,
называется потенциальным
Иначе силы называются диссипативными

6. Мощность

Мощность N – физическая величина,
численно равная работе, совершаемой за
единицу времени
A
N
t
A dA
N lim
t 0 t
dt
N Ватт (Вт)
- мгновенная мощность

7. Механическая энергия

Энергия – это физическая величина,
показывающая
способность
тела
совершать механическую работу
A1 2 E2 E1 dE
Энергия выступает как единая мера
движения
материи
и
является
характеристикой
состояния
данной
системы,
т.е.
является
функцией
состояния системы

8.

Механическая энергия
Кинетическая
T
Потенциальная
U
Полная механическая энергия – сумма
кинетической и потенциальной энергии тела
или системы тел
E T U

9. Кинетическая энергия

Работа силы F на пути, который тело прошло за
время возрастания скорости от 0 до ,идет на
увеличение кинетической энергии тела
dA dT
d
F m
второй закон
dt
Ньютона
d
m
ds F ds dA
dt
dA m d dT
m 2
T m d
2
0
Кинетическая
энергия
–
физическая
величина, численно
равная работе при
переходе тела из
состояния
со
скоростью, равной
нулю, в состояние
со скоростью

10. Потенциальная энергия

Потенциальная энергия U – часть общей
механической энергии системы, определяемая
взаимным расположением тел и характером сил
взаимодействия между ними
dA=-dU
Потенциальная энергия деформации
Потенциальная гравитационная энергия
Потенциальная энергия в однородном поле
тяжести
1
U k ( x x0 ) 2
2
mM
U G
R
U mg h

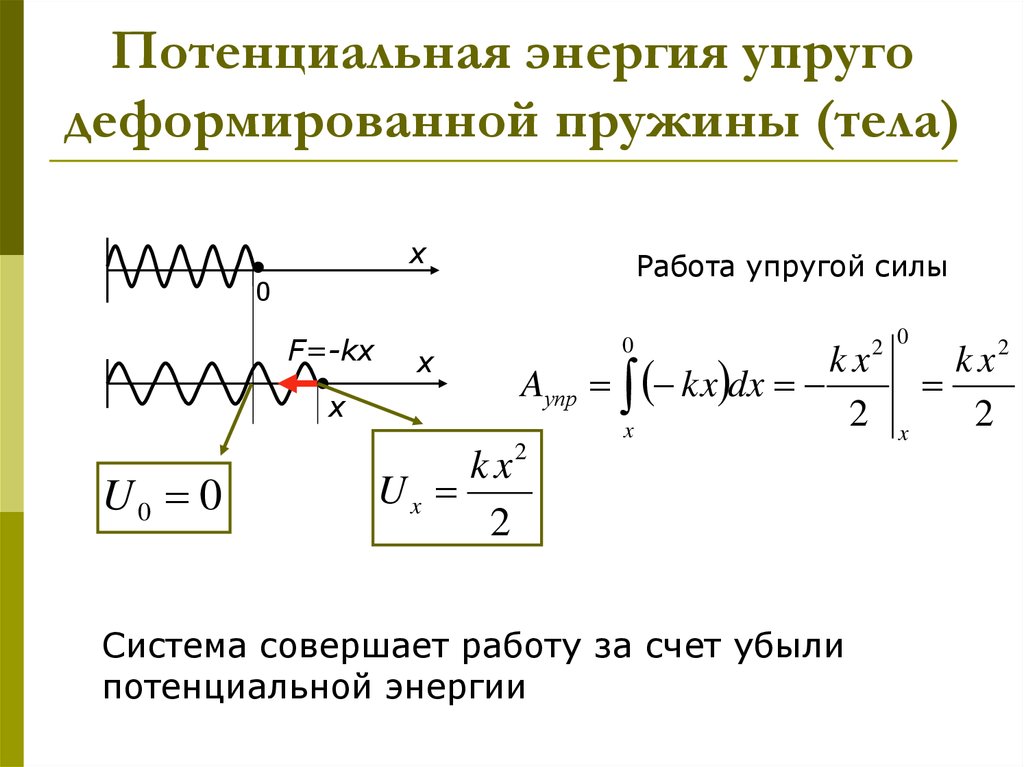
11. Потенциальная энергия упруго деформированной пружины (тела)

x
Работа упругой силы
0
F=-kx
x
x
U0 0
kx
Ux
2
0
Aупр
kx
kx dx
2
x
2
Система совершает работу за счет убыли
потенциальной энергии
2 0
x
k x2
2

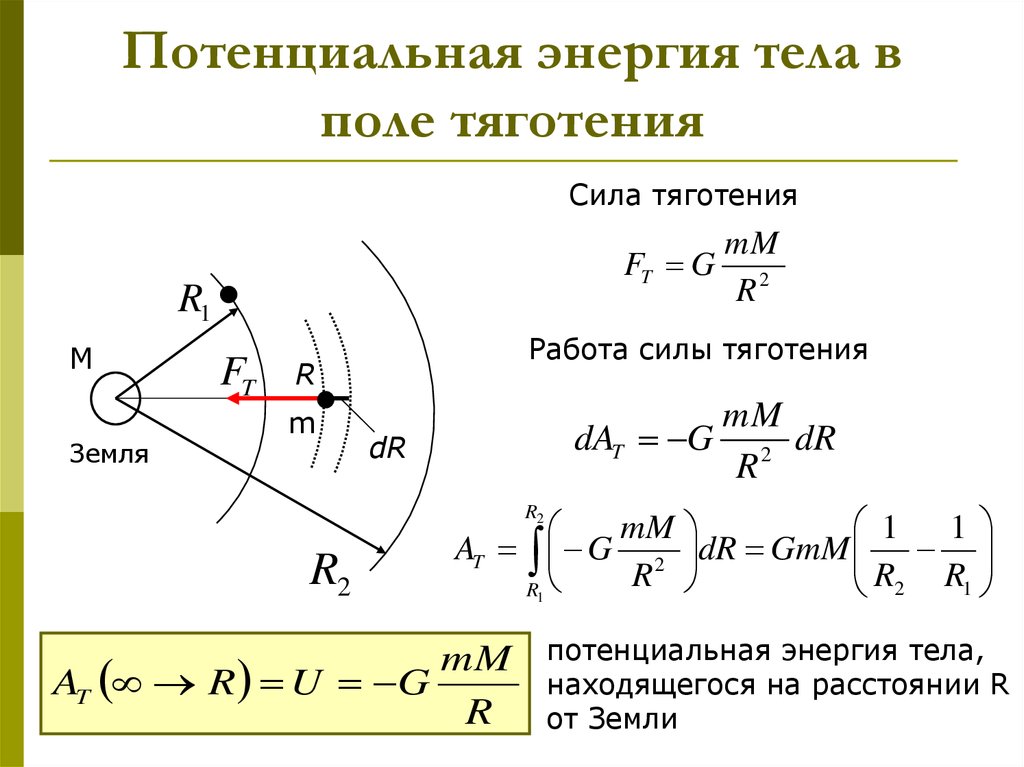
12. Потенциальная энергия тела в поле тяготения

Сила тяготения
mM
FT G 2
R
R1
М
Земля
FT
Работа силы тяготения
R
m
mM
dAT G 2 dR
R
dR
1
mM
1
AT G 2 dR GmM
R
R2 R1
R1
R2
R2
mM
AT R U G
R
потенциальная энергия тела,
находящегося на расстоянии R
от Земли

13. Потенциальная энергия тела в однородном поле тяжести

x
h
U=mgh
Работа внешней силы:
h
0
Земля
F mg
U=0
Aвн mg dx mgh
0
Потенциальная энергия системы тело – Земля
увеличивается за счет работы внешней силы

14. Взаимное превращение кинетической и потенциальной энергии

15. Вывод закона сохранения энергии в механике

+
d 1
Система
m1
F1 F1 d x1 материальных
m1 , , mn
dt
точек массой
dU - изменение
потенциальной
энергии
движется
со скоростями
d n
,
,
1
mn
Fn Fn d xn dT - изменение n
равнодействующая
dt
кинетической
энергии
Fn внутренних консервативных
n
n
сил
dT+dU=0
0
внешних
mi i d i Fi dxi Fi dxi равнодействующая
n
i 1
i 1
dU
=
dT
Fn
i 1
сил
0
(замкнутая система)
или
E=T+U

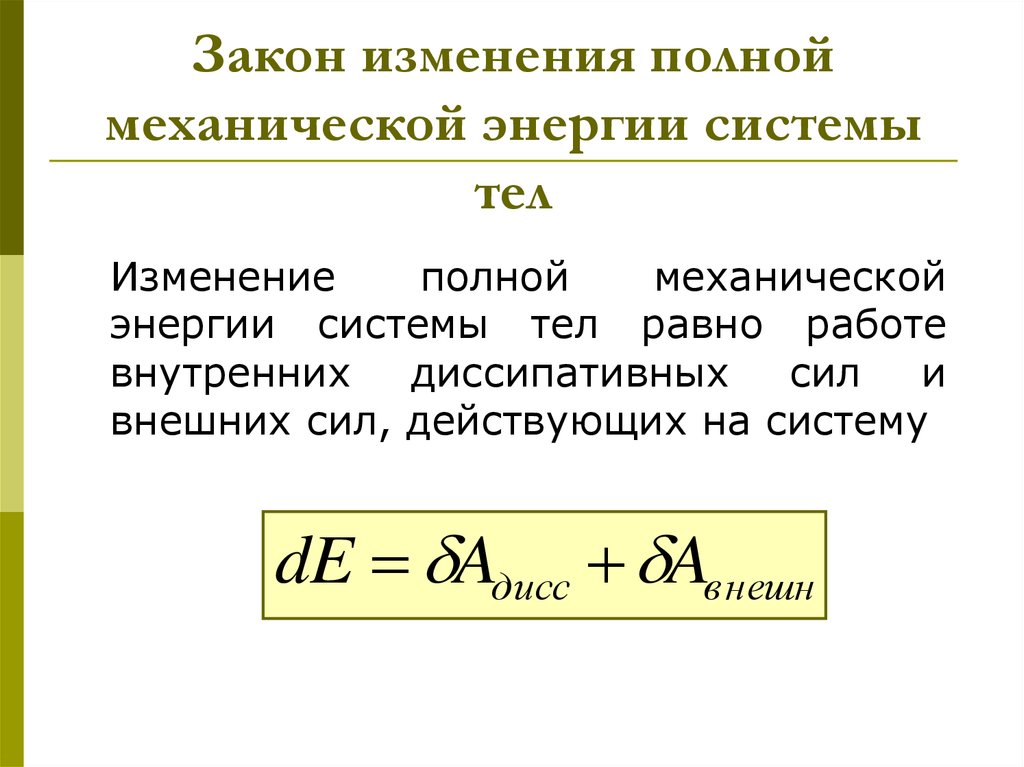
16. Закон изменения полной механической энергии системы тел

Изменение
полной
механической
энергии системы тел равно работе
внутренних
диссипативных
сил
и
внешних сил, действующих на систему
dE Aдисс Aвнешн

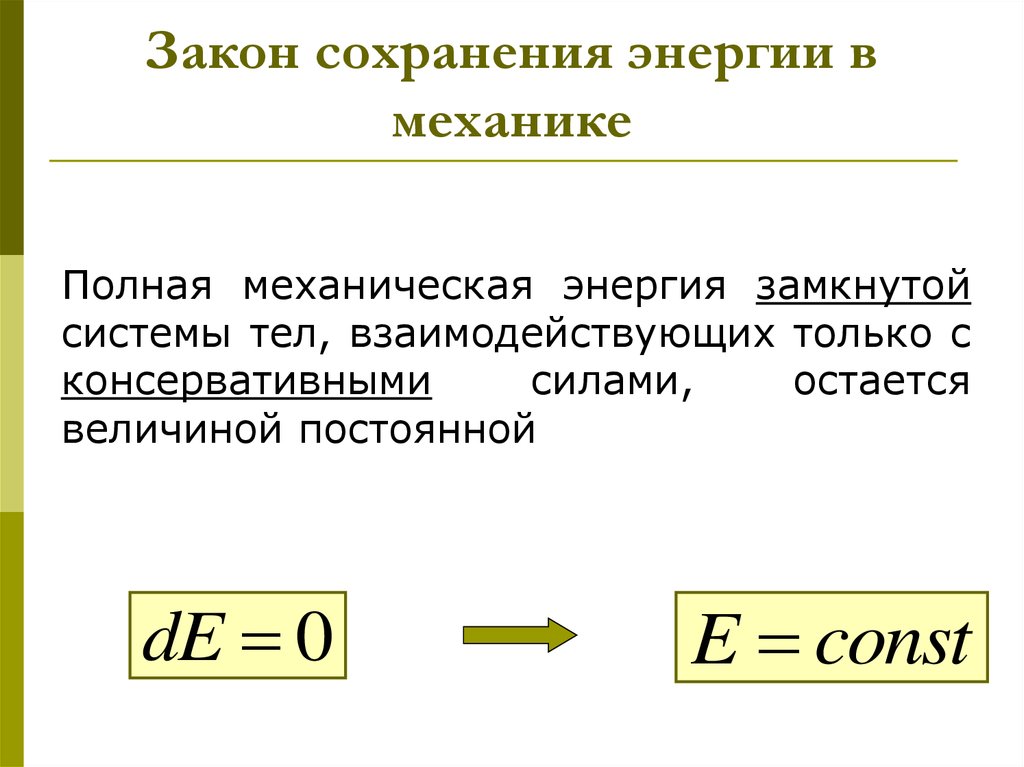
17. Закон сохранения энергии в механике

Полная механическая энергия замкнутой
системы тел, взаимодействующих только с
консервативными
силами,
остается
величиной постоянной
dE 0
E const

18. Закон сохранения энергии в механике

19. Замечания

Закон
сохранения
полной
механической
энергии связан с однородностью времени
Закон
сохранения
полной
механической
энергии – фундаментальный закон природы,
справедливый как для макроскопических тел,
так и для микроскопических тел
Физическая
сущность
закона
сохранения
полной
механической
энергии:
материя
неуничтожима, как и ее движение