Similar presentations:
Энергия, работа
1.
Энергия, работаЭнергия - универсальная мера различных форм движения и
взаимодействия. С различными формами движения материи связывают
различные формы энергии: механическую, тепловую, электромагнитную,
ядерную и другие.
Чтобы количественно характеризовать процесс обмена энергией между
взаимодействующими телами, в механике вводится понятие работы
силы.
Элементарная работа силы F: проекция силы на направление
перемещения, умноженная на величину самого перемещения.
company name
dA F dr F cos dr Fs dr
кг м2
A 2 H м Дж
с
2.
Энергия, работаПри прямолинейном движении тела под действием постоянной силы :
F
dA Fs s Fs s cos
Если сила переменна по величине и направлению:
2
2
n
company name
dAi Fsi ds
A dAi
i 1
Работа силы при движении тела по
произвольной криволинейной траектории
вычисляется
путем
интегрирования
элементарных работ:
2
A1,2 F dr
1
Fs
A dA Fdr cos
1
V
1
F
V
dS
2
1
3.
Энергия, работаFs
Если
2
Если
, то A 0
2
Если
, то A 0
2
dA
S
company name
S1
dS
S2
геометрический смысл выражения
для работы
, то
A 0
4.
МощностьМощность – быстрота совершения работы:
dA
N
dt
Дж
Вт
N
с
F dr dr
N
F F V
dt
dt
company name
dA F dr
N F V F V cos
5.
Мощность, кинетическая энергияМощность – быстрота совершения работы:
dA
N
dt
dA N dt
A1,2 N t dt
t1
Кинетическая энергия
Работа силы на конечном перемещении:
Выполним преобразования:
company name
t2
dV
F ma m
dt
dr
V
dt
d r V dt
2
A1,2 F dr
1
6.
Кинетическая энергияКинетическая энергия одной материальной точки:
2
dV
A1,2 F d r m
Vdt m dV V
dt
1
1
1
2
2
2
2
m V dV m VdV
company name
1
mV
A1,2
2
1
2 V2
V1
2
mV2
2
2
mV1
2
mV 2
Eкин
2
7.
Кинетическая энергия2
1
A1,2 Eкин Eкин
Eкин
работа силы при перемещении
материальной точки равна
приращению кинетической
энергии этой точки
Кинетическая энергия системы материальных точек:
Кинетическая энергия – величина аддитивная. Кинетическая энергия
с.м.т. равна сумме кинетических энергий отдельных м.т., из которых
эта система состоит, или, на которые ее можно мысленно разделить.
miV 2 V 2 n
mV 2
Eкин Eкин i
mi
2
2 i 1
2
i 1
i 1
company name
n
n
8.
Работа и кинетическая энергия с.м.т.n
A Ai
i 1
i
i
i
A1,2 Eкин2 Eкин1
n
i
Работа всех сил, действующих на
систему материальных точек,
равна приращению кинетической
энергии этой системы
A1,2 Eкин2 Eкин1
Eкин Eкин
company name
i 1
Приращение кинетической энергии системы материальных точек
определяется работой всех сил, действующих на систему, как
внешних, так и внутренних.
9.
Консервативные и неконсервативные силыконсервативные силы
Силы, работа которых при перемещении
с.м.т.
из
произвольного
начального
положения
в произвольное конечное
положение не зависит от пути перехода, а
определяется только начальной и конечной
конфигурацией с.м.т.
Работа консервативных сил по
любому замкнутому пути равна
нулю
F конс d r 0
L
company name
Силы, не являющиеся консервативными, называются
неконсервативными (диссипативными)
Работа неконсервативных сил
зависит от вида траектории и на
замкнутом пути не равна нулю
F конс d r 0
L
10.
Консервативные и неконсервативные силыСила тяжести – консервативная сила
h
m
dr
h dh
Элементарная работа
dA F d r
F dr cos
dh
F mg
company name
dr cos dh
h
F mg
dA mgdh
11.
Консервативные и неконсервативные силыm
dr
1
Работа на конечном
перемещении
dh
dA mgdh
2
F mg
2
2
1
1
company name
A1,2 dA mg dh mgh1 mgh2
Работа тяжести на произвольной траектории не зависит от вида
траектории
12.
Неконсервативные силыНеконсервативные силы
company name
Гироскопические силы, зависящие от
скорости и всегда перпендикулярные к
вектору скорости. Работа
гироскопических сил по любой
траектории равна нулю.
Например, сила Лоренца.
F л q V B
Диссипативные силы,
полная работа которых при
любых условиях в
замкнутой системе всегда
отрицательна
(сила трения).
F тр V
13.
Потенциальная энергияТела, находясь в потенциальном поле сил, обладают потенциальной
энергией.
Потенциальная энергия - механическая энергия системы тел,
определяемая их взаимным расположением и характером сил
взаимодействия между ними.
Работа консервативных сил при элементарном (бесконечно малом)
изменении конфигурации системы равна приращению потенциальной
энергии, взятому со знаком «-» (работа совершается за счет убыли
потенциальной энергии).
dA dU U 2 U1
1
A1 2 U1 U 2
2
2
company name
A1 2 dA
1
dA F d r
dA dU
2
F d r U1 U 2
1
F d r dU
14.
Система материальных точекРабота консервативных сил не зависит от
пути перехода, следовательно,
потенциальная энергия с.м.т. является
функцией только ее координат
1
2
n 2
A1 2 F i d r i U1 U 2
i 1 1
company name
2
F d r U U
i
1
i
i
i
1
2
A1 2 U1 U 2
15.
Силы и потенциальная энергияЗная действие силы как функции координат материальных точек
системы, интегрированием можно найти потенциальную энергию
системы.
Если известна потенциальная энергия системы как функция координат
взаимодействующих тел, то дифференцированием можно вычислить
действующие силы.
а)
F r U
известна сила
company name
2
1
1
F d r dU
F d r dU
2
2
F d r U 1 U 2 U1 U1 U 2
1
2
16.
Силы и потенциальная энергияб) известна потенциальная
энергия
U r F
a b a b a b a b
F F ,F ,F
F dx F dy F dz dU
F d r dU
company name
x
y
x x
z
U
dU
Fx
x
dx y , z const
dU
U
Fy
y
dy x , z const
U
Fz dU
z
dz x , y const
x
y y
y
z
d r dx , dy , dz
компоненты
вектора силы
z z
17.
Силы и потенциальная энергияFx dx Fy dy Fz dz dU
U
Fx
x
U
Fy
y
U
Fz
z
U
U
U
F Fx i F y j Fz k
i
j
k
x
y
z
Введем оператор
company name
«набла»
i
j k
x
y
z
оператор Гамильтона или
«набла» - оператор, grad
(градиент)
F gradU U
18.
Условия равновесия механической системыНеобходимое условие равновесия
U
U
U
F
i
j
k
y
z
x
U
0
xi
U
0
yi
Fi 0
U
0
zi
company name
gradU 0
U const
U U min
U U max
19.
Условия равновесия механической системыа) U const
Тривиальный случай безразличного
равновесия
U
x
б)
U U min
U
Устойчивое равновесие.
При отклонении точки от положения
равновесия возникают силы,
направленные в сторону убывания
потенциальной энергии, т.е. к
положению равновесия
x
company name
в)
U U max
U
x
Неустойчивое равновесие.
При отклонении точки от положения
равновесия возникают силы,
направленные в сторону убывания
потенциальной энергии, т.е. от
положения равновесия
20.
Закон сохранения механической энергииРассмотрим механическую систему,
состоящую из n тел, масса и скорость
которых равны
m1, m2, ... mn ; V 1, V 2, ... V n
company name
'
'
'
F 1 , F 2 ,... F n
равнодействующие
консервативных сил
внутренних
F 1, F 2, ... F n
равнодействующие
консервативных сил
внешних
f 1, f 2, ... f n
равнодействующие
неконсервативных сил
внешних
21.
Закон сохранения механической энергииЗапишем второй закон Ньютона для n тел механической системы:
Двигаясь
под
действием
сил,
материальные точки системы за интервал
времени dt совершают
перемещения,
соответственно равные dr1 , dr 2 , dr n
company name
dV1
'
F1 F1 f 1
m1
dt
dV2
'
F2 F2 f 2
m2
dt
dVn
'
Fn Fn f n
mn
dt
Умножив каждое из уравнений скалярно на
соответствующее перемещение и сложив
после этого уравнения получим:
m V dV F 1' F 1 d r 1 f d r 1
1
1 1 1
'
m2 V 2 dV 2 F 2 F 2 d r 2 f 2d r 2
m V dV ' F ' F d r f d r
n
n
n
n
n
n n n
22.
Закон сохранения механической энергииСложив эти уравнения, получим:
m V i dV i
n
i 1
n
n
i
mi V i dV i
company name
i 1
'
Fi Fi
i 1
d r f d r
i
i 1
i
i
2
mi V i
d
dE кин
2
i 1
n
n
работа внешних
неконсервативных сил
приращение кинетической
энергии
приращение потенциальной
энергии
23.
Закон сохранения механической энергииm V i dV i
n
i 1
n
i
i 1
'
Fi Fi
d r f d r
n
i
i 1
i
i
d Eкин Eпот dA
1)
fi 0
если внешние неконсервативные силы отсутствуют, то
company name
d Eкин Eпот 0
Eкин Eпот const
полная механическая энергия замкнутой
системы тел, между которыми действуют
лишь консервативные силы, остается
постоянной
24.
Закон сохранения механической энергии2)
fi 0
dE dAвнеш
система не замкнута
2
d Eкин Eпот A1,2
1
изменение полной механической энергии
системы при переходе из одного
состояния в другое равно работе,
совершенной при этом внешними
неконсервативными силами
company name
Графическое представление энергии
1) графическое представление
поле тяжести
E пот
для тела в однородном
2) графическое представление
упругодеформированного тела
E пот
для
25.
Графическое представление энергии1) графическое представление
поле тяжести
E пот
E пот
E
E Eкин Eпот
E
E кин
для тела в однородном
h hmax , то
Если
Eпот m ghmax
E пот
h
hmax
E кин 0
h
company name
Из приведенного графика можно найти скорость тела на высоте h :
Eкин E Eпот
2
, т.е.
mV
m ghmax m gh
2
V 2 g hmax h
26.
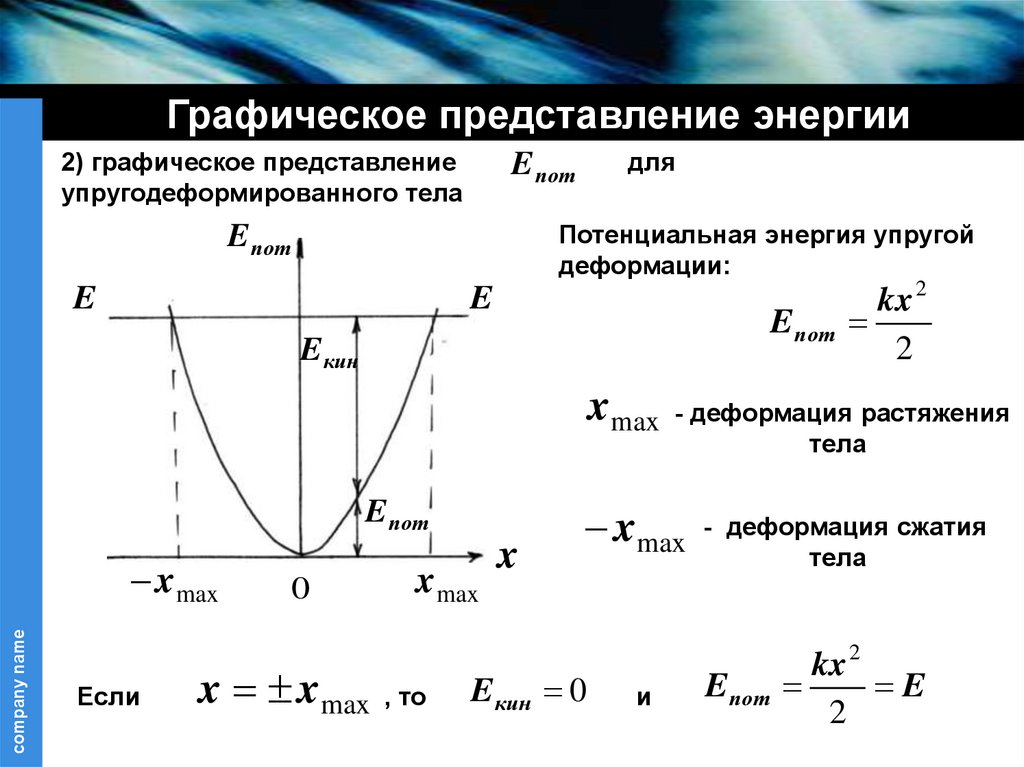
Графическое представление энергии2) графическое представление
упругодеформированного тела
для
E пот
Потенциальная энергия упругой
деформации:
E пот
E
kx 2
E пот
2
E
E кин
x max - деформация растяжения
тела
E пот
company name
x max
Если
0
x max
x xmax , то
x
x max - деформация сжатия
E кин 0
тела
и
kx 2
Eпот
E
2
27.
Графическое представление энергииПотенциальная кривая может иметь более сложный вид:
E пот
E
D
C
A
K
E
B
1
xA
x0
3
2
xC
Частица может находится только там , где
областях I и III.
company name
x
x 0'
Eпот E , т.е. в
x 0 - положение устойчивого равновесия
'
x 0 - положение неустойчивого равновесия


























 physics
physics








