Преобразование выражений, содержащих операцию извлечения квадратного корня

1.

Преобразование
выражений, содержащих
операцию извлечения
квадратного корня.

2.

ab a b
a
b
a
a
b
a
2n
n
a a
2
а 0
b 0
(b 0)

3.

Цель:
1.Учиться выполнять операцию
извлечения квадратного корня.
2.Учиться использовать эту
операцию в преобразовании
выражений.

4.

№1
Представьте заданное число в виде произведения двух таких
множителей, чтобы один из них являлся квадратом некоторого
натурального числа.
Например: 12=4 3.
1
2
3
18
20
24
40
44
45
54
56
60
27
48
63

5.

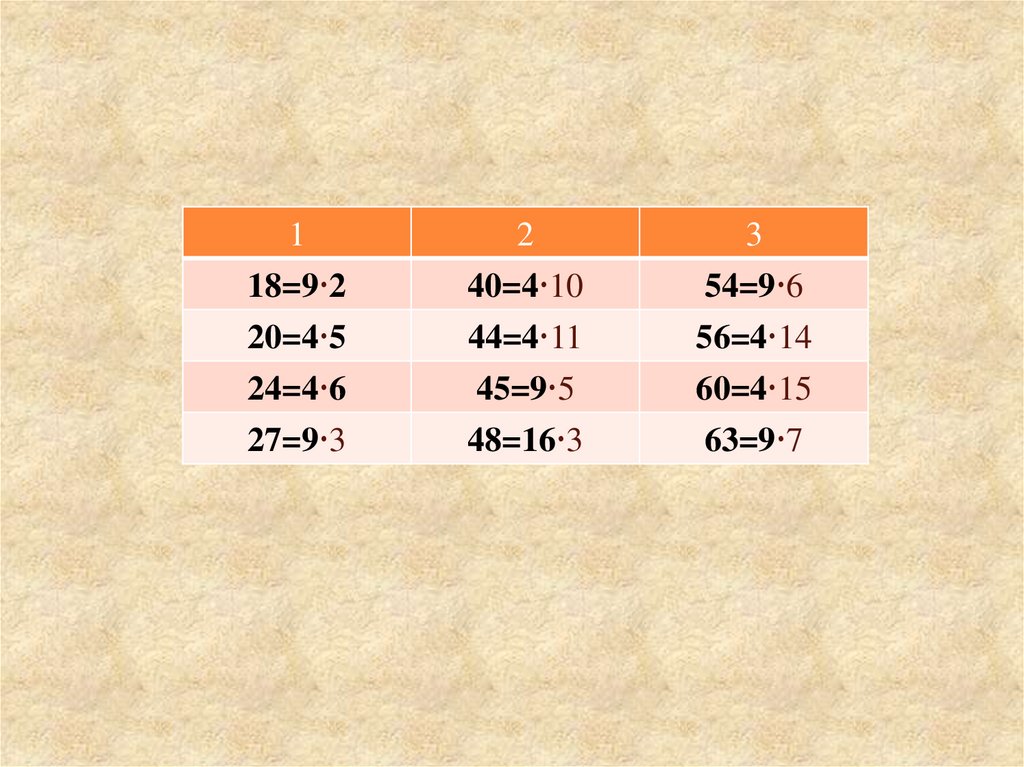
1
18=9 2
20=4 5
24=4 6
27=9 3
2
40=4 10
44=4 11
45=9 5
48=16 3
3
54=9 6
56=4 14
60=4 15
63=9 7

6.

№2.
Представьте в виде произведения
степеней, так чтобы показатель первого
множителя был на 1 меньше.
25 2 4 2
5
4
4
4
4
2 2 2 5 5 5
3
2
4
5
4
5
5 5 5 7 7 7 2 2 2
11
10
6
3
2
7
a a a x x x b b b
3
2
9
8

7.

Знак
используется для упрощения
записей многих иррациональных чисел.
Знак
иногда называют радикалом, от
латинского radix. В 1626 году
нидерландский математик А.Ширар ввел
близкое к современному обозначение корня
V. Если над этим знаком стояла цифра 2, то
это означало корень квадратный, если 3 –
кубический. Лишь в 1637 году Рене Декарт
соединил знак корня с горизонтальной
чертой, применив в своей «Геометрии»
современный знак корня . Этот знак вошёл
во всеобщее употребление лишь в начале
XVIII века.

8.

1.
2.
Учиться выполнять операцию
извлечения квадратного корня.
a a
2n
n
125 25 5 25 5 5 5
2 10 2 10 4 5 4 5 2 5
3
а
7
34 1 34 31 34 3 9 3
а
6 1
а а а
6
3
а
a
ab а b
48 16 3 16 3 4 3
5
a
2
a
b
а
b

9.

2. Учиться использовать эту
операцию в преобразовании
выражений.
81а
a a a a
ab а b
2n
n
a
b
2
а
b
81 а 9 а
9а в 9 а 6 1в 4 1 3 а 3 а в 2 в 3а 3в 2 ав
7 5
10 1
5
27 х11
9 3 х
3х 3х
6
3
6
25m
5m
25m