Similar presentations:
Преобразование выражений, содержащих операцию извлечения квадратного корня
1.
ПРЕОБРАЗОВАНИЕВЫРАЖЕНИЙ,
СОДЕРЖАЩИХ ОПЕРАЦИЮ
ИЗВЛЕЧЕНИЯ
КВАДРАТНОГО КОРНЯ
2.
( a ) a;2
ab a b ;
a
a
;
b
b
a
2n
a .
n
а и b – неотрицательные числа
3.
Пример: Упростите выражение4.
Пример: Сократите дробь5.
Пример: Освободить дробь от иррациональности(от знака корня в знаменателе):
6.
Пример: Освободить дробь от иррациональности(от знака корня в знаменателе):
7.
Пример: Выполнить действия:а) ( a b )( a b )
( a b )( a b ) ( a ) 2 ( b ) 2 a b.
2
2
(
a
)
2
a
b
(
b
)
б) ( a b )
2
a 2 ab b.
8.
Пример: Выполнить действия:A)
6 2 6 2 6 2 6 2 4;
Б)
2 5 5 2 2 5 2 2 5 5 2 5 2
2
2
2
2
2
2
2
2 5 2 2 5 5 2 5 2 4 5 20 10 25 2
2
2
20 20 10 50 70 20 10;
3 x 9 3 x x 3 x 27 x x ;
Г) 1 x 1 x 1 x 1 x .
В)
3
2
2
Д)
a 7 a
2
3
2
7 a 7 a 7 .
2
9.
Пример : Разложить на множители:2
а) 4a 4 ab b 2 a 2 2 a b
b .
2
4a 4 ab b 2 a b .
2
3
б) x x 1 x x 1 x 1 .
3
3
2
2
a b (a b)(a ab b )
3
x 1 x 1 x x 1 1
x 1 x x 1 .
3
2
3
2
2
2
10.
Пример : Упростить выражение:a a 3 3
a 3 .
a 3 3a
1) a a 3 3 a 3 a 3 a a 3 3
a 3 a 3a 3 ;
2
3
2
a 3 3a a 2 a 3 3 3a
2
2)
3
2
2
a 2 3a 3 3a a 3a 3.
a 3 a 3a 3
3)
a 3.
a 3a 3
4)
a 3 a 3 a 3 a 3.
2
2
2
11.
Пример : Преобразовать заданное алгебраическоевыражение к такому виду, чтобы знаменатель дроби не
содержал знаков квадратных корней:
a)
1
2
1
б)
3 2
Значение дроби не изменится, если ее числитель и знаменатель
одновременно умножить
на одно и то же отличное от нуля число или выражение
1
1 2
2
2 2
б)
2
2
.
2
2
2
1 3 2
1
3 2
3 2
3 2
3 2 3 2 3 2 3 2
2
3 2.
2
12.
Если знаменатель алгебраической дроби содержитзнак квадратного корня, то говорят, что
в знаменателе содержится иррациональность
Преобразование выражения к такому виду,
чтобы в знаменателе дроби
не оказалось знаков квадратных корней, называют
освобождением от иррациональности в знаменателе
- если знаменатель имеет вид а , то числитель и
знаменатель дроби следует умножить на а
b , то
- если знаменатель имеет вид а
b или а
числитель и знаменатель дроби надо умножить
соответственно на а
b или на а
b (сопряженное
выражение)
13.
72
4
.
7
7 5
5 3
Пример : Упростить выражение
7
7 7
7 7
1)
7;
7
7
7 7
2
2 7 5
2 7 5
2 7 5
2)
2
2
7 5
7 5 7 5
7 5
7 5
2 7 5
7 5;
2
4 5 3
4 5 3
4 5 3
4
3)
2
2
5 3
5 3 5 3
5 3
5 3
4 5 3
2 5 3 ;
2
4) 7 ( 7 5 ) 2( 5 3 ) 7 7 5 2 5 2 3
5 2 3.



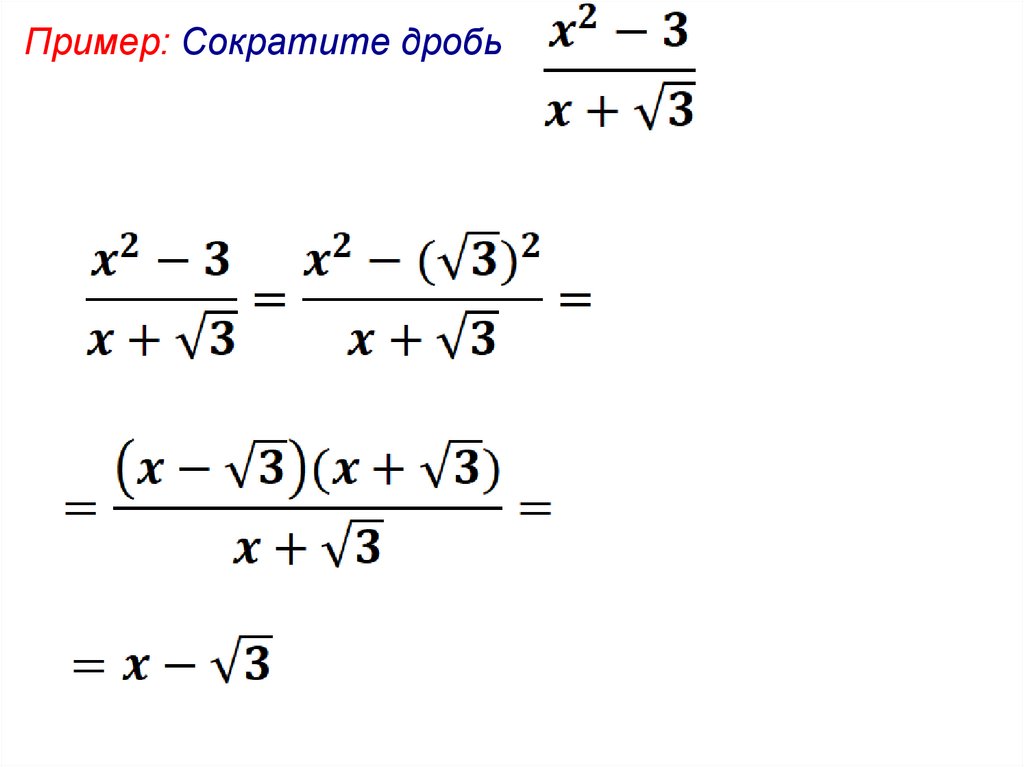











 mathematics
mathematics








