Similar presentations:
Преобразование выражений, содержащие квадратные корни
1.
2.
1. Вынесение множителя из под знака корня:a)
12
b)
8a
6
5
2a
2. Внесение множителя под знак корня:
a)
3 2
b)
a
3. Разложение на множители:
a)
a 5
2
b)
14 2
4. Избавление от иррациональности в знаменателе:
a)
3
5
b)
1
?
3 1
3.
4.
5.
Тест №11)
Арифметиче
ским
квадратным
корнем из
числа а
называется
Число, квадрат которого
равен а.
Свойства
Число равное а.
Неотрицательное число,
квадрат которого равен
а.
2).Завершить утверждение.
а) Корень из произведения неотрицательных множителей равен
произведению корней из этих множителей.
оценка -2 балла
б) Всякая бесконечная непериодическая десятичная дробь называется
иррациональным числом.
оценка -2 балла
в) Корень из дроби, числитель которой является неотрицательным
числом, а знаменатель положительным, равен корню из числителя,
деленного на корень из знаменателя.
6.
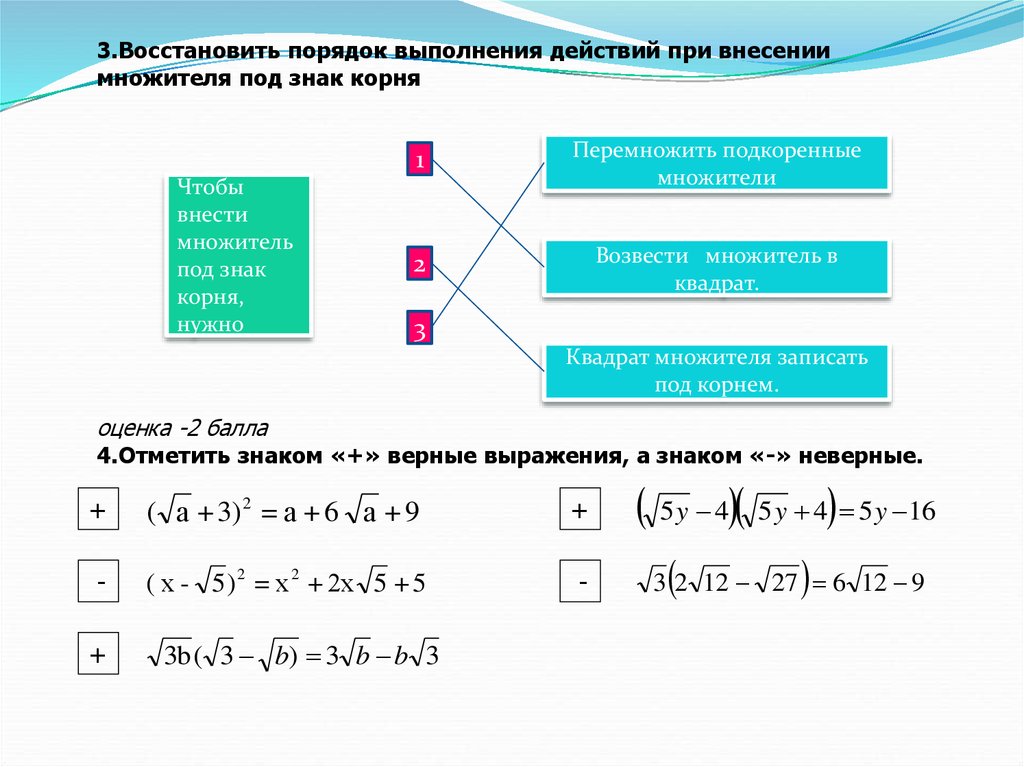
3.Восстановить порядок выполнения действий при внесениимножителя под знак корня
Чтобы
внести
множитель
под знак
корня,
нужно
1
Перемножить подкоренные
множители
2
Возвести множитель в
квадрат.
3
Квадрат множителя записать
под корнем.
оценка -2 балла
4.Отметить знаком «+» верные выражения, а знаком «-» неверные.
+
( а + 3) 2 = а + 6 а + 9
+
-
( х - 5 ) 2 = х 2 + 2х 5 + 5
-
+
3b ( 3 b) 3 b b 3
5 y 4 5 y 16
3 2 12 27 6 12 9
5y 4
7.
ТЕСТ 2 Соединить линией многочлен с соответствующим емуспособом разложения на множители.
Вариант I
Ответ:
2 3 15
4a 2 5a 9
4 a b x a b 12 x 3x 2
3 x2
Вынесение общего
множителя за
скобки
Формула
сокращенного
умножения
9x2 y 4
5 2x 5 x
2
2b x 3a y 6b y a x
13x 10 x 4 x
Не раскладывается
на множители
Способ
группировки
8.
ТЕСТ 2 Соединить линией многочлен с соответствующим емуспособом разложения на множители.
Вариант II
Ответ:
7a 7b
9 x 5x 4
2
a 2 3 ab 3 a 7 b 7
49b 2 a
4a 25b
4
2
b 2 2b 3 3
2 b b 2 a ab
b a 5 c a 5
Вынесение общего
множителя за
скобки
Формула
сокращенного
умножения
Не раскладывается
на множители
Способ
группировки
9.
Задание.Разложить на множители:
1.
2 3 15
7.
2.
7a 7b
8.
b a 5 c a 5
13x 10 x 4 x
2b x 3a y 6b y a x
3.
a 2 3 ab 3 a 7 b 7
4.
49b a
10.
5 2x 5 x2
5.
b 2 2b 3 3
11.
3 x
6.
2 b b 2 a ab
12.
4 a b x a b 12 x 3x 2
2
9.
2
10.
Ответы:1.
2.
7
3 2 5
a b
3.
a b a
4.
7.
a 5 b c
x 13 10 4
8.
9.
2b a
7b a 7b a
10.
5 x
5.
b 3
11.
3 x
6.
2 b
12.
4 x
3 7
2
b a
x 3 y
2
3 x
a b x3
11.
Получение новойинформации
12.
Вопрос: В чем отличие друг от друга следующихвыражений и как они называются?
1) -4 и 4
2) а-1 и -а+1
3) 12х-у и -(12х-у)
Вопрос: В чем отличие друг от друга следующих
выражений?
1) а+в и а-в
3) -4+х и 4+х
2) 3а- 7 и 3а+ 7
Определение:
Два выражения, отличающиеся друг от друга
знаком только перед одним из слагаемых,
называются сопряженными.
13.
Избавление от иррациональности взнаменателе:
1
3 1
1)
3 1
3 1
2
2
1 3 1
3 1 3 1
3 1
3 1
3 1
2
14.
2)15b
2 7 = 15b 2 7
2
2
2 7
2 7 2 7
15b 2 7 15b 2 7
=
2 7
5
3b 2 7
Задание из учебника №169 стр.41
15.
16.
Задание самостоятельной работыВариант 1
Вариант 2
Упростите выражение:
3 c 8 c 9 c
2 a 6 a 7 a
27 48 75
32 18 50
Сократите дробь:
a 3
a2 3
c 2
c2 2
14 7
2 2
15 5
3 15
Освободитесь от иррациональности в знаменателе дроби:
12
6
5 7
5 7
15
5
10 8
10 8
17.
Ответы к задачам для самостоятельного решенияI- вариант
1.
2.
3.
2 с
4 3
1
a 3
II - вариант
1.
2.
3.
a
2 2
1
c 2
4.
7
2
4.
5
3
5.
2 6
5.
3 5
6.
35 6
6.
9 4 5
Назад
Далее
18.
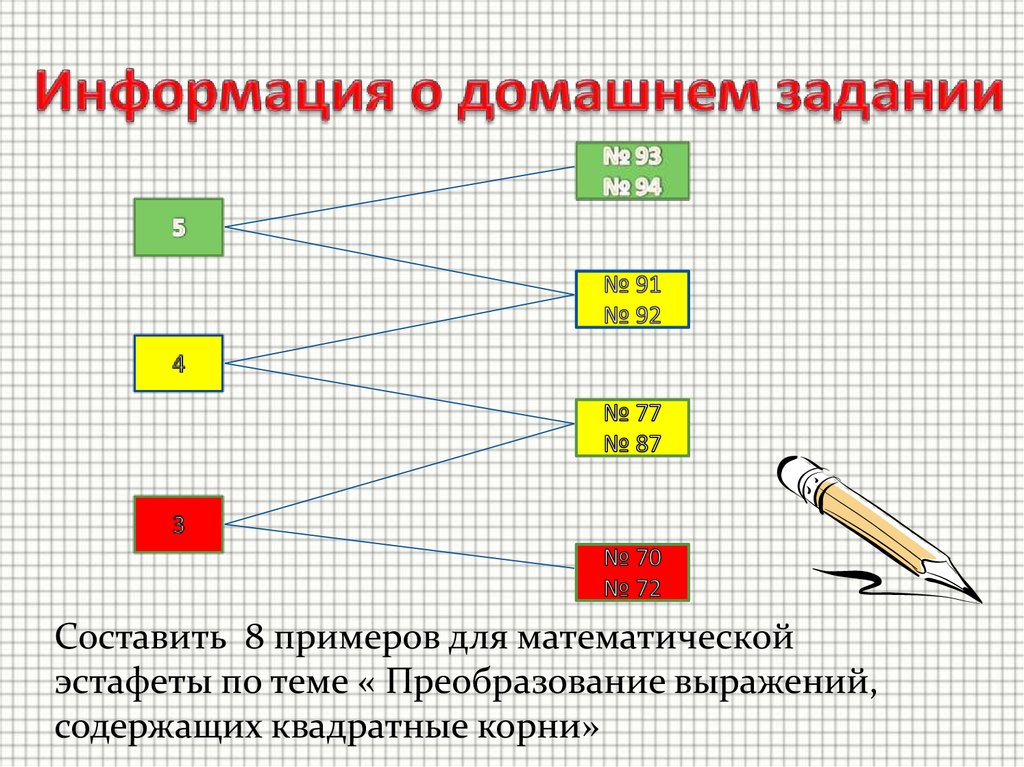
Составить 8 примеров для математическойэстафеты по теме « Преобразование выражений,
содержащих квадратные корни»

















 mathematics
mathematics








