Преобразование выражений, содержащих операцию извлечения квадратного корня

1. Тема:

Преобразование выражений,
содержащих операцию извлечения
квадратного корня

2. Знание – самое превосходное из владений. Все стремятся к нему, само оно не приходит. Абу Рейхан ал-Беруни

04.09.973-9.12.1048 - великий ученый из Хорезмa

3. Цель урока:

Повторить свойства квадратных корней;
объяснить правила вынесения множителя
из-под знака корня, внесения множителя
под знак корня
Проверить знания и умения с помощью
обучающей самостоятельной работы

4.

План урока:
Математическая разминка
Рассмотреть правила вынесения
множителя из-под знака корня, внесения
множителя под знак корня
Закрепление свойств квадратного корня на
примерах
Самостоятельная работа
Подведение итогов
Задание на дом

5.

Повторим:
Как называется выражение а ?
При каком значении а выражение а имеет смысл?
В формулировках и записях свойств
арифметических корней заполните пропуски:
а) корень из произведения неотрицательных
множителей равен_____________корней из этих
множителей;
б) корень из дроби, числитель которой
неотрицателен, а знаменатель______, равен корню
из числителя, делённому на _______;

6. Математическая разминка

Вариант 1
Вариант 2
1. Вычислить квадратный
корень из заданных
7
64
;
0
,
04
;
2
.
выражений:
9
2. Найти корень
квадратный из
произведения чисел 16 и
0,01.
3. Вычислить произведение
корней квадратных
чисел 20 и 5.
4. Вычислить квадратный
корень разности
квадратов 13 и 12.
1. Вычислить квадратный
корень из заданных
15
49
;
0
,
81
;
1
.
выражений:
49
2. Найти квадратный корень
из произведения чисел 25
и 0,0004.
3. Найти частное
квадратных корней 192 и
75.
4. Вычислить квадратный
корень разности
квадратов 41 и 40.

7. Ответы:

Вариант 1
№1. а)
№2.
7 б) 0,9 в)
0,1
№3 1 3
№4.
5
9
Вариант 2
1
1 №1.
7
№2.
а) 8 б) 0,2 в) 1 2
0,4
№3 10
№4. 5
3

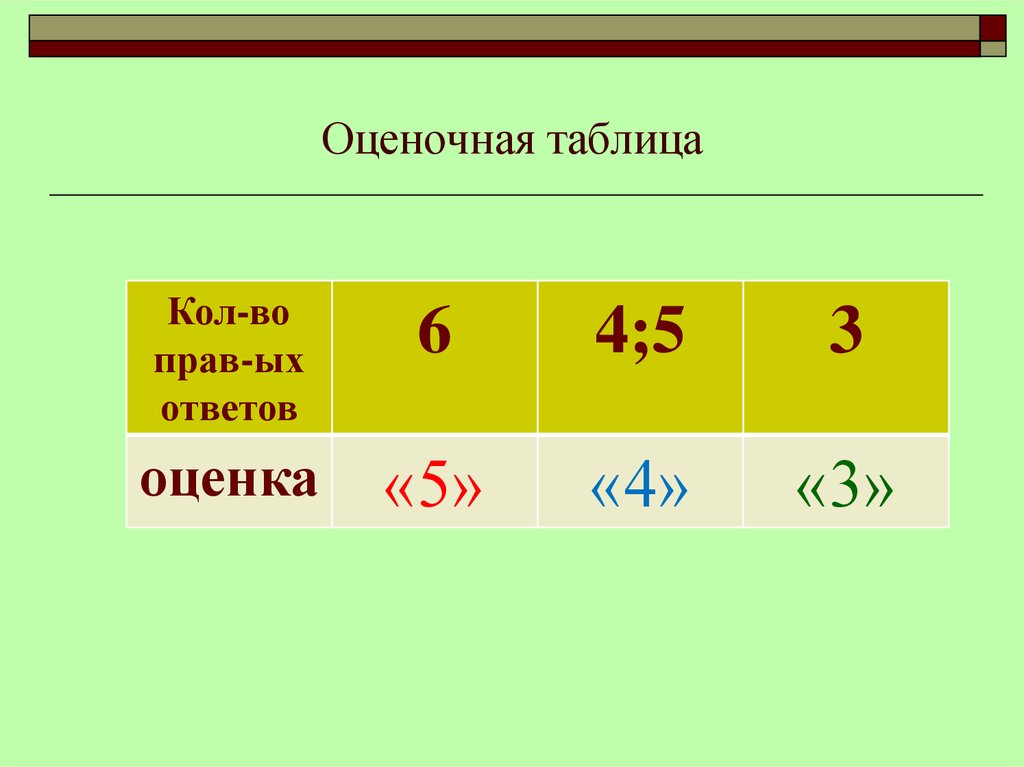
8. Оценочная таблица

Кол-во
прав-ых
ответов
6
4;5
3
оценка
«5»
«4»
«3»

9. Повторим свойства квадратных корней:

а
2
а;
аb
a
b
a b;
a
;
b
а 2n a n
Используя эти формулы, можно выполнять
различные преобразования выражений, содержащих
операцию извлечения квадратного корня.

10. Рассмотрим несколько примеров, причем во всех примерах будем предполагать, что переменные принимают только неотрицательные

значения.
Пример 1. Упростить выражение:
а)
аb
2 4
=
б)
4
16a 4
4
16a
9b 6
a b ab;
2
=
9b
6
4a 2
3.
3b
2

11. Пример 2. Вынести множитель из-под знака квадратного корня:

а) 81a =
81 a 9 a
б) 32a 2 =
16 a 2 2 16 a 2 2 4a 2
7 5
в) 9a b = 9 a 6 a b4 b
3a b
3
2
ab
9 a a b b
6
4

12. Пример 3. Внести множитель под знак квадратного корня:

а) 2 2 = 4 2 4 2 8
б)
3а b
3a
=
9а 2 b
3a
9a 2 b
3ab
3a

13. Закрепление нового материала:

Устно: № 15.1; 15.2.
№ 15.5 (а,б);
№ 15.8 (а,б);
№ 15.10 (а,б);
№ 15.13 (а,б);
№ 15.16 (а,б);
№ 15.20 (а,б).

14.

Предлагаю вам примеры для самостоятельного
решения

15. Обучающая самостоятельная работа

1. Вынесите множитель из–под знака корня:
а) 36 7 = 6 7
б) 75 = 5 3
в) 52 6 = 5 6
г) 12m 2 = 2m 3
3
18
у
д)
= 3у 2 у
е) 3а 2 = а 3
а)
б)
в)
г)
д)
е)
3 64 = 8 3
90 = 3 10
3 5 = 9 5
4
=х 7
20b 2 = 2b 5
16c 9 = 4c 4 c
7х 2
2. Внесите множитель под знак корня:
а) 10 3 =
б) х 3 =
300
3х
2
а) 3 8 = 72
б) у 2 =
2 у2

16. Подведём итоги:

Кол-во
прав-ых
ответов
8
6;7
4;5
оценка
«5»
«4»
«3»

17.

Дом. Задание:
№ 15.7; № 15.12;
№ 15.15