Симметрия тензора упругости. Лекция 3

1.

СИММЕТРИЯ ТЕНЗОРА УПРУГОСТИ
Число компонент тензора упругости n 4 81
Закон Гука
ij Cijkl kl
ij Sijkl kl
Плотность упругой энергии
1
1
kl kl Cijkl ij kl
2
2
ij
2
2
Cijkl
Cklij
kl ij kl kl ij
ij ji
Cijkl Cklij C jikl Cijlk C jilk
21 компонента

2.

МАТРИЧНАЯ ЗАПИСЬ ТЕНЗОРА
УПРУГОСТИ
Тензорная запись
ij Cijkl kl
Матричная запись
ij Sijkl kl
11 → 1
22 → 2
23 → 4
13 → 5 12 → 6
31 → 5 21 → 6
32 → 4
Cijkl Cmn
p C pq q
p S pq q
33 → 3
ij m ,
Sijkl Smn , m, n 1, 2,3
2Sijkl Smn , m или n 1, 2,3
ij m , m 1, 2,3
4Sijkl Smn , m, n 4,5, 6
2 ij m , m 4,5, 6

3.

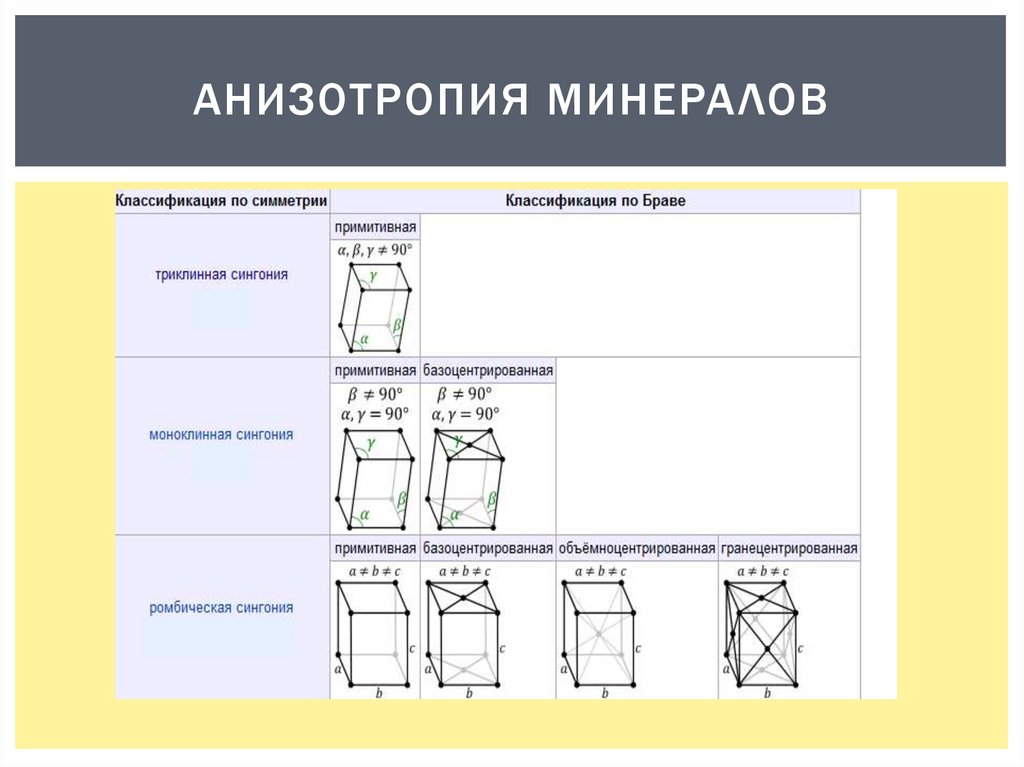
АНИЗОТРОПИЯ МИНЕРА ЛОВ
«Минералами называются естественные дискретные
органически целостные системы
взаимодействующих атомов, упорядоченных с
трёхмерной неограниченной периодичностью их
равновесных положений…»
Юшкин, 1977
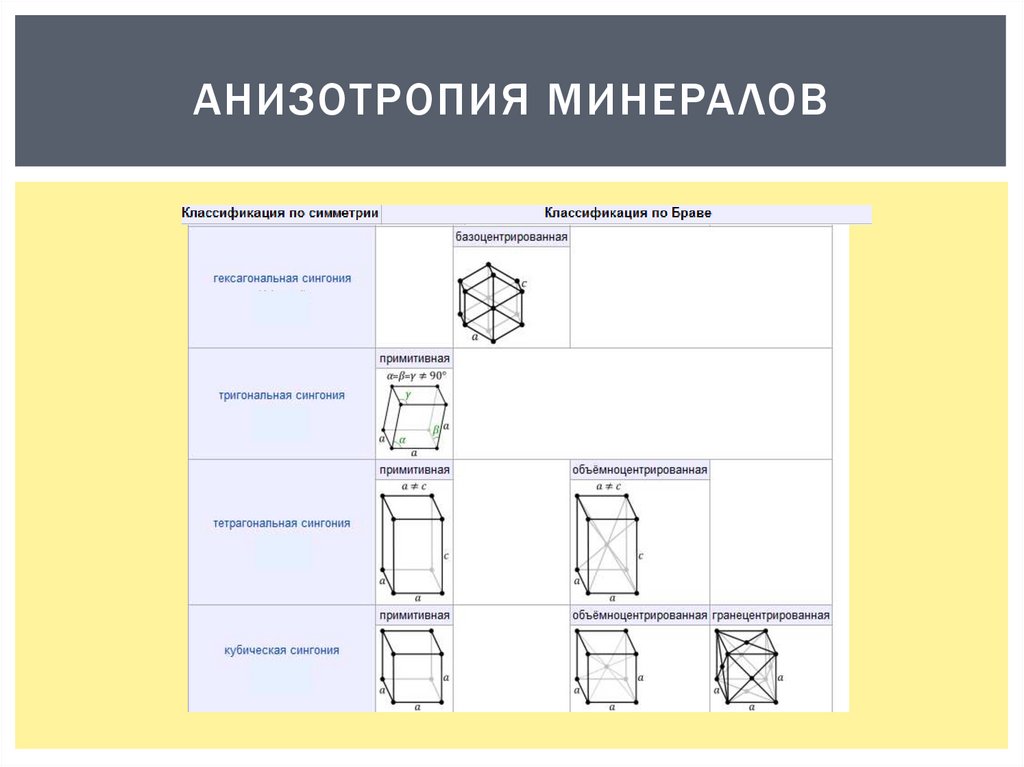
Типы симметрии (сингонии, системы)
1. триклинная,
32 группы симметрии
2. моноклинная
подразделяются на 7
3. орторомбическая
типов (классов, сингоний)
4. кубическая
5. тетрагональная
Кристаллы – симметричные тела,
6. тригональная
свойства которых не меняются в
7. гексагональная
изотропная среда
результате некоторых
преобразований.
Например, отражение в плоскости
или поворот вокруг оси.

4.

АНИЗОТРОПИЯ МИНЕРА ЛОВ

5.

АНИЗОТРОПИЯ МИНЕРА ЛОВ

6.

ТЕНЗОР УПРУГОСТИ – МАТРИЦА
УПРУГОСТИ
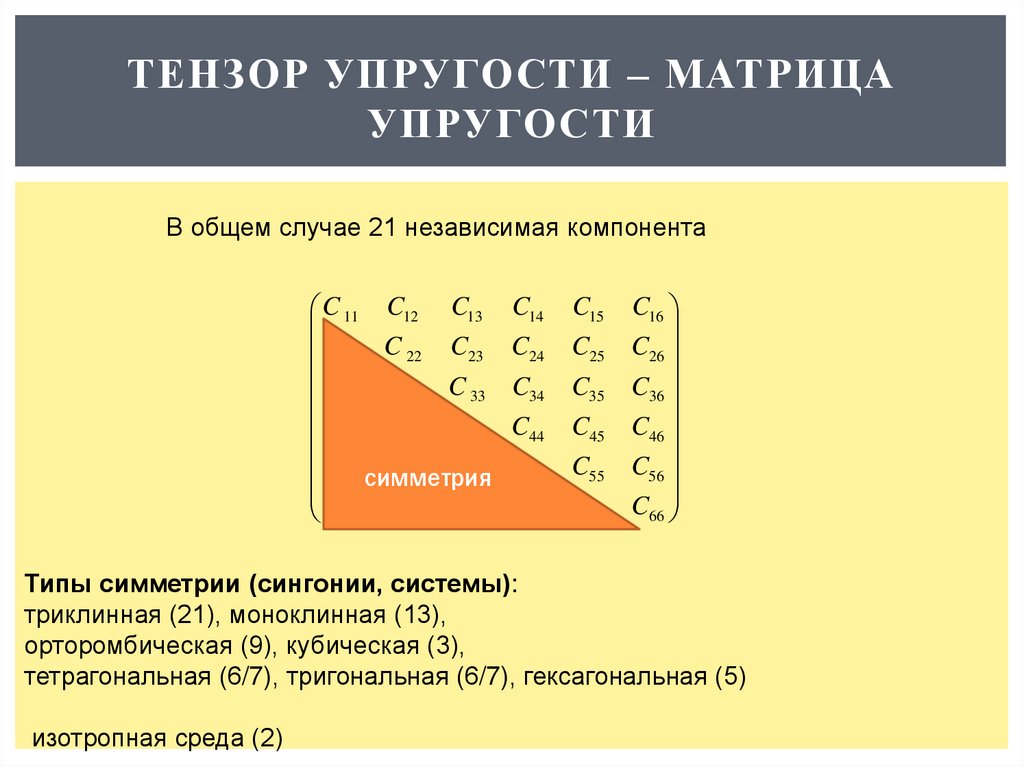
В общем случае 21 независимая компонента
C 11 C12 C13
C 22 C23
C 33
симметрия
C14
C24
C34
C44
C15 C16
C25 C26
C35 C36
C45 C46
C55 C56
C66
Типы симметрии (сингонии, системы):
триклинная (21), моноклинная (13),
орторомбическая (9), кубическая (3),
тетрагональная (6/7), тригональная (6/7), гексагональная (5)
изотропная среда (2)

7.

ТЕНЗОР УПРУГОСТИ – МАТРИЦА
УПРУГОСТИ
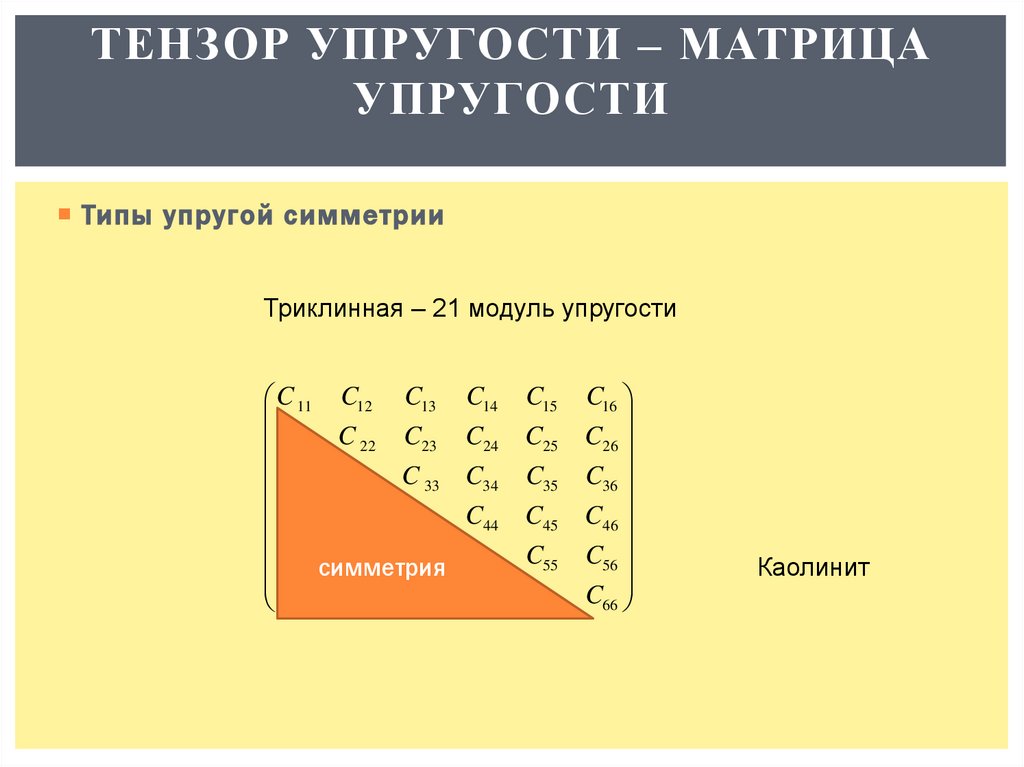
Типы упругой симметрии
Триклинная – 21 модуль упругости
C 11 C12 C13
C 22 C23
C 33
симметрия
C14
C24
C34
C44
C15 C16
C25 C26
C35 C36
C45 C46
C55 C56
C66
Каолинит

8.

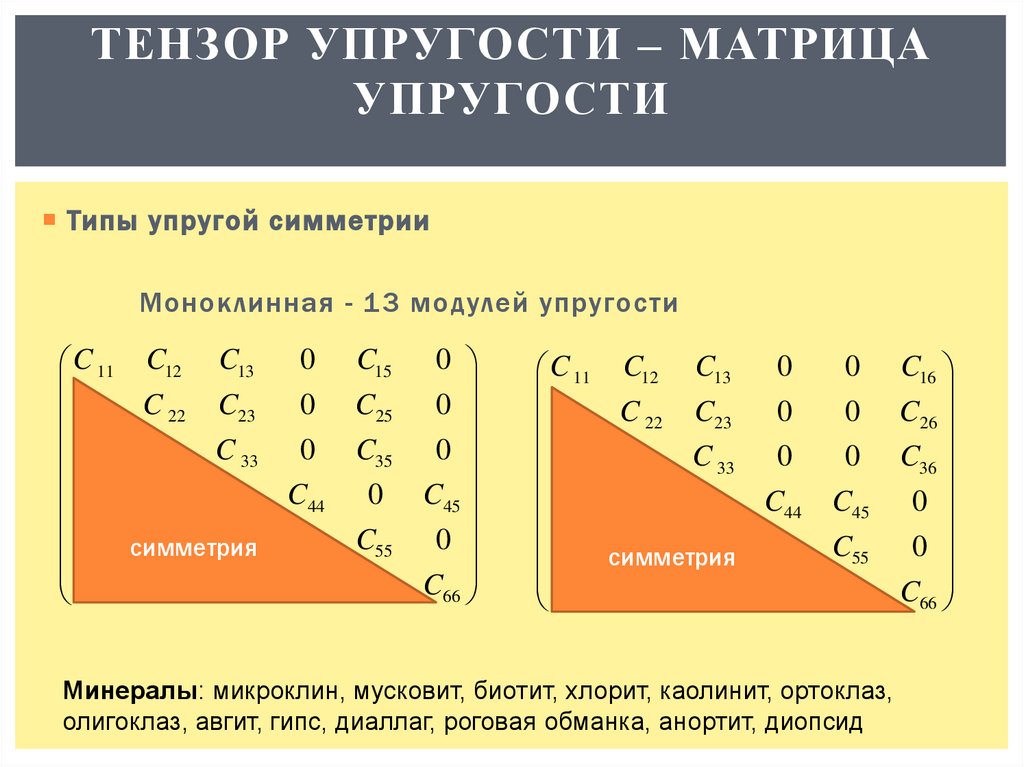
ТЕНЗОР УПРУГОСТИ – МАТРИЦА
УПРУГОСТИ
Типы упругой симметрии
Моноклинная - 13 модулей упругости
0
C 11 C12 C13
C12 C 22 C23 0
C13 C23 C 33 0
0
0 C44
0
0 симметрия
0
0
0
0
0
0
0
C15
C25
C35
0
C55
0
0
0
0
C45
0
C66
0
C 11 C12 C13
C12 C 22 C23 0
C13 C23 C 33 0
0
0 C44
0
0
0
0
0
симметрия
0
0
0
0
0 C16
0 C26
0 C36
C45 0
C55 0
0 C66
Минералы: микроклин, мусковит, биотит, хлорит, каолинит, ортоклаз,
олигоклаз, авгит, гипс, диаллаг, роговая обманка, анортит, диопсид

9.

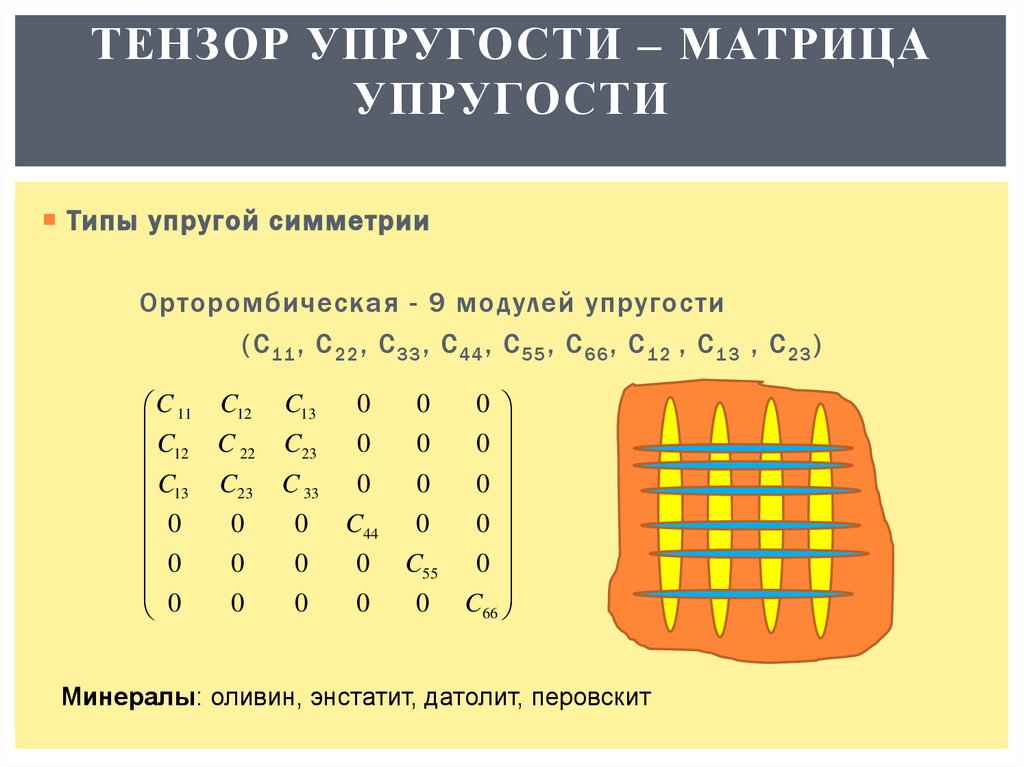
ТЕНЗОР УПРУГОСТИ – МАТРИЦА
УПРУГОСТИ
Типы упругой симметрии
Орторомбическая - 9 модулей упругости
(C 11 , C 22 , C 33 , C 44 , C 55 , C 66 , C 12 , C 13 , C 23 )
0
C 11 C12 C13
0
C12 C 22 C23
C13 C23 C 33 0
0
0 C44
0
0
0
0
0
0
0
0
0
0
0
0
0
C55
0
0
0
0
0
0
C66
Минералы: оливин, энстатит, датолит, перовскит

10.

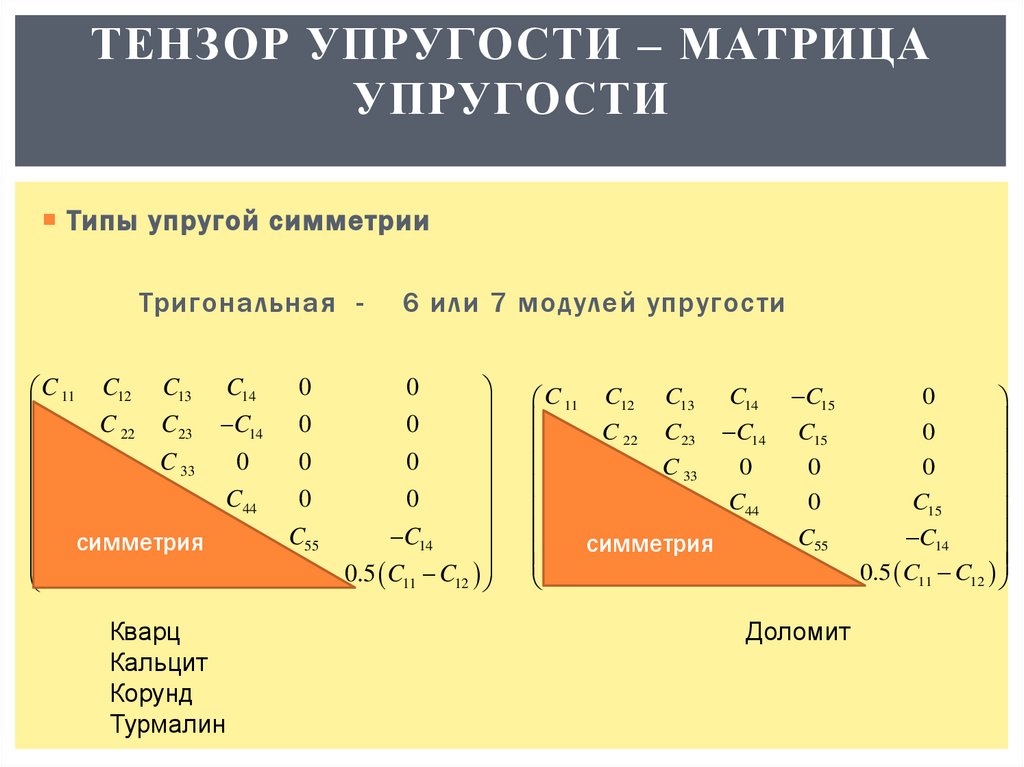
ТЕНЗОР УПРУГОСТИ – МАТРИЦА
УПРУГОСТИ
Типы упругой симметрии
Тригональная C 11 C12 C13 C14
C12 C 22 C23 C14
C13 C23 C 33
0
0
0
C44
0
0 симметрия
0
0
0
0
0
0
0
Кварц
Кальцит
Корунд
Турмалин
0
0
0
0
C55
0
6 или 7 модулей упругости
0
0
0
0
C14
0.5 C11 C12
C 11 C12 C13 C14
C12 C 22 C23 C14
C13 C23 C 33
0
0
0
C44
0
0
0
0
0
симметрия
0
0
0
0
C15
C15
0
0
C55
0
Доломит
0
0
0
C15
C14
0.5 C11 C12

11.

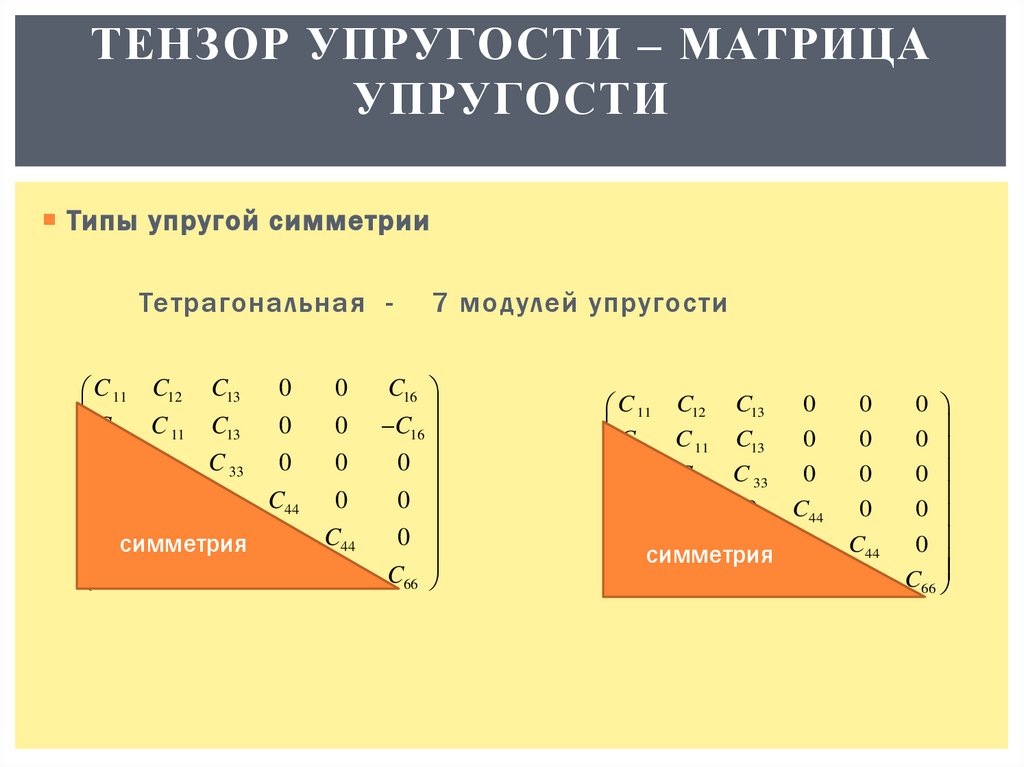
ТЕНЗОР УПРУГОСТИ – МАТРИЦА
УПРУГОСТИ
Типы упругой симметрии
Тетрагональная 0
C 11 C12 C13
0
C12 C 11 C13
C13 C23 C 33 0
0
0 C44
0
0 симметрия
0
0
0
0
0
0
0
0
0
0
0
C44
0
7 модулей упругости
C16
C16
0
0
0
C66
0
C 11 C12 C13
0
C12 C 11 C13
C13 C23 C 33
0
0
0 C44
0
0
0
0
0
симметрия
0
0
0
0
0
0
0
0
C44
0
0
0
0
0
0
C66

12.

ТЕНЗОР УПРУГОСТИ – МАТРИЦА
УПРУГОСТИ
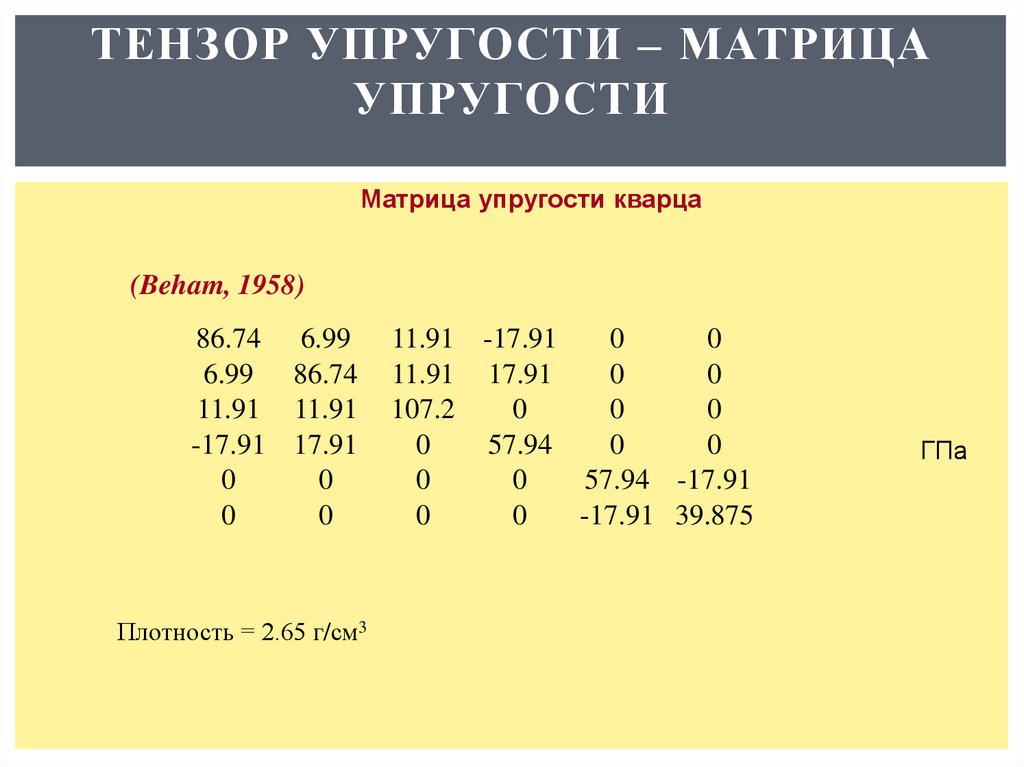
Матрица упругости кварца
(Beham, 1958)
86.74 6.99
6.99 86.74
11.91 11.91
-17.91 17.91
0
0
0
0
Плотность = 2.65 г/см3
11.91 -17.91
0
0
11.91 17.91
0
0
107.2
0
0
0
0
57.94
0
0
0
0
57.94 -17.91
0
0
-17.91 39.875
ГПа

13.

ТЕНЗОР УПРУГОСТИ – МАТРИЦА
УПРУГОСТИ
Типы упругой симметрии
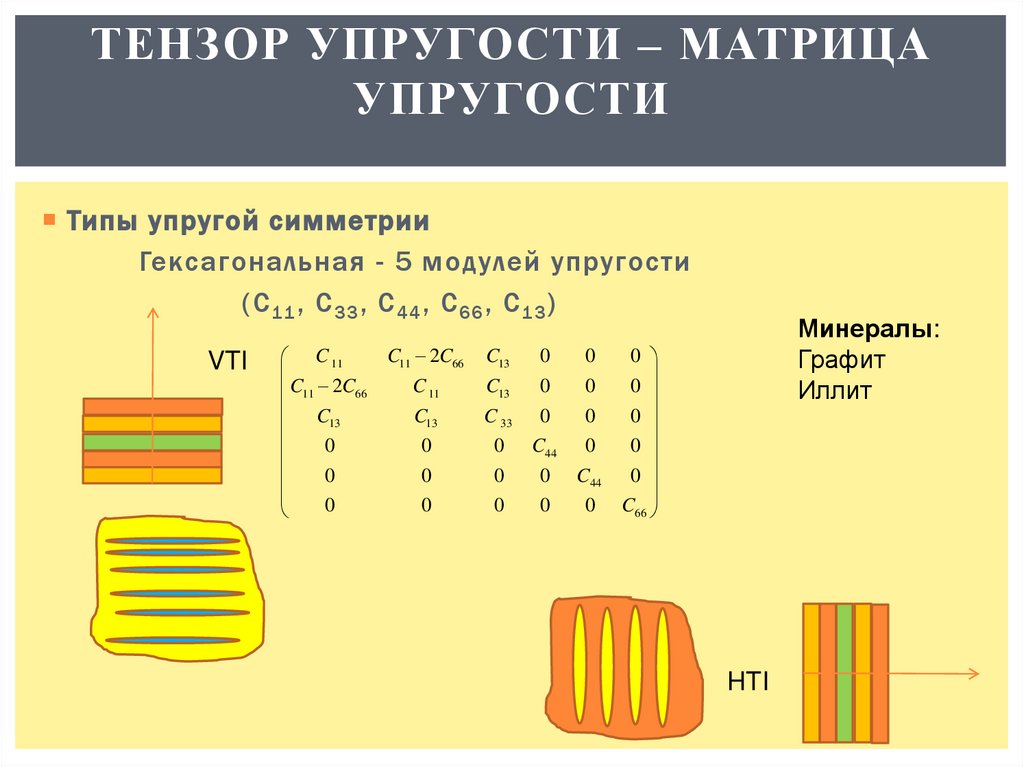
Гексагональная - 5 модулей упругости
(C 11 , C 33 , C 44 , C 66 , C 13 )
VTI
C 11
C11 2C66
C13
0
0
0
C11 2C66
C 11
C13
0
0
0
C13
0
C13
0
C 33 0
0 C44
0
0
0
0
0
0
0
0
C44
0
Минералы:
Графит
Иллит
0
0
0
0
0
C66
HTI

14.

ТЕНЗОР УПРУГОСТИ – МАТРИЦА
УПРУГОСТИ
Типы упругой симметрии
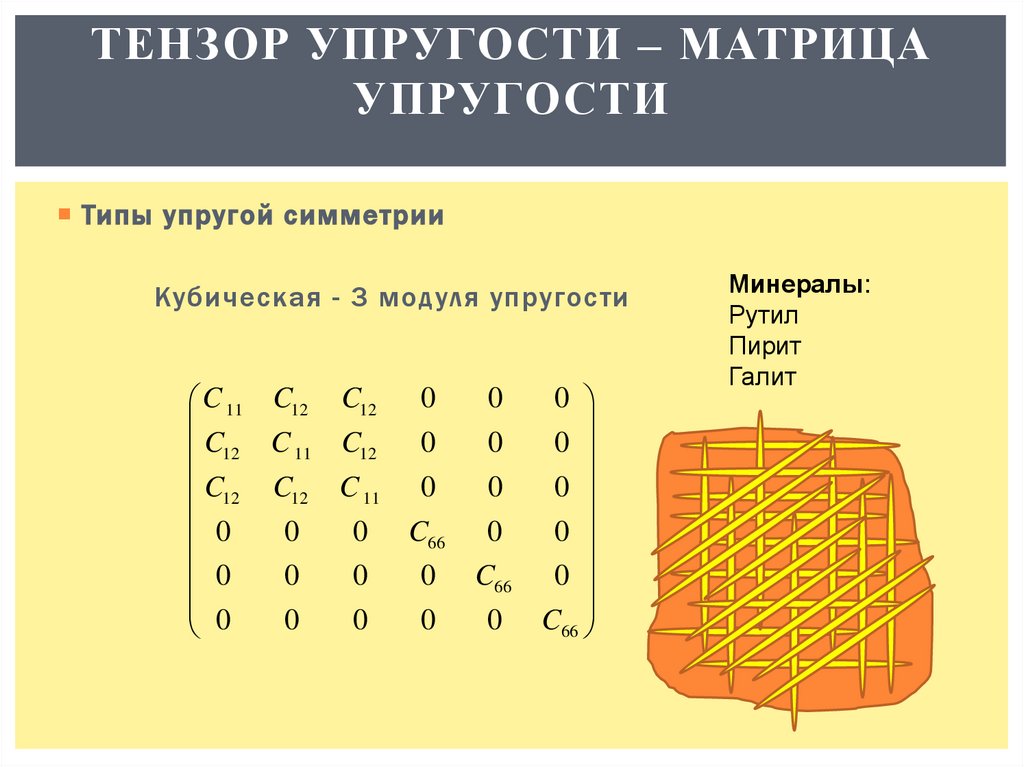
Кубическая - 3 модуля упругости
0
C 11 C12 C12
0
C12 C 11 C12
C12 C12 C 11 0
0
0 C66
0
0
0
0
0
0
0
0
0
0
0
0
0
C66
0
0
0
0
0
0
C66
Минералы:
Рутил
Пирит
Галит

15.

ТЕНЗОР УПРУГОСТИ – МАТРИЦА
УПРУГОСТИ
Типы упругой симметрии
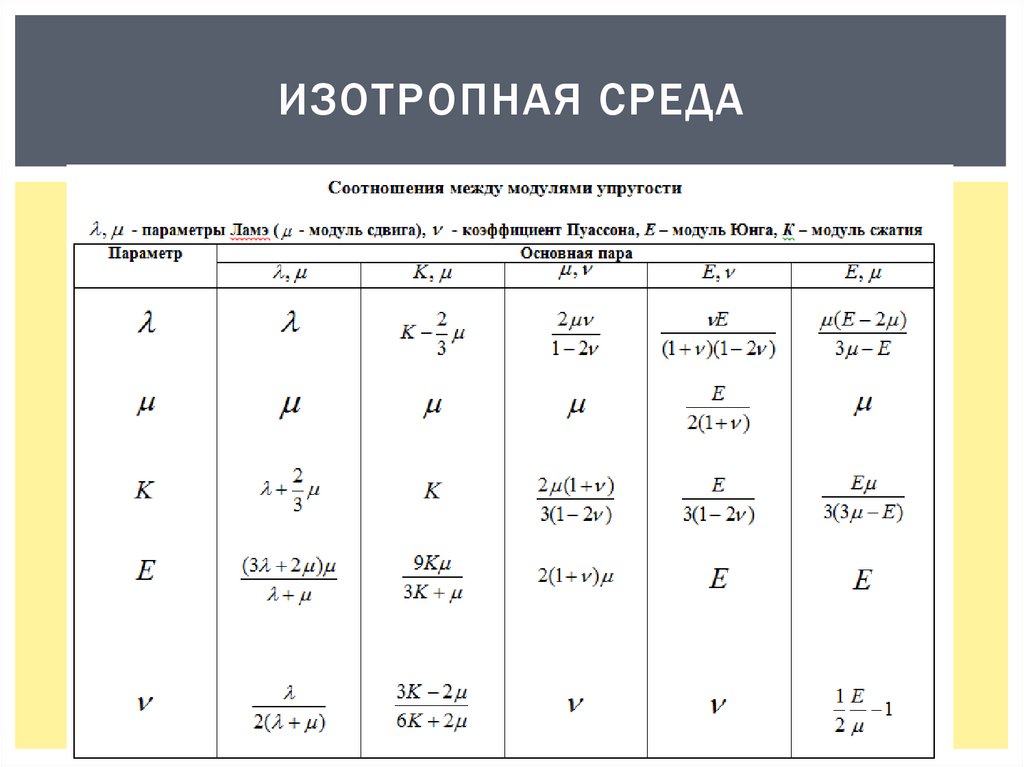
Изотропная среда - 2 модуля упругости –
(сжатия, сдвига), (Юнга, Пуассона), параметры Ламэ
C 11 C12 C12
C12 C 11 C12
C12 C12 C 11
0
0
0
0
0
0
0
0
0
0
0
0
C11 C12
2
0
0
0
0
0
C11 C12
2
0
0
0
0
C11 C12
2
0
0
0
4
C11 K
3
C44

16.

ИЗОТРОПНАЯ СРЕДА

17.

ЭФФЕКТИВНЫЕ ФИЗИЧЕСКИЕ
СВОЙСТВА КОМПОЗИТОВ
Эффективная среда - микроскопически неоднородная, макроскопически
однородная среда (композитный материал)
Общее определение
A(r) X* B(r)
Статистически однородная среда:
Статистические характеристики для
представительного объема не зависят от
координат
Эффективные упругие свойства
σ(r) C* ε(r)
Закон Гука
Эффективная электропроводность
j(r) S* (r) Закон Ома
Эффективная теплопроводность
q(r) λ* T (r)
Эффективные физические
свойства определяются с
помощью теории
эффективных сред
x
1
x(r )dr
V V
Закон Фурье
Эффективная гидравлическая
проницаемость
Закон Дарси
Q(r) K* h(r)
h
P
g

18.

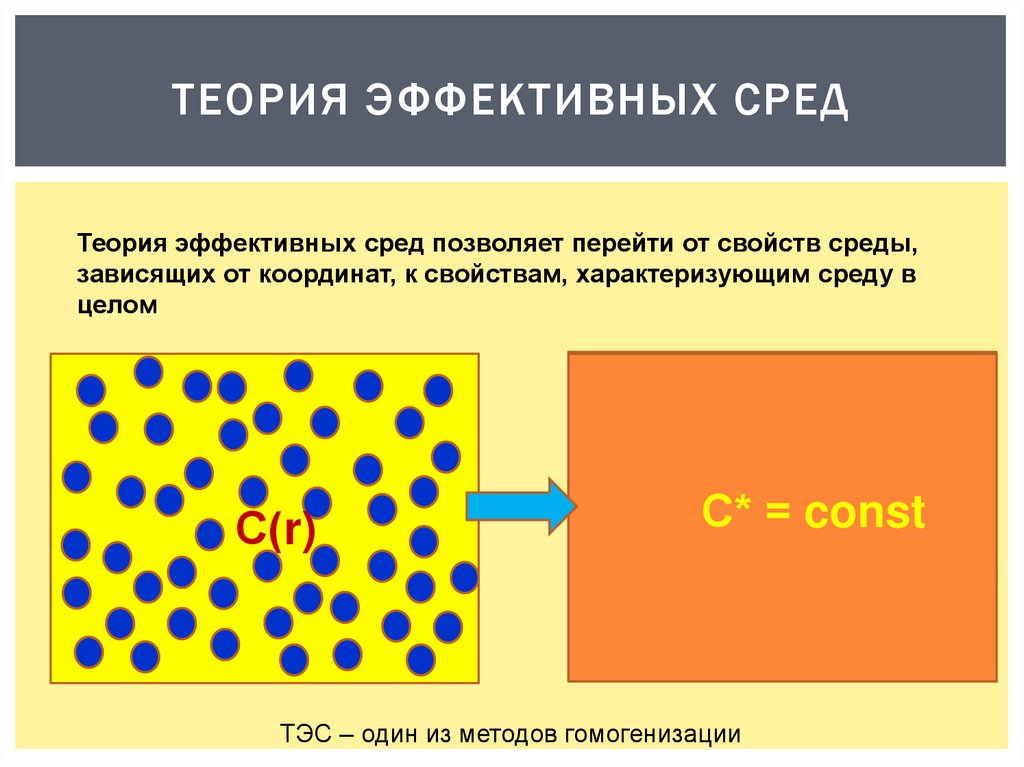
ТЕОРИЯ ЭФФЕКТИВНЫХ СРЕД
Теория эффективных сред позволяет перейти от свойств среды,
зависящих от координат, к свойствам, характеризующим среду в
целом
С(r)
С* = const
ТЭС – один из методов гомогенизации

19.

ЭФФЕКТИВНЫЕ ФИЗИЧЕСКИЕ
СВОЙСТВА ГОРНЫХ ПОРОД
Горная порода - природный микроскопически неоднородный,
макроскопически однородный композитный материал
Общее определение
Статистически однородная среда:
*
A
(
r
)
X
B(r)
Статистические характеристики для
представительного объема не зависят от
Эффективные упругие свойства
координат
σ(r) C* ε(r)
Закон Гука
Эффективная электропроводность
j(r) S* (r) Закон Ома
Эффективная теплопроводность
q(r) λ* T (r)
Закон Фурье
Эффективная гидравлическая
проницаемость
Закон Дарси
Q(r) K* h(r)
h
P
g

20.

ГОРНАЯ ПОРОДА КАК ПОРОВОТРЕЩИНОВАТАЯ СРЕДА
Порово-трещиноватая среда – как
композитная среда

21.

УСЛОВИЯ ПРИМЕНИМОСТИ ТЭС
ТЭС применима, если длина волны много больше
размера неоднородностей (для упругих свойств)
ТЭС применима, если масштаб рассмотрения
проблемы много больше размера
неоднородностей (для транспортных свойств)
Транспортные свойства: электропроводность,
теплопроводность, гидравлическая и диэлектрическая
проницаемость

22.

ЭФФЕКТИВНЫЕ ФИЗИЧЕСКИЕ
СВОЙСТВА ГОРНЫХ ПОРОД
Неоднородности в горной породе – зерна минералов,
поры, трещины, заполненные различными веществами
Форма неоднородностей (включений) в
теории эффективных сред- эллипсоид
общего вида
Чаще используют эллипсоид вращения

23.

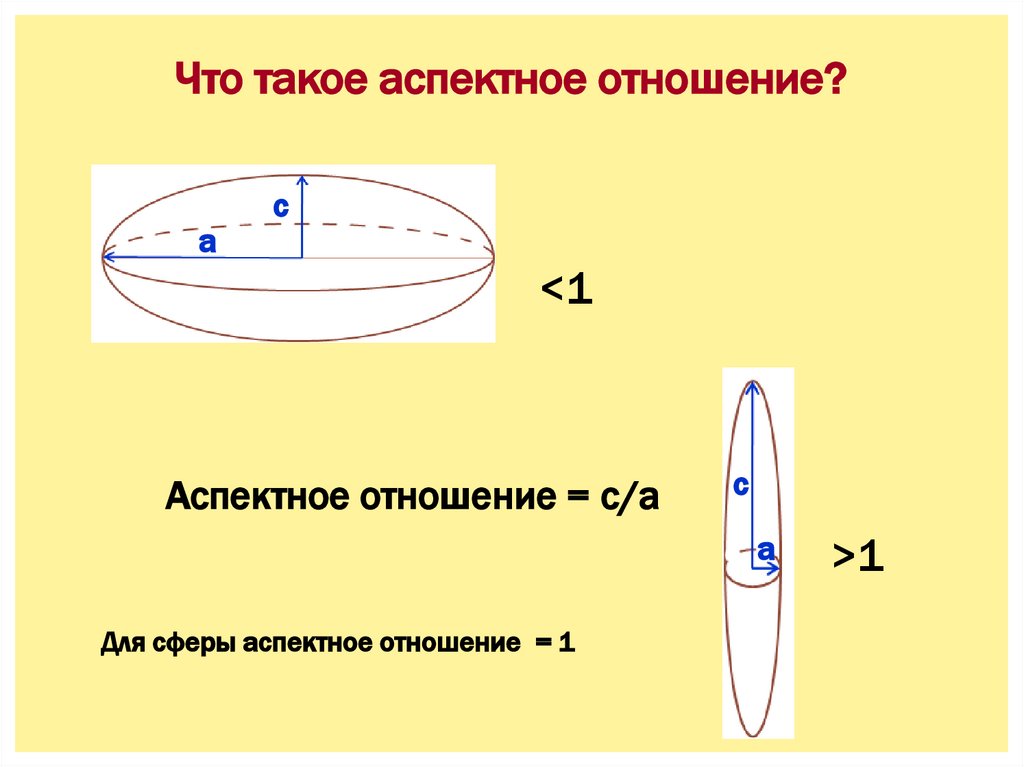
Что такое аспектное отношение?
a
c
<1
Аспектное отношение = c/a
c
a
Для сферы аспектное отношение = 1
>1

24.

ГОРНАЯ ПОРОДА КАК АНИЗОТРОПНЫЙ
КОМПОЗИТНЫЙ МАТЕРИА Л
Горная порода как анизотропный композитный материал
Причины анизотропии физических свойств горных пород
1. Анизотропия физических свойств минералов, имеющих
преимущественную ориентацию в породе
2. Преимущественная ориентация неоднородностей с контрастными
свойствами по отношению к другим включениям (например,
преимущественная ориентация трещин)
3. Тонкослоистость

25.

ПОСТРОЕНИЕ РЕШЕНИЯ ДЛЯ
ЭФФЕКТИВНЫХ ФИЗИЧЕСКИХ СВОЙСТВ
Эффективные упругие свойства
σ(r) C* ε(r)
Закон Гука
C(r) C(r) C' (r)
σ(r) σ(r ) σ ' (r )
ε(r ) ε(r ) ε ' (r )
ε ' (r ) σ ' (r ) C' (r ) 0
σ(r) C(r) ε(r) C' (r)ε ' (r)
ε (r ) P ε(r )
'
C* C(r) C' (r )P(r )
Проблема определения эффективных физических свойств является
проблемой учета взаимодействия многих тел и, в общем случае, может
быть решена лишь приближенно

26.

МЕТОДЫ ТЕОРИИ ЭФФЕКТИВНЫХ СРЕД
ε' (r ) P ' ε(r )
C* C(r ) C' (r )P' (r )
S C
1
σ (r) Q σ(r)
'
Тензор податливости
S* S(r) S' (r)Q' (r)
Метод Фойгта: ε (r ) 0
C* CV C(r )
Метод Ройсса: σ (r ) 0
S S S(r )
'
'
*
R
C S
R
R 1
Применяются для определения эффективных свойств поликристаллов
C C C
R
ii
*
ii
V
ii
«вилки» для диагональных компонент»

27.

МЕТОДЫ ТЕОРИИ ЭФФЕКТИВНЫХ СРЕД
Метод Фойгта – Ройсса - Хилла
Cij*
CijV CijR
S(r)
C S
R
C C(r )
V
2
R
1
1
Как определять среднее по объему?
Среднее по объему = статистическое среднее
(верно для статистически однородных сред)
Углы Эйлера
2 2
y’
z
z’
ij
k’
C
V
ij
k
A
x
C ( , , ) f , , sin d d d
y
x’
i1
x1
0 0 0
2 2
f , , sin d d d
0 0 0