Similar presentations:
Основы физики прочности и пластичности
1.
Основы физики прочности и пластичностиДЕФОРМАЦИИ И НАПРЯЖЕНИЯ
2.
1.Зависимость между напряжением и деформацией в идеальных кристаллах.Двухатомная модель.
3.
С развитием представлений о кристаллическом строениитвердых тел и взаимодействии атомов (молекул) в
кристаллической решетке металлов появилась возможность
теоретически рассмотреть такое взаимодействие в терминах
деформация – напряжение.
Выражение для сил связи в кристаллической решетке
является частным случаем общего уравнения А.Иоффе:
U A
e2
1
3
B
2
3
4 3
r0
3
где - атомный объем.
e2
C
(2.1)
4.
Отсюда металлическая связь может быть записана какA B
U m n;
r
r
n m
(2.2)
U min U 0
и
Рис. 2.1. Модель взаимодействия между частицами вещест
Условие минимума энергии взаимодействия:
U min U 0
5.
иAm
Bn
dU
0 m 1 n 1
dr
r
r
Отсюда
(2.3)
Am r0n 1
B
n r0m 1
И выражение для U принимает вид:
A Am r0n 1 1
U m
r
n r0m 1 r n
(2.4)
Сила взаимодействия P:
m 1
m 1
1
dU Am Am r0n 1 n
1 r0n 1 Am r0m 1 r0n 1 Am r0
r0
P
Am m 1 n 1 m 1 m 1 m 1 n 1 m 1
dr r m 1
n r0m 1 r n 1
r r0 r0 r
r r0 r
r
r
(2.5)
Для взаимодействия всех Ni –тых и Nj –тых атомов,
образующих пары в кристаллах,
1 N
U U (ri rj )
2 i , j 1
(2.6)
6.
где.
энергия взаимодействия пары атомов с
координатамиr i
и rj
U ( ri rj )
-
При механическом воздействии
r r0 r
При одноосном растяжении величина внешнего
приложенного напряжения не должна превышать max или
Pmax. Условие для Pmax можно записать как
r0m 1
r0n 1
dP
0 0 m 2 (m 1)( 1) n 2 (n 1) 0
dr
r0
r
ri
Отсюда получаем, что
r0n 1 n 1 r n 2
m 2
m 1
r0 m 1 r
и
n m
0
r
(2.8)
n 1
n 1 n m
n
m
r ; rmax r0
m 1
m 1
(2.9)
(2.7)
7.
"Мягкие" кристаллы имеют m=1, n=3 и для нихrmax = 1,41 ro
При перекрытии электронных оболочек m=1, n=11 и
r=0,2 ro.
Если же преобладают силы Ван дер Вальса, , то
r=0,115 ro.
r
т.е.
В лагранжевых представлениях
r r (1 )
r0
и из (2,5) получаем величину напряжения:
0
A1m
1
1
m 1
m 1
r0 (1 )
(1 ) n 1
(2.10)
Реально = 0,005-0,2%. При = 10-4 – 2 10-3 уже появляется
остаточная деформация.
8.
Небольшие смещения или деформации могут вызватьостаточную деформацию только в том случае, если в
реальном кристалле есть причины, повышающие его
энергетический уровень, в частности, внутренние
напряжения. Это наводит на мысль о существовании
дефектов кристаллической решетки.
Разлагая в биноминарный ряд выражение (2.10 ), получаем
(m 1)( m 2) (n 1)( n 2) 2 (m 1)( m 2)( m 3) (n 1)( n 2)( n 3) 3
(
n
m
)
...
r0m 1
(m n)2!
(m n)3!
A1
Здесь
A1 m
m 1
E аналог модуля упругости.
(2/11)
(n m) E
9.
Это одна из форм записи закона Гука. Таким образом законГука справедлив только для очень малых деформаций.
Иеншем предложил такую связь между напряжение и
деформацией:
2
3
(2.12)
2
k k ...
E
E
E
Уравнение (2.12) можно получит из (2,10), полагая, что
m=1, n=3.и пренебрегая 2, 3, 4 и т.д.
A1 1 1
1 Ai 1
1 2 2 1
Ai 2
2
E
r0 (1 )2 (1 )4
r02 1 2 2 2 4 3 2 2 2 2 3 4 r02 (1 4 )
1 4
2A
E 2i
r0
E
E
4
1 4
E
E
1 4
E
E
1
10.
Разлагая1
1 4
в биноминальный ряд, получаем
E
1
2
3
2
1 z 1 z z z ... E 4 E 4 E ...
2
3
(2.13)
Отсюда можно определить значение коэффициентов в
формуле Иеншема.
Таким образом закон Гука оправдан только для Е
Исходя из анализа сил связи в кристаллической решетке,
особенностью
деформации
кристаллов
является
неидентичность их поведения при растяжении и сжатии. При
растяжении rmax достигается при Pmax, а при сжатии (- r)
нет.
11.
Теоретическую прочность в двухатомной модели можно оценитьследующим образом. Подставим P Pmax
Pmax
Отсюда
Am r0
m 1
r0 rmax
m 1
rmax r0
r0
rmax
n m
n 1
n 1
m 1
(2.14)
(2.15)
Следовательно, можно представить напряжение max как
max
r0m 1
r0n 1
A1m(n m)
m 1
n 1
r0m 1
n
m
n
m
m 1 n 1
n 1 n 1
r
r
0
0 m 1
m 1
max
m 1
n 1
m
n
m
A1m(n m) n 1
n 1 n
m 1
r0m 1
m
1
(2.16, а)
(2.16, б)
12.
Тогда можно записатьA1m(n m)
E 2G (1 )
m 1
r0
Здесь коэффициент Пассона.
В этом случае
m 1
max
n 1 m n n 1
2G(1 )
1
m
1
m
1
При m=1 n=3 max =0,325 G.
При m=1 n=11 max =0,105 G
При m=6 n=11 max =0,15 G
n 1
m 1
(2.17)
(2.18)
Теоретическая прочность на сдвиг кристалла впервые была
вычислена Френкелем, исходя из простой модели двух рядов
атомов, смещаемых друг относительно друга под действием
напряжения сдвига (рис. 2.2). Межплоскостное расстояние
(расстояние между рядами) равно а, а расстояние между
атомами в направлении скольжения равно b.
13.
Под действием напряжения сдвига эти ряды атомовсмещаются друг относительно друга, попадая в равновесные
позиции в таких точках, как А и В, где напряжение сдвига,
необходимое для сохранения данной конфигурации, равно
нулю.
Точно так же это напряжение равно пулю, когда атомы в обоих
рядах располагаются точно друг над другом в положениях С и
D. В промежуточных положениях напряжение имеет конечные
значения, которые, периодически меняются в объеме
решетки. Если для напряжения сдвига смещение равно х, то
напряжение будет периодической функцией х с периодом b.
Проще всего предположить, что эта зависимость является
синусоидальной (рис. 2.2)
14.
Рис. 2.2. К расчету прочности по А.Френкелю(2.19)
Для малых смещений
Используя закон Гука, где G — модуль сдвига,
получаем другое выражение
где G – модуль сдвига, а х/а — деформация сдвига.
15.
Приравнивая приведенные выражения для , получаемПодставляя это значение k в соотношение (2.19), имеем
(2.20)
Максимальное значение , отвечающее напряжению, при
котором решетка переводится в неустойчивое состояние,
достигается при смещении b/4, откуда
(2.21)
где 0 критическое напряжение сдвига.
16.
напряжение сдвига приближенно равно G/2 . Длякристаллов меди G = 4000 кгс/мм2; таким образом,
теоретическое значение 0 составляет 760 кгс/мм2 по
сравнению со значением 100 гс/мм2 для реальных
кристаллов (табл. 2.2). Отсюда ясно, что теоретическое
значение прочности на несколько порядков величины
больше наблюдаемого значения.
Модули Юнга некоторых веществ Таблица 2.1
Модуль
Юнга,
ГПа
Металлы
Модуль
Юнга,
ГПа
Резина
0,7
Al
70
Пластик
17
Cu
125
Древесина
15
W
415
Стекло
55
Mo
320
Алмаз
400
Fe
210
Волокно
бора
480
Mg
45
Неметалл
ы
17.
Такоерасхождение
воспринимается
вначале
как
свидетельство того, что проведенный анализ является
ошибочным, по более детальные исследования показывают,
что, хотя упрощающие предположения приводят к получению
лишь приблизительного ответа, общие выводы являются
правильными. Расчет может быть уточнен главным образом
за счет использования более близкого к действительности
закона периодического изменения в зависимости от х; кроме
того, следует учесть тот факт, что в реальных плотно
упакованных
металлических
структурах
могут
быть
устойчивые положения атомов, отличные от A и В, например
двойниковая конфигурация. Однако даже с учетом этих
факторов значение 0 уменьшается только до величины
G/30, что все еще на несколько порядков величины больше
наблюдаемого значения.
18.
Из такого теоретического рассмотрения неизбежноследует заключение, что использованная простая модель
не соответствует поведению реальных кристаллов,
которые в действительности должны содержать дефекты,
уменьшающие механическую прочность.
Еще в 1921 г. Гриффитс предположил, что относительно
малая прочность хрупких твердых тел, таких, как стекло,
объясняется наличием в них микроскопических трещин, на
которых напряжение разрушения падает до значительно
более низкого уровня, чем предсказанный теоретически.
Однако лишь в 1934 г. Поляни, Орован п Тейлор
независимо друг от друга ввели представление о
дислокациях в кристаллическом твердом теле.
19.
Дислокация является линейным дефектом, пли нарушениемнепрерывности смещения между двумя частями кристалла,
из которых одна претерпела сдвиг, а другая нет; таким
образом, деформация осуществляется последовательным
прохождением дислокаций по плоскости скольжения, а не
путем одновременного однородного сдвига по всему
кристаллу.
max
G
0.16 G
2
Реальные значения предела прочности в = 400 – 1500 –
3500 МПа, теор = 10000 МПа
20.
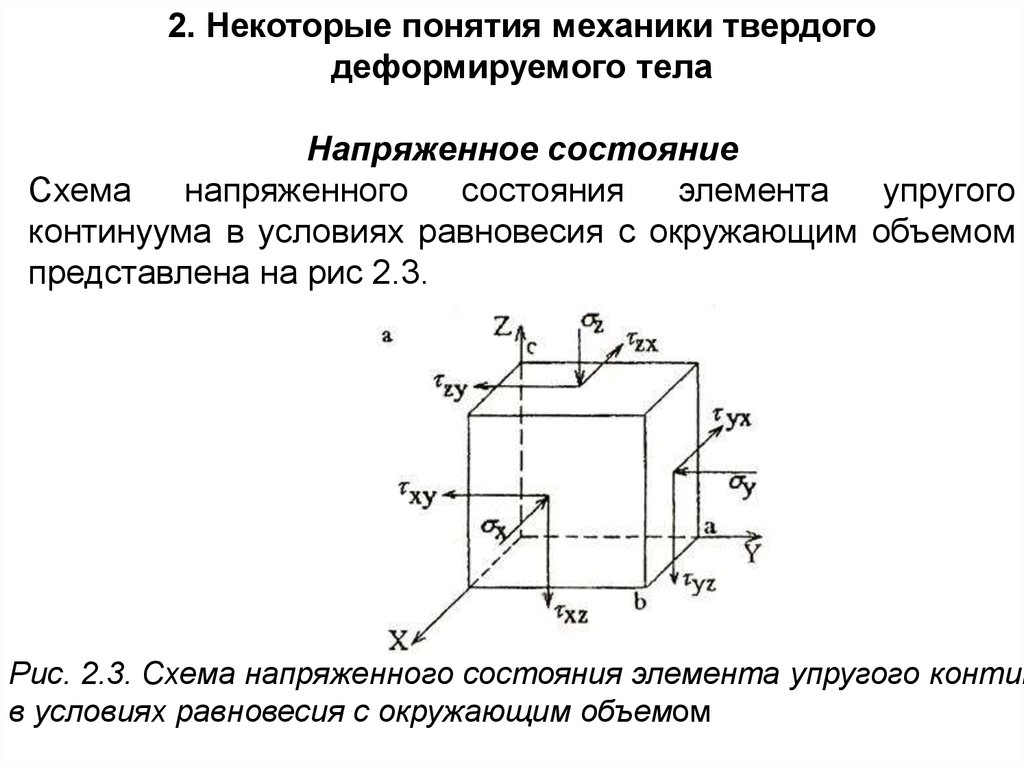
2. Некоторые понятия механики твердогодеформируемого тела
Напряженное состояние
Схема
напряженного
состояния
элемента
упругого
континуума в условиях равновесия с окружающим объемом
представлена на рис 2.3.
Рис. 2.3. Схема напряженного состояния элемента упругого контин
в условиях равновесия с окружающим объемом
21.
В этом случае тензор напряженного состояния можно записатьx xy xz
yx y yz
zx zy z
(2.22)
где x . y. z – нормальные напряжения, ij – касательные
напряжения.
Согласно правилу Онзагера
xy yx ; zy yz ; zx xz
Когда
xy yz xz 0
то x 1 ; y 2 ; z 3
Среднее гидростатическое напряжение можно записать
n
1 2 3
3
x y z
3
(2.23)
22.
Соответственно главные касательные напряжения можноопределить как:
1 3
1 2
2 3
1
; 2
; 3
(2.24)
2
2
2
Тогда тензор деформации можно представить как сумму
шарового тензора и девиатора поля напряжение
x xy xz n 0 0 n x
xy
xz
(2.25)
yx y yz 0 n 0 yx
n y
yz
zx zy z 0 0 0 n
zx
zy
n z
Гидростатическое напряжении шарового тензора равно нулю
( n x ) ( n y ) ( n z ) 3 n x y z
0 (2.26)
3
3
3
Шаровой тензор характеризует деформацию тела без
изменения его формы.
Девиатор отвечает за дефолиацию, связанную с
изменением формы твердого тела.
23.
Для тензора поля напряжений можно записатьJ i J 2 J 3 0
3
2
(2.27)
где J1. J2. J3 – инварианты тензора напряжения:
J1 x y z
J 2 x y z
J 3 x z x y y z
Деформации в поле напряжений
Рис. 2.4. К определению деформаций в поле напряжений
24.
l2 l0 ll1
l
(2.28)
Истинная деформация описывается уравнением:
l
dl
dl
l
ln 1
l
l l0 l
l0
l1
(2.29)
Если считать, что при деформации объем тела не
изменяется (V = const), то удлинение тела в одном
направлении должно сопровождаться его сокращением в
двух
других
направлениях.
Это
учитывается
коэффициентом Пуассона .
y x ; z x
Обычно = 0,25-0,5. Для абсолютно не сжимаемого тела
= 0,5.
25.
Средняя (гидростатическая) деформация определяется какn
x y z
(2.30)
3
Сдвиговую деформацию для чистого сдвига определяют как
показано на рис.2.4.
В этом случае тензор поля деформаций можно записать как
x
1
xy
2
1
yx
2
1
zx
2
y
1
zy
2
1
xz
2
n
1
yz 0
2
0
z
0
0
n
0
0
n
n x
1
xy
2
1
yx
2
1
zx
2
n y
1
zy
2
1
xz
2
1
yz
2
(2.31)
n z
Здесь шаровой тензор отвечает за деформацию без
изменения формы, девиатор – за деформацию с
изменением формы.
26.
c ji cijВ этом случае обобщенный закон Гука – Коши записывается
как:
x c11 x c12 y c13 z c14 xy c15 xz c16 yz
y c21 x c22 y c23 z c24 xy c25 xz c26 yz
z c31 x c32 y c33 z c34 xy c35 xz c36 yz
xy c41 x c42 y c43 z c44 xy c45 xz c46 yz
xz c51 x c52 y c53 z c54 xy c55 xz c56 yz
(2.32)
yz c61 x c62 y c63 z c64 xy c65 xz c66 yz
Здесь 36 const в соотношениях между напряженьями и
c ji cij
деформациями. Если применить правило Онзагера
то число const становится равным 21. А езди расположить оси
по ребрам куба, то,
c11 c22 c33
c44 c55 c66
c12 c13 c23
(2.33)
27.
Константы Ламэ: модуль нормальной упругости, модульЮнга Е: модуль сдвига, модуль Гука – G; коэффициент
Пуассона - .
Соотношение между ними:
G
E
1
S
2(1 2 ) c
K
E
3(1 2 )
К – объемный модуль упругости.
xy c44 xy
c11 c12
c'
2
- напряжение действует в плоскости (100) в
направлении 010 (ребро куба).
- напряжение действует в плоскости (110)
направлении 110 (диагональ грани куба).
Податливость S, величина, обратная модулю
S
1
c
28.
S11 2 S12S11 S12
S 44
1
1
, S11
c11 2c12
E
1
S
, 12 M
c11 c12
S11
1 1
,
G
c44 S 44
Анизотропия упругих свойств кристалла определяется
константой анизотропии А из соотношением
c44
2c44
A
c1 '
c11 c12
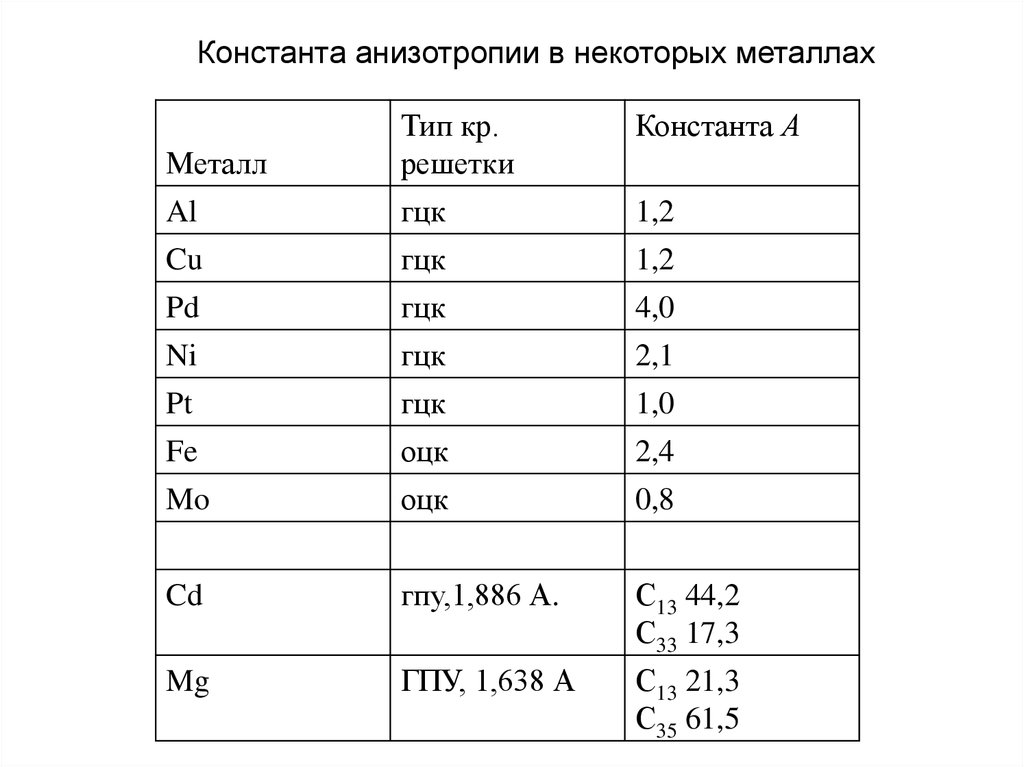
29.
Константа анизотропии в некоторых металлахКонстанта А
Металл
Тип кр.
решетки
Al
гцк
1,2
Cu
гцк
1,2
Pd
гцк
4,0
Ni
гцк
2,1
Pt
гцк
1,0
Fe
оцк
2,4
Mo
оцк
0,8
Cd
гпу,1,886 А.
С13 44,2
С33 17,3
Mg
ГПУ, 1,638 А
С13 21,3
С35 61,5
30.
В общем случае трехосного напряженного состояниярезультирующая деформация вдоль выбранного направления
вычисляется из соотношения:
x
Таким образом
E
y
E
z
E
1
x ( y z )
E
1
y y ( x z )
E
1
z z ( y x )
E
x
Или
x
1
1 1 ( 2 3 )
E
1
2 2 ( 1 3 )
E
1
3 3 ( 2 1 )
E
(2.34)
31.
Объемная компонента деформации равна.v
V
V
Если положить, что V= 1, то
1 V (1 1 )(1 2 )(1 3 ) 1 1 2 3 1 2 1 3 2 3 1 2 3
Пренебрегая члены более высокого порядка и зная что
величина <<1, можно записать
V
v
1 2 3
1
32.
Работа упругой деформацииПусть F площадь поперечного сечения образца, lo первоначальная длина. Тогда запасенная энергия W может
быть представлена как
W Fl0 d и в единице объема W d E d
т.к.
E
0
0
0
1
1
Или
1
1 2 1
12
W1 E 1 1 1
2
2
2E
W W1 W2 W3
В общем случае
1
1 2 3 W
( 12 22 32 ) 2 ( 1 2 1 3 2 3 )
2E
Часть энергии деформации связана с деформацией без
изменения форумы, часть только с формоизменением. То
есть,
W WS WV
33.
Тогда после соответствующих преобразований получаем:1
1 1 2 3
1
( 1 2 3 )( 1 2 3 ) 2 ( 1 2 3 )
WV V V
( 1 2 3 )
2
2
3
6E
(1 2 )
( 1 2 2 ) 2
6E
WS W WV
1
( 12 22 32 ) 2 ( 1 2 1 3 2 3 )
2E
(1 2 )
( 1 2 2 ) 2 2( 1 2 1 3 2 3 )
6E
2
[3( 12 22 32 ) 6 ( 1 2 1 3 2 3 ) ( 12 22 32 ) 2( 1 2 1 3 2 3 )
6E
2 ( 12 22 32 ) 4 ( 1 2 1 3 2 3 )]
1
2( 12 22 32 ) 2( 1 2 1 3 2 3 ) 2 ( 12 22 32 ) 2 ( 1 2 1 3 2 3 )
6E
2(1 ) ( 12 22 32 ) ( 1 2 1 3 2 3 )
2
6E
2
2(1 ) 12 2 1 2 22 22 2 2 3 32 12 2 1 3 32
3E
2
2
2
2
2(1 ) 1 2 1 2 2 3
3E 2 2 2
34.
Таким образом, в запасенной энергии, связанной сформоизменением объекта, входят только касательные
напряжения, выраженные через разницу нормальных
напряжений.
35.
Теории эквивалентностиПри нагружении макроскопического тела в нем, как
правило, возникает объемное напряженное состояние.
Однако экспериментально можно определить только либо
напряжение растяжения, либо напряжение сжатия.
Поэтому предлагаются некоторые подходы, позволяющие
получить представление об объемном напряженном
состоянии по данным испытания на растяжение. Такие
подходы называются гипотезами эквивалентности.
Гипотезы эквивалентности показывают связь между
линейным и пространственным напряженными
состояниями. При этом делаются следующие допущения:
а). тело считается однородным и изотропным по всему
объему;
б). материал заполняет весь объем без пор и трещин;
в). выполняется во всем объеме закон Гука;
г). отсутствуют в материале внутренние напряжения.
36.
1. Гипотеза наибольших нормальных напряжений.Системы считаются эквивалентными, если наибольшие
напряжения равны:
= 1
(2.36)
2. Гипотеза наибольших линейных деформаций
max 1 2 3 1 2 3
E
E
E
E
(2.37)
. 3. Гипотеза
наибольших касательных напряжений. Состояние
считается эквивалентным, если наибольшие касательные
напряжения , возникающие в каждом из них, равны между
собой. Критерий Мора.
max
2
max
1 3
2
1 3
(2.38)
37.
4.Гипотеза
одинаковой
энергии
формоизменения.
Состояние считается эквивалентным, если энергия
формоизменения элементарного объема при линейном и
объемном напряженном состояниях равны. Критерий Генки
и Мозеса.
1
2
2
2
1 2 2 3 1 3
2
(2.39
Правая часть уравнения – приведенные (касательные)
напряжения.
38.
Схемы напряженного состояния39.
Диаграмма напряженного состояния Я.Б.Фридмана.Коэффициент мягкости нагружения:
max
пр.
max
Наибольшие приведенные напряжения по второй гипотезе
эквивалентности:
1 3
пр.
max 1 ( 2 3 )
m
2
То есть,
1 3
2 1 0,5( 2 3 )
(2.40)
40.
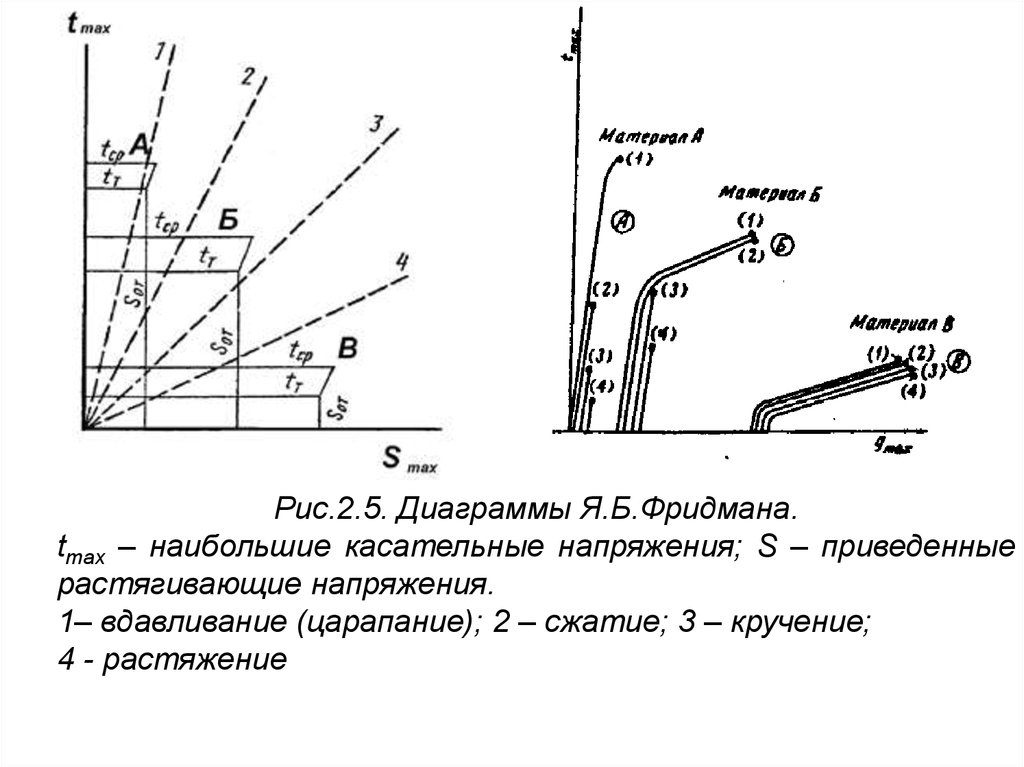
Рис.2.5. Диаграммы Я.Б.Фридмана.tmax – наибольшие касательные напряжения; S – приведенные
растягивающие напряжения.
1– вдавливание (царапание); 2 – сжатие; 3 – кручение;
4 - растяжение
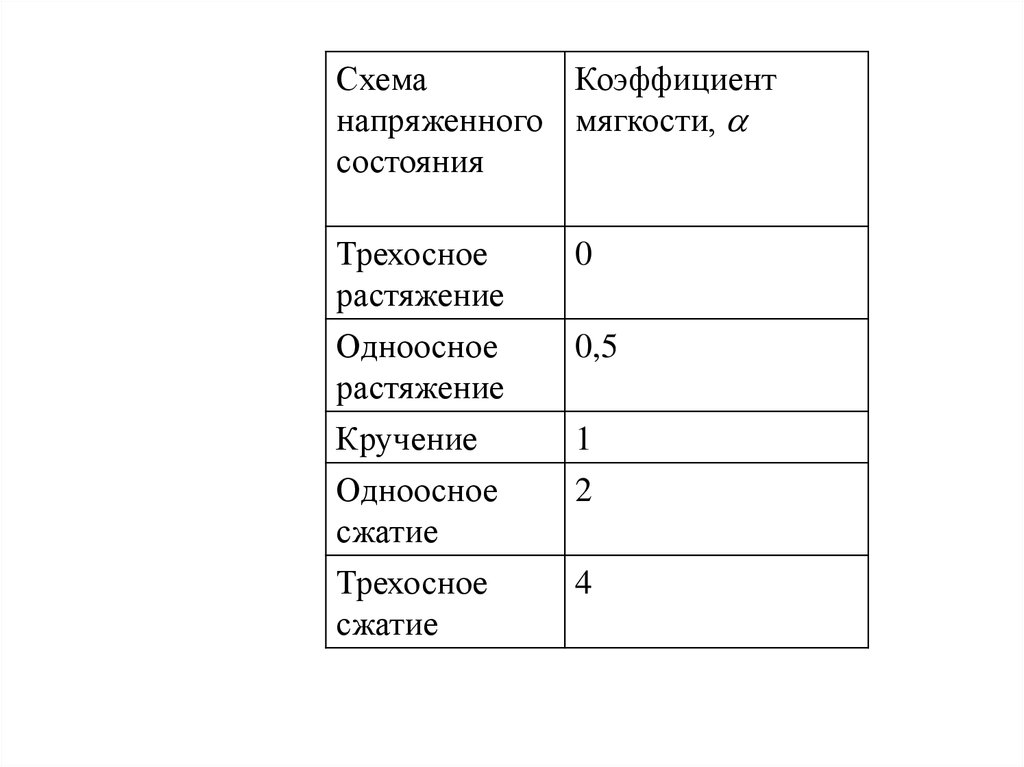
41.
СхемаКоэффициент
напряженного мягкости,
состояния
Трехосное
растяжение
Одноосное
растяжение
0
Кручение
1
Одноосное
сжатие
2
Трехосное
сжатие
4
0,5
42.
Уравнения пластичностиВсе что ранее рассматривалось относилось к
деформации в упругой области. Заманчиво рассмотреть
ситуация на начальном участке деформационной кривой
немного выше предела пропорциональности. В этом случае
происходит переход в область пластических деформаций.
Но поскольку захватывается только начальный этап этого
процесса, полагают, что прежние соотношения между
напряжениями
и
деформациями
сохраняются
с
определенной степени отклонений.
1
1
1 1 ' 2 3 d p1 1 2 3 dc
2
2
1
1
2 2 ' 1 3 d p2 2 3 1 dc
2
2
1
1
3 3 ' 2 1 d p3 3 2 1 dc
2
2
(2.41)
43.
Здесь с – свойство, зависящее от степени деформации.P1 > P2 > P3 – индексы компонент деформации по разным
осям. ≈ 0,5
Работа пластической деформации на единицу объема
dW p d1d p1 d 2 d p1 d3d p3
d 1 v ; d 2 v ; d 3 v ;
1
2
3
v – объемные напряжения.
Уравнение Райса для этого случая:
dW p
3 2
d1 d22 d23 dc
2
Для одноосного растяжения
d p dc
(2.42)
44.
Здесь - напряжение течения. Коэффициентd
деформационного упрочнения
k
d
1 d
dc
отсюда
k
Приближенные методы учитывают равенство объемов
до и после деформирования
l*
W p (l )
l0
dl
l
F
* ln * * ln *
l
l0
F0
(2.43)
Коэффициент процесса =0,5 – 0,8.
* F0
Wp ln
F
Если х – путь, P – сила. То работа на этом пути равна P x.
Объем тела равен F1 x.
В этом случае полная работа деформации равна:
W p F1 x P1 x W p
P1
F
P1 * ln 1 F1
F1
F2
(2.44)








































 physics
physics








