Главные центральные моменты инерции

1.

1.2. Главные центральные моменты инерции
J x J xy J xz
J yx J y J yz 0.
J zx
J zy
Jz
Частный случай:
J i
Jx J y
2
i x, y
J x , J y и J z
J xz J yz = 0, J xy 0 :
2
Jx J y
2
J
xy
2
Угловое положение главных центральных осей относительно связанных.
J xz J yz = 0, J xy 0
Частный случай:
x
y
x cos sin
y sin cos
z
0
... tg 2
0
z
x x cos y sin
0
x y dm 0 ...
y y cos x sin J xy
0
z z
1
2 J xy
J y Jx
1

2.

1.3. Ориентация связанных осей 0xyz
относительно опорных 0x0y0z0
Ракетная система поворотов
x a11 a12
y a21 a22
z a
31 a32
& & &
a13 x0
a23 y0
a33
z0
a11 cos cos ,
a12 sin cos ,
a13 sin ,
a21 cos sin sin sin cos ,
a22 cos cos sin sin sin ,
a sin cos ,
23
a31 cos sin cos sin sin ,
a32 cos sin sin sin cos ,
a cos cos .
33
2

3.

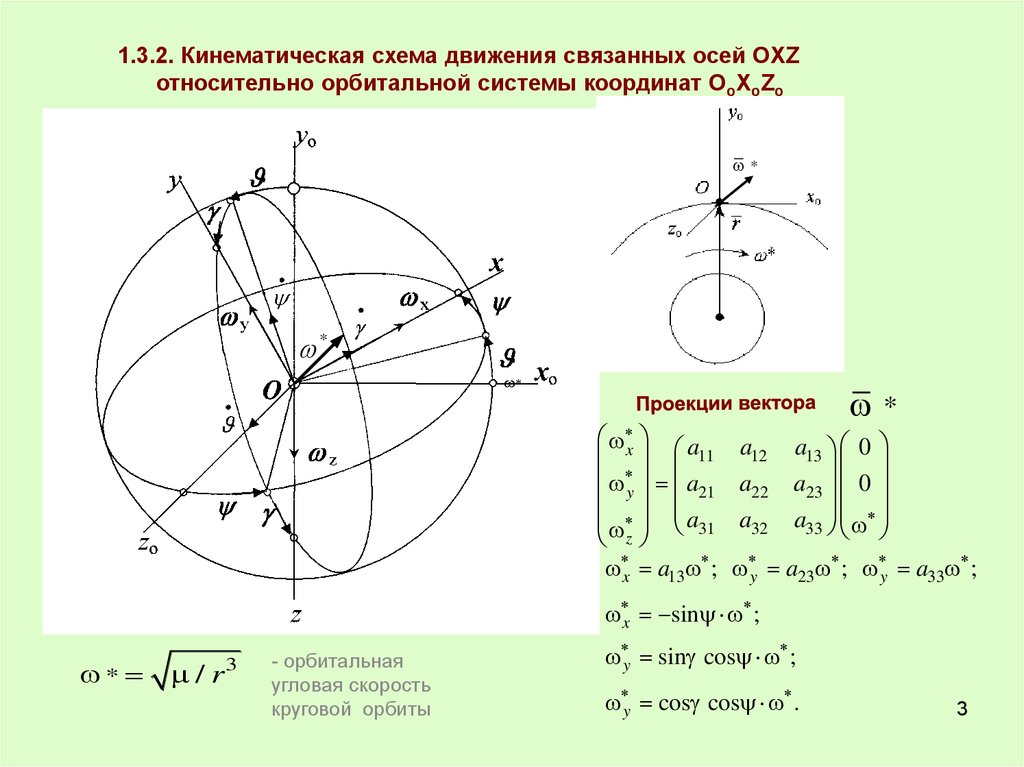
1.3.2. Кинематическая схема движения связанных осей ОXZ
относительно орбитальной системы координат ОоXоZо
*
*
*
x
y
a
11
a21
a31
z
x a13 ;
*
a12
a22
a32
a13 0
a23 0
a33
y a23 ; y a33 ;
x sin ;
*
/r
3
- орбитальная
угловая скорость
круговой орбиты
y sin cos ;
y cos cos .
3

4.

1.4. Кинематические уравнения движения связанных осей
относительно орбитальных
& (
& * ) sin ,
x
& * )sin cos ,
&cos (
y
& * cos cos
&sin .
z
Из (1.4.1) получаем значения производных углов по времени
1
&
*
(
cos
sin
)
,
z
y
cos
& x tg ( z cos y sin ),
&
y cos z sin .
Выражения (1.4.2) позволяют выполнить интегрирование уравнений движения
&(t )dt 0 ,
&(t )dt 0 ,
&(t )dt 0
4

5.

1.5. Динамические уравнения
Теорема об изменении кинетического момента:
dH
M,
dt
dH
H M
dt
В скалярной форме:
Проекции вектора
кинетического
момента:
Уравнения
движения:
H x J x x J xy y J xz z ,
H y J y y J yx x J yz z ,
H z J z z J zx x J zy y .
H&x H z y H y z M x ,
H&y H x z H z x M y ,
&
H z H y x H x y M z .
5

6.

Уравнения движения в развёрнутом виде:
J x &x J xy &y J xz &z J&x x J&xy y J&xz z
( J z J y ) z y ( J xy z J xz y ) x J yz ( 2z 2y ) M x ,
J y &y J xy &x J yz &z J&y y J xy x J&yz z
2
2
( J x J z ) x z ( J yz x J xz z ) y J xz ( x z ) M y ,
J z &z J xz &x J yz &y J&z z J&xz x J&yz y
( J J ) ( J J ) J ( 2 2 ) M .
y
x
x y
xz y
yx x
z
xy
y
x
z
6

7.

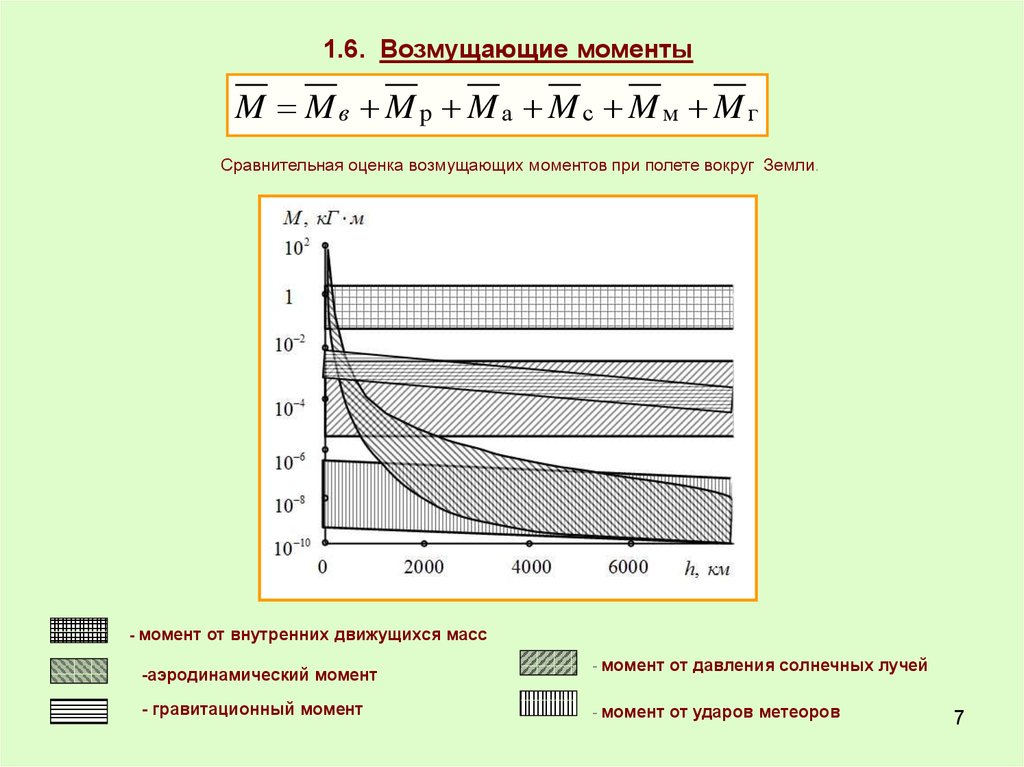
1.6. Возмущающие моменты
M Mв Mp Mа Mc Mм Mг
Cравнительная оценка возмущающих моментов при полете вокруг Земли.
- момент
от внутренних движущихся масс
-аэродинамический момент
- гравитационный момент
- момент
от давления солнечных лучей
- момент
от ударов метеоров
7

8.

1.6.1. Внутренние моменты
H L,
L
MД
dH
dL
H
L,
dt
dt
dL
M Д kL ,
dt
- Кинетический момент вращающихся на борту масс,
- момент электропривода,
H , H
kL
- Вентиляционный момент,
- гироскопические моменты.
1.6.2. Моменты реактивных сил
M р P
P
M px y Pz z Py
M py z Px x Pz
M pz x Py y Px
- тяга реактивного двигателя ОДУ,
- эксцентриситет вектора тяги
8

9.

1.6.3. Аэродинамический момент
M а (r d F )
S
mi mio mi mi ,
mai mi q Sl , i x, y, z,
mio – const,
mi , mi
dmi dmi
,
d d
В случае плоских движений по тангажу и курсу :
maz cSql sin , maz cSql sin ,
1.6.4. Момент сил солнечного давления:
M с r F c
dFc pc cos dS
уголпадения (между нормалью к поверхности и направлением лучей);
2
– коэффициент отражения ( 0 1); E - мощность потока 1400 Вт / м ;
R, R 0 - расстояние от Солнца, средний радиус орбиты Земли; p c давление света;
2
E
R
p c (1 ) 4,505 10 6 0 (1 );
R 0 1, 495 10 11 м
c
R
2
1
R
F с p c 0 S cos 1 2 2 cos 2
2
R
Рис. 5
9

10.

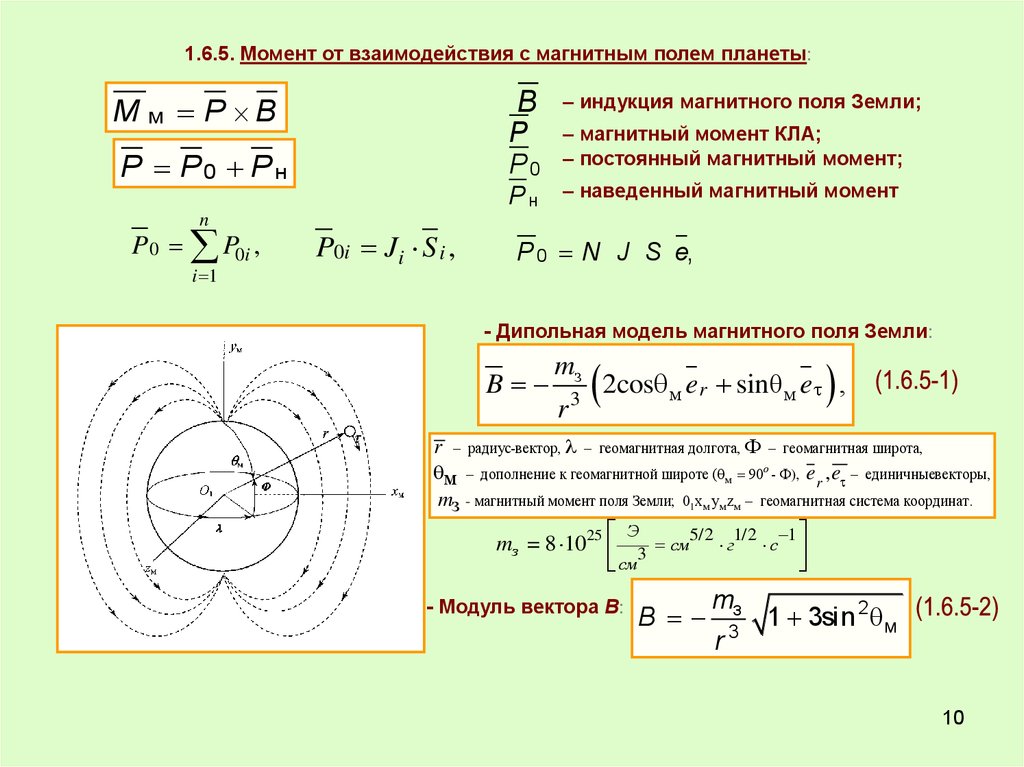
1.6.5. Момент от взаимодействия с магнитным полем планеты:
M м P B
B
P P0 Pн
n
P 0 P0i ,
i 1
P0i Ji S i ,
– индукция магнитного поля Земли;
P
P0
– магнитный момент КЛА;
– постоянный магнитный момент;
Pн
– наведенный магнитный момент
P 0 N J S e,
- Дипольная модель магнитного поля Земли:
B
mз
r
3
2cos м er sinθм e ,
r радиус-вектор, геомагнитная долгота, геомагнитная широта,
м дополнение к геомагнитной широте ( м 90о - ), e r , e единичныевекторы,
mз - магнитный момент поля Земли; 01x м yм zм геомагнитная система координат.
Э
mз = 8 1025 3 см5/2 г1/2 с 1
см
- Модуль вектора В:
B
mз
r3
1 3sin 2 м
10

11.

Магнитное поле Земли
в проекциях на орбитальные оси координат
Bxo Bэh cos u sin i, Byo 2 Bэh sin u sin i,
3
Bzo Bэh cos i,
Bэh
h
Bэh Bэo 1 .
R
(7)
– индукция МПЗ на высоте h над поверхностью
Земли у её геомагнитного экватора;
Bэo 0,313 гс
при h = 0;
u – аргумент широты;
i – угол наклона плоскости орбиты к плоскости
геомагнитного экватора;
11

12.

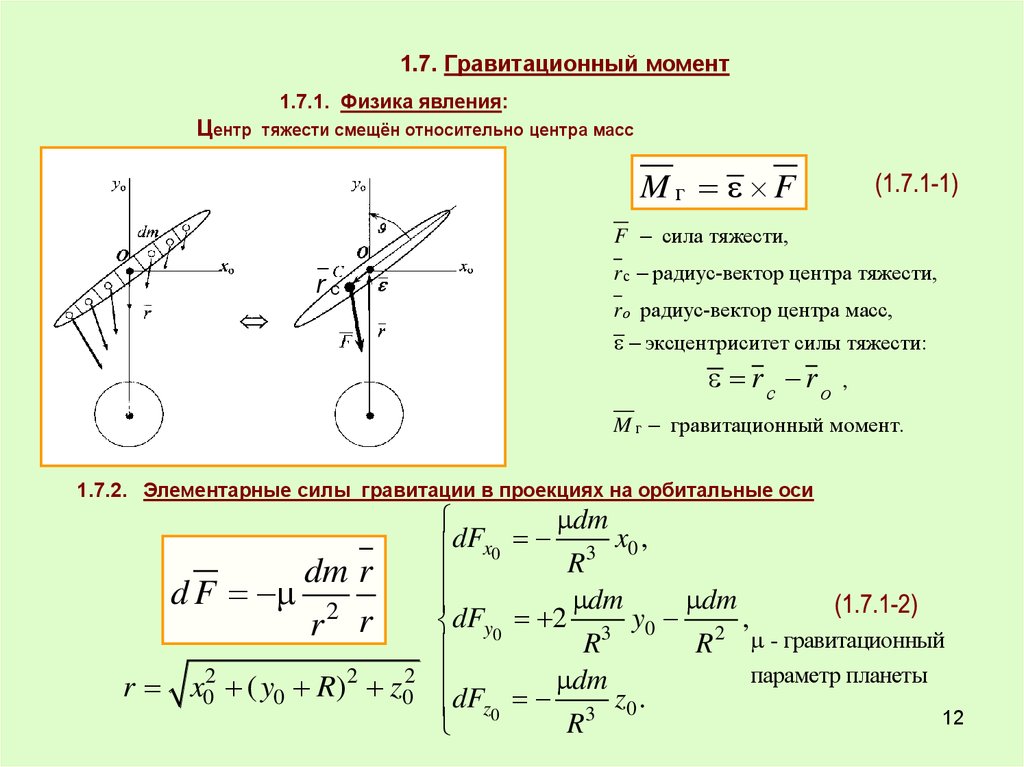
1.7. Гравитационный момент
1.7.1. Физика явления:
Центр
тяжести смещён относительно центра масс
Mг F
F сила тяжести,
rс
r с радиус-вектор центра тяжести,
r о радиус-вектор центра масс,
эксцентриситет силы тяжести:
rс rо
,
M г гравитационный момент.
1.7.2. Элементарные силы гравитации в проекциях на орбитальные оси
dm r
d F 2
r r
r x02 ( y0 R)2 z02
dm
dFx0 R3 x0 ,
dm
dm
dFy0 2 3 y0 2 ,
R
R - гравитационный
параметр планеты
dm
dFz0 3 z0 .
12
R

13.

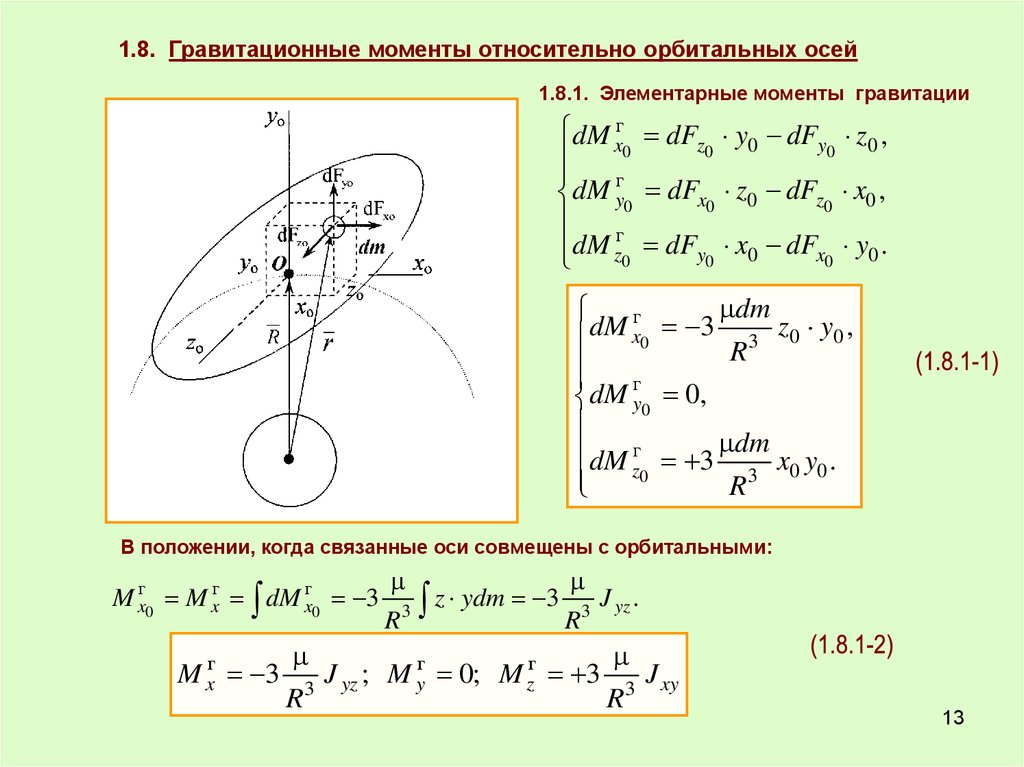
1.8. Гравитационные моменты относительно орбитальных осей
1.8.1. Элементарные моменты гравитации
dM xг dFz y0 dFy z0 ,
0
0
0
г
dM
y0 dFx0 z0 dFz0 x0 ,
г
dM z0 dFy0 x0 dFx0 y0 .
dm
г
dM x0 3 R 3 z0 y0 ,
г
dM y0 0,
dM г 3 dm x y .
z0
0 0
R3
В положении, когда связанные оси совмещены с орбитальными:
M xг0 M xг dM xг0 3
M xг 3
R
3
R
3
z ydm 3
R
3
J yz .
J yz ; M yг 0; M zг 3
R
3
J xy
13

14.

1.8.2. Гравитационные моменты относительно связанных осей
x0 , y0 , z0 x, y, z dM xг0 , dM yг0 , dM zг0 dM , dM yг , dM zг
dM xг x, y, z dxdydz, dM yг x, y, z dxdydz , dM zг x, y, z dxdydz
V
V
V
2
2
M xг 3 2 ( J y J z )a22 a32 ( J xz a22 J xy a32 )a12 J yz (a22
a
32 ) ,
г
2
2
2
M y 3 ( J z J x )a32 a12 ( J yx a32 J yz a12 )a22 J xz (a32 a12 ) ,
2
2
M zг 3 2 ( J x J y )a12 a22 ( J zy a12 J zx a22 )a32 J yx (a12
a
22 ) .
a12 sin cos ,
a22 sin sin sin cos cos ,
a32 sin sin cos cos sin .
- Пример для проверки: идеальная стабилизация (связанные оси совмещены с орбитальными осями):
J 0
a22 1,
a12 a32 0.
M xг 3 2 J yz , M yг 0, M zг 3 2 J xy ,
14

15.

- Гравитационные моменты при движении в плоскости тангажа и произвольном тензоре инерции
г
2 1
2
M
3
J
sin
2
J
cos
x
xz
yz
2
г
2 1
2
M y 3 J yz sin 2 J xz sin
2
г
2 1
M z 3 ( J x J y ) sin 2 J yx cos2
2
0, 0 :
a12 sin ,
a22 cos ,
a32 0.
- Гравитационные моменты при движении в плоскости курса и произвольном тензоре инерции
M xг 3 2 J yz ,
г
M y 0,
г
2
M z 3 J yx .
0, 0
a12 0,
a22 1,
a32 0.
- Гравитационные моменты при движении в плоскости крена и произвольном тензоре инерции
г
2 1
M
3
( J z J y )sin2 J yz cos 2 ,
x
2
г
2 1
2
M y 3 J yx sin2 J xz sin ,
2
г
2 1
2
M z 3 J zx sin2 J yx cos .
2
0, 0
a12 0,
a22 cos ,
a32 sin .
15

16.

- Гравитационные моменты, можно выразить через углы ориентации связанных осей относительно главных
центральных осей инерции:
M zг
J yx
3 2
( J x J y ) sin 2 2
Jx J y
2
cos2
3
sin 2
2 ( J x J y ) sin 2
cos2
2
cos2
3
1
2 ( J x J y )
sin 2 cos2 sin 2 cos2
2
cos2
sin 2
3 2
( J x J y )
2
cos2
3
sin 2
При 0 M zг 2 ( J x J y )
3 2 J xy
2
cos2
M zг
M xг
tg 2
2 J xy
J y Jx
- угол между строительной осью Oz
и главной центральной осью инерции Oz .
2 J yz
3 2
( J z J y ) sin2
cos 2
2
Jz J y
sin2
3
M xг 2 ( J z J y )
,
2
cos 2
2 J zy
tg 2
Jz J y
- угол между строительной осью Ox
и главной центральной осью инерции
Ox .
16

17.

- Гравитационные моменты в плоских движениях при диагональном тензоре инерции:
3
M XГ *2 ( J z J y )sin 2 ,
2
3
M ZГ *2 ( J x J y )sin 2 .
2
M yГ 0,
При J z J x J y :
M XГ момент, стабилизирующий по крену относиткльно
Г
Г
положения = 0 ( >0 M X 0; 0 M X 0 ),
M ZГ момент, стабилизирующий по тангажу относиткльно
Г
Г
положения = 0 ( >0 M Z 0; 0 M Z 0 ),
M YГ по курсу стабилизирующий момент от гравитации отсутствует.
Гравитационный момент поворачивает ось минимального момента инерции
в направлении к радиус-вектору (к местной вертикали).
17

18.

1.9. Гироскопические моменты корпуса при неподвижном положении
связанных осей относительно орбитальной системы координат
1.9.1. Общий случай ориентации при недиагональном тензоре инерции
M * *2 ( J z J y )а33 а23 ( J xy а33 J xz а23 )а13 J yz (а 2 а 2 ) ,
33
23
x
*
*2
2
2
M y ( J x J z )а13 а33 ( J yz а13 J xz а33 )а23 J xz (а13 а 33 ) ,
M * *2 ( J y J x )а13 а23 ( J xz а23 J yx а13 )а33 J xy (а 2 а 2 ) .
23
13
z
а13 sin , а23 cos sin , а33 cos cos .
- Связанные оси повёрнуты в плоскости тангажа:
M *x *2 J yz ; M *y *2 J xz ; M *z 0.
- Связанные оси повёрнуты в плоскости курса:
1
M x J xy sin 2 J yz cos 2
2
1
M *y *2 ( J z J x )sin 2 J xz cos 2
2
*
*2
M *z *2 J yx sin cos J xy sin 2
0, 0, 0
а13 0, а23 0, а33 1
0, 0
а13 sin ,
а23 0,
а33 cos
18

19.

Связанные оси повёрнуты в плоскости крена:
0, 0 а13 sin , а23 0, а33 cos
*
*2 1
M
(
J
J
)
sin
2
J
cos
2
y
yz
x
2 z
,
*
*2
2
M y J xz sin 2 J xz cos ,
M * *2 1 J sin 2 J sin 2 .
xy
2 xz
z
Гироскопические моменты при плоских отклонениях и при диагональном тензоре инерции:
1
M x *2 ( J z J y )sin 2
2
*
1
M y *2 ( J z J x )sin 2
2
*
M *z 0
Влияние гироскопических моментов
орбитального движения
- В плоскости тангажа: отсутствует
- В плоскостях крена и курса: оказывает стабилизирующее действие,
если момент инерции по тангажу максимальный;
19

20.

1.10. Движение в плоскости тангажа
под действием гравитационного момента
1.10.1. Случай невозмущённого плоского движения при диагональном тензоре инерции
Уравнения движения:
Jz
Исключаем время:
d 2
dt
2
d 2
dt 2
M xГ
Jz
d 2
3 2
( J x J y )sin 2 0
2
2
dt
d d d
d
d 2 d d
dt
2
,
dt dt dt
dt d
dt
Jx J y
d
3
*2
sin 2 0
d
2
Jz
Интеграл энергии:
3
J z d = *2 (J x J y ) sin 2 d E
2
J z 2
Кинетическая энергия: E к = d
;
2
3
Потенциальная энергия: E п = *2 (J x J y ) sin 2 d
2
J z 2 3 2
Уравнение фазовой траектории:
J x J y sin 2 d E
2
2
h b cos 2
h - const, находится из начальных условий
20

21.

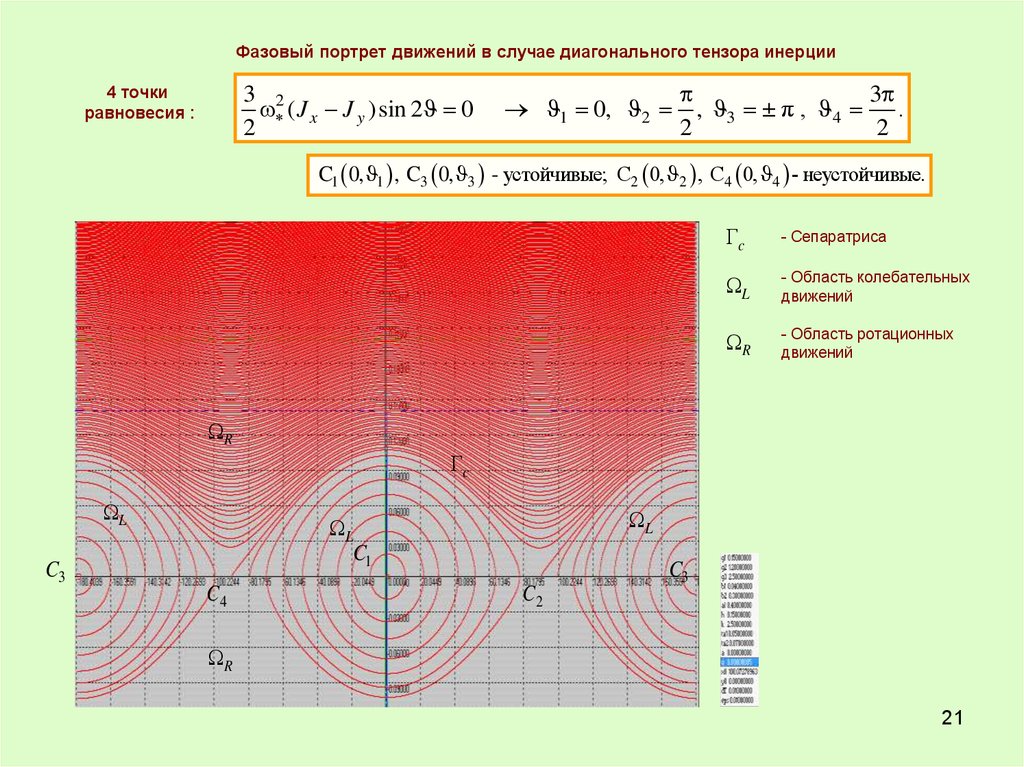
Фазовый портрет движений в случае диагонального тензора инерции
4 точки
равновесия :
3 2
( J x J y )sin 2 0
2
1 0, 2
3
, 3 ± π , 4 .
2
2
C1 0, 1 , C3 0, 3 - устойчивые; C2 0, 2 , C4 0, 4 - неустойчивые.
c
- Сепаратриса
L
- Область колебательных
движений
R
- Область ротационных
движений
R
c
L
C3
L
L
C1
C4
C2
C3
R
21

22.

1.10.2. Случай невозмущённого плоского движения по тангажу при недиагональном тензоре инерции
d 2
3 2
J z 2 ( J x J y )sin 2 3 2 J yx cos2 0
2
dt
В точке равновесия :
Следовательно, в точке равновесия:
d 2
dt 2
0
1
( J x J y )sin 2 J yx cos2 0
2
2 J yx
1
( J x J y ) sin 2 J yx cos2 tg2
tg2 ,
2
Jx J y
где - угол между
главной центральной осью инерции и строительной осью.
Положения равновесия C1 0, 1 , C3 0, 3 , C2 0, 2 и C 4 0, 4 определяются
значениями:
1 , 2
3
, 3 и 4
.
2
2
Относительно местной вертикали колеблется ось минимального
момента инерции. Поэтому фазовый портрет в плоскости ( , ) смещается
по оси 0 на угол .
22

23.

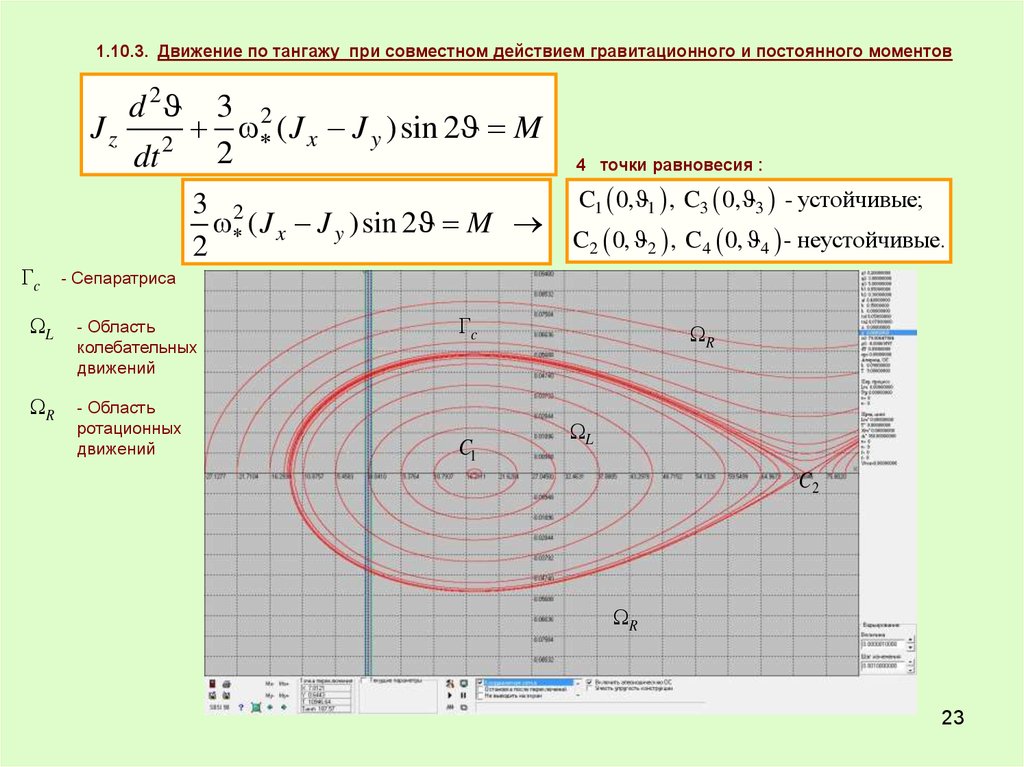
1.10.3. Движение по тангажу при совместном действием гравитационного и постоянного моментов
d 2
3 2
J z 2 ( J x J y )sin 2 M
2
dt
c
4 точки равновесия :
C1 0, 1 , C3 0, 3 - устойчивые;
3 2
( J x J y )sin 2 M
C2 0, 2 , C4 0, 4 - неустойчивые.
2
- Сепаратриса
L
- Область
колебательных
движений
R
- Область
ротационных
движений
c
C1
R
L
C2
R
23

24.

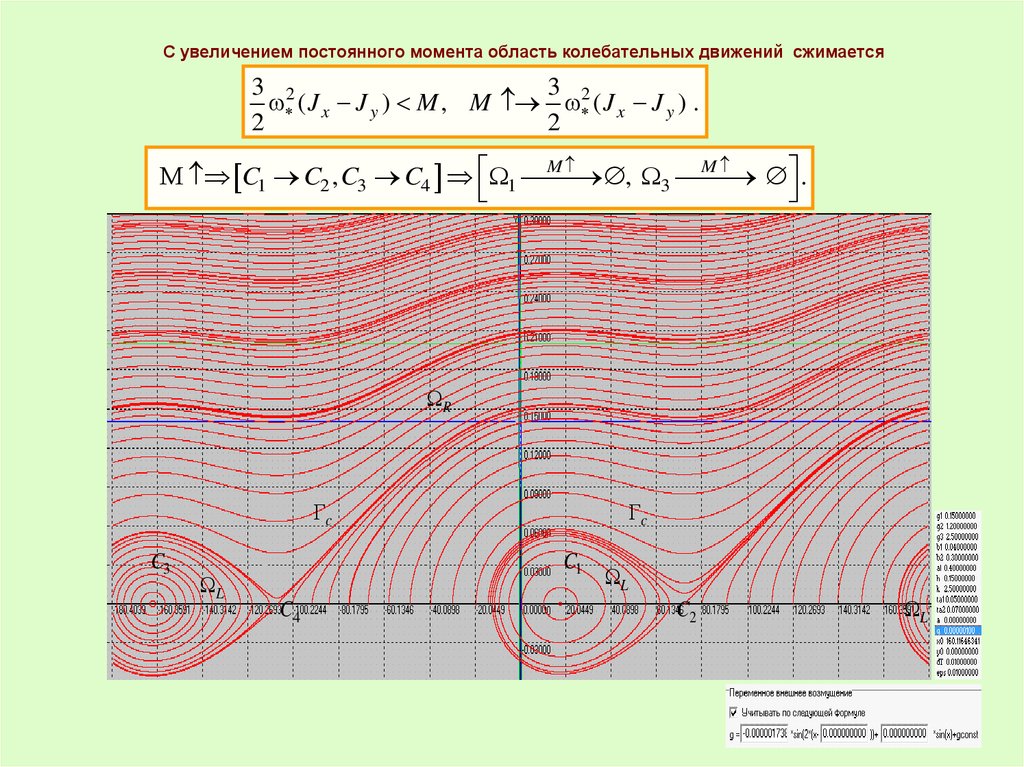
С увеличением постоянного момента область колебательных движений сжимается
3 2
3
( J x J y ) M , M 2 ( J x J y ) .
2
2
M
M
C1 C2 , C3 C4 1
, 3
.
R
c
C3
L
c
C1
C4
L
C2
L
24

25.

Критический случай: область колебательных движений исчезла – возможны только
ротационные движения.
3 2
( J x J y ) M .
2
C1 C2 , C3 C4 , L
R
C3 , C4
C1 , C2
R
Из любого начального положения на оси абсцисс (состояния покоя) тело переходит в ротацию.
25

26.

1.10.4. Условия захвата градиентом гравитации
Тело захвачено градиентом гравитации, если его ось минимального момента инерции совершает лишь
колебательные движения относительно местной вертикали (без ротации относительно осей 0x, 0y) .
Условие захвата. Фазовые координаты начальной точки движений по тангажу и крену должны
принадлежать внутренним областям фазовых плоскостей, ограниченных сепаратрисами:
0 , 0 k ,
, ;
d
dt
Условие захвата можно сформулировать как требование достаточной малости полной
механической энергии тела в движении относительно местной вертикали:
Eк Eп Eдоп .
Для захвата градиентом гравитации, необходимо погасить избыток кинетической энергии тела.
Если выполнены условия захвата градиентом гравитации, тело приобретает в движении по тангажу
постоянную составляющую угловой скорости, равную угловой скорости орбитального движения
При этом возникают гироскопические моменты по курсу и по крену, притягивающие ось максимального
момента инерции к бинормали.
Для того, чтобы управлять ориентацией тела захваченного гравитационном градиентом, необходимо
располагать управляющим моментом, который по модулю больше суммы максимального гравитационного и
максимального гироскопического моментов:
.
3 2
M z ( J x J y ), M y > 2 ( J z J x ) ,
2
M x 2 2 ( J z J y )
26

27.

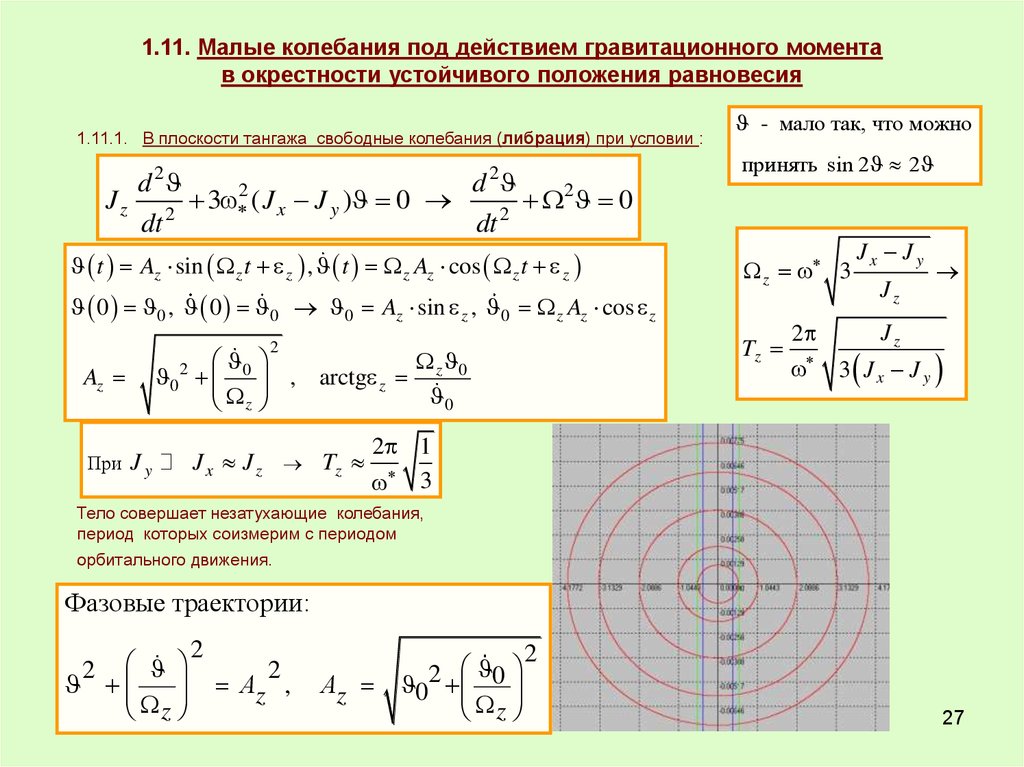
1.11. Малые колебания под действием гравитационного момента
в окрестности устойчивого положения равновесия
1.11.1. В плоскости тангажа свободные колебания (либрация) при условии :
Jz
d 2
dt 2
3 2 ( J x J y ) 0
d 2
dt 2
принять sin 2 2
2 0
t Az sin z t z , t z Az cos z t z
0 0 , 0 0 0 Az sin z , 0 z Az cos z
2
0 2 0 ,
z
Az
При
arctg z
J x J z Tz
Jy
- мало так, что можно
z
Tz
z 0
0
2
3
Jx Jy
Jz
Jz
3 Jx Jy
2 1
3
Тело совершает незатухающие колебания,
период которых соизмерим с периодом
орбитального движения.
Фазовые траектории:
2
z
2
2
Аz ,
Аz
02 0
z
2
27

28.

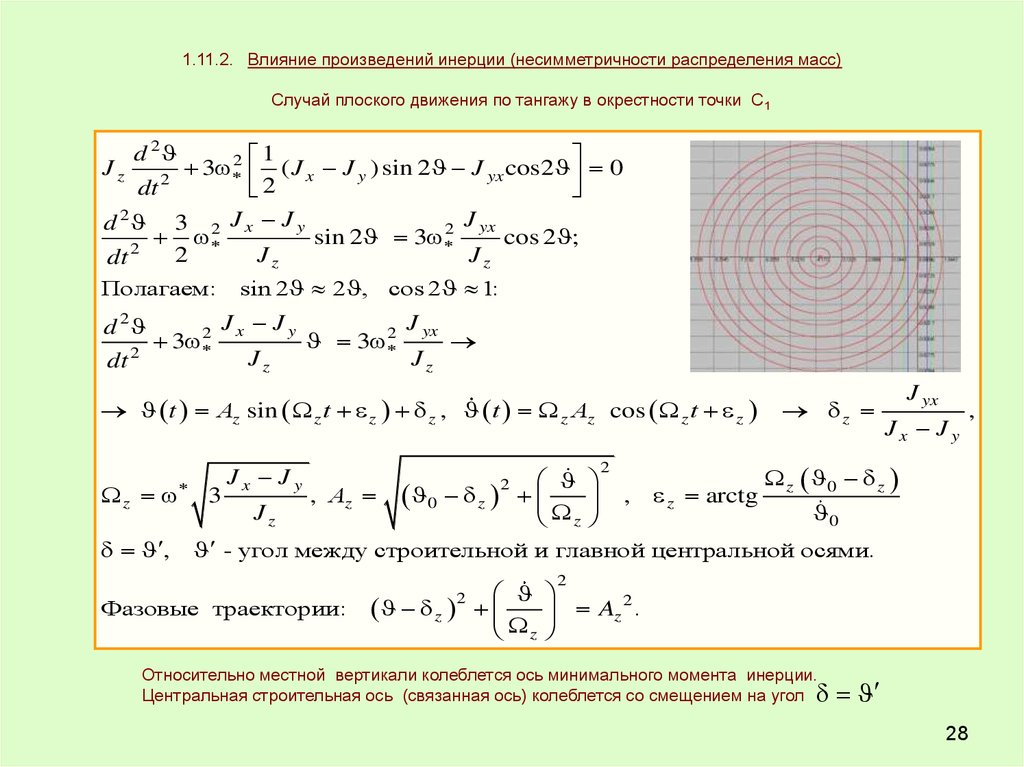
1.11.2. Влияние произведений инерции (несимметричности распределения масс)
Случай плоского движения по тангажу в окрестности точки С1
d 2
2 1
3
(
J
J
)
sin
2
J
cos2
0
x
y
yx
2
dt
2
J yx
d 2 3 2 J x J y
2
sin 2 3
cos 2 ;
2
Jz
Jz
dt 2
Jz
Полагаем:
d 2
dt 2
3 2
sin 2 2 , cos 2 1:
Jx J y
Jz
3 2
J yx
Jz
t Аz sin z t z z , t z Аz cos z t z
z
J yx
Jx J y
,
z 0 z
z 3
, Аz 0 z
,
arctg
z
Jz
0
z
, - угол между строительной и главной центральной осями.
2
Jx J y
Фазовые траектории:
2
z
2
2
2
Az .
z
Относительно местной вертикали колеблется ось минимального момента инерции.
Центральная строительная ось (связанная ось) колеблется со смещением на угол
28

29.

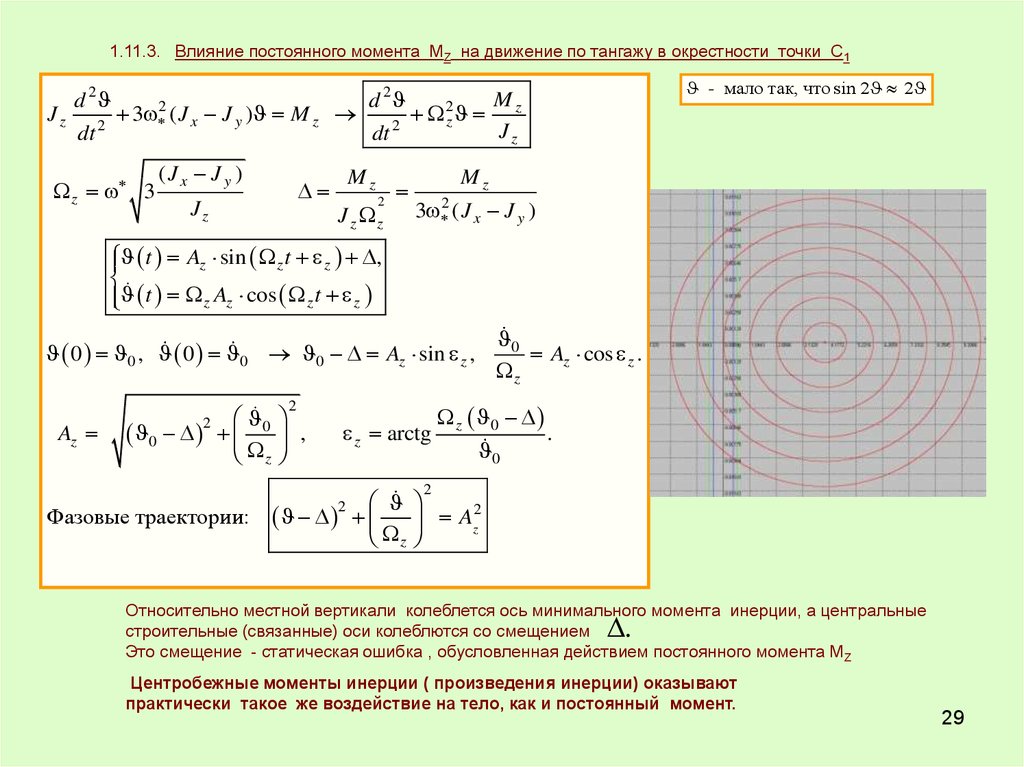
1.11.3. Влияние постоянного момента МZ на движение по тангажу в окрестности точки С1
Jz
d 2
dt
2
(J x
3
2
z
3
J y ) M z
(J x J y )
Jz
d 2
dt
Mz
2
J z z
2
z
2
- мало так, что sin 2 2
M
z
Jz
Mz
3 2 ( J x J y )
t Az sin z t z ,
t z Az cos z t z
0
Az cos z .
z
0 0 , 0 0 0 Az sin z ,
Az
0
2
2
0 ,
z
Фазовые траектории:
z arctg
z 0
0
.
2
2
2
Az
z
Относительно местной вертикали колеблется ось минимального момента инерции, а центральные
строительные (связанные) оси колеблются со смещением
Это смещение - статическая ошибка , обусловленная действием постоянного момента МZ
.
Центробежные моменты инерции ( произведения инерции) оказывают
практически такое же воздействие на тело, как и постоянный момент.
29

30.

1.11.4. Компенсация постоянным моментом недиагональности тензора инерции
Компенсировать негативное влияние недиагональности тензора инерции (смещение z )
можно надлежащим выбором постоянного возмущающего момента. На рисунке для наглядности
совмещены фазовые портреты для трёх случаев:
о
1) слева - колебание тела при M z = 0, главная ось инерции которого смещена на 4 ;
2) справа - колебания тела при таком значении M z , которое в случае диагонального тензора инерции
о
даёт статическую ошибку + 4 ;
о
2) в центре - колебания тела, ось инерции которого смещена на 4 , но при том же значении M z ,
что и во втором случае.
z
z
30

31.

1.12 . Плоское движение по курсу под действием
гироскопического момента
1.12.1.
Постоянный момент при недиагональном тензоре инерции
Полагаем, что ось минимального момента инерции тела захвачена градиентом гравитации и , отслеживая
местную вертикаль, совершает вращение в плоскости орбиты.
Jy
d 2
dt 2
1
*2 ( J z J x ) sin 2 J xz cos 2 M y
2
d 2
1
0 *2 ( J z J x ) sin 2 J xz cos 2 M y .
dt
2
При M y = 0 ось максимального момента инерции стремится к бинормали 0 z0 .
В положении равновесия:
2
4 положения равновесия : B1 0, 0 , B2 0,
, B3 0, , B4 0, 3
.
2
4
Точки с нечётными индексами устойчивы, с чётными неустойчивы.
*
*2 1
Связанная ось 0 zM
в состоянии
равновесия
отклонена
от
0
z
на
угол
(
J
J
)sin
2
J
cos
2
x
xz0
2 z
, который
y
2 J xz
1
находим из условия:
( J z J x ) sin 2 J xz cos 2 0 arctg
.
2
Jz Jx
Это угол отклонения связанной оси 0 z от оси максимального момента инерции.
В малой окрестности устойчивого положения равновесия, полагая sin 2 2 , cos 2 1,
находим линейное уравнение колебаний:
Jy
d 2
dt
2
*2 ( J z J x ) M y *2 J xz .
Из него легко находим все параметры колебаний.
31

32.

1.13. Плоское движение по крену под действием гравитационного
и гироскопического моментов
1.13.1.
Общий случай – постоянный момент при недиагональном тензоре инерции
Как и случае движения по курсу полагаем, что ось минимального момента инерции тела захвачена
градиентом гравитации и , отслеживая местную вертикаль, совершает вращение в плоскости орбиты.
Если по тангажу действует только гравитационный момент, а по курсу – только гироскопический, то по оси
крена действуют как гравитационные, так и гироскопические моменты.
Jx
d 2
2 1
2
s
co
J
)sin2
J
J
(
4
yz
y
z
Mx
2
dt 2
Ось минимального момента инерции в плоскости крена имеет 4 равновесных положения
на фазовой плоскости , : D1 0, 0 ; D1 0, ; D1 0, ; D1 0, .
2
2
При J z J y 0 точки с нечётными индексами усточивы, с чётными - не устойчивы.
В малой окрестности устойчивого положения равновесия тело совершает колебания
в соответствии с уравнением:
Jx
d 2
dt
2
4 2 ( J z J y ) M x 4 2 J yz ,
из которого можем найти все параметры колебаний.
32

33.

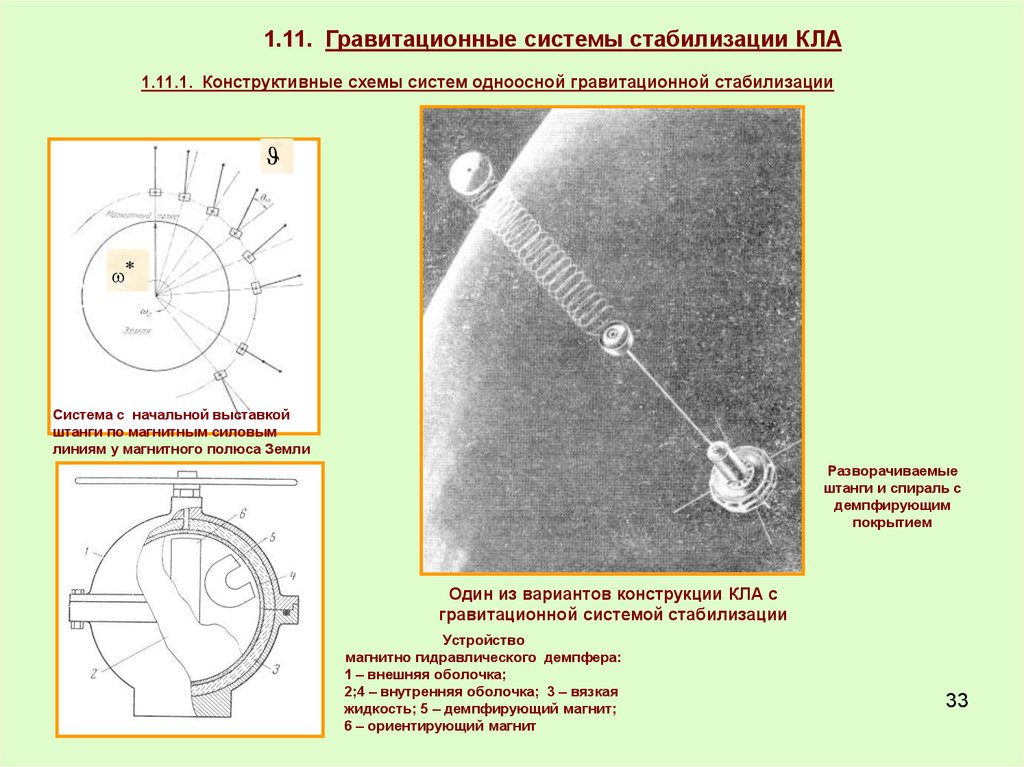
1.11. Гравитационные системы стабилизации КЛА
1.11.1. Конструктивные схемы систем одноосной гравитационной стабилизации
Система с начальной выставкой
штанги по магнитным силовым
линиям у магнитного полюса Земли
Разворачиваемые
штанги и спираль с
демпфирующим
покрытием
Один из вариантов конструкции КЛА с
гравитационной системой стабилизации
Устройство
магнитно гидравлического демпфера:
1 – внешняя оболочка;
2;4 – внутренняя оболочка; 3 – вязкая
жидкость; 5 – демпфирующий магнит;
6 – ориентирующий магнит
33

34.

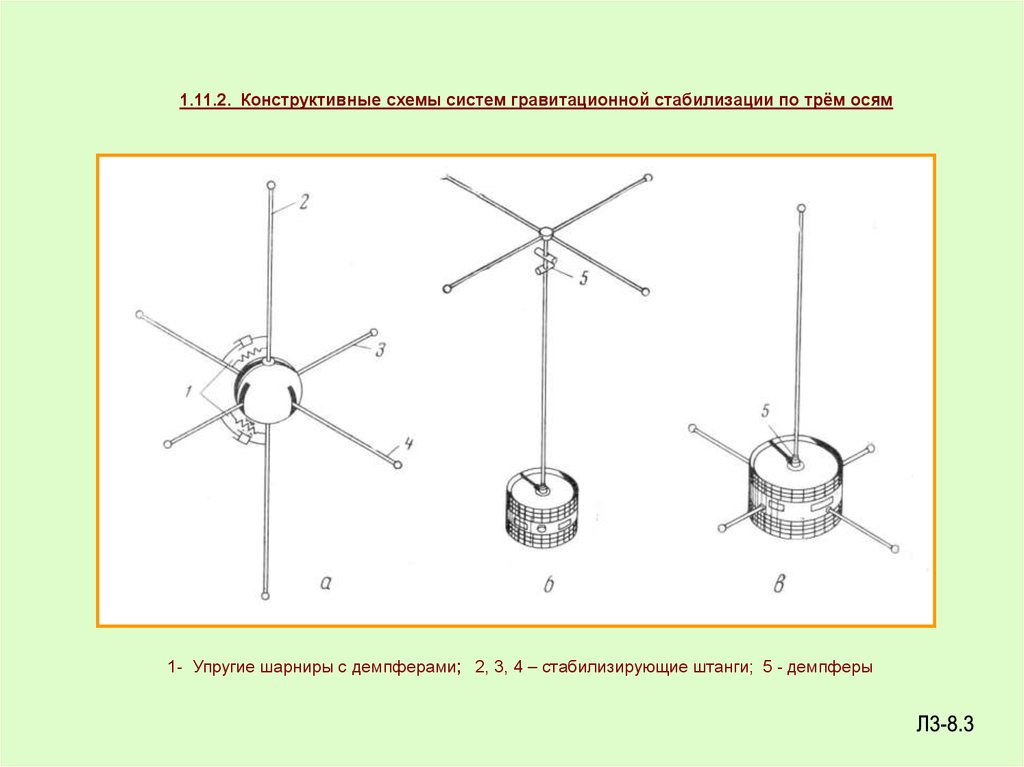
1.11.2. Конструктивные схемы систем гравитационной стабилизации по трём осям
1- Упругие шарниры с демпферами; 2, 3, 4 – стабилизирующие штанги; 5 - демпферы

35.

1.13.1. Сброс избытка кинетической энергии и демпфирование
Eк Eп Eдоп
- Условие захвата градиентом гравитации обеспечивает переход
движения от ротации к колебаниям. Чтобы уменьшить амплитуду колебаний, нужно погасить
избыток кинетической энергии.
E
k
Задача 1: 0 , 0 R
1 , 1 L , Ek : Ek E0k E1k 12 J 02 12
E
k
Задача 2: 1 , 1 L
1 0, 1 0 , Ek : Ek
1
2
J 12 .
Задача 1 решается системой предварительного успокоения. Она может быть как активной (использовать датчики,
исполнительные органы, энергию или топливо) , так и пассивной, например на основе магнитно- гистерезисных
стержней. При этом за каждый оборот в магнитном поле Земли от кинетической энергии отнимается её часть и
выделяется в виде тепла. Она затрачивается на перемагничивание стержней:
E BdH ,
V- объём стержня; B, H магнитная индукция и напряжённость магнитного поля поля Земли
V
Задача 2 решается системой специальных демпферов. Используются конструкции, в которых отдельные шарнирно
или упруго закреплённые части, перемещаясь друг относительно друга в вязкой жидкости, энергию колебаний корпуса
переводят в тепло и рассеивают.
35

36.

1.12. Динамика стабилизации вращением
1.12.1. Устойчивость вращения тела произвольной формы
dH
0 H const ,
dt
H H J
H2
H2
E
E min E
2J
2 J max
движение устойчиво
относительно оси
максимального
момента инерции
1.12.2. Динамика свободного вращения симметричного тела
dH
0 H const ,
dt
Рассмотрим случай J z J y J x J .
Покажем, что в свободном вращении всякое твёрдое тело при избытке энергии движения возбуждено,
стремится сбросить этот избыток энергии и прийти к состоянию относительного покоя –
равномерного вращения вокруг прямой, совпадающей с направлением вектора кинетического момента.

37.

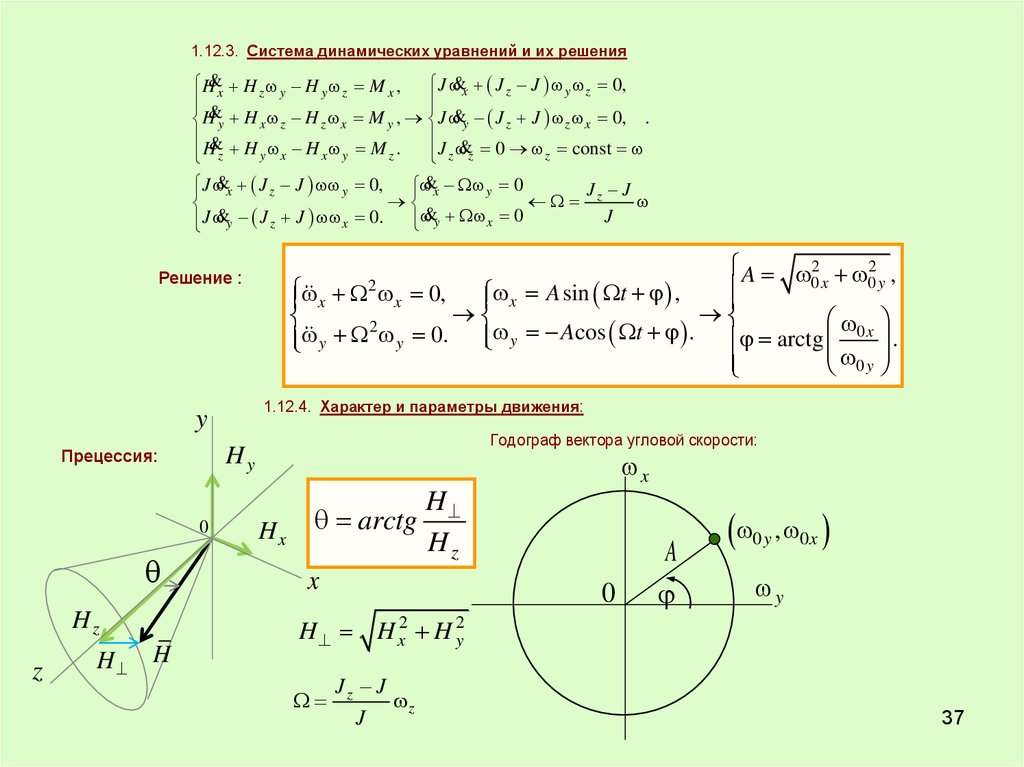
1.12.3. Система динамических уравнений и их решения
H&x H z y H y z M x , J &x J z J y z 0,
H&y H x z H z x M y , J &y J z J z x 0, .
&
H z H y x H x y M z . J z &z 0 z const
J &x J z J y 0, &x y 0
J J
z
&
&
0
J
J
J
J
0.
x
z
x
y
y
A 2 2 ,
0x
0y
x 2 x 0,
x A sin t ,
0 x
2
A
cos
t
.
0.
y
arctg
.
y
y
0 y
Решение :
1.12.4. Характер и параметры движения:
y
0
Hz
z
H H
Годограф вектора угловой скорости:
Hy
Прецессия:
x
Hx
arctg
H
Hz
x
0
A
0 y , 0x
y
H H x2 H y2
Jz J
z
J
37

38.

1.12.4. Силовые поля в прецессирующем теле:
Угловые скорости свободно вращающегося тела изменяются по гармоническому закону. Следовательно, во
всём объёме тела действуют гармонические поля инерционных и центробежных сил.
Частота инерционных сил равна . Действительно, на каждый элемент массы dm на радиусе r
по касательной в плоскостях 0 x при движении с угловым ускорением x действует элементарная
сила инерции dF
x rdm A rdm cos t.
Частота центробежных сил равна 2 . Действительно, на каждый элемент массы dm по радиусу r
в плоскостях 0 x при движении с угловой скоростью x действует центробежная сила
dF
r
dm 2x r dm A2 2 r sin 2 t dm A2 2 r 12 1 cos 2 t .
Аналогичный результат получаем, рассматривая движение вокруг оси
0 y,
т.е. в плоскостях
0y .
1.12.4. Прецессия как следствие избытка энергии вращения
Прецессия тела признак избытка кинетичкской энергии его вращения.
Избыток энергии это разность её значений для текущего состояния и для
состояния равномерного вращения вокруг оси максимального момента инерции.
H2
Минимум энергии : min Ek
2 J max
Избыток энергии:
J
Ek
min
Ek
H 2 J max J
2J
J max
момент инерции относительно оси мгновенного вращения
38

39.

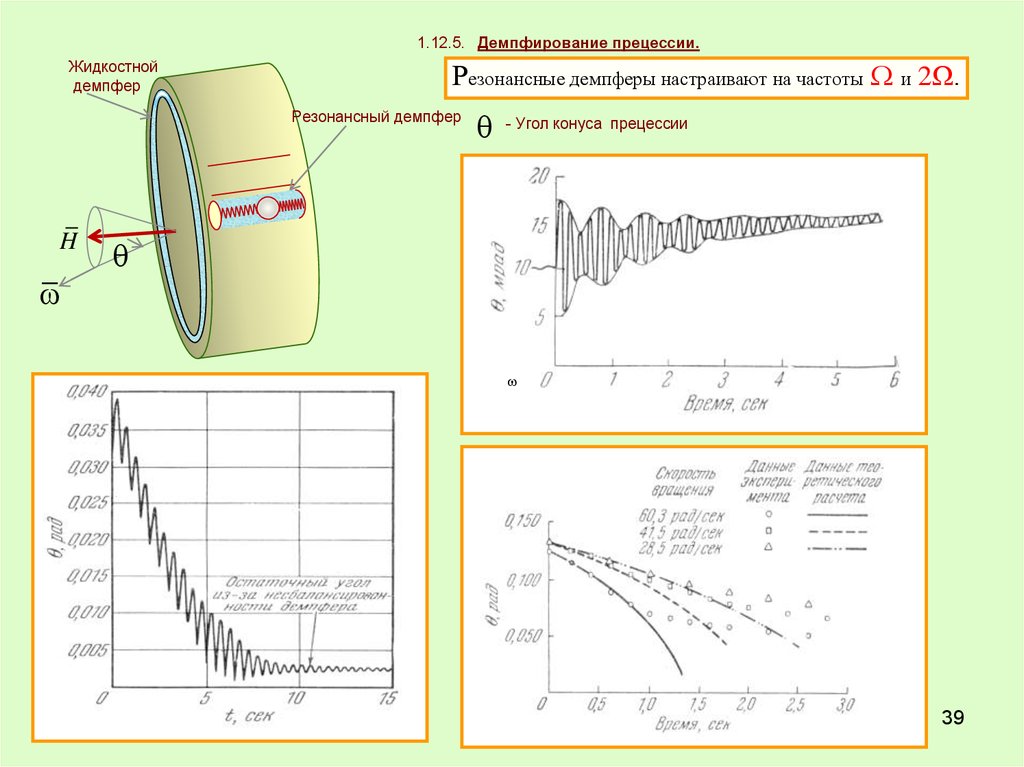
1.12.5. Демпфирование прецессии.
Жидкостной
демпфер
Резонансные демпферы настраивают на частоты и 2Ω.
Резонансный демпфер
H
- Угол конуса прецессии
39

40.

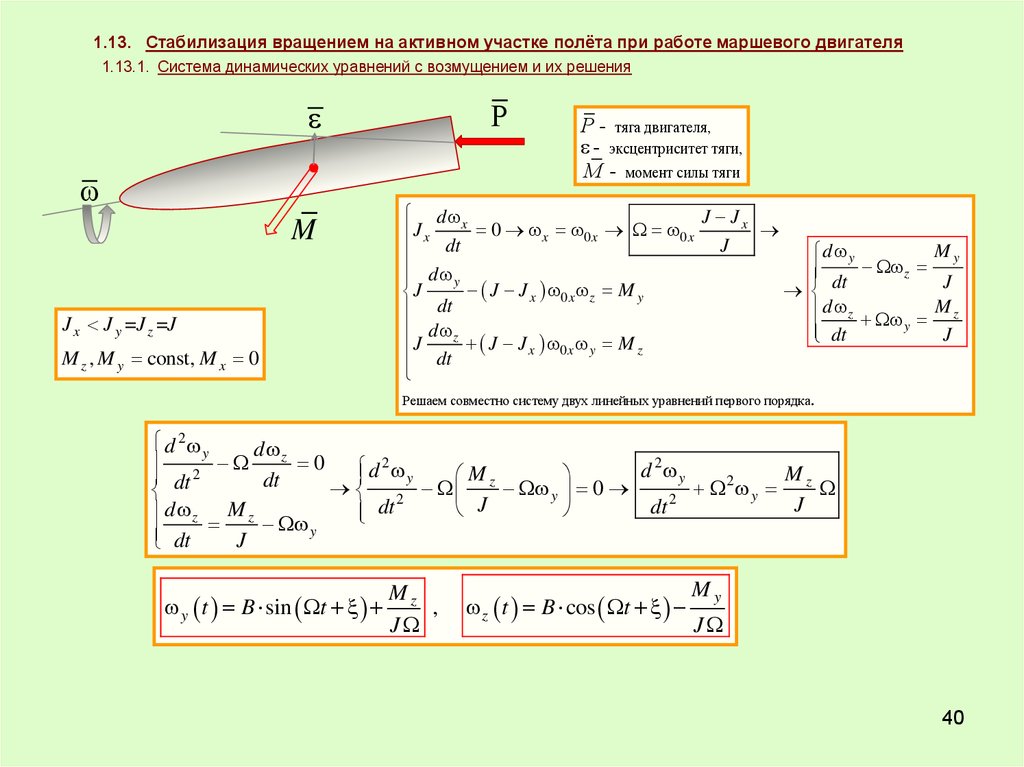
1.13. Стабилизация вращением на активном участке полёта при работе маршевого двигателя
1.13.1. Система динамических уравнений с возмущением и их решения
M
J x J y =J z =J
M z , M y const, M x 0
Р - тяга двигателя,
- эксцентриситет тяги,
М - момент силы тяги
d x
J Jx
0 x 0 x 0 x
J x
dt
J
My
d y
z
d
y
J
J J x 0 x z M y
dt
J
dt
d z M z
y
d z
dt
J
J
J
J
M
x
0x y
z
dt
Решаем совместно систему двух линейных уравнений первого порядка.
d 2 y
d z
2
0 d 2
d 2 y
Mz
Mz
dt
y
2
dt
2
y 0
y
2
J
J
dt
d z M z
dt
y
dt
J
y t B sin t
Mz
,
J
z t B cos t
My
J
40

41.

1.13.1. Характер движения
Годограф вектора угловой скорости
2
My
Mz
B y
z
J
J
2
2
0
H
z
M
x
B
0 y , 0z
My
J
1.13.2. Параметры прецессионно-нутационного движения
2
B
2
My
Mz
,
0
y
0
z
J
J
arctg
J
,
J x x
H J ,
arc tg
0 y
0 z
Mz
J
My
J
y
0
Mz
J
2y 2z .
Вектор возмущающего момента М вместе со связанными осями вращается,
делая за время 2
x
полный оборот вокруг H . Поэтому вектор H совершает
коническое движение с угловым отклонением . Продольная ось 0 x и вектор
тяги участвуют в прецессионно-нутационном движении. Угловое отклонение
оси 0 x в этом движении определяется велечиной .
41

42.

1.13.3. О стабилизации вращением вокруг оси минимального момента инерции
Вращение вокруг оси минимального момента инерции неустойчиво.
По мере диссипации энергии угол конуса прецессии увеличивается,
тело переходит к вращению вокруг оси максимального момента инерции 0x и, в
конечном счёте, завершается постоянным вращением вокруг этой оси (кувыркание).
При стабилизации вращением вокруг оси минимального момента инерции 0x
необходимо обеспечить максимальную жёсткость конструкции, исключить возможность
колебаний элементов конструкции или оборудования, тем более резонансных (на равных
или кратным частотам , 2 ).
Влияние возмущающего моментана на точность ориентации стабилизируемой вращением оси
будет тем меньше, чем больше вытянуто тело (J J x ) и чем больше скорость вращения x .
42

43.

1.14. Внутренние моменты от вращающихся масс
dH
dL
dL
H M
L ;
M Д kв L .
dt
dt
dt
H L ;
L
- Кинетические момента вращающихся на борту масс (маховика),
MД
kв
- Крутящий момент от электродвигателя,
- Коэффициент вентиляционного момента вращающихся масс (маховика).
1.14.1. Маховик с постоянной скоростью
y0
z0
x0
L
0
L,
L J м ;
- Момент инерции и
угловая скорость
маховика
dL
0 L L0 const
dt
Гироскопические моменты от маховика
z0
Jм,
L :
Lz y L y z M x L , x a13 sin ;
L
a
sin
cos
;
y
23
L
L
M
,
x z
z x
y
L
a
cos
cos
.
z
33
L y x Lx y M z .
43

44.

1.14. Маховик с постоянной скоростью по оси тангажа
Стабилизирующие гироскопические моменты маховика
L Lx Lx 0, Lz 0 , Lz J м ,
Уравнения движения в предположении,
что на тело действуют только эти моменты:
H 0 Это возможно при J x J y J z :
M x L , M y L 0
M x L Lz y , M L L sin cos ,
x
z
L
L
M y Lz x , M y Lz sin ,
L
M z L 0.
M z 0.
d 2 Lz
sin cos 0,
2
Jx
dt
d 2
J
L
sin 0,
y
z
2
dt
d 2 Lz
Lz
0,
2
Jx
J
dt
x
2
2
d Lz
d Lz 0
Lz
0
dt 2
Jy
Jy
dt 2
J
y
Lz
0,
Jx
dt 2
Jy
d 2
dt 2
0 0 .
d 2
Lz
,
Jx
Lz
Jy
В окрестности устойчивого положения равновесия:
t =A sin t , & t =A cos t
&0
A 0
2
&
t =A sin t , & t =A cos t A 20 0
44

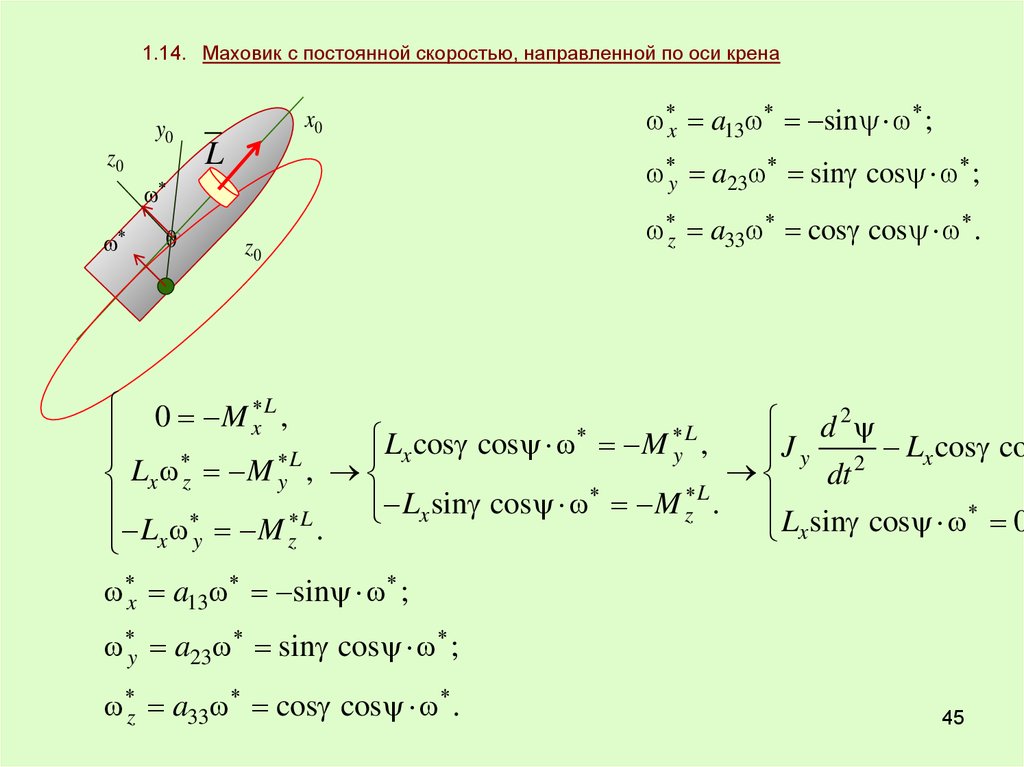
45.

1.14. Маховик с постоянной скоростью, направленной по оси крена
y0
z0
x0
L
y a23 sin cos ;
0
x a13 sin ;
z0
z a33 cos cos .
0 M L ,
d 2
x
L
J y 2 Lx cos co
Lx cos cos M y ,
L
dt
Lx z M y ,
L
Lx sin cos M z . L sin cos 0
L
x
Lx y M z .
x a13 sin ;
y a23 sin cos ;
z a33 cos cos .
45

46.

Уравнения плоских управляемых движений
При условии:
d 2
Jz 2
dt
J xy J xz J yz 0; i j i 0
2
M âi M F , [u( ),V (
d
)]
dt
d & d &
,
g F , , h ,
dt
dt
u , i kv &, j
1 , & , & ,
F 1 , & , & ,
0
0 , & , & .
Fτ t F t ,
1 если F t 0 0, F t 0 1,
2 если F t 0 1, F t 0 0.
46

47.

Двигатели коррекции и
управления.
Схема размещения
корректирующего и
управляющих двигателей
Схема расположения
реактивных двигателей
для управления движением
относительно центра масс:
1, 2 - по тангажу;
3, 4 - по рысканию;
5, 6 - по крену
47

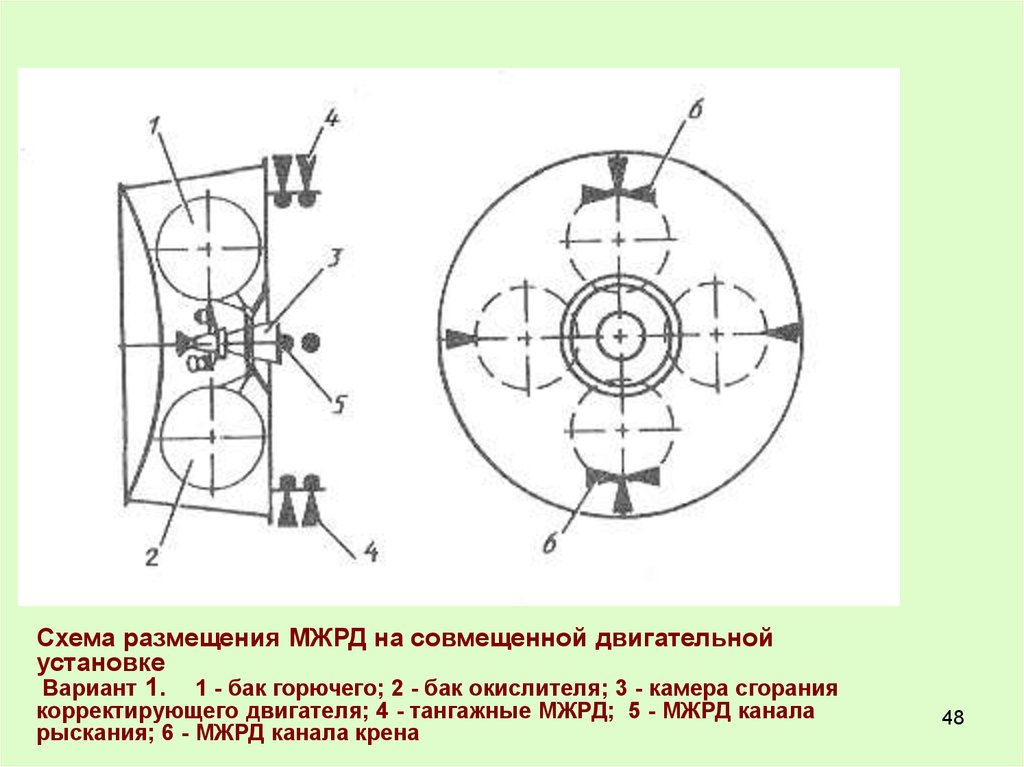
48.

Схема размещения МЖРД на совмещенной двигательной
установке
Вариант 1. 1 - бак горючего; 2 - бак окислителя; 3 - камера сгорания
корректирующего двигателя; 4 - тангажные МЖРД; 5 - МЖРД канала
рыскания; 6 - МЖРД канала крена
48

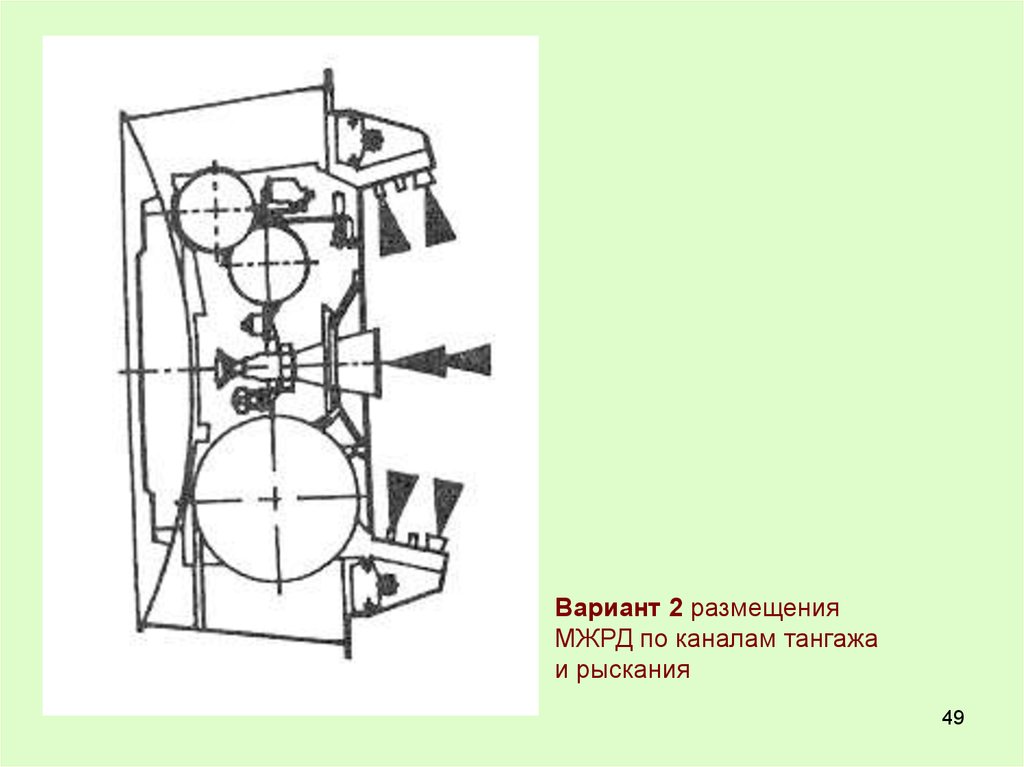
49.

Вариант 2 размещения
МЖРД по каналам тангажа
и рыскания
49

50.

Математические модели нелинейных элементов
u ( x, i ) k v( y, j ),
x
1 , 1
0 x
x 3 ,
u x x 1 sgn x x 1 , 2 ,
2 1 sgn x x 2 , 3 .
y x
0 y 1 , 1 ,
V y y 1sgn y y 1 , 2 ,
2 1 sgn y y 2 .
u
1 2
3
v
1 2
dx
x , , , y x
dt
50

51.

1
F
-h
-1
F
1
sign h F0 sign h F0
2
1 при ,
или F 1 при
h h ,
0
при
h , если F0 F t 0 0
51

52.

Линии переключения ( границы листов ) фазовой поверхности
Li : x, y u ( x, i ) k v ( y , j ),
x , , , y x
L1 :
L2 :
L3 :
L :
4
L1 :
L2 :
L3 :
L4 :
x, y
dx
, i 1, 2,3; j 1, 2.
dt
x, y h
x, y
x, y h
u x, i k v y , j
u x, i k v y , j h
u x, i k v y, j
u x, i k v y, j h
52

53.

Линии переключения при линейных датчиках
u x, i x,
L1 :
L :
2
L3 :
L4 :
v y, j y
x k y
x k vy h
x k y
ux ky h
53

54.

Линии переключения при нелинейном датчике скорости
54

55.

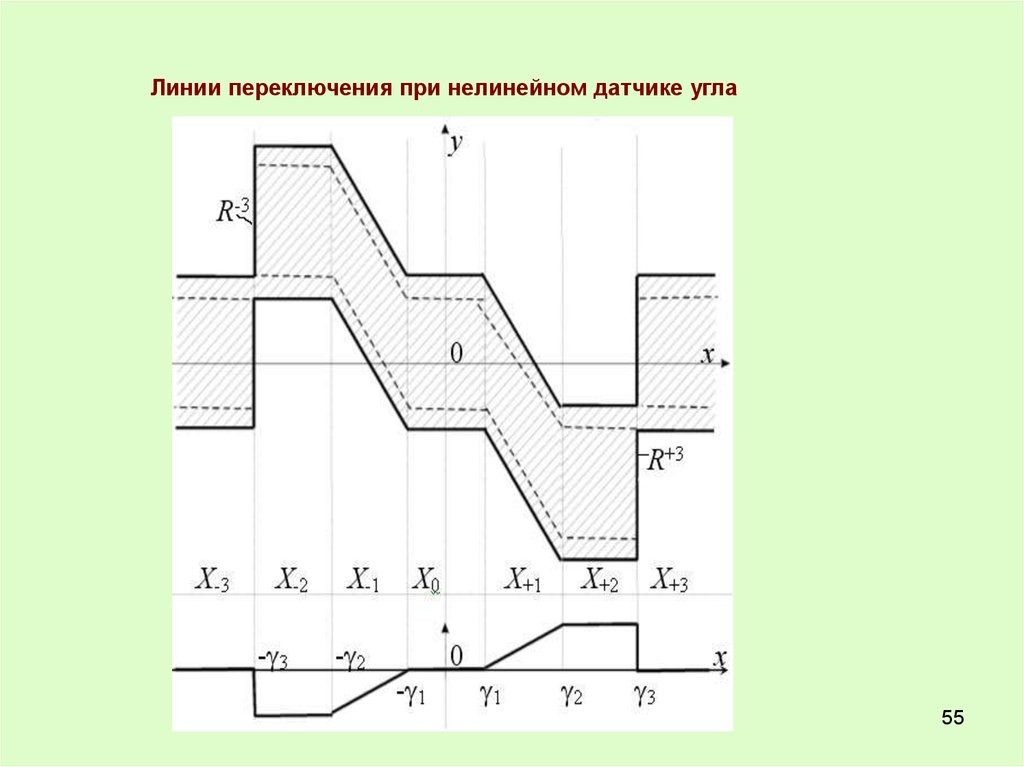
Линии переключения при нелинейном датчике угла
55

56.

Структура разбиения фазовой поверхности в общем случае
56

57.

Бифуркации структуры фазовой поверхности
Параметры нелинейностей датчиков
= 2 - 1,
= k · ( 2 - 1)
Параметр структуры
S = n1 + 2 n2
n1 - число наклонных участков,
n2 - число вертикальных участков
S24
= - , > 2
S57
= - , < 2
S47
= > /2
S25
= < /2
S34
= >
S67
= <
S36
= >
S79
= - , < 2
S89
= < /2
S68
= - , > 2
57

58.

Полибифуркации структур
S2457 :
при = = /2;
S3467 :
при = = ;
S6789:
при = = /2.
58

59.

Фазовые траектории при постоянном
возмущении ( g = const)
Общий вид
Г F : y 2 y02 2( g a F )( x x0 ),
Г : y 2 y02 2( g a )( x x0 ),
Г 0 : y 2 y02 2 g ( x x0 ),
Г : y 2 y02 2( g a )( x x0 )
или
y02
y2
Г :x
c , c x0
,
2( a g )
2( a g )
y2
Г :x
c0 ,
2g
0
2
y
Г : x
c ,
2( a g )
y02
c x0
,
2g
0
2
y
0
c x0
2( a g )
59

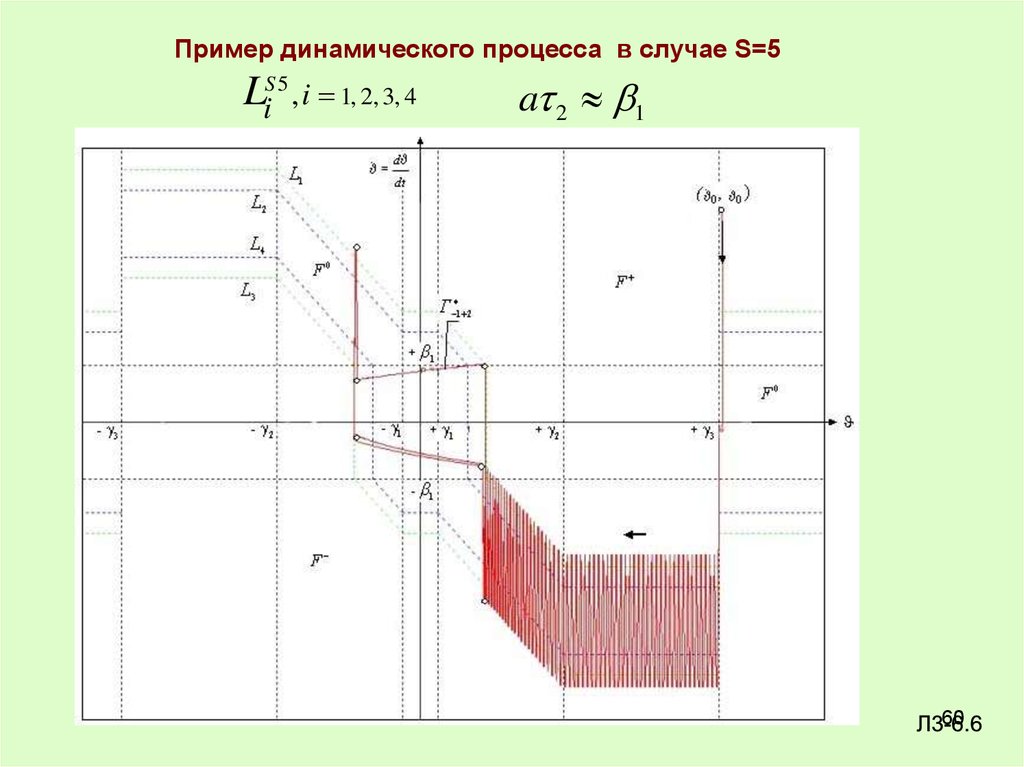
60.

Пример динамического процесса в случае S=5
LiS 5 , i 1, 2, 3, 4
a 2 1
60

61.

Автоколебания. Простые предельные циклы
*
1
*
2
61

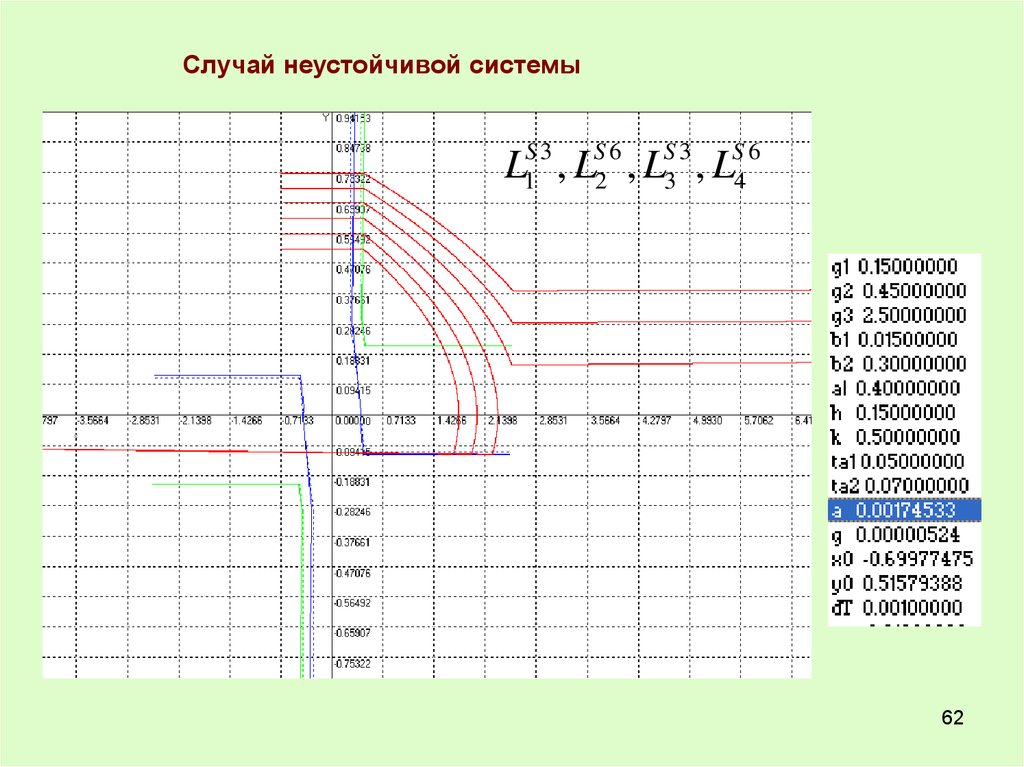
62.

Случай неустойчивой системы
L1S 3 , LS2 6 , LS3 3 , LS4 6
62

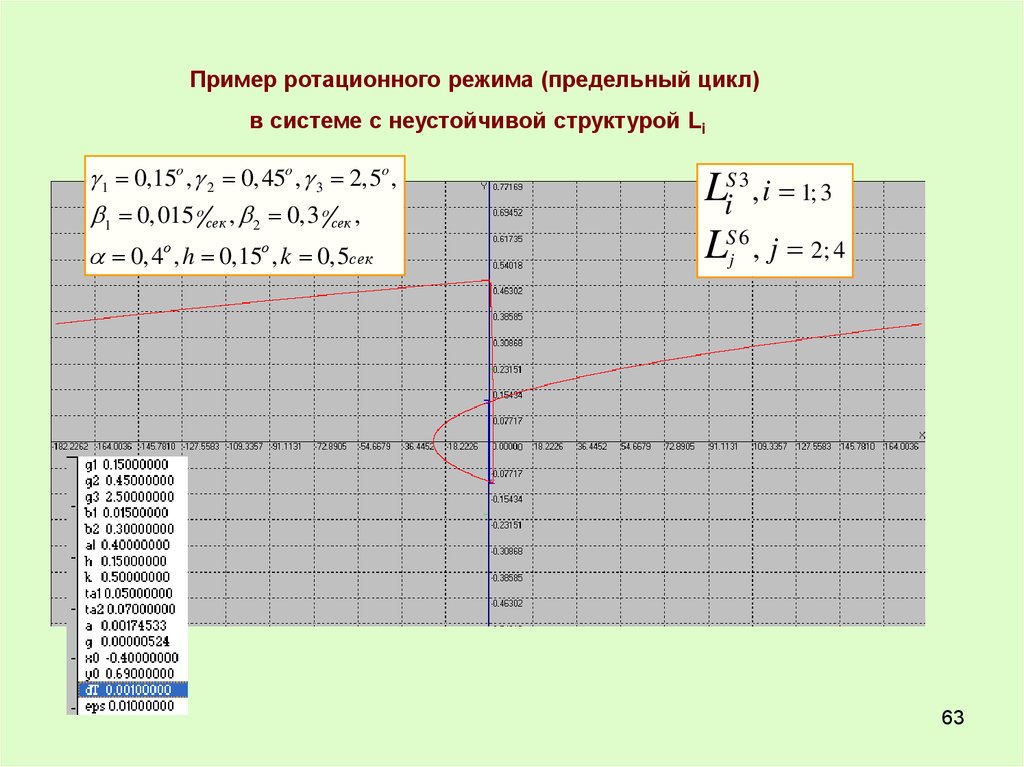
63.

Пример ротационного режима (предельный цикл)
в системе с неустойчивой структурой Li
1 0,15o , 2 0, 45o , 3 2,5o ,
1 0,015 o сек , 2 0,3 o сек ,
0, 4о , h 0,15o , k 0,5сек
LiS 3 , i 1; 3
LSj 6 , j 2; 4
63

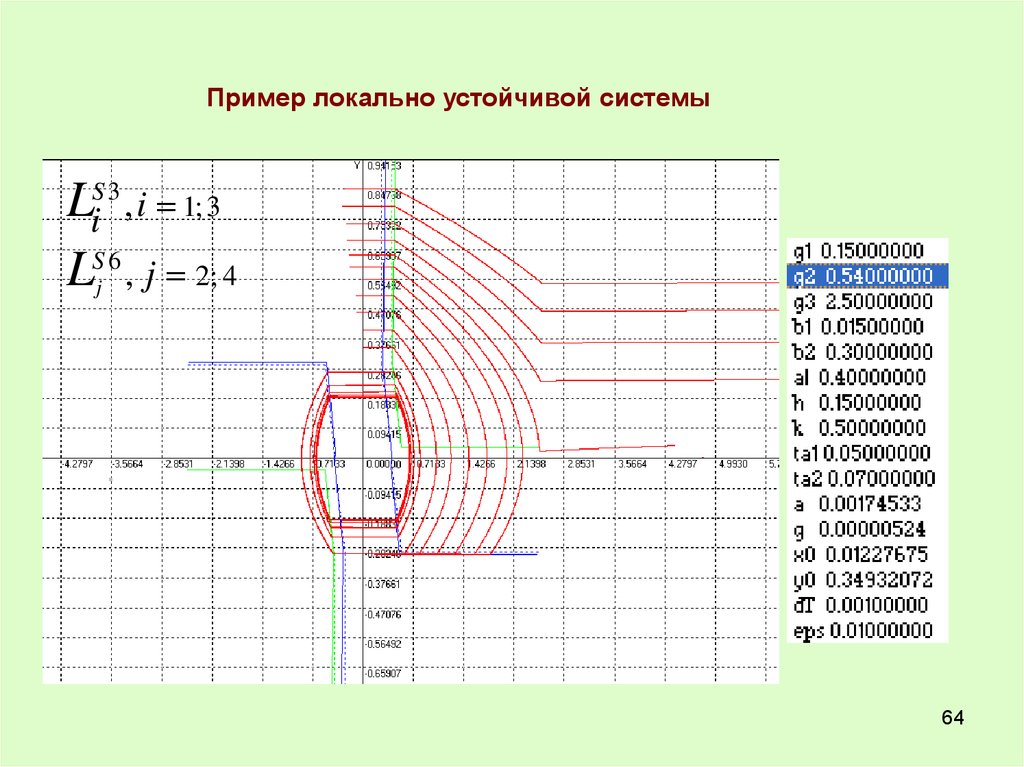
64.

Пример локально устойчивой системы
LiS 3 , i 1; 3
LSj 6 , j 2; 4
64

65.

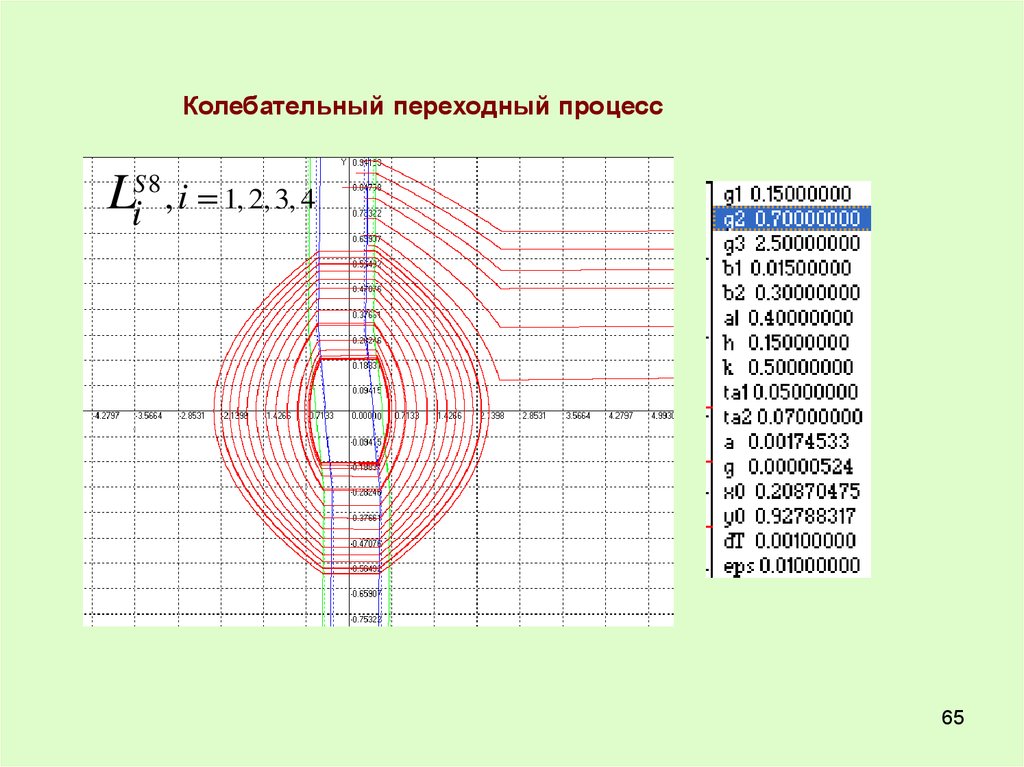
Колебательный переходный процесс
LiS 8 , i 1, 2, 3, 4
65

66.

Система глобально (тотально) устойчива.
Ротационный переходный процесс
LiS 8 , i 1, 2,3, 4
66

67.

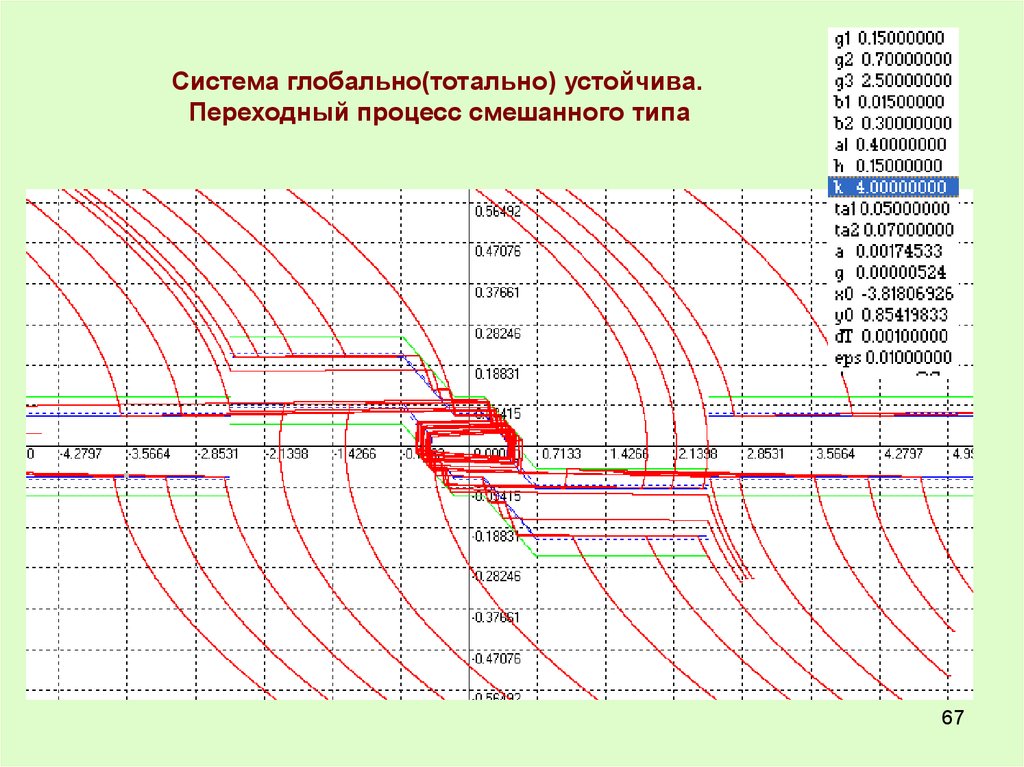
Система глобально(тотально) устойчива.
Переходный процесс смешанного типа
67

68.

Скользящий режим
68

69.

Три предельных цикла и сягивающиеся к ним траектории
Гр
Г2
Г1
Гр – Ротационный, Г2 – двухимпульсный, Г1 –одноимпульсный
предельные циклы
69

70.

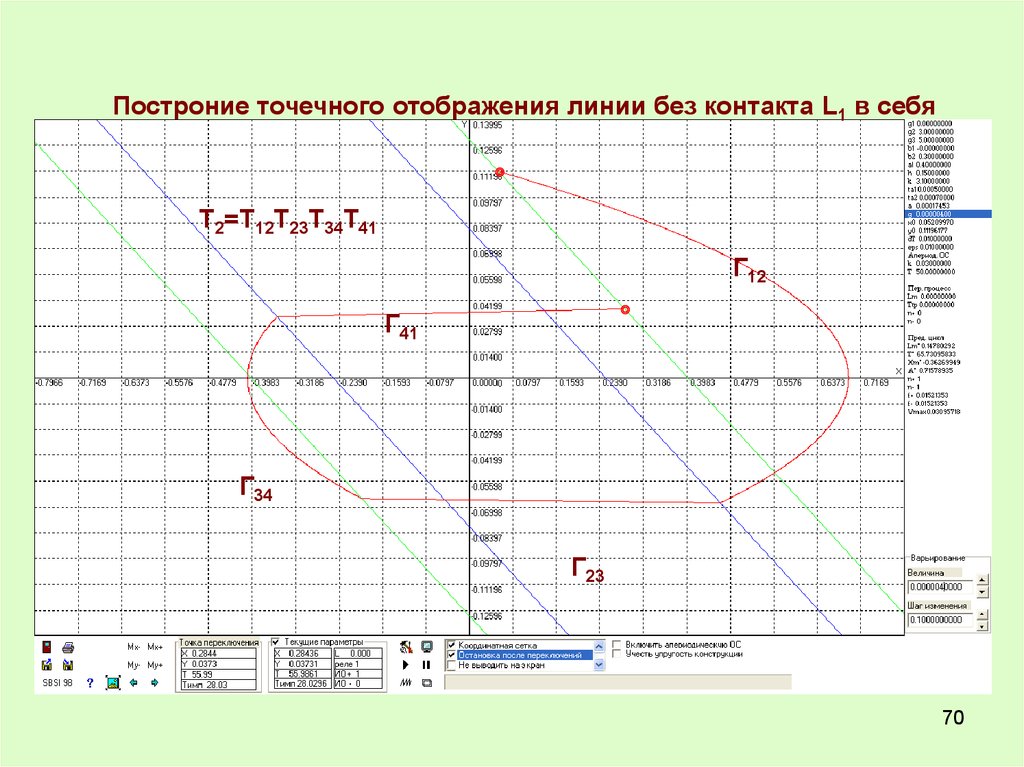
Построние точечного отображения линии без контакта L1 в себя
Т2=Т12Т23Т34Т41
Г12
Г41
Г34
Г23
70

71.

Преобразование Т1=Т12Т21
L1
L2
71

72.

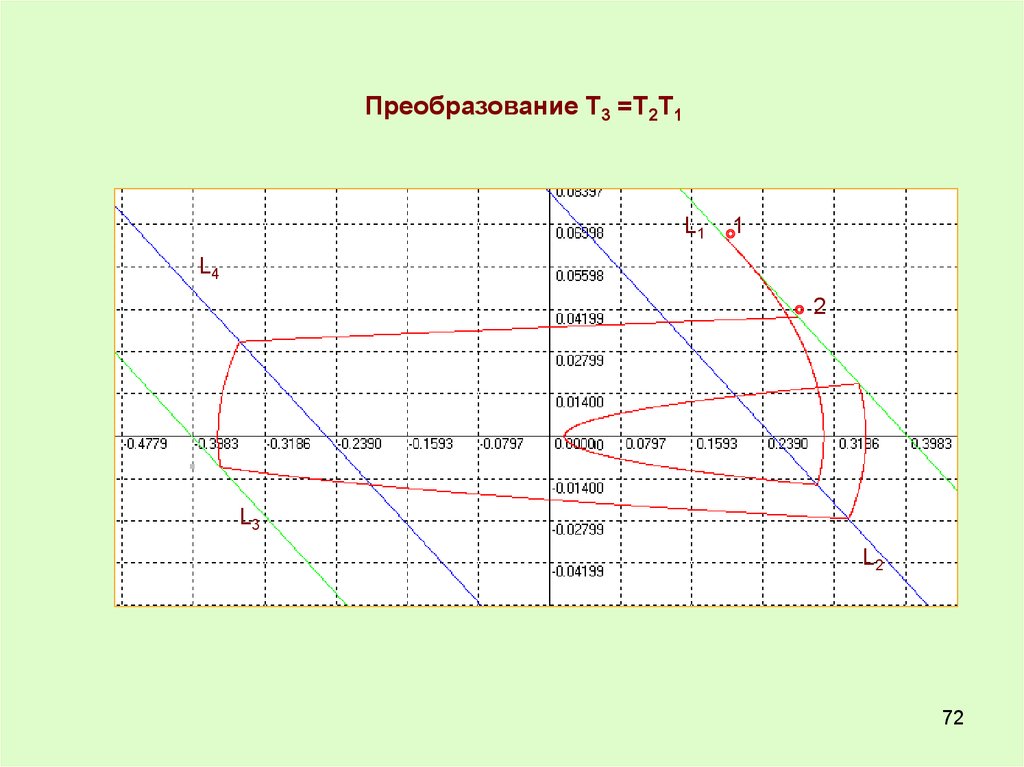
Преобразование Т3 =Т2Т1
L1
1
L4
2
L3
L2
72

73.

Построние отображения Т12
L1
ɣ12
L2
73

74.

Отображение Т23
ɣ23
L3
ɣ23
L2
74

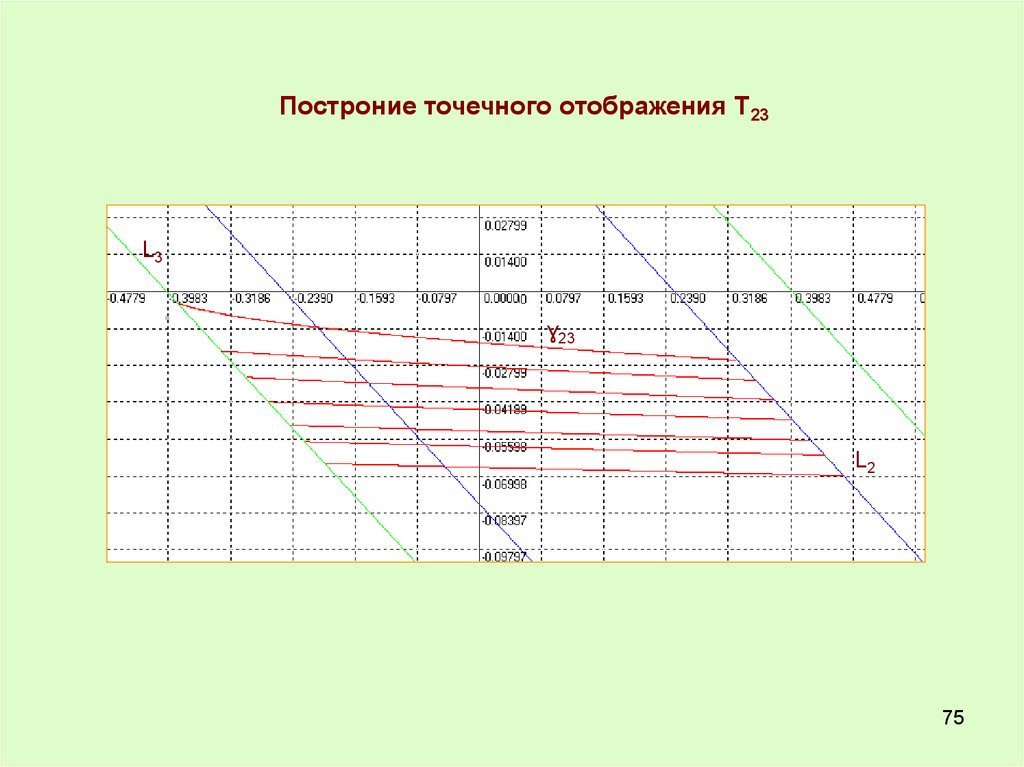
75.

Построние точечного отображения Т23
L3
ɣ23
L2
75

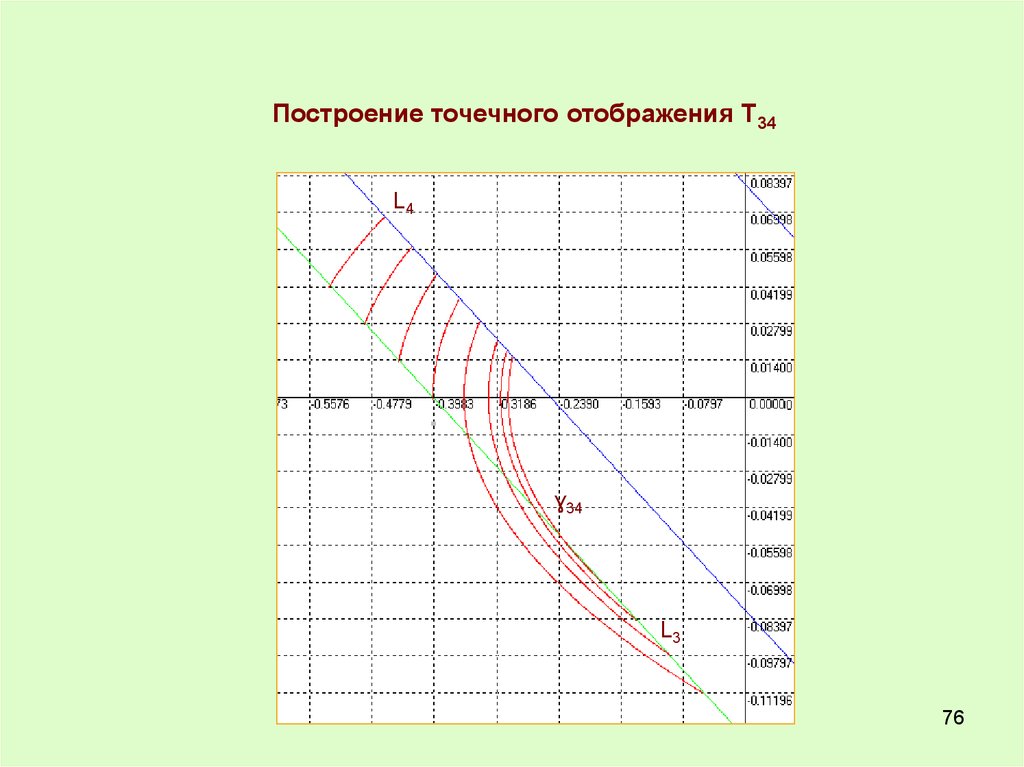
76.

Построение точечного отображения Т34
L4
ɣ34
L3
76

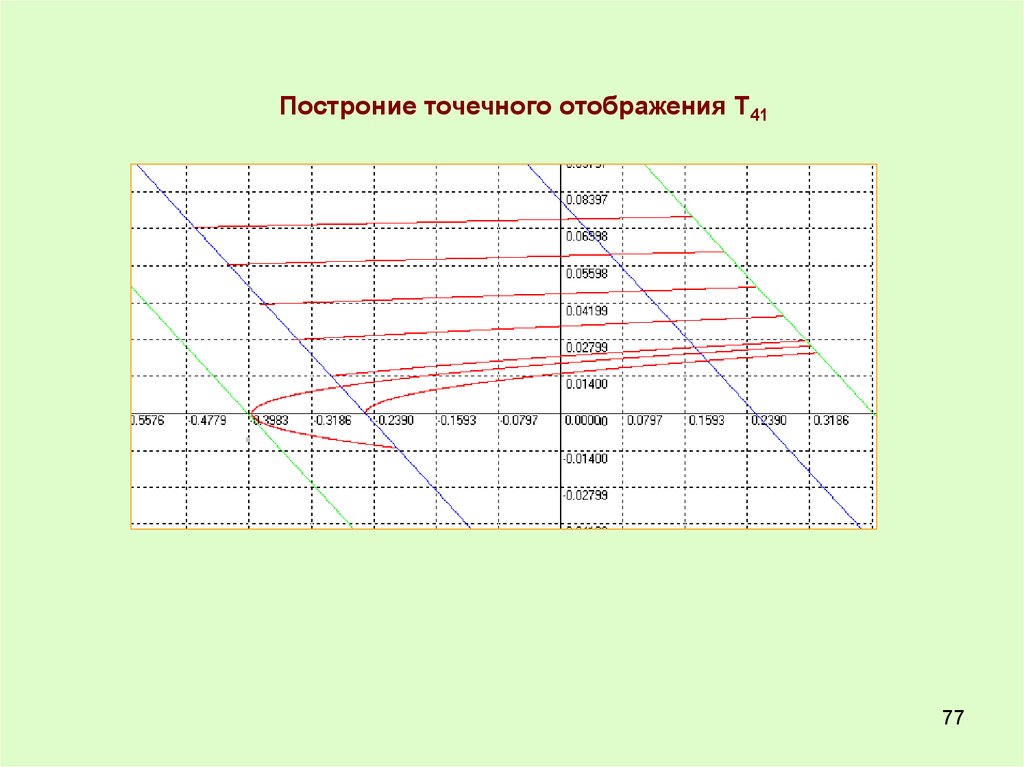
77.

Построние точечного отображения Т41
77

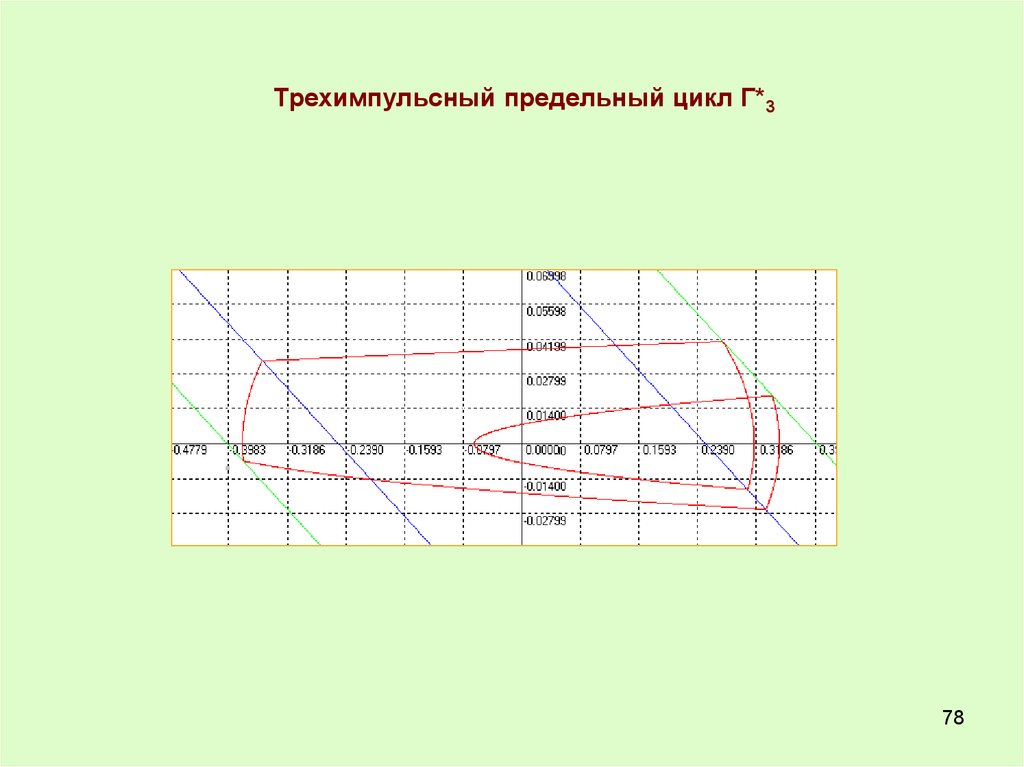
78.

Трехимпульсный предельный цикл Г*3
78

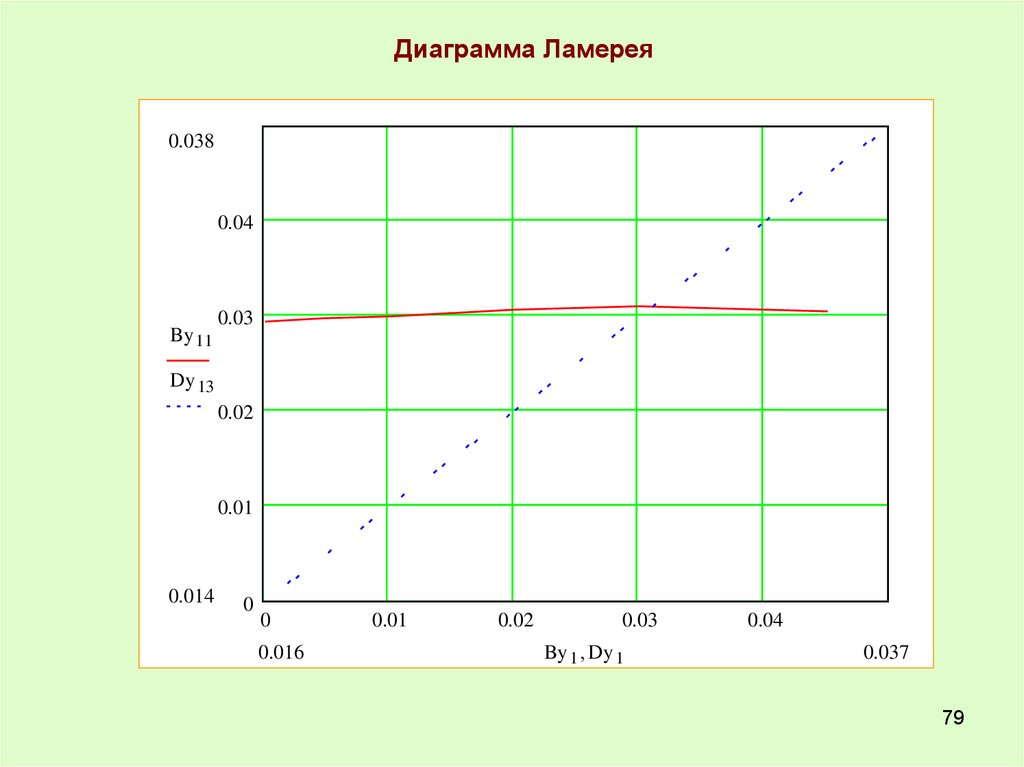
79.

Диаграмма Ламерея
0.038
0.04
By 11
0.03
Dy 13
0.02
0.01
0.014
0
0
0.016
0.01
0.02
0.03
By 1 Dy 1
0.04
0.037
79

80.

a :=0.010
b := a-g
g :=0.0002292
1 :
d := a+g
T12 By2 : bk
B
y2
bk
2
2b 1 2
T23 By3 : gk
gk B
T34 By4 : dk
dk B
By11 : gk
gk B
2
2 g 3 2
2
2d 4 3
y2
y3
Dy13 : Dy1
y4
:=0.4
h :=0.15
2 : h 3 :
2
2 g 1 4
0
Dy1
0.05
k :=3.1
4 : h
0.045
0.04
0.035
0.03
0.025
By1 :
0.02
0.015
0.01
0.005
0
80