Момент инерции материальной точки относительно оси, перпендикулярной плоскости её обращения

1.

Момент инерции материальной точки относительно
оси, перпендикулярной плоскости её обращения
LZ L
МТ движется по окружности в плоскости,
перпендикулярной оси (z), проходящей через центр
окружности.
R
Момент импульса МТ относительно точки О :
LZ [ R p]
Проекция момента импульса на ось z
m
p
2
mR
R
m
R
Lz Lz Rp sin Rm
2
2
I z mR - момент инерции материальной точки относительно оси z.
Момент инерции материальной точки относительно оси – это величина,
равная произведению массы материальной точки на квадрат расстояния
до оси вращения.

2.

Момент инерции материальной точки относительно
оси, перпендикулярной плоскости её обращения
I z mR 2
LZ L
Lz mR 2 I z
R
Lz I z
m
В векторной форме:
Lz I z
p m
p

3.

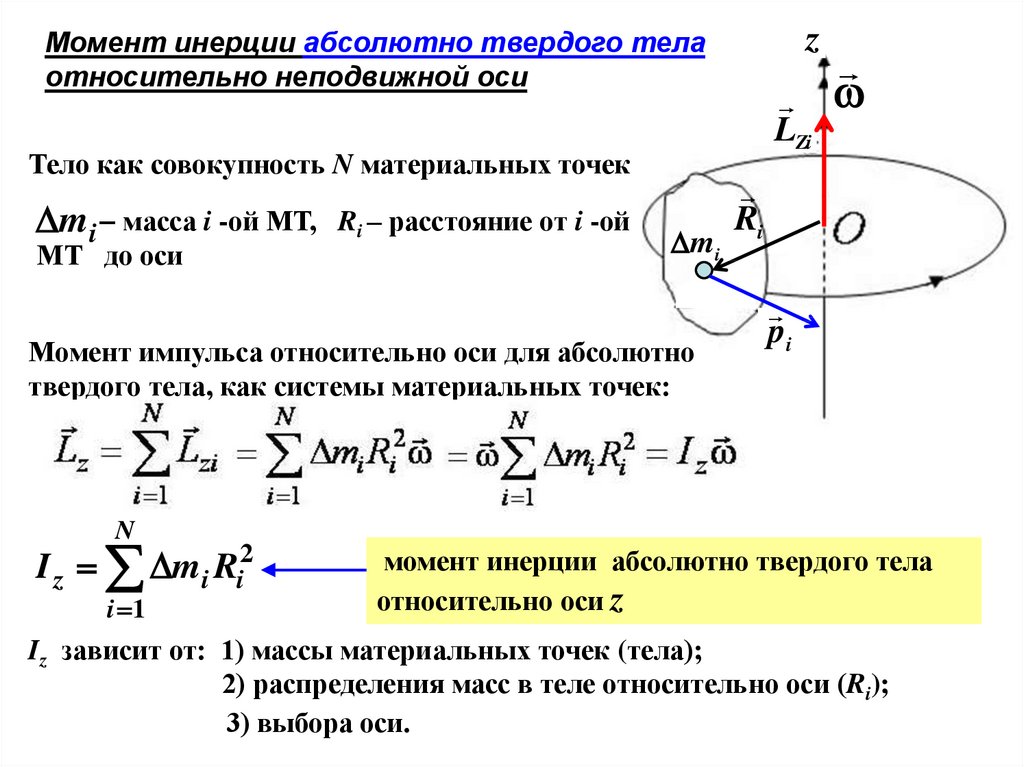
z
Момент инерции абсолютно твердого тела
относительно неподвижной оси
Тело как совокупность N материальных точек
mi – масса i -ой МТ,
МТ до оси
Ri – расстояние от i -ой
m i
Момент импульса относительно оси для абсолютно
твердого тела, как системы материальных точек:
N
I z mi Ri2
i 1
LZi
Ri
pi
момент инерции абсолютно твердого тела
относительно оси z
Iz зависит от: 1) массы материальных точек (тела);
2) распределения масс в теле относительно оси (Ri);
3) выбора оси.

4.

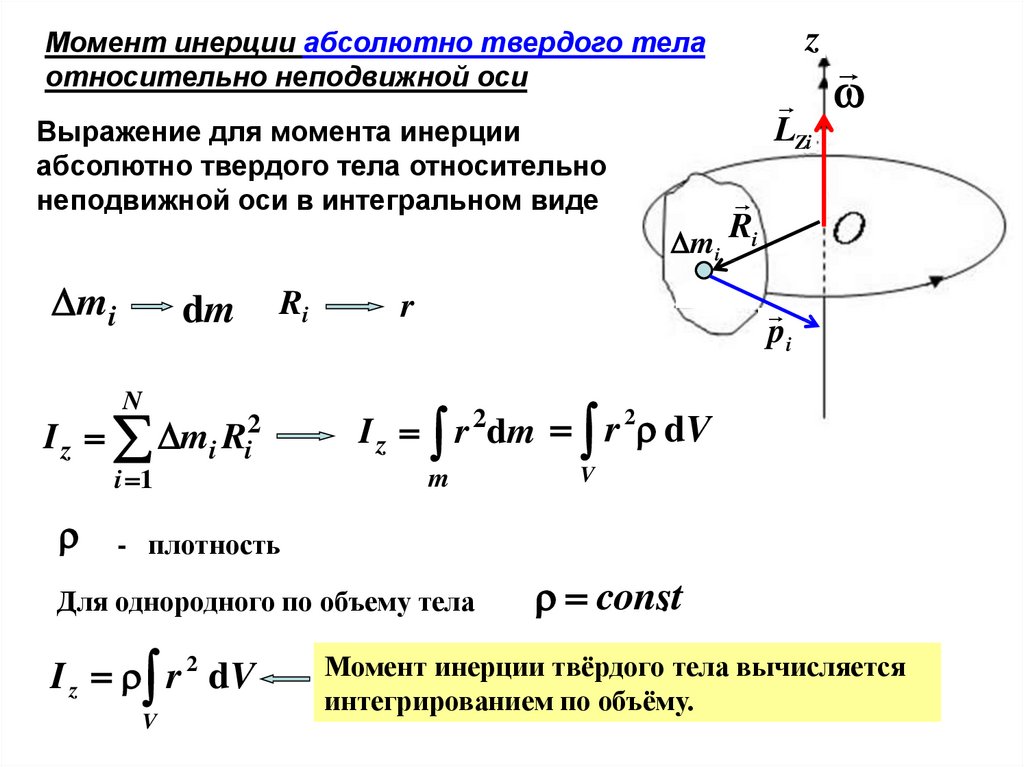
Момент инерции абсолютно твердого тела
относительно неподвижной оси
Выражение для момента инерции
абсолютно твердого тела относительно
неподвижной оси в интегральном виде
m i
dm
N
Iz
i 1
Ri
mi Ri2
z
LZi
mi Ri
pi
r
2
I z r 2dm r dV
m
V
- плотность
Для однородного по объему тела
I z r 2 dV
V
const
.
Момент инерции твёрдого тела вычисляется
интегрированием по объёму.

5.

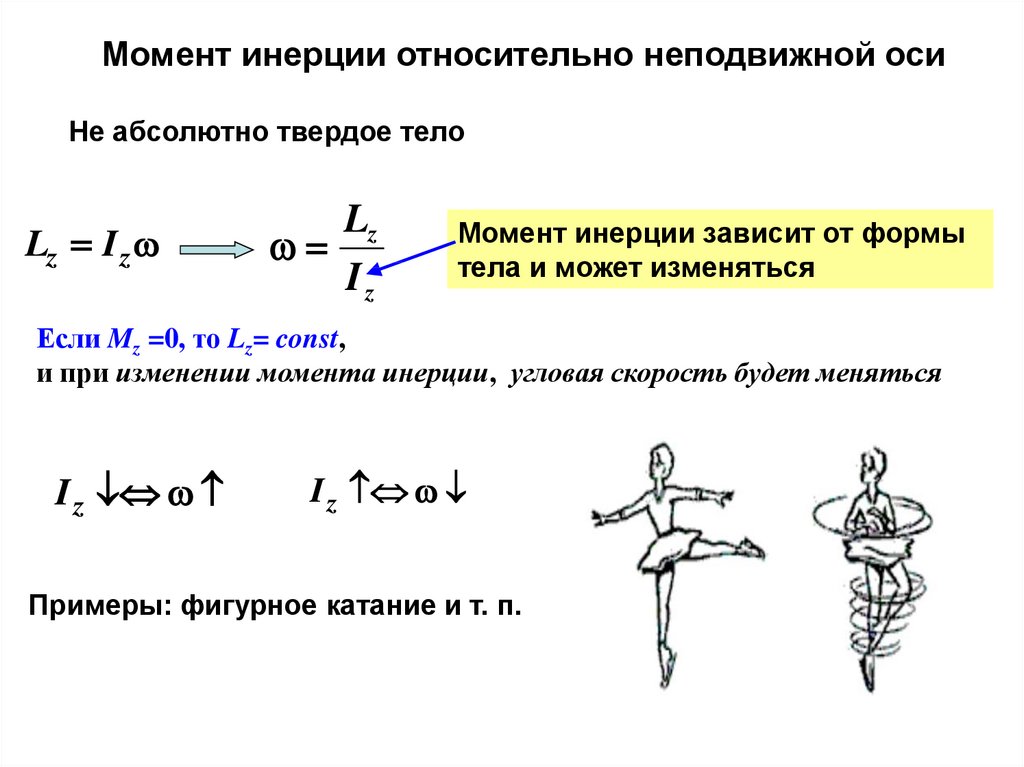
Момент инерции относительно неподвижной оси
Не абсолютно твердое тело
Lz I z
Lz
Iz
Момент инерции зависит от формы
тела и может изменяться
Если Mz =0, то Lz= const,
и при изменении момента инерции, угловая скорость будет меняться
I z
I z
Примеры: фигурное катание и т. п.

6.

Основное уравнение динамики вращательного движения
Рассмотрим абсолютно твердое тело, вращающееся относительно
неподвижной оси.
Момент импульса тела относительно оси
Lz I z
Под действием внешних сил
Lz
и
dLz
d
Iz
dt
dt
dLz
Mz
dt
d
dt
Mz
Iz
будут меняться.
F
a
m
основное уравнение динамики вращательного движения

7.

Примеры расчета момента инерции абсолютно твердого
тела
1. Тонкое кольцо, полый тонкостенный цилиндр
Найдём момент инерции относительно оси
симметрии
I z mi ri2 mi R 2 R 2 mi mR 2
i
i
I z mR 2
i
2. Однородный диск, сплошной цилиндр
Найдём момент инерции относительно оси
симметрии, проходящей через центр масс.
I z r dV
2
dr
r
dV 2 r hdr
V
R
h
R
4
R
3
2
2
h
r
I z r 2 r hdr
0 dr 2 h 4
0
R h V V m
2
mR
Iz
2
2
2R

8.

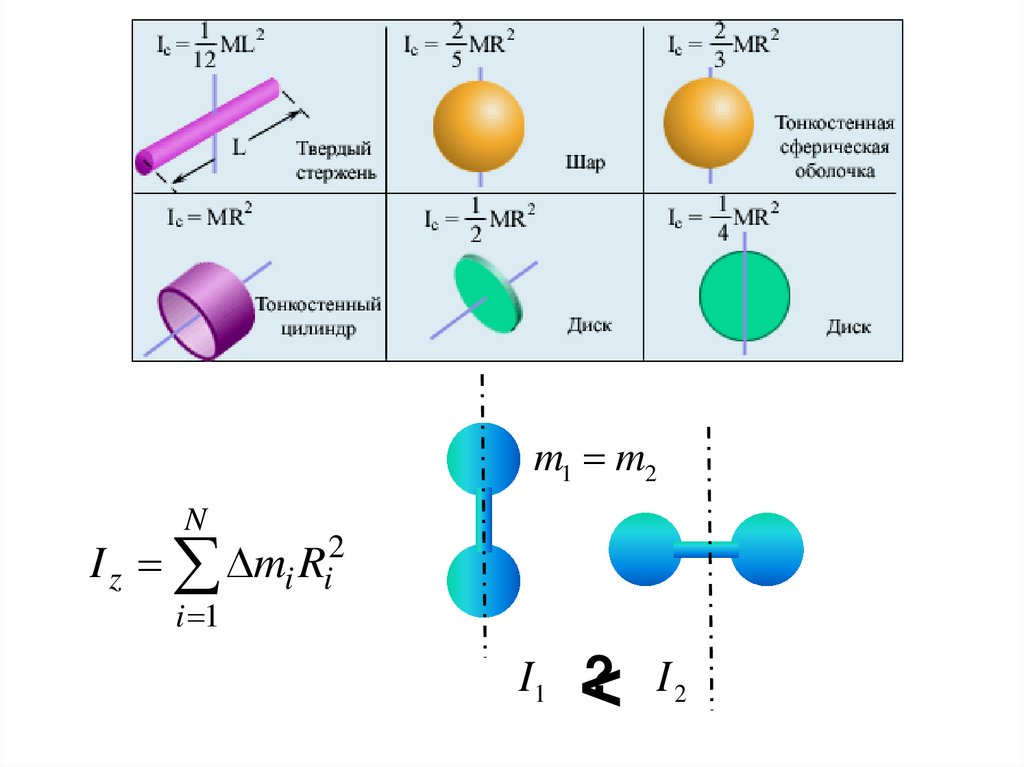
m1 m2
N
Iz
i 1
2
mi Ri
<
I1 ? I 2

9.

Теорема Штейнера
ZC
Z
d
Момент
инерции
тела
относительно
произвольной оси Z равен сумме момента
C
инерции этого тела относительно оси,
параллельной данной и проходящей через
центр масс этого тела, и произведения массы
тела на квадрат расстояния между осями
I Z IC md 2
Iz– искомый момент инерции тела относительно оси Z;
IC - момент инерции тела относительно оси , параллельной оси Z и
проходящей через центр масс тела – точку С ;
d – расстояние между осями;
m – масса тела

10.

Момент инерции однородного стержня.
ZC
Z
1. Момент инерции стержня относительно
оси ZC, перпендикулярной стержню и
проходящей через его центр (центр масс).
r
C
Pазобьем стержень на элементарные участки
длиной dr.
m
dm dr
l
l 2
3 l/2
l 2
r
2
2
r
d
r
2
I c 2 dI C
0
3
0
0
l
2
l
2
dI c r 2dm r 2dr
1
IC ml 2
12
l 3 ml 2
2
24
12
2. Момент инерции относительно оси Z, проходящей
через конец стержня параллельной оси ZC .
Согласно теореме Штейнера
2
2
2
ml
ml
ml
l
I Z IC m
12
4
3
2
2
dr
1 2
I Z ml
3

11.

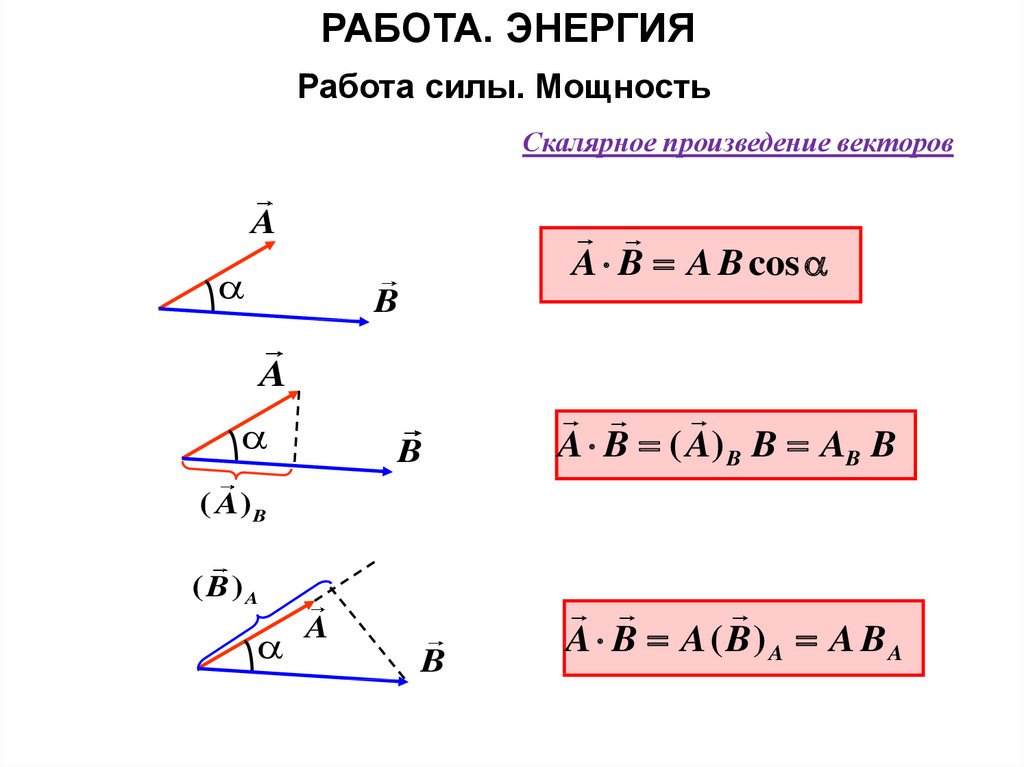
РАБОТА. ЭНЕРГИЯ
Работа силы. Мощность
Скалярное произведение векторов
A
A B A B cos
B
A
B
A B ( A) B B AB B
( A) B
( B)A
A
B
A B A ( B ) A A BA

12.

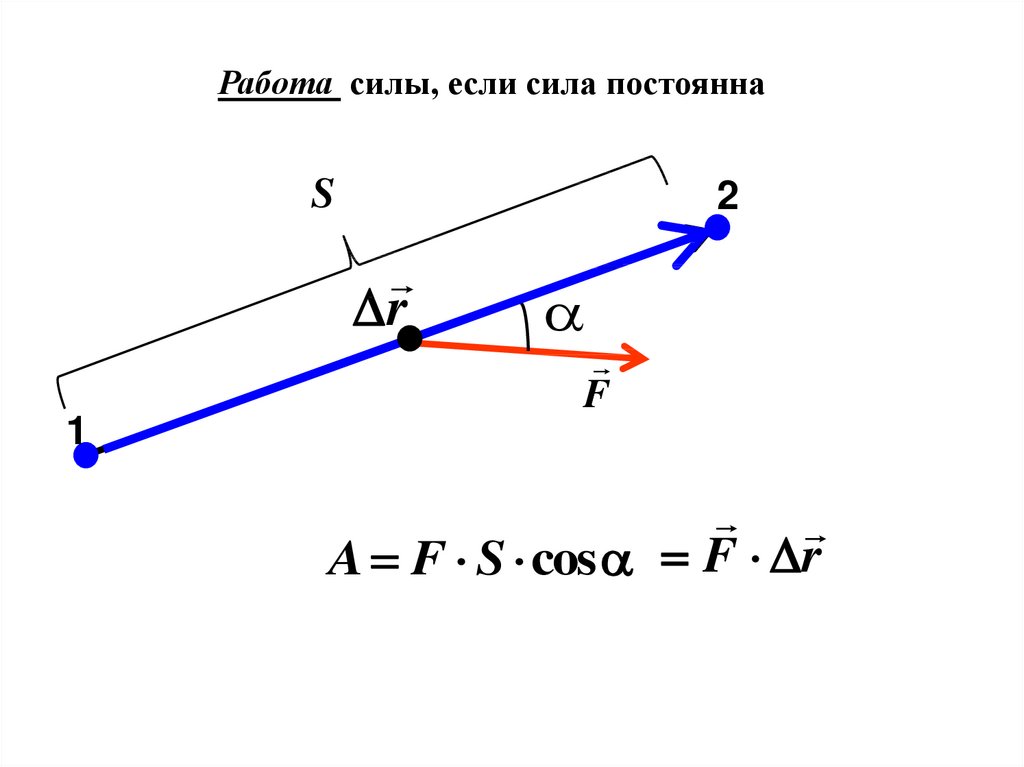
Работа силы, если сила постоянна
S
2
r
1
F
A F S cos F r

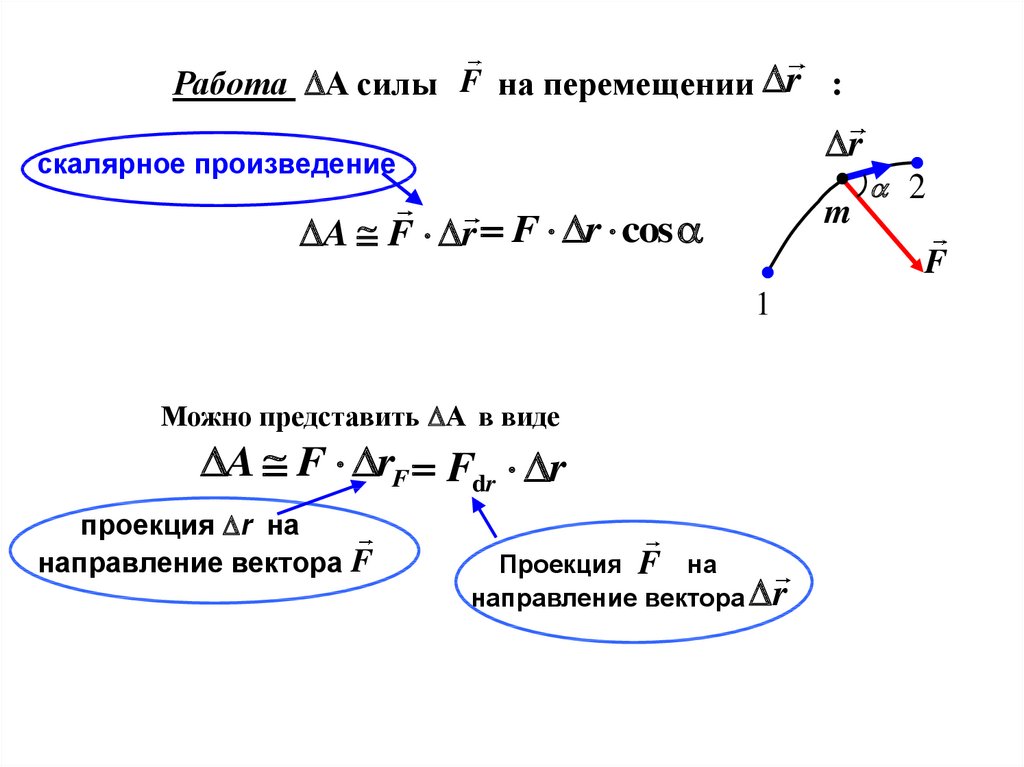
13.

Работа A силы F на перемещении r :
drr
скалярное произведение
A F r F r cos
m
F
1
Можно представить A в виде
A F rF Fdr r
проекция r на
направление вектора F
F
2
Проекция
на
направление вектора r

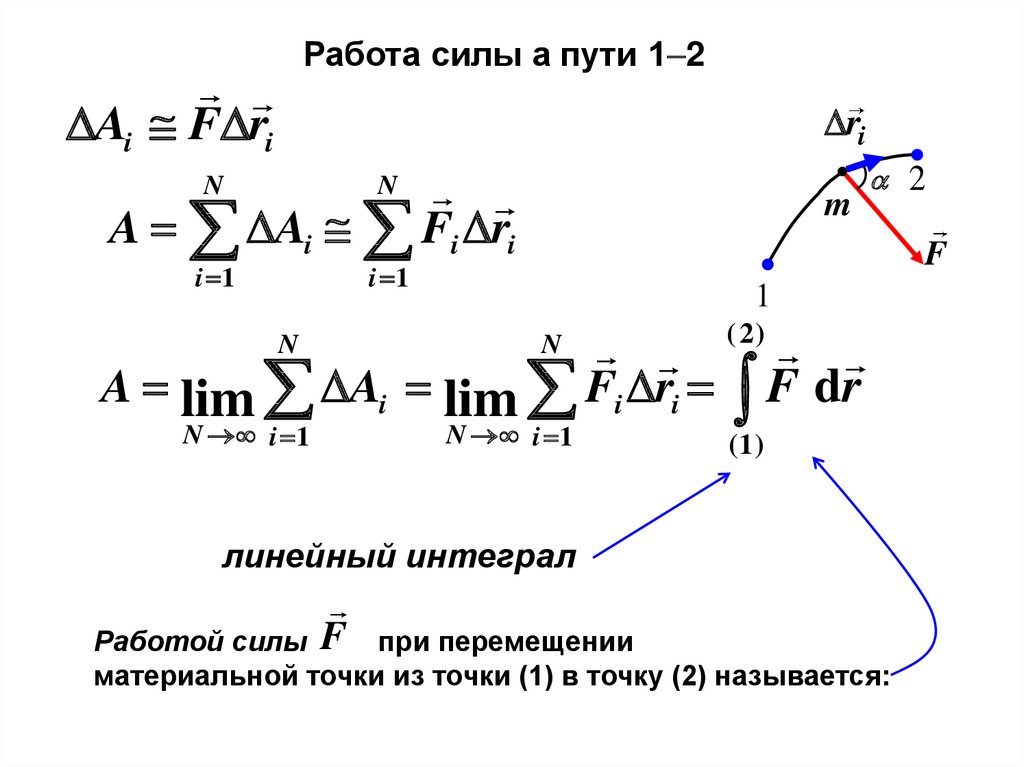
14.

Работа силы а пути 1 2
Ai F ri
dr
ri
A Ai Fi ri
N
N
i 1
m
2
F
i 1
1
( 2)
A lim Ai lim Fi ri F dr
N
N
N i 1
N i 1
(1)
линейный интеграл
F
Работой силы
при перемещении
материальной точки из точки (1) в точку (2) называется:

15.

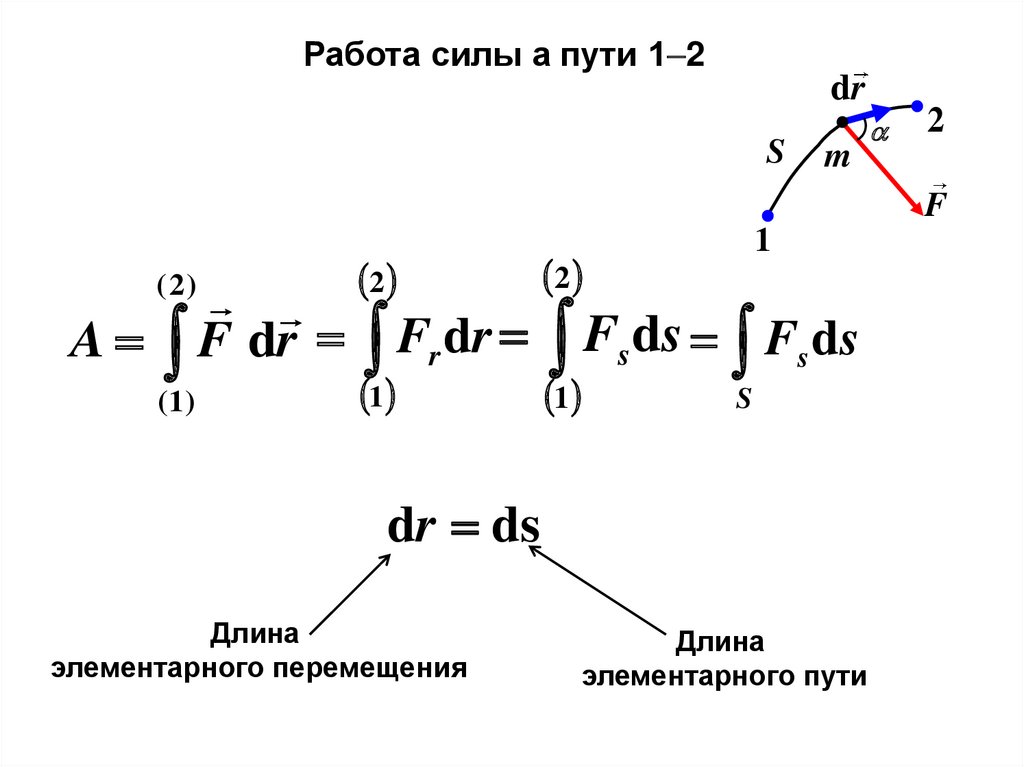
Работа силы а пути 1 2
dr
S
m
2
F
( 2)
2
2
(1)
1
1
A F dr
F
dr
r
1
F
ds
s
Fsds
S
dr ds
Длина
элементарного перемещения
Длина
элементарного пути

16.

Элементарная работа dA силы F на элементарном
перемещении dr :
dr
m
2
F
1
dA F dr F dr cos F drF
Fdr dr Fs ds

17.

Мощность
Мощность характеризует быстроту с которой
совершается работа:
F dr
dA
P
dt
dt
F
Размерность работы: [A]=[F]L=MLT-2*L=ML2T-2
Единица измерения работы в системе СИ:
Размерность мощности:
Дж = кг*м2/сек2
[P]=[A]T-1=ML2T-3
Единица измерения мощности в системе СИ: Вт= Дж /c = кг*м2/сек3

18.

Работа центральной силы
f r
r
O
Сила упругости
r
Felastic
r
Felastic
Felastic kr

19.

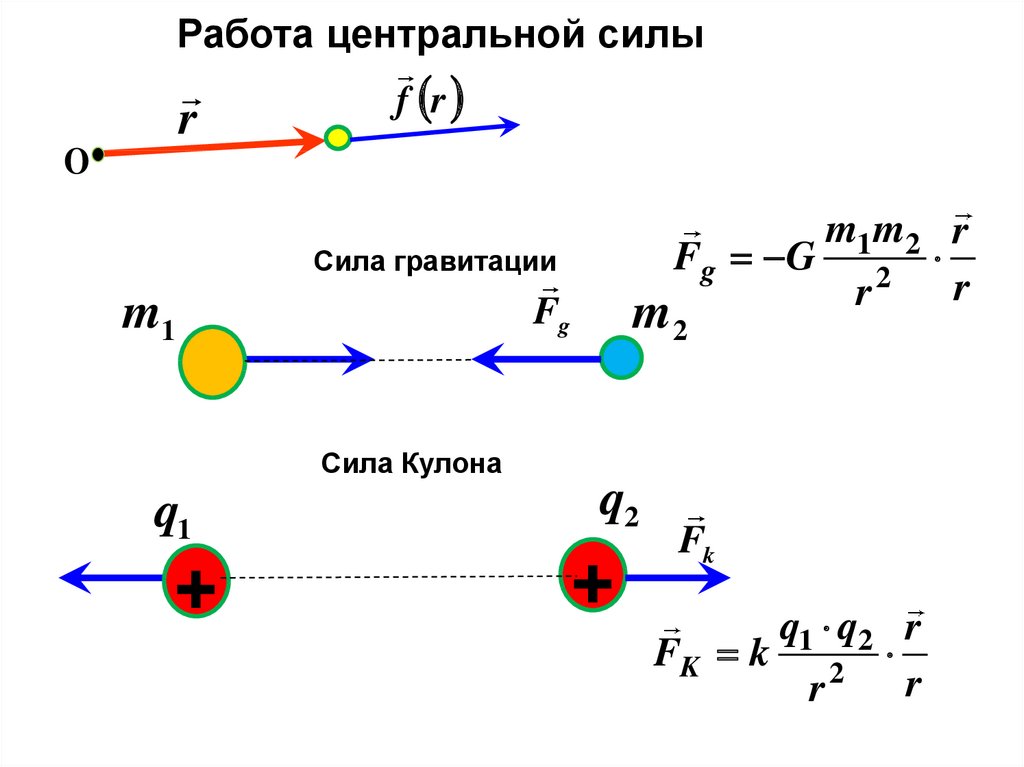
Работа центральной силы
f r
r
O
m1m2 r
Fg G 2
r
r
Сила гравитации
Fg
m1
m2
Сила Кулона
q1
+
q2
+
Fk
q1 q2 r
FK k 2
r
r

20.

.
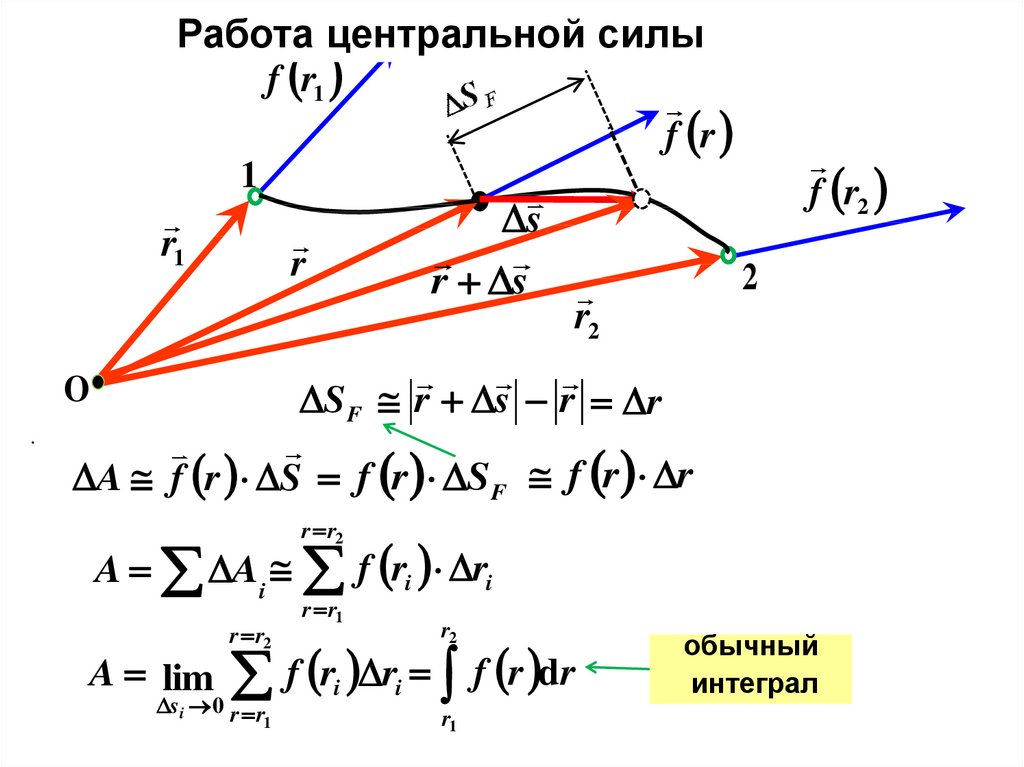
Работа
центральной силы
f r1
f r
1
s
r1
r
2
r s
r2
O
S F r s r r
A f r S f r SF f r r
f r2
r r2
A Ai f ri ri
A lim
r r2
r r1
r2
f r r f r dr
s i 0 r r
1
i
i
r1
обычный
интеграл

21.

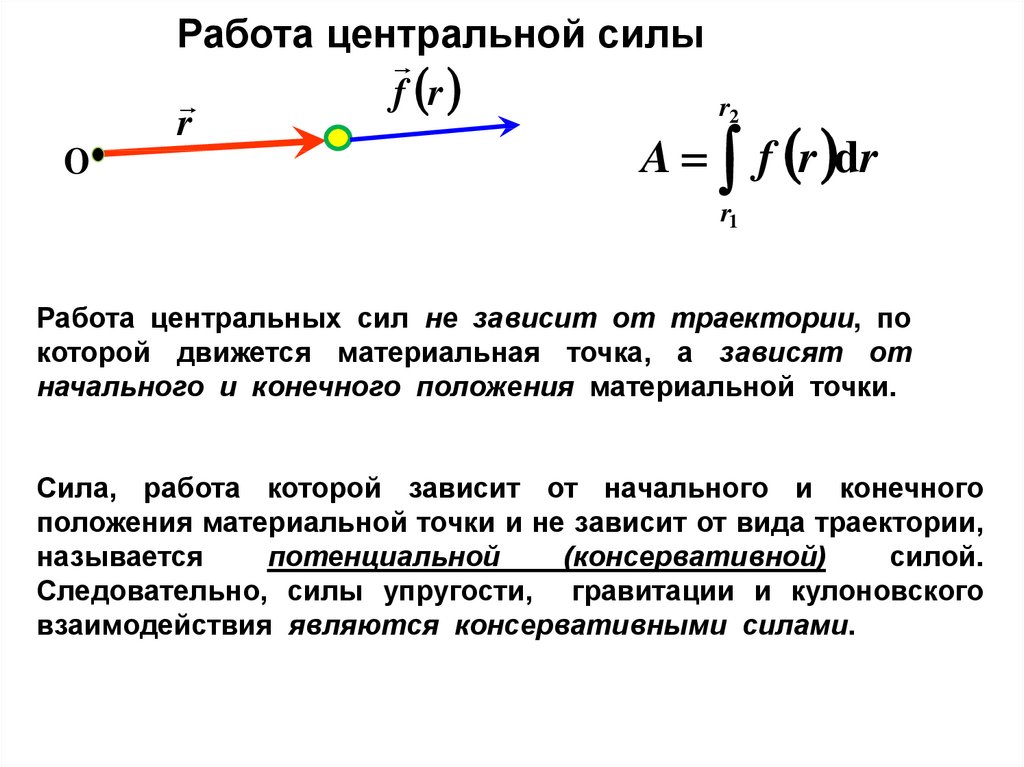
Работа центральной силы
f r
r
O
r2
A f r dr
r1
Работа центральных сил не зависит от траектории, по
которой движется материальная точка, а зависят от
начального и конечного положения материальной точки.
Сила, работа которой зависит от начального и конечного
положения материальной точки и не зависит от вида траектории,
называется
потенциальной
(консервативной)
силой.
Следовательно, силы упругости, гравитации и кулоновского
взаимодействия являются консервативными силами.

22.

Работа силы гравитации
r2
A f r dr
r1
m1m2 r
Fg G 2
r
r
G 6,67 10 11 м³/(кг с²)
r2
r2
m1 m 2
Ag Fg r dr - G 2 dr
r
r1
r1
m1m2
G
r
r2
r1
m1m2
m1m2
G
G
r1
r2

23.

Работа силы Кулона
r2
A f r dr
r1
q1q2 r
FK k 2
r
r
k 9 109 Н·м2/Кл2
r2
r2
q1q2
AK FK r dr k 2 dr
r
r
1
r
1
q1q2
k
r
r2
r1
q1q2
q1q2
k
k
r1
r2

24.

Работа силы упругости
Felastic kr
r2
A f r dr
r1
r
Felastic
0
r2
r2
r1
r1
Aelastic Felastic r dr k r dr
r2
k
2
r2
r1
2
2
r1
r2
k
k
2
2

25.

Работа силы тяжести (работа в однородном поле)
m1m2
G
Fg Fg
r2
сила тяжести
Вблизи поверхности Земли h<<R
MЗ
Fg G 2 m gm Fт const (h)
RЗ g
Элементарная работа силы тяжести на
элементарном перемещении dr
z
h1
drF dz
dAT FT dr FT drF FT dz mgdz
AT
h2
h2
dr
h2
mg dz mg dz mgh1 mgh2
h1
h1
1
0
2
FT mg
Сила тяжести – консервативная сила
Не зависит от траектории

26.

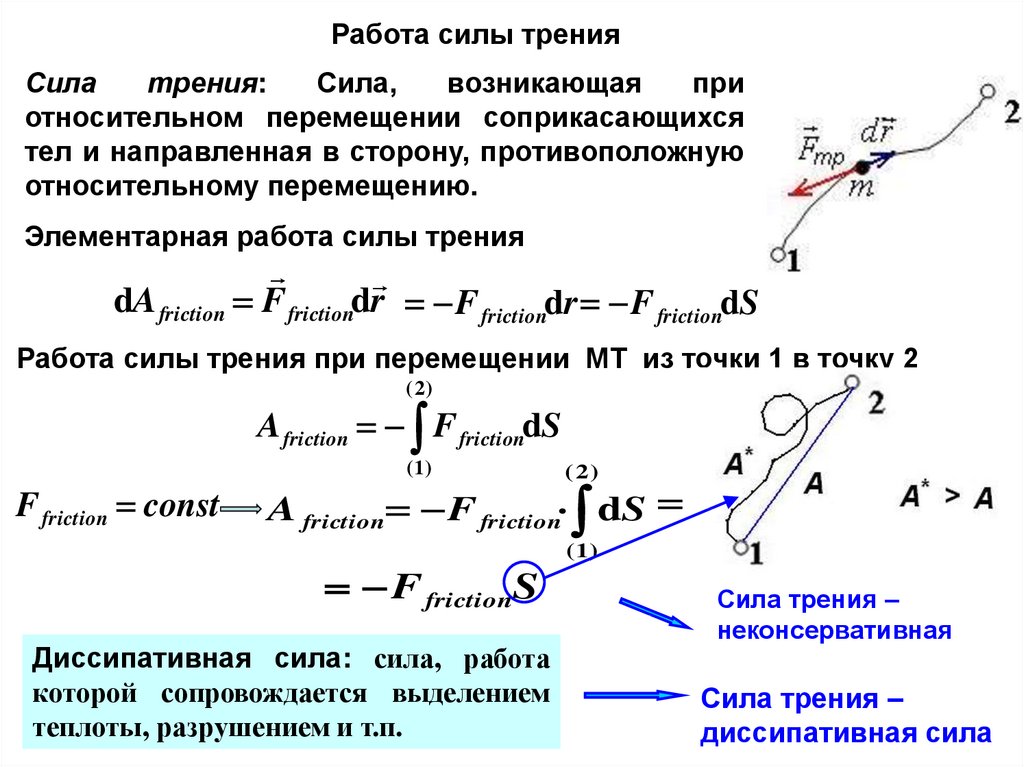
Работа силы трения
Сила
трения:
Сила,
возникающая
при
относительном перемещении соприкасающихся
тел и направленная в сторону, противоположную
относительному перемещению.
Элементарная работа силы трения
dA friction F frictiondr F frictiondr F frictiondS
Работа силы трения при перемещении МТ из точки 1 в точку 2
( 2)
A friction F frictiondS
(1)
F friction const
( 2)
A friction F friction dS
(1)
F frictionS
Диссипативная сила: сила, работа
которой сопровождается выделением
теплоты, разрушением и т.п.
Сила трения –
неконсервативная
Сила трения –
диссипативная сила

27.

Потенциальная энергия
Примеры потенциальных полей и работы сил этих полей
m1m2
m1m2
Ag G
G
r1
r2
q1q2
q1q2
AK k
k
r1
r2
консервативной
силы:
AKC Wn1 Wn2
AT mgh1 mgh2
kr12 kr22
Aelastic
2
2
Работа консервативной силы
Работа
=
разность значений функции,
зависящая от относительного
положения взаимодействующих
тел (или от координат тела в
потенциальном поле).
Обозначим эти значения функции Wn1 и Wn2 и назовем их
потенциальными энергиями взаимодействия.

28.

Потенциальная энергия
Akc=Wn1 - Wn2= - ΔWn
Работа консервативной силы равна взятому со знаком минус
изменению потенциальной энергии тела.

29.

Akc=Wn1 - Wn2= - ΔWn
Akc=(Wn1 +C)- (Wn2+C)= - ΔWn
m1m2
m1m2
Ag G
G
r1
r2
q1q2
q1q2
Ak k
k
r1
r2
AT mgh1 mgh2
kr12
2
2
kr
Aelastic
2
2
m1m2
Wg G
+C
r
q1q2
+C
Wk k
r
WT mgh +C
Welastic
k r2
+C
2
Потенциальная энергия системы в данном ее положении численно равна работе,
которую совершают действующие на систему консервативные силы при
перемещении системы из этого положения в то, где потенциальная энергия
условно принимается равной нулю.

30.

Потенциальная энергия системы МТ
Потенциальная энергия - часть механической энергии
системы, зависящая от взаимного расположения
материальных точек, составляющих эту систему, и
от их положения во внешнем силовом поле.
Wп
Felasic Felasic
Fg
ik – потенциальная энергия взаимодействия i-й МТ с k-й МТ.
N
W
k 1
k i
1
2
N
n ik –
потенц. энергия взаимодействия i-й МТ со всеми МТ системы.
N
– полная потенциальная энергия взаимодействия МТ друг
W
n ik
i 1 k 1
k i
с другом
W n i потенц. энергия взаимодействия i-й МТ
с внешними телами (полями).
Wn i – полная потенциальная энергия взаимодействия системы с
внешними телами (полями)
i 1
N
N
Wn Wn i
i 1
1 N N
Wn ik
2 i 1 k 1
k i
– полная потенциальная энергия
системы МТ

31.

Потенциальная энергия системы МТ
Взаимодействие между
МТ системы
Взаимодействие с
внешними телами (полями)
N
Wn Wn i
i 1
1 N
2 i 1
N
W
k 1
k i
n ik
Изменение потенциальной энергии системы МТ
Aкс=Wn1-Wn2= - ΔWn
Работа всех консервативных сил (включая внутренние),
действующих на систему, равна взятому со знаком минус
изменению потенциальной энергии системы.

32.

Связь консервативной силы с
потенциальной энергией тела
Работа консервативной силы на элементарном
перемещении в произвольном направлении
dA Fsds
С другой стороны
dA dWn
Проекция консервативной силы на
произвольное направление
Fsds dWn
dWn
Fs
ds
В частности для проекций на оси координат
Wn ( x, y, z ) F Wn ( x , y , z ) ; F Wn ( x , y , z )
z
Fx
; y
z
y
x
W
W
W
n
n
n
F Fx i Fy j Fz k
x i y j z k grad Wn
F grad Wn

33.

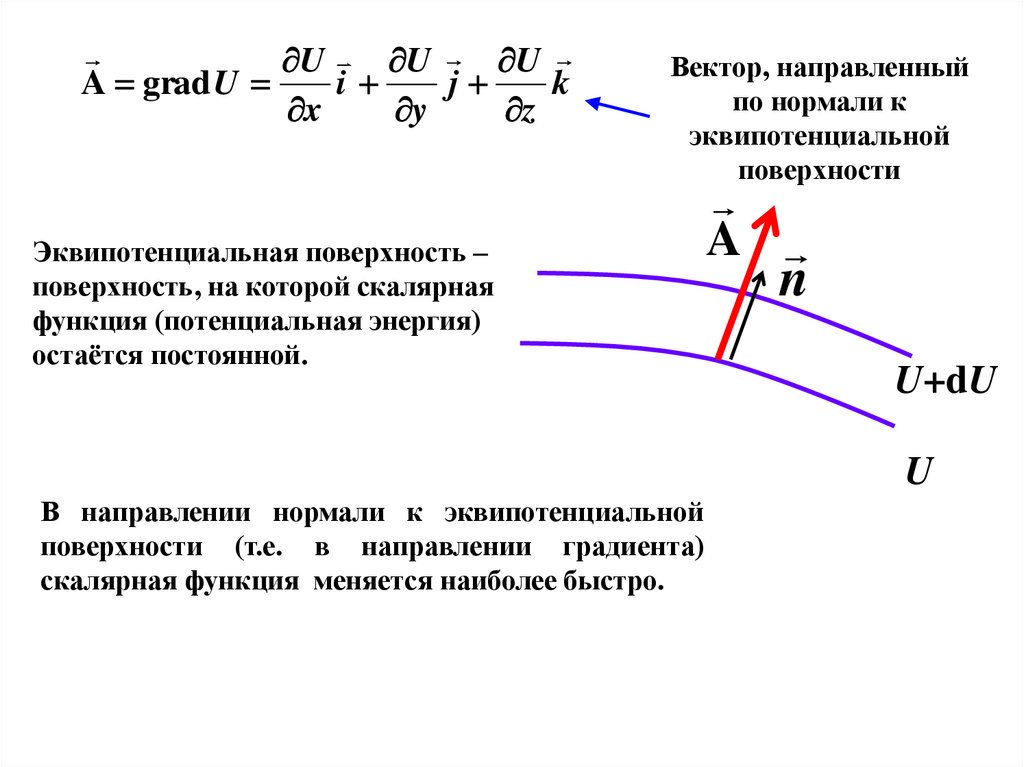
U U U
A grad U
i
j
k
x
y
z
Вектор, направленный
по нормали к
эквипотенциальной
поверхности
Эквипотенциальная поверхность –
поверхность, на которой скалярная
функция (потенциальная энергия)
остаётся постоянной.
A
n
U+dU
U
В направлении нормали к эквипотенциальной
поверхности (т.е. в направлении градиента)
скалярная функция меняется наиболее быстро.

34.

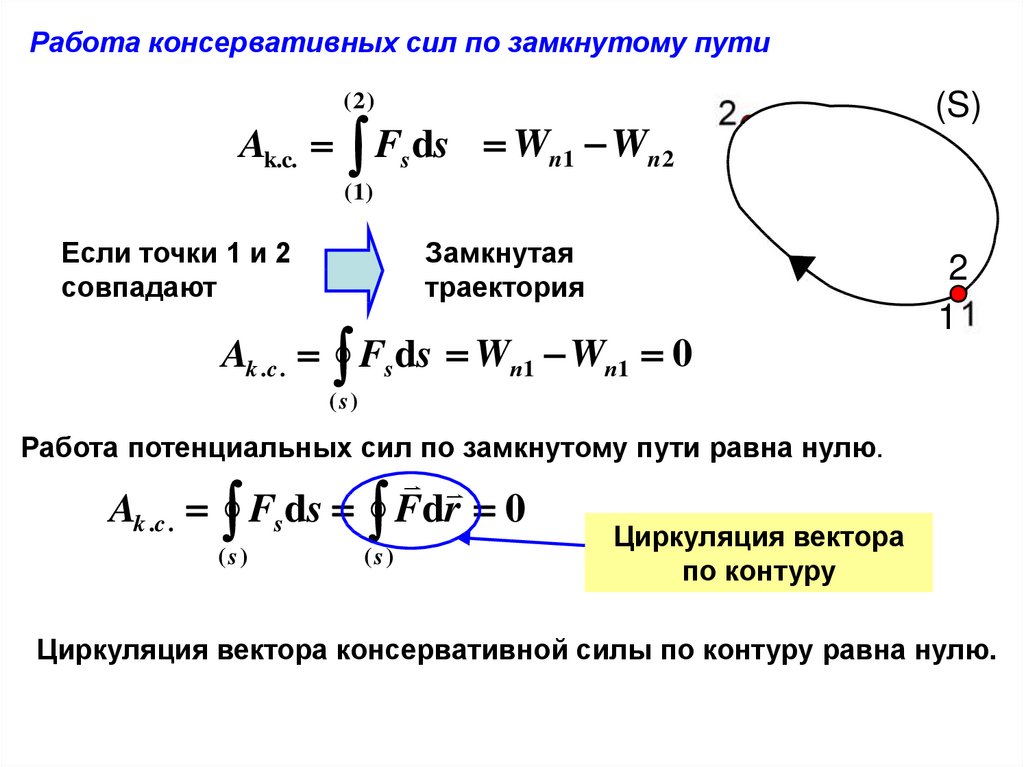
Работа консервативных сил по замкнутому пути
( 2)
Ak.c.
F ds
s
Wn1 Wn 2
(S)
(1)
Если точки 1 и 2
совпадают
Замкнутая
траектория
Ak .c . Fsds Wп1 Wп1 0
2
1
(s)
Работа потенциальных сил по замкнутому пути равна нулю.
Ak .c .
Fsds Fdr 0
(s)
(s)
Циркуляция вектора
по контуру
Циркуляция вектора консервативной силы по контуру равна нулю.

35.

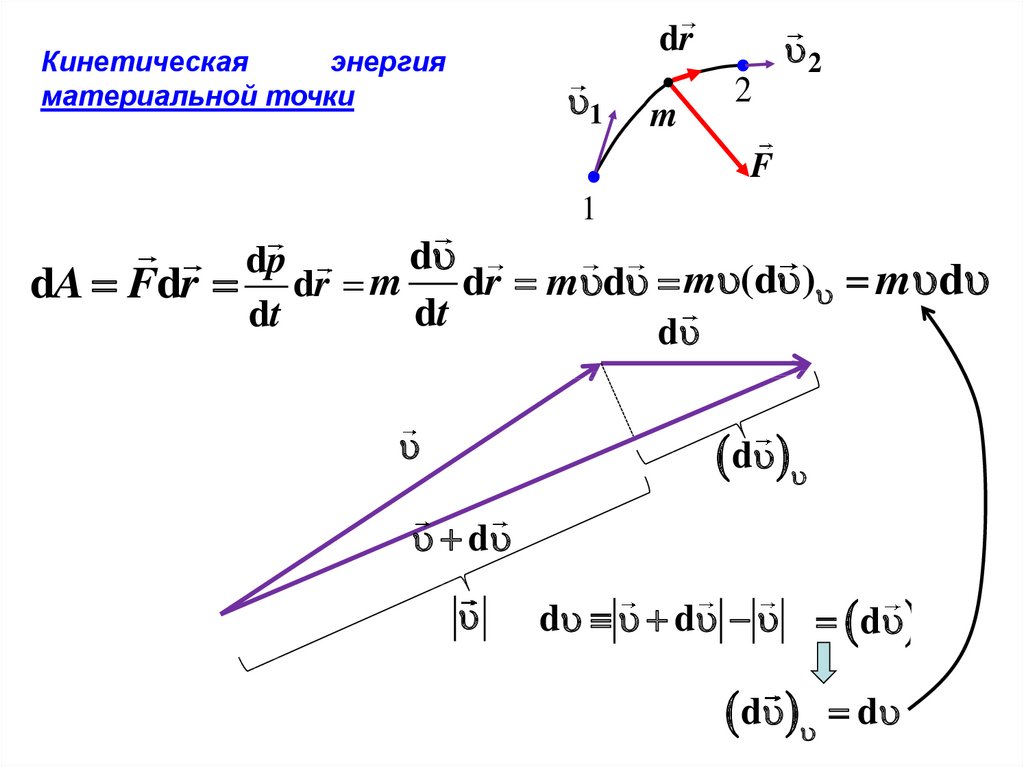
dr
Кинетическая
энергия
материальной точки
1
m
2
2
F
1
dp
d
dA Fdr dr m dr m d m (d ) m d
dt
dt
d
d
d
d d d
d d

36.

Кинетическая
энергия
материальной точки
dr
1
m
2
2
F
1
dp
d
dA Fdr dr m dr m d m (d ) m d
dt
dt
Кинетическая энергия
Работа результирующей всех сил,
при перемещении м.т. из (1) в (2)
2
( 2)
m 22 m 12
AF Fdr m d m d
2
2
(1)
(1)
( 2)
1

37.

m
m
A
2
2
2
2
2
1
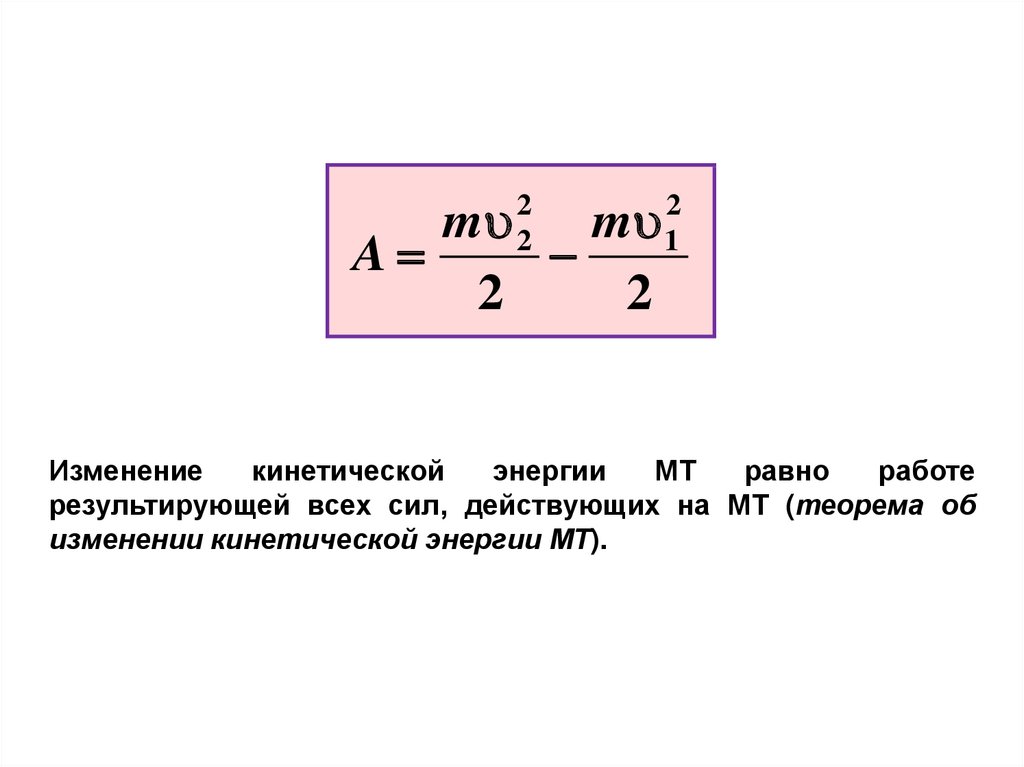
Изменение
кинетической
энергии
МТ
равно
работе
результирующей всех сил, действующих на МТ (теорема об
изменении кинетической энергии МТ).

38.

Кинетическая энергия поступательного движения системы
материальных точек
Система N материальных точек
Кинетическая энергия i-ой МТ
WKi
2
m
WK WKi i i
2
i 1
i 1
N
N
Суммарная кинетическая энергия
Работа всех сил: внешних и сил
взаимодействия с другими МТ системы
Теорема об изменении кин.энергии МТ: A W
i
i
K2
N
A WK 2 W K 1
W
i
K1
N
N
i 1
i 1
i
i
i
A
W
W
K 2 K1
Просуммируем обе части уравнения по всем МТ:
i 1
A WK 2 WK 1
Изменение кинетической энергии системы МТ равно работе всех
сил, действующих на каждую МТ (как внутренних так и внешних).
Отличие от закона изменения импульса

39.

Кинетическая энергия поступательного и вращательного
движения абсолютно твёрдого тела
Поступательное движение АТТ
Разобьём тело массой m на кусочки с массами
можно считать материальными точками.
mi
Wk
2
i
2
mi
, которые
2
2
m
mi
2 i
2
m
Wk
2
2

40.

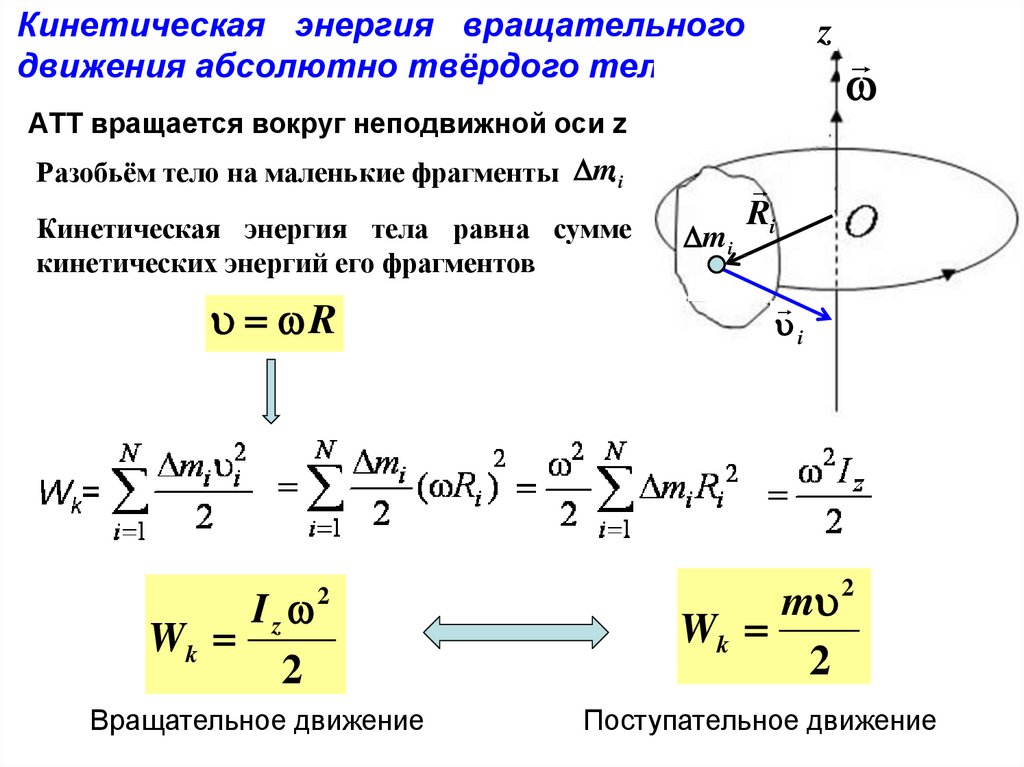
Кинетическая энергия вращательного
движения абсолютно твёрдого тела
z
АТТ вращается вокруг неподвижной оси z
Разобьём тело на маленькие фрагменты m. i
Кинетическая энергия тела равна сумме
кинетических энергий его фрагментов
R
Iz
Wk
2
2
Вращательное движение
m i
Ri
i
m
Wk
2
2
Поступательное движение

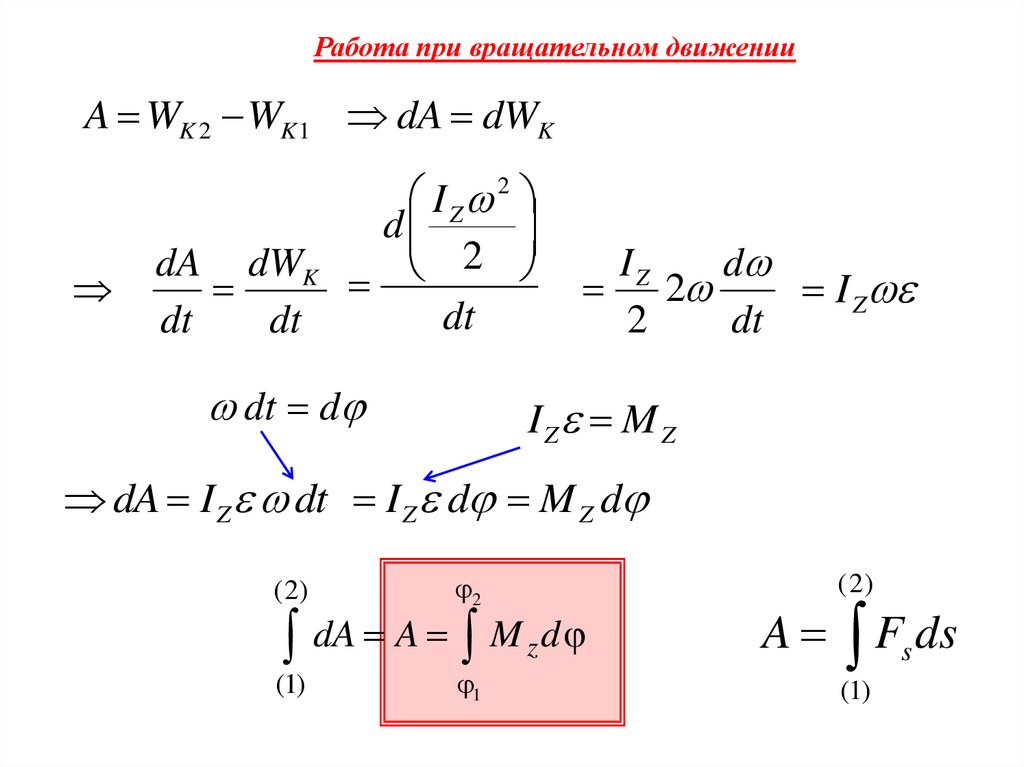
41.

Работа при вращательном движении
A WK 2 WK1 dA dWK
dA dWK
dt
dt
I Z 2
d
2
dt
dt d
IZ
d
2
I Z
2
dt
IZ M Z
dA I Z dt I Z d M Z d
(2)
2
dA A M z d
(1)
1
( 2)
A
F ds
s
(1)

42.

43.

Закон сохранения полной механической энергии
Полная механическая энергия системы
=
N
кин
W
сумма кинетических энергий тел, входящих в систему i
i 1
+
сумма потенциальных энергий, обусловленных их
взаимодействием друг с другом и внешними телами (полями)
1 N N пот N пот
Wik Wi
2 i 1 k 1
i 1
W W кин W пот
N
N N
N
1
Wi кин Wikпот Wi пот
2 i 1 k 1
i 1
i 1

44.

Закон сохранения полной механической энергии
W W кин W пот
N
N N
N
1
Wi кин Wikпот Wi пот
2 i 1 k 1
i 1
i 1
W ?
Теорема об изменении кинетической энергии для системы МТ
W кин A
– работа всех сил, приложенных к МТ системы
A Aк .с . Aн. к .с .
W кин Aк .с . Aн . к .с .
По определению
потенциальной
энергии
Aк .с . W пот
W W кин W пот
Aк .с . Aн.к .с . Aк .с . Aн.к .с .

45.

Закон сохранения полной механической энергии
W W кин W пот Aн . к .с .
Что такое неконсервативные силы?
• Силы трения (диссипативные силы), действующие между
телами системы
• Внешние неконсервативные силы, например, мускульная сила,
силы со стороны каких-либо механизмов и т.п.
Cилы вихревых полей
В системе с одними только
консервативными силами полная
механическая энергия остаётся постоянной.

46.

Закон сохранения полной механической энергии
Отличия законов сохранения импульса (момента импульса) и
полной механической энергии:
1. Роль внешней силы
Чтобы сохранялся импульс, результирующая
внешняя сила должна быть равна 0.
Полная механическая энергия сохраняется
при действии внешних консервативных сил.
Примеры: тело на пружине, свободное падение
2. Роль диссипативных сил
Импульс сохраняется независимо от вида внутренних сил, в том
числе, это могут быть силы трения между телами системы.
Полная механическая энергия не сохраняется при действии сил
трения (она переходит в тепло, полная энергия сохраняется).
Пример: неупругие столкновения.

47.

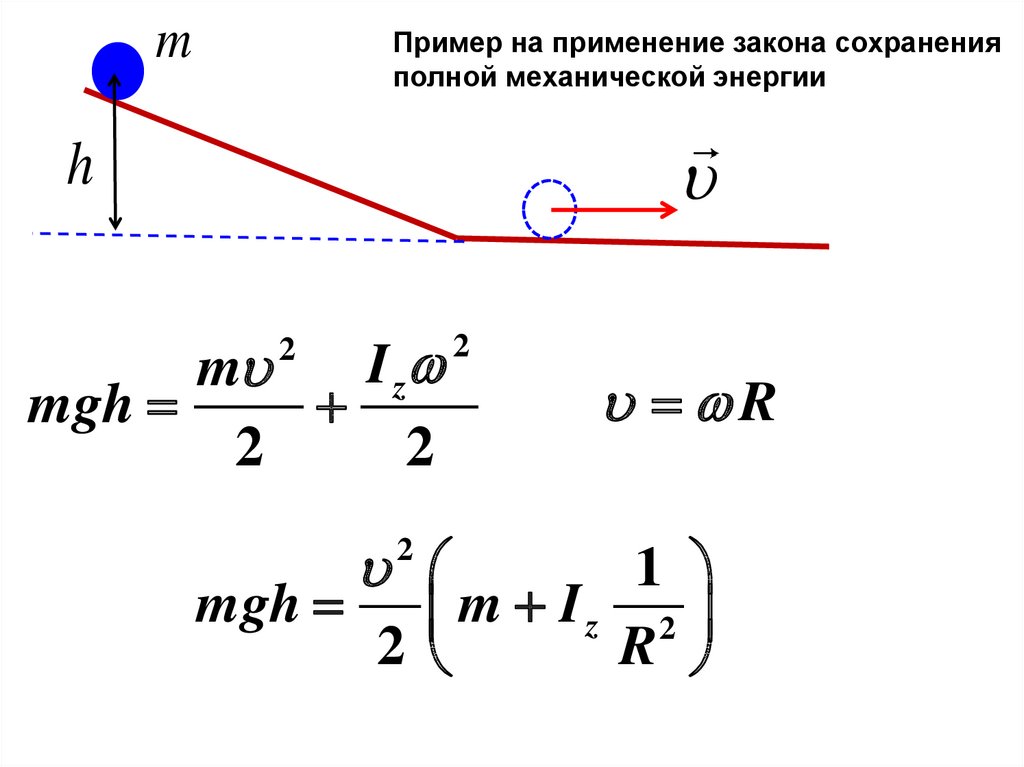
m
Пример на применение закона сохранения
полной механической энергии
h
I z
m
mgh
2
2
2
2
R
1
mgh
m Iz 2
2
R
2

48.

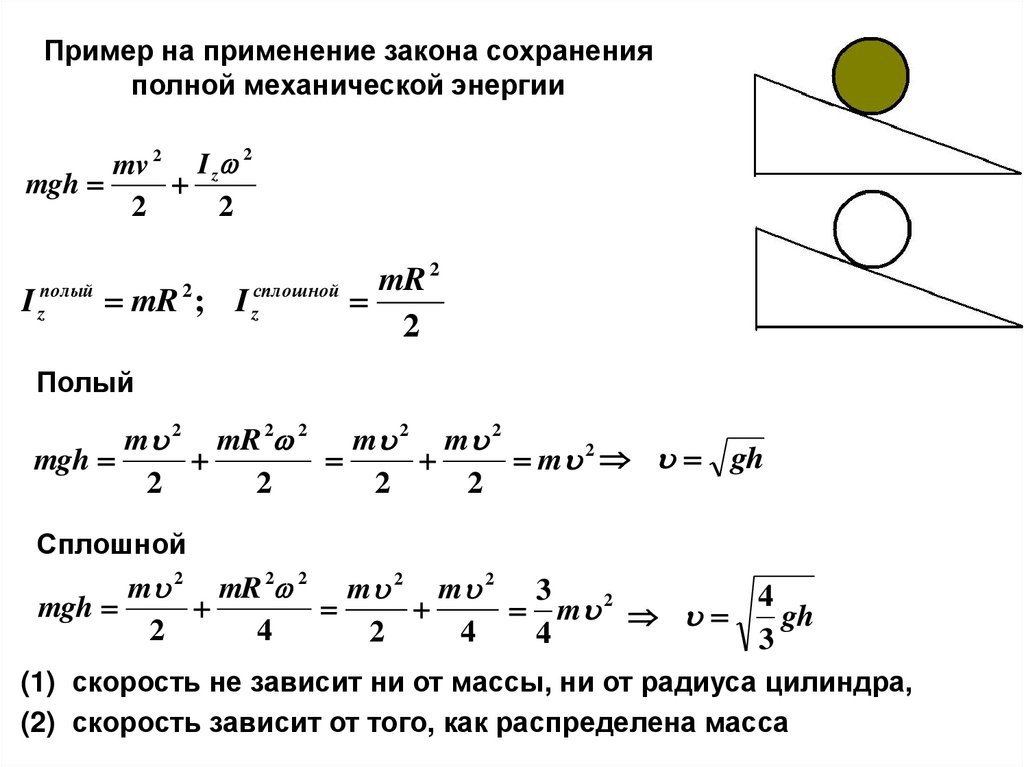
Пример на применение закона сохранения
полной механической энергии
mv 2 I z 2
mgh
2
2
I zполый
2
mR
mR 2 ; I zсплошной
2
Полый
m 2 mR 2 2 m 2 m 2
mgh
m 2 gh
2
2
2
2
Сплошной
m 2 mR 2 2 m 2 m 2 3
mgh
m 2 4 gh
2
4
2
4
4
3
(1) скорость не зависит ни от массы, ни от радиуса цилиндра,
(2) скорость зависит от того, как распределена масса

49.

Закон сохранения полной механической энергии
Согласно теореме Нётер (Эмми Нётер),
закон сохранения механической энергии является следствием
однородности времени.
закон сохранения импульса — однородности пространства,
закон сохранения момента импульса — изотропности
пространства.

50.

Закон сохранения и превращения энергии
Диссипативные силы:
механическая энергия системы тел уменьшается
внутренняя энергии тел увеличивается (нагрев
при трении) на ту же величину.
Виды энергии: механическая, внутренняя, электрическая,
магнитная, ядерная и др.
Энергия не исчезает бесследно и не возникает
из ничего, она превращается из одного вида
энергии в другой, либо передается от одних
тел к другим в эквивалентном количестве. При
этом суммарное количество энергии остается
постоянным.
Следствие закона сохранения и превращения
энергии - невозможность создания «вечного
двигателя».

51.

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
Вопросы к коллоквиуму
Кинематика материальной точки.
Кинематика вращательного движения.
Законы Ньютона. Принцип относительности Галилея.
Постулаты специальной теории относительности А.Эйнштейна. Относительность
одновременности, сокращение продольных размеров, замедление времени.
Второй закон Ньютона. Движение центра инерции.
Третий закон Ньютона. Закон изменения и сохранения импульса.
Момент импульса. Момент силы. Связь между ними.
Момент инерции. Моменты инерции тонкостенного кольца и сплошного цилиндра.
Теорема Штейнера. Применение для расчета МИ стержня относительно оси, проходящей
через его конец.
Основное уравнение динамики вращательного движения.
Работа силы. Мощность.
Работа силы тяготения. Работа сил Кулона.
Работа силы тяжести.
Работа силы упругости.
Поле силы. Потенциальная энергия. Связь поля силы с потенциальной энергией.
Кинетическая энергия (мат. точки, системы мат. точек, кинетическая энергия
поступательного и вращательного движения АТТ).
Полная механическая энергия.
Закон изменения и сохранения полной механической энергии.