Similar presentations:
Динамика относительного движения материальной точки. (Лекция 3)
1. Динамика относительного движения материальной точки Лекция 3
2. Дифференциальные уравнения относительного движения материальной точки
3. Дифференциальные уравнения относительного движения материальной точки
Силыинерции
Переносная
Кориолисова
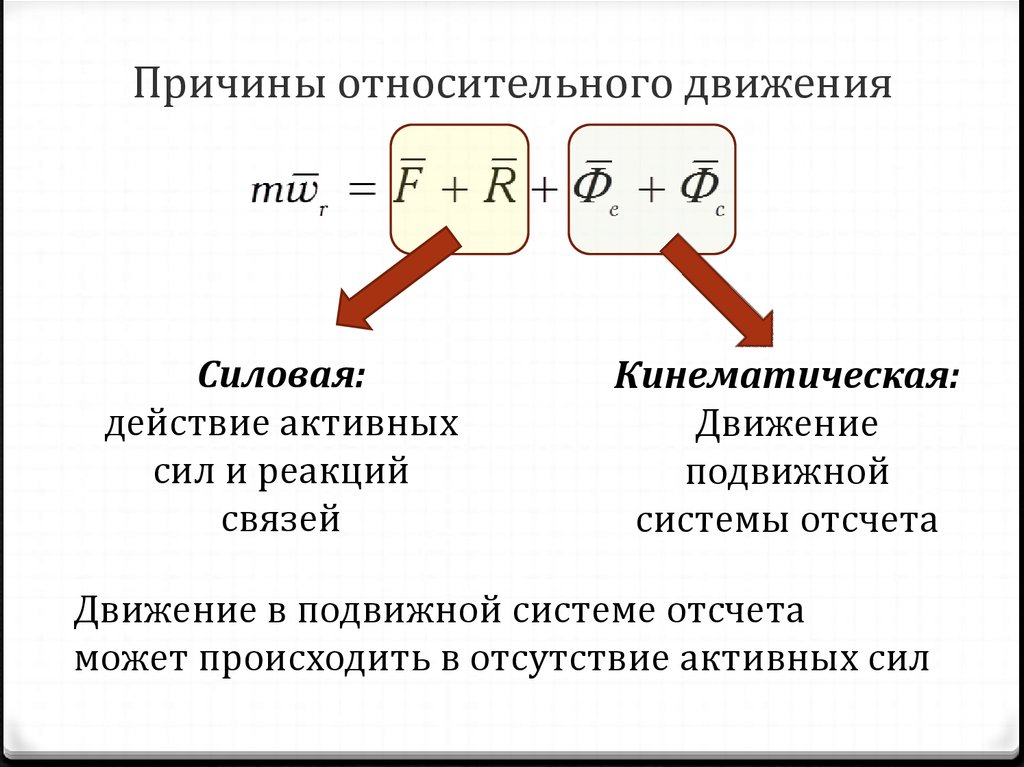
4. Причины относительного движения
Силовая:действие активных
сил и реакций
связей
Кинематическая:
Движение
подвижной
системы отсчета
Движение в подвижной системе отсчета
может происходить в отсутствие активных сил
5. Частные случаи относительного движения
1 Переносное движение –вращение вокруг неподвижной оси
Центробежная сила инерции
Вращательная сила инерции
6. Частные случаи относительного движения
2 Переносное движение – равномерноевращение вокруг неподвижной оси
3 Переносное движение - поступательное
7. Частные случаи относительного движения
4 Переносное движение – равномерное,прямолинейное поступательное движение
Никакими опытами в механической системе нельзя
определить покоится подвижная система отсчета или
движется поступательно прямолинейно и равномерно.
Если существует хотя бы одна инерциальная система
отсчета, то инерциальной также будет любая
система отсчета, которая движется относительно
нее поступательно прямолинейно и равномерно
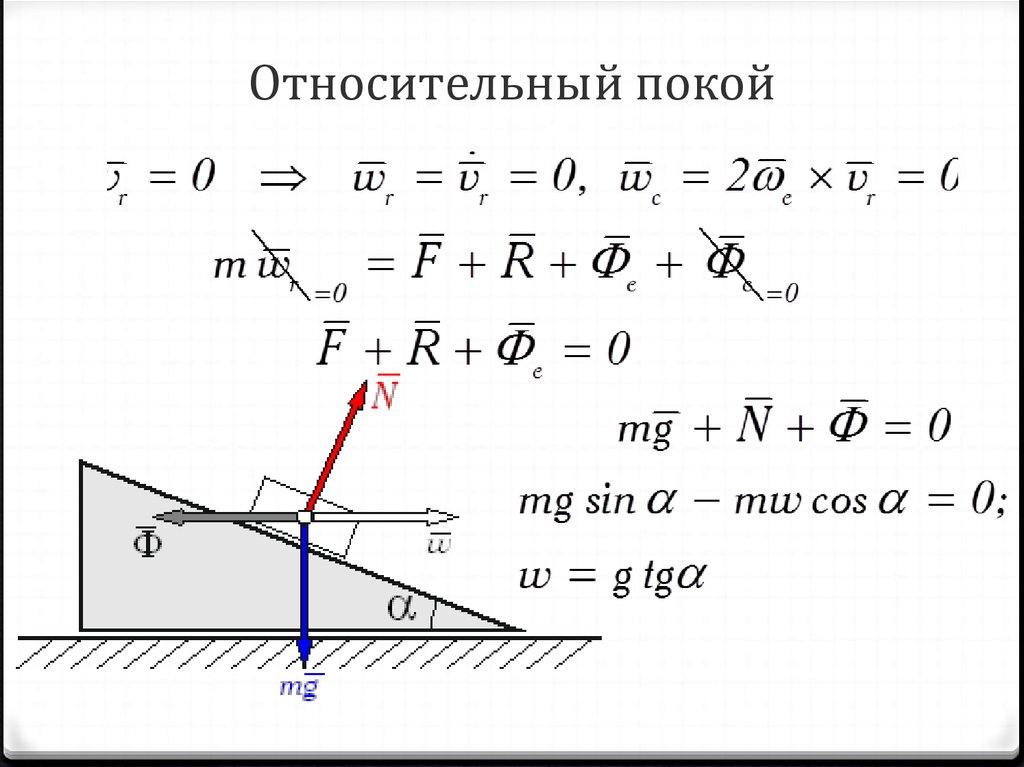
8. Относительный покой
9. Сила тяжести
10. Движение несвободной материальной точки
Механическойсвязью
называется
любое
ограничение на движение материального тела или
точки.
Аксиома освобождаемости от связей:
Движение материального тела не
изменится, если заменить действие связей
реакциями связей.
mw F R
F F t, r , r
R ?
11. Механические связи
Если ограничения, накладываемые связямина движение точек и тел, можно описать
аналитически, то соответствующие
соотношения называются уравнениями
связей.
f r , r , t 0
f x, x, t 0
fk x, x, t 0 , k 1,..., h
12. Классификация связей
yСтационарные связи
f r, r 0
f1 x, y xM 0;
f2 x, y yM 0 .
y
Нестационарные связи
О
M( x,y,z)
x
( t)
f1 x, y xM t 0;
f2 x, y yM 0 .
О
M( x,y,z)
x
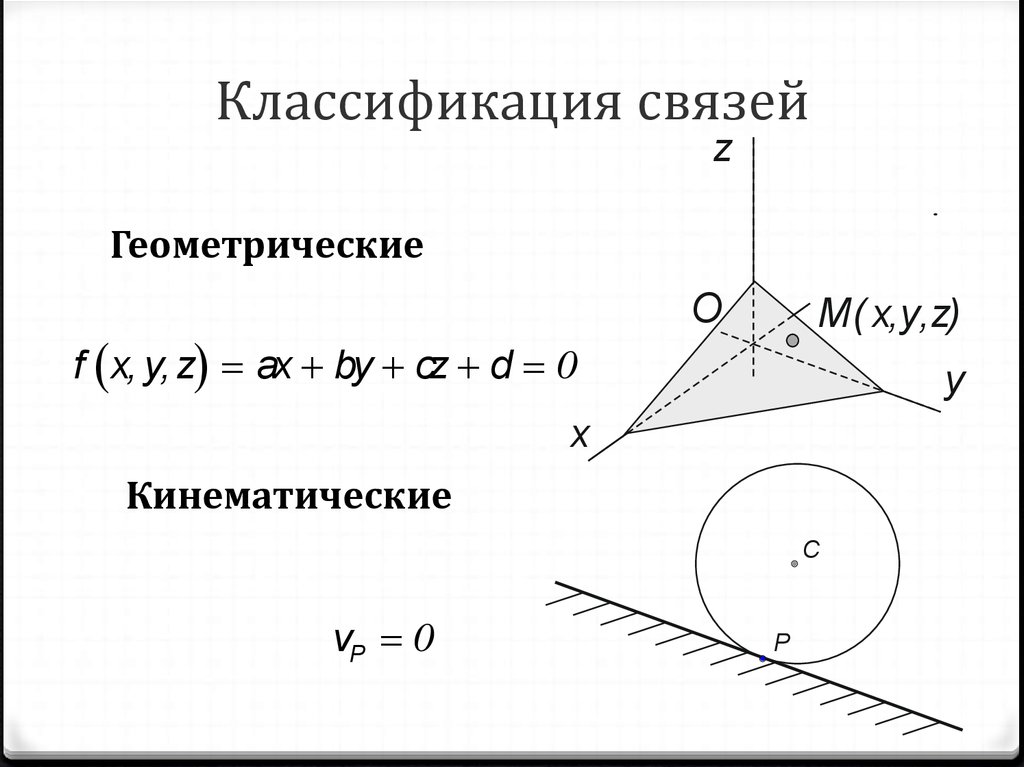
13. Классификация связей
zГеометрические
f x, y, z ax by cz d 0
О
M( x,y,z)
y
x
Кинематические
C
vP 0
P
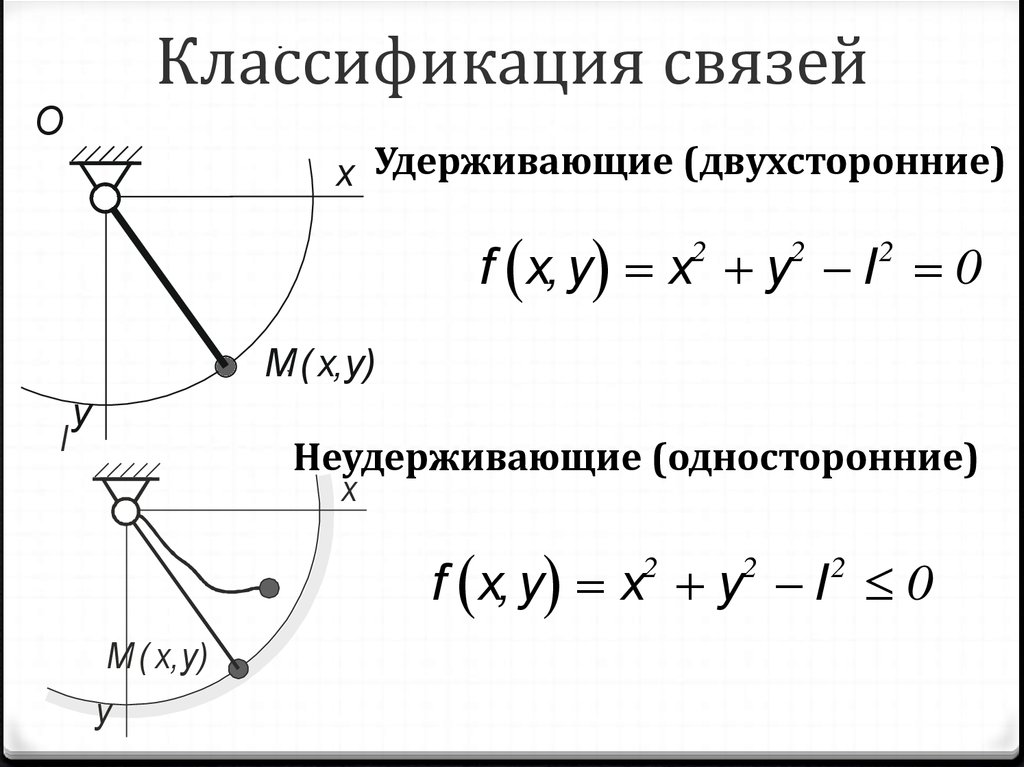
14. Классификация связей
Оx Удерживающие (двухсторонние)
f x, y x y l 0
2
2
2
M( x,y)
I
y
Неудерживающие (односторонние)
x
f x, y x y l 0
2
M ( x,y)
y
2
2
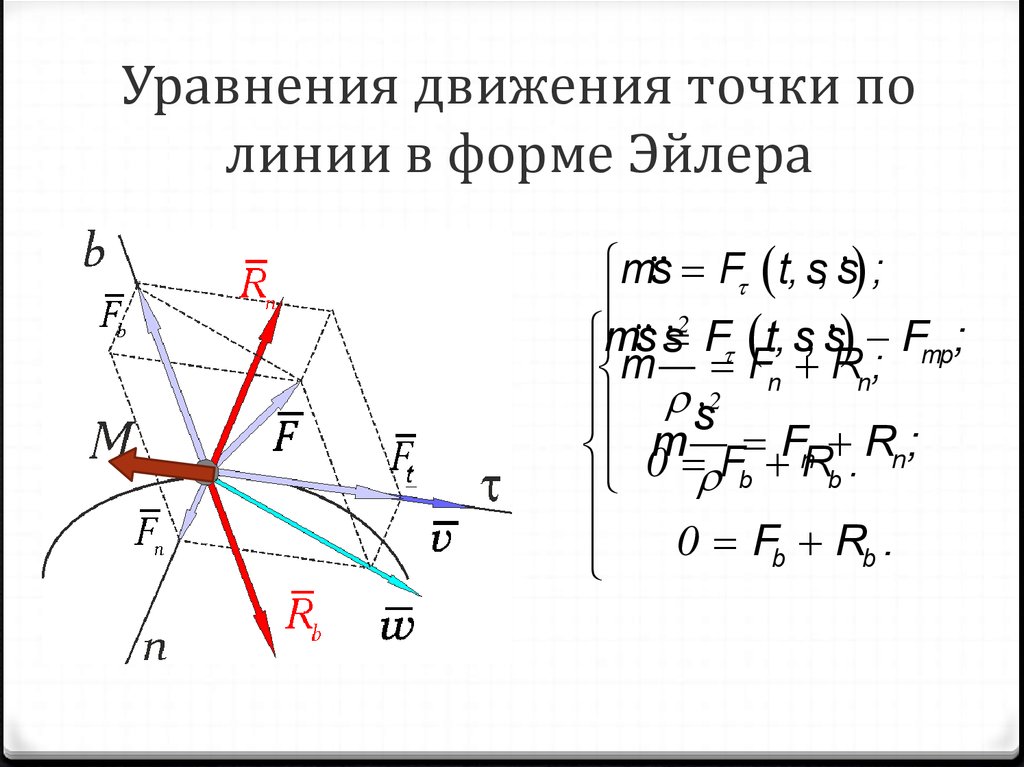
15. Уравнения движения точки по линии в форме Эйлера
ms F t, s, s ;2
ms s F t, s, s Fтр;
m 2 Fn Rn;
s
0m F FnR . Rn;
b
b
0 Fb Rb .
16. Движение МТ по гладкой поверхности.
zR
mr F N
mx Fx Nx;
F
my Fy Ny ;
f( x,y,z) = 0
mz Fz Nz.
y
f
f
f
N gradf i
j k
y
z
x
M
O
x
= (t) - неопределенный множитель Лагранжа
17. Уравнения Лагранжа первого рода
fmx Fx x ;
f
my Fy ;
y
f
mz Fz ;
z
f x, y, z 0 .
Неизвестные функции
x(t) , y(t) , z(t) , (t)
N t t grad f
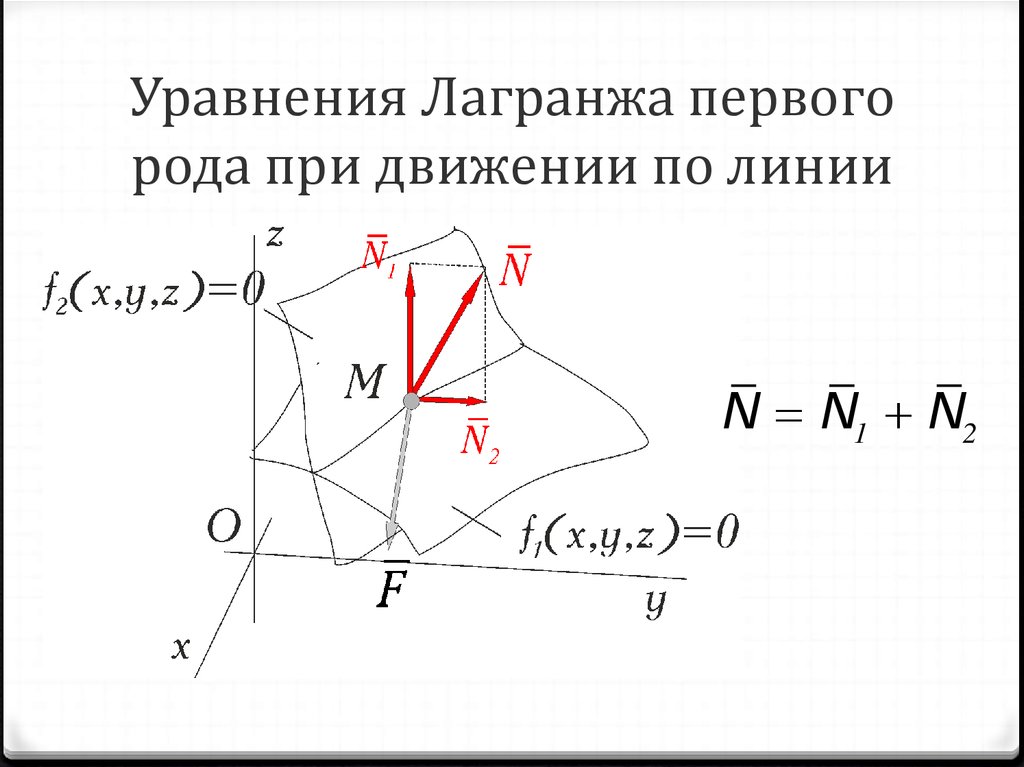
18. Уравнения Лагранжа первого рода при движении по линии
N N1 N219. Уравнения Лагранжа первого рода при движении по линии
f1f2
mx Fx 1 x 2 x ;
f1 f1 f1 f2 f1
N1 1 grad
myf1 F y1 x1 i y2 j ; z k ;
y
y
f2 f1 f2 f2 f2
2 j ;
N2 2 grad
k .
mz f2 F
z 2 1 i
x z y z z
f1 x, y, z 0 ;
f2 x, y, z 0 .













 physics
physics








