Similar presentations:
Движение несвободной материальной точки. Лекция 2
1.
Зная массу точки и закон ее движения определитьдействующую на точку силу. Разложить силу на составляющие
и определить реакции связей.
По заданным массе точки, силам, начальным условиям и связям
определить движение точки и силы реакции связей.
2.
Уравнение поверхности:f x , y , z 0. Неизвестная нормальная реакция поверхности: N .
Дифференциальные
уравнения движения
точки по поверхности:
z
N
2
F
O
y
d x
m 2 Fx N x ;
dt
2
d y
m 2 Fy N y ;
dt
2
d z
m 2 Fz N z ;
dt
Направляющие косинусы
нормали к поверхности:
1 f
cos( N , x )
;
f x
1 f
cos( N , y )
;
f y
1 f
cos( N , z )
;
f z
где
2
x
2
2
f f f
f ;
x y z
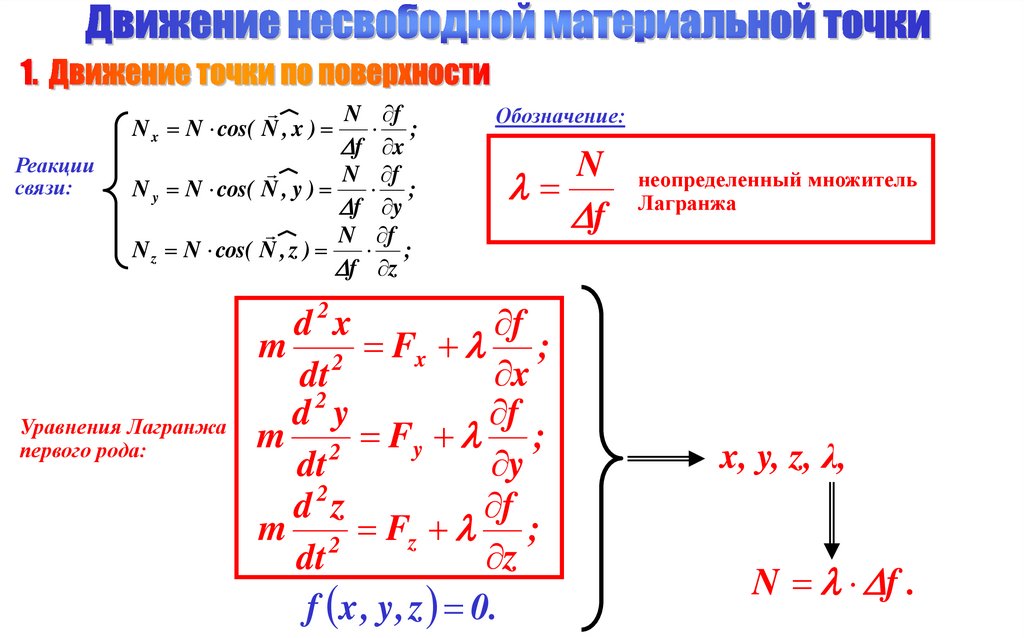
3.
Реакциисвязи:
N f
N x N cos( N , x )
;
f x
N f
N y N cos( N , y )
;
f y
N f
N z N cos( N , z )
;
f z
Обозначение:
N
f
d x
f
m 2 Fx ;
x
dt
2
d y
f
m 2 Fy ;
y
dt
2
d z
f
m 2 Fz ;
z
dt
f x , y , z 0.
неопределенный множитель
Лагранжа
2
Уравнения Лагранжа
первого рода:
x, y, z, λ,
N f .
4.
трmax
F
fтр N :
x
тр v x
F F cos( v , x ) Fmax fтр N
;
2
2
2
v
x y z
y
тр
тр
тр v y
Fy Fmax cos( v , y ) Fmax fтр N
;
2
2
2
v
x y z
z
тр
тр
тр vz
Fz Fmax cos( v , z ) Fmax fтр N
;
2
2
2
v
x y z
тр
x
тр
max
5.
Неподвижная кривая в пространстверассматривается как линия пересечения двух поверхностей: f1 x , y , z 0 ,
f2 x , y , z 0.
Поверхности создают две неизвестные нормальные реакции: N 1 , N 2 .
Равнодействующая сил реакции: N N 1 N 2 ,
2
d
x
f1
f2
Уравнения Лагранжа первого рода: m
Fx 1
2
;
N
2
z
N2
N1
x
x
dt
;
где 1
, 2
2
d y
f1
f2
f 2
f1
m 2 Fy 1
2
;
2
2
2
y
y
dt
f1 f1 f1
f1 ;
d 2z
f1
f2
N1
m 2 Fz 1
2
;
x y z
N2
z
z
2
dt
2
2
f2 f2 f2
;
x y z
f 2
F
O
x
y
x, y, z, λ1, λ2
N 1 1 f1 , N 2 2 f2
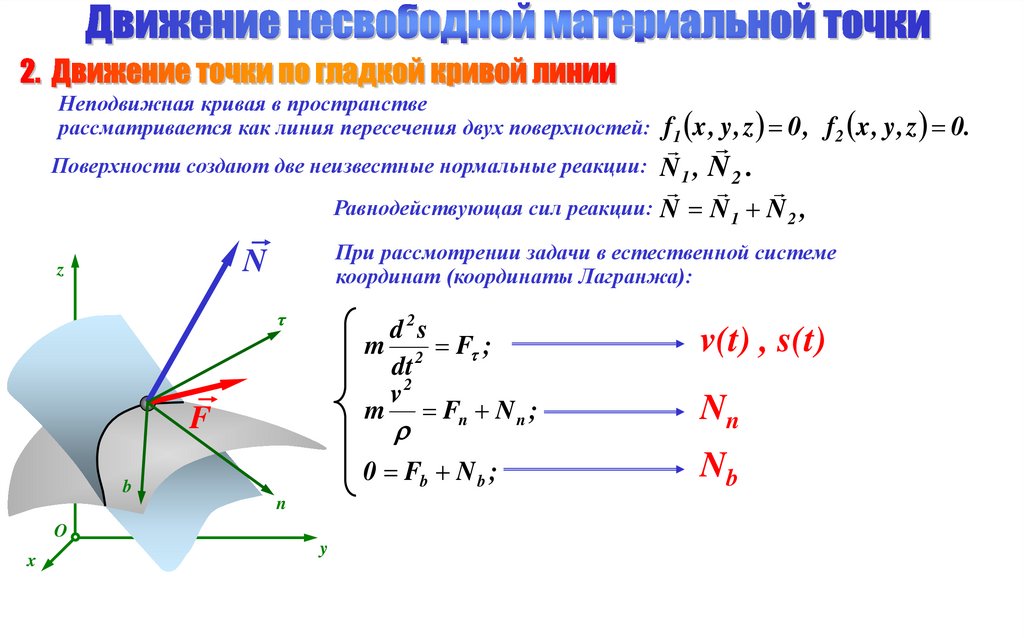
6.
Неподвижная кривая в пространстверассматривается как линия пересечения двух поверхностей: f1 x , y , z 0 ,
Поверхности создают две неизвестные нормальные реакции: N 1 , N 2 .
Равнодействующая сил реакции: N N 1 N 2 ,
При рассмотрении задачи в естественной системе
координат (координаты Лагранжа):
N
z
τ
d 2s
m 2 F ;
dt
v2
m Fn N n ;
F
0 Fb N b ;
b
n
O
x
f2 x , y , z 0.
y
v(t) , s(t)
Nn
Nb
7.
Точка массы m движется под действием силы тяжести по внутренней частиповерхности сферы радиуса R вблизи устойчивого положения равновесия. В
начальный момент при t = 0, x = x0 , y = 0, vx = 0, vy = v0 .
Определить движение точки и силу реакции сферы.
Решение: Задача о сферическом маятнике.
O
x
y
R
N
Дифференциальные уравнения движения точки по поверхности сферы:
N
f
f
f где
,
mx ; m y ; m z mg ,
f
y
x
z
2
2
2
2
Уравнение поверхности сферы: R x y z 0.
f
f
2 y ;
2 x ;
y
x
R x y z ;
2
2
2
z
P
2
2
2
f
2 z ;
z
f f f
2
2
2
f
2 x y z 2 R.
x y z
8.
Точка массы m движется под действием силы тяжести по внутренней частиповерхности сферы радиуса R вблизи устойчивого положения равновесия. В
начальный момент при t = 0, x = x0 , y = 0, vx = 0, vy = v0 .
Определить движение точки и силу реакции сферы.
Решение: Задача о сферическом маятнике.
Окончательные дифференциальные уравнения движения точки по поверхности сферы:
mx 2 x ;
z
α
R
m y 2 y;
N
.
m z mg 2 z , где
2R
Полученные дифференциальные уравнения интегрируем приближенно, для
случая малых движений точки около положения устойчивого равновесия:
z R cos ; При малом угле α: cos 1 (например: cos(1 ) = 0.9998;
cos(2 ) = 0.9994;
cos(3 ) = 0.9986;
Тогда: z R ;
cos(4 ) = 0.9975;
0 mg 2 R; cos(5 ) = 0.9962 и т.д.).
z 0.
mg
; N f mg
2R
0
0
0
0
0
9.
Точка массы m движется под действием силы тяжести по внутренней частиповерхности сферы радиуса R вблизи устойчивого положения равновесия. В
начальный момент при t = 0, x = x0 , y = 0, vx = 0, vy = v0 .
Определить движение точки и силу реакции сферы.
Решение: Задача о сферическом маятнике.
g
g
x ; y y ;
Дифференциальные уравнения движения точки с учетом приближений: x
R
R
Общее решение:
Первые производные:
g
x x 0 ; x C1 sin kt C2 ;
x C1k cos kt C2 ;
R
или
y C 3 sin kt C4 ,
g
y C 3 k cos kt C4 ,
y y 0.
где k g R .
R
Произвольные постоянные:
x0 C1 sin C 2 ;
0 C 3 sin C 4 ;
0 C1k cos C2 ;
v0 C 3 k cos C 4 ;
C1 x0 ;
C2 2 ;
C 3 v0 k ;
C4 0.
Уравнения движения точки:
x x0 sin kt ;
v0
y cos kt ;
k
z R.
Уравнение траектории:
2
2
x
y g
2 1; z R .
2
x0 Rv0
эллипс в плоскости z = R
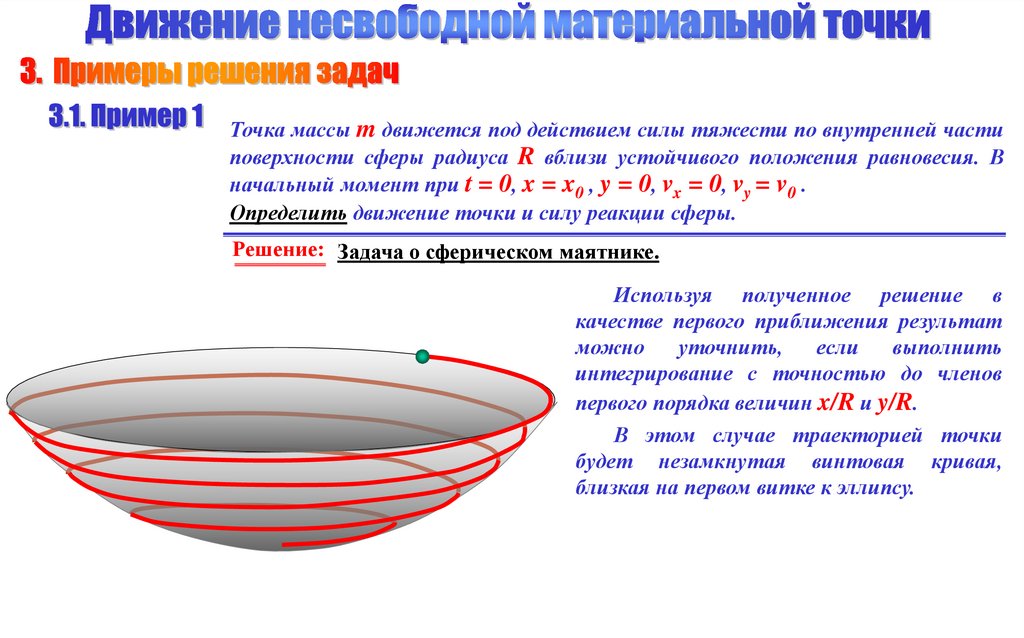
10.
Точка массы m движется под действием силы тяжести по внутренней частиповерхности сферы радиуса R вблизи устойчивого положения равновесия. В
начальный момент при t = 0, x = x0 , y = 0, vx = 0, vy = v0 .
Определить движение точки и силу реакции сферы.
Решение: Задача о сферическом маятнике.
Используя полученное решение в
качестве первого приближения результат
можно
уточнить,
если
выполнить
интегрирование с точностью до членов
первого порядка величин x/R и y/R.
В этом случае траекторией точки
будет незамкнутая винтовая кривая,
близкая на первом витке к эллипсу.
11.
z1ФК
R
z
y1
x1
y
x
– переносная сила инерции
Ф
m
a
e
e
– кориолисова сила инерции
ФK m aK
aK
o1
o
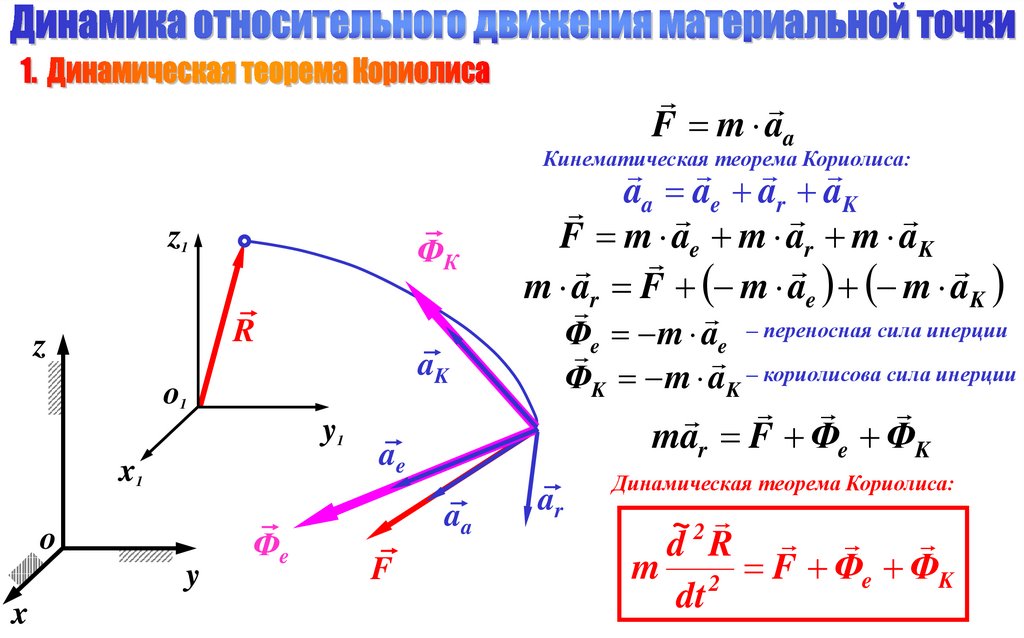
F m aa
Кинематическая теорема Кориолиса:
a
a
a
a
a
e
r
K
F m ae m ar m aK
m a r F m ae m aK
Фe
mar F Фe ФK
ae
aa
F
ar
Динамическая теорема Кориолиса:
~2
d R
m 2 F Фe ФK
dt
12.
0.
e
aK 2 e vr 0 ; ФK m aK 0 ;
m ar F Фe
Переносное движение - поступательное:
ae
R
z
Переносное движение – равномерное и прямолинейное:
m ar F
z1
Относительное движение – равномерное и прямолинейное:
aa
x1
o1
ar
o
y
x
y1
ar 0 ; F Фe ФK 0
vr
Относительное равновесие точки:
vr 0 ;
aK 0 ; F Фe 0
13.
Невесомость – отсутствие давления материальнойточки на каждое из тел, с которым она может
соприкасаться.
Собственная система отсчета – система отсчета, относительно
которой точка находится в покое
v
0
.
a
0
,
r
r
N
В собственной системе отсчета: a 0 ; F N Ф 0. В невесомости: N 0 ; F Ф 0.
e
K
e
Для того, чтобы материальная точка находилась в состоянии невесомости необходимо и достаточно, чтобы
равнодействующая активных сил, не соприкасающихся с точкой, и переносная сила инерции в собственной системе
отсчет образовывали равновесную систему сил
Абсолютное движение
a ae ar aK – в инерциальной системе отсчета;
F
Переносное движение
– движение собственной системе отсчета;
ar 0 ,
vr 0 ;
a K 0.
a ae
Фe Ф
В состоянии невесомости равнодействующая активных сил, не соприкасающихся с точкой, уравновешивается силой
инерции в в инерциальной системе отсчета
14.
Внутри гладкой трубки движется шарик массой m = 1 кг под действием силы притяженияк центру О, пропорциональной расстоянию до центра F = cx, с =4.9 н/м. Трубка
наклонена к вертикали под углом α = 600 и вращается вокруг вертикальной оси с
постоянной угловой скоростью ω = 1 рад/с. В начальный момент шарик находился в точке
М0, ОМ0 = 2.4 м имел начальную скорость относительно трубки v0 = 4 м/с .
Определить закон движения шарика по трубке, силу давления его на стенку трубки и силу
притяжения в момент времени t = π/2 c.
z1
y
ωe
Решение:
N ωe
α
M0
O
Дифференциальное уравнение относительного движения:
ФK
x
vr
M
F
P
Фe
mar P N F Фe ФK .
В проекциях на подвижные оси:
mx F P cos Фe sin ;
0 N y P sin Фe cos ;
0 N z ФK .
Фe mx sin 2 3 x ;
2
ФK 2 m x sin 3 x ;
F c x 4.9 x ;
15.
Внутри гладкой трубки движется шарик массой m = 1 кг под действием силы притяженияк центру О, пропорциональной расстоянию до центра F = cx, с =4.9 н/м. Трубка
наклонена к вертикали под углом α = 600 и вращается вокруг вертикальной оси с
постоянной угловой скоростью ω = 1 рад/с. В начальный момент шарик находился в точке
М0, ОМ0 = 2.4 м имел начальную скорость относительно трубки v0 = 4 м/с .
Определить закон движения шарика по трубке, силу давления его на стенку трубки и силу
притяжения в момент времени t = π/2 c.
Решение:
Окончательно дифференциальные уравнения относительного движения:
c
2
x sin x g cos ;
m
N y m sin g x 2 cos ;
N z 2 m x sin .
x 4 x 4.9 ;
3
x
Ny
9.8 ;
2
2
N z 3 x .
16.
Внутри гладкой трубки движется шарик массой m = 1 кг под действием силы притяженияк центру О, пропорциональной расстоянию до центра F = cx, с =4.9 н/м. Трубка
наклонена к вертикали под углом α = 600 и вращается вокруг вертикальной оси с
постоянной угловой скоростью ω = 1 рад/с. В начальный момент шарик находился в точке
М0, ОМ0 = 2.4 м имел начальную скорость относительно трубки v0 = 4 м/с .
Определить закон движения шарика по трубке, силу давления его на стенку трубки и силу
притяжения в момент времени t = π/2 c.
Решение:
Интегрирование дифференциального уравнения:
x 4 x 4.9 ;
4
.
9
x x1 x2 ;
частное решение неоднородного дифуравнения: x2
1.2 ;
4
общее решение однородного дифуравнения: x
1 4 x1 0 ;
характеристическое уравнение: 2 4 0
x1 C1 cos 2 t C2 sin 2 t .
2i
x C1 cos 2 t C2 sin 2 t 1.2 ;
определение
C1 1.2 ;
2.4 C1 1.2 ;
x 2C1 sin 2 t 2C2 cos 2 t ;
произвольных
C2 5.
10 2C2 ;
начальные условия: при t 2 :
постоянных:
x x0 2.4 м; x v0 10 м c .
17.
Внутри гладкой трубки движется шарик массой m = 1 кг под действием силы притяженияк центру О, пропорциональной расстоянию до центра F = cx, с =4.9 н/м. Трубка
наклонена к вертикали под углом α = 600 и вращается вокруг вертикальной оси с
постоянной угловой скоростью ω = 1 рад/с. В начальный момент шарик находился в точке
М0, ОМ0 = 2.4 м имел начальную скорость относительно трубки v0 = 4 м/с .
Определить закон движения шарика по трубке, силу давления его на стенку трубки и силу
притяжения в момент времени t = π/2 c.
Решение:
Уравнение движения шарика:
При t
x 1.2 cos 2 t 1 5 sin 2 t
2 : x 1.2 cos 1 5 sin 2.4 м;
x 2.4 sin 10 cos 10 м c .
Сила притяжения:
F c x 4.9 2.4 11.8 н;
Давление шарика на трубку:
3
9.8 1.2 7.3 н;
Ny
2
N z 3 10 17.3 н;
N N y2 N z2 18.8 н;
Ответ: x 1.2 cos 2 t 1 5 sin 2 t ; F 11.8 н ;
N 18.8 н .













 physics
physics








