Similar presentations:
Кинематика поступательного и вращательного движения материальной точки
1.
КРАТКИЙМУЛЬТИМЕДИЙНЫЙ
КУРС ЛЕКЦИЙ
ПО ОБЩЕЙ ФИЗИКЕ
Ч.1
Чужков Ю.П.
2.
Мультимедийный курс лекций для использования на очном и заочномотделении разработан в соответствии с Государственным образовательным
стандартом и рабочей программой дисциплины.
Данный курс лекций предназначен для самостоятельного изучения
студентами всех специальностей содержания дисциплины. Прежде всего, он
адресован студентам заочного отделения ввиду специфики формы обучения.
Студентам очного отделения (бакалаврам) курс будет полезен как учебное
пособие, дополняющее лекционный курс.
Элементы этого курса могут быть использованы преподавателями для
наглядного представления изучаемого на лекциях материала (в качестве
мультимедийных презентаций).
После названия темы лекции приводится перечень вопросов,
изучение которых предполагается в ней. Каждая лекция сопровождается
разбором типовых задач по пройденной теме и задачами (тестами) для
самостоятельного решения.
В конце каждого раздела приводится список используемой литературы,
рекомендуемой для дополнительного, более глубокого изучения темы.
3.
Содержание1. Механика.
2. Молекулярная физика и
термодинамика
3. Механические колебания
и волны
4. Электричество.
Постоянный электрический
ток
4.
МЕХАНИКА5.
Лекция № 1Кинематика поступательного и
вращательного движения
материальной точки
6.
Рассматриваемые вопросы1. Введение.
2. Выбор системы отчета.
3. Скорость и ускорение движения
материальной точки.
4. Кинематика поступательного движения
материальной точки.
5. Кинематика вращательного движения
материальной точки.
6. Решение задач и тестов.
7. Введение
ФИЗИКАКлассическая
(Ньютоновская)
Квантовая
Теория
относительности
Эйнштейна
МЕХАНИКА
кинематика
статика
динамика
8. Система отсчёта.
Zz(t)
M (x1, y1,z1,t1)
Уравнение движения
точки в векторной форме:
x(t)
y(t)
Y
r r t xe x ye y ze z
X
Уравнения движения точки
в координатной форме:
x x t , y y t , z z t
9. Система отсчёта.
Z∆S
z(t)
r
M (x1, y1,z1,t1)
∆S
N(x2, y2,z2 ,t2)
y(t)
x(t)
X
Мгновенная скорость точки
в положении M:
Y
- пройденный путь
- вектор перемещения
S
t
- средне
путевая
скорость
r
t
- средняя
скорость
r
dr
lim
t 0
t
dt
10. Система отсчёта.
Zx ex y ey z ez
z(t)
M (x1, y1,z1,t1)
∆S
t
2
x
2
y
N(x2, y2,z2 ,t2)
y(t)
Y
x(t)
X
x , y , z
-
dx
x
dt
dy
y
dt
dz
z
dt
проекции вектора скорости на координатные оси.
2
z
11. Выбор системы отсчёта.
Z’Z
Y’
Y
- закон сложения
скоростей
X’
X
Инерциальная система отсчета – система
отсчета, в которой тело движется
равномерно и прямолинейно.
12. Задача 1. Радиус-вектор начального положения частицы определяется выражение . Частица движется с постоянной скоростью . Найти
Задача 1. Радиус-вектор начальногочастицы
положения
определяется выражение r t 3ex 6e y 8ez . Частица движется с
v
7
e
9
e
2
e
постоянной скоростью
.z Найти координаты
x
y
частицы через t = 2 c после начала движения.
Решение:
r t xex ye y zez
r t a0 ex b0 e y c0 ez
x ex y ey z ez
В начальный момент времени координаты радиус-вектора (a0,b0,c0), а
через время t:
a0=-3;
b0= 6;
c0= -8;
a1= 7;
b1= 9;
c1= 2;
x= -3+7*2=11
y= 6+9*2=24
z= -8+2*2=-4
a1ex b1ey c1ez
Ответ: 11; 24;-4
13. Тема: «Криволинейное движение под действием силы тяжести». Задача 2. Камень брошен горизонтально со скоростью . Найти радиус
Тема: «Криволинейное движение под действием силытяжести».
Задача 2. Камень брошен горизонтально со скоростью x 10м/с
.
Найти радиус кривизны траектории камня через t = 3 c
после начала движения.
Необходимо помнить:
y
1)
t полета t падения
2)
x const
R
3)
0
x
y g
(всегда)
g - ускорение
свободного
падения
R – радиус кривизны траектории
2x 2 y
Модуль скорости
2
gt
2
x
14. Тема: «Криволинейное движение под действием силы тяжести». Задача 2. Камень брошен горизонтально со скоростью . Найти радиус
Тема: «Криволинейное движение под действием силытяжести».
Задача 2. Камень брошен горизонтально со скоростью x 10м/с
.
Найти радиус кривизны траектории камня через t = 3 c
после начала движения.
Решение:
y
По рисунку:
0
Тангенциальное ускорение
показывает быстроту
изменения модуля
скорости.
x
Ответ: 305 м.
Нормальное ускорение показывает быстроту
изменения направления скорости
15. Падение тела под действием сил земного притяжения
1) С какой высоты упало тело, еслирасстояние до земли оно преодолело
за 2 с?
Y
Vy = 0
h
X
2) С какой скоростью упадет камень на
землю, если время падения длилось
3с?
16. Падение тела под действием сил земного притяжения
YVy = 0
h
X
17.
Материальная точка А движется по траектории, указаннойна рисунке с постоянным нормальным ускорением. Что
можно сказать о скорости материальной точки?
1) Скорость изменяется по
направлению и уменьшается
по величине.
2) Скорость изменяется по
направлению и
увеличивается по величине.
3) Скорость не изменяется.
18.
Задача № 3Тело брошено под углом к горизонту
Камень брошен под углом к горизонту 300 со скоростью 20 м/с.
Определить: 1) время подъёма камня на максимальную высоту;
2) максимальную высоту поднятия камня; 3) максимальная дальность полета.
Y
Решение:
1)
A
2)
0
X
3)
Ответы: t подъёма= 1,02 c; hmax = 5,1 м; Smax = 35,3 м.
19. Два тела одновременно брошены под углом к горизонту, как показано на рисунке.
ТестДва тела одновременно брошены под углом к
горизонту, как показано на рисунке.
Сравните:
Y
V01
1) Время полета двух тел
V02
а) t1 t 2 б)
t 2 t1
в) t1 = t2
2) Высоту полета
0
X
а) h1 h2
б) h2 h1
в) h1 = h2
20.
Ответы:Y
V01
V02
V01 sin V02 sin
a b
0
1)
V01 cos V02 cos
V01 sin V02 sin
t1 t 2
g
g
V01 sin
V02 sin
h1 h2
2g
2g
2
2)
X
2
2
2
21. Вращательное движение материальной точки
∆ϕ - угол поворота радиус-вектораZ
0 t
ε>0
∆ϕ
r
X
ε<0
0t
r(t)
Y
t
2
2
2
2 N
2
a R
an 2 R
a a an
2
2
Угловая скорость характеризует быстроту изменения угла
поворота со временем при вращательном движении
Угловое ускорение характеризует быстроту изменения
угловой скорости при вращательном движении
22. На каком из рисунков при указанных направлениях вращениях правильно отображено направление углового ускорения?
ТестНа каком из рисунков при указанных
направлениях вращениях правильно
отображено направление углового ускорения?
1
2
3
4
23. Тема “Вращательное движение материальной точки”
Задача 4 Шарик движется по окружности радиусом 5 см с постояннымтангенциальным ускорением 5 см/ с2. Определить: 1) угловую скорость шарика к
концу пятого оборота; 2) нормальное ускорение к концу пятого оборота; 3) полное
ускорение.
Решение:
1)
0
0 t
0t
t
2
0
2 N
2
a R a
R
an 2 R
3) a
Ответ:
an 4 Na
a an
2
t
2
R
2)
t
2
an 0,63 м/с2 ; a = 0,885 м/с2
2 N
t 2
2
24.
Вопросы для самоконтроля:1. Что изучает кинематика?
2. Дайте определение мгновенной скорости материальной
точки.
3. В чём отличие средней скорости от мгновенной.
4. Что определяет тангенциальное и нормальное ускорение?
5. Что такое угловая скорость и угловое ускорение?
6. Что такое инерциальная система отсчета?
7. Почему нельзя при вращательном движении вычислять
пройденный путь в метрах?
25. Динамика поступательного движения.
Лекция № 2Динамика поступательного
движения.
26.
Рассматриваемые вопросы27. Введение
МЕХАНИКАкинематика
статика
динамика
Инертность - свойство различных тел по-разному изменяют
свою скорость под воздействием одной и той же силы.
m - масса – мера инертности тела при поступательном движении,
[m]= кг
28. Рассматриваемые вопросы
1. Силы в механике.2. Законы Ньютона.
3. Импульс тела. Закон сохранения импульса.
4. Механическая работа и энергия.
5. Неинерциальные системы отсчета.
29. Законы Ньютона.
Первый закон Ньютона. Тело сохраняет состояние покоя илиравномерного и прямолинейного движения до тех пор, пока
воздействие других тел не выведет его из этого состояния.
Инерциальной называется такая система отсчета, в которой
свободное тело покоится или движется равномерно и
прямолинейно.
В инерциальной системе отсчета координаты
изолированной точки изменяются пропорционально
времени, т.е.
x x t xo
y y t yo
z z t zo
Уравнения динамики не изменяются при переходе от одной инерциальной
системы к другой.
30. Законы Ньютона
Второй закон Ньютона. Произведение массы тела на его ускорение равнодействующей на тело силе :
F ma
Второй закон Ньютона. Скорость изменения импульса тела равна
dp
действующей на тело силе :
F
dt
Третий закон Ньютона. Силы, с которыми действуют друг на друга
взаимодействующие тела, равны по модулю и противоположны по
направлению: F12 = F
- 21
31. ДИНАМИКА. Практическое применение законов Ньютона
yFтр
Fтр
N
N
mg
x
mg
- сила трения
- сила реакции
-сила тяжести
Запишем второе уравнение Ньютона:
ma mg N Fтр
- векторное уравнение движения
32. ДИНАМИКА. Практическое применение законов Ньютона
Запишем уравнения движения в проекциях на оси координат:max mgx N x Fтр x
may mg y N y Fтр y
a x a, mg x mg sin , N x 0, Fтр x Fn
a y 0, mg y mg cos , N y N , Fтр y 0
a g sin cos
33.
12
3
4
34.
Силы в механике1. Сила упругости
2. Сила сопротивления
0
35.
Силы в механике3. Сила тяжести
Сила тяжести определяется силой притяжения
Земли
- ускорение свободного падения тела
- гравитационная постоянная
N
N
mg
P=N
mg
36.
Силы в механике4. Сила трения
N
mg
Сила трения не зависит от размеров площади соприкосновения тел.
37. Законы сохранения
Система называется замкнутой, когда внешние силы отсутствуют.1. Закон сохранения импульса
dp dt 0,
p const
Импульс замкнутой системы материальных точек остается
постоянным
Пример. Мячик массой 100 г брошен с начальной скоростью 20 м/с под углом
600 к горизонту. Импульс мячика в высшей точке траектории равен
1) 0;
2) 1 кг∙м/с;
3) 1.7 кг∙м/с;
4) 2 кг∙м/с.
38. Задача 3. Пуля массой m = 10г, летящая со скоростью υ = 400 м/с, пробивает навылет подвешенный пластмассовый шар, масса
которого М = 1 кг. Послевылета из шара скорость пули уменьшилась в к = 5 раз. С какой скоростью U
будет двигаться шар в первый момент после вылета из него пули? Временным
взаимодействием шара и пули пренебречь.
Решение:
m M ш m MU
k
υш = 0
U
m m
MU
k
m( k 1 )
kM
После подстановки числовых данных имеем: U = 3,2м/с.
Ответ: U = 3,2м/с.
39. Тема «Закон сохранения энергии» Задача 2. Пренебрегая трением, определить наименьшую высоту h, с которой должна скатиться
тележка с человеком по желобу, переходящему в петлюрадиуса R.
Решение:
Запишем закон сохранения энергии:
m 2
2
mgh
mg 2 R
gh
g 2R
2
2
В верхней точке петли на тележку
действуют две силы: сила тяжести
FT = mg и центростремительная сила
m 2
Fцс
R
Чтобы тележка не оторвалась под действием силы тяжести в верхней точке, необходимо
(как минимум) равенство этих сил.
5R
Rg
h
2 Rg
gh
g 2R
2
2
Ответ: h = 15 м.
40. Работа и энергия.
Работа A характеризует изменение энергии, обусловленное действием силы надвижущуюся частицу. Работу совершают только силы.
dA Fds
dA Fds cos
dA Fs ds [Джоуль]
Мощность – работа, совершаемая в единицу
времени.
[Ватт]
Кинетическая энергия – энергия движения
Потенциальная энергия – энергия взаимодействия
Eп -
1
4 0
ze e
r
Eп mgh
kx2
Eп
2
Закон сохранения механической энергии: в замкнутой системе
полная энергия остаётся постоянной
41. Задача 4. С башни высотой h = 20 м горизонтально со скоростью υ0 = 10 м/с брошен камень массой m = 400 г. Пренебрегая
сопротивлениемвоздуха, определить кинетическую и потенциальную энергию камня для
момента времени t = 1 c после начала движения. Ускорение свободного
падения принять равным 10 м/с2.
Решение:
Для нахождения кинетической энергии необходимо знать скорость
камня υ для момента времени t = 1с после начала движения
m 2
Ek
x 0 y gt
2x 2 y
2
0 ,4 2
m 2
10 10 2 12 40 Дж
Ek
0 g 2t 2 Ek
2
2
gt 2
h 0 yt
2
t = 0 0 y
gt 2
5м .
0;h
2
Через 1 с камень оказался на высоте H h над землей и потенциальная энергия
камня будет: Eп mg H h
Подставляем числовые данные: Eп 0 ,4 10 20 5 60 Дж
Ответ: Ek 40 Дж Eп 60 Дж
42. Задача 4. С башни высотой h = 20 м горизонтально со скоростью υ0 = 10 м/с брошен камень массой m = 400 г. Пренебрегая
сопротивлениемвоздуха, определить кинетическую и потенциальную энергию камня для
момента времени t = 1 c после начала движения. Ускорение свободного
падения принять равным 10 м/с2.
Решение:
Для нахождения кинетической энергии необходимо знать скорость
камня υ для момента времени t = 1с после начала движения
m 2
Ek
x 0 y gt
2x 2 y
2
0 ,4 2
m 2
10 10 2 12 40 Дж
Ek
0 g 2t 2 Ek
2
2
gt 2
h 0 yt
2
t = 0 0 y
gt 2
5м .
0;h
2
Через 1 с камень оказался на высоте H h над землей и потенциальная энергия
камня будет: Eп mg H h
Подставляем числовые данные: Eп 0 ,4 10 20 5 60 Дж
Ответ: Ek 40 Дж Eп 60 Дж
43. Задача 5. Два шарика массами 8 г и 4 г висят на нитях одинаковой длины. Между нитями зажата пружина. Нить, связывающая шарики,
пережигают. Найти отношениемаксимальных высот h2 /h1, на которые поднимутся шарики.
Решение:
В момент пережигания нити импульсы шариков
равны. Закон сохранения импульса: m1 1 m2 2
h2
h1
Кинетическая энергия каждого шарика после их
расхождения переходит в потенциальную энергию
(согласно закону сохранения механической энергии)
m1 12
2
m1gh1
2
h2 2
,
h1 1
h2 m1
h1 m2
2
h2
4
h1
m2 2
2
2
m2 gh2
2 m1
1 m2
44. Задача 6. Тело сначала скользит по наклонной плоскости, составляющей угол = 450 с горизонтом, а затем по горизонтальной
Задача 6. Тело сначала скользит по наклонной плоскости,составляющей
угол
= 450 с горизонтом, а затем по горизонтальной поверхности. Найти
коэффициент трения , если тело проходит по горизонтальной
поверхности такое же расстояние, как и по наклонной плоскости.
Решение:
Введем обозначения: h - высота, с которой начинается
движение тела; L – расстояние по наклонной (по
горизонтальной ) плоскости
y
Fтр
N
h
mg
На наклонном участке:
Когда тело находится на высоте, оно обладает
потенциальной энергией Eп mgh
При скольжении тела по наклонной поверхности
x эта энергия расходуется на совершение работы А
1
по преодолению сил трения на этом участке пути.
A1 Fтр1 L mg cos L
На горизонтальном участке пути A1 Fтр 2 L mgL
mgh A1 A2
mgh mg cos L mg L,
Ответ: 0,41
sin
1 cos
0,41
h L sin
45. 1. Сила инерции (поступательное движение)
Неинерциальные системы отсчета.1. Сила инерции (поступательное
движение)
а
Т
a=0
a =- a`
a>0
Fин
F = - ma`
Р
2. Центробежная сила
2
Fцб m R
z*
y*
x*
Fцб
F
46. Сила Кориолиса.
z*Fk
B
y*
O
x
*
При движении тел во вращающейся
системе отсчета кроме центробежной
силы инерции возникает сила
Кориолиса
Fцб
Fk 2m
Решение:
?
Fk 2m sin
2 - угловая скорость вращения Земли ;
T
Т – период вращения Земли Т = 24∙3600с
2 3,14
Fk 2 5 106 30
sin 60 18 ,75кН
24 3600
Ответ: Fk 18,75кН
Fk
Rз
47.
Лекция №3Динамика вращательного
движения твердого тела
48. Рассматриваемые вопросы
1. Динамика вращательного движения твердого тела- Момент инерции. Теорема Штейнера.
- Момент силы (относительно центра, относительно оси).
-Момент импульса (относительно центра, относительно
оси).
2. Закон сохранения момента импульса.
3. Абсолютно упругий удар. Абсолютно неупругий удар.
4. Статика. Центр инерции (центр масс).
49. Момент инерции.
I кг м 2Момент инерции – скалярная величина.
Момент инерции – аддитивная величина.
МОМЕНТ ИНЕРЦИИ – МЕРА ИНЕРТНОСТИ ТЕЛА ПРИ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ.
При поступательном движении мерой инертности тела является
масса.
50. Задача 1. Рассчитать момент инерции однородного диска массой m = 1,6 кг , имеющего радиус R = 1,0 м.
Решение:R
I dm r 2
dm dV
0
R
R4
I 2 h r dr 2 h
4
0
3
m V R 2 h
mR 2
I
2
Ответ: I = 0,8 кг∙м2
dV 2 rh dr
51. Теорема Штейнера.
Момент инерции тела I относительно произвольной оси равен сумме его моментаинерции относительно оси, проходящей через центр инерции тела, параллельно
рассматриваемой, и произведения массы m тела на квадрат расстояния d между
осями.
I I 0 md 2
Пример:
Рассчитать момент инерции диска , вращающегося относительно оси,
отстоящей от оси симметрии диска на два радиуса.
mR 2
I
md 2
2
d 2R
mR2
9
2
I
m 2 R mR2
2
2
Момент инерции увеличился в 9 раз
52. МОМЕНТ СИЛЫ
F относительно центра 0Моментом силы
называется
векторная величина
, где - радиус вектор
точки приложения сил, проведенный из центра.
Направление вектора момента сил
определяется по правилу правого винта.
Момент силы – векторная величина
Момент силы – аддитивная величина
Момент силы характеризует в динамике способность силы вызывать вращение
тела и изменять угловую скорость:
M rF sin
M F R
F ma a R
Работа при вращательном движении:
M mR I
2
M I
dA M d
I 2
Ek
Кинетическая энергия вращающегося тела:
2
Если тело принимает одновременно участие в поступательном и вращательном
m 2
I 2
движении, кинетическая энергия равна:
E
k
2
2
53. Момент импульса.
Момент импульса – аддитивная величина.Пример: При движении электрона по орбите возникает момент импульса L.
Закон сохранения момента импульса
В замкнутой системе момент импульса остается
постоянным
L= const I1ω1=I2ω2
54. Задача 2. Две гири с массами m1 = 2 кг и m2 = 4 кг соединены нитью и перекинуты через блок массой mб = 1 кг. Найти ускорение, с
которым движутся гири. Блоксчитать однородным диском. Трением пренебречь.
Решение:
a1 a2 a
Масса блока отлична от нуля: Т1 ≠ Т2
Возникает момент сил
Для каждого из грузов и для блока запишем уравнения
динамики:
m1a T1 m1 g (поступательное)
m2 a m2 g T2
I M
(поступательное)
(вращательное)
mб R 2
По условию задачи блок считать диском. Момент инерции однородного диска I
2
a
2
mб R a
a R
T2 m2 g m2a
T1 m1a 1 m1 g
R T2 T1
R
m2 m1
a
g
mб
m1 m2
2
2
R
Ответ: a 0,93 м / с
2
55. Задача 3. На барабан радиусом R = 20см, момент инерции которого I = 0,1кг∙м2 , намотан шнур, к которому привязан груз массой m1
= 0,5кг. До началавращения барабана высота груза над полом h = 1 м, Найти: 1) через сколько
времени груз опуститься до пола: 2) кинетическую энергию груза в момент
удара о пол; 3) Натяжение нити. Трением пренебречь.
Решение:
m
a
m
g
T - для поступательного движения;
Запишем 2 закон Ньютона:
I M - для вращательного движения.
a
ma mg T I T R
R
mgR 2
a
Ia
Ia
T mg ma
T 2 mg ma 2
mR 2 I
R
R
0 ,5 9 ,8 0 ,22
a
1,64 м / с 2
2
0 ,5 0 ,2 0 ,1
at 2 t
1) Найдем время опускания груза h 2 ,
2h t 2 1 1,1c
1,64
a ,
2) Кинетическая энергия (по закону сохранения энергии) при падении груза равна
2ah
потенциальной энергии груза до падения m 2
2 gh
Ek
m
m2ah
mah
2
2
2
Ek mah
mgh
2
Ek 0,82 Дж
3) натяжение нити ma mg T ; T m( g a ) ; T 4,1Н
Ответы: 1) t 1,1c ; 2) Ek 0,82 Дж ; 3) T 4,1Н
56. Закон сохранения момента импульса.
Задача 4. Платформа в виде диска радиусом R = 3 м и массой M = 120 кгвращается по инерции с частотой ν = 6 об/мин. На краю платформы стоит
человек, масса которого
m = 60 кг. С какой частотой будет вращаться платформа, если человек перейдет
в ее центр? Момент инерции человека рассчитать, как для материальной точки.
Решение:
Закон сохранения момента импульса: I1 1 I 2 2
I1 – момент инерции системы (диск - человек) в исходном положении.
MR 2
2
I1 I д I ч ; I д
- момент инерции диска. I ч mR .
2
I2 – момент инерции системы с человеком в центре. I 2 I д .
R
Момент инерции человека в центре платформы равен нулю
(материальная точка не имеет размеров).Учитывая, что ω = 2πν,
Закон сохранения момента импульса запишется:
MR 2
MR 2
2
I д I ч 2 1 I д 2 2 ; 2 mR 1 2 2
MR 2 2mR 2
2m
2
1
1 . 2 12об / мин 0.2об / с
1
2
M
MR
Ответ: ν2 = 0,2 об/с
57. Задача 5. Шарик массой m = 200 г, привязанный к концу нити длиной l1 = 1 м, вращается в горизонтальной плоскости (опираясь на
неё) с частотой ν1 = 2 об/с .Нить укорачивают и шарик приближается к оси вращения до расстояния l2 = 0,5 м.
Определить работу внешней силы, укорачивающей нить.
Решение:
Работа внешней силы, укорачивающей нить, равна убыли кинетической энергии
2
I 2 2 I1 1
A
;
2
2
2
вращающегося шарика A E k 2 E k1
1 2 1 ;
I1 ml1 ; I 2 ml2 2
2
2 2 2 ;
I1 1 I 2 2
2 найдем из закона сохранения момента импульса L1 = L2
2
2
I
ml 2 1 1
2
2
I2
ml1 1
A
2
2
2
I1
1 ;
I2
После преобразований получаем формулу для расчета работы
2 2
A
2 2 m 1 l1 l1 l 2
l2
2
2
Ответ: А = 47,3 Дж
2
;
A
2 3,14 2 0 ,2 2 2 12 1 0 ,52
0 ,52
2
47 ,3 Дж
58. Задача 6. Невесомая доска покоится на двух опорах. Правая опора делит длину доски в соотношении 1:3. На её правый конец падает
тело массой m2 = 2 кг, теряя при ударе всю свою скорость. Если послеудара тело массой m1 = 1 кг начинает двигаться со скоростью
υ1 = 12 м/с, то какова скорость тела υ2?
Решение:
Закон сохранения момента импульса:
L1 L2 ;
m1 1l1 m2 2 l 2
2
m1l1
1
m2 l 2
22 22м
м // сс
59. АБСОЛЮТНО УПРУГИЙ УДАР
Абсолютно упругим называется такой удар, при котором, механическая энергиятел не переходит в другие, немеханические, виды энергии.
При абсолютно упругом ударе выполняется и закон сохранения механической
энергии, и закон сохранения импульса.
(υ1,2 - скорость до удара)
(U1.2 - скорость после удара)
1) Закон сохранения энергии:
m1 21 m2 2
mU
mU
1 1 2 2
2
2
2
2
2
2
2
m1 m2 1 2m2 2
U1
m1 m
2) Закон сохранения импульса:
m1 1 m2 2 m1U 1 m2U 2
m1 1 U 1
2
2
m U
2
2
2
2
m1 1 U1 m2 U 2 2
2
m2 m1 2 2m1
U2
m1 m2
1
60. Задача 7. Два шарика подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Масса первого шарика m1 = 10
г,масса второго m2 = 50 г. Первый шар отклоняют так, что его центр
поднимается на высоту 18 см и отпускают. На какую высоту поднимутся
шары после упругого удара?
Решение:
Закон сохранения энергии:
m
m1 gh 1 1
2
2
- для первого шарика; 1 2gh - с такой скоростью первый
шарик сталкивается со вторым. После упругого удара скорость первого шарика
будет равна U1
U1
m1 m2 1 2m2 2
m1 m2
;
2 0
U1
;
2
Второй шарик в результате удара начинает движение со скоростью U2
m2 m1 2 2m1 1
2m1 1
U2
U2
2 0
m1 m2
m1 m2
2
m1 m2
U 21 m1 m2 h
h1
2g
m1 m2 2
2
m1U 1
m1 gh1
2
m2U 2
m2 gh2 2
m1 m2 1
2m1 h
U 22
h1
2 g m1 m2 2
2
h2 2см
h1 8см1
61.
АБСОЛЮТНО НЕУПРУГИЙ УДАРАбсолютно неупругий удар – кинетическая энергия тел частично или полностью
превращается во внутреннюю энергию; после удара столкнувшиеся тела движутся с
одинаковой скоростью, либо покоятся.
При абсолютно неупругом ударе закон сохранения механической энергии не
выполняется. Часть механической энергии переходит в тепловую.
- Выполняется закон сохранения импульса
m1 21 m2 2
m1 m2 U 2
Q
2
2
2
2
Q
Закон сохранения импульса:
- количество выделившегося тепла
m1m2
2 2
2 m1 m2
m1 1 m2 2
U
m1 m2
62.
Задача 8. Два тела массами 1 кг и 3 кг движутся со скоростями 7 м/с и 3 м/ссоответственно, навстречу друг другу. Определить увеличение внутренней энергии
шаров после абсолютно неупругого соударения.
Закон сохранения механической энергии не выполняется.
Часть механической энергии переходит в тепловую.
Выполняется закон сохранения импульса
2
2
m1 21 m2 2
m1 m2 U 2
m1 21 m2 2
m1 m2 U 2
Q
Q
2
2
2
2
2
2
2
m1 21 m2 2
m1 m2 U 2
Q
;
2
2
2
Скорость движущихся вместе двух тел найдем из закона сохранения импульса:
m m2 2
U 1 1
U 0 ,5 м / с
m1 1 m2 2 m1 m2 U ;
m1 m2 ;
1 7 2 3 32 1 3 0 ,52
Q
37 ,5 Дж
2
2
2
Ответ: Q = 37,5 Дж
63. Статика
Для равновесия тела, имеющего неподвижную осьвращения, необходимо, чтобы алгебраическая
сумма моментов сил, действующих на тело,
относительно этой оси, равнялась нулю:
В разделе механики “Статика” изучаются
условия равновесия тела или системы тел.
Состояние механической системы называется
равновесным, если все точки системы покоятся
по отношению к выбранной системе отсчета.
64.
СтатикаДля равновесия твердого тела это
условие является необходимым, но
недостаточным. Движение, вызванное
силой F, действующей на тело, зависит
не только от величины и направления
этой силы, но также и от точки ее
приложения. Поэтому для оценки
воздействия силы на твердое тело
вводится понятие – момент силы.
65.
Момент силы – произведение силына плечо.
Плечо силы – это кратчайшее расстояние
от оси вращения до линии действия силы
Для равновесия тела, имеющего неподвижную
ось вращения, необходимо, чтобы
алгебраическая сумма моментов сил,
действующих на тело, относительно этой оси,
равнялась нулю:
66.
СтатикаЦентр тяжести – это точка приложения
результирующих всех сил тяжести, действующих на
каждую частицу тела при любом его положении.
Центр масс – это точка твердого тела или
системы тел, которая движется так же, как и
материальная точка, на которую действует та же
результирующая сила, что и на твердое тело.
xц . м .
m1 x1 m2 x2 ...
m1 m2 ...
m x
i
i
m
i
67. Задача 9. Однородная балка лежит на платформе так, что один ее конец свешивается с платформы. Длина свешивающегося конца балки
равна четверти всей ее длины. Ксвешивающемуся концу прикладывают силу, направленную вниз. Когда эта сила
становится равной 1 кН, противоположный конец балки начинает подниматься.
Определить
массу
балки.
На балку действуют три силы: сила тяжести mg, сила
реакции опоры N и внешняя сила F. При этом сила тяжести
приложена к средней точке однородной балки (к центру
масс). За ось вращения рационально выбрать ось,
проходящую через точку В, в этом случае момент силы N
относительно точки В равен нулю, т.к. ее плечо равно 0.
Запишем условие равновесия балки относительно опоры В
mg CB F DB 0
Учитывая, что CB L / 4 ;
Ответ: m = 100 кг.
DB L / 4 ,
68. Задача 10. Cистема состоит из трёх шаров с массами m1 = 1 кг, m2 = 2 кг, m3 = 3 кг, которые двигаются так, как показано на
рисунке. Если скоростишаров равны V1 = 3 м/с, V2 = 2 м/с, V3 = 1 м/с, то величина скорости центра
масс
этой
системы
равна:
Ответы: 1) 1/3 м/с; 2) 2/3 м/с; 3) 4/3 м/с; 4) 5/3 м/с.
69.
Лекция №4 ?Работа и энергия
Законы сохранения
70.
Лекция № 4Механические колебания
71. Рассматриваемые вопросы
1.2.
3.
4.
Гармонические колебания.
Амплитуда, фаза колебаний.
Энергия колебаний.
Сложение однонаправленных колебаний.
Биения.
5. Сложение взаимно перпендикулярных
колебаний.
72.
ВведениеКолебаниями называются процессы, которые обладают той или иной степенью
повторяемости во времени.
В зависимости от природы
Механические колебания
Электрические колебания
В зависимости от характера воздействия
Свободные колебания
Вынужденные колебания
Автоколебания
Параметрические
Рассмотрим механические колебания. Из всех видов колебаний наибольший
интерес представляют гармонические колебания.
73. Гармонические колебания
Гармоническими называются такие колебания, при которых колеблющаяся величинаизменяется со временем по закону косинуса (синуса).
Пружинный маятник
x – Смещение тела от положения равновесия
ω0 – Частота собственных колебаний
(циклическая частота, угловая)
А - амплитуда колебаний
A = xmax
Кинематическое уравнение
гармонических колебаний:
x A cos 0t 0
- Фаза колебаний
0
T
Начальная фаза колебаний
2
- Период колебаний
74. Характеристики гармонических колебаний
Определим скорость и ускорение колеблющейся материальной точки.x A cos 0 t 0
dx
A 0 sin 0 t 0 A 0 cos 0 t 0
dt
2
d 2x
2
2
a 2 A 0 cos 0 t 0 A 0 cos 0 t 0
dt
• Из рисунка 1 видно, что
скорость и ускорение
колеблющейся точки
изменяются со
временем также по
гармоническому закону.
• Колебания
скорости опережают
колебания координаты
на угол , колебания
2
ускорения происходят в
противофазе с
колебаниями
координаты x.
75.
76. Задача 1. Груз, висящий на пружине, оттянули вниз и отпустили. За какое время от начала движения груз пройдет путь, равный
половине амплитуды? Период колебаний груза равен 2,4 с. Ответдать в единицах СИ.
Решение:
x A sin t 0 ; x 0 A ;
sin 0 1
0
2;
x t A sin t
2 ;
1
A
A cos t ; cos t ;
x t A cos t
2
2
t
3
Ответ:
t 0,4c
2
T
t
T
6
t 0,4c
77. ЭНЕРГИЯ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
Кинетическая энергия Ек материальной точки массой ,совершающей колебания:
Полная энергия
m 0 A 2
E Ek Em
2
2
Потенциальная энергия Еп:
kx2 m 0 A 2
En
cos 2 0 t
2
2
2
2 2
m
A
Кинетическая и потенциальная энергии периодически изменяются от 0 до
2
по гармоническому закону с частотой (рис.2).
Колебания кинетической энергии происходят в противофазе с колебаниями
потенциальной энергии, а их сумма в любой момент времени одинакова.
При решении задач необходимо помнить: Энергия пропорциональна квадрату
амплитуды
78. Задача 2. Начальная фаза гармонических колебаний равна нулю. При смещении точки из положения равновесия равном x1=1 см скорость
точки 1 15см / с .При смещении, равном x2=6 см, скорость 2 10см / с .Найти период колебаний x1 A cos 0t1
1 A 0 sin 0t1
2 A 0 sin 0t2
x2 A cos 0t2
Решение:
Закон сохранения механической энергии:
E Ek En
kx1
m 1
2
2
2
k x 2 x1 m 1 1
2
2
k
1 2 22
m
x2 x1
Ответ:
2
2
T 3,32c
2
2
2
kx
m 2
2
2
2
2
T
2
T 2
0
0
x 2 x1
2
1 2
2
2
2
2
k
m
T 3,32c
79. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
Получим дифференциальное уравнение свободных гармонических колебаний. Длямеханических колебаний воспользуемся уравнением динамики (второй закон Ньютона)
a
ma F
2
d x
dt 2
;
F kx ;
d 2x
k
x 0
2
dt
m
0
ma kx 0
d 2x
2
0 x 0
2
dt
- ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
СВОБОДНЫХ НЕЗАТУХАЮЩИХ
ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
k
- Частота собственных колебаний
m
Решением дифференциального уравнения является:
x A sin 0 t
или
x A cos 0 t
- Кинематическое
уравнение гармонических
колебаний
80. Математический маятник
Математический маятник – это идеализированная система, состоящая изматериальной точки массой , подвешенной на невесомой нерастяжимой нити, и
совершающая колебания под действием силы тяжести.
Период колебаний математического маятника
l
T 2
g
Круговая (циклическая) частота собственных колебаний
0
g
l
0 2
T
2
0
ν – частота колебаний (число колебаний в единицу времени)
81. Задача 3. Длина одного из математических маятников на 1,5 см больше длины другого. В то время как первый маятник делает 7
колебаний, второй делает на одно колебание больше. Определить вмиллисекундах период колебаний второго маятника. Принять ускорение
свободного падения g = 10 м/с2.
Решение:
Период колебаний второго маятника определяется выражением:
T2 2
l2
g
За одно и то же время t маятники совершают различное число
t
t
T
T
колебаний, поэтому их периоды отличаются: 1 N и 2
N2 .
1
N 2 T1
l
1 ;
N
T2
l2
Отсюда видно, что
l2
N2
l l
1
N
l2
l1 l 2 l
l
N
2
N
1
2
l2 0,049 м
1/ 2
0 ,049
T2 2
10
Ответ: T2 = 439,6 мс
0 ,14 0 ,4396 с
T2 = 439,6 мс
82. ФИЗИЧЕСКИЙ МАЯТНИК
Физический маятник – это твердое тело, совершающее в поле сил тяжестиколебания относительно горизонтальной оси, которая проходит через точку, не
совпадающую с центром инерции.
Период колебаний физического маятника:
T 2
I
mglпр
Частота собственных колебаний физического маятника:
0
mglпр
I
lпр- приведенная длина физического маятника – расстояние
от точки подвеса до центра масс.
83. ФИЗИЧЕСКИЙ МАЯТНИК
Физический маятник – это твердое тело, совершающее в поле сил тяжестиколебания относительно горизонтальной оси, которая проходит через точку, не
совпадающую с центром инерции.
Период колебаний физического маятника:
T 2
I
mglпр
Частота собственных колебаний физического маятника:
0
mglпр
I
lпр- приведенная длина физического маятника – расстояние
от точки подвеса до центра масс.
84. Задача 4. К потолку лифта на шарнире подвешен стержень за один конец. При этом его второй конец может свободно качаться. Длина
стержня 31 см. Определить период колебаний стержня, еслилифт движется вверх с ускорением 1,79 м/с2.
Решение:
Период колебаний стержня в поле тяготения земли: T 2
Поскольку лифт движется с ускорение вверх, ускорение будет
g1 g a
2
ml
Момент инерции стержня относительно центра масс I
12
Применяя теорему Штейнера, получим выражение для момента
инерции при вращении около одного из концов.
α
2
ml 2
ml 2
l
I
m
12
3
2
Учитывая, что l пр l / 2 , получаем окончательную формулу для
расчета периода колебаний стержня:
T 2
2l
3 g a
После подстановки числовых данных получаем: Т = 0,84 с.
Ответ: Т = 0,84 с.
I
mglпр
85. Задача 4. К потолку лифта на шарнире подвешен стержень за один конец. При этом его второй конец может свободно качаться. Длина
стержня 31 см. Определить период колебаний стержня, еслилифт движется вверх с ускорением 1,79 м/с2.
Решение:
Период колебаний стержня в поле тяготения земли: T 2
Поскольку лифт движется с ускорение вверх, ускорение будет
g1 g a
2
ml
Момент инерции стержня относительно центра масс I
12
Применяя теорему Штейнера, получим выражение для момента
инерции при вращении около одного из концов.
α
2
ml 2
ml 2
l
I
m
12
3
2
Учитывая, что l пр l / 2 , получаем окончательную формулу для
расчета периода колебаний стержня:
T 2
2l
3 g a
После подстановки числовых данных получаем: Т = 0,84 с.
Ответ: Т = 0,84 с.
I
mglпр
86. Метод векторной диаграммы.
Если изображать колебания графически в видевекторов на плоскости, то такая схема колебаний
называется векторной диаграммой.
a
Рассмотрим произвольный вектор , образующий с
осью x угол . Если привести этот вектор во
вращение относительно точки О, с угловой
скоростью , то проекция конца вектора будет
перемещаться по оси x в пределах от a до a .
Координата этой проекции будет изменяться со
временем по закону
0
x A cos 0 t
Гармоническое колебание может быть задано с помощью вектора, длина
которого равна амплитуде колебания, а направление вектора образует с осью
x угол, равный начальной фазе колебания.
87. Сложение гармонических колебаний.
x1 A1 cos 0 t 1 x 2 A2 cos 0 t 2x x1 x 2
x A cos 0 t 0
0 2 1
A2 A12 A22 2 A1 A2 cos 2 1
0 2 1
tg 0
A1 sin 1 A2 sin 2
A1cos 1 A2 cos 2
Метод векторной диаграммы позволяет свести сложение нескольких гармонических
колебаний одной частоты к операции сложения векторов.
88. Задача 5. Грузик, подвешенный на легкой пружине, совершает гармонические колебания в вертикальной плоскости с амплитудой 5 см.
В некоторый момент времени точка подвеса сама начинает колебаться ввертикальной плоскости с амплитудой 5 см и тем же периодом. Найти
разность фаз складываемых колебаний, если амплитуда
результирующего колебания равнялась5 см.
Решение:
При сложении однонаправленных гармонических
колебаний амплитуда результирующего колебания
определяется по формуле:
A2 A12 A22 2 A1 A2 cos 2 1
A 2 A1 A2
cos 2 1
2 A1 A2
2
2
52 52 52
25
cos 2 1
0 ,5
2 5 5
50
2 1 2,09 рад
Ответ:
2 1 2,09 рад
89. Биения
Пусть два складываемых гармонических колебания одинакового направления малоразличаются по частоте. Результирующее движение при этих условиях можно
рассматривать как гармоническое колебание с пульсирующей амплитудой. Такое
колебание называется биениями.
x1 A cos t
x2 A cos t
cos x cos y 2 cos
x y
x y
cos
2
2
2
x 2 A cos
t cos
t 2 A cos
t cos t
2
2
2
Частоту называют циклической частотой биений.
Aбиений 2 A cos
t
2
Tбиений 2
Б
- период биений.
90. Сложение взаимно перпендикулярных колебаний.
x A cos ty B cos t
x 2 y 2 2 xy
2
cos
sin
2
2
AB
A
B
Формы кривых, определяемых данным уравнением.
1)
0
2)
3)
2
x y
0
A B
x y
0
A B
x2 y2
2 1
2
A
B
y
B
x
A
y
B
x
A
91. Фигуры Лиссажу.
1 mЕсли частоты взаимно перпендикулярных колебаний неодинаковы ( 2 n ), то
траектория результирующего движения может иметь вид сложных кривых,
называемых фигурами Лиссажу.
Пример. Пусть отношение частот взаимно перпендикулярных колебаний равно
1:2 и разность фаз .
2
Уравнения колебаний:
x A cos t
y B cos 2 t
2
Результирующее колебание показано на рисунке.
Траектория вырождается в незамкнутую кривую, по
которой точка движется туда и обратно.
Это одна из простейших фигур Лиссажу.
92. СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
Свободные затухающие колебания– это такие свободные колебания, амплитуда
которых из-за потерь энергии реальной колебательной системой с течением времени
уменьшается.
d2x
dx
2
2
0x 0
2
dt
dt
или
x 2 x 02 x 0
const - коэффициент затухания, 0 - циклическая частота свободных
незатухающих колебаний той же колебательной системы в отсутствие
потерь энергии (при 0 ). Её называют собственной частотой
колебательной системы.
В случае малых затуханий ( 0 ) решение уравнения затухающих колебаний
имеет вид:
t
A
A
e
- амплитуда затухающих
0
x Ae t cos t
колебаний,
A0 - начальная амплитуда
Амплитуда затухающих колебаний убывает по экспоненциальному закону.
A A0 e t
93. СВОБОДНЫЕ ЗАТУХАБЩИЕ КОЛЕБАНИЯ
Промежуток времени 1 , втечение которого амплитуда
колебаний уменьшится в e раз,
называется временем релаксации.
Частота затухающих колебаний
связана ω с собственной частотой
ω0 соотношением:
0 2
2
Пример:
Амплитуда колебаний уменьшилась в е раз за 4 с. следовательно, можно
определить коэффициент затухания β.
β = 1/4 с = 0,25 с-1.
94. Задача 6. Амплитуда затухающих колебаний математического маятника уменьшилась за 8 минут в 7 раз. Во сколько раз она уменьшится
за 1 минуту?Решение:
Выразим время в системе СИ: t1 = 480 c; t2 = 60c.
A0
7
A1
A1 A0 e
A0
?
A2
t1
A
ln 0 t1
A1
A
ln 0 t 2
A2
Ответ: 1.28 раз
A2 A0 e
t 2
A0
e t1
A1
A0
e t 2
A2
ln A0 / A1 ln 7
3 1
4.05 10 c
t1
480
A0
t 2
4 10 3 60
e e
e 0.243 1.28
A2
95. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
F F0 cos t , гдеF0 и соответственно амплитуда и собственная частота
вынуждающей силы.
Рассмотрим пружинный маятник.
В уравнении динамики помимо силы упругости появляется сила
F F0 cos t
сопротивления F r и вынуждающая сила
ma kx r
d 2x
dx
m 2 kx r F0 cos t
dt
dt
d 2x
dx
m 2 kx r F0 cos t
dt
dt
Преобразуем это выражение. Разделим обе части на m и введем
k
r
- коэффициент затухания
обозначения 0
,
m 2m
пружинного маятника.
F0
d2x
dx
- дифференциальное уравнение
2
2
x
cos
t
0
вынужденных колебаний
2
dt
dt
m
96. ЯВЛЕНИЕ РЕЗОНАНСА
Явление резонанса – это резкое возрастание амплитуды колебаний при частотевынуждающей силы, равной или близкой к собственной частоте системы.
Амплитуда вынужденных колебаний связана с
частотой вынуждающее силы соотношением:
A
F0 m
2
0
2
2
4 2 2
При некоторой определенной для системы частоте амплитуда колебаний достигает
максимального значения. Колебательная система оказывается наиболее отзывчивой
на действие вынуждающей силы именно на этой частоте. Это явление называется
резонансом, а соответствующая частота – резонансной частотой.
рез 02 2 2
Из этого выражения следует, что при отсутствии сопротивления среды ( 0 )
амплитуда при резонансе обращалась бы в бесконечность.
97. Задача 7. Определить амплитуду вынужденных колебаний груза массой 423 г, подвешенного на пружине с коэффициентом жесткости 16
Н/м, если действует вынуждающая сила с амплитудой 3 Н и частотой в2 раза большей частоты собственных колебаний груза. Коэффициент
затухания равен 8 с-1
Решение:
A
F0 m
2
0
2
2
4 2 2
2 0 ;
По условию задачи
A
0
k
m
F0 m
2
0
2 0
4
2 2
2
2 0 2
Подставляем числовые данные
A
3 0 ,423
6 ,15 9 6 ,152 16 82
Ответ: А = 3,12∙10-2 м
3,12 10 2
ω0 =
A
6,15 рад/с
F0 m
0 9 0 16 2
2
98.
Лекция № 5Механические волны
Механика жидкости
99. Рассматриваемые вопросы
1. Волны в упругих средах2. Уравнение плоской и сферической среды
3. Наложение волн. Стоячие волны
4. Звуковые волны, эффект Доплера
5. Уравнение Бернулли
6. Ламинарное и турбулентное течение
7. Движения тел в жидкостях и газах
100. Механические волны.
Волна – процесс распространения колебаний в пространствеВ зависимости от природы
Механические волны
(звуковые, акустические)
Электрические волны
(электромагнитные, световые)
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой
поверхностью.
Геометрическое место точек, до которых доходят колебания к некоторому моменту
времени t, называется фронтом волны или волновым фронтом.
101. Плоские и сферические волны.
В плоской волне волновые поверхности представляют собой множество параллельных друг другуплоскостей, в сферической волне – множество концентрических сфер.
T
102. Уравнение плоской волны.
Уравнение волны – это уравнение, выражающее зависимость смещенияколеблющейся частицы, участвующей в волновом процессе, от координаты ее
равновесного положения и времени:
x , y , z; t
Пусть колебание точки с координатой x = 0(источник колебаний) задается функцией:
0 , t A cos t 0
Задача. Найти вид колебания точек в плоскости, соответствующей произвольному
значению x
Для того, чтобы пройти путь от плоскости x=0 до этой
плоскости, волне требуется время: x
103. Уравнение плоской волны.
Уравнение колебаний частиц в плоскости x будет иметь вид:x
x ,t A cos t 0 A cos t 0
В итоге получаем уравнение плоской волны, распространяющейся в направлении x:
x
x , t A cos t 0
A - амплитуда волны
x
t
0
- фаза плоской волны.
104. Уравнение плоской волны.
0 , t A cos t 0Обычно уравнению плоской волны придают симметричный
относительно x и t вид. Для этого вводится величина
k 2 – волновое число
T , k
2
T
Подставим это выражение в уравнение плоской волны:
x ,t A cos t kx 0
x ,t A cos t kx 0
Амплитуда плоской волны не зависит от расстояния.
105. Уравнение плоской волны.
В том случае, когда волна проходит через среду, обладающую потерями, уравнениеволны имеет вид:
x , t A e x cos t kx 0
Амплитуда волны зависит от расстояния по экспоненциальному закону:
A A0e x
106. Задача1. Уравнение бегущей звуковой волны в некоторой среде имеет вид: где Т – время в секундах, ω – круговая частота, x –
Задача1. Уравнение бегущей звуковой волны в некоторой среде имеет вид:10 cos T 2x
где Т – время в секундах, ω – круговая частота, x – координата в метрах. Найти
отношение амплитуды колебаний скорости частиц среды к скорости
распространения волны.
Необходимо найти:
d
dt
Acos t kx
A cos t
x
d
dt
A A k
/k
d
dt 2 10 5
Ответ:
d
A
dt
k
k
d
dt 10 10 6 2 2 10 5
107. Задача2. В однородной среде распространяется плоская упругая волна. Длина волны равна 20 см, а коэффициент затухания волны
равен 0,12 1/м. Найтиразность фаз волны в точках, для которых отношение амплитуд смещения
частиц среды равно 1,2
Уравнение плоской волны в среде с
потерями: x ,t Ae r cos t kx
Амплитуды волны в точках на расстояниях:
0
1 A1e r
1
A2e r
2
2
Фазы волны на расстоянии r1 и r2 равны: 1 t kx1 0 и 2 t kx2 0
Искомая разность фаз: 2 1 k x2 x1
k
2
2
Обозначим отношение амплитуд смещения частиц таким образом:
1
e
x2 x1
6 ,28 ln1,2
47 ,7 рад
0 ,2 0 12
x2 x1 ln
2 ln
108. Сферические волны.
r1r2
r
t 0
1
Амплитуда колебаний в этом случае убывает с расстоянием от источника по закону r
Уравнение сферической волны имеет вид:
r ,t
A
cos t kr 0
r
При распространении сферической волны в среде с потерями амплитуда будет
убывать по экспоненциальному закону (как и в случае плоской волны):
A r
e cos t kr 0
r
r ,t
2
Интенсивность волны пропорциональна квадрату амплитуды: I A
Максимальное значение интенсивности волны на расстоянии r:
A
I
r
2
109. Задача3. Найти коэффициент затухания звуковой волны, если на расстояниях 6 м и 12 м от точечного изотропного источника звука
интенсивности порождаемойим волны отличаются друг от друга в 6 раз.
A r
e cos t kr 0
r
Уравнение сферической волны в среде с потерями: r ,t
Интенсивность волны пропорциональна квадрату
2
амплитуды:
A 2 r1
I1
r
e
1
I A2
2
A 2 r2
I 2 e
r2
Обозначим отношение интенсивностей таким образом:
2
r1 2 r2 r1
e
r2
2
r
ln 2
r1
2 r2 r1
I2
I1
12 2
ln 6 / 2 12 6 3,4 10 2 м 1
6
110. Волновое уравнение.
Распространение волн в однородной изотропной среде описывается дифференциальнымуравнением в частных производных вида:
2ξ 2ξ 2ξ
1 2ξ
2 2 2 2
2
x
y
z
t
2 2 2
2 2 2
x
y
z
2
или
1 2
2 2
t
- волновое уравнение
2
- оператор набла или оператор Лапласа
Для плоской волны, распространяющейся в направлении x, волновое уравнение имеет вид:
d 2ξ
1 2ξ
dx 2 2 t 2
Решением этого уравнения является уравнение плоской волны:
x ,t A cos t kx 0
k
или
фазовая скорость волны
x
x , t A cos t 0
k
2
волновое число
111. Интерференция волн.
При распространении в упругой среде одновременно нескольких волн возникает ихналожение. Волны при наложении подчиняются принципу суперпозиции.
Если частоты складываемых волн имеют одну и ту же частоту, то возникает явление
интерференции волн.
Важное условие наблюдения интерференции:
когерентность складываемых волн
(волны должны иметь одну природу и иметь одинаковые частоты)
112. Интерференция волн. Стоячие волны.
Запишем уравнения этих волн: x ,t A cos t kx 0x ,t A cos t kx 0
Суперпозиция этих волн дает: 1 2 A cos t kx cos t kx
Преобразуем выражение, воспользовавшись тригонометрической формулой:
cos x cos y 2 cos
x y
x y
cos
2
2
В итоге получим уравнение стоячей волны: 2A cos kx cos t
2A cos kx
Амплитуда стоячей волны
В точках, где cos kx 1 - максимумы (пучности)
k x
cos kx 0
x
k 2
- минимумы (узлы)
113. Отличие стоячей волны от бегущей.
• Длина стоячей волны равна половине бегущей.• В стоячей волне в отличие от бегущей отсутствует перенос энергии, поскольку
встречные бегущие волны одинаковой амплитуды переносят равную по величине
энергию в противоположных направлениях. Энергия колебания между двумя
узлами остается постоянной, совершается лишь превращение кинетической
энергии в потенциальную и наоборот. Другими словами, нет никакого
распространения возмущения вдоль оси x. Именно поэтому такая волна
называется стоячей.
114. Задача4. Найти длину волны λ колебаний, если расстояние между первой и четвертой пучностями стоячей волны l = 15 см.
Длина стоячей волны равна половине длины бегущей: ст2
По условию задачи n1 = 1 и n2 = 4 – порядковые номера пучностей.
Длину стоячей волны можно представить в виде:
Приравняем левые и правые части.
l
2 3
2l
10cм 0 ,1м
3
ст
l
n2 n1
115. Звуковые волны.
Звуковые волны (звук) – это распространяющийся в упругой среде волновой процесс,воспринимаемый человеческим ухом.
Диапазон звуковых частот – 20 Гц – 20 кГц.
Волны с частотами < 20 Гц называются инфразвуком, > 20 кГц – ультразвуком.
Инфра- и ультразвук человеческое ухо не воспринимает.
Учение о звуке называется акустикой.
Источником звука может быть любое тело, колеблющееся в упругой среде со
звуковой частотой (например, в струнных инструментах источником звука является
струна, соединенная с корпусом инструмента).
Скорость распространения звука различна в различных средах.
RT
– скорость звука в газах
116. Эффект Доплера.
Эффект Доплера - это явление, состоящеев том, что испускаемая и регистрируемая
частоты волны различаются, если источник
и приемник движутся относительно друг
друга.
ист
- скорость движения источника
пр - скорость движения приёмника
зв пр
0
зв ист
- сближение
зв - скорость распространения волны
ν0 - частота колебания источника
зв пр
0
зв ист - удаление
117. Задача5. Два поезда идут навстречу друг другу (по разным путям) со скоростями 54 км/ч и 72 км/ч. Второй поезд дает свисток с
частотой 800 Гц. Найти частотуколебаний звука, который слышит пассажир первого поезда после встречи
поездов. Скорость звука принять равной 340 м/с.
Скорости поездов переведем в систему СИ.
1
54 1000
15 м / c
3600
2
72 1000
20 м / с
3600
По условию задачи υ2 – источник звука; υ1 - приемник
После встречи поездов приемник и источник удаляются друг от друга
зв пр
0
зв ист
Ответ: 732,4 Гц
800
340 15
732 ,4 Гц
340 15
118. Механика жидкости.
Гидродинамика представляет собой раздел механики сплошных сред, в которомизучаются движение несжимаемых жидкостей и взаимодействие несжимаемых
жидкостей с твердыми телами
Жидкости и газы обладают свойством текучести
119. Теорема о неразрывности струи.
Поле векторов скорости – совокупность векторовυ, заданных для всех точек пространства
Линия тока – линия, в каждой точке которой
вектор скорости направлен по касательной
Трубка тока
ТЕОРЕМА О НЕРАЗРЫВНОСТИ СТРУИ
120. Уравнение Бернулли.
Жидкость, в которой внутреннее трение(вязкость) полностью отсутствует,
называется идеальной жидкостью
Стационарное течение – течение, при котором
в каждой точке пространства вектор скорости
остается постоянным
В стационарно текущей жидкости вдоль любой линии
тока выполняется условие:
2
2
gh p const
p – статическое давление
gh – гидростатическое давление
2
2
Для горизонтальной линии тока выражение
уравнение Бернулли можно представить в виде:
– динамическое давление
1
2
2
p1
2
2
2
p2 так как h1 = h2
Давление оказывается меньшим в тех точках, где скорость течения жидкости больше.
Формула Торричелли:
h1
h2
2 gh
h h1 h2
121. Задача6. На столе стоит сосуд с водой, в боковой поверхности которого имеется малое отверстие на расстоянии h1 и на расстоянии
h2 от уровня воды. Уровень воды в сосудеподдерживается постоянным. На каком расстоянии l от сосуда (по горизонтали) струя воды
падает на стол в случае, если: а) h1 = 25 см, h2 =16 см; б) h1 = 16 см, h2 =25 см?
По теореме Бернулли:
2 gh 2
2
2 2gh2
1
2
2
gh1 p1
2
2
2
gh2 p2
l 2 t
(t – время прохождения струи расстояния l с высоты h1 отверстия)
gt 2
h1
2
l 2 h1h2
t
2h1
g
l 4 gh1h2 / g 2 h1h2
В обоих случаях вода падает на одинаковые расстояния: l 2 25 16 0 ,4 м
Ответ: l 0,4 м
122. Внутреннее трение. Вязкость.
Ламинарное – это такое течение жидкости или газа, при котором жидкость как быразделяется на слои, которые скользят относительно друг друга, не перемешиваясь.
Турбулентное - это такое течение жидкости или газа, при котором возникает
энергичное перемешивание жидкости так, что скорости частиц в рассматриваемом
месте изменяются беспорядочным образом. Такое течение нестационарно.
Распределение поля скоростей в слое жидкости при движении
одной пластины относительно другой
F S
x
y
Число Рейнольдса
l ρ – плотность жидкости; υ – средняя по
Re
сечению потока скорость течения;
l – размер потока (или тела)
η – коэффициент вязкости
Число Рейнольдса определяет характер
движения. При малых числах Re течение
носит ламинарный характер.
123. Внутреннее трение. Вязкость.
Ламинарное – это такое течение жидкости или газа, при котором жидкость как быразделяется на слои, которые скользят относительно друг друга, не перемешиваясь.
Турбулентное - это такое течение жидкости или газа, при котором возникает
энергичное перемешивание жидкости так, что скорости частиц в рассматриваемом
месте изменяются беспорядочным образом. Такое течение нестационарно.
Распределение поля скоростей в слое жидкости при движении
одной пластины относительно другой
F S
x
y
Число Рейнольдса
l ρ – плотность жидкости; υ – средняя по
Re
сечению потока скорость течения;
l – размер потока (или тела)
η – коэффициент вязкости
Число Рейнольдса определяет характер
движения. При малых числах Re течение
носит ламинарный характер.
124.
Лекция № 6Теория относительности
Релятивистская динамика
125. Рассматриваемые вопросы
1. Принцип относительности Галилея2. Постулаты специальной теории
относительности Эйнштейна
3. Преобразования Лоренца.
4. Следствия из преобразования Лоренца
5. Релятивистская динамика
126. Основы теории относительности.
Принципиальное отличиеспециальной теории
относительности от классической
механики Ньютона – введение
четырехмерного пространства –
единого пространство – время.
Событию в воображаемом четырехмерном пространстве
отвечает точка с координатами (x,y,z,ct) – мировая точка
Обычное пространство
обладает евклидовой
метрикой
4-х мерное пространство -псевдоевклидовое
S 2 c 2 t 2 x 2 y 2 z 2
S - интервал (расстояние между двумя мировыми точками)
127. Принцип относительности Галилея.
Инерциальная система отсчета – система, котораянаходится в состоянии покоя или равномерного
прямолинейного движения
Все инерциальные
системы отсчета –
равноправны.
r r 0t
ПРОСТРАНСТВО И ВРЕМЯ - АБСОЛЮТНЫ.
ВРЕМЯ ВО ВСЕХ ИНЕРЦИАЛЬНЫХ СИСТЕМАХ
ПРОТЕКАЕТ ОДИНАКОВО
128. Преобразования Галилея.
Согласно принципу относительности Галилея, любое механическое явление протекает одинаковово всех инерциальных системах отсчета.
Никакими механическими опытами, проводимыми в инерциальной системе отсчета, нельзя
установить, движется ли эта система отсчета прямолинейно и равномерно, или покоится.
Принципу относительности Галилея соответствуют
преобразования координат Галилея:
Прямые преобразования
Галилея
x x 0t
y y' z z'
'
' 0
Обратные
преобразования Галилея
x' x 0t
'
t t
'
y' y
z' z
t' t
– закон сложения скоростей в классической механике
Уравнения динамики не изменяются при переходе от одной инерциальной системы к другой
(инвариантны по отношению к преобразованию координат)
129. Специальная теория относительности Эйнштейна.
Скорость света в вакууме равна 2,99793∙108 м/с130. Относительность временных интервалов.
События, которые в системе K’ были одновременными, в системе К оказываютсянеодновременными
131. Элементы релятивистской механики. Преобразования Лоренца.
11 0 / c 2
2
132. Следствия из преобразований Лоренца.
1. Одновременность событий в разных системах отсчета133. Следствия из преобразований Лоренца.
2. Длина тел в разных системах отсчета134.
Решение.l l0 1 2 / c 2
По условию:
l0 l
l
1 0 ,25
l0
l0
2
2
1
c
2
0 ,75
1
c2
0 ,5625
c 1 0 ,5625 1,98 108 м / с
Ответ: 1,98 108 м / с
l 0,75l0
135. Следствия из преобразований Лоренца.
3.Промежуток времени между событиямиВ одной и той же точке системы К’ происходят два события.
xи1 момент
a времени
'
Первому событию соответствует координата
'
'
второму – tкоордината
и момент
x2времени
a
1
t1
1 0 / c 2
2
t' 2
2
1 0 / c
2
t 1 0 / c a
'
t2 t1
t
,
2
t t
'
2
'
1
1 / c
2
t2
t' 2 0 / c 2 a
t
2
1 0 / c 2
2
t'
1 0 / c 2
2
Время, отсчитанное по часам, движущимся вместе с телом,
называется собственным временем этого тела τ
“Парадокс близнецов”
t 1 2 c2
136.
Задача 3. В лабораторной системе отсчета удаляются друг от друга две частицы содинаковыми абсолютными скоростями. Их относительная скорость U в той же системе
отсчета равна 0,5 с. Определить скорость этих частиц.
Решение.
u
0
0
1
c2
2 c 2
u 2
0 ,5
2
c
0,5 2 2 c 0,5c 2 0
2c 4c 2 4 0 ,5 0 ,5c 2
2c 4c 2 c 2 c 2 3
2 0 ,5
0,81 108 м / с
Ответ: 0 ,81 108 м / с
137.
ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ(краткие сведения)
В основе ОТО лежит экспериментальный факт равенства инертной массы (входящей во 2 –й
закон Ньютона)и гравитационной массы (входящей в закон тяготения для любого тела).
Чем больше поле тяготения, тем медленнее течет время
Равенство инертной и гравитационной масс проявляется в том, что
движение тела в поле тяготения не зависит от его массы
Экспериментальное
обоснование ОТО
Перигелий Меркурия (ближайшая к Солнцу точка орбиты) за 100 лет поворачивается на 34
секунды!
138.
Молекулярная физикаТермодинамика
139.
Лекция № 7Физические основы
молекулярно-кинетической
теории
140.
План занятия:1 Введение. Предмет “Молекулярная физика и
термодинамика”
2 Статистическая физика и термодинамика;
3 Молекулярно – кинетическая теория
идеального газа;
4 Состояние термодинамической системы;
5 Термодинамические процессы. Равновесные,
обратимые, круговые;
6 Газовые законы
7 Основные термины, используемые в
молекулярной физике.(атомная единица массы,
молярная масса, моль, число Авогадро).
141.
Физические основы молекулярно – кинетическойтеории
Молекулярная физика – раздел физической науки, в котором рассматриваются
зависимости агрегатных состояний и свойств тела , от их строения,
взаимодействия между частицами, из которых состоят вещества, и характера
движения частиц
Основой молекулярной физики является молекулярно – кинетическая
теория (МКТ), родоначальником которой был М.В.Ломоносов.
Основа термодинамики – фундаментальные законы, установленные
путем обобщения опытных данных
142.
Физические основы молекулярно – кинетической теорииАгрегатные состояния вещества
Газообразное
состояние
Жидкое
Твердое
Плазма
Число молекул в 1 см3 очень велико. Например, в каждом см3 воздуха (при нормальных условиях)
содержится 2,7∙1019 молекул! Если расположить эти молекулы рядом, то получится длина, которая в 375 раз
превышает длину земного экватора! Размеры молекул ~ 3∙10-8 см. Средняя скорость движения порядка 450
Физические основы молекулярно –
м/с. За 1 с каждая молекула испытывает ~7,5 млрд столкновений.
кинетической
В газах молекулы перемещаются произвольно, хаотически (броуновское движение).Вводится понятие длина
теории
свободного пробега - расстояние, которое проходят молекулы от столкновения между собой до
столкновения.
Формула для расчета длины свободного пробега:
l
1
2 d 2 n
В твердом теле число частиц в 1 см3 примерно 1023 . Атомы совершают колебания около узлов
кристаллической решетки под действием сил притяжения и отталкивания. Атомы не могут приблизиться
до определенного расстояния и удалиться под действием сил притяжения.
В жидкости молекулы находятся в непрерывном движении, но благодаря большей плотности, чем в газах,
нет понятия длина свободного пробега
143.
Основные положения молекулярно-кинетической теории.1.Все тела состоят из мельчайших частиц – молекул.
(1 см3 газа содержит в среднем 1019 молекул).
2.Все
молекулы
находятся
в
состоянии
непрерывного
хаотического движения (броуновское движение).
3. Молекулы взаимодействуют между собой.
Идеальный газ – газ молекулы которого не взаимодействуют
между собой (инертные газы, воздух, Н2, О2, N2)
144.
Физические основы молекулярно – кинетическойтеории
Основное уравнение молекулярно – кинетической теории
1
P nm 2
3
2
P n Eпост
3
P nkT
Eпост
3
kT
2
Уравнение Клаузиуса
P – давление; n = N/V – концентрация частиц;
m – масса молекулы;
2
Средняя квадратичная скорость;
Eпост
Средняя энергия поступательного
движения
k-постоянная Больцмана
T - температура (К)
k = 1.38∙10-23
Дж/К
145.
Физические основы молекулярно – кинетическойФизические основы молекулярно – кинетической
теории теории
Два метода описания свойств макросистем
Статистический метод
Термодинамический метод
Основан на использовании
теории вероятностей и
определенных моделей
строения изучаемых систем
(распределение Максвелла
распределение Больцмана)
Основан на анализе условий и
количественных соотношений
при различных превращениях
энергии происходящих в
системе (первое, второе и
третье начала термодинамики)
Статистическая физика
Термодинамика
146.
Термодинамические параметры и процессыТермодинамическая система – это
совокупность макроскопических тел
любой физико – химической природы
Пар
O
He
Вода
Изолированная термодинамическая система – это система,
которая не взаимодействует внешними телами
Термодинамические параметры – это
Величины, характеризующие состояние системы
Давление (Паскаль)
Объем (м3)
P
V
T
Температура (Кельвин)
Термодинамический процесс – всякое изменение термодинамической
системы, связанное с изменением хотя бы одного из ее параметров
147.
Термодинамические параметры и процессыТермодинамические параметры при нормальных условиях
Температура Т0 = 273К. Перевод
20 0 C 20 273 293K
t 0 C TK
Температура абсолютного нуля -273 К
Нормальное давление (СИ) P 10 5 Па
0
(760 мм. рт. ст).
Пример перевода давления, выраженного в мм. рт. ст. в Паскаль:
720 мм . рт.ст. 133,3 0 ,96 105 Па
P P He P O2 P N 2
Объем V
м3
1 литр = 10-3 м3
Закон Дальтона
He
O2
N2
Объем газа совпадает с объемом сосуда
148.
Термодинамические параметры и процессы2
Круговой (циклический) процесс - это процесс,
при котором система после ряда изменений
возвращается в исходное состояние
1
0
Равновесной (обратимой) называется термодинамическая
система, при которой все параметры системы имеют
определенные значения, остающиеся при неизменных
внешних условиях постоянными сколь угодно долго
Изолированные системы со временем неизбежно и самопроизвольно
переходят в равновесное состояние (состояние теплового равновесия) и
никогда из него самопроизвольно выйти не могут.
149.
Термодинамические параметры и процессыРелаксация – процесс перехода термодинамической системы из
неравновесного состояния в равновесное
Время релаксации – время, за которое первоначальное отклонение какой
– либо величины от равновесного значения уменьшается в е раз.
(е = 2,72) – основание натурального логарифма
Все количественные выводы термодинамики применимы только к
равновесным состояниям и обратимым процессам.
Все реальные процессы являются неравновесными и могут лишь
приближенно считаться равновесными
150.
Термодинамические параметры и процессыГазовые законы
1 Изотермический процесс
Закон Бойля - Мариотта
Изотермический процесс – процесс, происходящий в
физической системе при постоянной температуре
2 Изобарный процесс
T = const
Закон Гей -Люссака
Изобарный процесс – процесс, происходящий в
физической системе при постоянном давлении
P = const
151.
Физические основы МКТОсновные термины, используемые в молекулярной
физике и термодинамике
Относительная атомная масса (Аr) химического элемента
- это отношение массы атома этого элемента к 1/12 массы
атома 12С (изотоп углерода с массовым числом 12).
Относительная молекулярная масса (Mr)- это отношение
массы молекулы этого вещества к 1/12 массы атома 12С.
Обозначается Mr. Масса молекулы: Mr mед
Атомная единицы массы (а.е.м.). равна 1/12 массы атома 12С
Обозначается: mед . Масса атома равна: Аr mед
152.
Физические основы МКТОсновные термины, используемые в молекулярной
физике и термодинамике
Моль – это количество вещества, в котором содержится число частиц, равное
числу атомов в 0,012 кг изотопа углерода 12С. Обозначается:
Постоянная Авогадро – число частиц, содержащихся в моле вещества.
Обозначается: NA = 6.02∙1023 моль-1
Молярная масса - масса одного моля вещества. Обозначается: M ( либо )
Универсальная газовая постоянная R = 8.31 Дж /мольК
Постоянная Больцмана k = 1,38*10-23 Дж/К
K
R
NA
153.
Примеры и задачи.Задача 1 153
Определить массу молекулы воды, если ее молярная масса равна 18 г/ моль.
Решение:
Примеры и задачи
m = μ / NA m = 18∙10-3/ 6,02∙1023 = 3∙1026 кг
Задача 2
При неизменной концентрации молекул идеального газа средняя квадратичная скорость теплового
движения его молекул увеличилась в 4 раза, при этом давление газа…
1) увеличится в 16 раз
3) увеличится в 4 раза
2) увеличится в 2 раза
4) не изменится
Решение:
P = 2/3 ∙nm<υ2>. Откуда следует ответ 1.
Задача 3
При неизменной концентрации молекул абсолютная температура идеального газа была увеличена
в 4 раза. При этом давление газа…
1) увеличилось в 4 раза
2) Увеличилась в 2 раза
3) не изменилась
4)Уменьшилась в 4 раза
Решение:
P = nkT , откуда ответ 1
154.
Примеры и задачиP
1
p
Примеры и задачи
p
p
p
2
3
4
0
Рис.1
V
Какой из графиков
рис.1
соответствует
процессу,
проведенному
при постоянной
температуре газа?
<E >
<E >
k
k
<E >
k
<E >
k
Рис.2
Какой график на рис.2 правильно изображает зависимость
давления идеального газа P от средней кинетической энергии
поступательного хаотического движения молекул или
атомов?
155.
Лекция № 8Уравнение состояния
156.
План занятия.1. Микропараметры и макропараметры.
2. Уравнение состояния идеального газа.
3. Давление газа на стенки сосуда.
4. Степени свободы сложной системы.
5. Закон равнораспределения энергии.
6. Примеры и задачи.
157.
Основы молекулярно – кинетической теорииМикропараметры
Координаты
x, y, z
молекулы
Импульс
молекулы p = mυ
Макропараметры
Давление P
Броуновское
движение
Температура T
P2>P1 T2>T1
V2<V1
Объем V
Задача статистической механики – выразить свойства системы в целом
через характеристики отдельных молекул, т.е. перекинуть мост между
макро – и микроскопическими описаниями системы.
158.
Уравнение состояния идеального газаИдеальный газ – газ, взаимодействием молекул которого
Идеальный
газ – газ, взаимодействием молекул
можно пренебречь.
которого можно пренебречь.
Соотношение, определяющее связь между параметрами
состояния какого-либо тела, называется уравнением
состояния
F(p,V,T) = 0
F(p,V,T) - некоторая функция параметров тела
T –Термодинамическая температура. Единица измерения - Кельвин (К)
Термодинамическая температура Т связана с температурой t по шкале
Цельсия соотношением: Т = t + 273.15
Температура, равная 0К, называется абсолютным нулем температуры
159.
Газовые законыЗакон Бойля – Мариотта
pV = const
Закон Гей – Люссака
Объем некоторой массы газа
при постоянном давлении
пропорционален его
абсолютной температуре
V
При изотермическом процессе
произведение объема данной
массы на его давление постоянно.
P = const
T= const
p
T1>T3
T3
0
T
0
pV
const
T
V
Уравнение Клапейрона
160.
Физические основы МКТУравнение состояния идеального газа
Моли всех газов при одинаковых условиях (при одинаковых
температуры и давлении) занимают одинаковый объем
При нормальных условиях (Т = 273 К и р = 105 Па) объем моля
любого газа равен 22,4 ∙10-3 кг/моль
Когда количество газа равно одному молю, величина константы R в
уравнении Клайперона одинакова для всех газов
pV/T = R
R =8.31Дж/моль∙К –универсальная газовая постоянная
pV RT
Уравнение состояния идеального газа для 1 моля.
161.
Уравнение состояния идеального газа.pV
m
RT
Уравнение Менделеева -Клайперона
Умножим и разделим правую часть на число Авогадро NA
N
m
N A - Число молекул в газе массой m
m NA
m
R
R
pV
RT N A
T N
T
NA
NA
NA
R
pV N
T
NA
R
8 ,31
23
k
1
,
38
*
10
Дж/К -постоянная Больцмана
23
N A 6 ,02 * 10
162.
Уравнение состояния идеального газа.pV NkT
N
n
V
p nkT
pV RT
- Концентрация молекул
pV
Уравнение состояния идеального газа
(уравнение Менделеева – Клайперона)
m
RT
163.
Термодинамические параметры и процессыДавление
газа на стенки сосуда
Основным уравнением кинетической теории газов принято называть
уравнение , устанавливающее связь между давлением газа, его
объемом и энергией.
1. Давление газа на стенку не зависит от формы сосуда
2. Отражение молекул происходит по зеркальному закону;
vx
x
vx
F
p n
S
3. Если газ находится в равновесии, все направления
движения молекул равновероятны
Давление, оказываемое молекулами на стенку численно
равно среднему значению силы, действующей на единицу
площади стенки нормально к ее поверхности и возникает
вследствие ударов о нее молекул.
164.
Давление газа на стенки сосудаFn
d m
dt
Согласно второму закону Ньютона
По третьему закону Ньютона молекула сообщает
стенке при ударе импульс 2m x
px 2nm x S
2
Fn
p
S
Полное изменение импульса всех молекул,
обладающих скоростью x соударяющихся за 1
секунду с элемента поверхности S
p 2n m 2 x
Со стенкой соударяются только
молекулы, движущиеся слева
направо, т.е. 1/2
165.
Термодинамические параметры и процессыДавление
газа на стенку сосуда
p nm x
2
Тепловое движение молекул происходит совершенно
беспорядочно, имеет место равновероятное распределение
по направлениям, поэтому
1
2x
3
2
Окончательное выражение для давления газа на стенку сосуда:
1
p nm
3
2
2
p n E пост
3
Основное уравнение молекулярно – кинетической
теории газа
Давление равно двум третям энергии поступательного
движения молекул, содержащихся в единице объема.
166.
Средняя энергия молекул.2
p n E пост
3
Основное уравнение
МКТ
E пост
p nkT
Уравнение
состояния
идеального газа
3
kT
2
Абсолютная температура есть величина прямо
пропорциональная средней энергии
поступательного движения молекул
167.
Степени свободы сложной системы.E пост
3
kT
2
Средняя энергия зависит только от температуры
и не зависит от массы молекулы
Эта формула определяет энергию только
поступательного движения молекулы
Наряду с поступательным движением возможны также вращение молекулы и
колебания атомов, входящих в состав молекул.
Статистическая физика устанавливает закон о равнораспределении
энергии по степеням свободы молекулы.
Числом степеней свободы механической системы называется
количество независимых величин, с помощью которых может быть
задано положение системы. Обозначается i.
168.
Число степеней свободы в молекулярной физике.z
Одноатомная молекула.
y
x
i=3
Три - поступательные
Ne , He , Ar
Двухатомная молекула i = 5
H2 , O2 , N2
Три – поступательные
Две - вращательные
С жесткой связью
С упругой связью i = 7
5 + (2 колебательных)
(Екинет + Епотенц )
Трехатомные и более i = 6
CO2 ,H2O, СH4
Три – поступательные
три - вращательные
169.
Закон распределения энергииНа каждую степень свободы (поступательную, вращательную
и колебательную) в среднем приходится одинаковая
кинетическая энергия, равная ½ кТ
i
E kT
2
i - сумма числа поступательных, числа вращательных и удвоенного
числа колебательных степеней свободы молекулы
i = nпост + nвращ +2nколеб
170.
Примеры и задачиЗадача 1
Решение
Сколько атомов водорода содержится в 50 г
водяного пара?
Число Авогадро
m
NA- число молекул в одном моле
m
- Моль – количество газа N N A
H 2O 2 16 10 кг / моль
3
Задача 2
H 2O H 2 O
50 10 3
23
23
N
6
,
02
10
16
,
7
10
18 10 3
Найти массу одной молекулы аммиака
NH3
Решение N m N N – число молекул. Для одной молекулы
A
3
Молярная масса аммиака NH 3 14 3 10 кг / моль
17 10 3
m
2,82 10 26 кг
23
6,02 10
m
NA
171.
Примеры и задачиЗадача 3
Определить число n молекул воздуха в единице объема при
температуре 00С и давлении 1,013∙105 Па.
Уравнение состояния идеального газа p nkT
Решение
p
n
kT
1.013 105
25
3
n
2
,
7
10
м
1.38 10 23 273
Найти плотность ρ воздуха при температуре 00С и давлении
1,0∙105 Па . Молярная масса воздуха μ = 29∙10-3 кг/моль.
Задача 4
Решение
pV
m
Уравнение состояния идеального газа
RT
m p
V RT
1.0 105 29 10 3
1,29кг / м 3 1,29г / л
8.31 273
172.
Примеры и задачиЗадача 5
Решение
m
pV RT
Какое давление на стенки сосуда производят 0,02 кг кислорода,
занимающего объем 0,2 м3 при температуре 400С?
Уравнение состояния идеального газа
p
m RT
V
t = 40 +273 =313 K
Молярная масса О2
32 10 3
кг
моль
0,02 8,31 313
4
0
,
8
10
Па
3
32 10 0,2
В закрытом сосуде емкостью 2 м3 находится 1,4 кг азота (N2) и
Задача 6 2 кг кислорода (О2 ). Найти давление газовой смеси в сосуде,
если температура смеси t = 270 C.
p
Решение
p
m RT
V
По закону Дальтона давление смеси газов равно сумме
p p N 2 p O2
парциальных давлений
RT
p
V
N 28 10 3 кг / моль
2
m N 2 m O2
p 8,31 300 1,4 2 1,4 10 5 Па
N O
2 10 3 28 32
2
2
О 32 10 3 кг / моль
2
t 27 273 300K
173.
Пример 1Примеры и задачи
В сосуде, закрытом поршнем, находится
идеальный газ. График зависимости
объема газа от температуры при изменения
его состояния приведен на рисунке.
Какому состоянию газа соответствует
наибольшее давление?
Пример 2
v
Укажите точку, в которой достигалась
наибольшая температура идеального газа
в ходе процесса, график которого
изображен на рисунке
3
1
4
0
T
2
p
1
Сравните объем данной массы
идеального газа в состоянии 1 и 2.
Пример 3
2
T
p
V
174.
Примеры и задачиПример 1
p 4 R
T4
V4
p4V4 RT4
R
p4
tg
V4
tg
T4
pmax соответствует Т.4
Пример 2
pV RT
T
R
R
V R
p p tg
T
Пример 3
v
Объем
максимальный в
т.2
3
2
1
4
β
0
T
2
p
1
T
p
T3
T3 T2 T1
T2
T1
V
175.
Примеры и задачиПример 1
p 4 R
T4
V4
p4V4 RT4
R
p4
tg
V4
tg
T4
pmax соответствует Т.4
Пример 2
pV RT
T
R
R
V R
p p tg
T
Пример 3
v
Объем
максимальный в
т.2
3
2
1
4
β
0
T
2
p
1
T
p
T3
T3 T2 T1
T2
T1
V
176.
Лекция № 9Первое начало
термодинамики
177.
План занятия1. Первое начало термодинамики.
2. Работа, теплота в термодинамике.
3. Внутренняя энергия.
4. Теплоемкость идеального газа.
5. Удельная, молярная теплоемкость.
6 Теплоемкость смеси газов.
178.
Q = ΔU + A1 начало
термодинамики
Количество теплоты, сообщенное системе, идет на приращение внутренней
энергии системы и на совершение системой работы над внешними телами
Q – количество сообщенной телу (системе) теплоты, Дж
U – внутренняя энергия, ΔU - изменение внутренней энергии, Дж
A – работа, совершенная системой, Дж
Если Q > 0 – к системе
подводится тепло
Если Q < 0 – от системы
отводится тепло
Если Q = 0 – без теплообмена (адиабатический процесс)
Взаимодействие термодинамических систем с окружающей средой
сопровождается обменом энергией. Этот обмен осуществляется
двумя качественно различными способами: путем совершения
работы и путем теплообмена.
179.
1 началотермодинамики
Работа, теплота в термодинамике
1 Совершение работы сопровождается перемещением внешних тел,
воздействующих на систему. При этом количество переданной механической
энергии измеряется совершенной работой.
Работа является мерой механической энергии, переданной другому телу
или телам .
2 Процесс обмена энергией между телами – передача тепла. Величину
переданной энергии теплового движения молекул измеряют количеством
теплоты Q.
Теплота есть мера переданной телу (или отданной им) энергии теплового
движения.
Работа и теплота обладают тем общим свойством, что они существуют
лишь в процессе передачи энергии.
180.
1 началотермодинамики
Три способа передачи теплоты
Теплообмен
Излучение
Конвекция
T2
T1
Теплообмен: механизм обмена энергией состоит в том, что
частицы соприкасающихся тел обмениваются энергией при
взаимных столкновениях
Излучение: обмен энергией без непосредственного контакта между
телами, когда они разделены какой – либо средой или даже вакуумом.
Конвекция: обмен энергией без непосредственного контакта между
телами, когда они разделены какой –либо средой (кроме вакуума)
181.
Работа1 начало
термодинамики
Теплота
Между теплотой и работой существует качественное различие.
Совершение работы над системой приводит к увеличению любого вида
энергии (кинетической, потенциальной, внутренней)
Сообщение телу или системе тел теплоты , т.е. увеличение энергии
хаотического теплового движения ее частиц, непосредственно ведет только
к увеличению внутренней энергии.
Работа и количество тепла – это не формы энергии, а только различные
способы ее изменения и передачи от одного тела к другому.
Энергия характеризует состояние рассматриваемой системы
Теплота и работа характеризуют изменение состояния, т.е.
происходящие в системе процессы.
182.
1 началотермодинамики
Внутренняя энергия термодинамической системы
Внутренняя энергия какого – либо тела слагается из
кинетической энергии поступательного и вращательного
движения молекул, кинетической и потенциальной
энергий колебательного движения атомов в молекулах,
потенциальной энергии взаимодействия между
молекулами.
Кинетическая энергия тела как целого и его
потенциальная энергия во внешнем силовом поле во
внутреннюю энергию не входят
i = nпост + nвращ + 2nколеб - число степеней свободы
183.
Внутренняя энергияидеального газа
1 начало
термодинамики
Вследствие того, что молекулы идеального газа на расстоянии не
взаимодействуют, внутренняя энергия такого газа будет складываться из
энергий отдельных молекул.
U NA
i
i
E N A kT RT
2
2
i m
U
RT
2
для одного моля газа
Внутренняя энергия зависит только от температуры!
Внутренняя энергия является функцией состояния системы
Приращение внутренней энергии при переходе системы из одного состояния в
другое всегда равно разности значений внутренней энергии в конечном и
начальном состояниях независимо от пути, по которому совершался переход
(независимо от характера процесса, приведшего к переходу)
i m
U
R T
2
U U 2 U1
184.
1 началотермодинамики
Работа, совершаемая телом при изменениях объема
Работа, совершаемая газом над внешними телами , может быть
выражена через давление и и изменение объема.
S
Δh
газ
Р
A F h
A p V
F pS
A pS h p V
A - элементарная работа
Если давление остается постоянным
A12 p V2 V1
Если при изменении объема давление меняется
Q dU A
A12
V2
pdV
V1
Первое начало термодинамики для элементарного процесса
185.
1 началотермодинамики
Теплоемкость идеального газа
Теплоемкостью какого – либо тела называется величина, равная
количеству тепла, которое нужно сообщить телу, чтобы
повысить его температуру на один Кельвин
С
C уд
m
С тел а
Q
dT
Дж/К
удельная теплоемкость –
теплоемкость единицы
массы вещества Дж/кг∙К
С уд
С
C
C
m
Молярная теплоемкость –
теплоемкость моля
вещества Дж/(моль∙К)
186.
Теплоемкостьидеального газа
1 начало
термодинамики
Q
i m
RdT pdV
2
Для газов теплоемкость существенно зависит от
процесса, в котором участвует газ.
Теплоемкость при
постоянном давлении
Теплоемкость при
постоянном объеме
CV
Для 1 моля
i
Q RdT
2
Для 1
моля
Разделим левую и правую часть на dT
Cp
i
Q RdT pdV
2
Q
dT
i
CV R
2
Для 1 моля
i 2
Cp
R
2
i dT
dV
R
p
2 dT
dT
i
dV i
Cp R p
R R
2
dT 2
187.
1 началотермодинамики
Теплоемкость идеального газа
U
m
CV T
С p CV R
Внутренняя энергия произвольной массы газа m .
Нагревание газа происходит при постоянном объеме
Уравнение Майера
i 2
i
2
i
1
R
СV
1
1
U
pV
1
Сp
CV
Коэффициент
Пуассона
(показатель
адиабаты)
Число степеней свободы
Внутренняя энергия
произвольной массы
идеального газа
188.
1 началотермодинамики
Теплоемкость смеси газов
При смеси нескольких газов
V1 + V2 + …+ Vn
V=const
C удV
Если задано:
какой газ (i ) и
количество газа
m1 + m2 + …+mn
CV 1 CV 2 CV 3
m1 m2 m3
m
m
p1 + p2 +… + pn
С удV
1 2 ... n
i m
i1 m1
i m
R 2 2 R 3 3 R
2 1
2 2
2 3
m1 m2 m3
С удV
i
i1
i
1R 2 2 R 3 3 R
2
2
2
1 1 2 2 3 3
189.
1 началотермодинамики
Теплоемкость смеси газов
При смеси нескольких газов
V1 + V2 + …+ Vn
V=const
C удV
Если задано:
какой газ (i ) и
количество газа
m1 + m2 + …+mn
CV 1 CV 2 CV 3
m1 m2 m3
m
m
p1 + p2 +… + pn
С удV
1 2 ... n
i m
i1 m1
i m
R 2 2 R 3 3 R
2 1
2 2
2 3
m1 m2 m3
С удV
i
i1
i
1R 2 2 R 3 3 R
2
2
2
1 1 2 2 3 3
190.
1 началотермодинамики
Теплоемкость смеи газов
P = const
C удр
C C P 2 C P3
P1
m1 m2 m3
Если известно:
какой газ (i) и
количество газа ν
Если известно только, какие
газы в смеси (i,μ)
(при равных условиях (p,V)
i1 2
i 2
i 2
1R 2 2 R 3 3 R
2
2
Ñ óäP 2
m1 m2 m3
i1 2
i 2
i 2
1R 2 2 R 3 3 R
2
2
Ñ óäP 2
1 2 2 3 3
m
pV
RT
i1 2 i2 2 i3 2
R
R
R
2
2
Ñ óäP 2
1 2 3
191.
1 начало термодинамики.
ПРИМЕРЫ И ЗАДАЧИ
Задача 1
Найти удельную теплоемкость при постоянном давлении газовой смеси из
3х киломолей гелия и 2х киломолей углекислого газа.
Дано: p = const; He 3 10 3 CO2 2 10 3 He 4 10 3 кг / моль
CO2 12 32 10 3 кг / моль
Найти: Судр смеси
Решение
i He 3
C p уд ( смеси )
i CO2 6
С p1 1 C p 2 2
m1 m2
i 2
Cp
R
2
кг
моль кг )
m (
моль
i CO2 2
i He 2
He R
CO2 R
2
2
C pуд ( смеси )
He He CO2 CO2
Ответ:
C pуд ( смеси ) 1.29 103 Дж / кгK
m
192.
1 начало термодинамики.
Примеры и задачи
Задача 2
Чему равна удельная теплоемкость при постоянном объеме некоторого двухатомного
газа, если плотность этого газа при нормальных условиях равна 1,43 кг/м3?
Дано: V = const; i = 5; p = 105 Па; Т = 273 К; ρ = 1,43 кг/м3.
Найти :CV уд
Решение
C v уд
C
V
m
p RT RT
V
CVУд
Ответ:
Молярная масcа газа μ
неизвестна
RT
p
5
10 5
640 Дж / кгК
2 1,43 273
CVУд 640 Дж / кгК
CVУд
i p
2 T
pV
m
RT
193.
1 начало термодинамикиПримеры и задачи
Задача 3
P, кПа
3
30
На диаграмме представлены изменения давления и
объема идеального одноатомного газа.
Какое количество теплоты было получено или
отдано газом при пере,vходе из состояния 1 в
состояние 3.
Решение
20
1
2
10
0
1
2
3
При переходе из начального в конечное состояние объем газа увеличился.,
следовательно, газ совершил работу А'. По первому закону т/д: Q U A'
U U 3 U 1
U1
3
p1V1
2
U3
3
p3V3
2
Работа А' при переходе из 1 в 3 равна: A' p1 V
( работа на участке 2-3 равна нулю, т.к. V = const).
Q
V,м3
3
( p3V3 p1V1 ) p1 V
2
Ответ:Q = 14∙1014 Дж
Q
3
(3 10 4 3 10 4 1) 10 4 2 14 10 4 Дж
2
194.
1 начало термодинамикиЗадача 4
Примеры и задачи
Для нагревания некоторой массы газа на 500С при постоянном
давлении необходимо затратить 160 кал. Если эту же массу газа
охладить на 1000Спри постоянном объеме, то выделяется 240 кал.
Какое число степеней свободы имеют молекулы этого газа?
Дано: T 50 0 C 323К ; T2 100 0 C 373К
Q1 160кал 670,4 Дж
Q2 240кал 1005,6 Дж
Найти: i
Решение
Q U A'
Q2
i T2
Q1 i 2 T1
Q2 i 2 T1 Q1i T2
Ответ: i = 6
i
i 2
Q1 R T1 R T
R T1
2
2 1
i
i
Q2 R T2 p V2 R T2
2
21
2Q2 T1
i
Q T2 Q2 T1
i
P -const
V - const
2 240 50
6
160 100 240 50
195.
Лекция № 11Второе начало термодинамики
Тепловые машины
196.
План занятия1. Обратимые и необратимые процессы.
2.Круговые процессы
3. Микро - и макросостояния системы.
4.Статистический вес (термодинамическая
вероятность).
5. Энтропия (по Больцману, по Клаузиусу)
6. Второе начало термодинамики. Формулировки.
7. Изменение энтропии при изопроцессах.
8. К вопросу о “тепловой смерти Вселенной”.
197.
Второе начало термодинамикиСтатистический метод
Основан на использовании
теории вероятностей и
определенных моделей
строения изучаемых систем
(распределение Максвелла
распределение Больцмана)
Термодинамический метод
Основан на анализе условий и
количественных соотношений при
различных превращениях энергии
происходящих в системе (первое,
второе и третье начала
термодинамики)
Q U A
I начало термодинамики
Количество теплоты, сообщенное системе, идет на изменение внутренней
энергии и совершение работы против внешних сил
198.
Второе начало термодинамикиТермодинамика – это наука о тепловых
процессах, о превращении тепловой
энергии.
Термодинамика – это наука о тепловых процессах, о
превращении тепловой энергии.
Для описания термодинамических процессов
первого начала термодинамики недостаточно
,
Выражая общий закон сохранения и
превращения энергии, первое начало не
позволяет
определить
направление
протекания процессов.
199.
Второе начало термодинамикиВторой закон термодинамики представляет собой ряд положений, относящихся к
различным состояниям и процессам в термодинамической системе.
Стационарное состояние системы
x
t = 1000C
t = 00C
Лед
Кипяток
dT
x
dx
dT
градиент температуры
dx
Стояние системы называется
стационарным, если параметры
системы во всех частях системы
остаются постоянными. Это
состояние может сохраняться само
собой или поддерживаться с
помощью каких – либо процессов.
Постоянство температуры в каждой точке стержня поддерживается с
помощью процесса теплопроводности
200.
Второе начало термодинамикиРавновесное состояние системы
Равновесное состояние – состояние, в котором каждый
параметр имеет одно и то же значение в каждой точке
системы и остается неизменным сколь угодно долго, если не
меняются внешние условия.
Равновесным ( квазиравновесным, квазистатическим)
называется процесс, состоящий из непрерывной
последовательности равновесных состояний
термодинамической системы.
Для осуществления равновесного процесса параметры внешней
среды должны изменяться бесконечно медленно.
Время перехода системы из неравновесного состояния в
равновесное называется временем релаксации.
201.
Второе начало термодинамикиОбратимые и необратимые процессы
Термодинамический процесс, совершаемый системой,
называется обратимым, если после него можно
возвратить систему и все взаимодействующие с ней тела в
их начальное состояние таким образом, чтобы в других
телах не возникло каких – либо остаточных изменений.
Процесс называется необратимым, если он
протекает так, что после его окончания систему
нельзя вернуть в начальное состояние через прежние
промежуточные состояния. Нельзя осуществить
необратимый круговой процесс, чтобы нигде в
окружающей среде не осталось никаких изменений.
202.
Второе начало термодинамикиОбратимые и необратимые процессы
не всякий
равновесный процесс
Необходимое условие
обратимости
термодинамического
обязательно обратим
процесса – его равновесность,
всякий обратимый процесс
всегда является равновесным (квазистатическим).
Однако, не всякий равновесный процесс – обратим.
Примером обратимого процесса является адиабатическое
расширение с последующим (адиабатическим) сжатием.
При адиабатическом процессе нет необратимого
теплообмена с окружающей средой Q 0
Все реальные процессы - необратимые
203.
Второе начало термодинамикиКруговые процессы
Термодинамических процессов, в результате которых
система возвращается в исходное состояние.
p
p
1
1
a
b
0
V1
2
V2
Прямой цикл
a
b
V
0
V1
2
V2
V
Работа совершаемая при
круговом процессе,
численно равна площади
охватываемой кривой.
Обратный цикл
После совершения цикла система возвращается в прежнее состояние.
Поэтому всякая функция состояния, в частности внутренняя энергия,
имеет в начале и в конце цикла одинаковое значение.
204.
Второе начало термодинамикиМикросостояния и макросостояния системы
Различные состояния, отвечающие одной и той
же энергии, обладают разной вероятностью
Изолированная система самопроизвольно переходит из менее
вероятных в более вероятные состояния, либо пребывают
преимущественно в состоянии, вероятность которого
максимальна.
Пример 1
Т1
Пример 2
Газ
Т2
Вакуум
Т
Газ
205.
Второе начало термодинамикиМакросостояние системы. Микросостояние системы
Состояние системы, заданное с помощью ее термодинамических
параметров: давлением p, объемом V, температурой Т, называется
макросостоянием
Состояние системы, заданное с помощью ее микропараметров
(координат и импульсов, непрерывно меняющихся), называется
микросостоянием
Всякое макросостояние может быть осуществлено различными
способами, каждому из которых соответствует некоторое
микросостояние системы.
206.
Второе начало термодинамикиСтатистический вес. Термодинамическая вероятность
Частицы, образующие систему, все время перемещаются и изменяют
свой импульс в результате соударений. В соответствии с этим
макросостояние системы все время изменяется
Всякое макросостояние осуществляется различными способами,
каждому из которых соответствует некоторое микросостояние
Число различных микросостояний, соответствующих
данному макросостоянию, называется статистическим
весом или термодинамической вероятностью
п
Л
1
2
п
Л
1
2
3
3
Макросостояние 1
Макросостояние 2
п
Л
2
3
1
Макросостояние 3
207.
Второе начало термодинамикиСтатистический вес. Термодинамическая вероятность
Число
молекул
слева
Число
молекул
справа
4
0
3
1
Левая половина
Правая половина
-
1 2 3 4
1
123 124
1 2 3 4
4
134 234
2
2
14
34
23 24 34
14
12
1
0
3
4
Число
способов
13
1 2 3 4
-
234
124
24
23
13
134
123
1 2 3 4
12
6
4
1
208.
Второе начало термодинамикиСтатистический вес. Термодинамическая вероятность
Наибольшее число способов реализации состояний
соответствует равномерному распределению частиц.
Термодинамическая вероятность равна шести
Статистический вес для системы, содержащей N частиц
может быть рассчитан по формуле:
4
1
6
4
1
N!
n! N n !
В отличие от математической вероятности, которая не может быть больше 1,
термодинамическая вероятность всегда больше или, в крайнем случае, равна 1
209.
Второе начало термодинамикиСтатистический вес. Термодинамическая вероятность
N!
n! N n !
N – Общее число частиц
n – Число частиц в одной части сосуда
(N – n) – Число частиц в другой части
N! – читается: эн факториал ; пример: 5! = 1ˑ2ˑ3ˑ4ˑ5
Статистический вес обычно выражается огромными
числами. Например, для одного моля кислорода при
атмосферном давлении и комнатной температуре
10
6 ,5 1021
210.
Второе начало термодинамикиЭнтропия
Итак, вероятность макросостояния пропорциональна его
статистическому весу (термодинамической вероятности) Ώ .
В качестве характеристики вероятности состояния можно было бы взять
число Ώ, но тогда бы не выполнялось свойство аддитивности. По закону
умножения вероятностей Ώ = Ώ1ˑΏ2.
Больцман предложил в качестве функции, характеризующей меру
беспорядочности теплового движения величину S , пропорциональную
логарифму термодинамической вероятности Ώ
S k ln
Энтропия по Больцману
211.
S k lnВторое начало термодинамики
Энтропия
Статистическое толкование энтропии:
Энтропия есть мера неупорядоченности системы
Энтропия является количественной мерой степени
молекулярного беспорядка в системе
Свойства энтропии:
1. В ходе необратимого процесса энтропия изолированной системы
возрастает. Предоставленная самой себе, система переходит из менее
вероятных в более вероятные состояния.
2.
Энтропия изолированной системы, находящейся в
равновесном состоянии, максимальна
3. Энтропия упорядоченного движения равна нулю
lim S 0
t 0
212.
Второе начало термодинамикиЭнтропия
Определение энтропии по Клаузиусу
dQ
dS
T
Если количество тепла dQ сообщается системе в ходе
необратимого процесса, энтропия возрастает как вследствие
сообщения тепла, так и вследствие необратимости процесса.
Поэтому имеет место неравенство
dS
dQ
T
Для обратимого процесса
dS
dQ
T
213.
Второе начало термодинамикиФормулировки второго начала термодинамики
1. Энтропия изолированной системы не может убывать при
любых происходящих в ней процессах
2. Невозможен процесс, единственным результатом
которого является совершение работы за счет
охлаждения одного тела ( Томсон)
3. Невозможен процесс, единственным результатом
которого является передача тепла от холодного тела к
горячему. (Клаузиус)
4. Невозможно построить вечный двигатель второго рода
(тепловой двигатель)
214.
Второе начало термодинамикиК вопросу о тепловой смерти Вселенной
В 1867г. Клаузиус сделал незакономерную попытку
обосновать гибель Вселенной.Он пришел к выводу, что
рано или поздно энтропия Вселенной должна достигнуть
своего максимума, что приведет к выравниванию
температур всех тел Вселенной. В результате прекратятся
все иные формы движения (механическая,электрическая,
световая), кроме хаотического теплового движения.
Клаузиус назвал такое состояние “тепловой смертью”.
В чем ошибочность подобных выводов?
215.
Второе начало термодинамикиК вопросу о тепловой смерти Вселенной
1. Во- первых, не учитывается тяготение. Вследствие
тяготения однородное изотермическое распределение
вещества во Вселенной не соответствует максимуму
энтропии, потому что не является наиболее
вероятным.
2. Вселенная не стационарна – она расширяется, и
первоначальное однородное вещество распадается
под действием сил тяготения, образуя скопления
галактик, галактики, звезды и т.д. Эти процессы
происходят с ростом энтропии, т.е. в согласии со
вторым началом термодинамики
216.
Второе начало термодинамикиЭнтропия при изопроцессах
Саму энтропию измерить нельзя (как нельзя измерить
меру , например, испуга, радости , голода и т.д.).
Можно измерить изменение энтропии при переходе системы из
одного состояния в другое
dQ
dS
T
2
2
dQ
dS
1
1 T
2
2
i mR dT
pdV
T 1 T
1 2
S
2
dQ
1 T
S S 2 S1
dQ
При необходимости делается замена термодинамических
параметров из уравнения состояния идеального газа
Первое начало
термодинамики
im
RdT pDV
2
pV
m
RT
217.
Второе начало термодинамикиЗадача 1
Найти изменение энтропии S при превращении массы m = 1 воды (t = 00C) в пар.
Дано: m = 1 г; tв = 00 С; tв = 1000 С; с = 4,19 кДж/кг.К; r = 2,26 МДж/кг
Найти : S
Решение Общее изменение энтропии S складывается изменения энтропии S1 при
нагревании массы воды m от температуры Т = 273 К до температуры Тп = 373 К и
изменения энтропии S 2 при испарении массы m воды.
S S1 S 2
Tп
S1 mc ln
T
S 2
mr
Tп
Tп r
S m c ln
T Tп
Вычисления
373 2,26 10 6
2260
3
10 3 10 3 4,19 0,31
S 10 4,19 10 ln
7,4Дж/К
273
373
373
3
Ответ:
S 7,4Дж/К
218.
Второе начало термодинамикиЗадача 3
Массу m = 640 г расплавленного свинца при температуре плавления
вылили на лед (t = 00 C). Найти изменение энтропии при этом процессе.
Дано: m = 640 г; tл = 00 С; Т1 = 600К; с(Pb) = 126 кДж/кг.К; 22,6 кДж/кг
Найти : S
Решение
Изменение энтропии системы “свинец – лед” будет складываться из:
1) изменения энтропии свинца при затвердевании S1 ,
2) изменения энтропии свинца при охлаждении до t = 00 C S 2 ,
3) изменения энтропии льда при таянии S 3
S S1 S 2 S 3
dQ
m
S1 1
T1
T1
1
2
В соответствии с
законом сохранения
энергии
2
mc dT
T
S 2 c
mcc ln 2
T
T1
1
Q3 Q1 Q2 m cm T1 T2
dS 3
dQ3
Q
или S 3 3
T
T2
S 3
m cm T1 T2
T2
219.
Задача 3продолжение
Второе
Второеначало
начало термодинамики
термодинамики
Полное изменение энтропии системы “свинец – лед” будет:
T2 m cm T1 T2
m
S
mcc ln
T1
T1
T2
Вычисления
0,64 22,6 10 3
22,6 10 3 0,64 126 0,64 600 273
S
0,64 126 0,79
62,2 Дж / К
600
273
Ответ: S 62,2 Дж / К
220.
Задача 4Второе начало термодинамики
Определить изменение энтропии S при изотермическом расширении азота
массой m = 10 г, если давление газа уменьшилось от 0,1МПа до 50 кПа.
Дано: m = 10 г; p1= 0,1МПа; p2= 50 кПа; T – const.
Найти : S
Решение
Изменение энтропии, учитывая, что процесс изотермический
2
2
dQ 1
Q
S
dQ
T
T 1
T
1
Для изотермического процесса Q = A
1
A
m
RT ln
V2 m
p
RT ln 1
V1
p2
После подстановки 2 в 1 найдем искомое изменение энтропии
S
Вычисления:
S 2,06 Дж / К
m
RT ln
p1
p2
10 2
10 5
S
8,31 ln
2,06 Дж / К
3
4
28 10
5 10
2
221.
Второе начало термодинамикиКонтрольные вопросы
1 Какие Вы знаете формулировки второго начала
термодинамики?
2 Что такое статистический вес?
3. Может ли энтропия убывать в ходе
необратимого процесса?
4 Почему для определения энтропии понадобилось
вводить логарифм от термодинамической вероятности?
5.Как Вы поняли, что такое энтропия?
6. Привести примеры обратимых и
необратимых процессов.
7. Может ли энтропия некоторой системы самопроизвольно
уменьшаться в результате теплообмена с окружающими
телами?
222.
Лекция № 12ТЕПЛОВЫЕ МАШИНЫ
ЦИКЛ КАРНО
223.
План занятия1. Обратимые и необратимые процессы.
2. Круговые процессы. Прямые и обратные
3. Устройство тепловых машин
4. Цикл Карно.
5.Термический КПД цикла Карно
6. Холодильники
Обзор пройденного материала
224.
Тепловые машиныОбратимые и необратимые процессы
Термодинамический процесс, совершаемый системой,
называется обратимым, если после него можно
возвратить систему и все взаимодействующие с ней тела в
их начальное состояние таким образом, чтобы в других
телах не возникло каких – либо остаточных изменений.
Процесс называется необратимым, если он протекает
так, что после его окончания систему нельзя вернуть в
начальное состояние через прежние промежуточные
состояния. Нельзя осуществить необратимый круговой
процесс, чтобы нигде в окружающей среде не осталось
никаких изменений.
225.
Тепловые машиныКруговые процессы
Ряд термодинамических процессов, в результате которых
система возвращается в исходное состояние, называется
круговым процессом
p
p
1
a
,
b
0
V1
1
b
2
V2
Прямой цикл
V
0
V1
Работа совершаемая при
круговом процессе,
численно равна площади
охватываемой кривой.
a
2
V2
V
Обратный цикл
После завершения цикла система возвращается в исходное состояние.
Поэтому всякая функция состояния, в частности внутренняя энергия
имеет в начале и в конце одинаковое значение
226.
Тепловые машиныПрямые и обратные циклы
Прямое преобразование тепловой энергии в работу
запрещается постулатом Томсона (см. Второе
начало термодинамики). Поэтому для этой цели
используются термодинамические циклы.
p
1
a
b
0
V1
2
V2
Прямой цикл
V
Цикл, совершаемый идеальным газом, можно разбить на
процессы расширения (1 – 2) и сжатия (2 - 1)газа. Работа,
совершаемая за цикл, определяется площадью, охваченной
замкнутой кривой.
Если за цикл совершается положительная работа
(цикл протекает по часовой стрелке), то он
называется прямым
A pdV 0
C
227.
ТЕПЛОВЫЕ МАШИНЫПрямые и обратные циклы
p
1
b
0
Если за цикл совершается отрицательная работа
(цикл протекает против часовой стрелке), то
он называется обратным
a
V1
2
V2
Обратный цикл
V
A pdV 0
C
Круговые процессы лежат в основе всех тепловых
машин: двигателей внутреннего сгорания, паровых и
газовых турбин, паровых и холодильных машин и т. д.
228.
ТЕПЛОВЫЕ МАШИНЫЦиклические процессы
A Q dU Q TdS
Q U A
1 Начало т/д
C
Q
dS
T
2 Начало т/д
Q TdS
Циклический процесс
p
Т
T2
p2
AAA
Q
Q=A
p1
0
C
T1
V1
V2
V
При расширении газа от V1 до V2 газ
совершает некоторую работу, а при сжатии
расходуется меньшая работа
0
S1
S2
S
При увеличении энтропии от S1до S2 в газ вводится
некоторая тепловая энергия Q1>0, а приуменьшения
энтропии от газа отводится меньшее количество теплоты
229.
ТЕПЛОВЫЕ МАШИНЫТепловыми машинами называются устройства, преобразующие
тепловую энергию в механическую работу (тепловые двигатели)
или механическую работу в тепло (холодильники)
Первые практически действующие универсальные паровые
машины были созданы русским изобретателем И. Ползуновым
(1776) и английским изобретателем Дж. Уаттом (1784).
Недостаток – низкий КПД ~9%
Первая паровая турбина, получившая практическое применение, была
изготовлена шведским инженером Густавом Ловалем (1889)
пар
t > 5000C
1000 м / с
генератор
Первый двигатель внутреннего сгорания создал фр. Ленуар (1860)
4-х тактный двигатель предложил фр. Бо де Роша (1862);
построил Отто (1870)
230.
ТЕПЛОВЫЕ МАШИНЫУстройство тепловой машины
Элементы тепловой машины:
Нагреватель, Рабочее тело (газ) ,
холодильник
В основе тепловой машины лежат
два принципа
Принцип первый
Принцип второй
В машине должно присутствовать тепло и оно
должно превращаться в работу
Тепловая машина должна работать циклически
Рабочее тело, получая тепло от нагревателя, меняет свое состояние. Изменяется
объем рабочего тела dV,совершается работа. Объем – это функция состояния.
231.
ТЕПЛОВЫЕ МАШИНЫВ тепловых двигателях стремятся достигнуть наиболее полного превращения
тепловой энергии в механическую. Максимальное КПД.
На рисунке изображены циклы, используемые в бензиновом карбюраторном
двигателе и в дизельном двигателе. В обоих случаях рабочим телом является
смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного
двигателя внутреннего сгорания состоит из двух изохор (1–2, 3–4) и двух
адиабат (2–3, 4–1). Дизельный двигатель внутреннего сгорания работает по
циклу, состоящему из двух адиабат (1–2, 3–4), одной изобары (2–3) и одной
изохоры (4–1). Реальный коэффициент полезного действия у карбюраторного
двигателя порядка 30%, у дизельного двигателя – порядка 40 %.
232.
ТЕПЛОВЫЕ МАШИНЫЦикл Карно
Французский физик С.Карно разработал работу идеального
теплового двигателя.
p
1
Адиабаты
Q1>0
Изотерма
Изотермы
2
A
4
3
Q2<0
0
Рабочую часть двигателя Карно
можно представить себе в виде
поршня в заполненном газом
цилиндре. Механическая работа
максимальна, если рабочее тело
выполняет цикл, состоящий из
двух изотерм и двух адиабат. Этот
цикл называют циклом Карно.
V
Двигатель Карно — машина чисто теоретическая, то есть идеальная,
силы трения между поршнем и цилиндром и тепловые потери считаются
равными нулю.
233.
ТЕПЛОВЫЕ МАШИНЫЦикл Карно
p
1
Q1
Т1
2
0
V1
V2
V
Пусть газ, занимающий
объем V1 и имеющий
температуру Т1 (температура
нагревателя), приводится в
тепловой контакт с
нагревателем и получает
возможность изотермически
расширяться и совершать
работу. Газ получает при этом
от нагревателя некоторое
количество теплоты Q1. Этот
процесс представлен на
изотермой 1 2
4
234.
ТЕПЛОВЫЕ МАШИНЫЦикл Карно
p
1
Q1
Т1
2
Q=0
Т2
0
V1
V2
3
V3
V
Далее газ должен быть сжат, но при более
низкой температуре, то есть изотерма
сжатия должна быть ниже изотермы
расширения. Только в этом случае работа
расширения будет больше работы сжатия.
температура рабочего тела не должна
изменяться без совершения работы.
Значит, остается единственная
возможность – охлаждать газ, предоставив
ему возможность адиабатически
расширяться.
Поэтому изотермический процесс расширения не доводят до конца хода поршня в
цилиндре. Когда объем газа становится равным V2, дно цилиндра изолируют от
нагревателя; после этого газ адиабатно расширяется до объема V3, соответствующего
максимальному ходу поршня в цилиндре (кривая 23). При этом газ охлаждается до
температуры Т2.
235.
ТЕПЛОВЫЕ МАШИНЫЦикл Карно
p
1
Q1
Т1
2
4
Q=0
Т2
3
Q2
0
V1 V4
V2
V3
V
Теперь охлажденный газ можно
изотермически сжимать при
температуре Т2. Для этого его нужно
привести в контакт с телом, имеющим ту
же температуру Т2 (холодильник), и
сжимать газ внешней силой.
Изотермическое сжатие доводят до
некоторого промежуточного объема,
кривая 34). В процессе изотермического
сжатия газ отдает холодильнику некоторое
количество теплоты Q2, равное
совершаемой над ним работе сжатия.
236.
ТЕПЛОВЫЕ МАШИНЫЦикл Карно
p
1
Q1
T1
Q=0
2
A
Q=0
Т2
4
3
Q2
0
V1 V4
V2
V3
V
После этого газ подвергают адиабатическому
сжатию, в ходе которого его
Т температура
повышается до значения ТЕ1 (кривая41).
П
После завершения цикла газ
Л вернулся в
первоначальное состояниеО и цикл можно
В
повторить.
Ы
Е
Итак, на участке123 газ совершает
работу
М
(A > 0), а на участке341работа
совершается
А
над газом (A < 0). На участках
23 и 41 работа
Ш
И изменения
совершается только за счет
Н
внутренней энергии газа. Ы
Полная работа за
цикл определяется разностью работ на
участках 12 и 34. Численно эта работа равна
площади фигуры, ограниченной кривой
цикла
237.
ТЕПЛОВЫЕ МАШИНЫКоэффициент полезного действия тепловых машин
p
1
Q1
T1
Q=0
2
A
Q=0
Т2
4
3
Q2
0
V1 V4
V2
Q1 Q2
Q
V3
V
На участке 1-2 газ получает от
нагревателя количество теплоты Q1,
а на участке 3-4 он непременно
должен отдать холодильнику
теплоту Q2, следовательно, в
полезную работу преобразуется
только часть полученной газом
теплоты, равная Q1 – Q2, и к.п.д.
цикла равен:
Для любого кругового процесса: работа А, совершаемая за прямой
цикл, всегда меньше количества теплоты Q, подводимого к рабочему
телу всеми нагревателями
238.
ТЕПЛОВЫЕ МАШИНЫКоэффициент полезного действия тепловых машин
Величина, равная отношению работы А,
совершенной рабочим телом в прямом обратимом
цикле, к количеству теплоты Q, сообщенному в этом
процессе рабочему телу, называется термическим
коэффициентом полезного действия цикла
A
Q
КПД цикла Карно определяет теоретический предел возможных
значений к.п.д. тепловой машины для данного температурного
интервала.
В реальных тепловых двигателях нельзя создать
условия, при которых их рабочий цикл был бы циклом
Карно. Так как процессы в них происходят быстрее, чем
это необходимо для изотермического процесса, и в то же
время не настолько быстрые, чтоб быть адиабатическими
239.
ТЕПЛОВЫЕ МАШИНЫКПД цикла КАРНО
Теорема 1
Теорема 2
Теорема 3
Теорема 4
Теорема 5
КПД цикла Карно не зависит от выбора рабочего тела
КПД Цикла Карно зависит только от отношения
температур нагревателя и холодильника и не
зависит от деталей конструкции машины
TH TХ
TH
КПД цикла Карно всегда меньше единицы и приближается к
ней только при стремлении температуры холодильника к
абсолютному нулю.
КПД цикла Карно больше КПД любого другого равновесного цикла,
имеющего максимальную температуру нагревателя и минимальную
температуру холодильника, равную соответствующим температурам
цикла Карно.
Из теорем 2 и 4 можно утверждать: КПД любой тепловой
машины всегда меньше единицы.
240.
241.
ТЕПЛОВЫЕ МАШИНЫХолодильники
В обратном цикле Карно
количество теплоты Q1отводится
от газа в процессе 2-1
изотермического сжатия при
температуре Т1, а количество
теплоты Q2 подводится к газу в
процессе 4-3 изотермического
расширения при температуре Т2
<Т1 . Следовательно, Q1<0, Q2>0 и
работа, совершаемая за один цикл,
отрицательна: A=Q1+Q2 <0
p
1
Q1<0
T1
Q=0
2
A
Q=0
Т2
4
3
Q2>0
0
V1 V4
V2
V3
V
При обратном цикле осуществляется
передача теплоты от холодного тела к
горячему за счет совершения внешними
силами соответствующей работы
242.
ТЕПЛОВЫЕ МАШИНЫХолодильники
Величина, равная отношению теплоты Qотв, отведенной в
обратном цикле от охлажденного тела к работе A1 , затраченной в
этом цикле, называется холодильным коэффициентом.
Qотв
A1
T2
T1 T2
Не противоречит ли работа холодильника 2 началу термодинамики?
Холодильник и воздух в комнате не составляют замкнутую систему!
Холодильник необходимо подключить к электрической сети. Электрическая энергия с помощью
электрического двигателя превращается в механическую энергию, затем механическая энергия в
результате работы компрессора превращается в конечном счете в энергию теплового движения
молекул. Следовательно, переход тепла от холодного тела к горячему не является единственным
результатом работы холодильника, т. К. сопровождается превращением энергии электрического
тока в энергию теплового движения.
243.
ТЕПЛОВЫЕ МАШИНЫЗадача 1
Дано:
Газ совершает цикл Карно, при этом 75% теплоты, полученной от
нагревателя, передается холодильнику, определить температуру
нагревателя, если температура холодильника равна 00С
QX= 0,75QН;; t = 00C = 273K
Определить ТН
Решение
Q
T
1 X 1 X
QH
TH
Ответ:
TH 364 K
QH QX
QH
Q X TX
QH TH
QH QX TH TX
QH
TH
TH TХ
TH
QH
TH TX
QX
4
TH 273 364 K
3
244.
Второе начало термодинамикиКонтрольные вопросы
1 Какие Вы знаете формулировки второго начала
термодинамики?
2 Что такое статистический вес?
3. Может ли энтропия убывать в ходе
необратимого процесса?
4 Почему для определения энтропии понадобилось
вводить логарифм от термодинамической вероятности?
5.Как Вы поняли, что такое энтропия?
6. Привести примеры обратимых и
необратимых процессов.
7. Может ли энтропия некоторой системы самопроизвольно
уменьшаться в результате теплообмена с окружающими
телами?
245.
Лекция № 12КЛАССИЧЕСКИЕ СТАТИСТИКИ
246.
План занятия1. Статистический метод описания макросистем.
2. Некоторые сведения из теории вероятностей.
3. Функция распределения Максвелла.
4. Распределение молекул газа по
абсолютным и относительным скоростям.
5. Распределение молекул газа по
кинетическим энергиям.
6. Барометрическая формула.
7. Распределение Больцмана.
247.
КЛАССИЧЕСКИЕ СТАТИСТИКИДва метода описания свойств макросистем
Статистический метод
Термодинамический метод
Основан на использовании
теории вероятностей и
определенных моделей
строения изучаемых систем
(распределение Максвелла
распределение Больцмана)
Основан на анализе условий и
количественных соотношений при
различных превращениях энергии
происходящих в системе (первое,
второе и третье начала
термодинамики)
Статистическая физика
Термодинамика
248.
КЛАССИЧЕСКИЕ СТАТИСТИКИНекоторые сведения из теории вероятностей
Теория вероятностей – раздел математики, изучающий закономерности
случайных явлений: случайные события, случайные величины, их свойства и
операция над ними
1.Вероятность события
Ведем обозначения:
,
А – некоторое событие
Если событие А не фиксируется, это событие В
N – полное число экспериментов
N A - число экспериментов, в которых событие А произошло
N B - число экспериментов, в которых событие А не
произошло (произошло событие В)
249.
КЛАССИЧЕСКИЕ СТАТИСТИКИ1. Вероятность события
Если значение одной из величин не зависит от того, какое значение
имеет другая, то величины А и В называются статистически
независимыми
NA
вероятность
события
А
P A
P A limN
,
P B
N
- вероятность события В, т.е. вероятность того, что
событие А не происходит
NB
P B limN
N
P A P B 1
250.
КЛАССИЧЕСКИЕ СТАТИСТИКИНекоторые сведения из теории вероятностей
2. Закон умножения вероятностей
Если А и В
- два независимых случайных события,
которые происходят с вероятностями P A и P В , то
вероятность того, что они произойдут одновременно,
равна
P A B P A * P B
Значок
в формуле означает “и”
251.
КЛАССИЧЕСКИЕ СТАТИСТИКИНекоторые сведения из теории вероятностей
3.Закон сложения вероятностей
Если А и В – два независимых случайных события,
которые происходят с вероятностями P(A) и P(B),
то вероятность того, что произойдет какое то
одно из этих событий, равна
P A B P A P B
Значок
в формуле означает “или”
252.
КЛАССИЧЕСКИЕ СТАТИСТИКИНекоторые сведения из теории вероятностей
4. Функция распределения
Пусть X – случайная величина
x; (x+Δx) – некоторый интервал значений этой величины
Попадание значения X в этот интервал – событие случайное
ΔP – вероятность этого события зависит
от ширины интервала Δx
Δx → 0
ΔP → 0
253.
КЛАССИЧЕСКИЕ СТАТИСТИКИНекоторые сведения из теории вероятностей
4. Функция распределения
При малых Δx величина ΔP и Δx пропорциональны друг другу
P f x
Вероятность ΔP зависит от того, в каком месте оси ox
располагается интервал x; (x+Δx)
Коэффициент пропорциональности f есть функция от x
P f x x
254.
КЛАССИЧЕСКИЕ СТАТИСТИКИНекоторые сведения из теории вероятностей
4. Функция распределения
f(x) называется функцией распределения
f x
P
x
P f x x
Функция распределения есть величина, численно
равная вероятности того, что значение случайной
величины X попадет в единичный интервал,
расположенный в окрестности точки x.
Функция распределения еще называется плотностью
вероятности
255.
КЛАССИЧЕСКИЕ СТАТИСТИКИФункция распределения Максвелла
Распределение молекул газа по скоростям
Все микропараметры системы (координаты молекул, их
скорости) – величины случайные
Состояние газа - равновесное
f(υ)
N
N- число зрителей
t - возраст
Число молекул
0
Распределение зрителей по возрасту –
( функция распределения зрителей по
возрасту)
υ
t 0
Распределение молекул газа по скоростям
Распределение Максвелла
256.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла
3
2
m 2
m
f
exp
2 kT
2kT
Пространство скоростей
z
dυz
dυx
dυy
υ
0
x
4 2 d
Объем шарового слоя
y
dN N f 4 2 d
2 x 2 y 2 z
3
2
N
4 m
m 2 2
d
exp
N
2kT
2kT
Относительное число молекул , скорости
которых находятся в интервале от υ до υ +dυ
m – масса молекулы, υ – скорость молекулы,
k - постоянная Больцмана, Т – термодинамическая температура
257.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла по абсолютным скоростям
f
Т1
T1 < T2 < T3
T2
T3
0
υ1
υ2
υ3
υ
Наибольшей является вероятность попадания в интервал, расположенный в
окрестности того значения υ, для которого f(υ) достигает максимума
Этот интервал и соответствующая ему скорость называются
наиболее вероятными.
258.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла по абсолютным скоростям
f(υ)
0
υ
υв υкв
<υ>
df
d
Вычислим наиболее вероятную скорость υв ,
используя правило нахождения экстремума
функции
2kT
в
m
в
2 RT
в
0
259.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла по абсолютным скоростям
f(υ)
Вычислим среднюю арифметическую
скорость <υ> молекул, используя закон
усреднения из теории относительностей
f d
υв υкв
<υ>
Вспомним:
υ
При расчете длины свободного пробега
молекул газа используется средняя
арифметическая скорость <λ> =<υ>/z
8kT
m
8RT
k – постоянная Больцмана;
R – газовая постоянная;
Т – термодинамическая
температура
260.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла по абсолютным скоростям
f(υ)
Вычислим среднюю квадратичную
скорость υкв, используя выражение для
средней кинетической энергии
поступательного движения молекул.
υ
υв υкв
<υ>
кв : : в 3 :
8
: 2 1 : 1,13 : 1,22
m 2
3
kT
2
2
3kT
k в
m
k в
3RT
261.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла по абсолютным скоростям
Определить температуру газообразного азота, при которой скоростям
υ1 = 250 м/с и υ2 = 2 υ1 соответствую одинаковые значения функции
распределения Максвелла
Задача 1
Дано:
μ(N2) = 28ˑ10-3 кг/моль; υ1 = 250 м/с и υ2 = 2 υ1 f(υ1) = f(υ2).
Определить: υ
1) Необходимо на графике уяснить суть вопроса задачи (пунктирны линии
указывают на равенство функций распределения.
Решение
2) Записываем выражения для функций распределения и приравниваем их
f(υ)
3
2
m 12 2
4 m
1
f 1
exp
2
kT
2kT
3
2
0
υ1
υ2
υ
m 2 2 2
4 m
2
f 2
exp
2kT
2kT
262.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла по абсолютным скоростям
Задача 2
Определить скорость молекул газа, при которой значение функции
распределения Максвелла при температуре 250 К будет таким же, как
при температуре в 2 раза большей (при одинаковой скорости).
Молярная масса газа 2ˑ10-3 кг/моль.
Дано:
μ= 2ˑ10-3 кг/моль; Т1 = 250 К; Т2= 2 Т1 f1(υ) = f2(υ).
Определить: υ
Решение
1) Запишем функции распределения для Т1 и Т2
3
2
f(υ)
T1
m 2 2
4 m
exp
f1
2
kT
2kT1
1
T2
T2 = 2T1
0
υ
3
2
m 2 2
4 m
exp
f 2
2
kT
2
kT
2
2
υ
263.
КЛАССИЧЕСКИЕ СТАТИСТИКИЗадача 2
Распределение Максвелла по абсолютным скоростям
2) По условию задачи f1(υ) = f2(υ).
3) Преобразуем выражение:
4) После преобразований
m 2
2 exp
2k
3
2
T2
T1
1
1
T 2T
1
1
6) Заменим k/m = R/μ
Ответ: υ = 2,1ˑ103 м/с
3
2
3
2
1
m 1
m 2
exp
exp
T1
2kT1 T2
2kT2
m 2
exp
2
kT
2
m 2
exp
2kT1
5) Возьмем ln
от левой м
правой части
6 RT1 ln 2
3
2
2
2T1
T1
3
2
m 2
exp
4
kT
1
m 2
exp
2kT1
3
m 2
ln 2
2
4kT1
2
4kT1 3
ln 2
m 2
6 8,31 250 0,69
2.1 10 3 м / с
3
2 10
264.
КЛАССИЧЕСКИЕ СТАТИСТИКИЗадача 2
Распределение Максвелла по абсолютным скоростям
2) По условию задачи f1(υ) = f2(υ).
3) Преобразуем выражение:
4) После преобразований
m 2
2 exp
2k
3
2
T2
T1
1
1
T 2T
1
1
6) Заменим k/m = R/μ
Ответ: υ = 2,1ˑ103 м/с
3
2
3
2
1
m 1
m 2
exp
exp
T1
2kT1 T2
2kT2
m 2
exp
2
kT
2
m 2
exp
2kT1
5) Возьмем ln
от левой м
правой части
6 RT1 ln 2
3
2
2
2T1
T1
3
2
m 2
exp
4
kT
1
m 2
exp
2kT1
3
m 2
ln 2
2
4kT1
2
4kT1 3
ln 2
m 2
6 8,31 250 0,69
2.1 10 3 м / с
3
2 10
265.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла по относительным
скоростям
Для упрощения расчетов вместо
абсолютной скорости вводится
понятие “относительная
скорость” путем нормировки
абсолютной скорости на наиболее
вероятную U = υ /υв
f(U)
U
0
4
f U
exp U 2 U 2
U
в
2kT / m
U
в
2kT / m
Функция распределения Максвелла по относительным скоростям
266.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение молекул газа по
относительным скоростям
Для подсчета числа молекул, относительные скорости которых
заключены в пределах от U до U + dU необходимо функцию
распределения f(u) умножить на число молекул N и на интервал ΔU
N N f u u
Интерес представляет не само число молекул, а относительное число
молекул, скорости которых заключены в интервале от u до u + Δu
N
4
exp u 2 u 2 u
N
267.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла по относительным скоростям
Какая часть молекул газа при температуре 250 К обладает
Задача 3
Дано:
скоростями в интервале от υ до (υ – 10) м/с, υ = 100 м/с?
Молярная масса газа 18 кг/кˑмоль. Ответ дать в %.
Т = 250 К; υ = 100 м/с; Δυ = 10 м/с; μ = 18ˑ10-3 кг/моль
Найти: ΔN/N
Решение 1) Запишем функцию распределения Максвелла
по относительным скоростям
2) Относительная скорость u = υ
/ υв;
Δu = Δυ / υв
3) Рассчитаем наиболее вероятную скорость υв
в
2 RT
N
4
exp u 2 u 2 u
N
268.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла по относительным скоростям
Какая часть молекул газа при температуре 250 К обладает
Задача 3
Дано:
скоростями в интервале от υ до (υ – 10) м/с, υ = 100 м/с?
Молярная масса газа 18 кг/кˑмоль. Ответ дать в %.
Т = 250 К; υ = 100 м/с; Δυ = 10 м/с; μ = 18ˑ10-3 кг/моль
Найти: ΔN/N
Решение 1) Запишем функцию распределения Максвелла
по относительным скоростям
2) Относительная скорость u = υ
/ υв;
Δu = Δυ / υв
3) Рассчитаем наиболее вероятную скорость υв
в
2 RT
N
4
exp u 2 u 2 u
N
269.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла по относительным скоростям
Задача3
4) Наиболее вероятная скорость
5) Относительная скорость
6) Найдем Δu
u
u
в
2 8,31 250
480 ,5 м / с
3
18 10
100
0 ,208
480 ,5
u 2 0,0436
10
2,08 10 2
480 ,5
7) Подставим числовые данные в формулу для нахождения ΔN/N
N
4
exp 0,0436 0,0436 2,08 10 2 1,96 10 3 0,2%
N 1,77
Ответ: ΔN/N = 0,2%
270.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла по относительным скоростям
Задача 4
Дано:
Найти относительное число молекул газа, скорости которых
отличаются не более чем на 0,1% от средней арифметической
скорости.
υ = <υ>; Δυ = ± 0,001 <υ>
N
N
Найти: ΔN/N
Решение
1) Обратимся к графику
2) По условию задачи интервал должен
быть не более 0,1% от <υ>. Это означает,
что он может быть как в меньшую сторону,
так и в большую, т.е. Δυ = 2ˑ0,001 <υ>.
υв υкв
<υ>±Δυ
υ
271.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла по относительным скоростям
Задача 4
3) Распределение Максвелла для нахождения относительного числа молекул со
скоростями в интервале от υ до υ +Δυ N
4
2
2
4) Найдем
u
в
u,u2,
N
Δu
8 RT
2
2 RT
u2
4
u
exp u u u
0,002 2 0,002
в
5) После подстановки числовых данных получим:
Ответ:
N
1,81 10 3
N
N
4
2
4 4
exp 0,004
1,81 10 3
N
272.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение молекул газа по энергиям
3
2
N
4 m
m 2 2
d
exp
N
2kT
2kT
Относительное число молекул
по абсолютным скоростям
Используя связь кинетической энергии со скоростью, можно
получить распределение молекул газа по энергиям
m 2
Ek
2
2
2E
m
1 / 2mE E
N
2
kT 3 / 2 exp E / kT E E
N
Относительное число молекул, кинетическая энергия поступательного
движения которых заключена в пределах от E до E+ΔE
273.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла по энергиям
Задача 5
Используя распределение Максвелла, определить относительное число
одноатомных молекул газа, имеющих кинетическую энергию,
отличающуюся от среднего значения на 0,1%. Газ находится в тепловом
равновесии. Ответ дать в %.
Дано: i = 3; E = <E> ΔE = ± 0,1%
Найти: ΔN/N
Решение
N
N
1) Обратимся к графику
2) По условию задачи интервал
должен быть не более 0,1% от <Е>.
Это означает, что он может быть
как в меньшую сторону, так и в
большую, т.е. ΔE = 2ˑ0,001 <E>.
0
E
<E>±ΔE
274.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла по энергиям
Задача 5
3) Распределение Максвелла по кинетическим энергиям имеет вид:
2
kT 3 / 2 exp E / kT E E
f E
4) Средняя кинетическая энергия молекул газа
5) С учетом сказанного
i
E 0,1% E 2 0.001 kT
2
3
N
2
kT 2 exp i i kT 0.002 i kT
N
2
2 2
6) После подстановки в формулу
7) После сокращений kT (i= 3) N
N
Ответ: N 0,092%
N
i
E kT
2
2
3
3 3
exp
0.002 9 ,2 10 4 0 ,092 %
2
2 2
275.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Максвелла по энергиям
Задача 6
С помощью распределения Максвелла по скоростям получить
распределение по кинетическим энергиям и определить наиболее
вероятное значение кинетической энергии при температуре 250 К.
Дано: Т = 250 К
Найти: Ев
f E A exp e / kT E
1) Запишем распределение Максвелла по кинетическим энергиям
Решение
2
kT 3 / 2 exp E / kT E
2) Для нахождения наиболее вероятной кинетической энергии используем правило
нахождения экстремума функции – равенство нулю производной функции df E 0
3) Представим функцию в виде:
f E
f E A exp E / kT E
А – константа, не зависящая от υ
dE
276.
КЛАССИЧЕСКИЕ СТАТИСТИКИЗадача 6
Распределение Максвелла по энергиям
4) Найдем производную от этой функции
e
E
kT
E 0
e
E
kT
u V u V uV
E
1
1
kT
E
e
0
kT
2 E
5) После преобразования имеем
1,38 10 23250
Eв
1,725 10 21 Дж
2
Ответ:
Вспомним:
Eв 1,725 10 21 Дж
E 1
2 E 0
kT
E
kT
2
277.
КЛАССИЧЕСКИЕ СТАТИСТИКИp f h
Барометрическая формула
p dp
dh
p
h
S
F
p
S
mg Vg
p
S
S
dp gdh
Ρ –плотность воздуха
на высоте h
При нормальных условиях воздух довольно хорошо
подчиняется уравнению состояния идеального газа
p
RT
pg
dp
dh
RT
p gh
dp
g
dh
p
RT
m
pV RT
278.
КЛАССИЧЕСКИЕ СТАТИСТИКИБарометрическая формула
dp
g
dh
p
RT
p
Предполагая, что
температура с высотой не
изменяется, имеем:
p
gh
ln
p0
RT
p p0 e
p0
2
gh
RT
p p0e
mgh
kT
m
R k
Молекулы газа находятся под действием
двух факторов: силы тяжести mg и
энергии теплового движения кТ
1
0
dp
g
p RT dh
h
279.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Больцмана
p p0e
mgh
kT
p nkT
Уравнение состояния
идеального газа
m
pV RT
n
n0
1
0
2
При абсолютном нуле все
молекулы окажутся на земле
n n0 e
mgh
kT
h Распределение
Максвелла –
распределение по
кинетическим
энергиям
m
R k
n n0 e
Распределение
Больцмана –
распределение по
потенциальным
энергиям
gh
RT
280.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Больцмана
Задача 7
Какова концентрация молекул воздуха на высоте 1,1 км , если
атмосферное давление на уровне моря 740 мм рт. ст.? Температуру
воздуха на высоте считать постоянной и равной – 200 С.
Дано: h = 1,1км; p0 = 740 мм рт. ст.= ; Т = - 200С = 253К; μ =29ˑ10-3 кг/моль
Найти: n
Решение
n
n0
1) Распределение Больцмана:
gh
n n0 exp
RT
n n0 e
gh
RT
2) Концентрация молекул на уровне моря n0 - не задана. Ее
можно выразить через известное давление на уровне моря p0,
используя уравнение состояния идеального газа
p nkT
0
h
p0
n0
kT
281.
КЛАССИЧЕСКИЕ СТАТИСТИКИln exp A A
ln e A A
Задача 7
Распределение Больцмана
3) Уравнение Больцмана принимает вид:
p0
gh
n
exp
kT
RT
4) Подставим числовые данные
740 133
29 10 39,8 1,1 10 3
25
n
exp
2
,
4
10
1,38 10 23
8,31 250
2,4 102525
Ответ: nn = 2.4ˑ10
282.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Больцмана
Задача 8
Определить массу одной из пылинок, взвешенных в воздухе,
если в толщине воздуха Δh = 1 см их концентрация различается
на 20% при температуре t = 100C.
Дано: μ = 29ˑ10-3 кг/моль; Δh = 1 см =10-2м; Т = 283К. (n1- n2)=20%
Определить: m
Решение
Δh
1) Для каждой высоты запишем
уравнение Больцмана
mgh2
n2 n0 exp
kT
n2
n1
h1
n0
mgh1
n1 n0 exp
kT
h2
Ход решения: разделить первое уравнение на второе
и взять натуральный логарифм от обеих частей
283.
КЛАССИЧЕСКИЕ СТАТИСТИКИРаспределение Больцмана
Задача 8
2) Результат деления:
n2
mg
h2 h1
exp
n1
kT
3) По условию задачи (n1- n2)=20%. Чему равно n2 /n1 ? Из рисунка: n2 /n1 = 0,8
4) После логарифмирования имеем:
5) Откуда получаем выражение
для расчета массы пылинок
Δh
n2= 80%
n1=100%
n0
h1 h2
ln
n2
mg
h2 h1
n1
kT
m ln
ln exp A A
ln e A A
n2 kT
n1 g h
1,38 10 23283
21
m 0,223
8
,
89
10
кг
2
9,8 10
m 8,89 10 21 кг
284.
Лекция № 13ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
285.
План занятия1. Электрический заряд. Закон Кулона
2. Напряженность электрического поля.
Принцип суперпозиции. Распределенные заряды.
3. Поток вектора напряженности.
Теорема Гаусса
4. Применение теоремы Гаусса к расчету
некоторых электрических полей.
5 Решение задач
286.
Известно четыре видафундаментальных взаимодействий:
• гравитационное;
• слабое
•электромагнитное.
• сильное
287.
Электрический зарядЭлектрический заряд –
физическая величина,
характеризующая способность
тел или их составных частей
вступать в электромагнитные
взаимодействия.
288.
ЭЛЕКТРИЧЕСКИЙ ЗАРЯДАтом
Ядро
Электроны
Нуклоны
Протоны
qp = +1,6∙10-19 Кл
Электромагнитное
поле
Нейтроны
qn = 0
Наименьший электрический заряд, встречающийся в природе, называется
элементарным зарядом и обозначается e. e = 1,6∙10-19 Кл
289.
ЭЛЕКТРИЧЕСКИЙ ЗАРЯДВ природе существует только два вида электрических зарядов –
положительные (протоны) и отрицательные (электроны)
ОСНОВНЫЕ СВОЙСТВА ЗАРЯДА:
• Закон сохранения электрического заряда
Q
i
const
i
Суммарный заряд электрически изолированной системы не может
изменяться при любых процессах, происходящих внутри этой системы
• электрический заряд квантуется.
Всякий заряд q есть величина, кратная e:
q Ne
• электрический заряд инвариантен по отношению к различным системам
отсчета. Во всех системах отсчета заряд тела или частицы имеет одно и то
же значение;
• электрический заряд – величина аддитивная. Заряд любой системы
равен сумме зарядов составляющих эту систему тел (частиц).
290.
электростатикаЗакон Кулона
Кулона
Закон
Взаимодействие зарядов подчиняется третьему закону
Ньютона: Силы взаимодействия между зарядами равны
по величине и направлены противоположно друг другу
вдоль прямой, связывающей эти заряды
F1
F2
+q1
r
+q2
F1 F2
,
+q
+q1
-q
-q2
291.
.Задача 2
Закон Кулона
+q1
В вершинах квадрата со стороной а = 0,1 м находятся
положительные одинаковые заряды q по 4ˑ10-9 Кл. Какой
отрицательный заряд qx нужно поместить в центр квадрата для
того, чтобы вся система зарядов находилась в равновесии?
+q2
-qx
F13
Дано: а = 0,1 м; q1 = q2 = q3 = q4 = + 4ˑ10-9 Кл.
Найти: qx .
+q3
+q4
F14
+q1
F12
1) Каждый из зарядов в вершинах квадратов находится в
эквивалентных условиях, поэтому достаточно рассмотреть
равновесие лишь одного (любого) заряда.
-qx
+q4
2) На любой из 4-х зарядов (например, на q1) со стороны других
трех зарядов действуют силы отталкивания, равнодействующая
которых направлена по диагонали квадрата в сторону от центра.
3) Между зарядами q1 и q2 действует отталкивающая сила
q2
F12 k 2 .
a
4) Между зарядами q1 и q4 действует такая же по величине сила
5) Векторное сложение этих сил по модулю дает:
q2
F1 2k 2
a
+q2
q2
F14 k 2
a
+q3
292.
Закон КулонаЗадача 2
.
6) В этом же направлении на заряд q1 со стороны
заряда q3 действует отталкивающая сила
F13 k
q2
a 2
F13
2
F12
F14
+q1
7) Результирующая сила, действующая на заряд q1 со стороны
зарядов равна:
q2
q2
F 2k 2 0,5k 2
a
a
q2
2 0,5 k 2
a
+q2
-qx
+q4
+q3
8) Для того, чтобы все заряды находились в равновесии необходимо приравнять
эту силу силе взаимодействия помещаемого в центр заряда q x с зарядом q
k
qx q
2
a
2
2
qx 3,84 10 Кл
9
q2
2 0 ,5 k 2
a
Откуда
qx
qx 0,96 4 10 9 3,84 10 9 Кл
2 0 ,5
q 0 ,96 q
2
293.
Задача 3Закон Кулона
На тонком кольце радиусом 58 см равномерно распределен заряд 54 нКл.
Определить силу, действующую на точечный заряд 66 нКл, находящийся
на осевой линии на расстоянии 23 см от центра кольца.
Дано: R = 0,58 см; Q = 54 нКл; q = 66 нКл; а = 0,23 см.
Найти: F.
Решение
dl
R
Q
1) Закон Кулона справедлив только для точечных
зарядов, поэтому необходимо заряд кольца представить
как множество точечных зарядов.
r dF
q
а
dF
dF
d
F
dF
dl
2) На элементарном участке кольца
заряда равна
dl величина
Q
dQ
dl
2 R
x
3) сила его взаимодействия с точечным зарядом :
dF k
dQq
Qq dl
k
r2
2 Rr 2
r 2 R2 a2
294.
Задача 3Закон Кулона
4) Вектор dF можно разложить на две составляющих
dF 0
dl
R
Q
r dF
q
а
F
dF
dF
d
F
dF
dl
2 R
a
a
cos
r
R2 a2
dF
2 R
F
k 2 Rr
0
Qqa
2
R a
2
dl k
Qqa
F k 2
R a2
F 9 10
Ответ: F = 30 мН
9
54 10 9 66 10 9 0,23
0,58
2
dF
dF dF cos
0
x
dF и
0,232
3/ 2
Qqa
2 R R a
2
2 R
dl ,
2 3/ 2
3 10 5 Н 30 мН
0
295.
НапряженностьНапряженность электрического
поля
поля
F
E
q0
Напряженность поля –
силовая характеристика
F qE
1 q
E
2
4 0 r
q
E k 2
r
E
Силовые линии
напряженности поля
+q
F
E
E
E
E
+q
E
-q
Распределенные заряды
dq
dS
Кл/м2
Поверхностная плотность
заряда
dq
dl
Кл/м
Линейная плотность
заряда
dq
dV
Кл/м3
Объемная плотность
заряда
296.
Напряженность электрическогополя
Задача 4
В электрическом поле Земли с напряженностью 490 В/м в равновесии
находится заряженная частица массой 5 миллиграмм . Определить. заряд
частицы. Ответ выразить в нанокулонах.
Дано: Е = 490 В/м; m = 5·10-6 кг.
Найти: q (нКл).
,
Решение
.
1) На заряд действуют две силы: сила тяжести и сила
F
e
E
действия электрического поля :
FТ mg
q
mg
2) Поскольку частица находится в равновесии
mg qE
5 10 6 9,8
q
10 7 Кл 100нКл
490
Ответ: q = 100 нКл.
Fe qE
q
mg
E
Ответить на вопрос:
Какой знак заряда должна иметь частица,
чтобы находиться в состоянии равновесия?
297.
E Ei.
Принцип суперпозиции
Напряженность поля, созданного системой неподвижных
зарядов, равна векторной сумме напряженностей полей,
создаваемых каждым зарядом в отдельности:
В вершинах равностороннего треугольника со стороной а = 0,1 м
находятся заряды q1=q2=+20 нКл и q3= - 20 нКл. Найти
напряженность электрического поля в центре треугольника.
Задача 5
Дано: а = 0,1 м; q1 q2 20 нКл q3= - 20 нКл
Найти:
E( 0 )
Решение
B q
3
EC
EB
E EC E A EB
EA
A
q1
0
a
1) Напряженность электрического поля в центре
треугольника (в т.0) равна векторной сумме
напряженностей, создаваемых каждым зарядом
C
q2
2) В равностороннем треугольнике высоты равны, а
расстояния от каждого заряда до т. 0
OA OB OC
a
3
298.
Задача 6Напряженность электрического
поля
Две плоские пластины площадью 60 см2, заряженные
равными по величине зарядами притягиваются с силой 6
Н, находясь в вакууме. Расстояние между пластинами
много меньше их линейных размеров. Определить
находящиеся на них заряды.
Дано: S 60см 2 ; F 6H
Найти: q
Решение.
q
q
S
q1 q2 q
1) Имеем заряженную пластину, создающую вокруг себя
электрическое поле . В этом поле находится другая пластина
с зарядом q, которая испытывает силовое действие поля.
2) Сила, с которой поле Е действует на заряд q, равна F qE
3) По условию задачи расстояние между пластинами много
меньше размеров пластин, что позволяет рассматривать
пластины, как бесконечные плоскости
299.
Задача 6Напряженность электрического
поля
4) Напряженность электрического поля бесконечной заряженной
плоскости в вакууме находится по формуле
q / S поверхностная плотность заряда
E
5) С учетом этого напряженность поля будет: E
6) Выражение для силы
q
q2
F q
2 0 S 2 0 S
7) Подстановка числовых данных
Ответ: q = 8 мкКл
2 0
q
2 0 S
q 2 0 SF
q 2 8,85 10 1260 10 4 6 8 10 6 Кл
q
q
S
300.
Теорема Гаусса для вектора напряженности EEЭлементарный поток вектора E
Элементарным потоком вектора
E
напряженности электрического поля сквозь
n
dS
малый участок поверхности, проведенный в
поле, называется величина
dФ E dS E dS cos
q
Поток напряженности Ф сквозь любую поверхность
S равен алгебраической сумме потоков
напряженности сквозь все малые участки этой
поверхности:
Ф E n dS EdS
S
S
dS dS n
301.
Теорема Гаусса для вектора напряженности Е1) Замкнутая поверхность охватывает заряд q , т.е. он
находится внутри области, ограниченной замкнутой
поверхностью S;
Поток напряженности dФi сквозь малый элемент dS равен:
dФi Ei dS i
Sсф
S
сф
S
SS
E
q
dS
d
ri
rсф
S сф 4 r
0
2
qi
4 0 ri
dS dS сф
qi
E dS
S
1
2
dS i
dФi
сф
qi
dS СФ i
4 0
ri
2
n
Ф EdS
S
q
i 1
0
i
302.
Теорема ГауссаПоток вектора напряженности электростатического поля в
вакууме сквозь произвольную замкнутую поверхность равен
отношению алгебраической суммы электрических зарядов,
охватываемых этой поверхностью, к электрической
постоянной ε0.
2) Замкнутая поверхность не охватывает заряд
E
q
n
q> 0
S1
S2
n
E
Ф EdS 0
S
Поток вектора напряженности
электростатического поля в вакууме
сквозь произвольную замкнутую
поверхность, не охватывающую
электрические заряды, равен нулю.
303.
Вычисление полей с помощью теоремы ГауссаМетод расчета электростатических полей, основанный на
использовании принципа суперпозиции полей, применим к расчету
поля любой системы зарядов. Это универсальный метод расчета.
Однако, как правило, он связан с трудоемкими математическими
операциями суммирования или интегрирования
Более простым оказывается метод, основанный на использовании
теоремы Остроградского – Гаусса. Этот метод особенно удобен
для расчета электростатических полей симметричных систем
зарядов.
Поле бесконечной однородно заряженной плоскости
Ф 2E S
S
E
+σ
E
+σ
E
E
Внутри поверхности S заключен заряд
2 E S
S
0
E
2 0
q S
304.
Вычисление полей с помощью теоремы ГауссаПоле двух равномерно заряженных плоскостей
+σ
-σ
E / 2 0
E / 2 0
E
0
Поле двух параллельных бесконечных
плоскостей, заряженных
разноименно, можно найти, как
суперпозицию полей, создаваемых
каждой из плоскостей в отдельности.
В области между плоскостями
складываемые поля имеют одинаковое
направление и равны по величине
(однородное поле). Вне объема,
ограниченного плоскостями, поле
равно нулю.
305.
Вычисление полей с помощью теоремы ГауссаПоле бесконечно заряженного цилиндра
E
Бесконечно длинный пустотелый цилиндр
dq
заряжен с линейной плотностью заряда
dl
Радиус цилиндра R.
l
EdS E r 2 r l
r
S
E
R
E
S
По теореме Гаусса
E
E
E
2 0 r
Е =0
0
R
r
E 2 r l
Внутри заряженного
цилиндра зарядов
нет (заряды
располагаются на
поверхности),
следовательно. поле
Е равно нулю,
q
0
q l
E
2 0 r
306.
Вычисление полей с помощью теоремы ГауссаE
Поле заряженной пустотелой сферы
q
4 R 2
r
R
E
E
0
R
1
r2
E
r
E r 4 r 2
q
0
q
4 0 r 2
Внутри пустотелой сферы зарядов
нет, поэтому при r < R
Е = 0.
Получим формулу для расчета напряженности
поля, создаваемого заряженной сферой с
поверхностной плотностью заряда σ. В формуле
выразим заряд через поверхностную плотность σ:
q 4 R 2
R2
E
0r 2
307.
Вычисление полей с помощью теоремы ГауссаПоле объемно заряженного шара
r
Для нахождения зависимости внутри
сферы выберем замкнутую поверхность
в виде сферы радиуса r<R. Теорема
Гаусса для этого случая:
R
E
E
1
r2
V
E r 4 r
0
2
0
r
R
4 r 3
E r 4 r
3 0
2
q
q 3
V 4 R 3
E r
Объем шара
4
V r 3
3
r
3 0
q r
E r
4 0 R 3
308.
309.
310.
311.
E Ei.
Принцип суперпозиции
Напряженность поля, созданного системой неподвижных
зарядов, равна векторной сумме напряженностей полей,
создаваемых каждым зарядом в отдельности:
В вершинах равностороннего треугольника со стороной а = 0,1 м
находятся заряды q1=q2=+20 нКл и q3= - 20 нКл. Найти
напряженность электрического поля в центре треугольника.
Задача 5
Дано: а = 0,1 м; q1 q2 20 нКл q3= - 20 нКл
Найти:
E( 0 )
Решение
B q
3
EC
EB
E EC E A EB
EA
A
q1
0
a
1) Напряженность электрического поля в центре
треугольника (в т.0) равна векторной сумме
напряженностей, создаваемых каждым зарядом
C
q2
2) В равностороннем треугольнике высоты равны, а
расстояния от каждого заряда до т. 0
OA OB OC
a
3






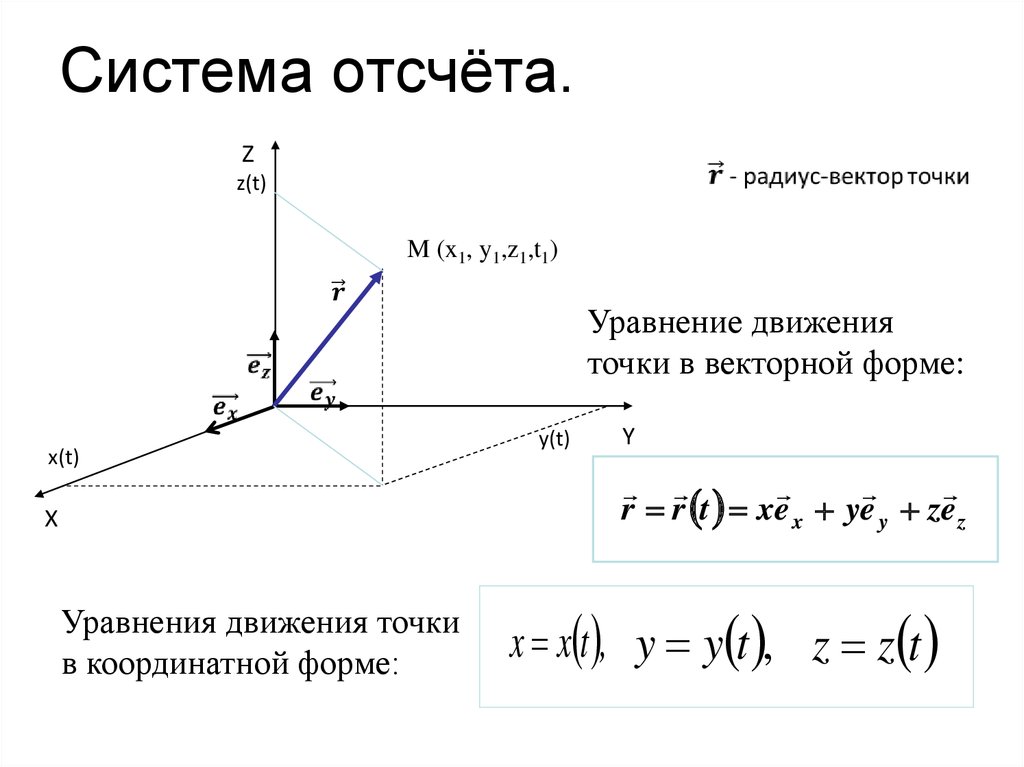
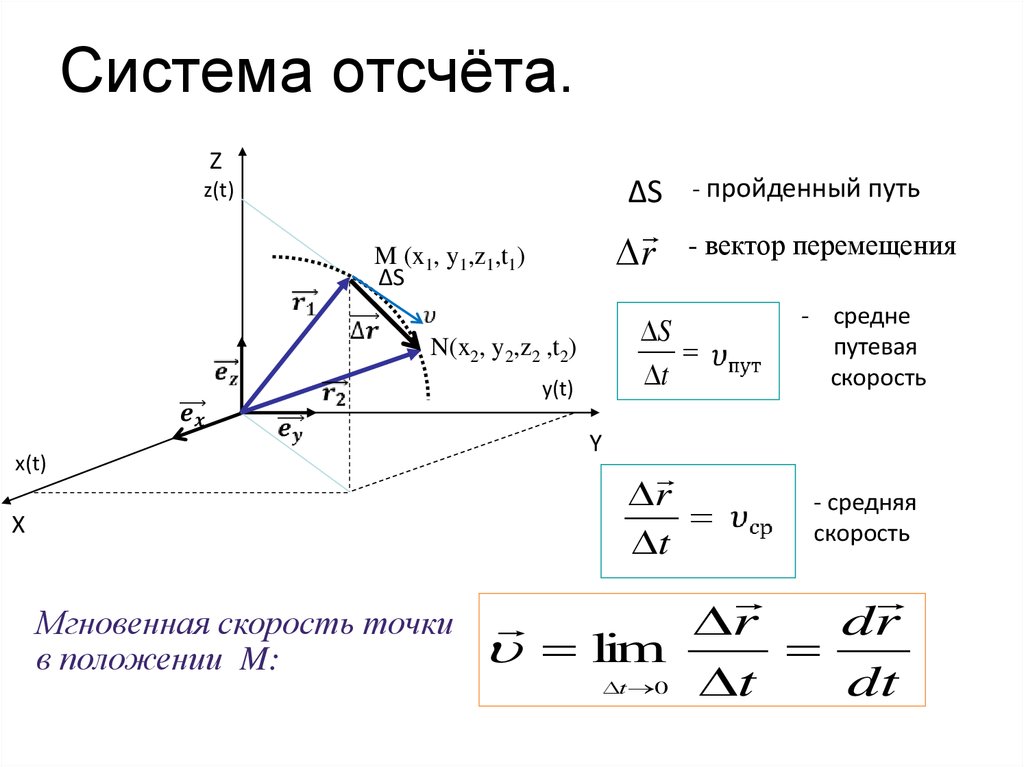
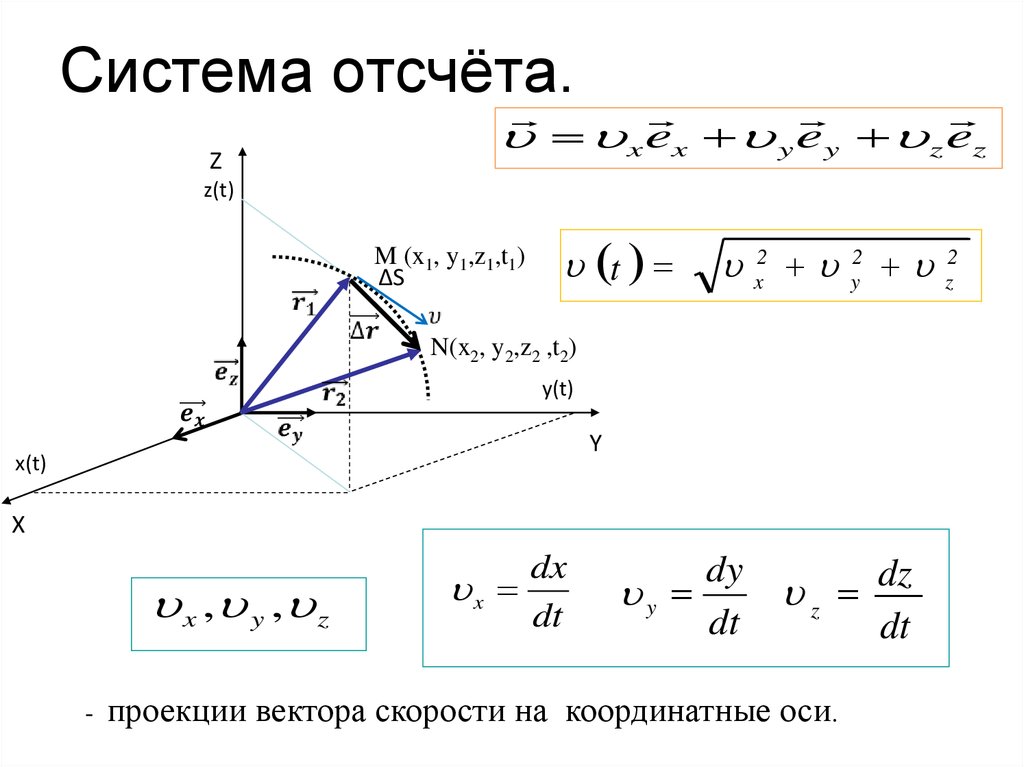
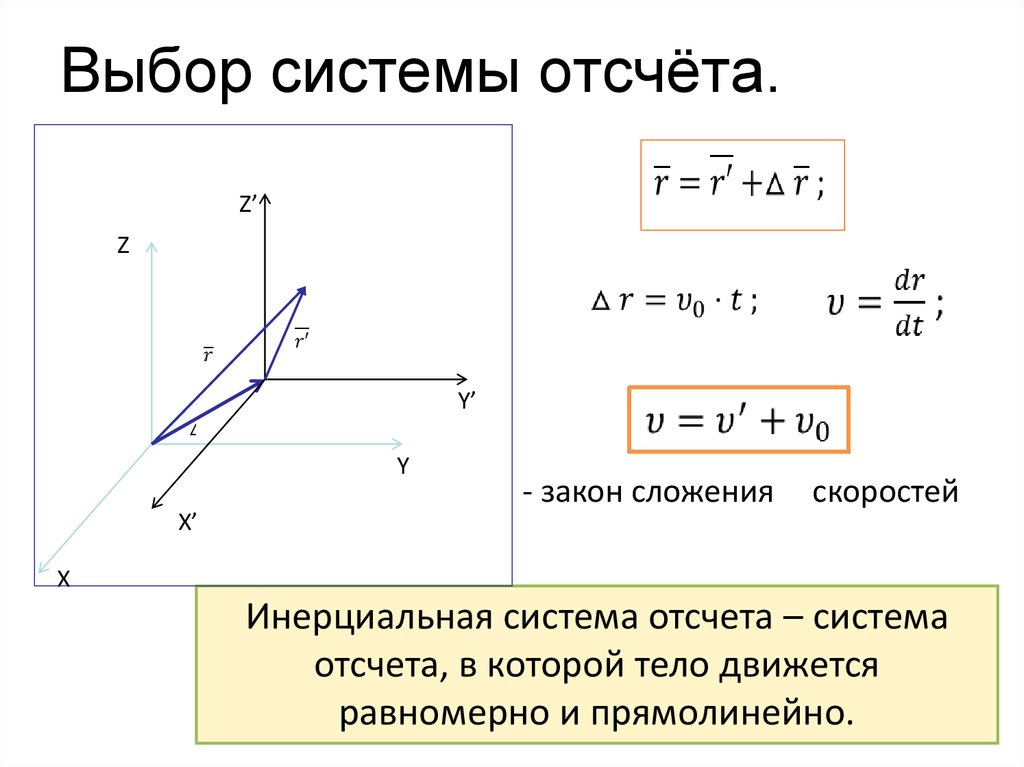

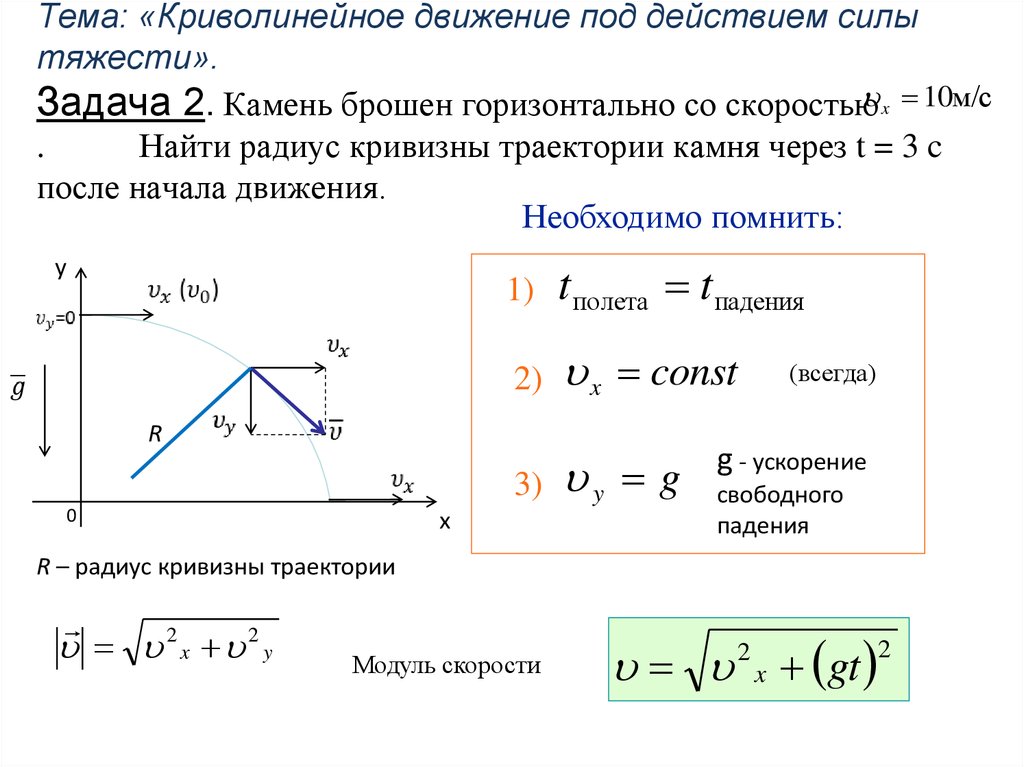
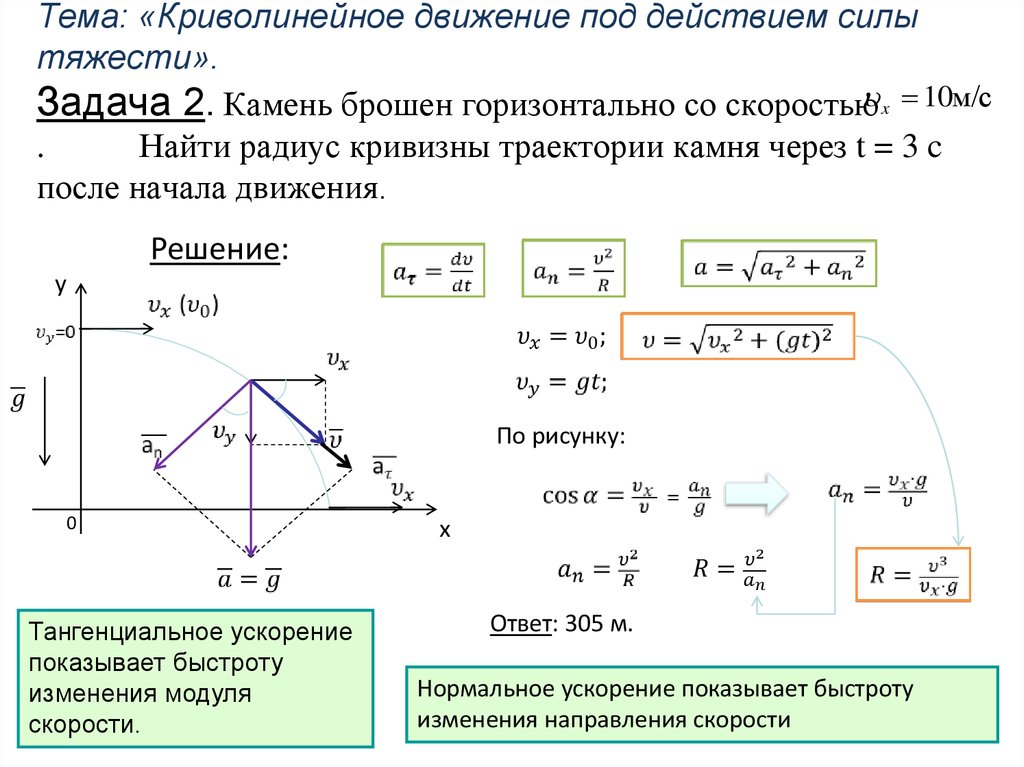


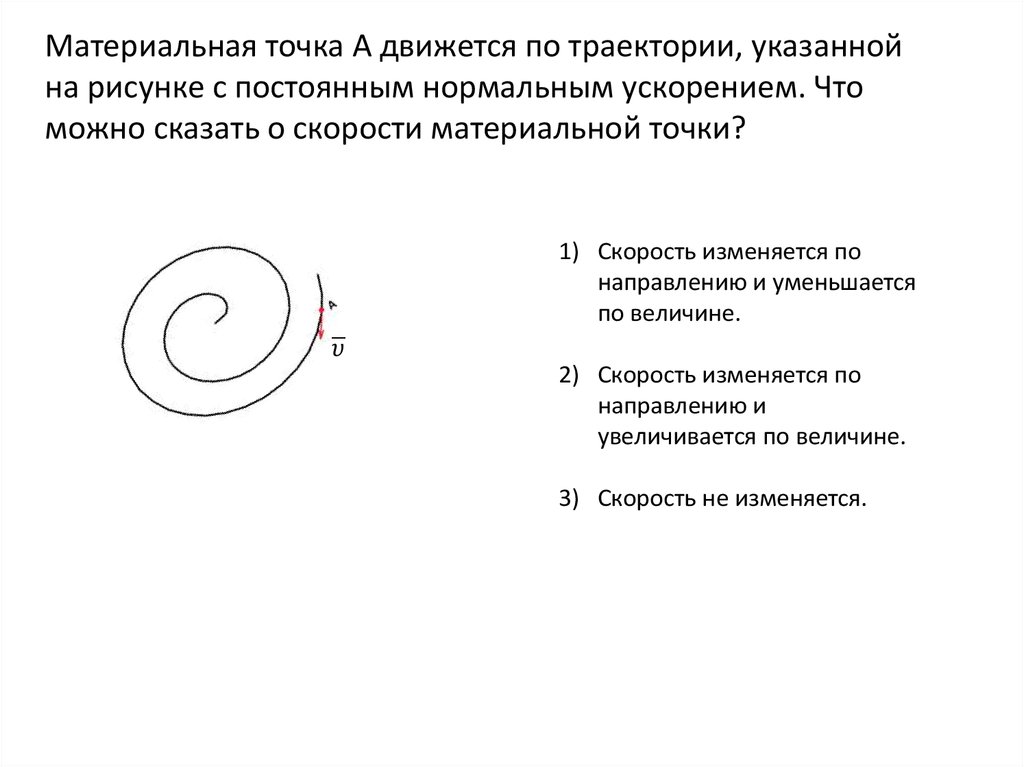
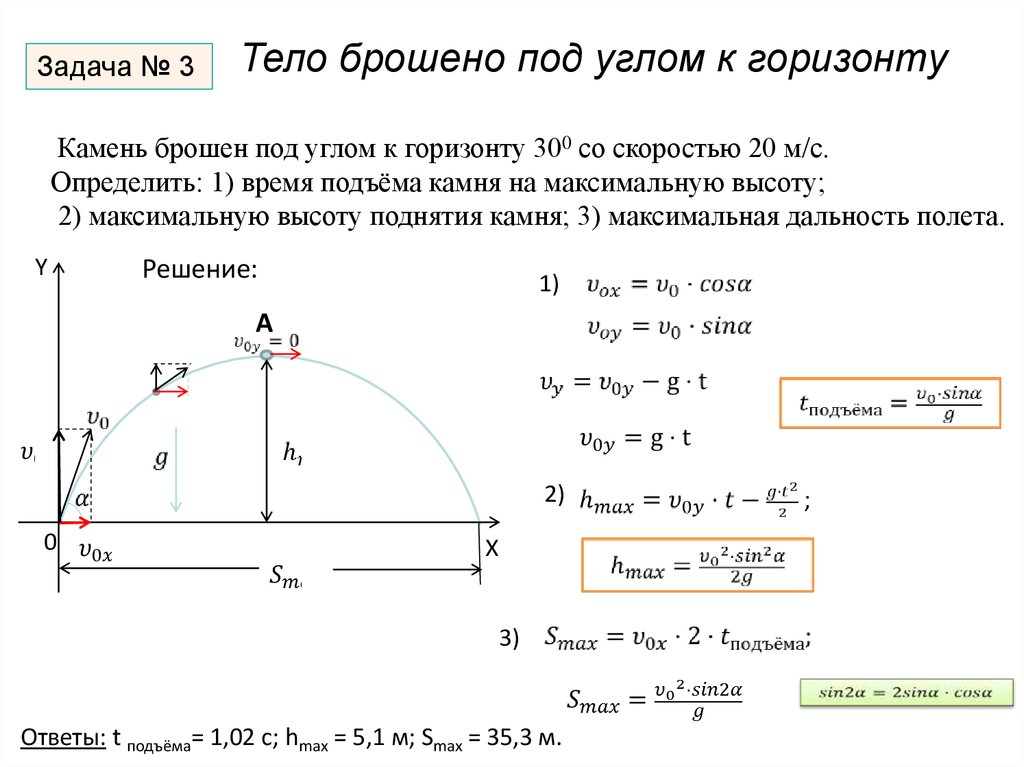
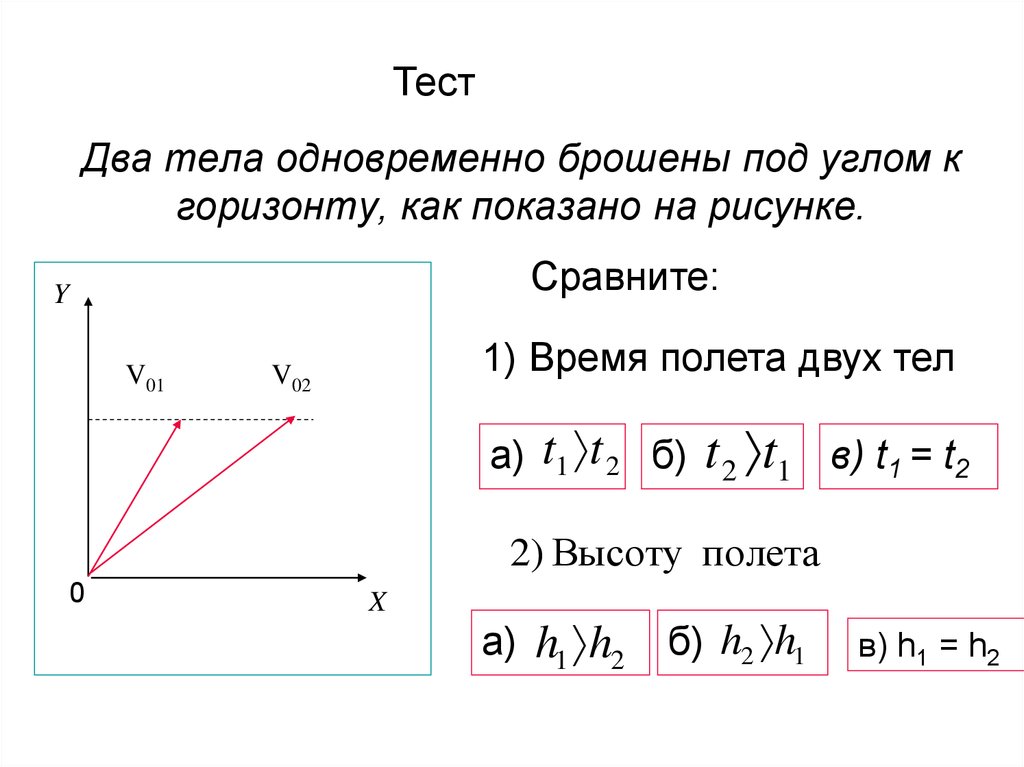


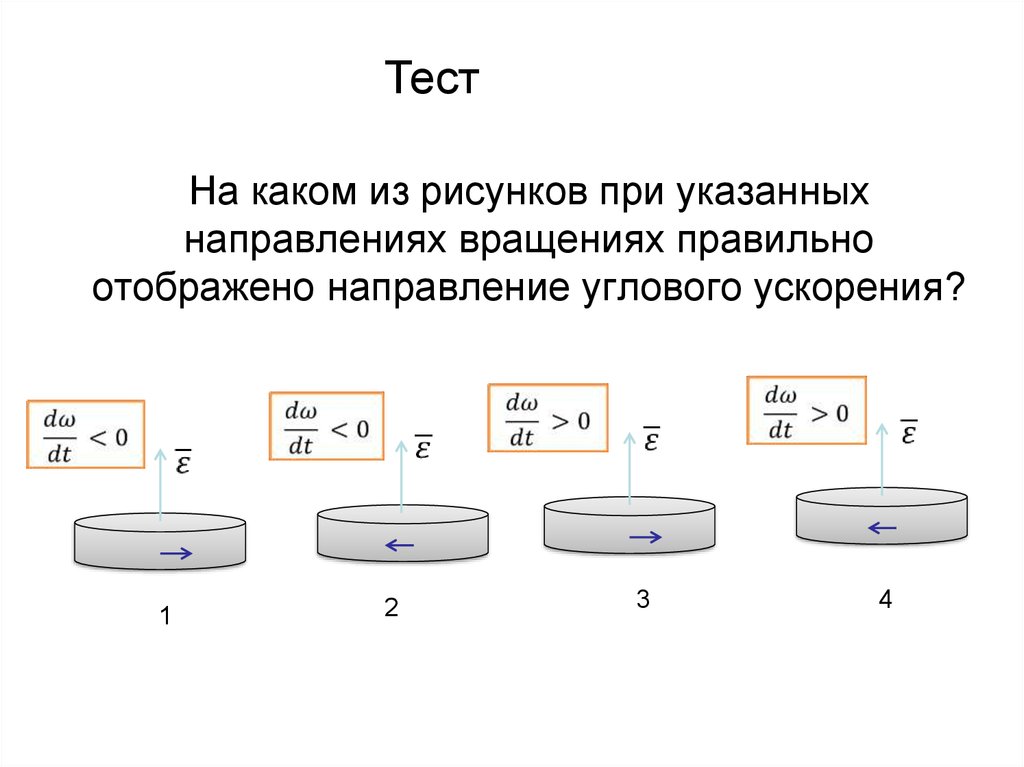
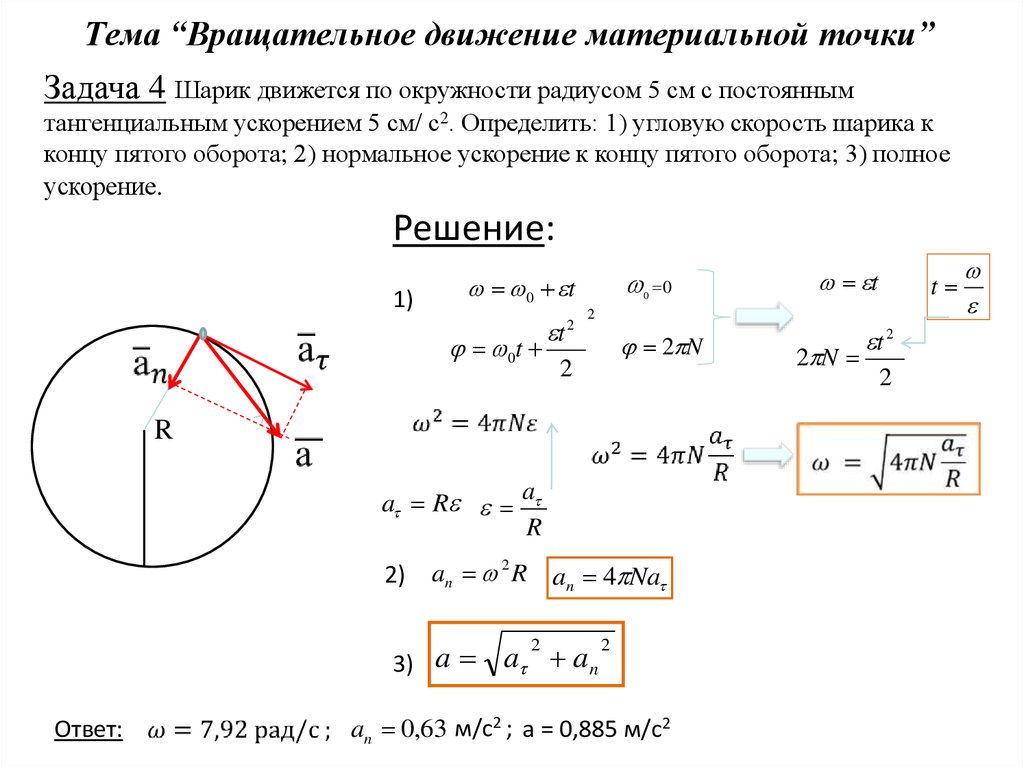



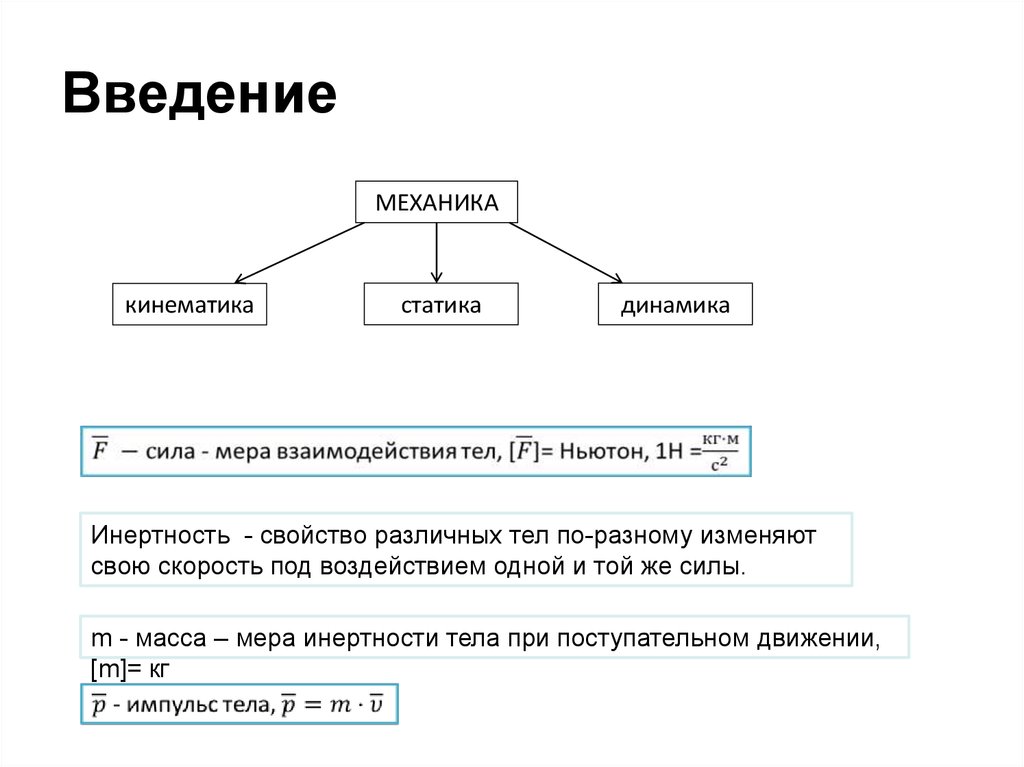



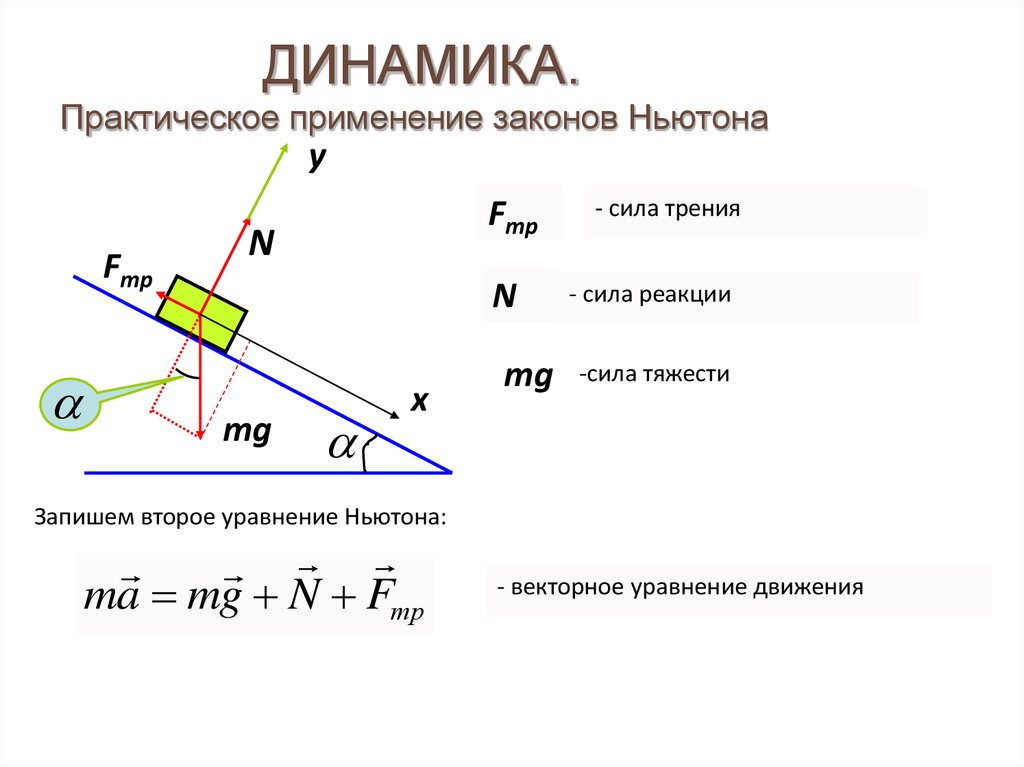

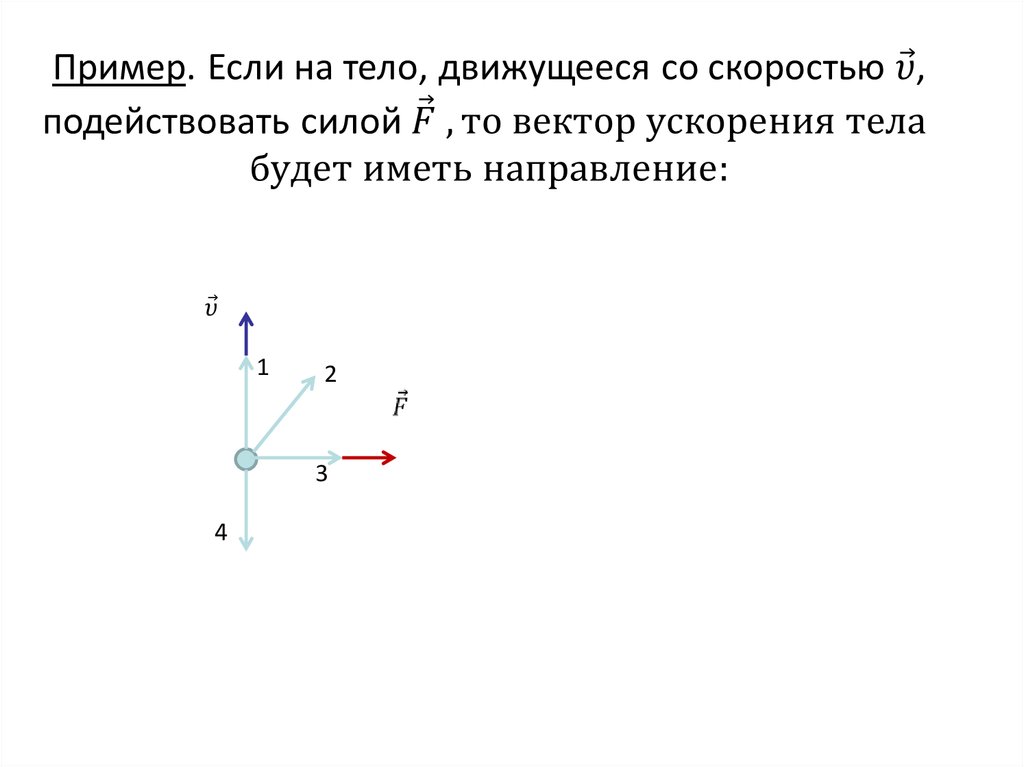
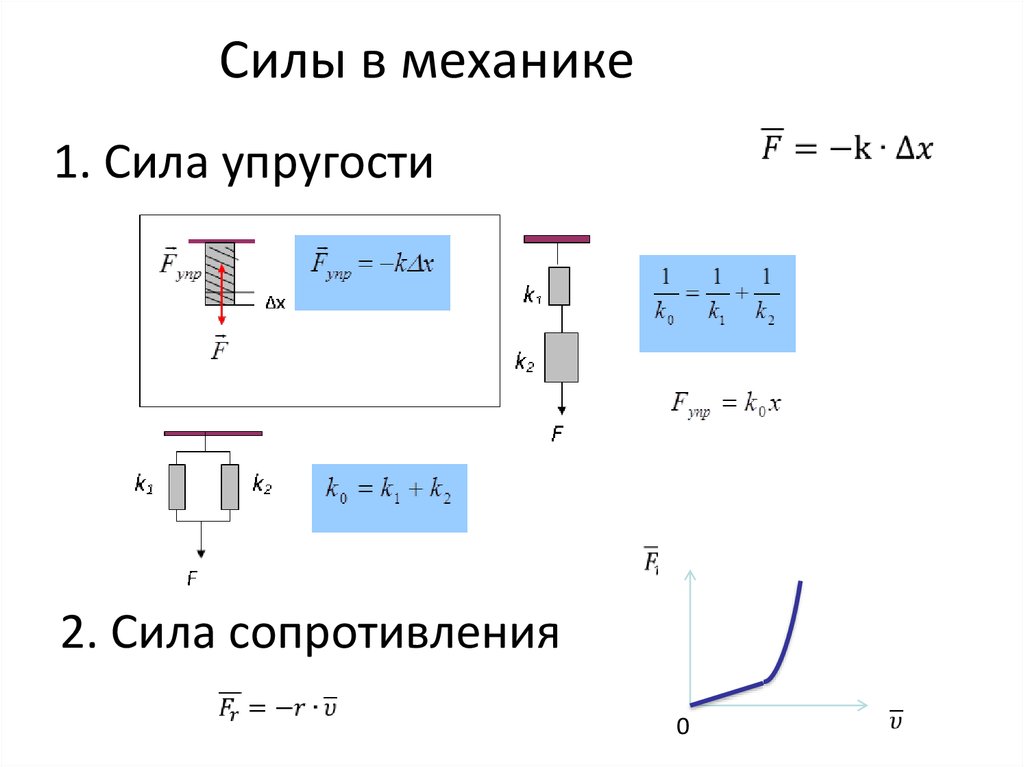

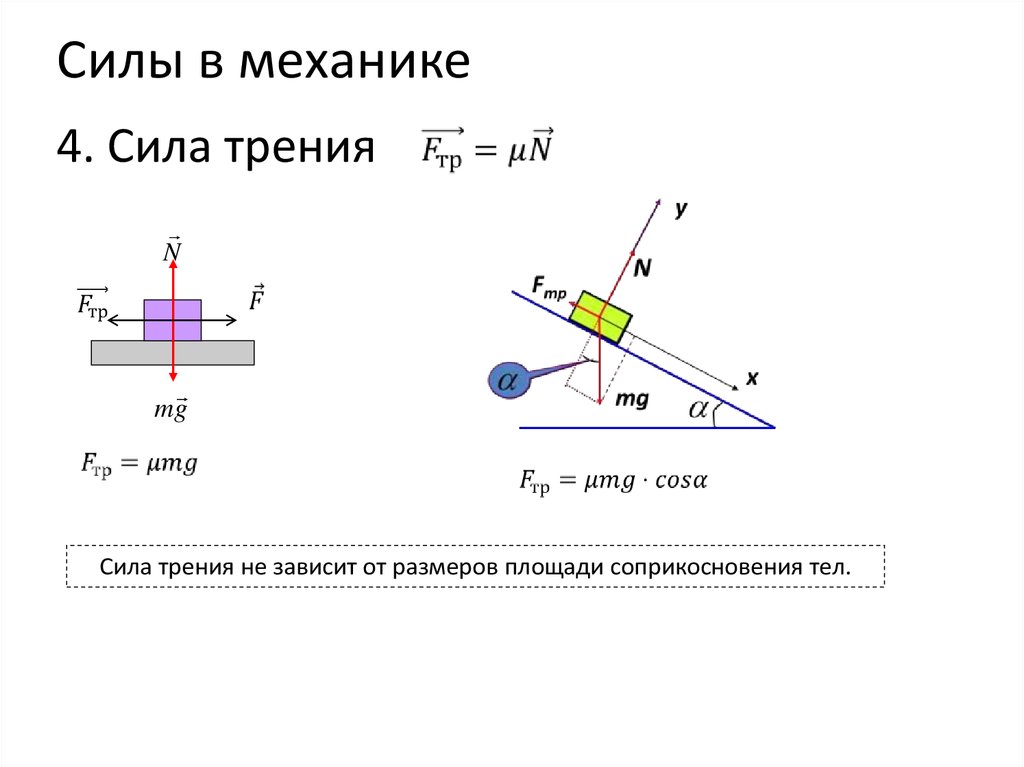

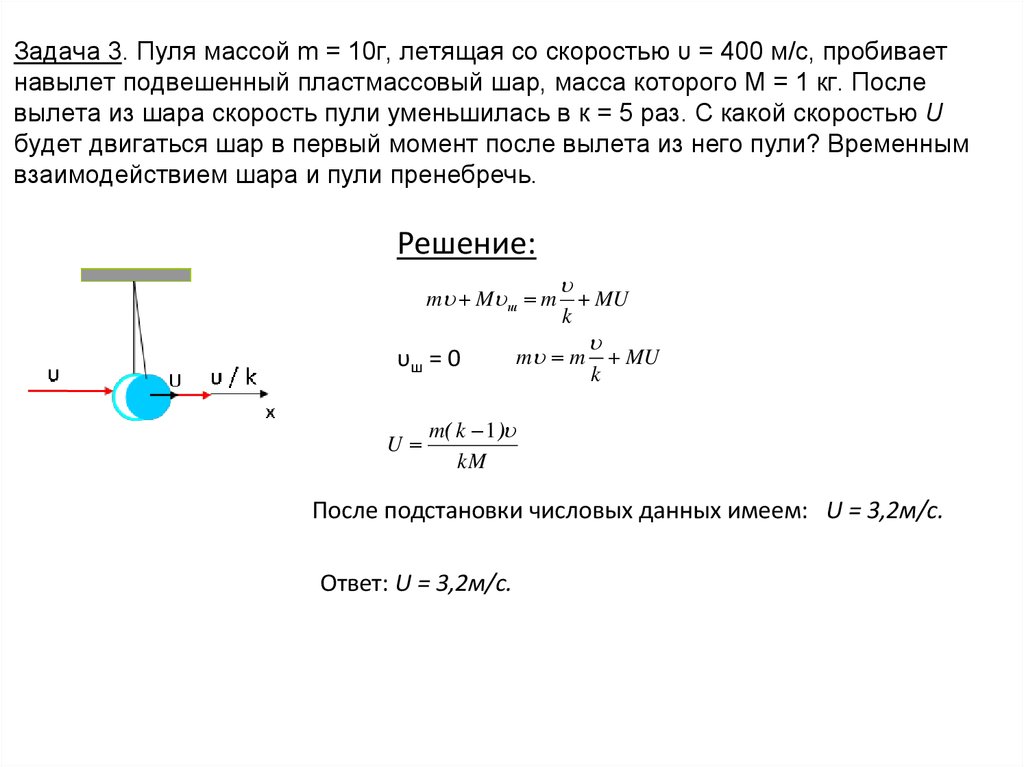
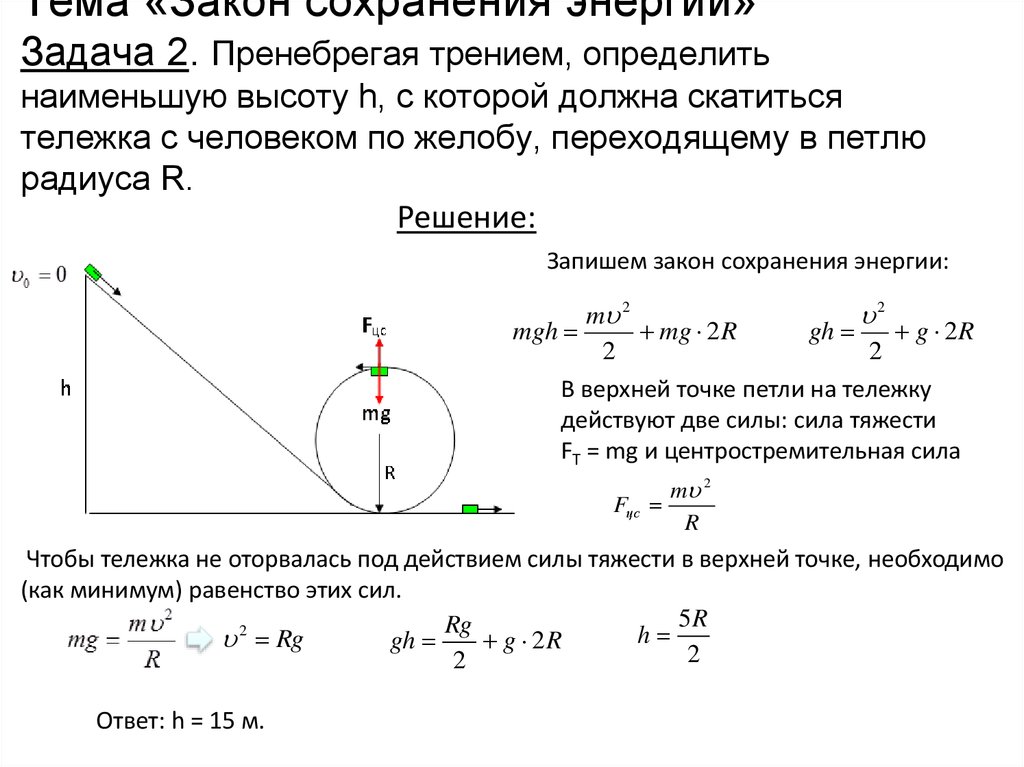



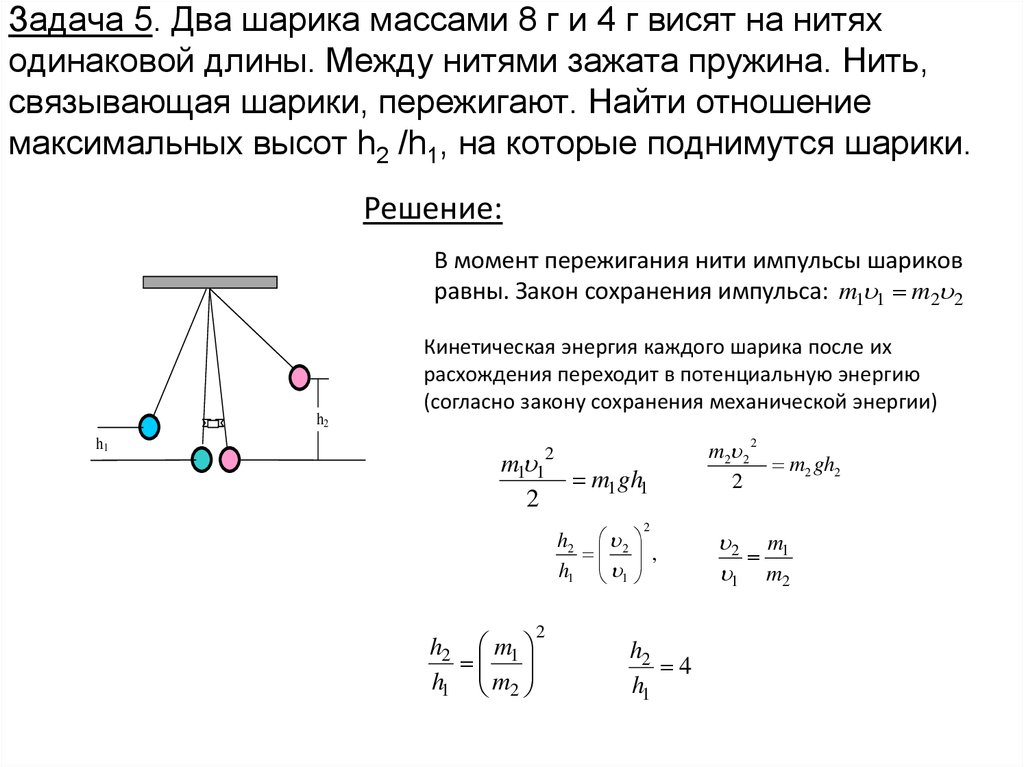

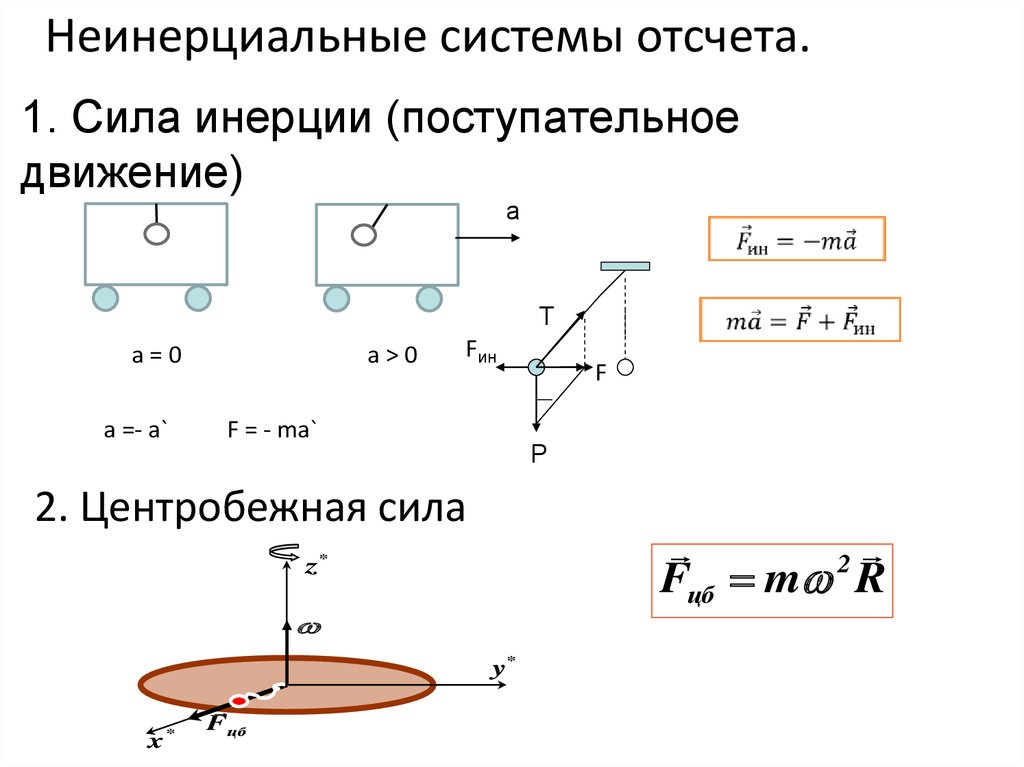
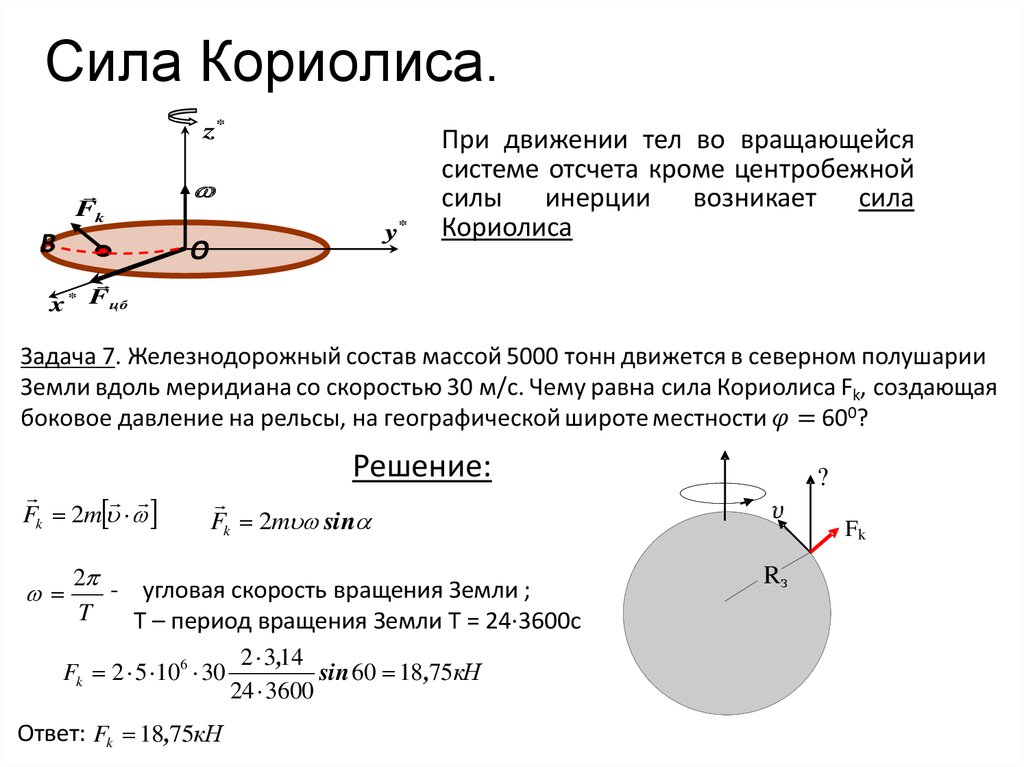


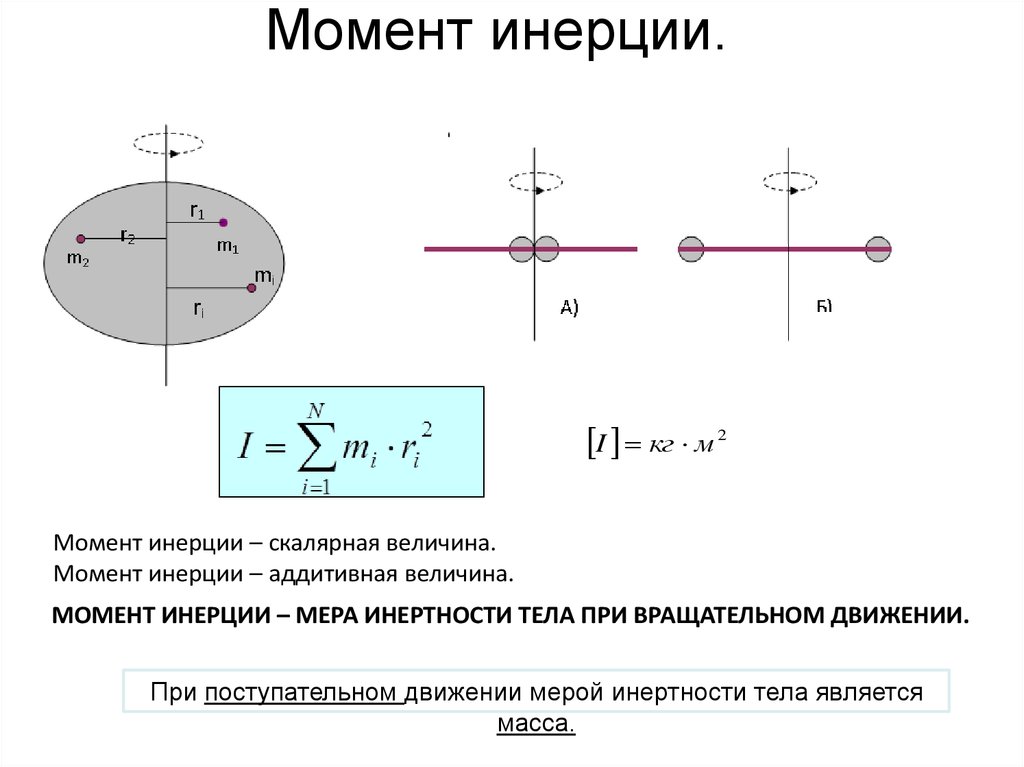
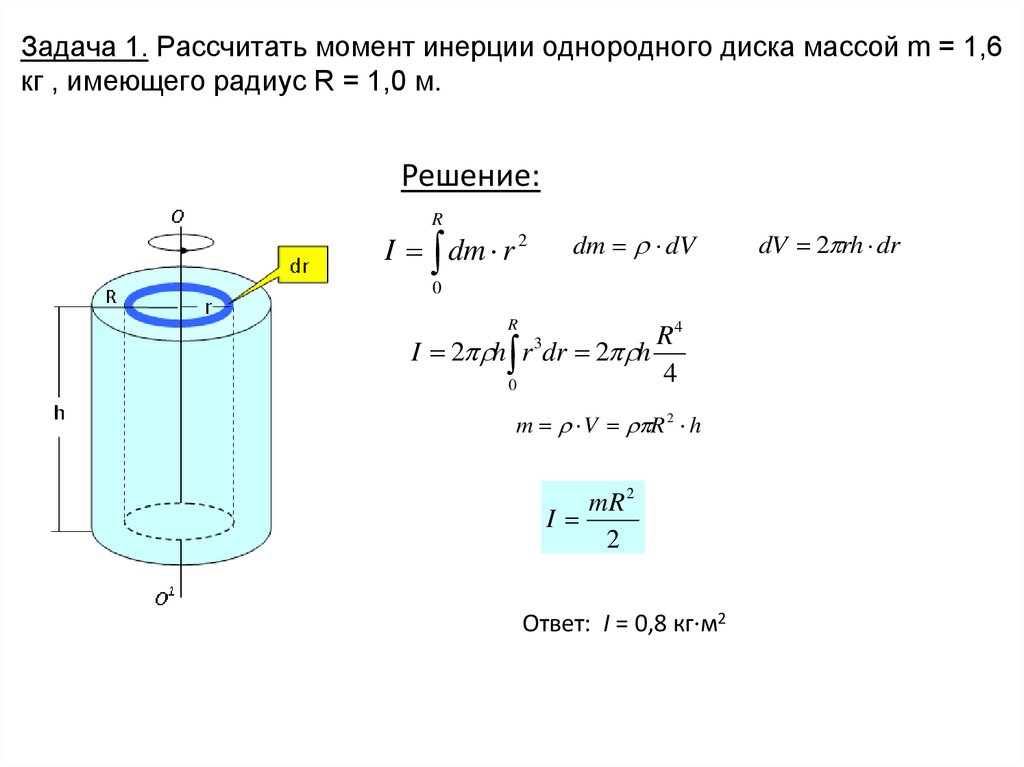

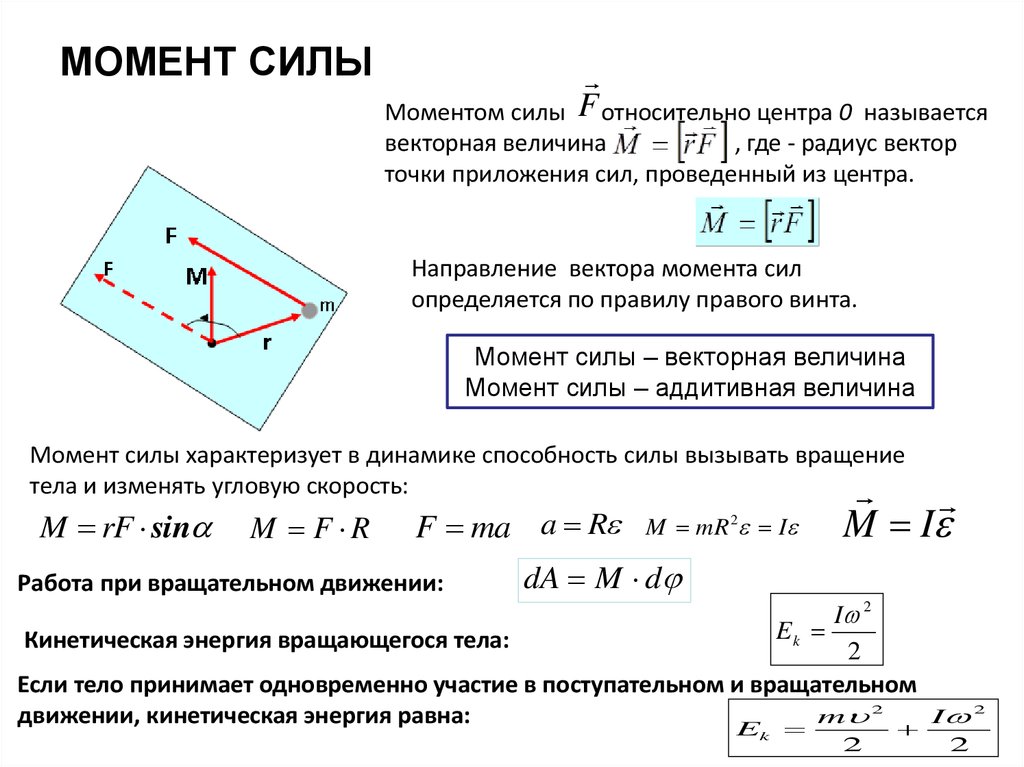
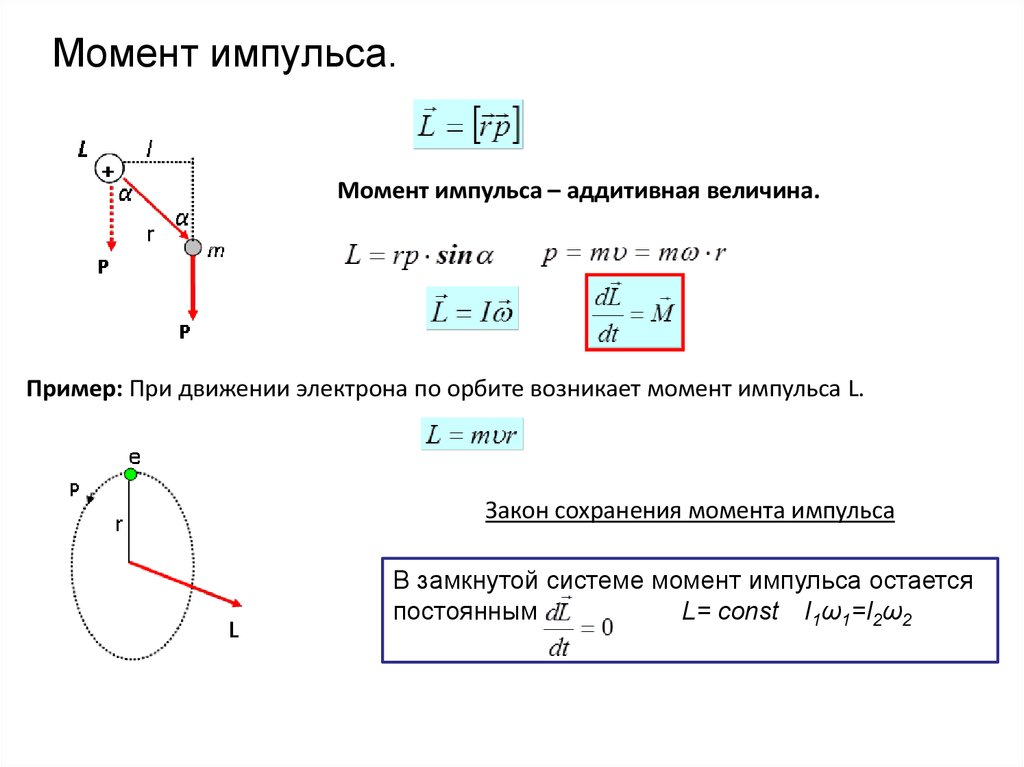











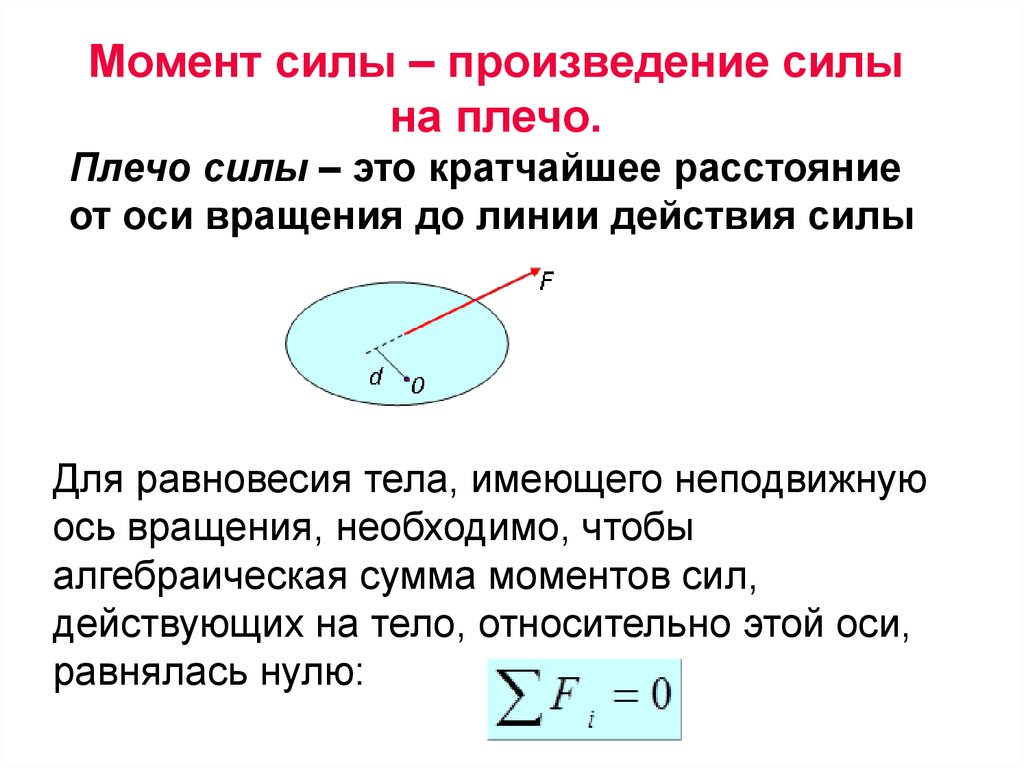






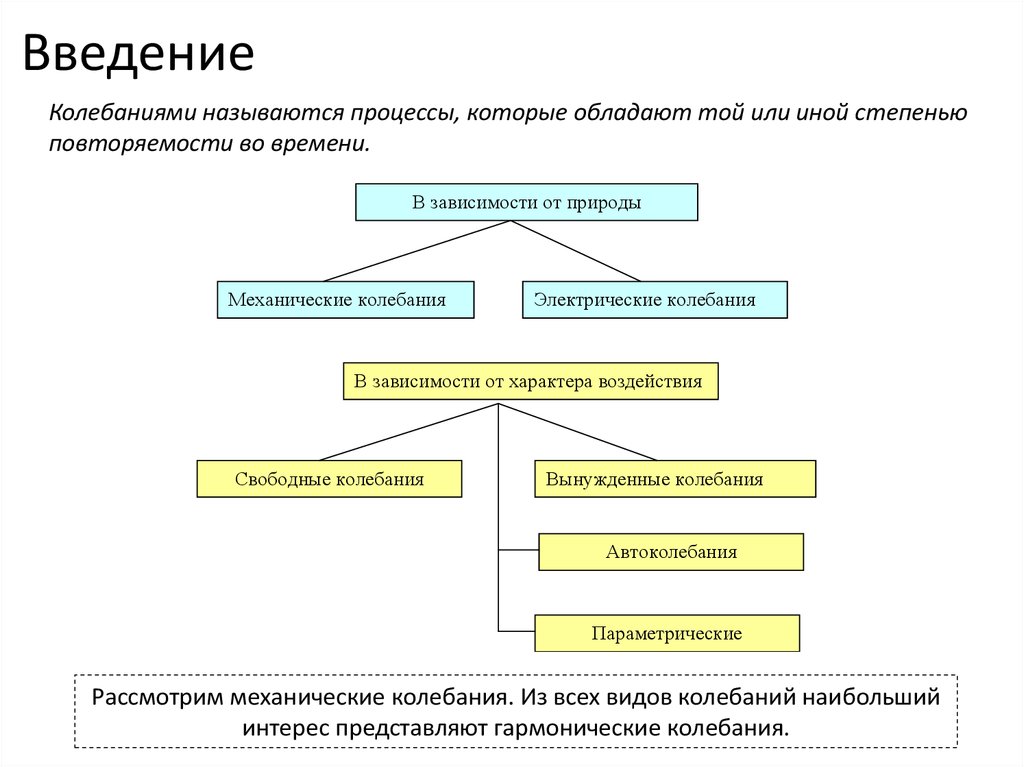
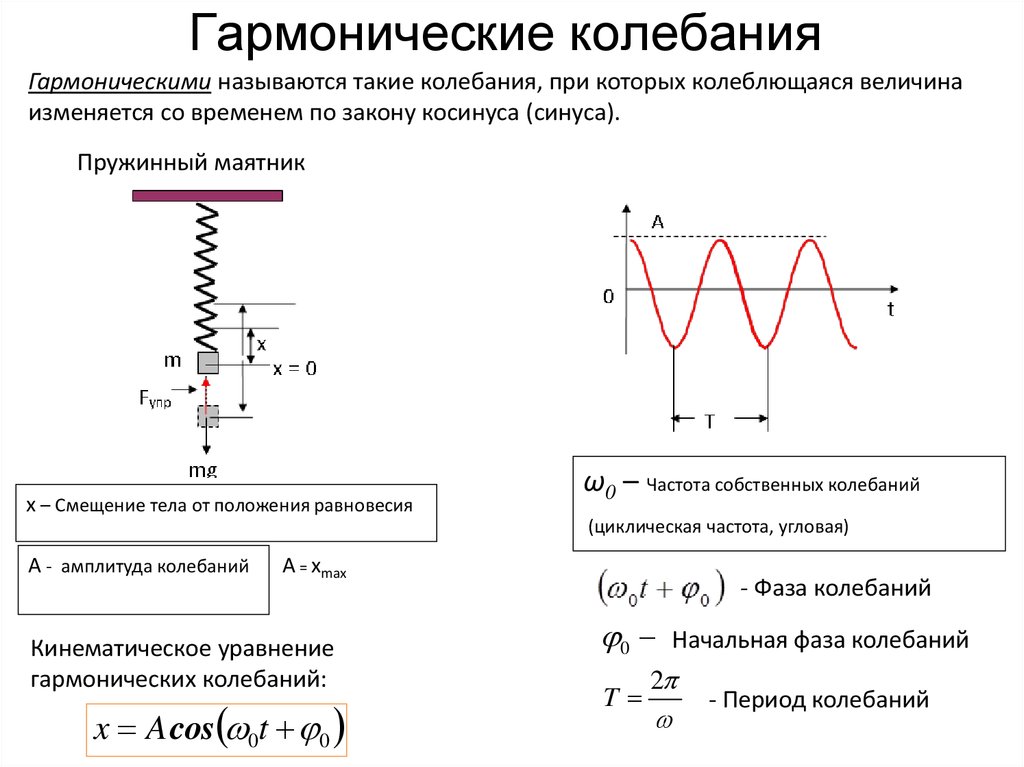
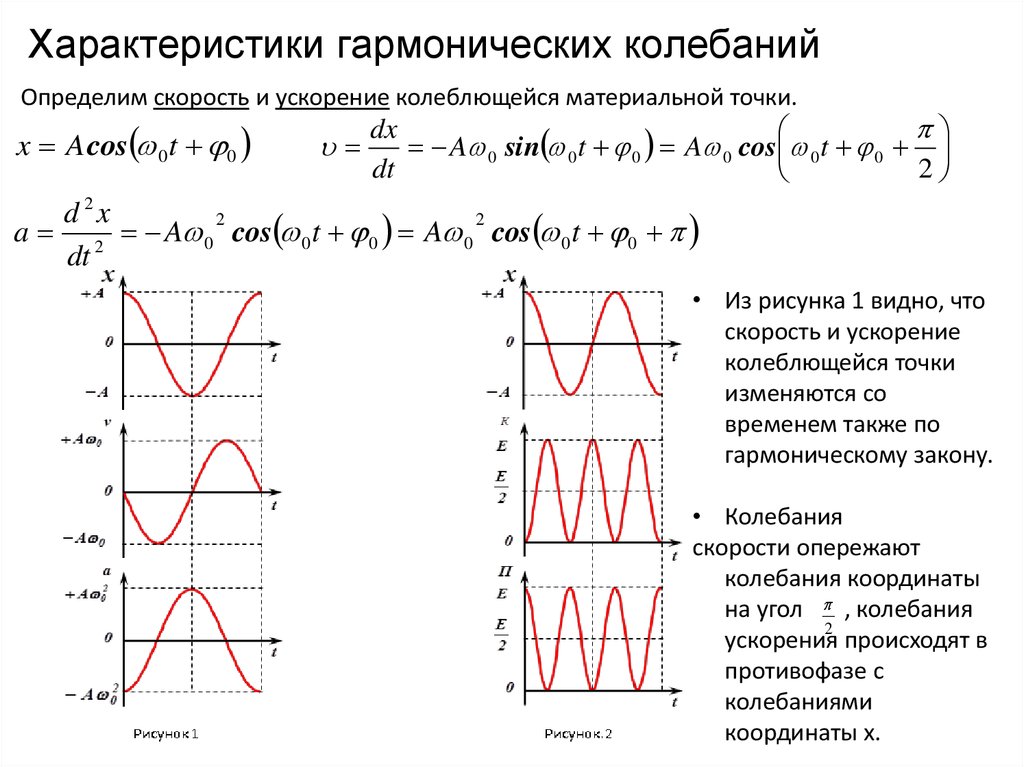
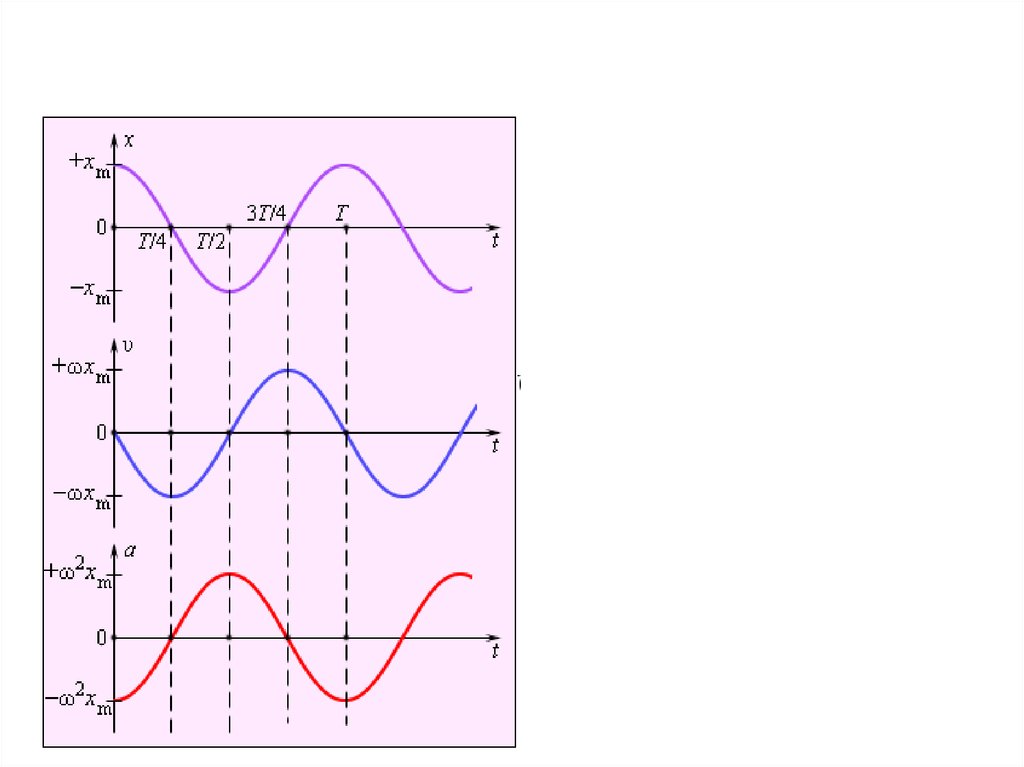




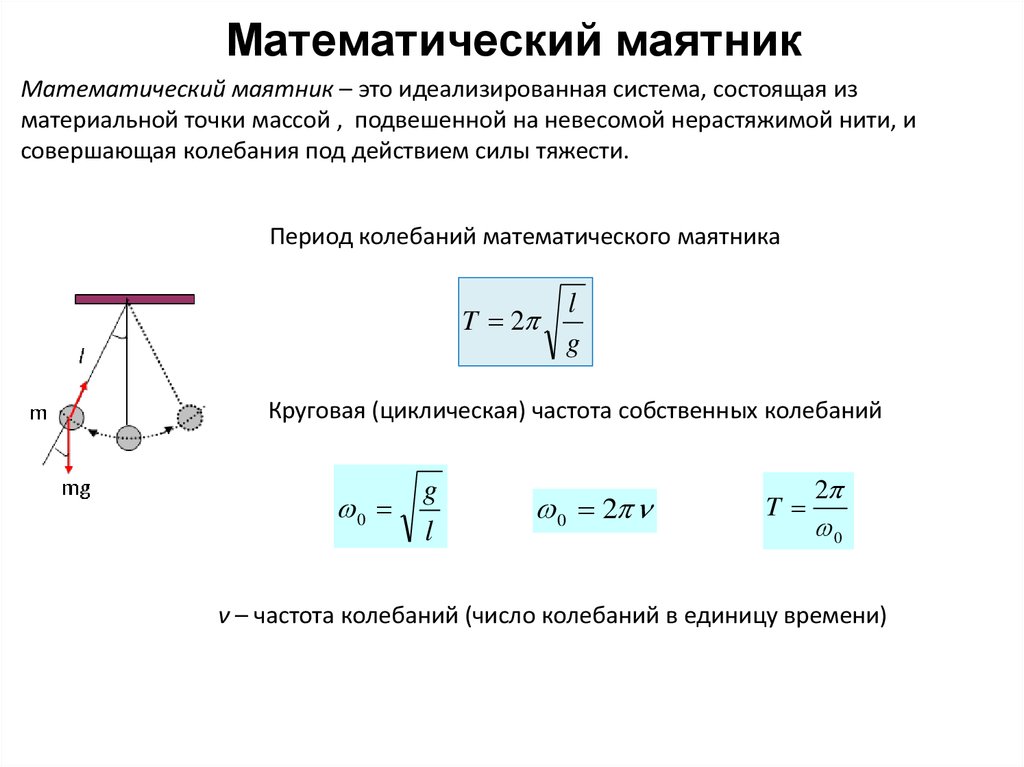

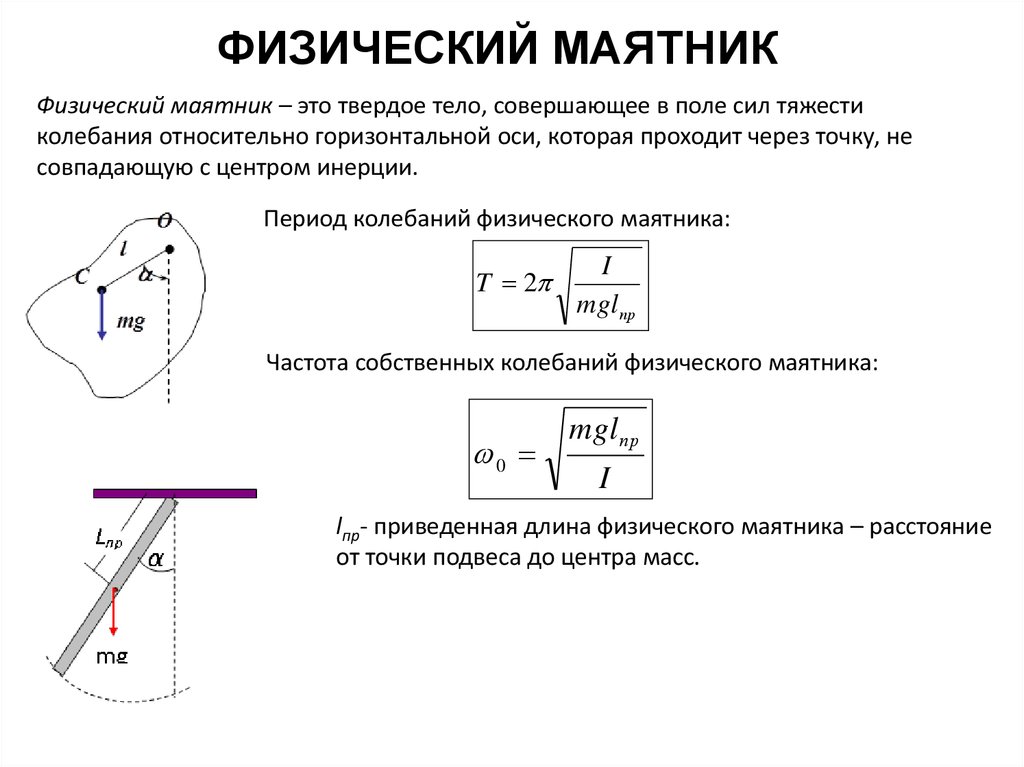
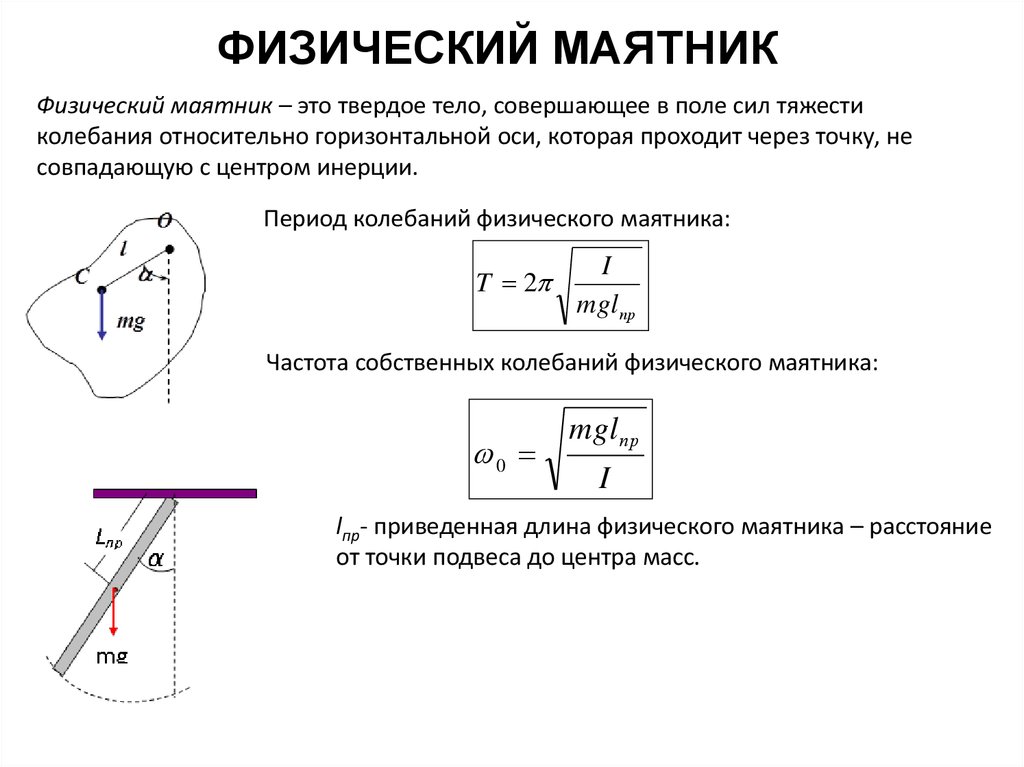



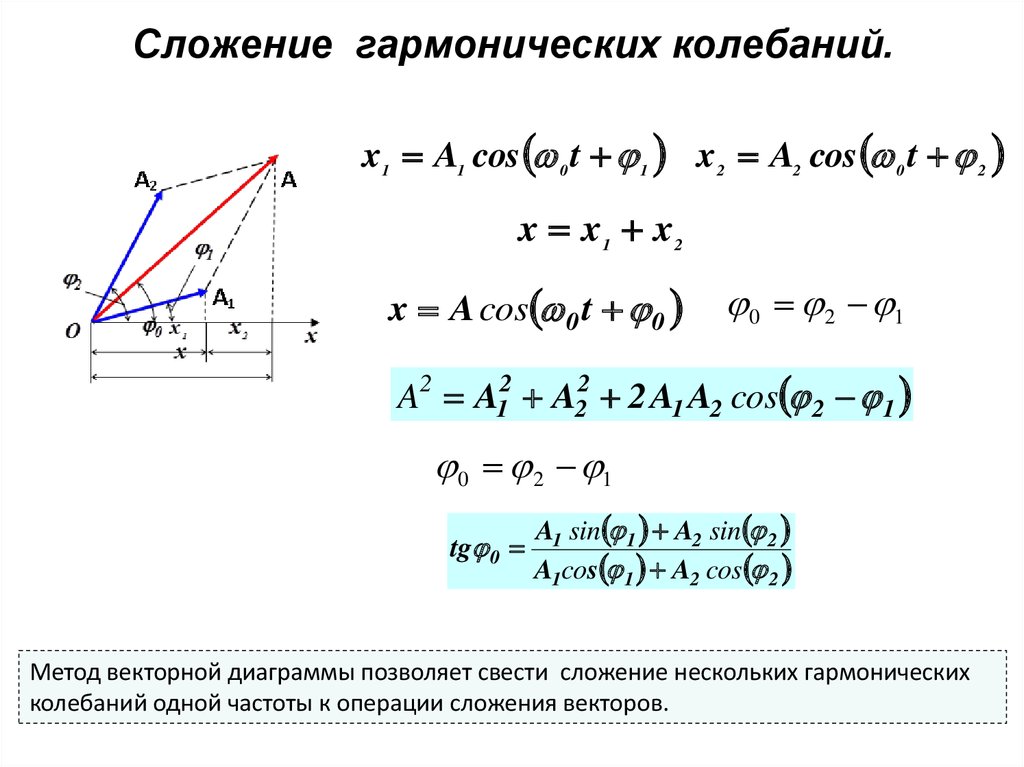





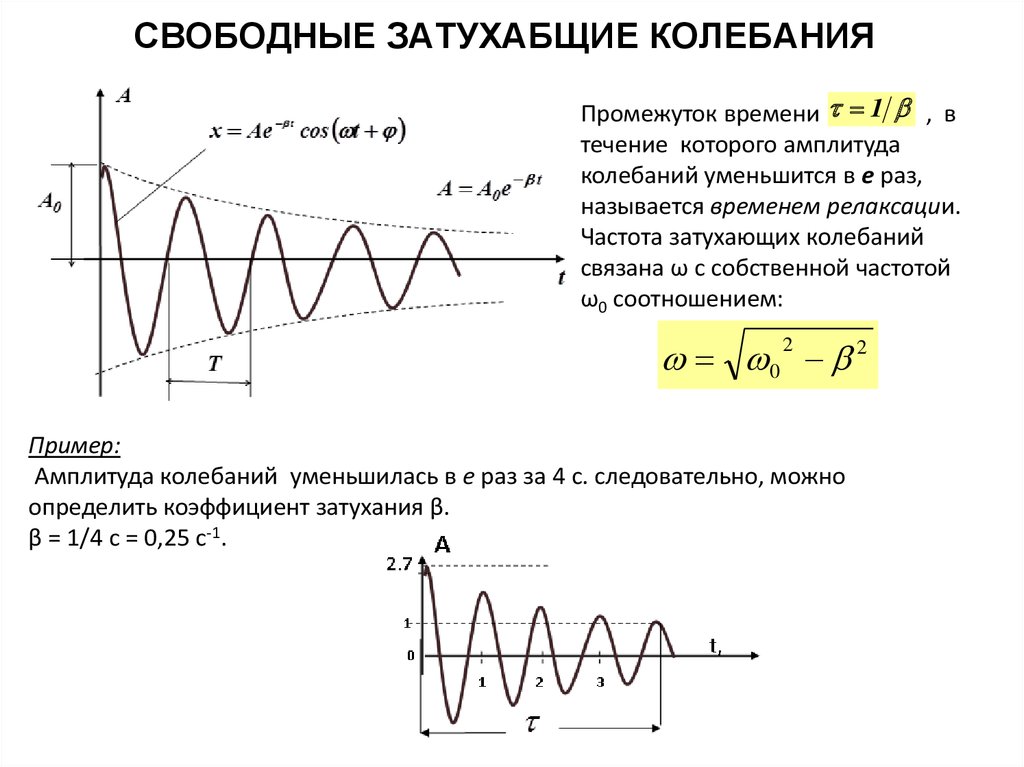


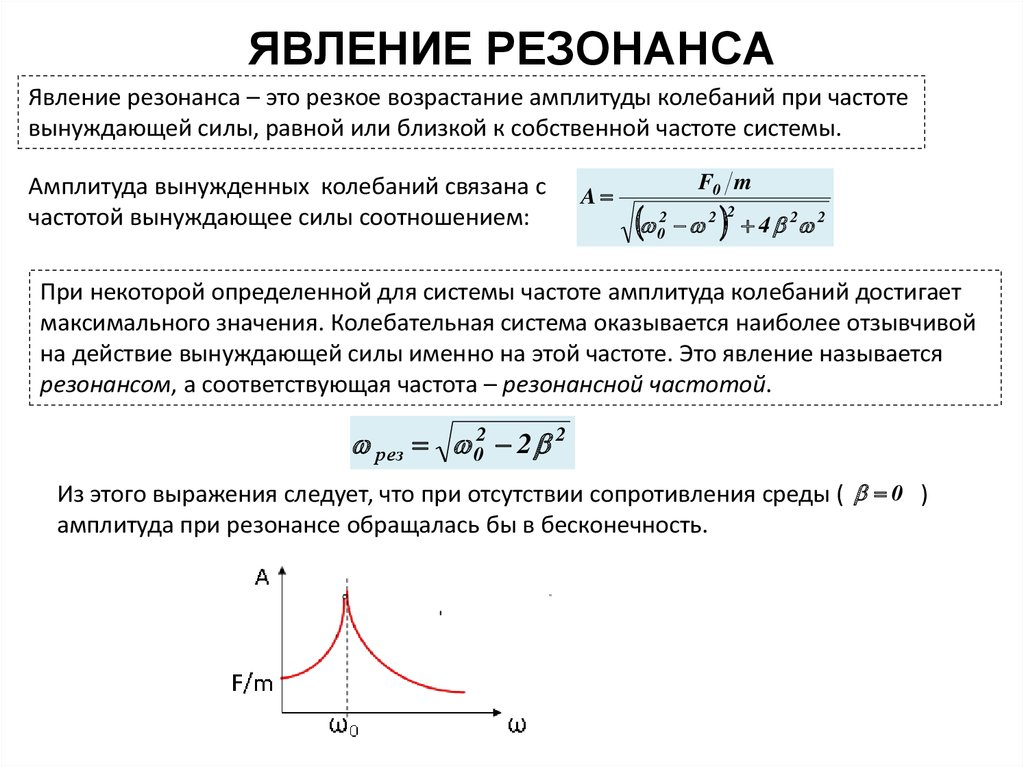



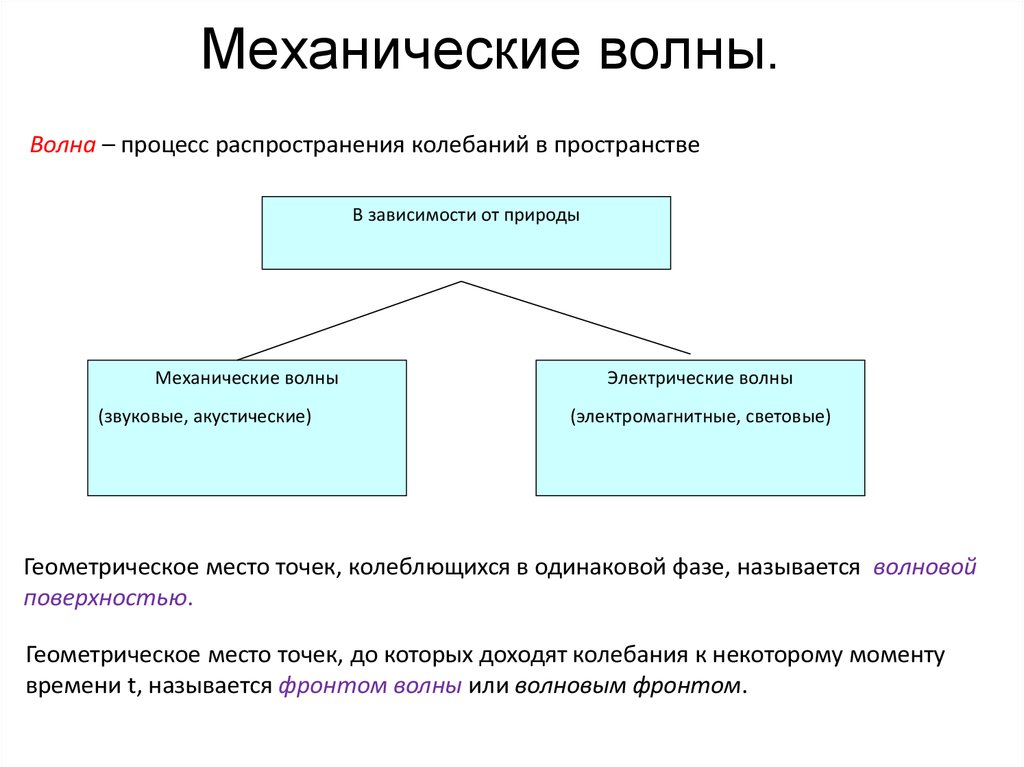
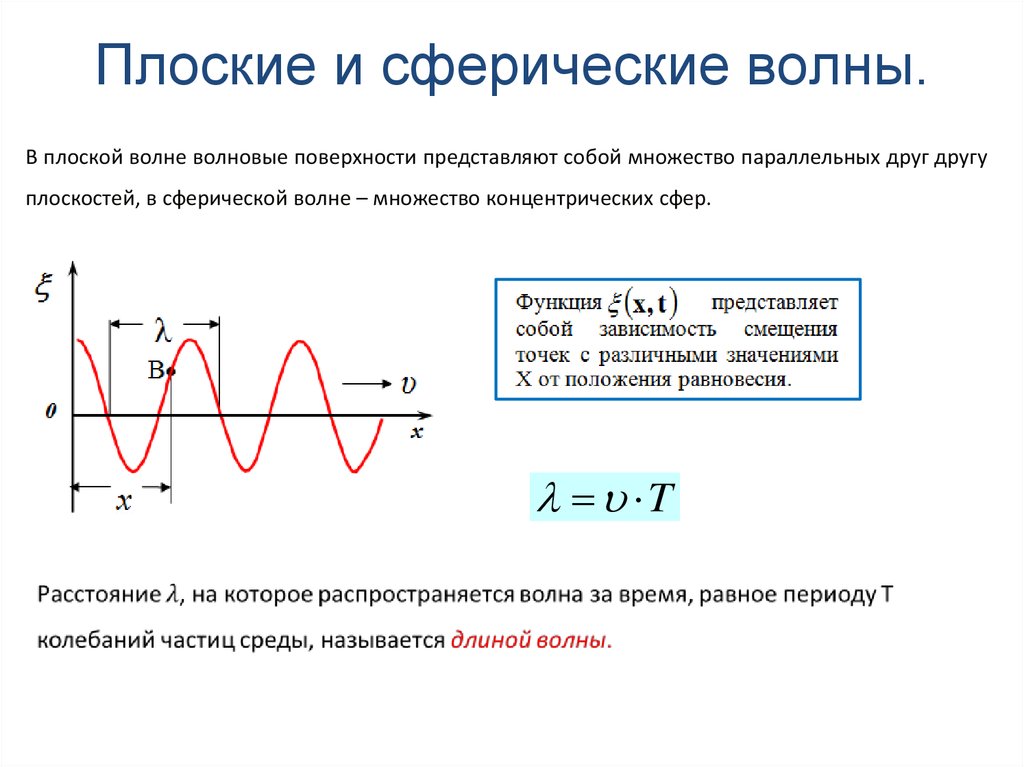


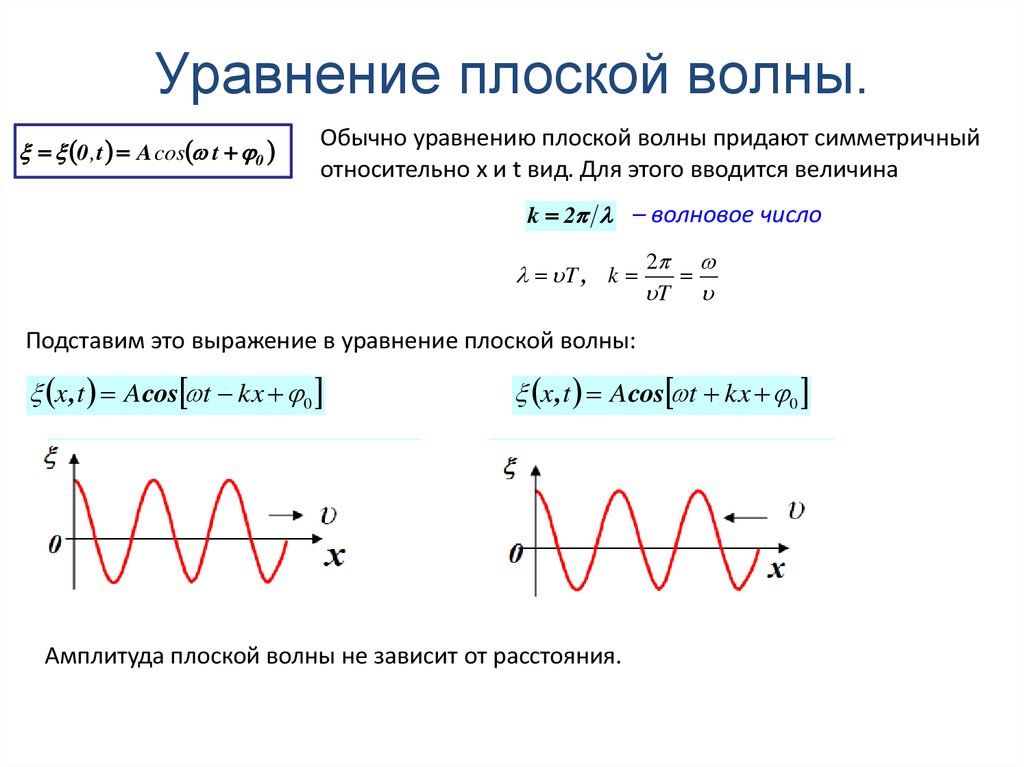











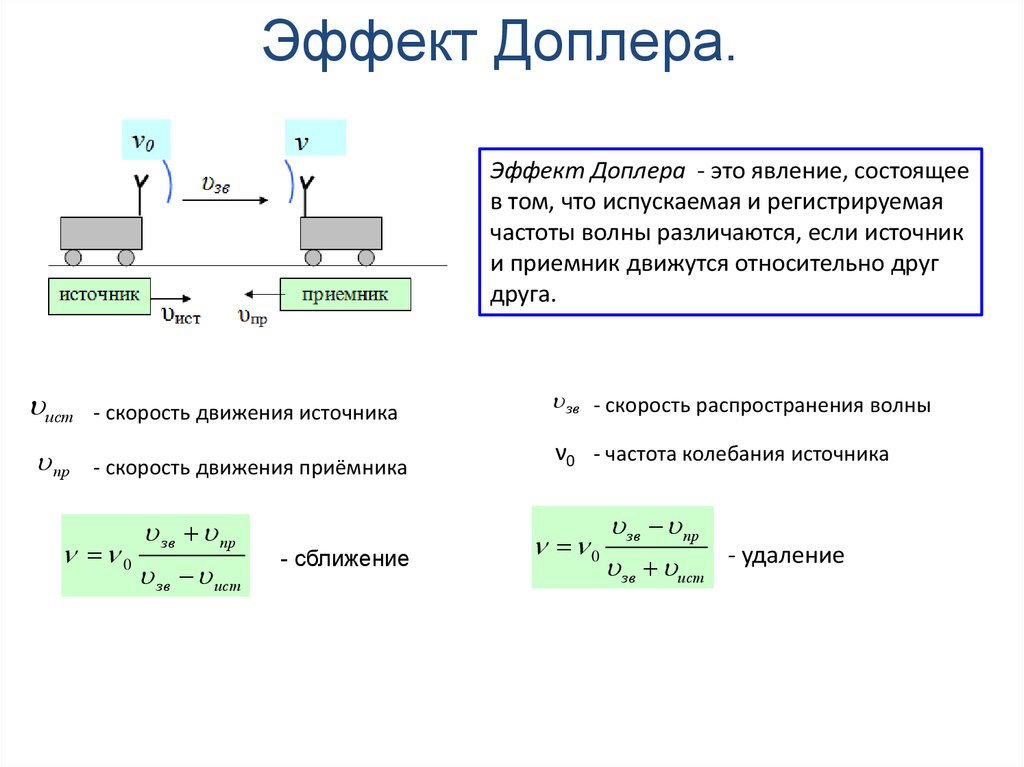

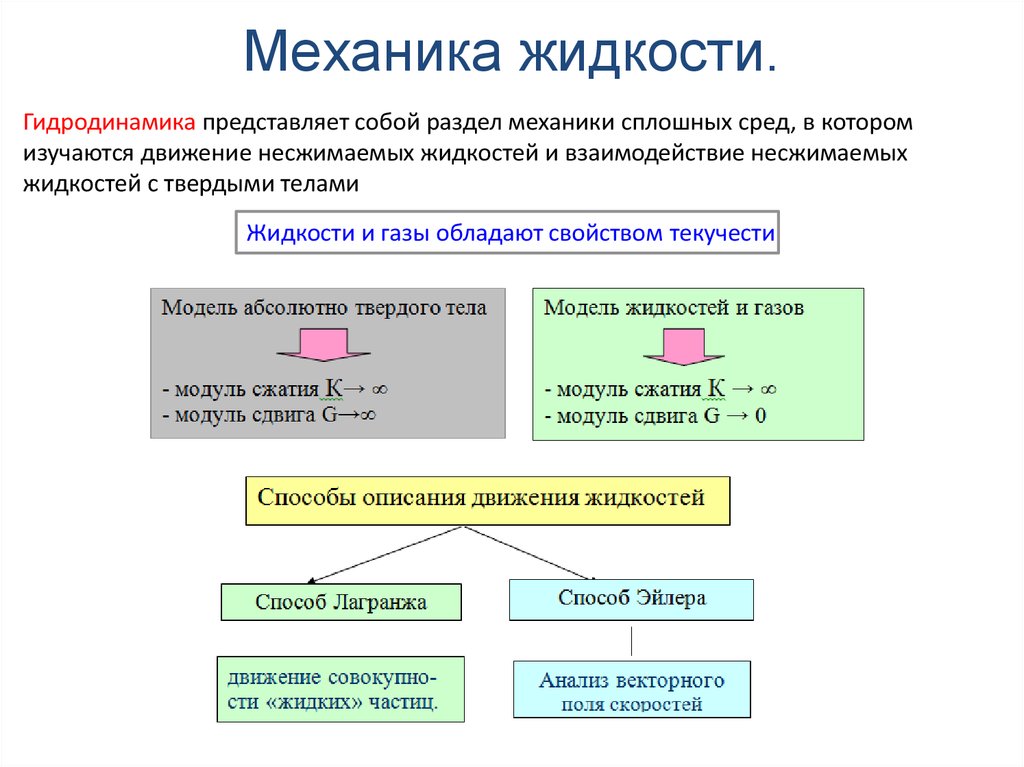
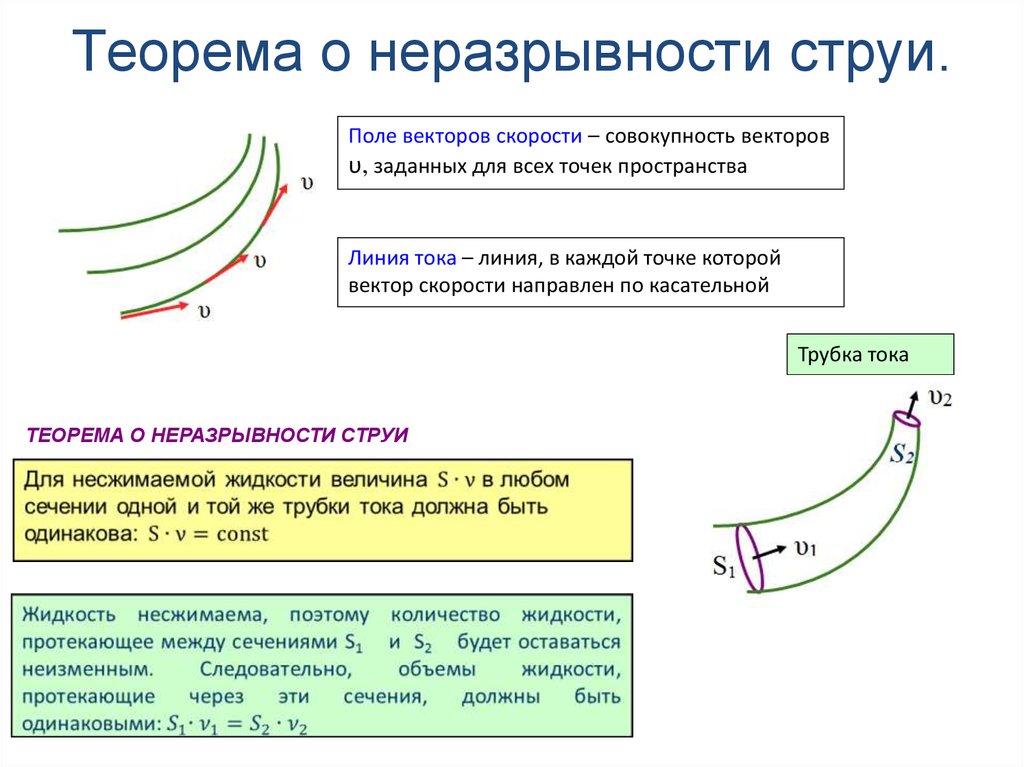



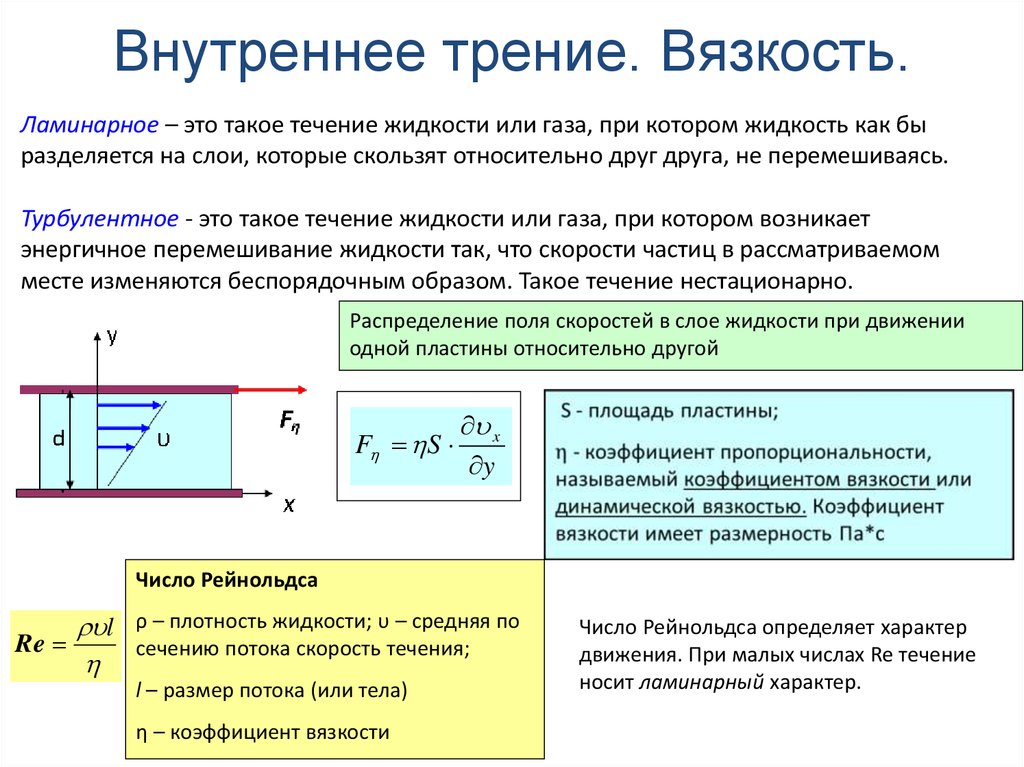


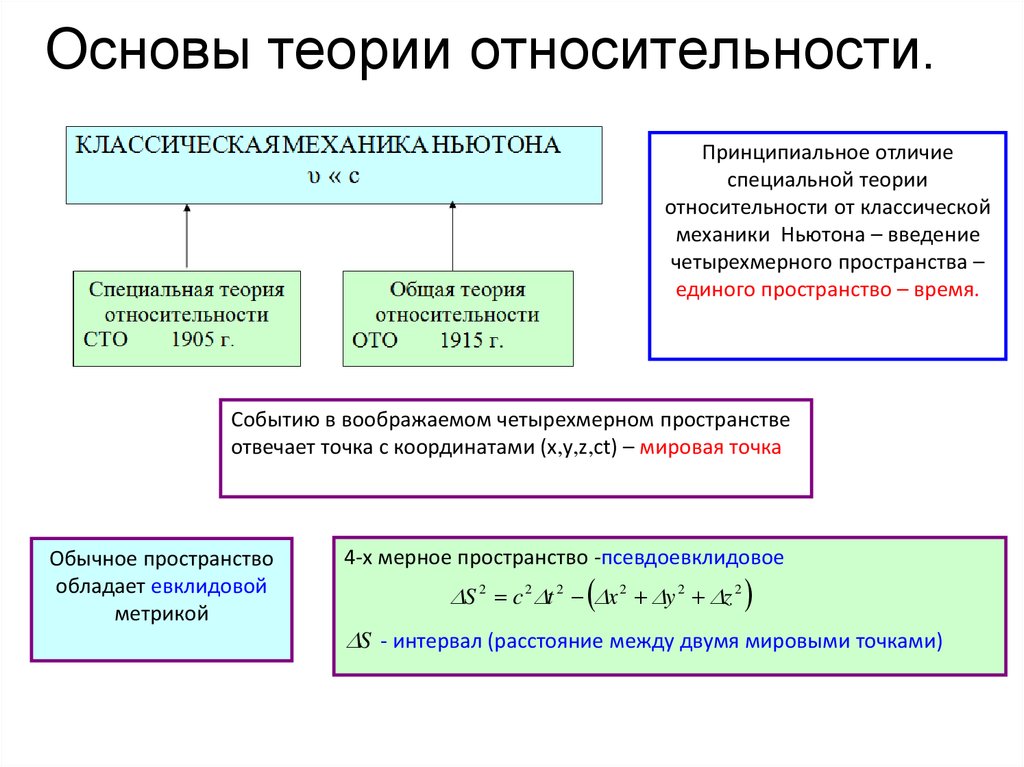
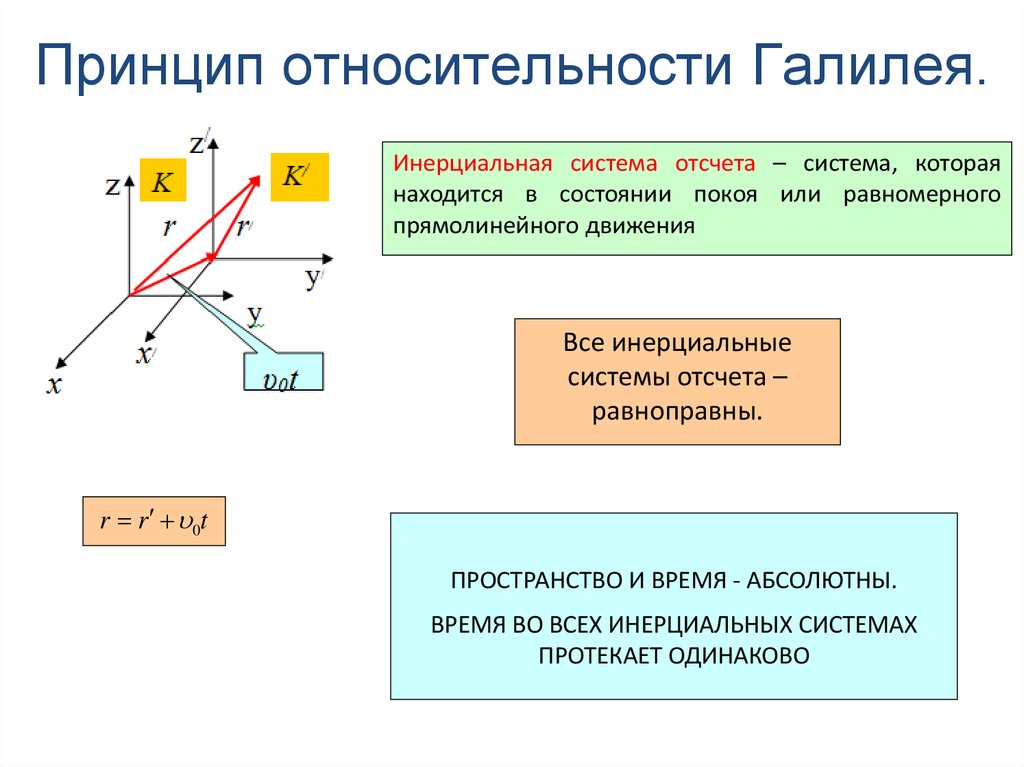

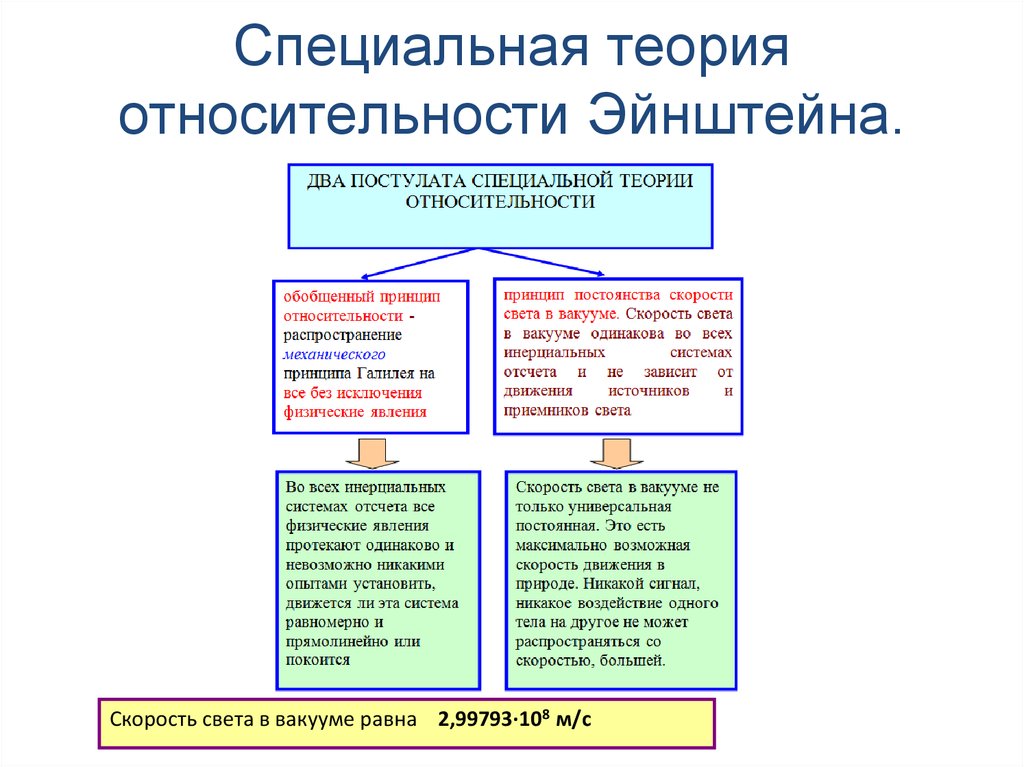
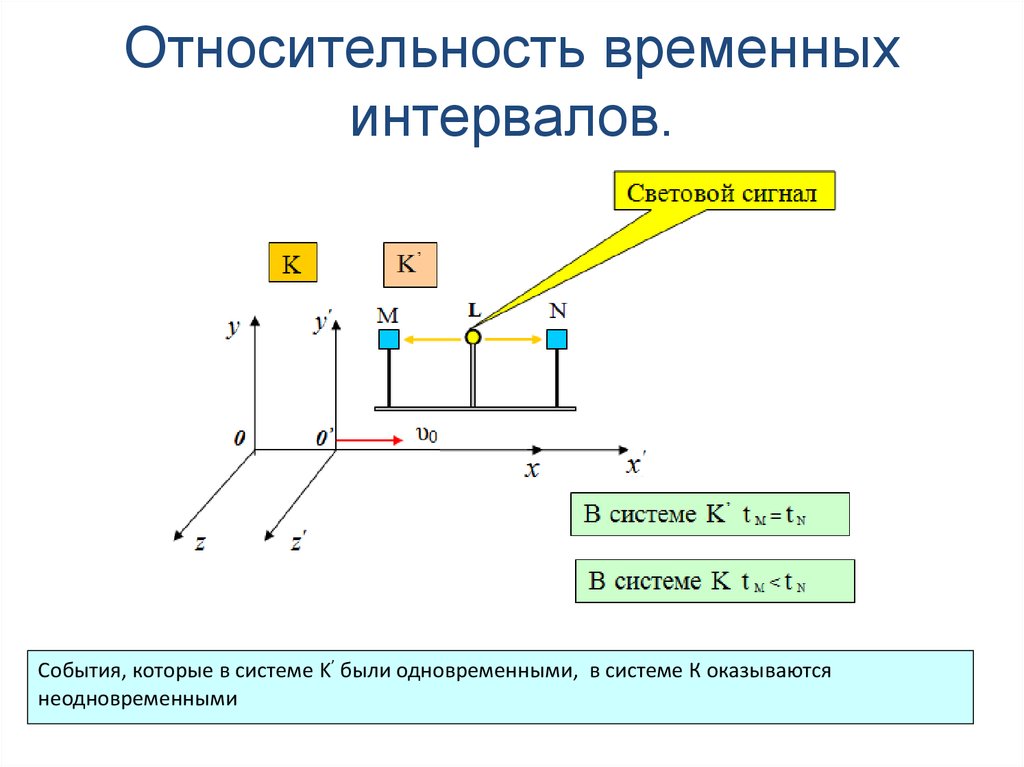

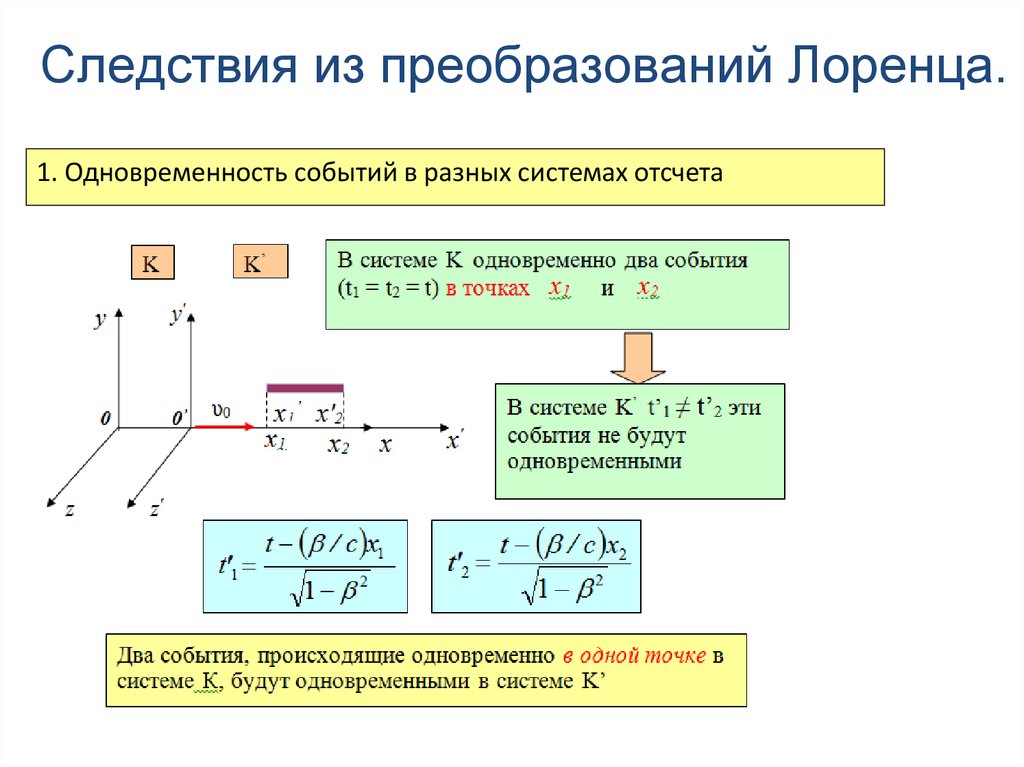
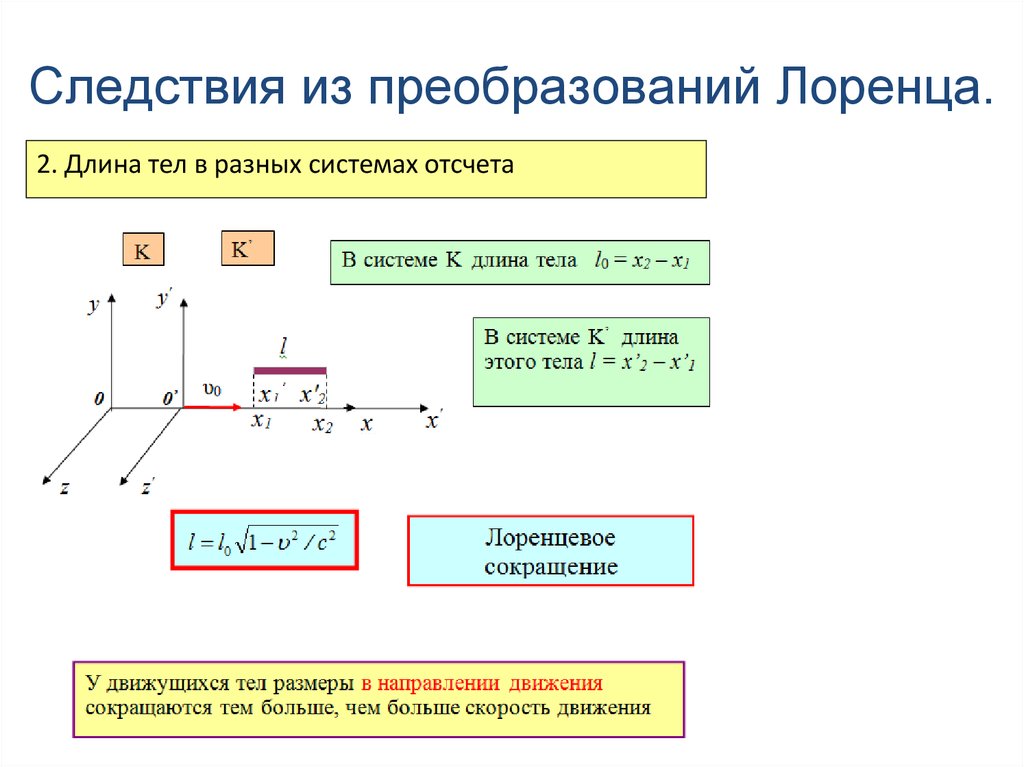
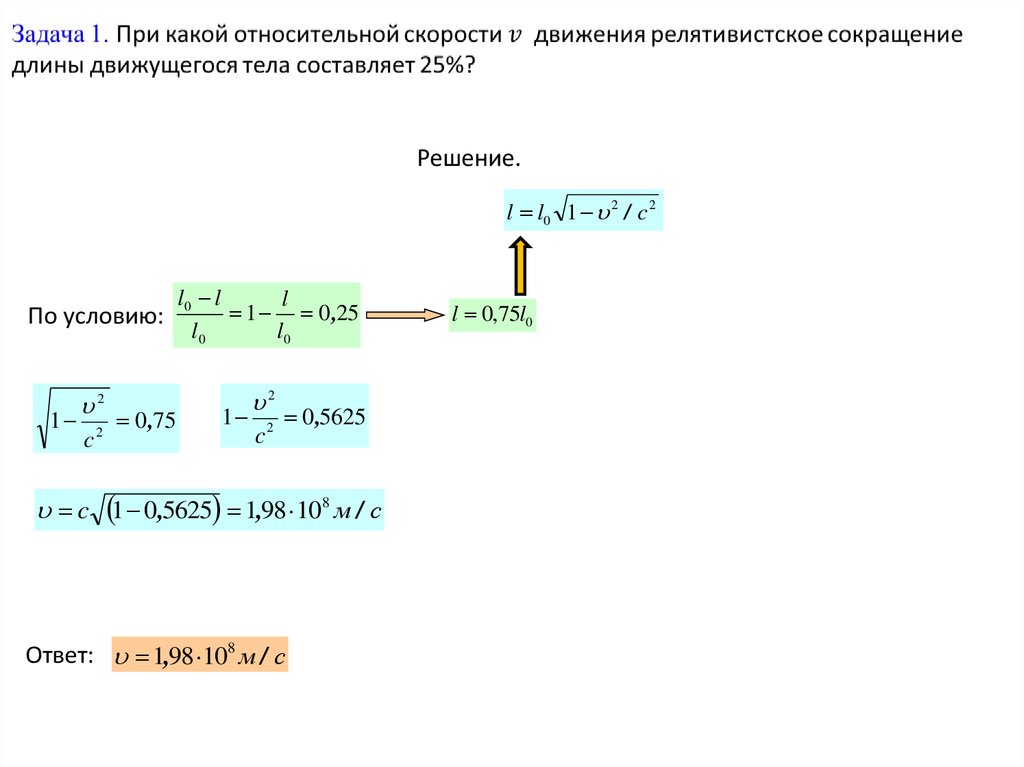


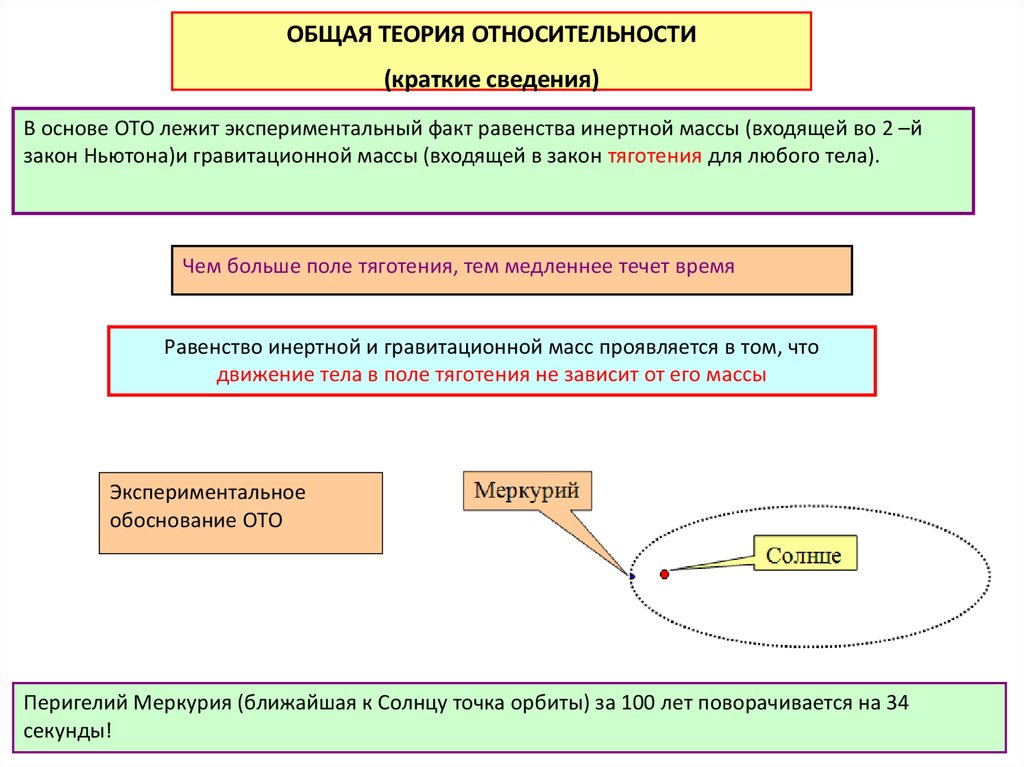









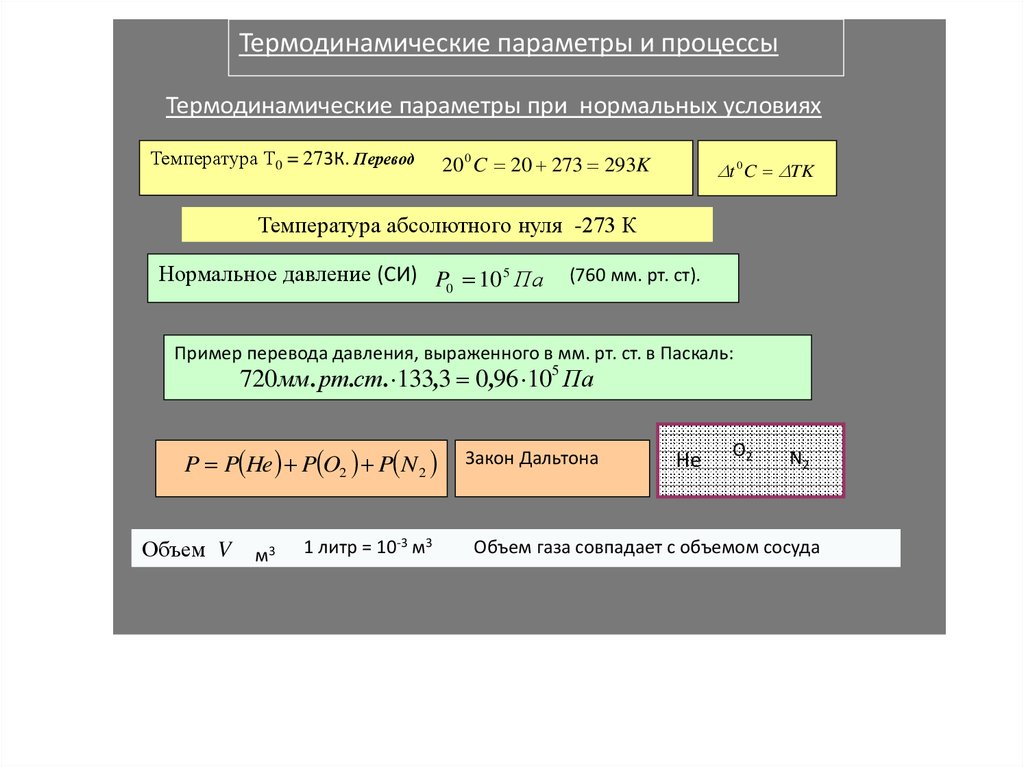
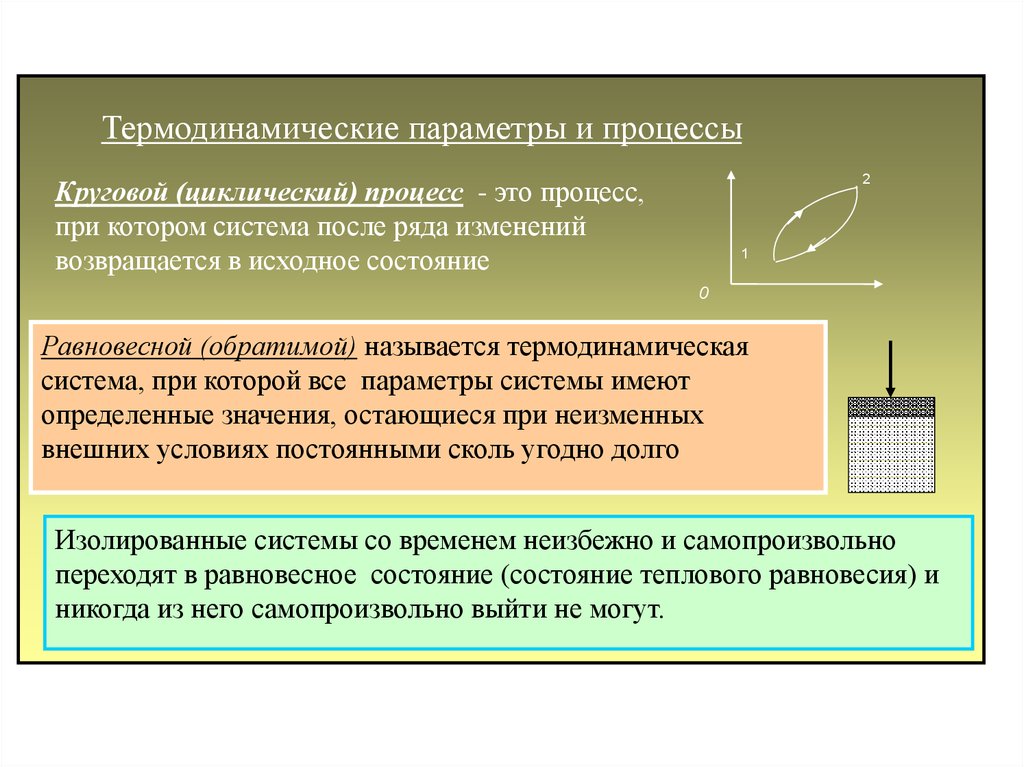





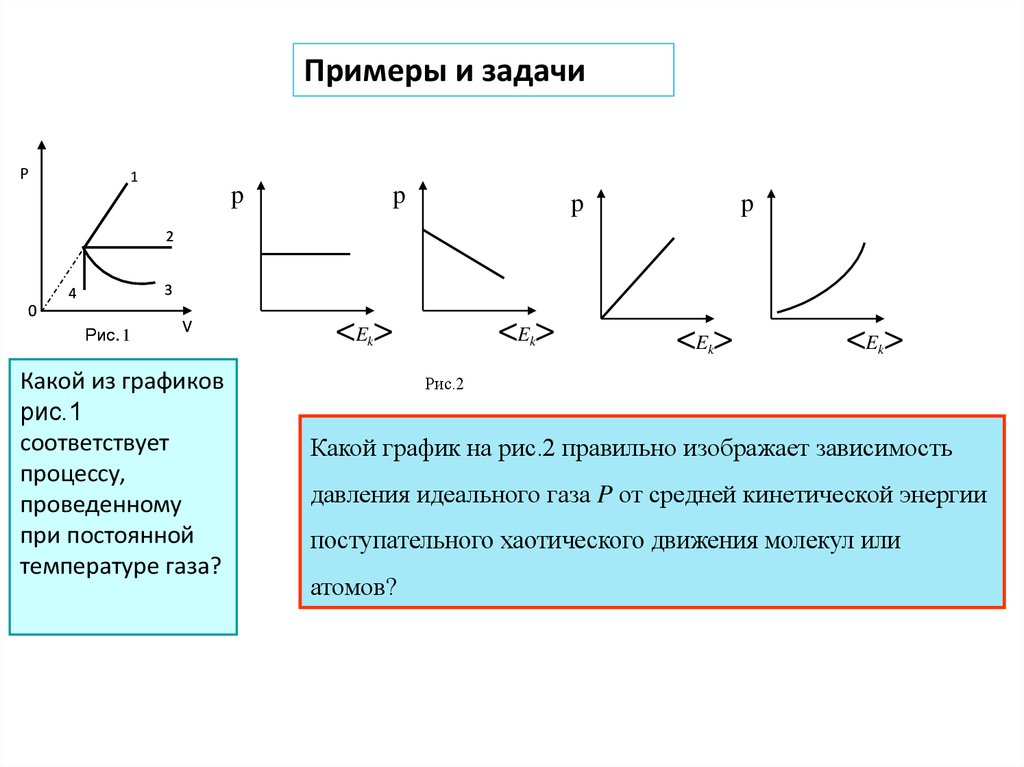


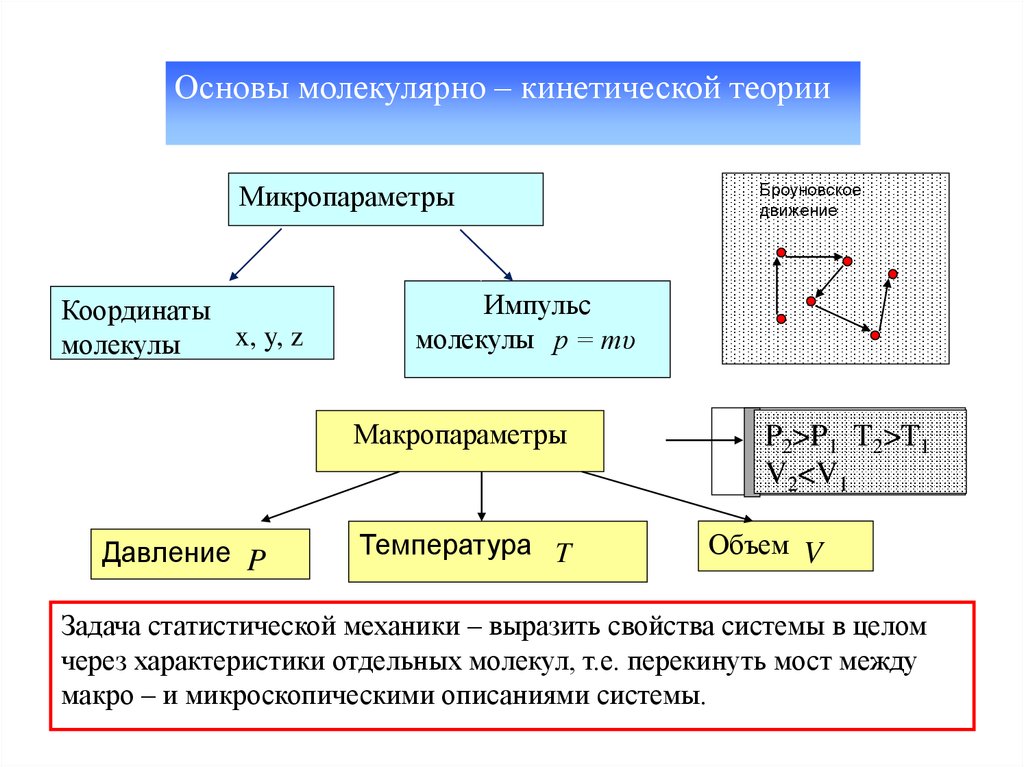

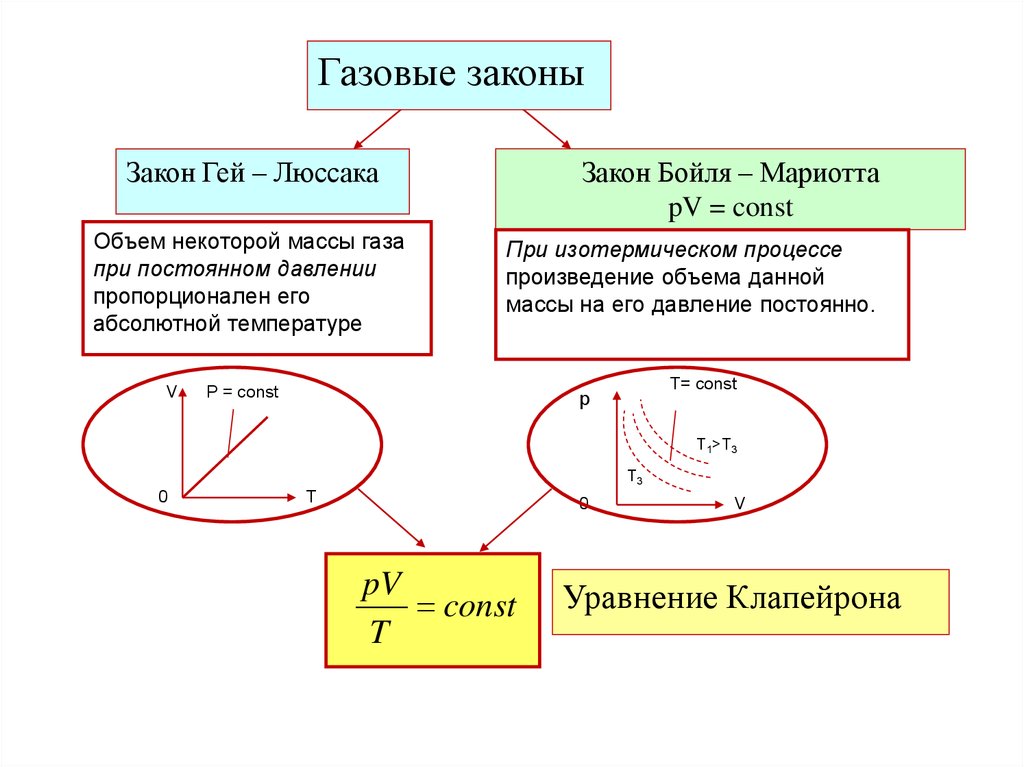
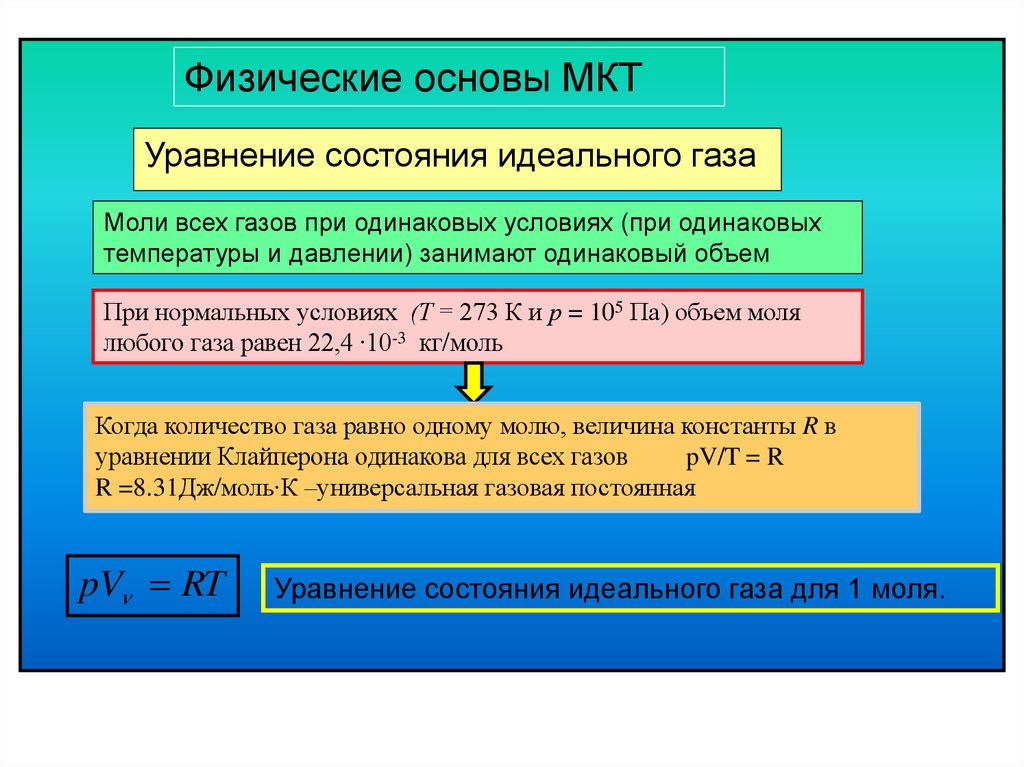

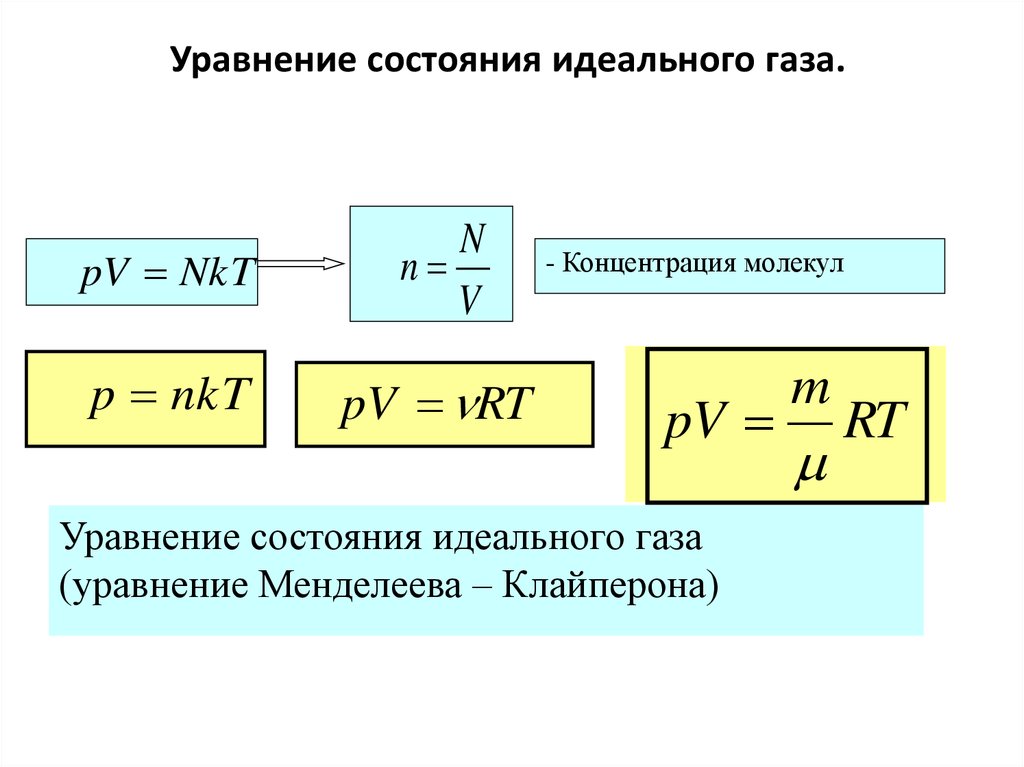
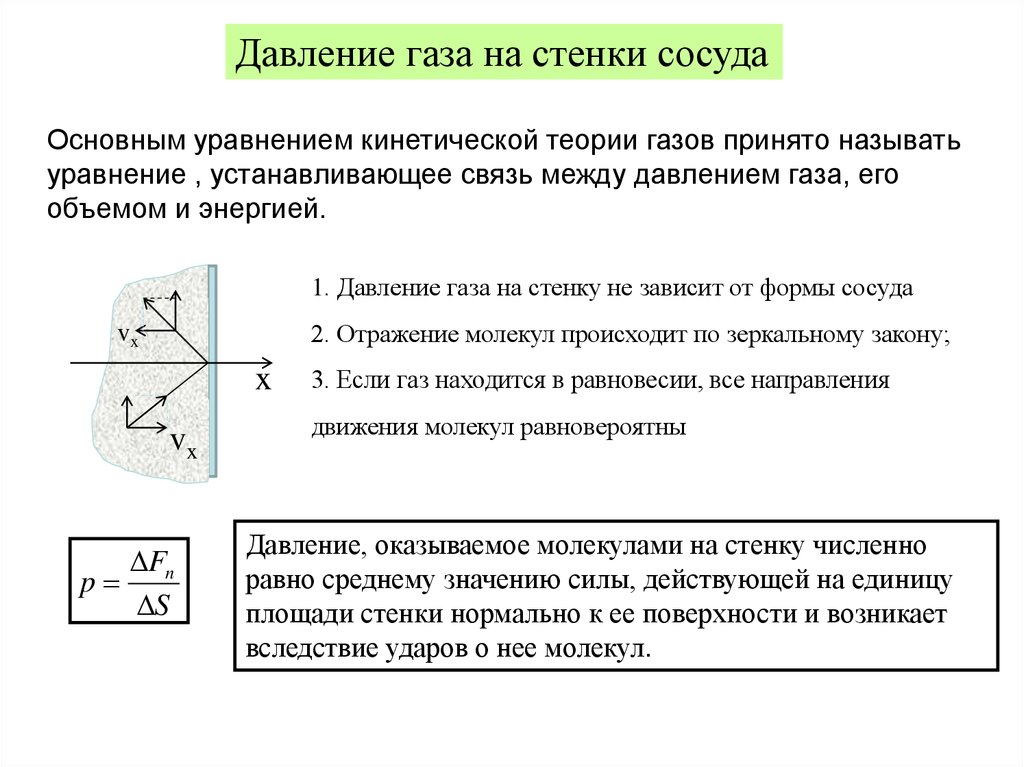
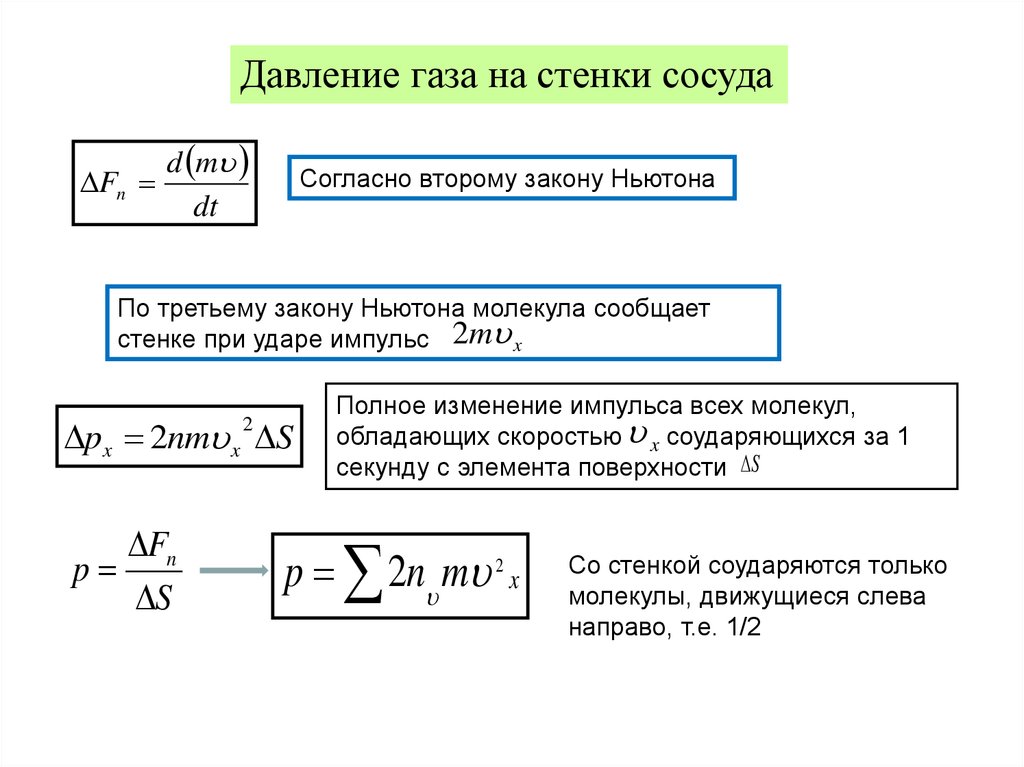

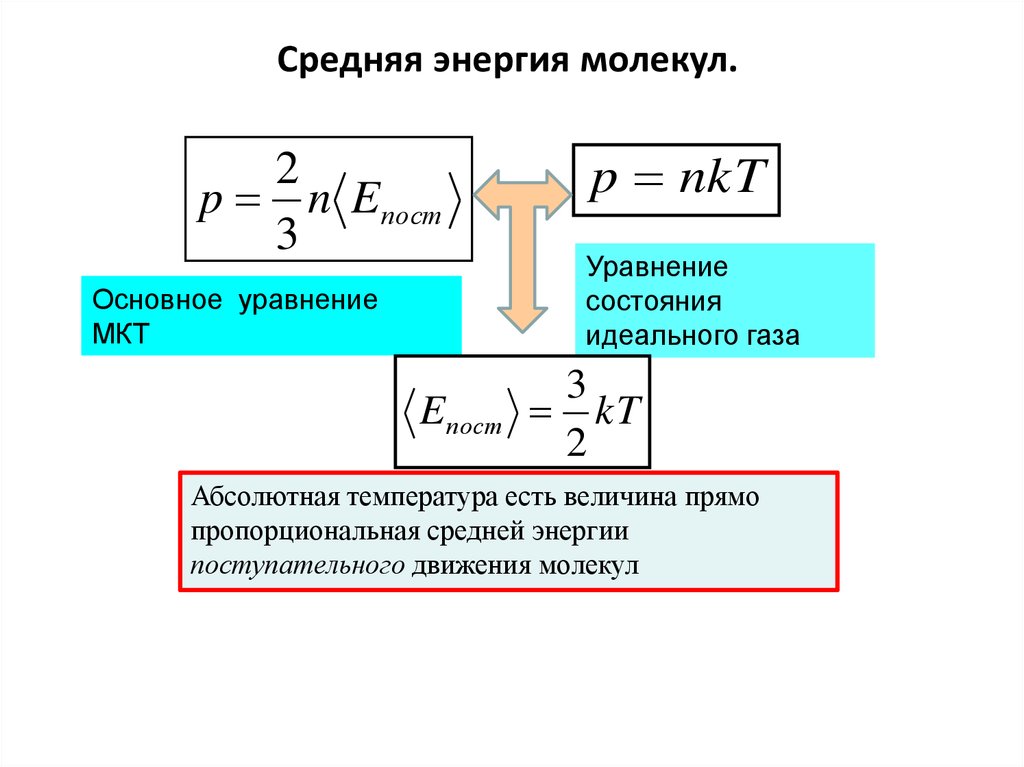

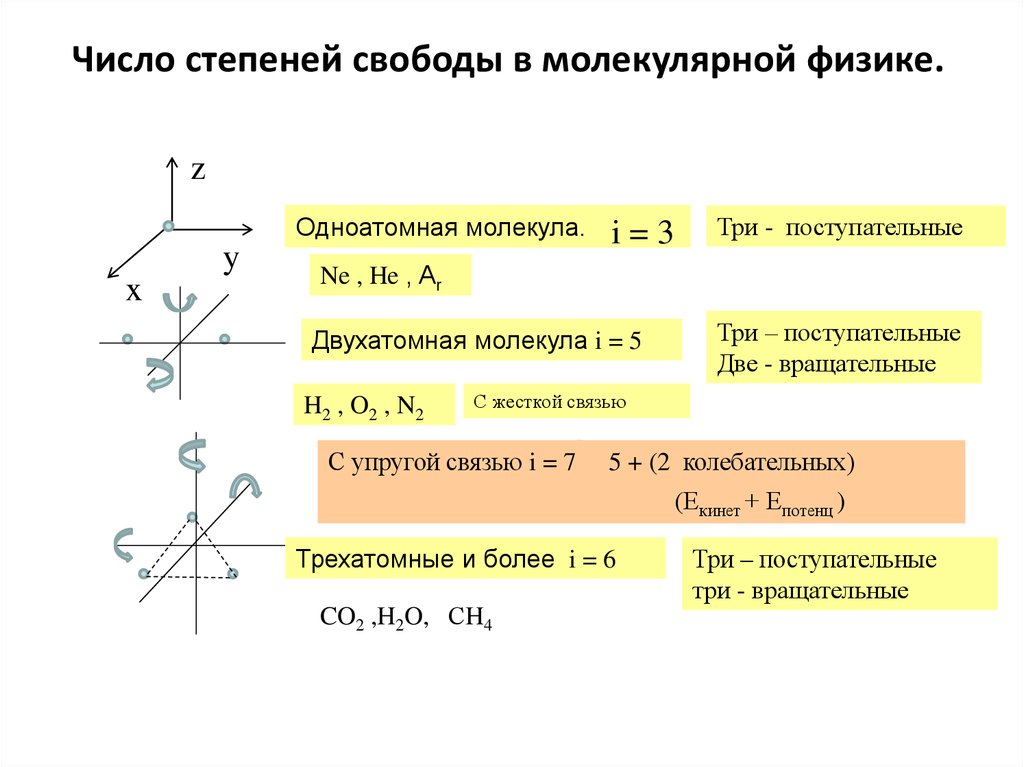












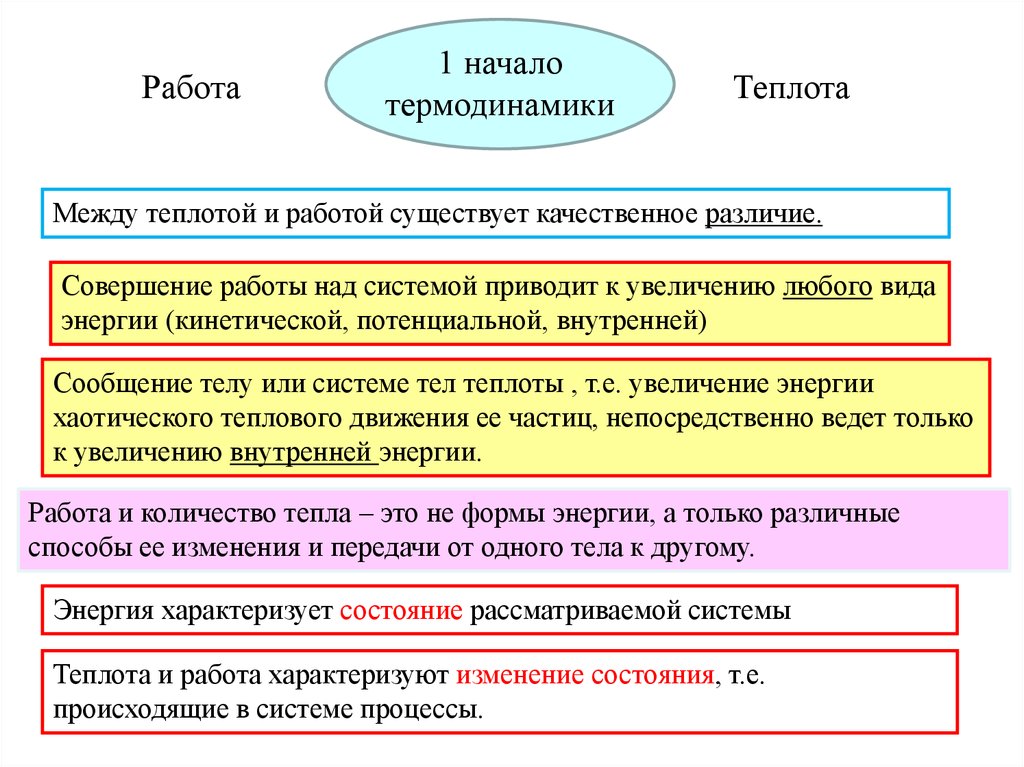



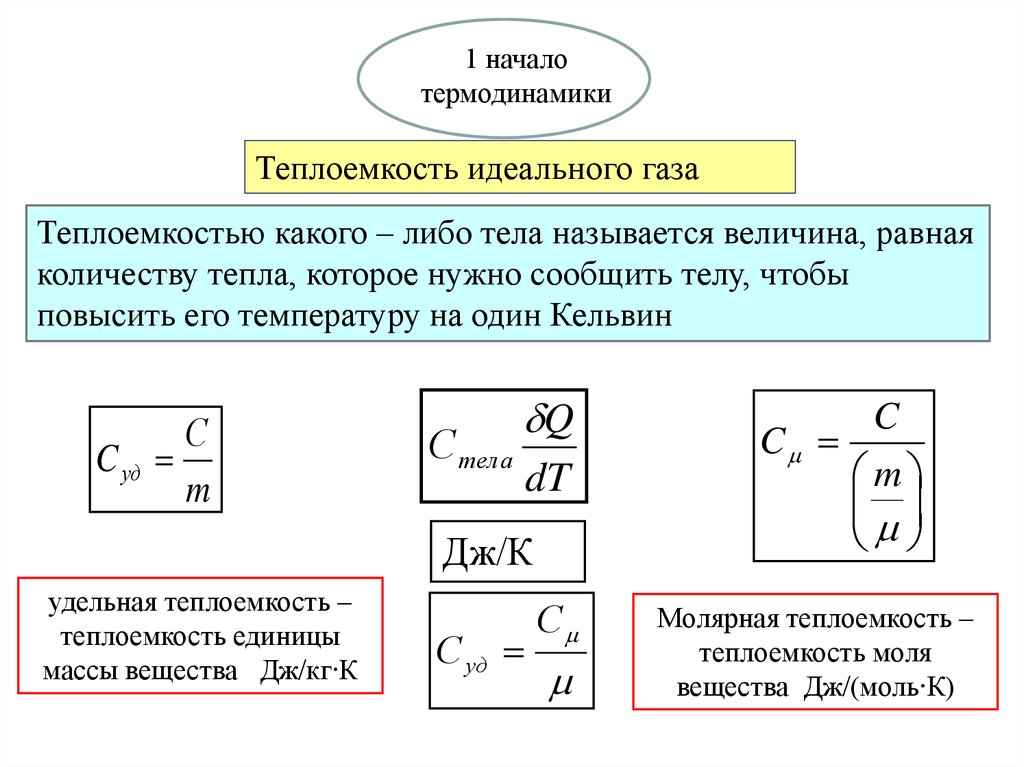
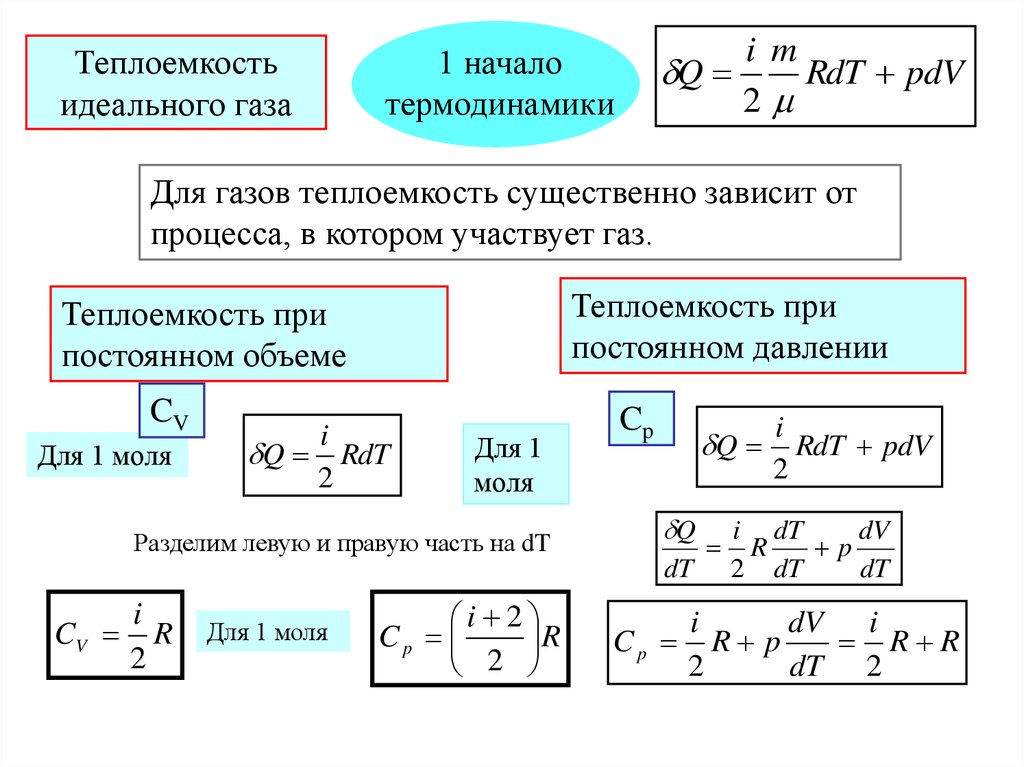
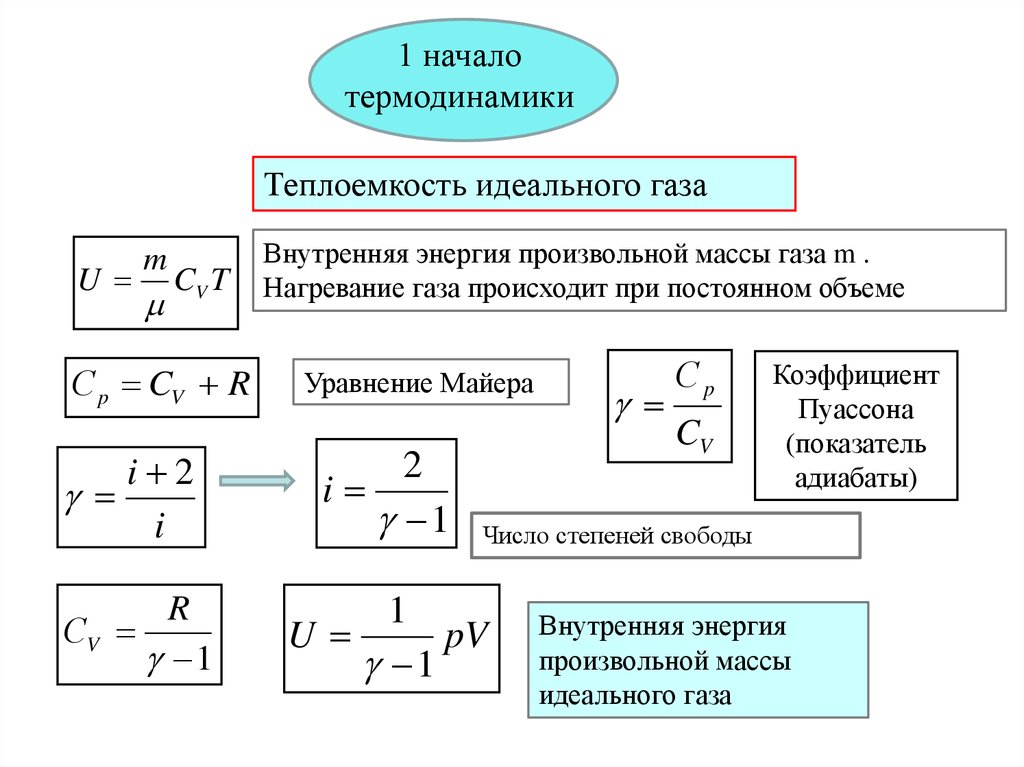
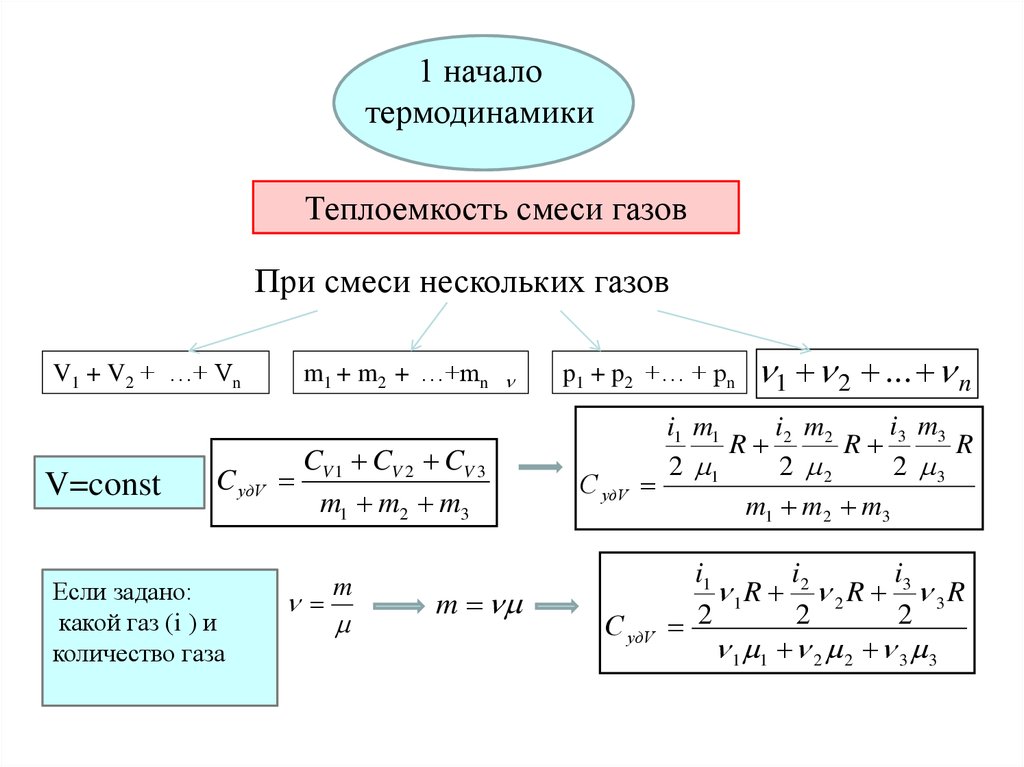
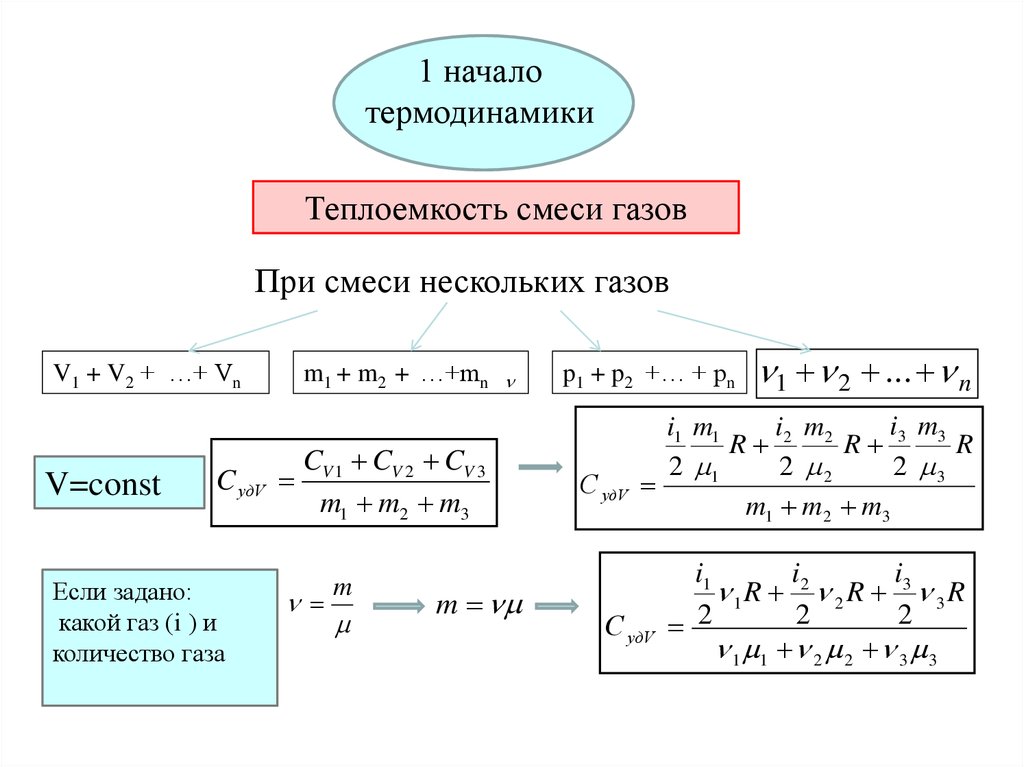
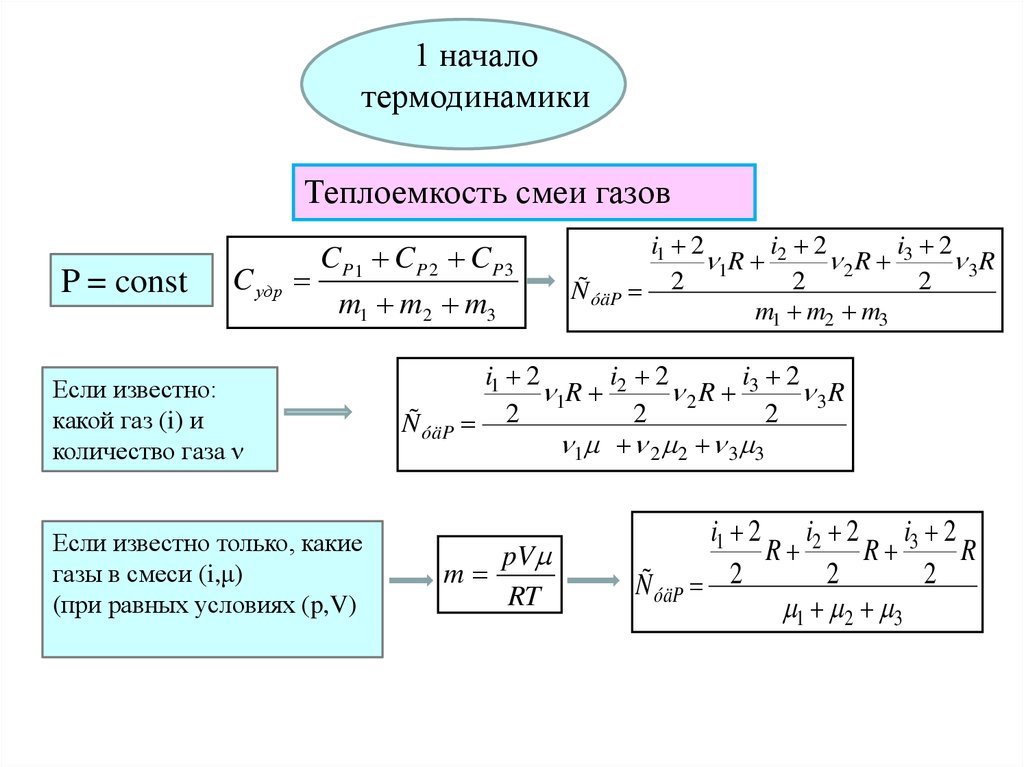








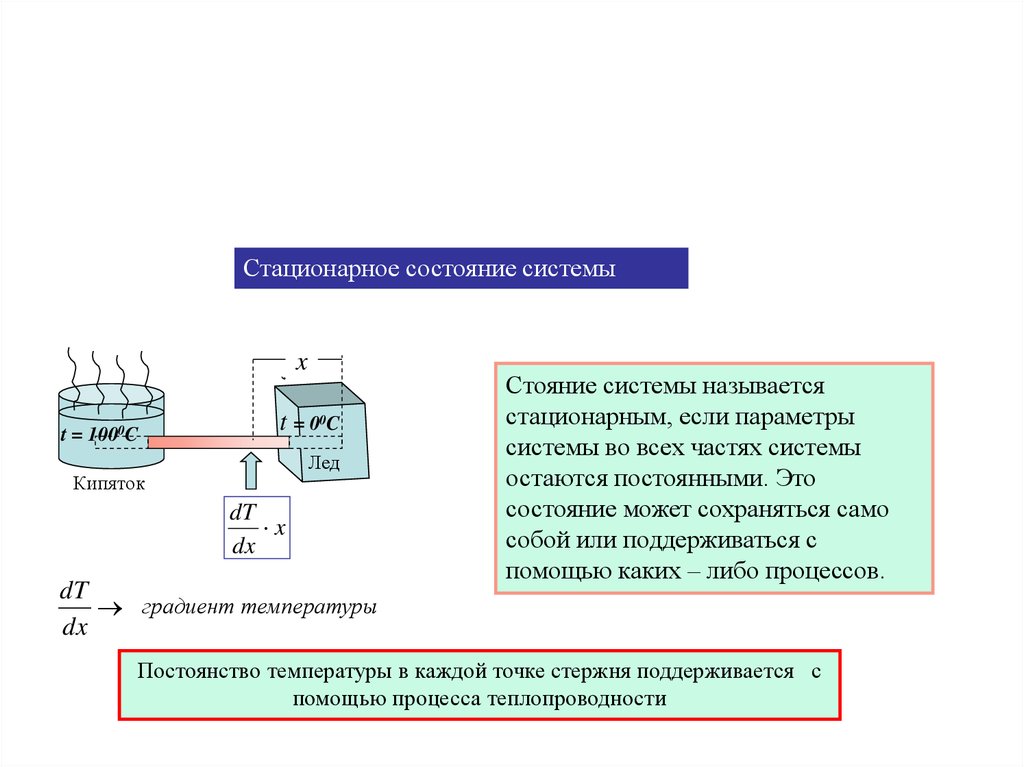




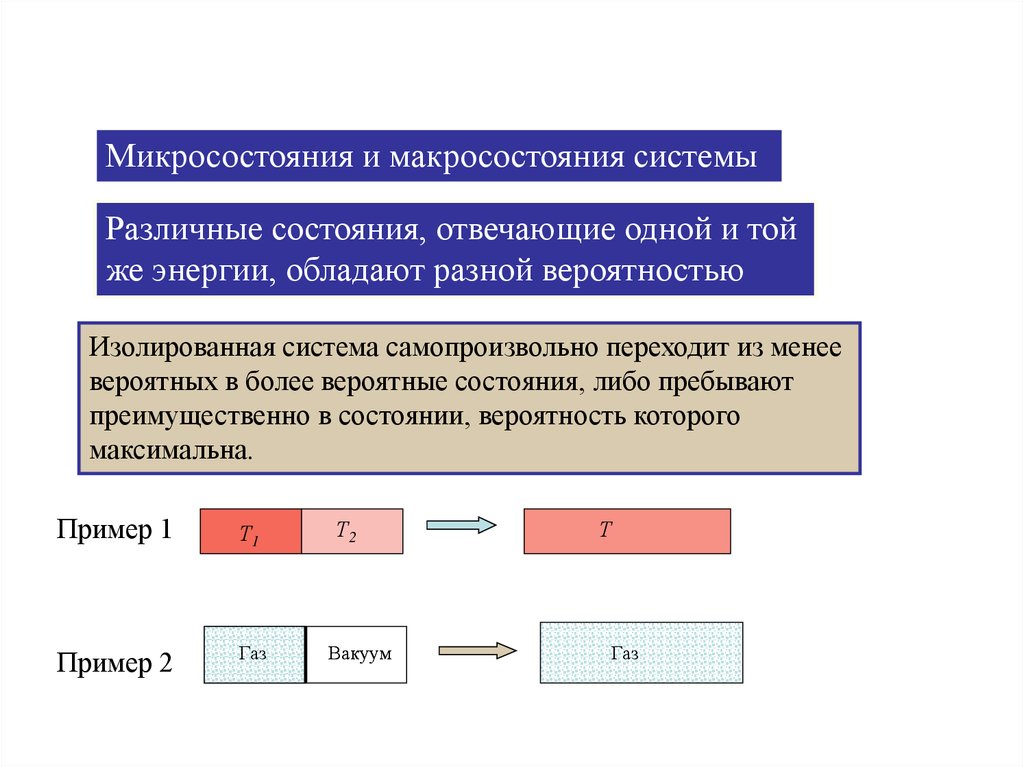


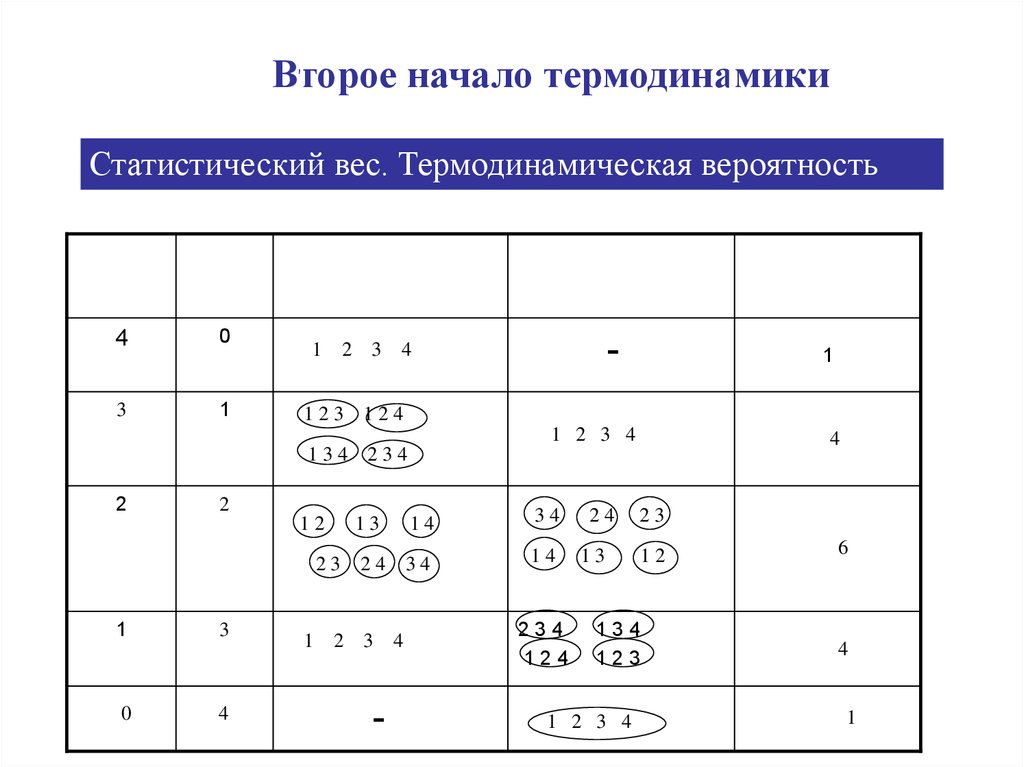



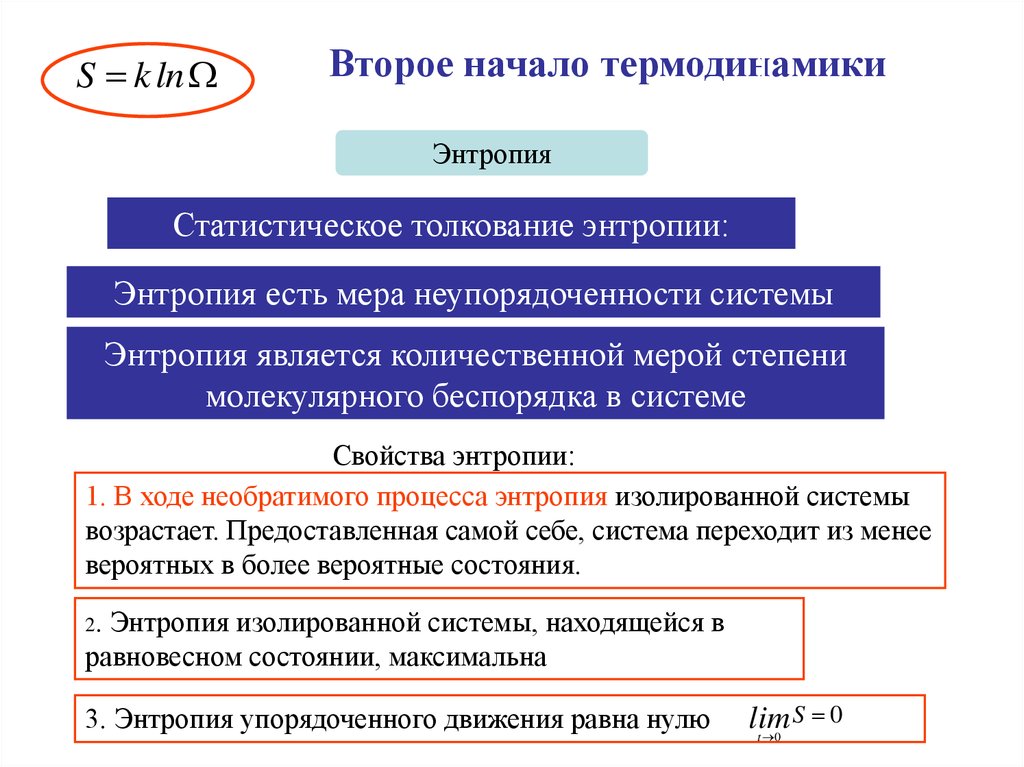
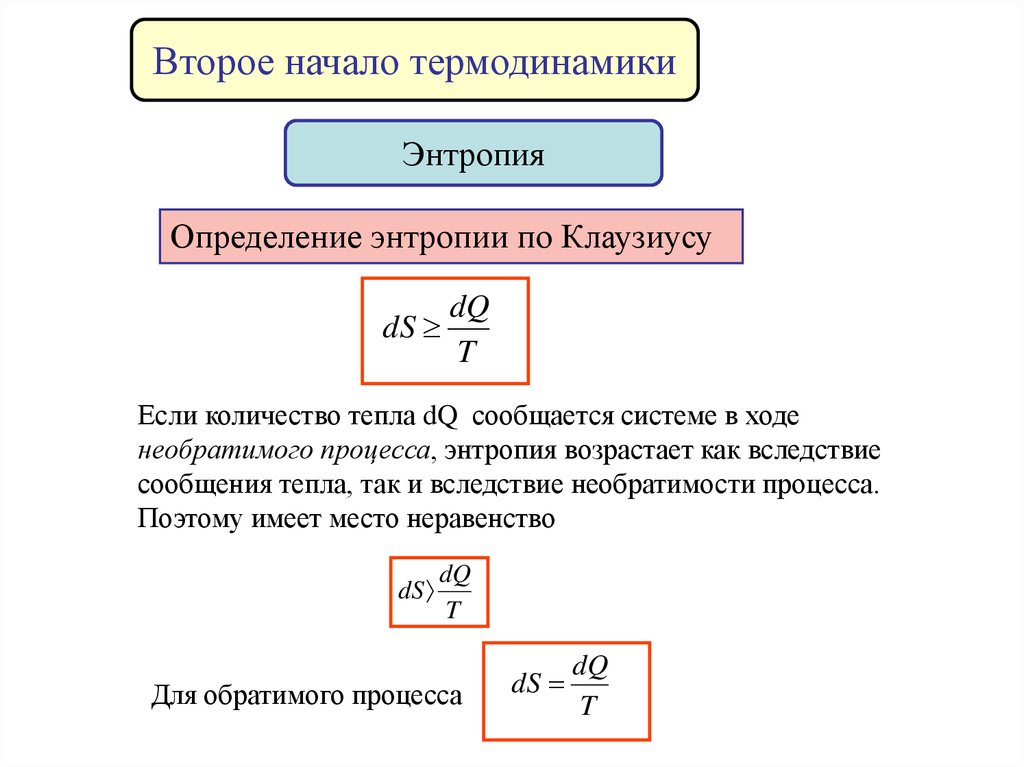

















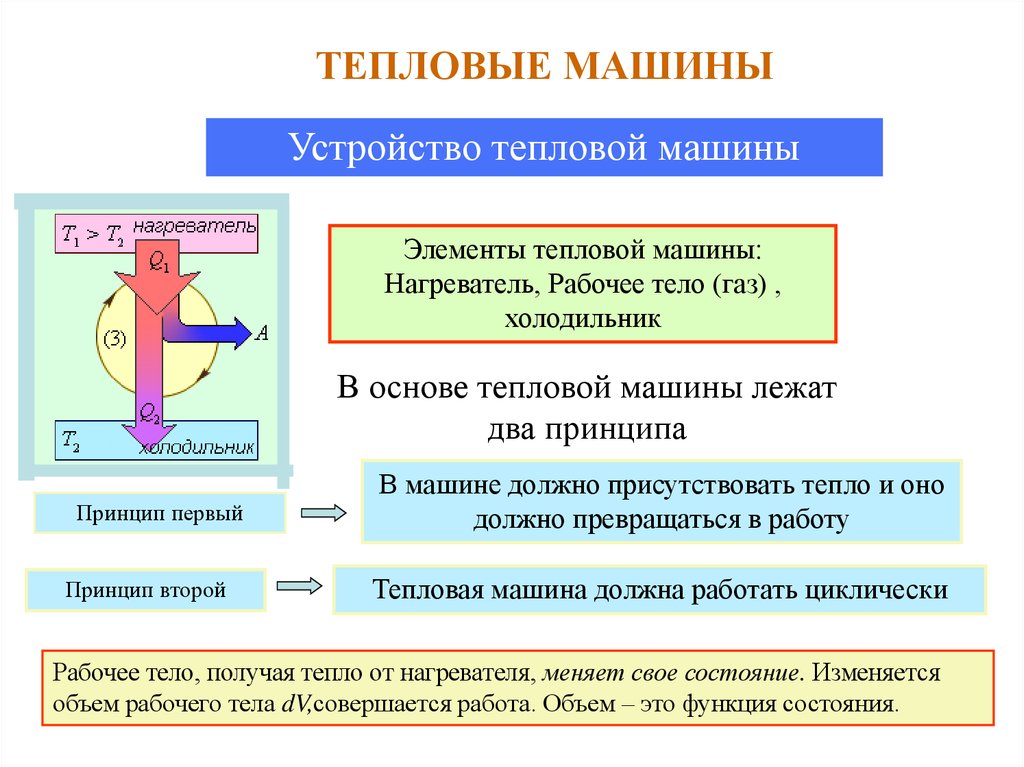

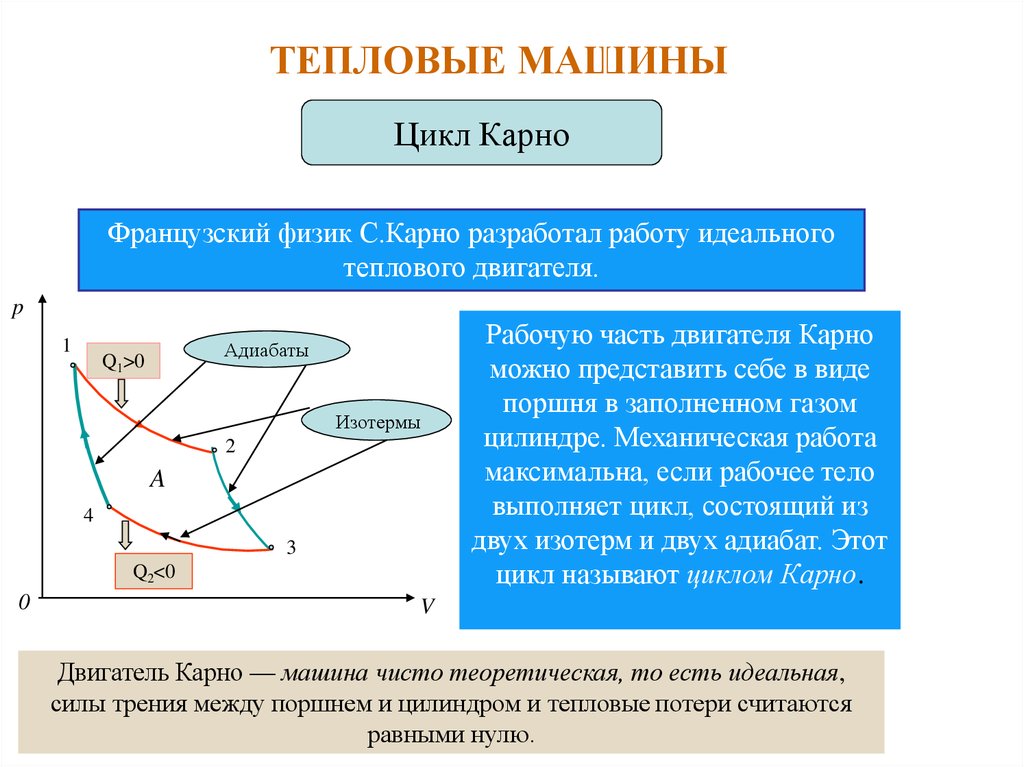
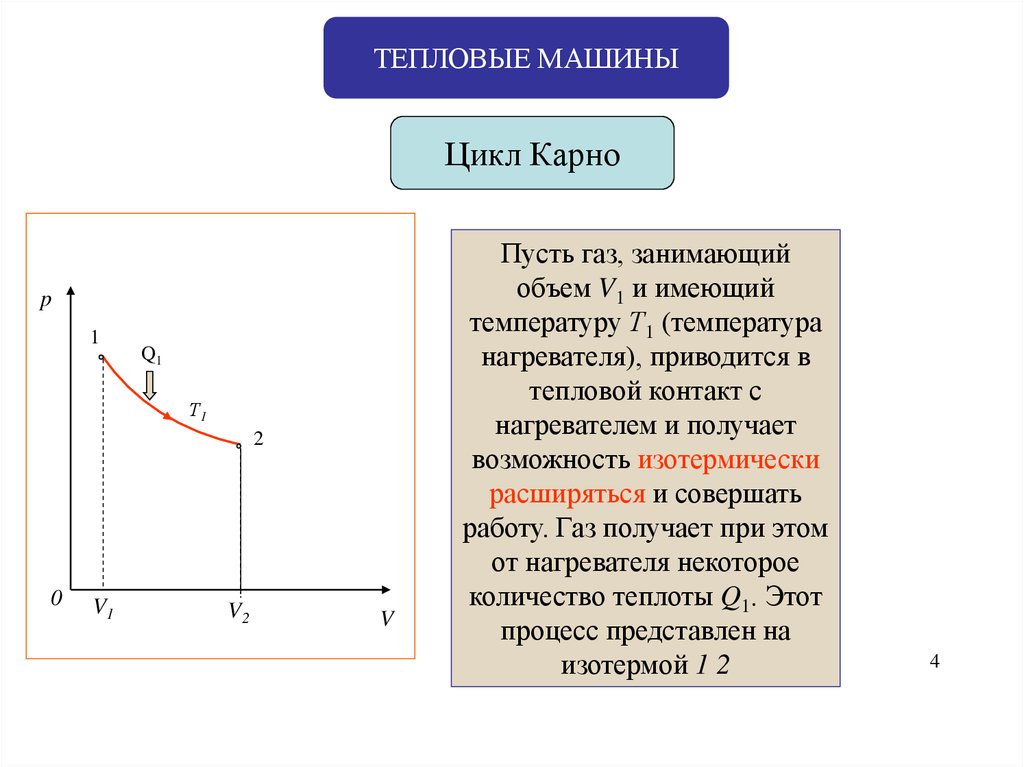
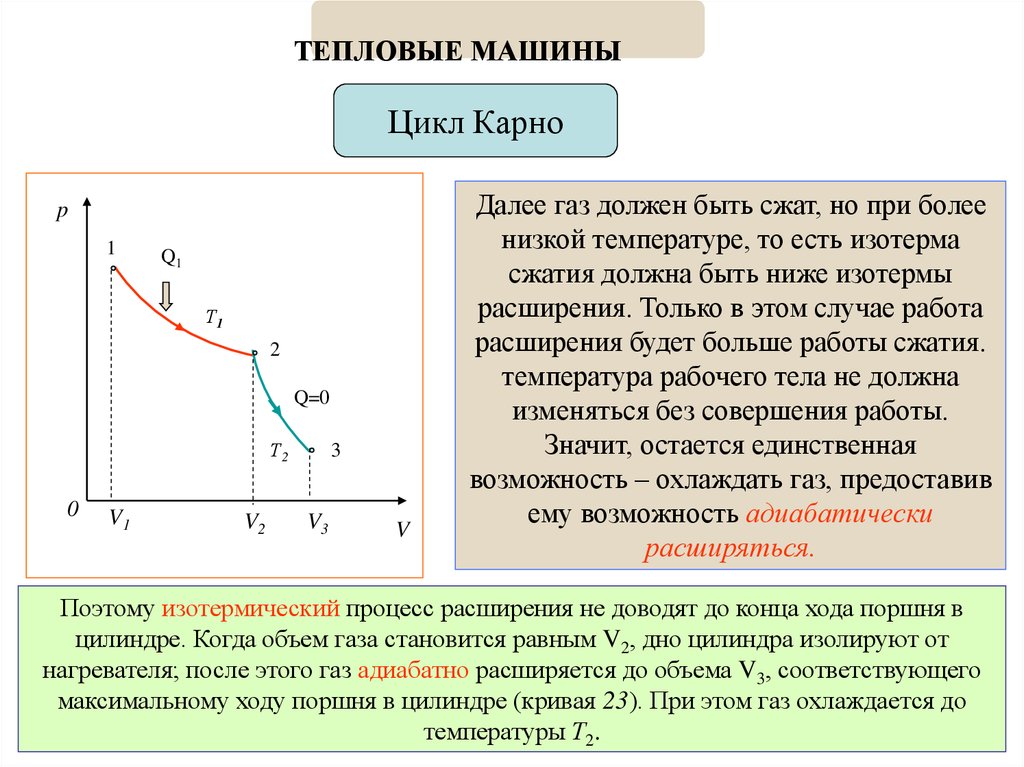
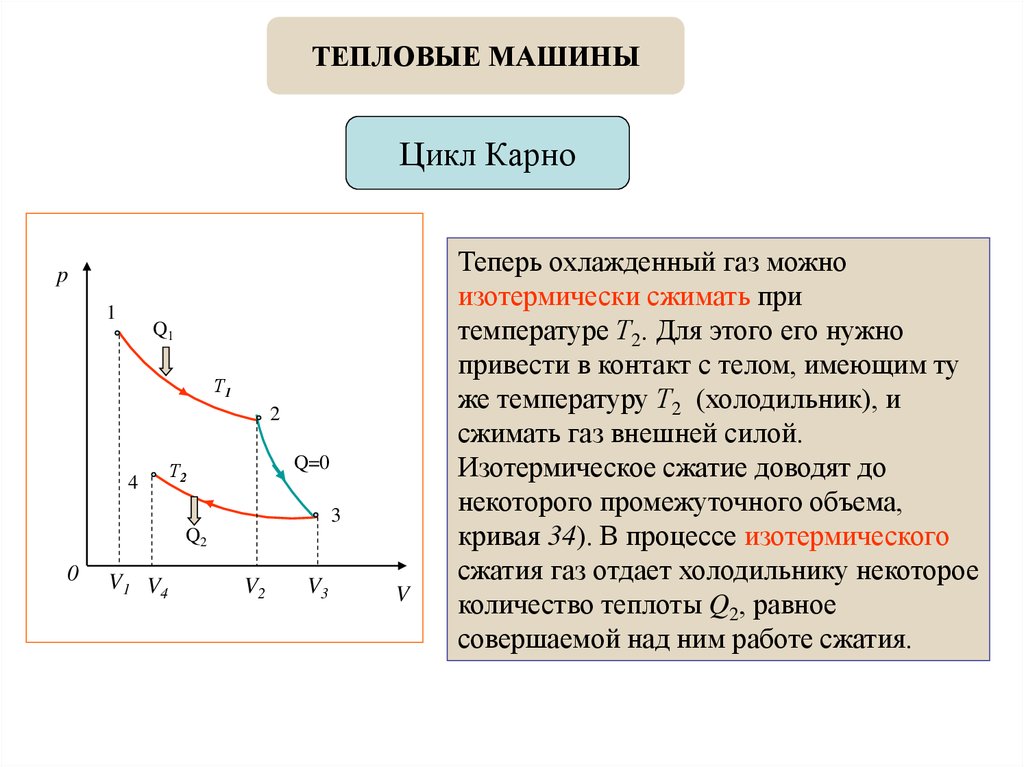



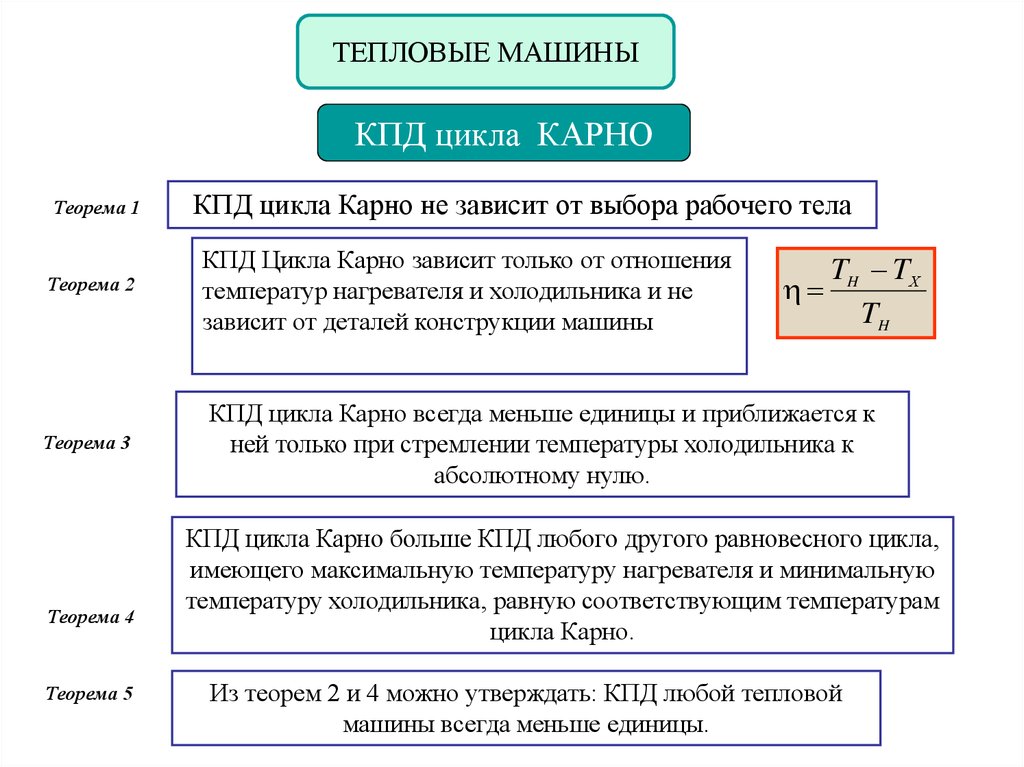

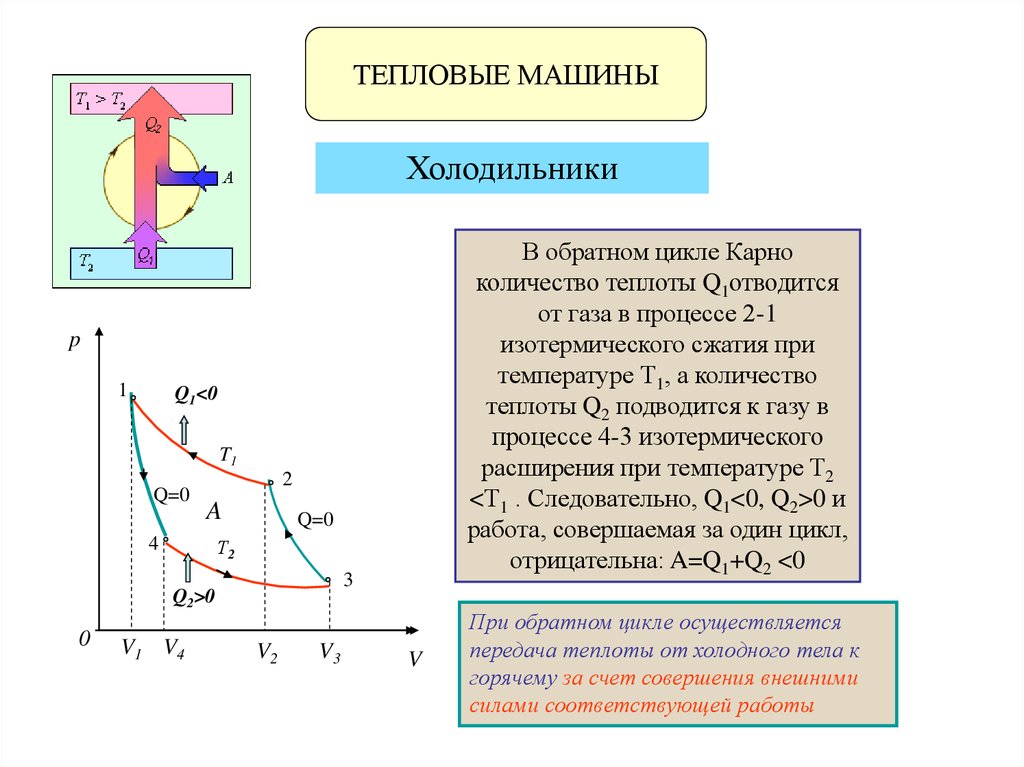
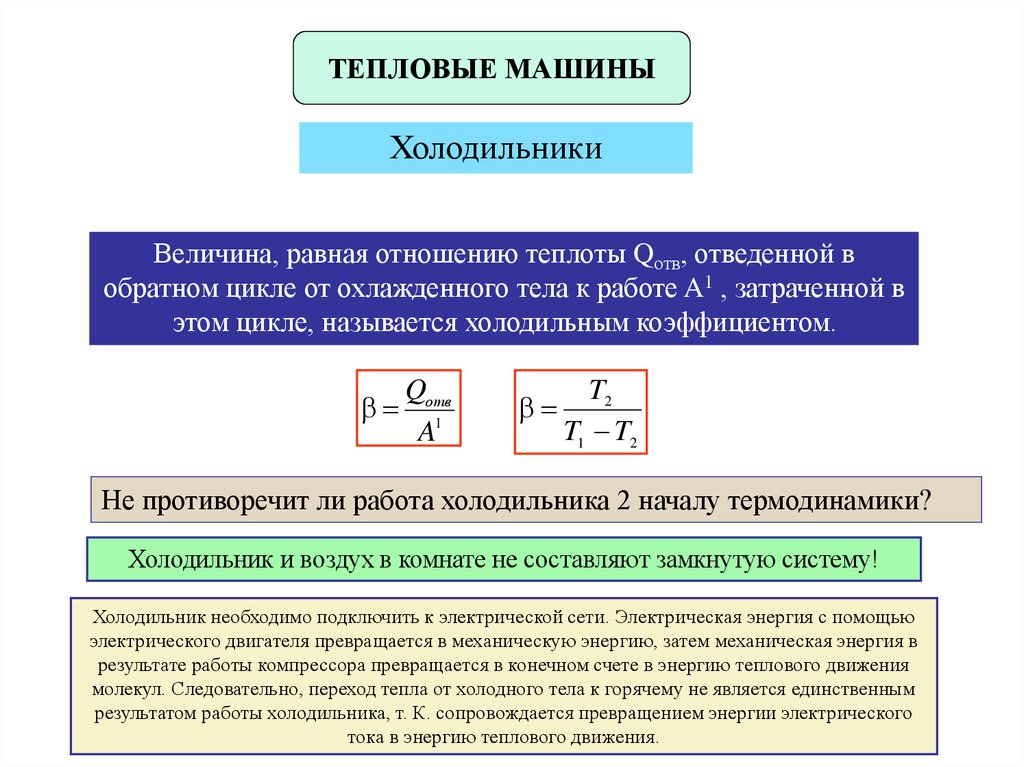
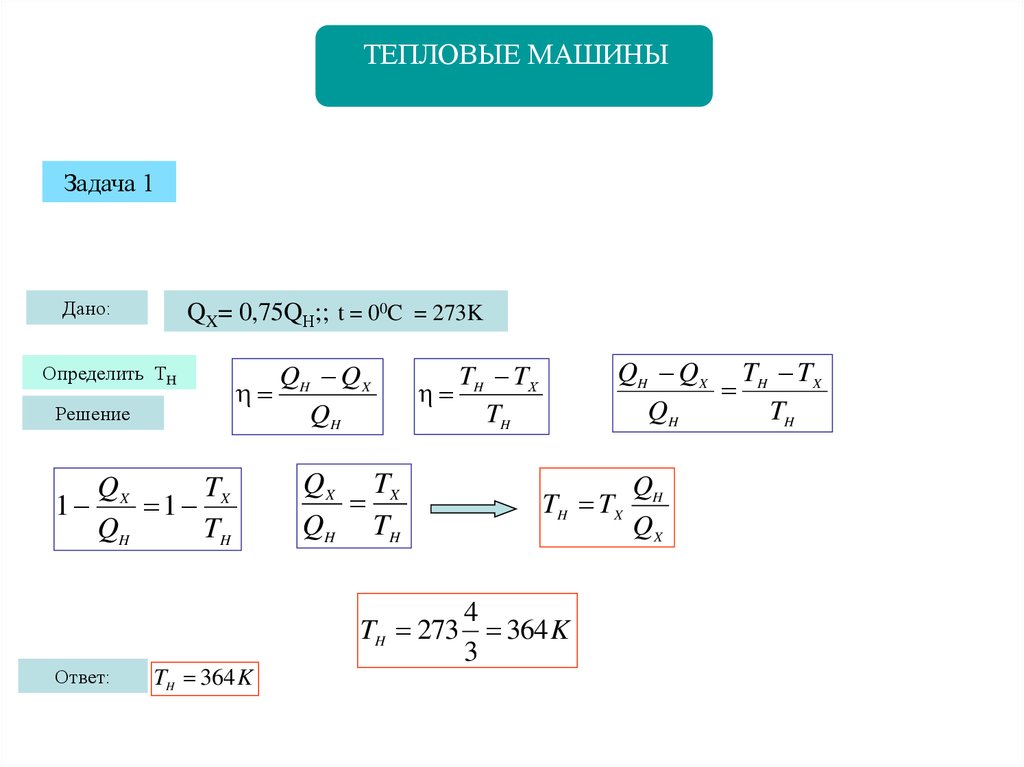



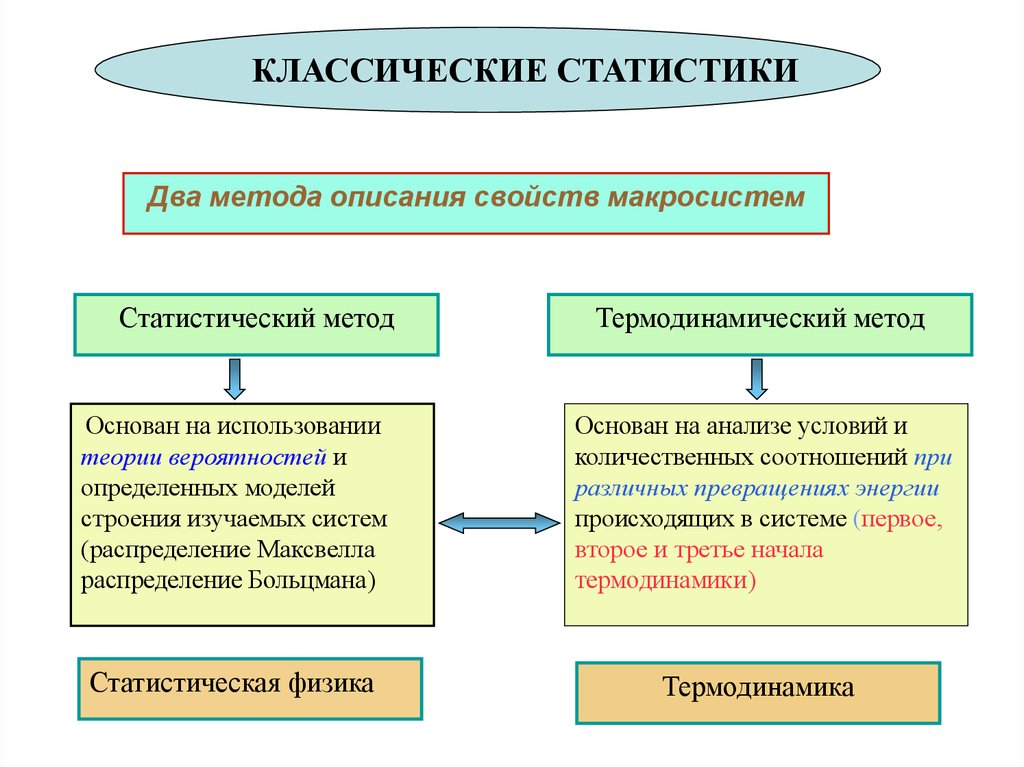






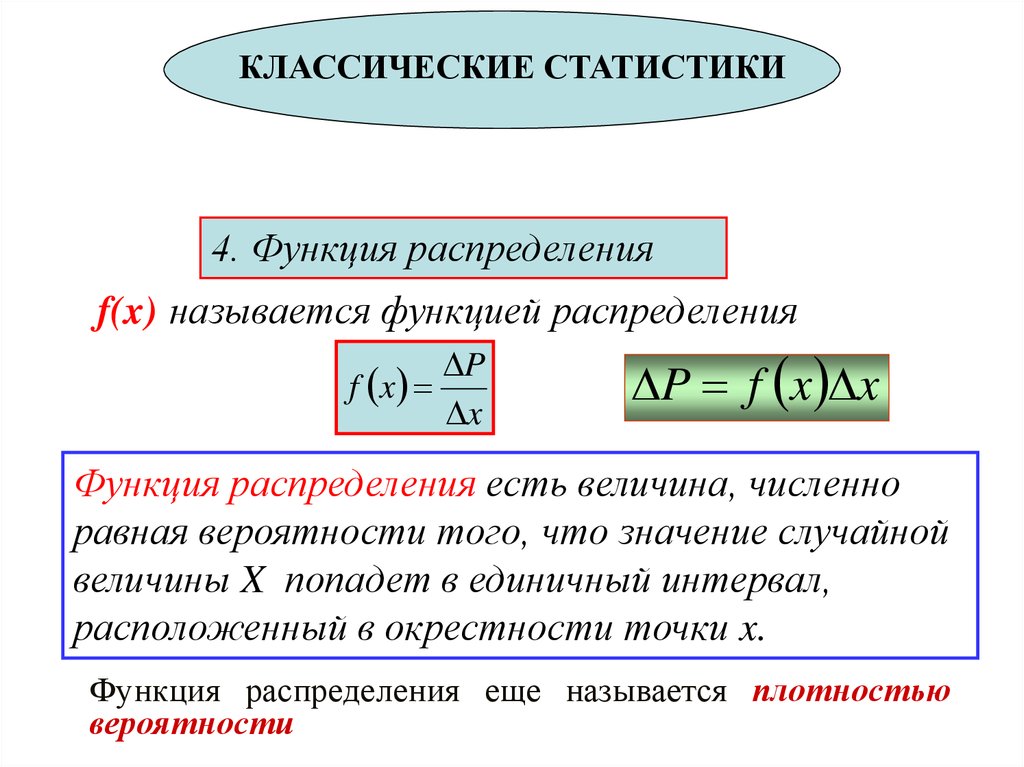
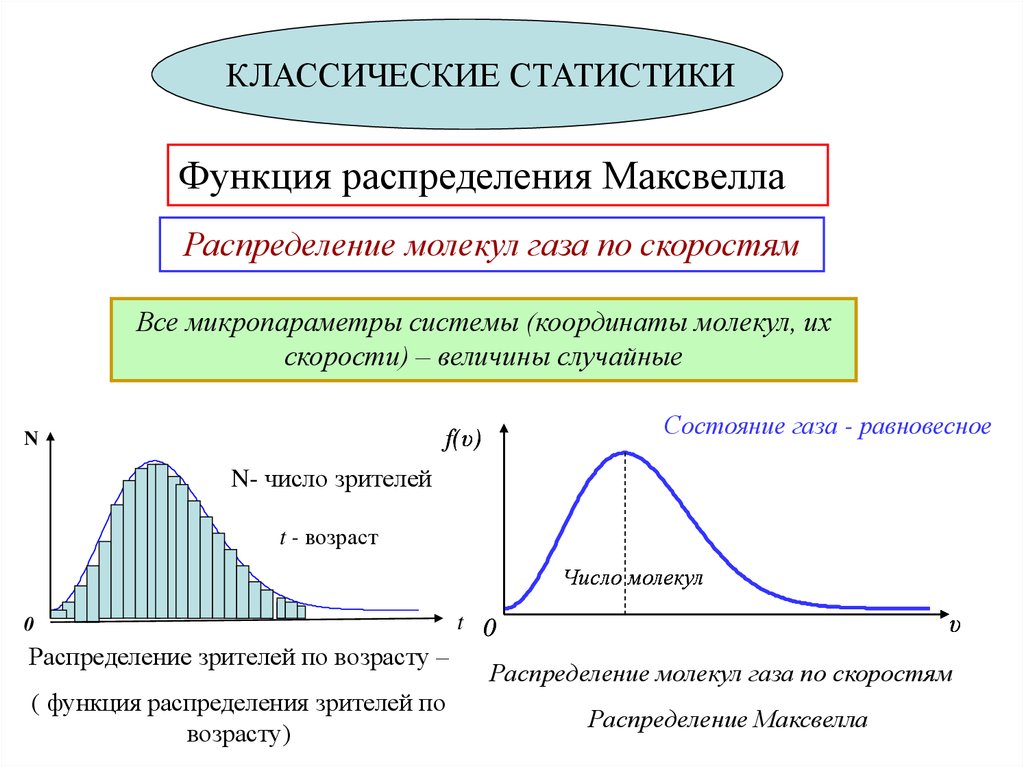
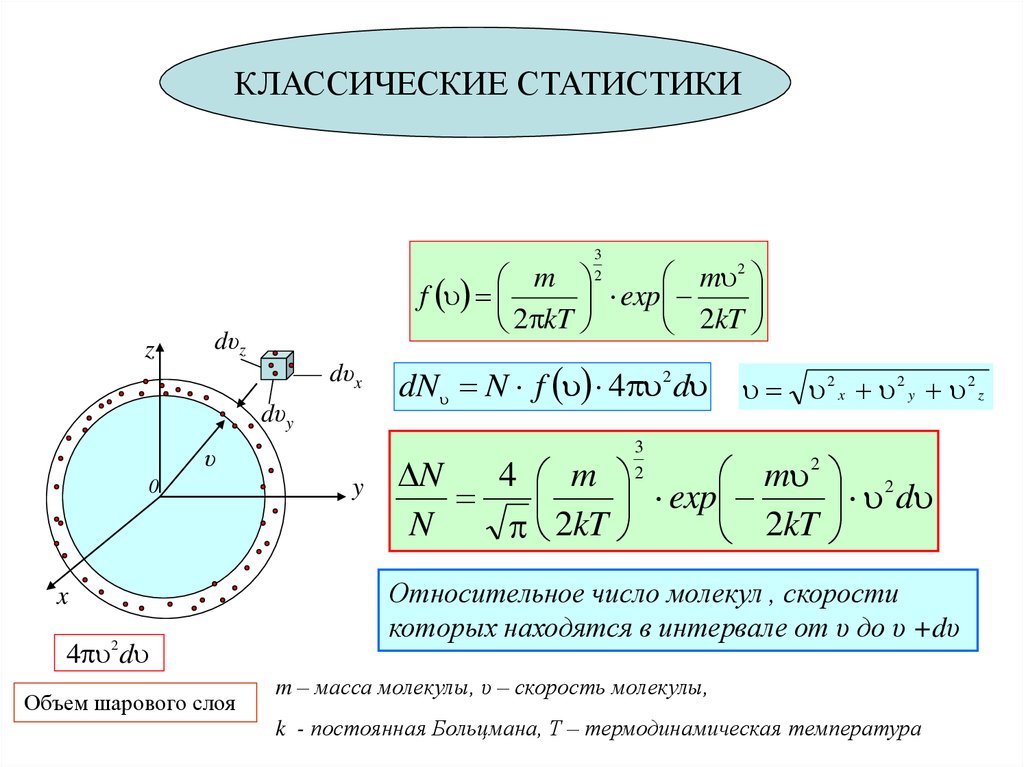
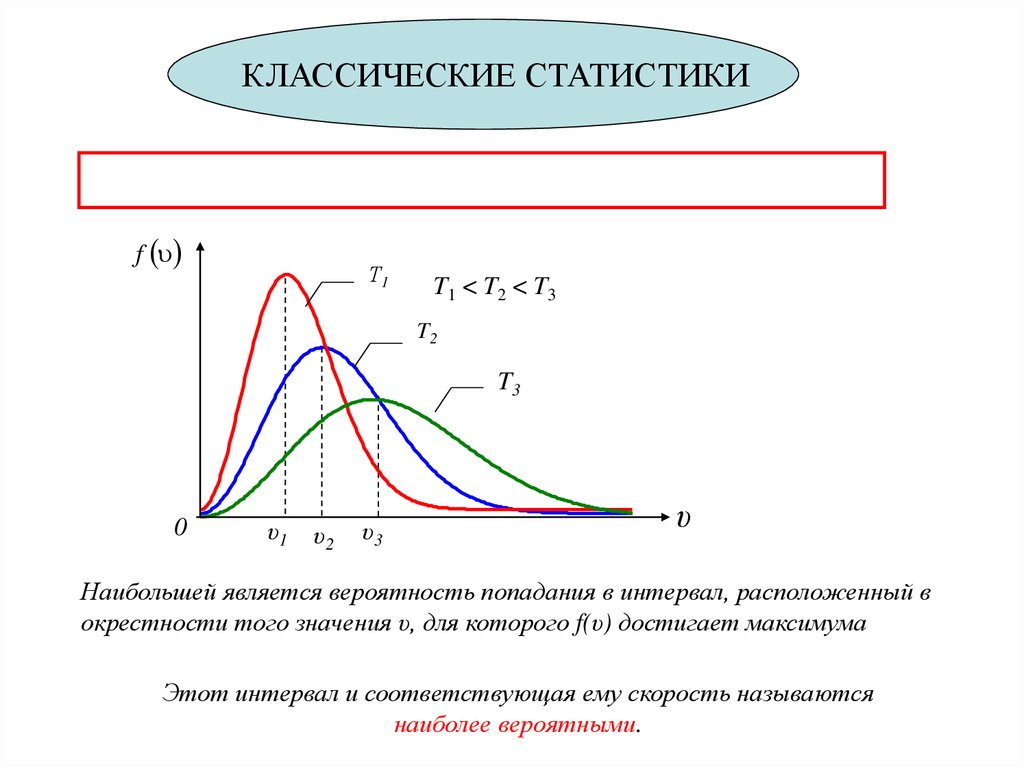
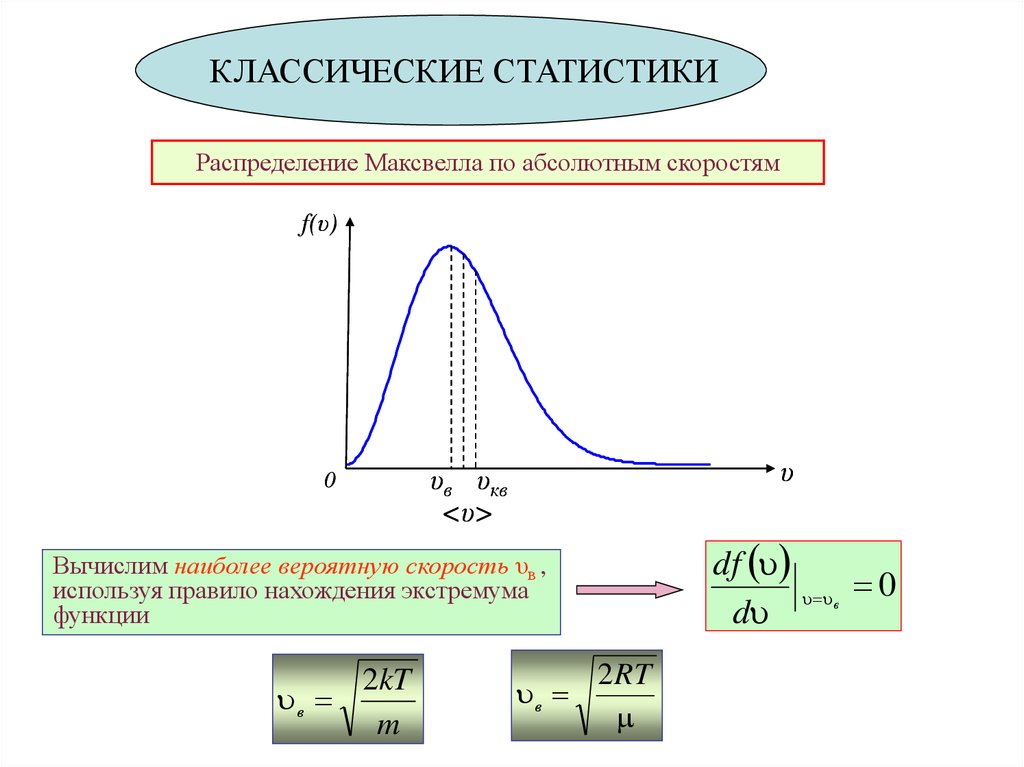
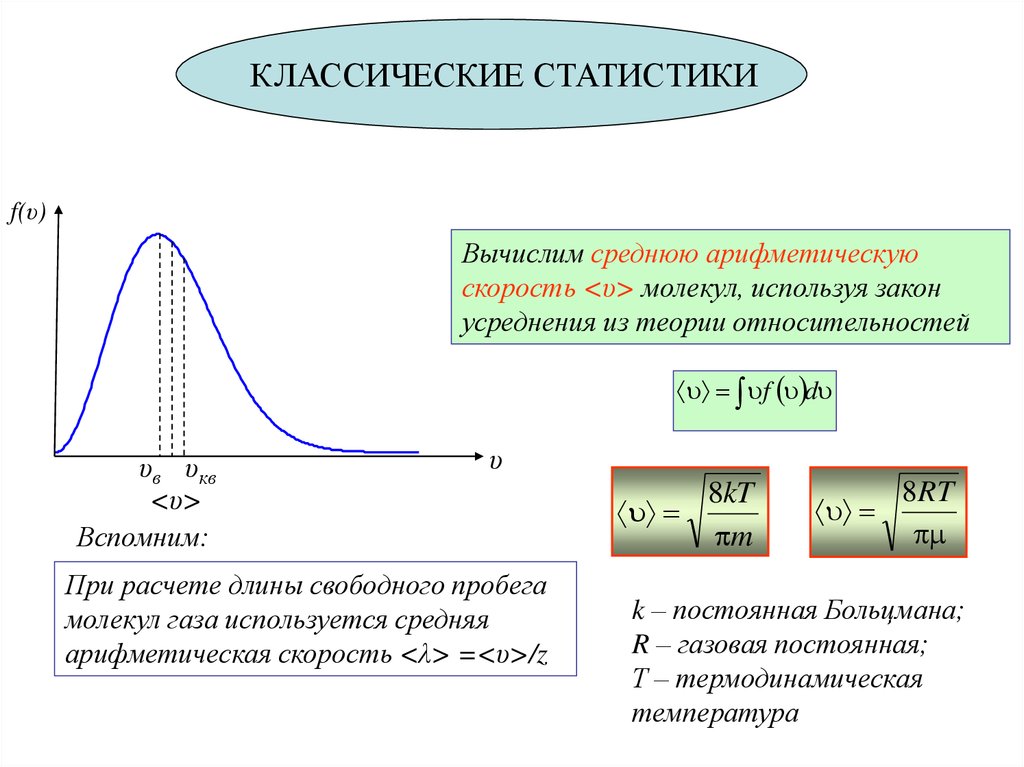

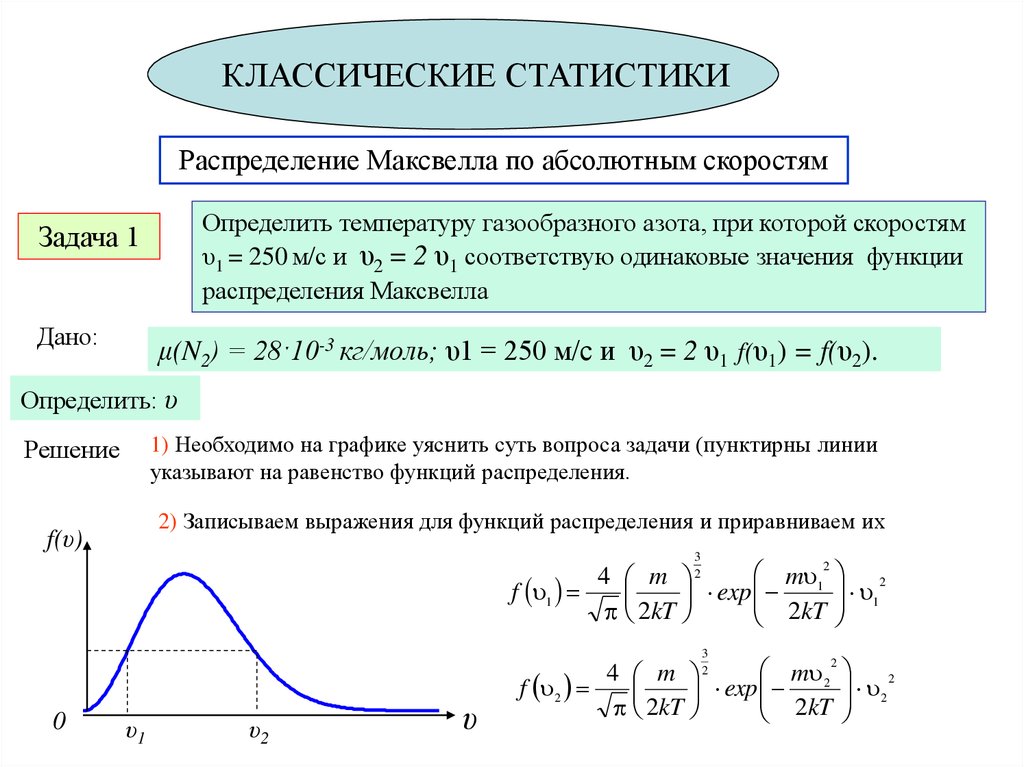
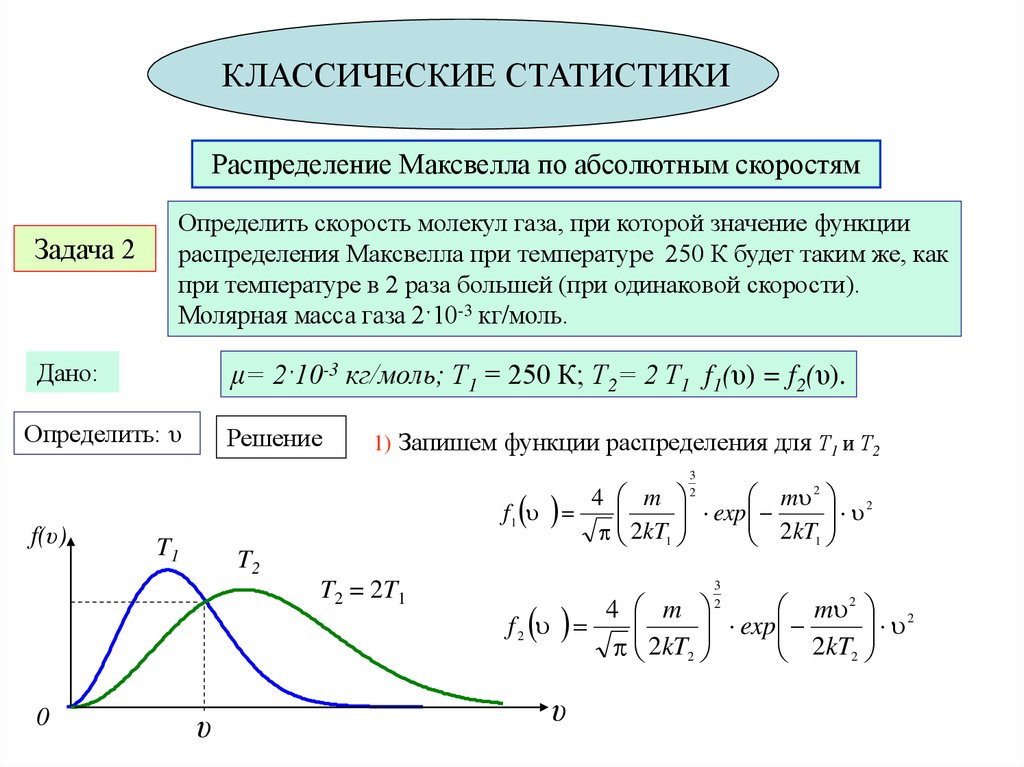
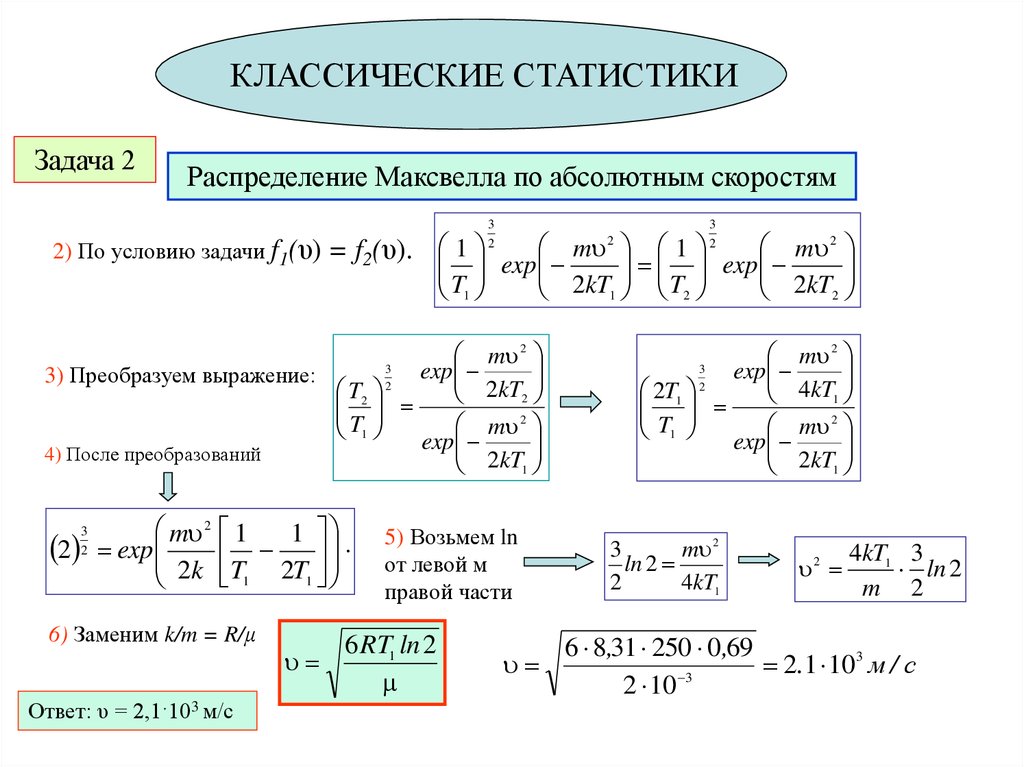

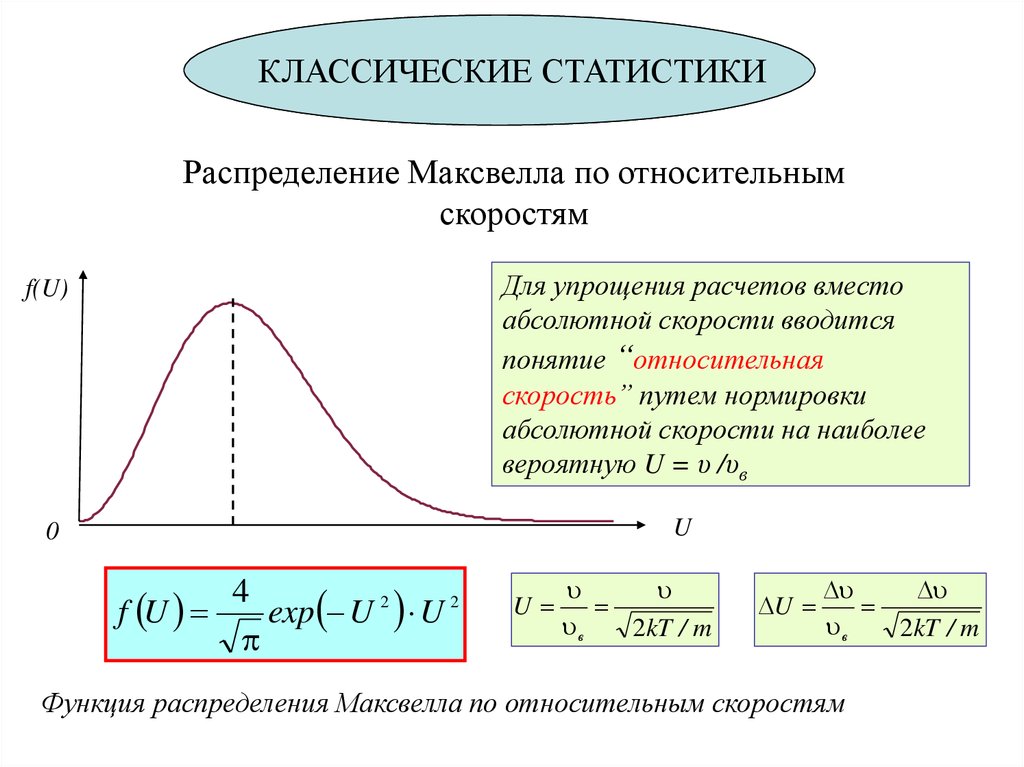







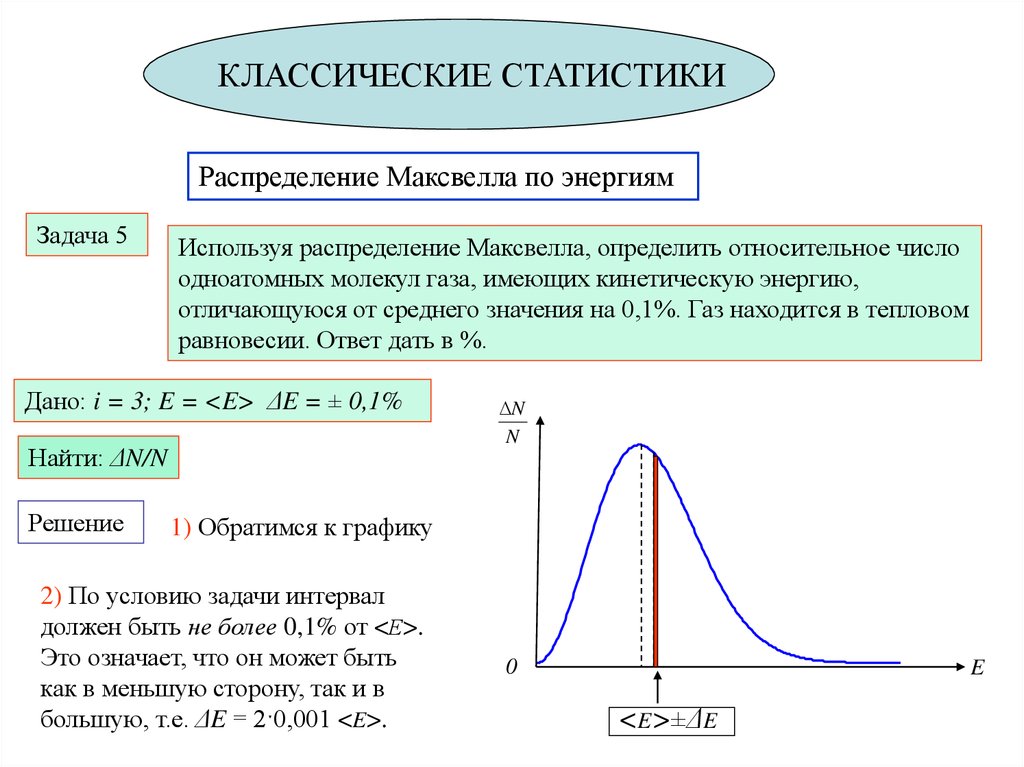




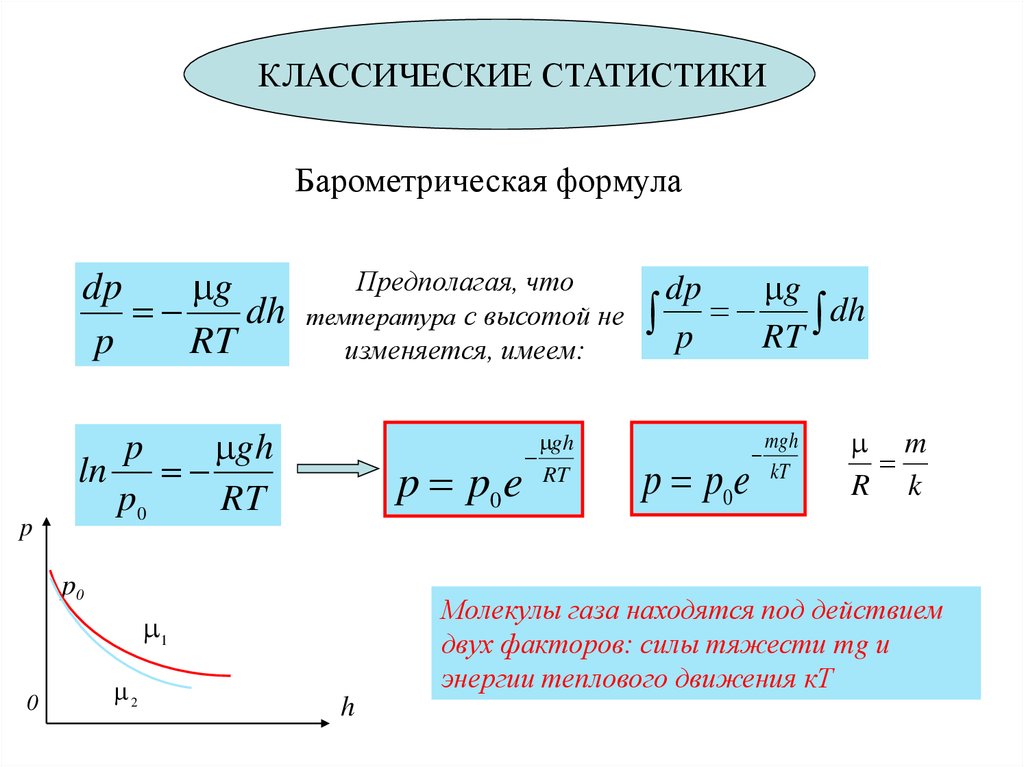
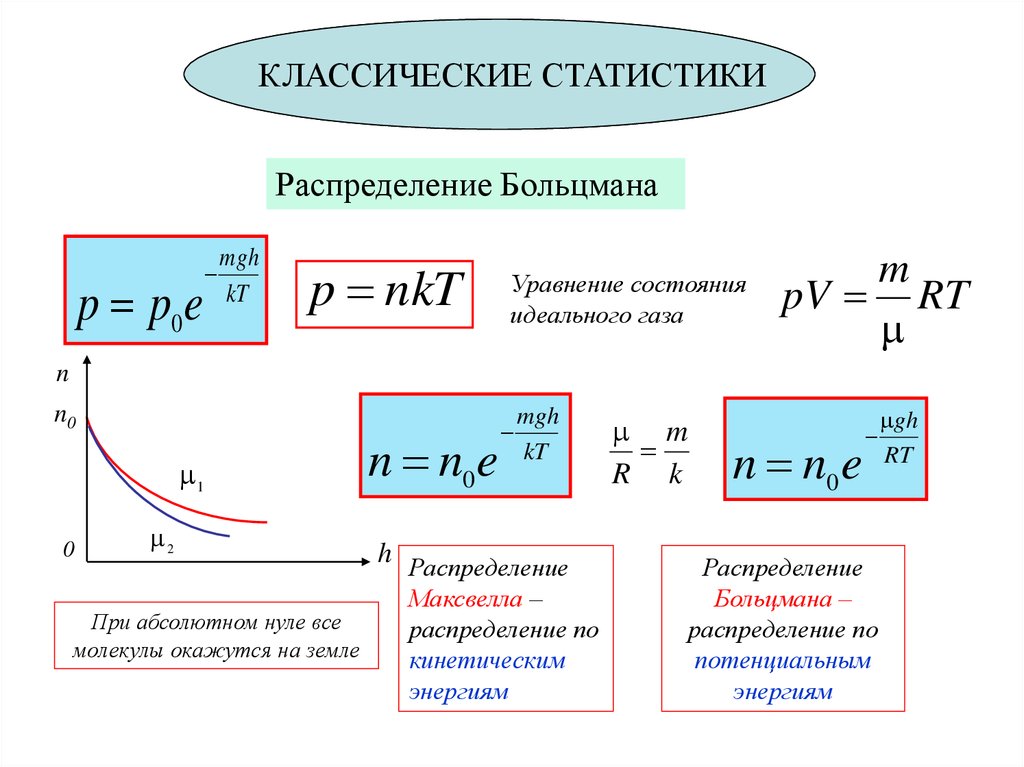
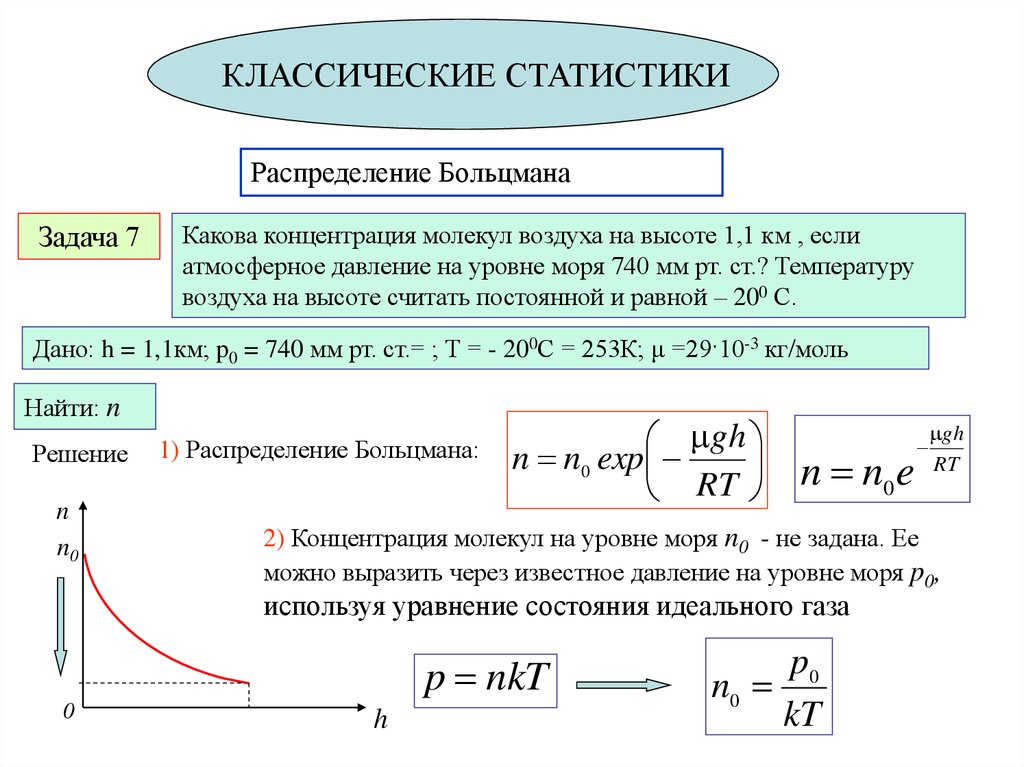
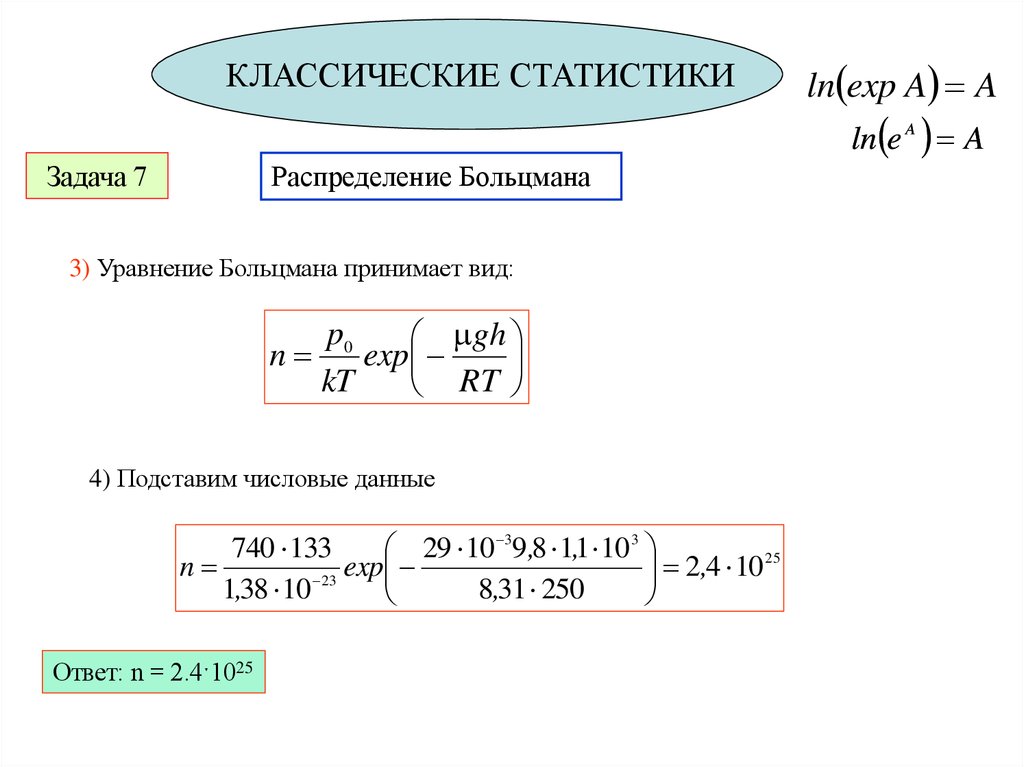
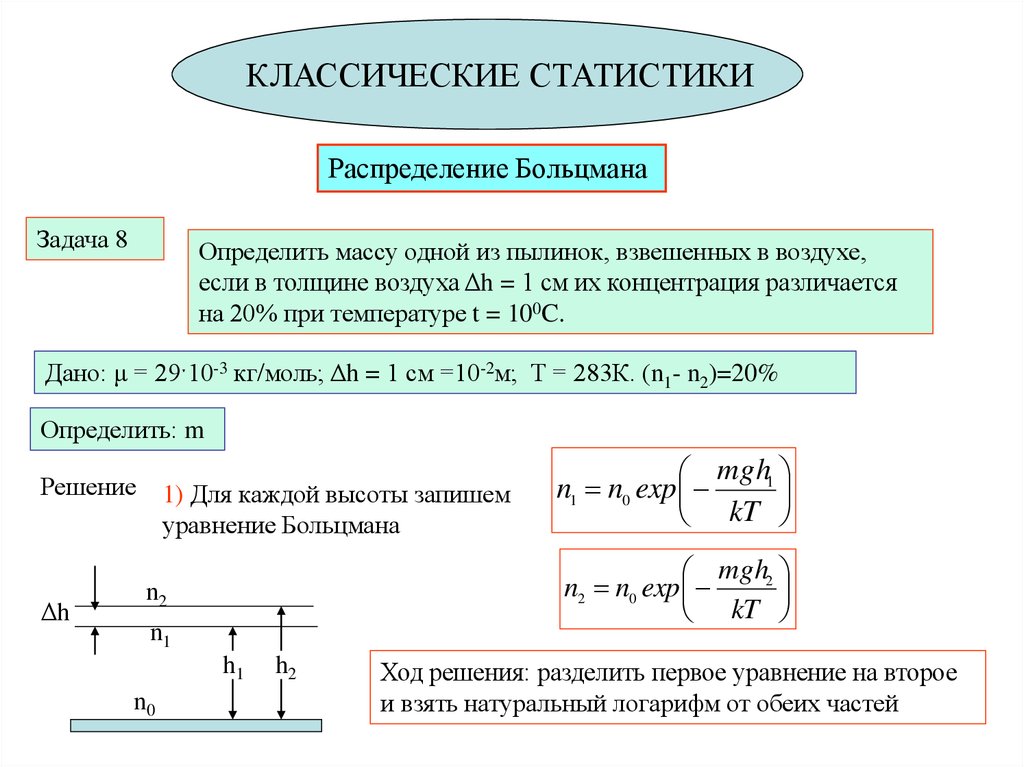
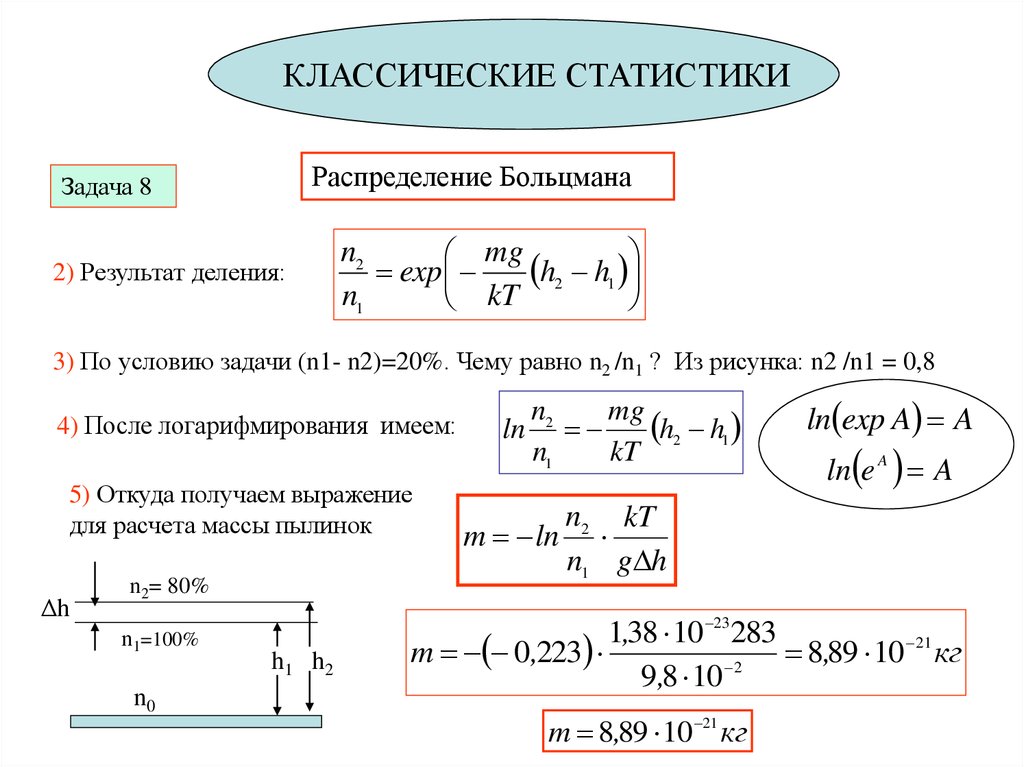






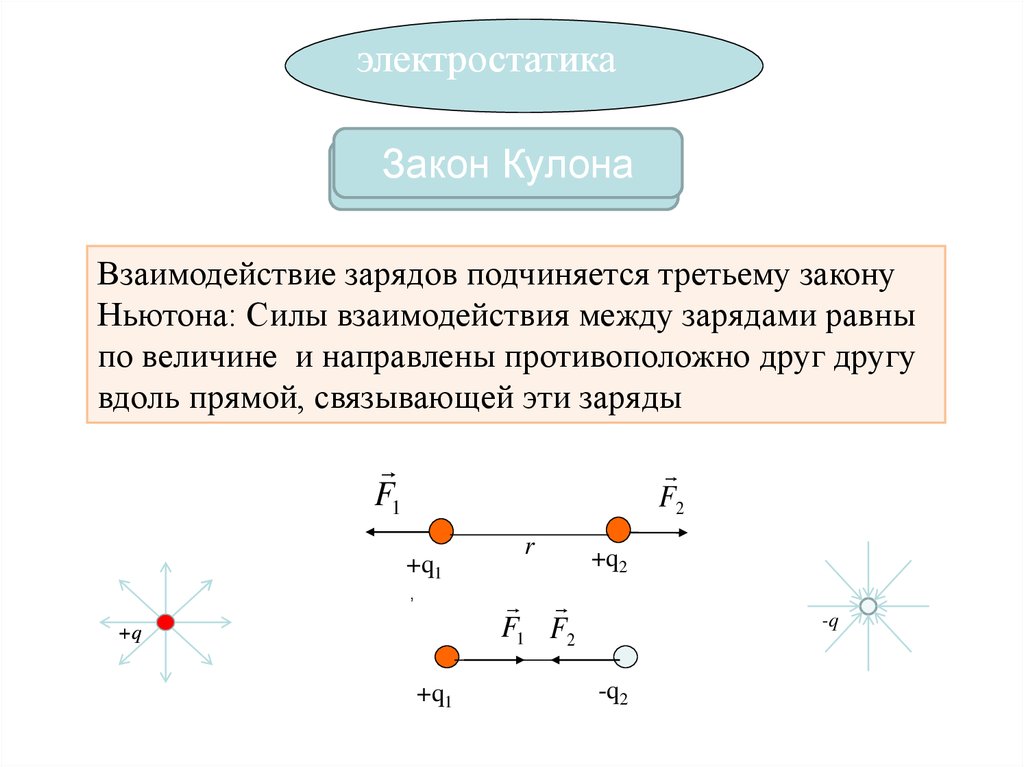
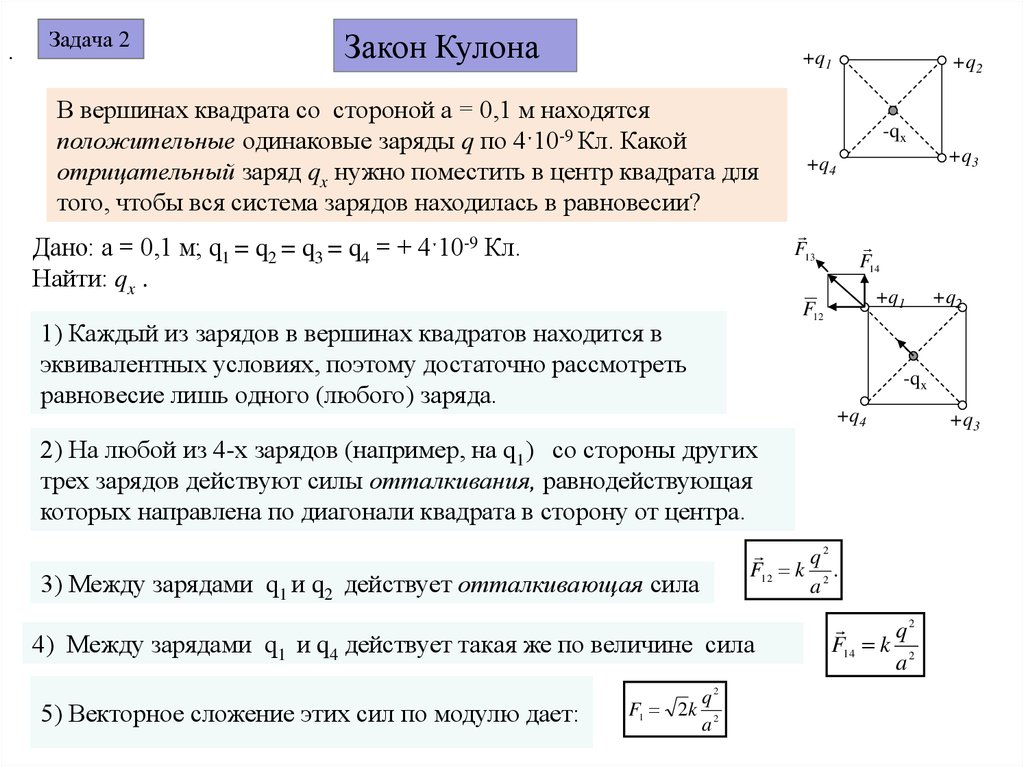

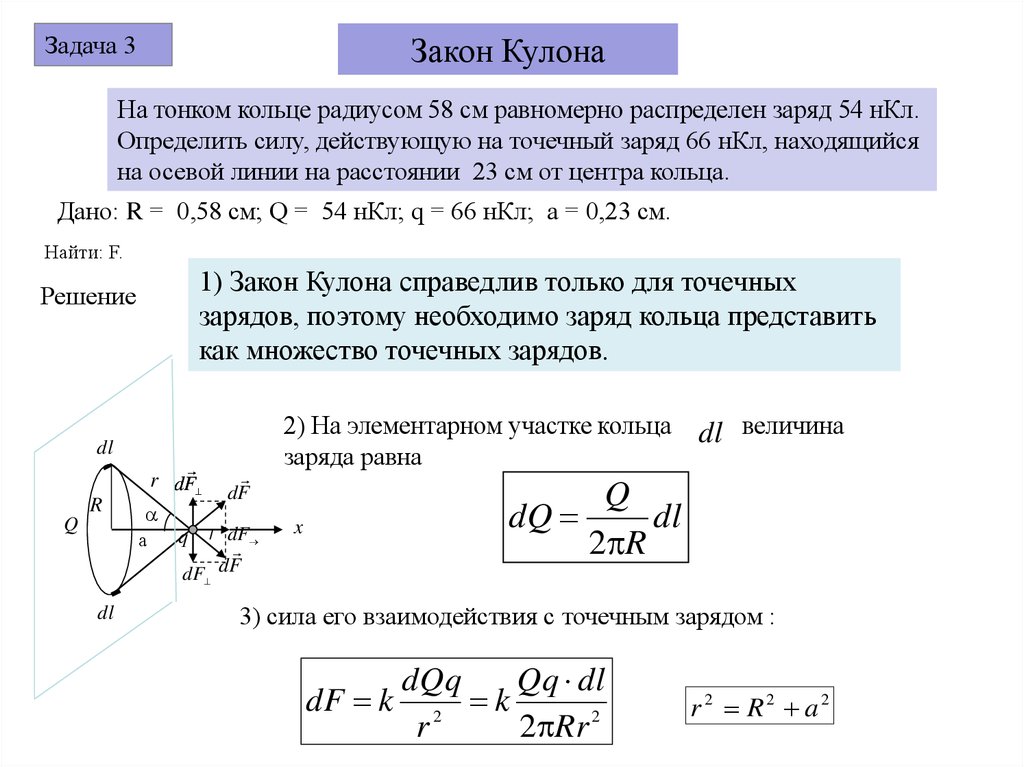
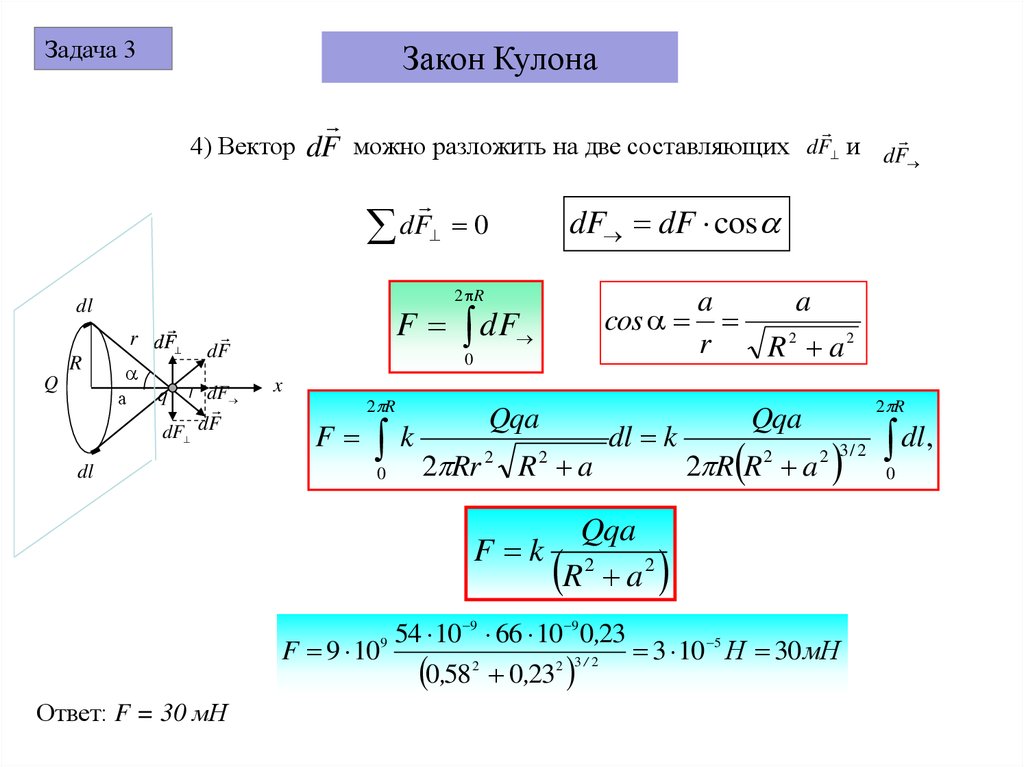




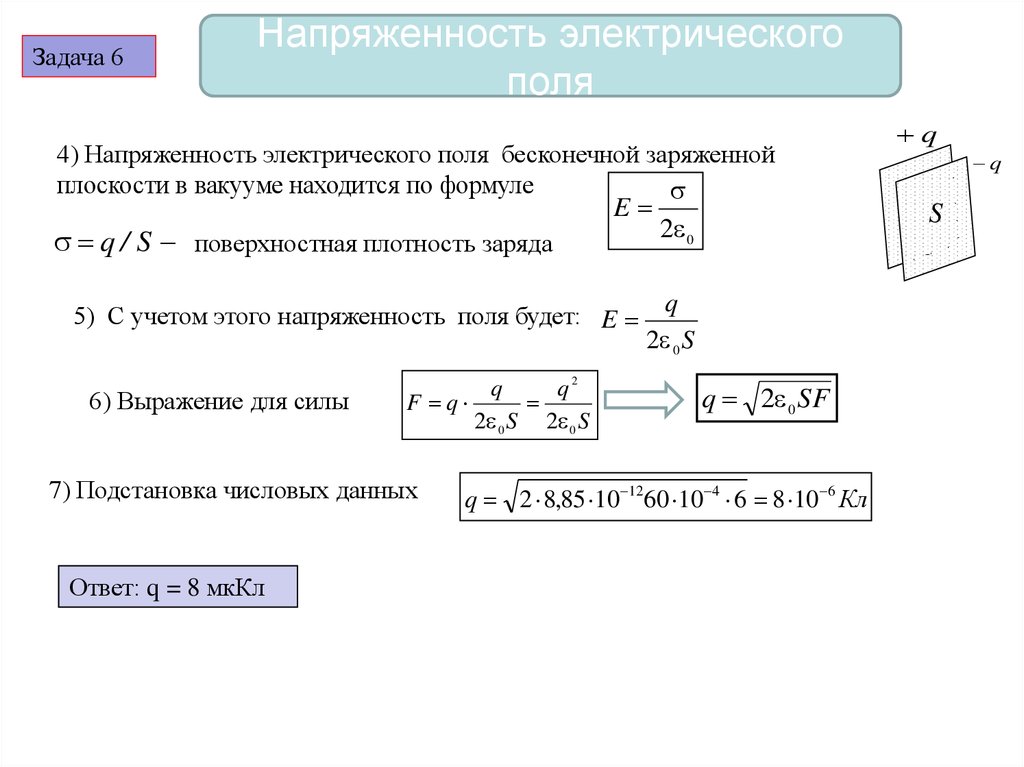






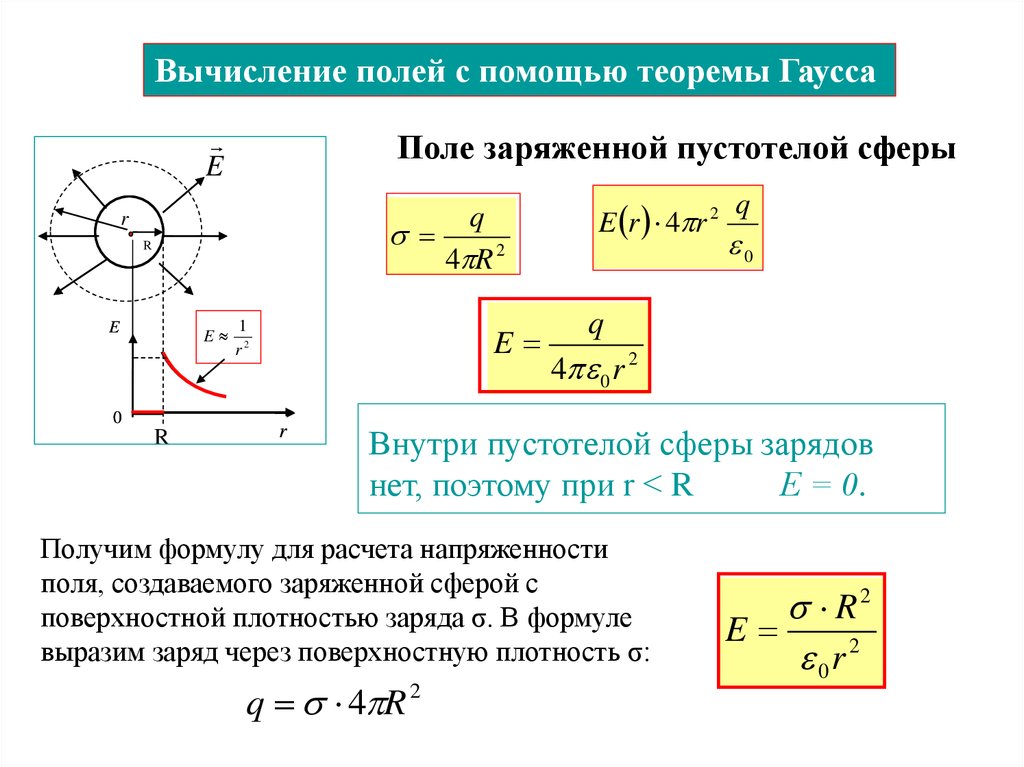
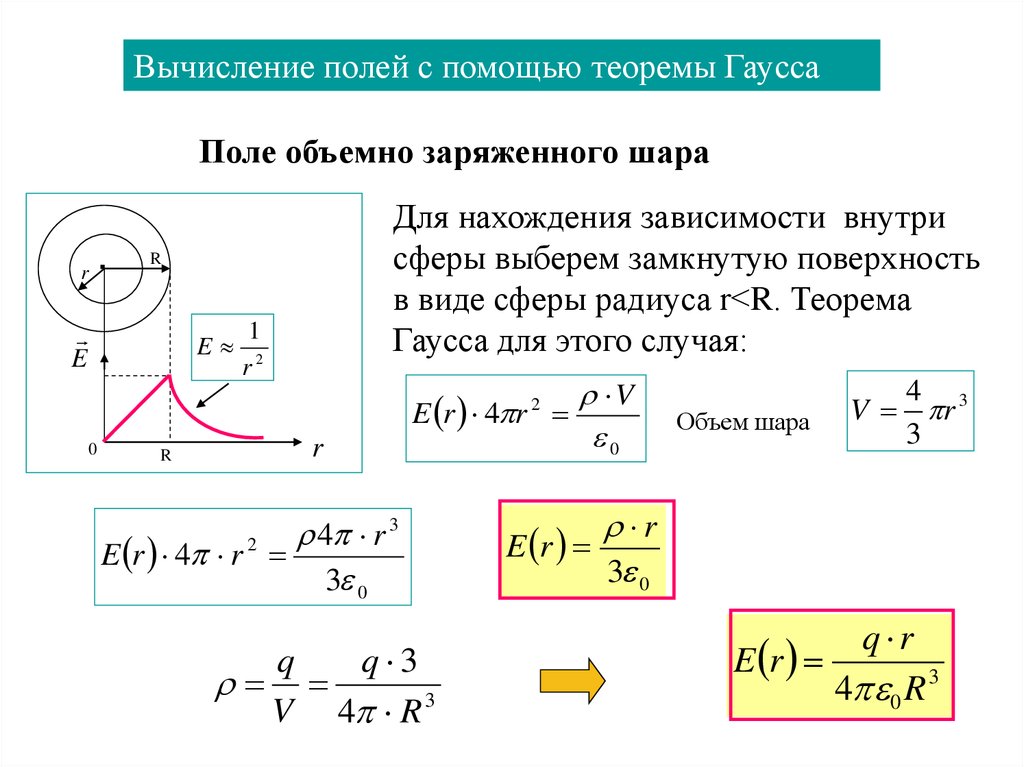




 physics
physics








