Кинематика поступательного и вращательного движения

1.

Литература:
1.Савельев И.В. Курс общей физики
(в 3-х томах). М.: Наука, СПб.: Лань,
2005-2008.
2.Трофимова Т.И. Курс физики. М.:
Высш. шк., 2004.

2. Кинематика поступательного и вращательного движения

1.
2.
3.
4.
5.
Система отсчета. Траектория материальной точки.
Скорость. Вычисление пройденного пути.
Ускорение и его составляющие.
Кинематика вращательного движения. Угловая
скорость и угловое ускорение.
Связь между векторами линейных и угловых
скоростей и ускорений.

3.

1.Система отсчета
Материальная точка – это тело, обладающее массой ,
размерами которого в данной задаче можно пренебречь.
Положение материальной точки определяется по отношению к какомулибо другому, произвольно выбранному телу, называемому телом
отсчета.
В систему отсчета входит: тело отсчета, связанная с ним
система координат и прибор для отсчета времени.
x x(t )
y y( t )
z z(t )
r r (t )
Уравнение траектории
Число независимых координат, полностью
определяющих положение точки в
пространстве, называется числом степеней
свободы.

4.

Траектория материальной точки
Траектория движения материальной точки — линия, описываемая этой
точкой в пространстве. В зависимости от формы траектории движение
может быть прямолинейным или криволинейным.
Рассмотрим движение материальной точки вдоль произвольной траектории:
Ds – длина пути
Dr r r0
– перемещение
Перемещение – направленный отрезок
прямой, соединяющий начальное положение
тела с его последующим положением.
r rx i ry j rz k

5.

2.Скорость
Для характеристики движения материальной точки вводится векторная
величина — скорость, которая определяет быстроту движения и его
направление в данный момент времени.
<v>
Dr
Dt
Dr dr
lim
Dt 0 Dt
dt
Средняя скорость движения
за время Dt.
Мгновенная скорость векторная величина, равная
первой производной радиусавектора движущейся точки по
времени.
Dr
Ds ds
lim
lim
Dt 0 Dt
Dt 0 D t
dt
Числовое значение мгновенной скорости равно
первой производной пути по времени:
Ds ds
Dt 0 Dt
dt
lim

6.

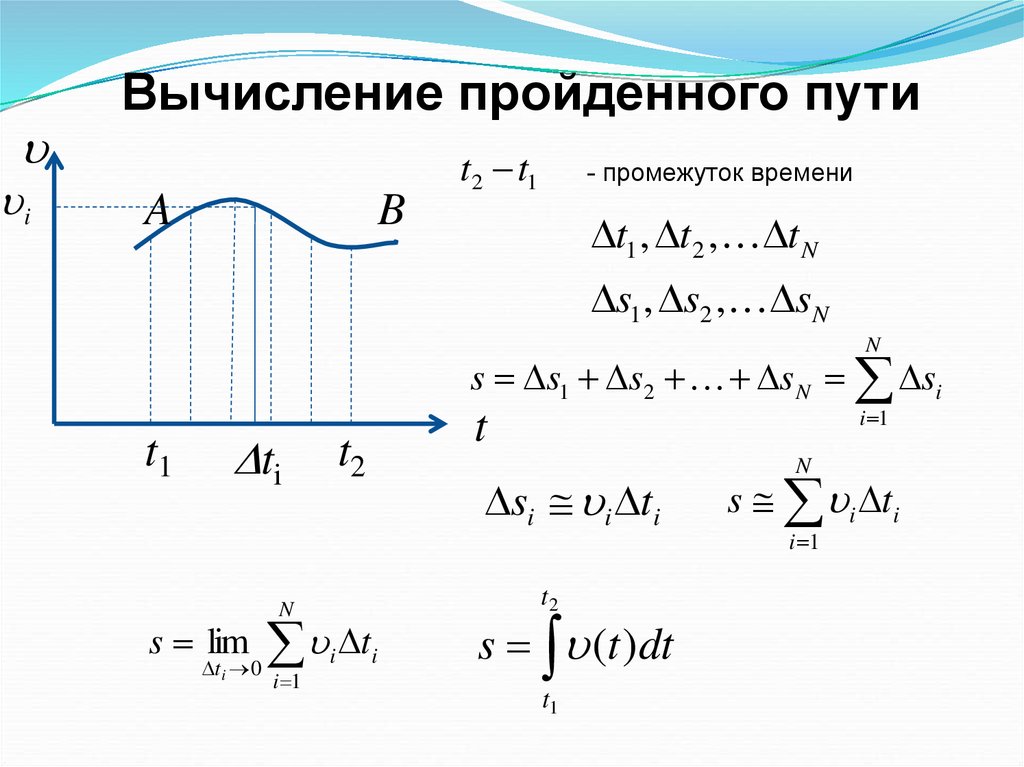
i
Вычисление пройденного пути
A
B
t2 t1
- промежуток времени
Dt1 , Dt2 , Dt N
Ds1 , Ds2 , DsN
N
s Ds1 Ds2 Ds N Dsi
t1
Dti
s lim
Dt i 0
t2
Dsi i Dti
t2
N
Dt
i 1
i
i 1
t
i
s (t )dt
t1
N
s i Dti
i 1

7.

Равномерное движение
Движение, при котором скорость, изменяясь как угодно по
направлению, остается постоянной по величине, называется
равномерным.
s= t
s
t
Проекция вектора скорости на
координатные оси:
Drx dx
x lim
Dt 0 D t
dt
s
t1
Dry
dy
y lim
Dt 0 D t
dt
Drz dz
z lim
Dt 0 Dt
dt
t2
t

8.

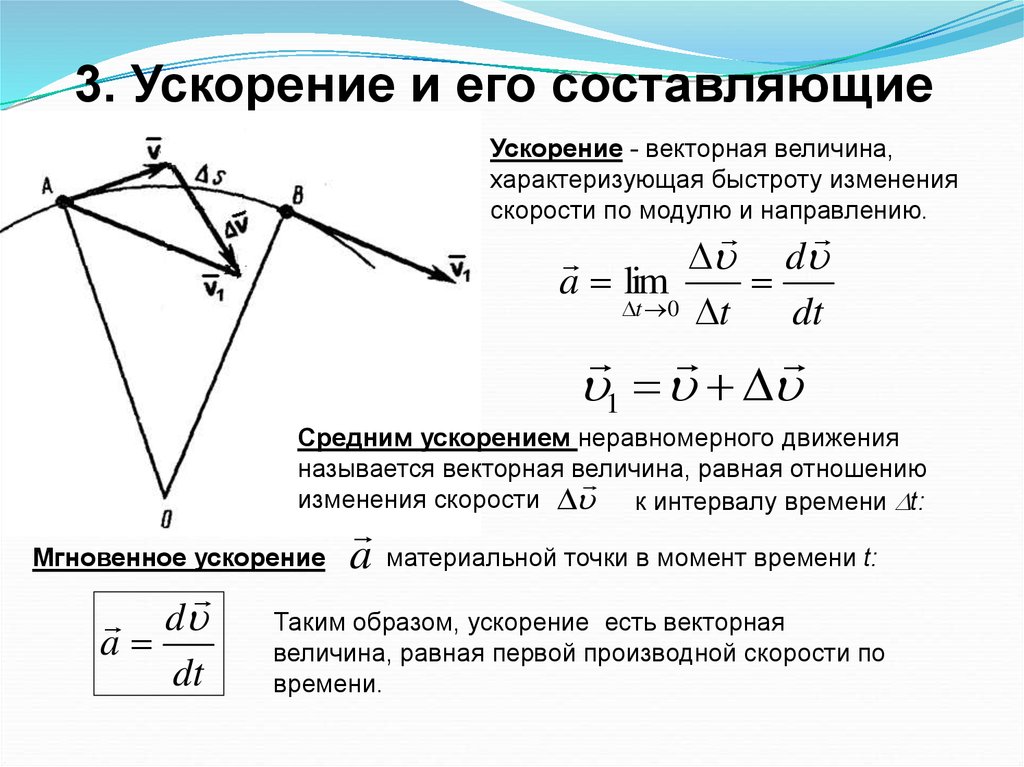
3. Ускорение и его составляющие
Ускорение - векторная величина,
характеризующая быстроту изменения
скорости по модулю и направлению.
D d
a lim
Dt 0 Dt
dt
1 D
Средним ускорением неравномерного движения
называется векторная величина,
равная отношению
изменения скорости D
к интервалу времени Dt:
Мгновенное ускорение
d
a
dt
a
материальной точки в момент времени t:
Таким образом, ускорение есть векторная
величина, равная первой производной скорости по
времени.

9.

t
D 1
D n
1 t Dt
- характеризует изменение скорости по
модулю
- характеризует изменение скорости по
направлению
D
a lim
D D D n
Dt 0 D t
D D n
D
D n
a lim
lim
lim
Dt 0
Dt 0 D t
Dt 0 D t
Dt
D n D
При малом D
D n
D
an lim
lim
Dt 0 Dt
Dt 0
Dt
2
2
D
D
s
D
s
D
an
an lim
lim
lim
R
Dt 0
D
t
0
D
t
0
Dt
Ds
R
Ds Dt

10.

D
a lim
Dt 0 Dt
a
an
d
a
dt
2
an n
R
- называется касательным или тангенциальным ускорением
- называется нормальным или центростремительным ускорением
2
2
a
a
a
n
Полное ускорение a an a
1. a 0, an 0 - прямолинейное
a
равномерное движение
2. a a const , an 0 - прямолинейное
an
равнопеременное движение
a
t
t
D
a a
Dt
a
at 2
s dt ( 0 at )dt 0t
2
0
0
0
t
0 a t
at 2
s 0t
2

11.

3. a 0; an const
an
2
R
const
- скорость по модулю не изменяется, а
изменяется по направлению
R=const - равномерное движение по
окружности
4. a 0; an f (t )
- равномерное криволинейное
движение, R - меняется
5. a f (t ); an 0
- прямолинейное движение с
переменным ускорением

12.

4. Кинематика вращательного движения.
Угловая скорость и угловое ускорение
D d
lim
Dt 0 Dt
dt
d
dt
рад
с
Угловой скоростью называется векторная
величина, равная первой производной
угла поворота тела по времени
d ,
- Направление векторов связано с
направлением движения по правилу
правого винта
2
T
Если const, то
2 R
T
1
T
2

13.

Угловым ускорением называется векторная величина, равная
первой производной угловой скорости по времени:
2
1
1
2
D d
lim
Dt 0 Dt
dt

14.

5. Связь между векторами линейных
и угловых скоростей и ускорений
Линейная скорость точки
Ds
RD
D
lim
R lim
R
Dt 0 Dt
Dt 0 Dt
Dt 0 Dt
lim
, r
R
Нормальное
ускорение:
an
2
R
an 2 R
Тангенциальное ускорение:
D
D ( R )
D
lim
R lim
R
a
Dt 0 D t
Dt 0
D
t
0
Dt
Dt
d
a
, r , r
Полное ускорение:
dt
a lim
R

15. Основные законы динамики

1.
2.
3.
Законы Ньютона и их физическое содержание
Масса, вес, сила, импульс силы, количество
движения
Закон сохранения количества движения.
Движение тела переменной массы

16. 1.Законы Ньютона и их физическое содержание

1-й закон Ньютона:
Всякое тело сохраняет состояние покоя или равномерного и прямолинейного
движения, пока воздействие со стороны других тел не заставит его поменять
это состояние.
2-й закон Ньютона:
Ускорение всякого тела прямо пропорционально действующей
на него силе и обратно пропорционально массе тела:
Если на тело действует несколько сил:
F
a
m
Fi
N
Дифференциальным уравнением
движения материальной точки
называется уравнение:
d 2r N
m 2 F Fi
dt
i 1
a
d 2x
m 2 Fx
dt
i 1
m
d2y
m 2 Fy
dt

17.

3-й закон Ньютона:
m1
m2
f12
f 21
Всякое действие тел друг на друга носит характер
взаимодействия: силы, с которыми действуют друг на друга
взаимодействующие тела, всегда раны по величине и
противоположны по направлению.
f12 f 21

18. 2. Масса, вес, сила, импульс силы, количество движения

2. Масса, вес, сила, импульс
количество движения
силы,
1. Масса
Масса – мера инертности тела.
Гравитационная масса – мера гравитационного притяжения.
Свойства массы:
1. Масса – величина аддитивная.
2. Масса изолированной системы тел остается постоянной при
всех происходящих в ней изменениях – закон сохранения
массы.
3. В классической механике масса не зависит от скорости. В
релятивистской механике с ростом скорости масса возрастает
m m0
1
1
,
2
c2
где m0 – масса покоя
Выполняется закон взаимосвязи массы и
энергии
E=mc2
В СИ [m]=кг

19.

2. Сила и вес
Если наблюдаем ускоренное движение тела, то всегда можно
указать другое тело, действие которого это ускорение вызвало.
При взаимодействии тел возникает ускорение. Количественная
мера этого взаимодействия называется силой.
Взаимодействие тел осуществляется двумя способами:
1. через поля,
2. при непосредственном контакте.
Различают:
1.
2.
3.
4.
Гравитационные взаимодействия;
Электромагнитные взаимодействия;
Ядерные или сильные взаимодействия;
Слабые взаимодействия.

20.

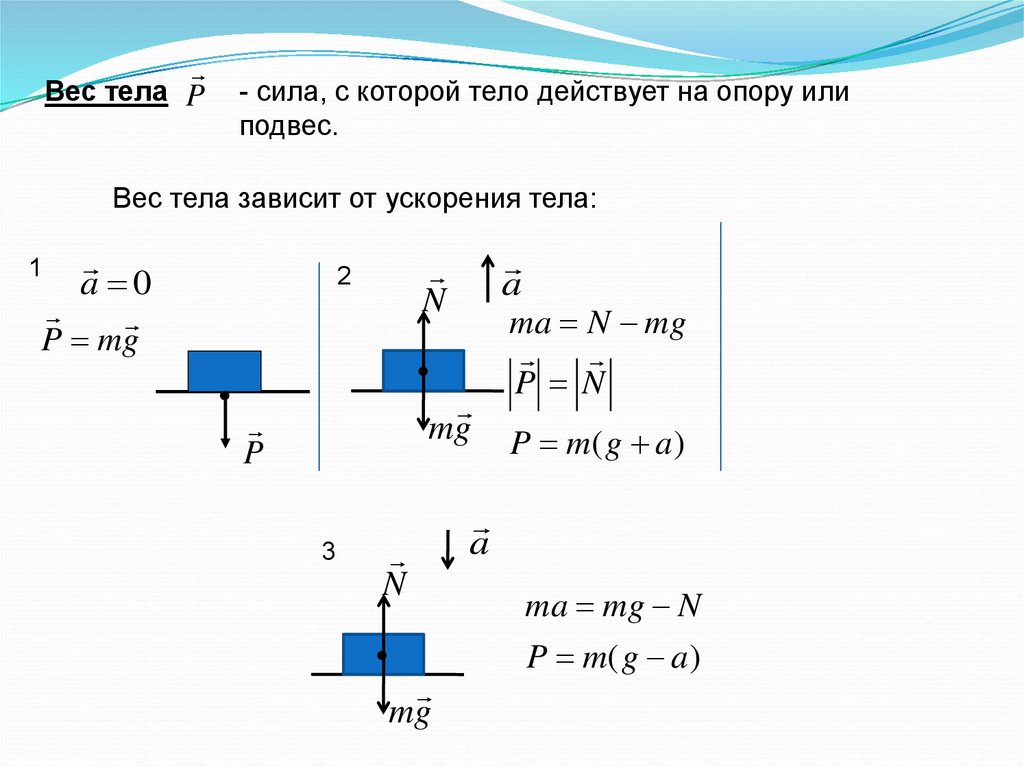
Вес тела P
- сила, с которой тело действует на опору или
подвес.
Вес тела зависит от ускорения тела:
a 0
P mg
1
N
2
mg
P
3
N
mg
a
ma N mg
P N
P m( g a )
a
ma mg N
P m( g a )

21.

3. Импульс силы и количество движения
Векторная величина
pi ,
mi
равная произведению массы
материальной точки на ее скорость
i ,
называется импульсом
или количеством движения этой материальной точки.
pi mi i
Импульсом системы материальных точек называется вектор
геометрической сумме импульсов всех материальных точек
системы:
а) Пусть действует
f ma
f const
D
a
Dt
D
f m
Dt
равный
p,
N
p pi
i 1
Dp
f
Dt
Сила – векторная физическая величина, равная отношению
изменения импульса тела ко времени, в течении которого это
изменение произошло.
б) при неравномерном движении
dp
f
dt
fdt - импульс силы

22.

3. Закон сохранения количества движения.
Рассмотрим систему, состоящую из 3-х материальных точек.
По 3-ему закону Ньютона:
f12 f 21;
dp1
f12 f13 f1
dt
dp2
f 21 f 23 f 2
dt
dp3
f 31 f 32 f 3
dt
Система замкнута:
Fвнешн. 0
dp
0
dt
f13 f31;
f32 f 23
d ( p1 p2 p3 )
f1 f 2 f 3
dt
f1 f 2 f3 Fвнешн
p const
Закон сохранения импульса: Импульс замкнутой системы
материальных точек остается постоянным при любых
взаимодействиях этих точек между собой.
dp
Fв нешн.
dt
pi const
N
i 1

23.

Движение тела переменной массы
масса
ракеты
время
t
m dm
t dt
m
скорость
ракеты отн.
Земли
d
импульс
ракеты
p1 (m dm)
p1' m( d )
u - скорость вытекающего газа относительно ракеты
u
p2 p1 Fdt ,
- скорость газов относительно Земли
p2
- импульс системы после взаимодействия
p2 m( d ) (u )dm m( d ) (u )dm (m dm) Fdt
m md udm dm m dm Fdt
md udm Fdt
Основное уравнение динамики тела
d
dm
переменной массы или уравнение Мещерского
m
F u
dt
dt
dm
- расход топлива
dt

24.

Работа, Мощность, Энергия
1.Работа. Мощность.
2.Потенциальное поле. Консервативные
и неконсервативные силы.
3.Энергия. Закон сохранения энергии.
4.Упругий и неупругий удары шаров.

25.

1.Работа. Мощность
Работой называется скалярная величина, равная произведению
проекции силы па направление перемещения fs и пути s,
проходимого точкой приложения силы:
f
A fs s
f s f cos
A fs cos
Работа – алгебраическая величина.
a) Если
б) Если
в)
cos 0
(сила и направление перемещения образуют
острый угол), то А > 0 (работа положительна)
cos 0 ( тупой угол), то А < 0 (работа отрицательна)
2,
то А = 0 (работа равна 0)

26.

fs
A DAi
DAi f si Dsi
i
A lim
f si
1
Dsi
Dsi 0
i
si
Dsi f s ds
s
A f S ds
s
2
f
[1 Дж ] 1Н м
Пусть на тело действуют одновременно несколько сил, результирующая
которых равна
Ds Dt
f fk
A DАК
k
k
A lim
Dti 0
i
t2
f i i Dti f dt
t1
DA
N
Dt
Мощность определяет быстроту совершения работы .
DA dA
N lim
Dt 0 Dt
dt
1 Дж
[1Вт ]
1с

27.

2. Потенциальное поле.
Консервативные и
неконсервативные силы.
Поле сил – это пространство, в каждой точке которого
на помещённую в него частицу действует сила,
закономерно меняющаяся от точки к точке.
Стационарное поле – пространство, в каждой точке
которого сила не зависит от времени.
Стационарное поле, в котором работа сил поля
зависит только от положения начальных и конечных
точек и не зависит от формы пути называется
потенциальным.

28.

Силы, действующие в потенциальном поле,
называются консервативными.
Силы, работа которых зависит от пути, по которому
тело переходит из одного положения в другое,
называются неконсервативными.
Свойства потенциальных полей
2
1. Если поле потенциально, то работа по
произвольному замкнутому пути равна нулю.
а
b
1
f s ds 0
A1a 2 A1b 2 A2b1
A1a 2 A2b1 0
2. Если в поле работа по произвольному замкнутому
контуру равна нулю, то поле является потенциальным.

29.

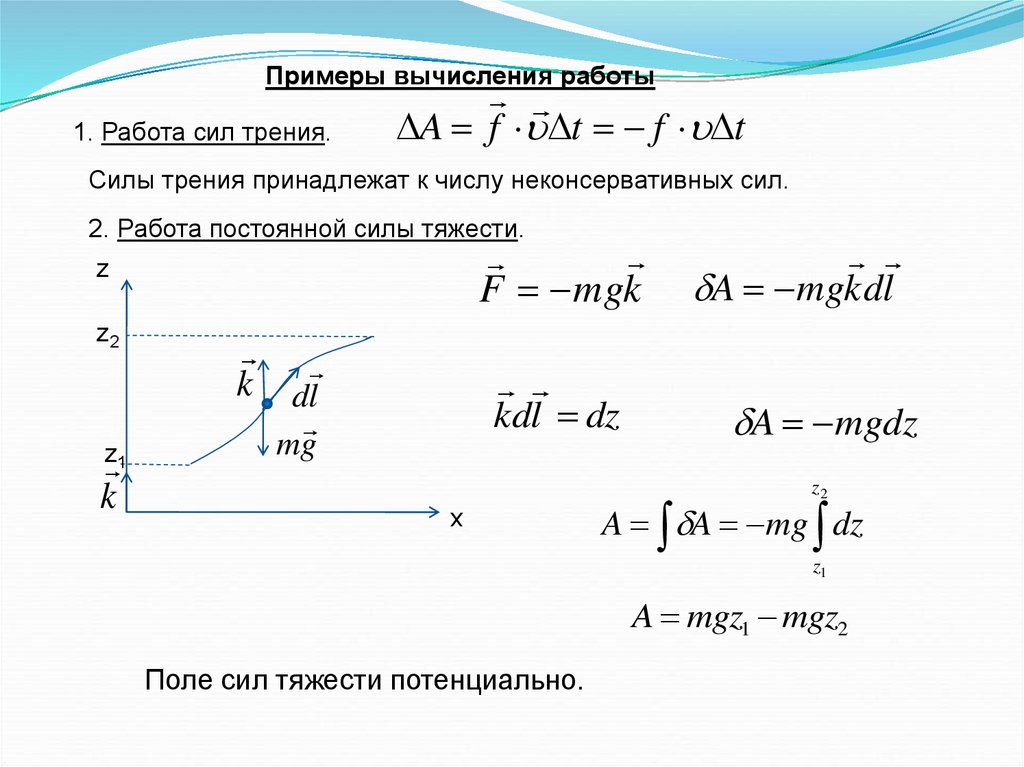
Примеры вычисления работы
1. Работа сил трения.
DA f Dt f Dt
Силы трения принадлежат к числу неконсервативных сил.
2. Работа постоянной силы тяжести.
F mgk
z
z2
z 1
k
k dl
kdl dz
mg
A mgk dl
A mgdz
z2
x
A A mg dz
z1
A mgz1 mgz2
Поле сил тяжести потенциально.

30.

3. Энергия. Закон сохранения энергии
Энергия – общая мера различных процессов и видов взаимодействия.
Энергия тела может быть обусловлена :
1) движением тела с некоторой скоростью (кинетическая энергия);
2) нахождением тела в потенциальном поле сил (потенциальная
энергия).
Потенциальная энергия
B
Ds
1
Dh
Рассмотрим работу, совершаемую при движении
материальной точки в однородном поле силы
тяжести.
DA mgDs cos
h
A DAi mg Dhi
i
B2
i
Работа зависит
только от разности
высот между
точками В1 и В2
- потенциальная энергия
A mgh
E p1 E p 2 A12
Ep
- полная работа

31.

Кинетическая энергия
Материальная точка А массы m движется под действием силы
ds
A
f
m 2
A d
2
A fds f dt
d
f m
dt
f
d
A m dt m d
dt
Часть механической энергии зависящая от скорости
называется кинетической энергией.
2
m 2 m 22 m 12
A dA d
2
2
1 2
A Eк 2 Eк1

32.

Полная механическая энергия
тела
m
x0
t0 x0 0 f 0 kx0
t x f kx
F
m
F
x
d
m
F kx
dt
d dx
Fdx m
x
dt
x0
0
kxdx
Второй закон
Ньютона дает:
d
m
F f
dt
d
F m
kx
dt
Fdx m d kxdx
x
A Fdx m d kxdx
x0
Полная механическая энергия
пружины в момент времени t:
dx
Проинтегрируем:
m 2
k 2
2
A ( 0 ) ( x x02 )
2
2
m 2 kx2
E
2
2
E E p Ek

33.

Закон сохранения энергии
а) Рассмотрим изолированную систему материальных точек, в которой
действуют только консервативные (потенциальные) силы.
Состояние системы в каждый момент времени определяется:
1. Конфигурацией системы;
2. Скоростью материальных точек.
A12 E p1 E p 2
A12 Ek 2 Ek1
E p1 E p 2 Ek 2 Ek1
E p1 Ek1 E p 2 Ek 2
Ek E p E
E1 E2
- полная энергия системы
Полная механическая энергия замкнутой системы тел, в
которой действуют только потенциальные силы, остается
постоянной. – закон сохранения энергии.
E const

34.

б) В системе кроме потенциальных сил действуют неконсервативные
(непотенциальные) силы (например, силы трения) и
рассматриваемая система незамкнутая и действуют внешние силы.
Изменение кинетической энергии:
Ek 2 Ek1 Aвнутр.потенц. Aтр. Aвнешн.
Изменение потенциальной энергии:
E p1 E p 2 Aвнутр.потенц.
Ek 2 Ek1 E p1 E p 2 Aтр. Aвнешн.
Ek 2 E p 2 Ek1 E p1 Aтр. Aвнешн.
E2 E1 Aтр. Aвнешн.
Изменение полной механической энергии системы равно
сумме работ внешних сил и сил трения (внутренних
непотенциальных сил).

35.

4. Упругий и неупругий удары шаров
Существуют два предельных вида удара:
1. Абсолютно упругий удар – это удар при котором механическая энергия
тел не переходит в другие, немеханические, виды энергии.
2. При абсолютно неупругом ударе кинетическая энергия тел полностью
или частично превращается во внутреннюю.
При абсолютно упругом ударе выполняются закон сохранения импульса
и закон сохранения энергии.
При абсолютно неупругом ударе выполнятся лишь закон сохранения
импульса, закон сохранения механической энергии не соблюдается.
Удар называется центральным, если шары до удара движутся вдоль
прямой, проходящей через их центры.
а)
б)
m1
10
20
m2
m1 10 m2
x
20
x

36.

Рассмотрим абсолютно неупругий удар:
Пусть m1 и m2
- массы шаров
10 и 20
- скорости шаров до удара
Закон сохранения количества движения:
m1 10 m2 20 m1 m2 (m1 m2 )
- одинаковая для обоих шаров скорость после удара
m1 10 m2 20
m1 m2
m1 10 m2 20
m1 m2
Знак «-» соответствует случаю а)
Знак «+» соответствует случаю б)

37.

Абсолютно упругий удар
m1 , m2
- массы шаров;
1 , 2
10 , 20
- скорости шаров до удара
- скорости шаров после удара
Уравнение закона сохранения импульса:
2
2
m1 10 m2 20 m1 1 m2 2
(1)
Закон сохранения энергии:
2
2
m1 10 m2 20 m1 1 m2 2
2
2
2
2
2m2 20 (m1 m2 ) 10
1
m1 m2
2m1 10 (m2 m1 ) 20
2
m1 m2
(2)