Similar presentations:
Динамика материальной точки. (Тема 2)
1. ТЕМА II. ДИНАМИКА
Исаак Ньютон1642 - 1727
2. ПЕРВЫЙ ЗАКОН НЬЮТОНА (ЗАКОН ИНЕРЦИИ)
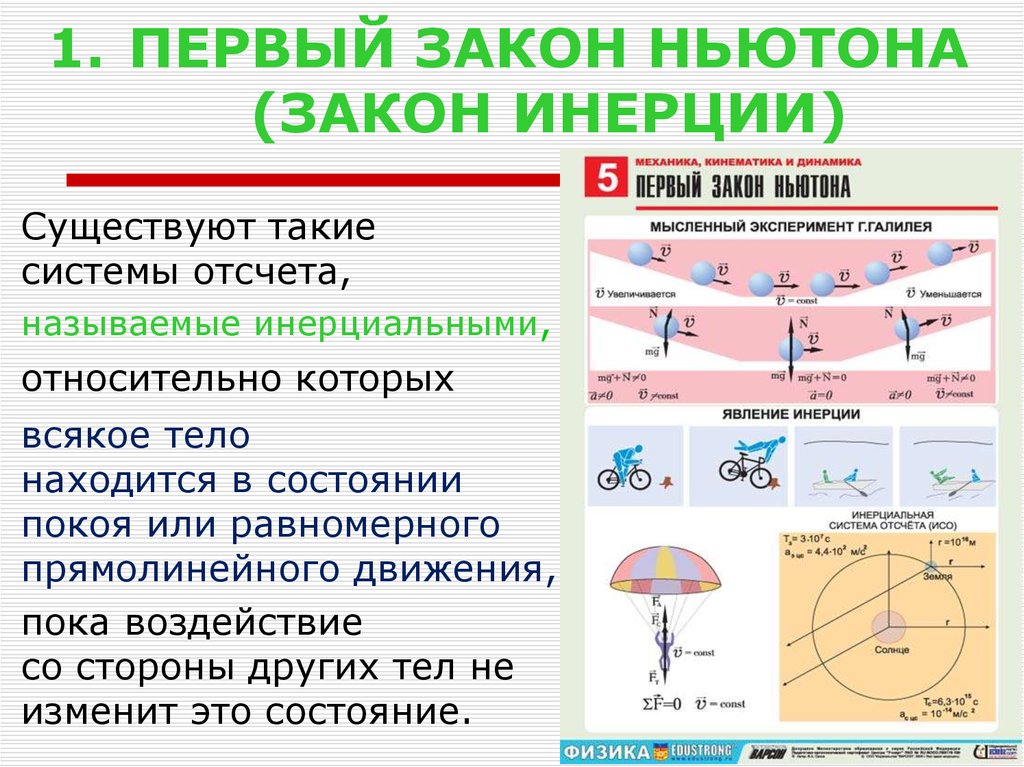
1. ПЕРВЫЙ ЗАКОН НЬЮТОНА(ЗАКОН ИНЕРЦИИ)
Существуют такие
системы отсчета,
называемые инерциальными,
относительно которых
всякое тело
находится в состоянии
покоя или равномерного
прямолинейного движения,
пока воздействие
со стороны других тел не
изменит это состояние.
3. 2. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ
Галилео Галилей1564 - 1642
4. 3. ИНЕРТНОСТЬ ТЕЛЛ. МАССА
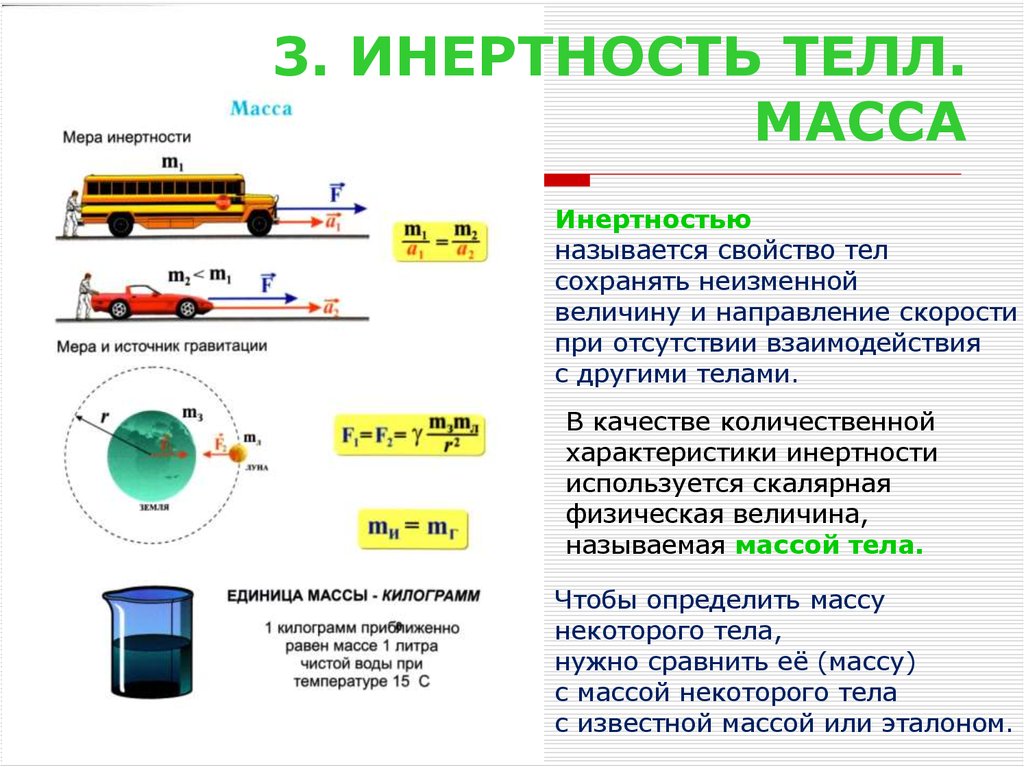
Инертностьюназывается свойство тел
сохранять неизменной
величину и направление скорости
при отсутствии взаимодействия
с другими телами.
В качестве количественной
характеристики инертности
используется скалярная
физическая величина,
называемая массой тела.
Чтобы определить массу
некоторого тела,
нужно сравнить её (массу)
с массой некоторого тела
с известной массой или эталоном.
5. 4. ВТОРОЙ ЗАКОН НЬЮТОНА
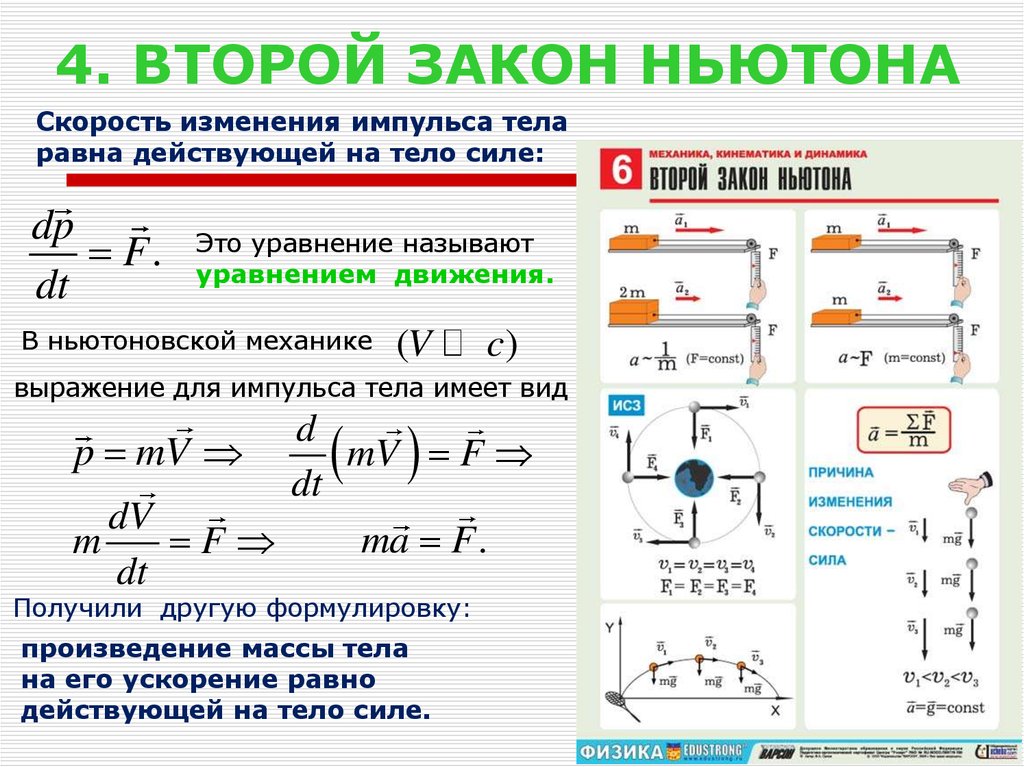
Скорость изменения импульса теларавна действующей на тело силе:
dp
F.
dt
Это уравнение называют
уравнением движения.
В ньютоновской механике
(V
c)
выражение для импульса тела имеет вид
d
p mV
mV F
dt
dV
ma F .
m
F
dt
Получили другую формулировку:
произведение массы тела
на его ускорение равно
действующей на тело силе.
6. 5. ТРЕТИЙ ЗАКОН НЬЮТОНА
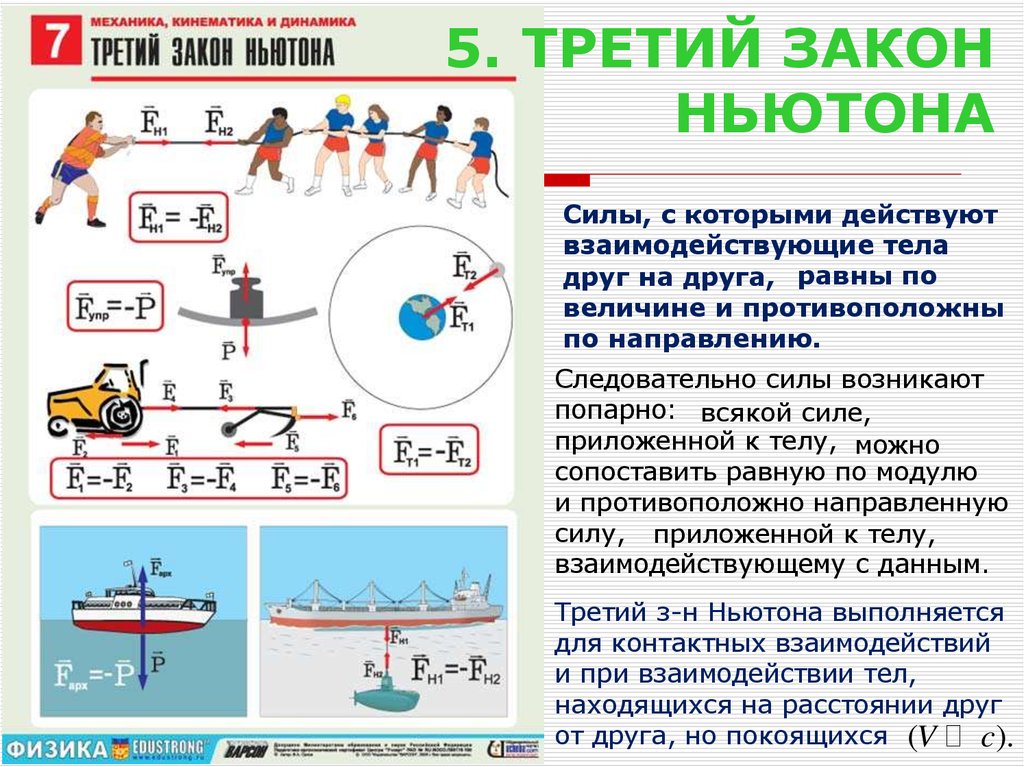
Силы, с которыми действуютвзаимодействующие тела
друг на друга, равны по
величине и противоположны
по направлению.
Следовательно силы возникают
попарно: всякой силе,
приложенной к телу, можно
сопоставить равную по модулю
и противоположно направленную
силу, приложенной к телу,
взаимодействующему с данным.
Третий з-н Ньютона выполняется
для контактных взаимодействий
и при взаимодействии тел,
находящихся на расстоянии друг
от друга, но покоящихся (V
c).
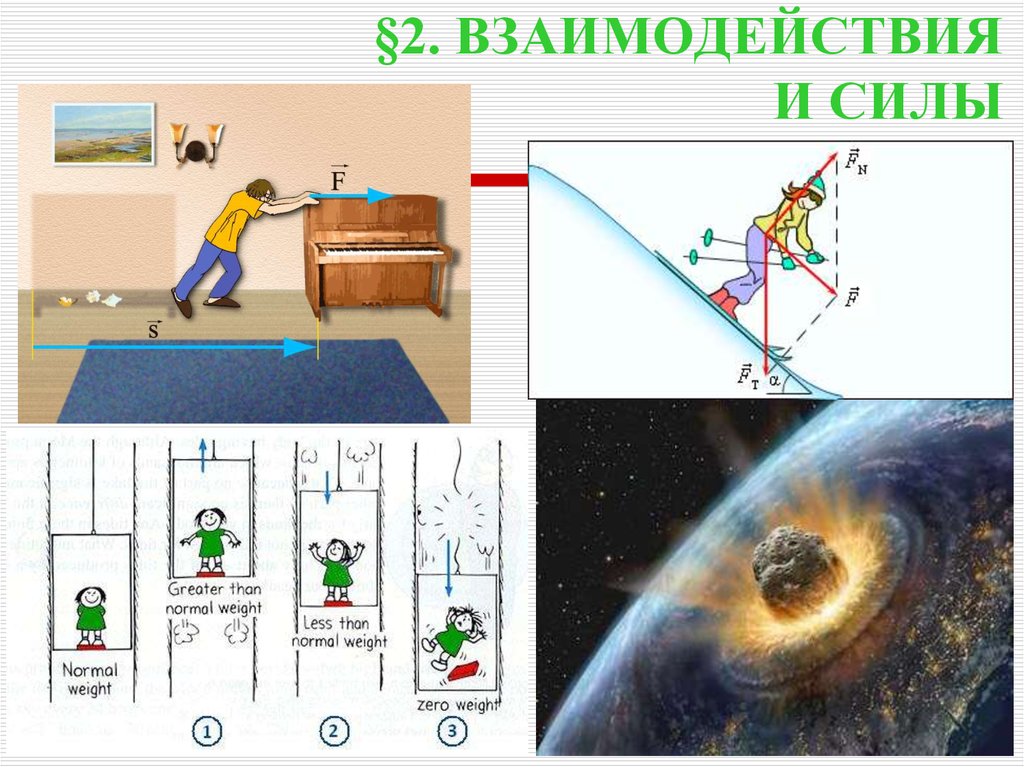
7. §2. ВЗАИМОДЕЙСТВИЯ И СИЛЫ
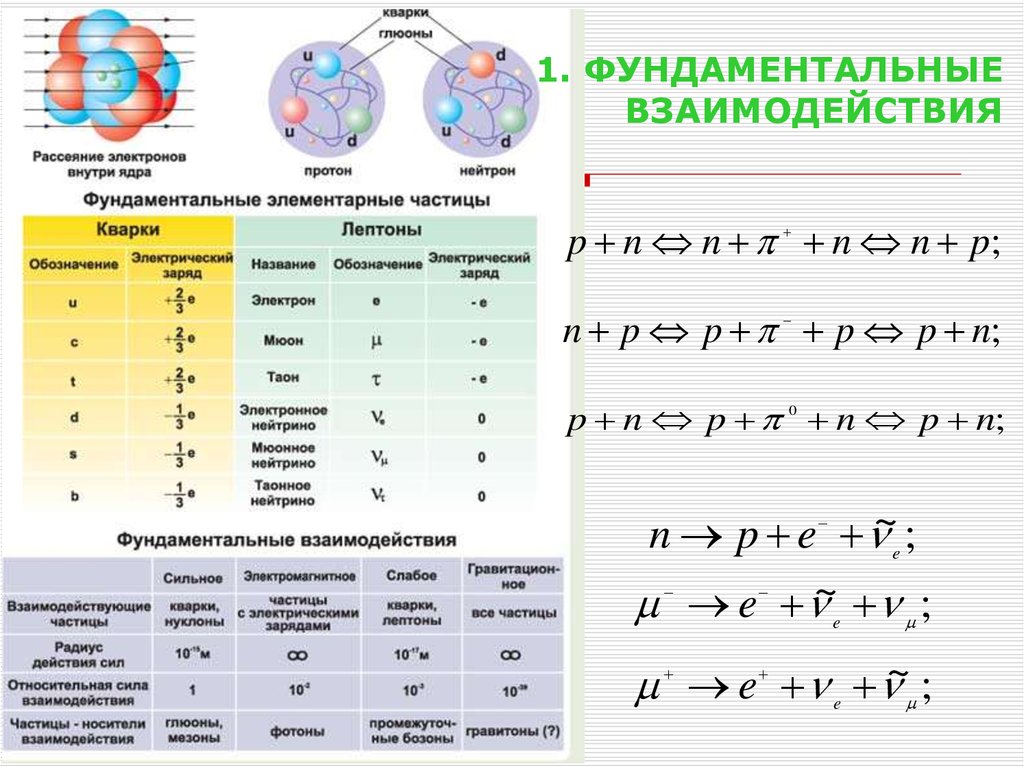
8. 1. ФУНДАМЕНТАЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ
p n n n n p;n p p p p n;
p n p 0 n p n;
n p e ~e ;
e ~ ;
e
e ~ ;
e
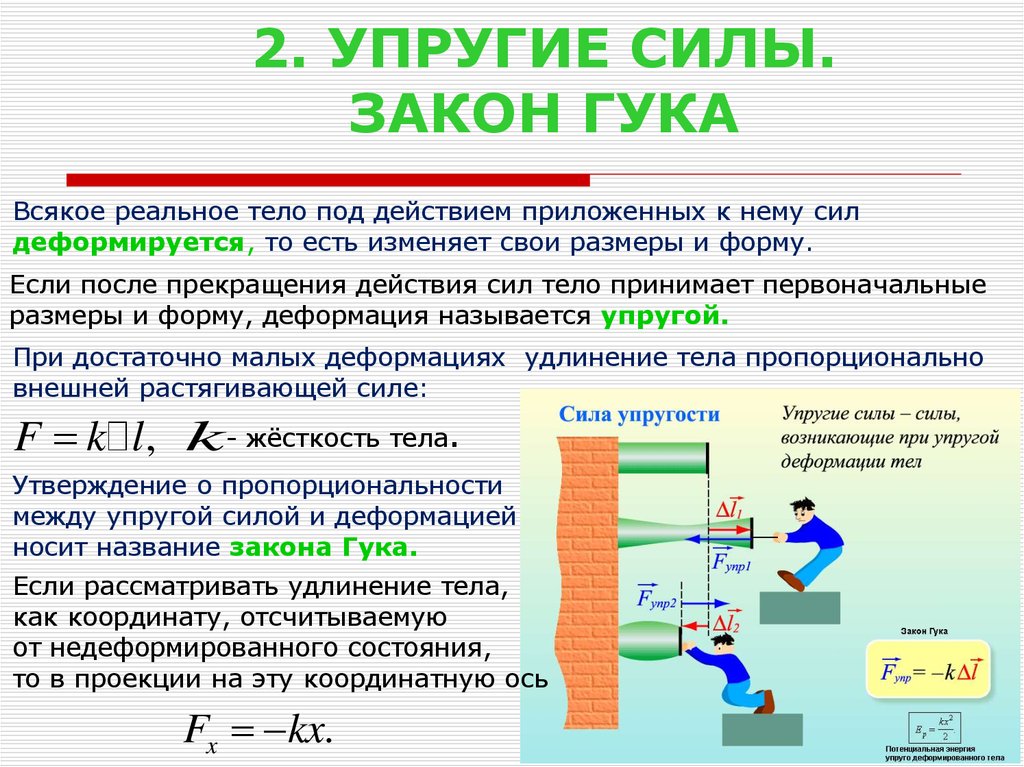
9. 2. УПРУГИЕ СИЛЫ. ЗАКОН ГУКА
Всякое реальное тело под действием приложенных к нему силдеформируется, то есть изменяет свои размеры и форму.
Если после прекращения действия сил тело принимает первоначальные
размеры и форму, деформация называется упругой.
При достаточно малых деформациях удлинение тела пропорционально
внешней растягивающей силе:
F k l , k- жёсткость тела.
Утверждение о пропорциональности
между упругой силой и деформацией
носит название закона Гука.
Если рассматривать удлинение тела,
как координату, отсчитываемую
от недеформированного состояния,
то в проекции на эту координатную ось
Fx kx.
10. 3. МОДУЛЬ ЮНГА И ЖЕСТКОСТЬ СТЕРЖНЯ
При упругой деформацию стержнявозникает сила упругости Fx kx.
Модуль этой силы F k l
будет одинаков во всех сечениях.
Это означает, что упругая сила
зависит не от абсолютного, а от
относительного удлинения стержня:
E , F , l ,
S
l0
– механическое напряжение,
E
– относительная деформация,
– модуль Юнга, характеристика упругих свойств материала стержня.
S
F
l
S
E F E l; F k l k E ,
S
l0
l0
l
Н
E 1 2 .
м
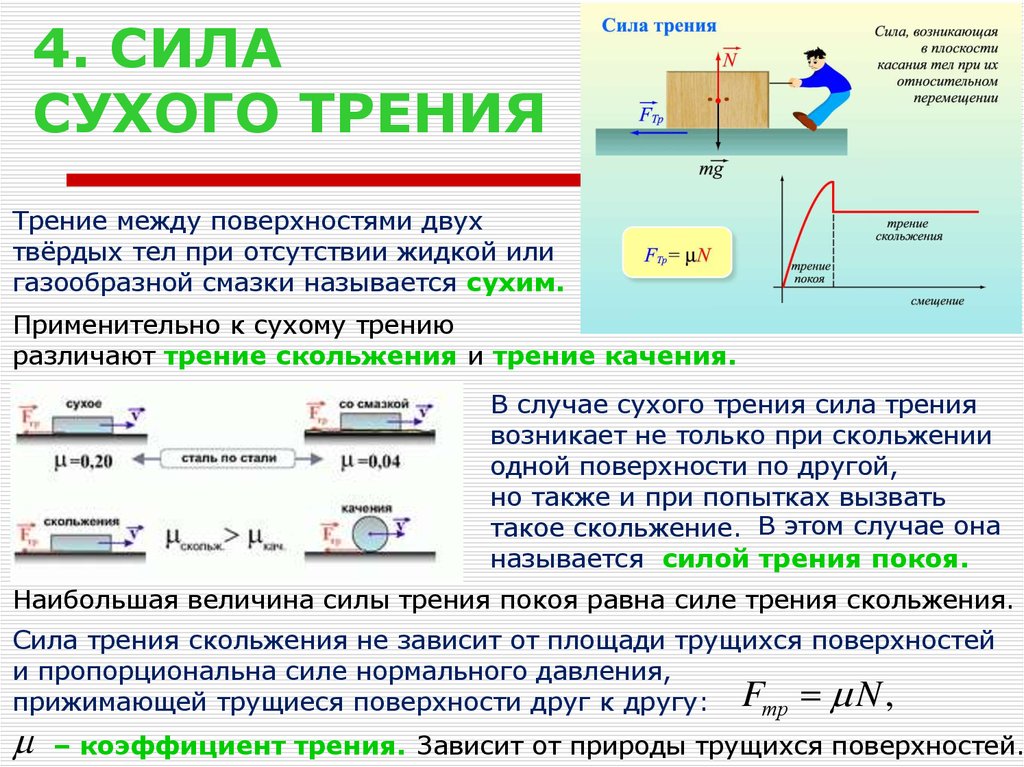
11. 4. СИЛА СУХОГО ТРЕНИЯ
Трение между поверхностями двухтвёрдых тел при отсутствии жидкой или
газообразной смазки называется сухим.
Применительно к сухому трению
различают трение скольжения и трение качения.
В случае сухого трения сила трения
возникает не только при скольжении
одной поверхности по другой,
но также и при попытках вызвать
такое скольжение. В этом случае она
называется силой трения покоя.
Наибольшая величина силы трения покоя равна силе трения скольжения.
Сила трения скольжения не зависит от площади трущихся поверхностей
и пропорциональна силе нормального давления,
прижимающей трущиеся поверхности друг к другу: Fтр N ,
– коэффициент трения. Зависит от природы трущихся поверхностей.
12. 5. СИЛА СОПРОТИВЛЕНИЯ
При небольших скоростях силасопротивления растёт
1 .
линейно со скоростью Fc rV
При больших скоростях линейный
закон переходит в квадратичный:
Fc r2V 2 , V V .
Зависимость силы сопротивления
от скорости приводит к тому,
что в вязкой среде под действием
постоянной внешней силы для тела
наступит состояние движения
с установившейся (постоянной скоростью).
В отличие от сухого вязкое трение
(сила сопротивления) обращается
в ноль вместе со скоростью.
Поэтому, как бы ни была мала внешняя сила, она вызовет движение тела
относительно вязкой среды. Т.е. отсутствует сила трения покоя.
13. 6. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЕНИЯ
Закон всемирного тяготения гласит,что материальные точки притягивают
друг друга с силой, величина которой
пропорциональна массам этих точек
и обратно пропорциональна квадрату
расстояния между ними.
Коэффициент пропорциональности
это гравитационная постоянная
G
G 6,672 10 11 Н м2 / кг.
Для характеристики гравитационного
поля вводится векторная величина
F
g ,
m
F – сила, действующая в
данной точке на тело массой
Напряжённость гравитационного
поля точечной массы равна
m.
g G
m
e.
2 r
r
14. 7. КОСМИЧЕСКИЕ СКОРОСТИ
Скорость, которую нужносообщить телу при запуске
с поверхности Земли,
чтобы оно вышло из сферы
земного притяжения, называется
второй космической скоростью.
V2
M
G
R h
( R h) 2
V
2
V2 2 gR 2 V1 11,2 км / c.
gR
. Скорость, которую нужно
R h
сообщить телу при запуске
с поверхности Земли,
чтобы оно покинуло пределы
Солнечной системы, называется
третей космической скоростью.
При запуске в направлении
движения Земли
V3 42 30 12 км / с.
15. §3. ЧАСТИЦА В СТАТИЧЕСКИХ СИЛОВЫХ ПОЛЯХ
16. ДВИЖЕНИЕ В ПОЛЕ СИЛЫ ТЯЖЕСТИ
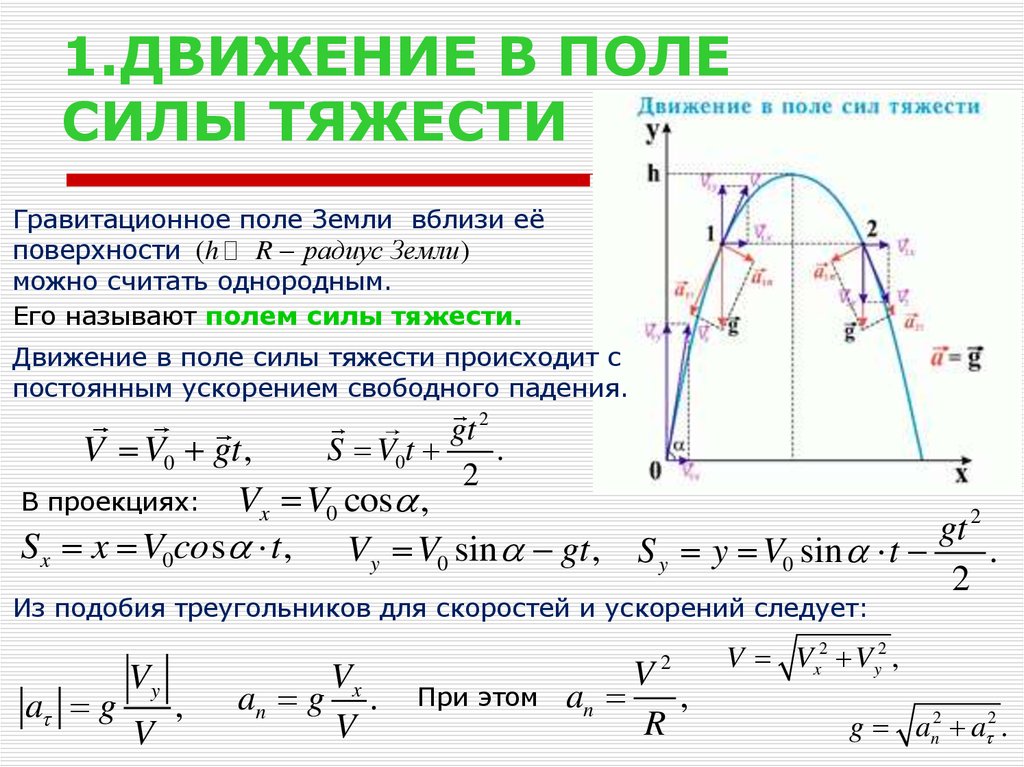
1.ДВИЖЕНИЕ В ПОЛЕСИЛЫ ТЯЖЕСТИ
Гравитационное поле Земли вблизи её
поверхности (h R радиус Земли )
можно считать однородным.
Его называют полем силы тяжести.
Движение в поле силы тяжести происходит с
постоянным ускорением свободного падения.
gt 2
S V0t
.
2
V V0 gt ,
В проекциях: Vx V0 cos ,
S x x V0co s t , Vy V0 sin gt ,
gt 2
S y y V0 sin t
.
2
Из подобия треугольников для скоростей и ускорений следует:
a g
Vy
V
,
Vx
an g .
V
2
При этом
V
an
,
R
V Vx2 Vy2 ,
g an2 a 2 .
17. 2. СИЛА, ДЕЙСТВУЮЩАЯ НА ЗАРЯД В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
FНапряжённостью электрического поля в данной точке называется
отношение силы, действующей на заряд, к величине этого заряда E q .
Наглядно электрическое поле можно описать
линиями напряжённости (силовыми линиями).
Силовые линии проводят таким образом, чтобы
касательная к ним в каждой точке совпадала
с напряжённостью электрического поля.
Зная напряжённость поля в данной точке,
можно определить силу,
действующую на заряд:
F qE;
F q E;
Н
В
E 1 1 ;
Кл
м
Сила, действующей на заряд, помещённый в данную
точку пропорциональна заряду и напряжённости поля.
Величина и направление напряжённости поля
в каждой точке определяется зарядами, создающими
данное электрическое поле (источниками поля).
18. 3. ДВИЖЕНИЕ ЧАСТИЦЫ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
Однородное электрическое поледействует на заряженную частицу также,
как сила тяжести на точечную массу.
F qE ,
F V0 , Vy V0 y const;
Fz qEz
Vz V0 z az t , az
,
m
m
Движение вдоль оси y (перпендикулярно полю) происходит равномерно,
а вдоль оси z (вдоль направления поля) – равноускоренно.
az t 2 az t 2
, V0 z 0,
z z0 S z , z0 0 z S z V0 z t
2
2
y y0 S y , y0 0 y S y V0t. К моменту вылета частицы
из области поля её вектор скорости изменит своё направление на угол:
tg V V0 ,
V az ,
l V0 ,
l
длина области поля.
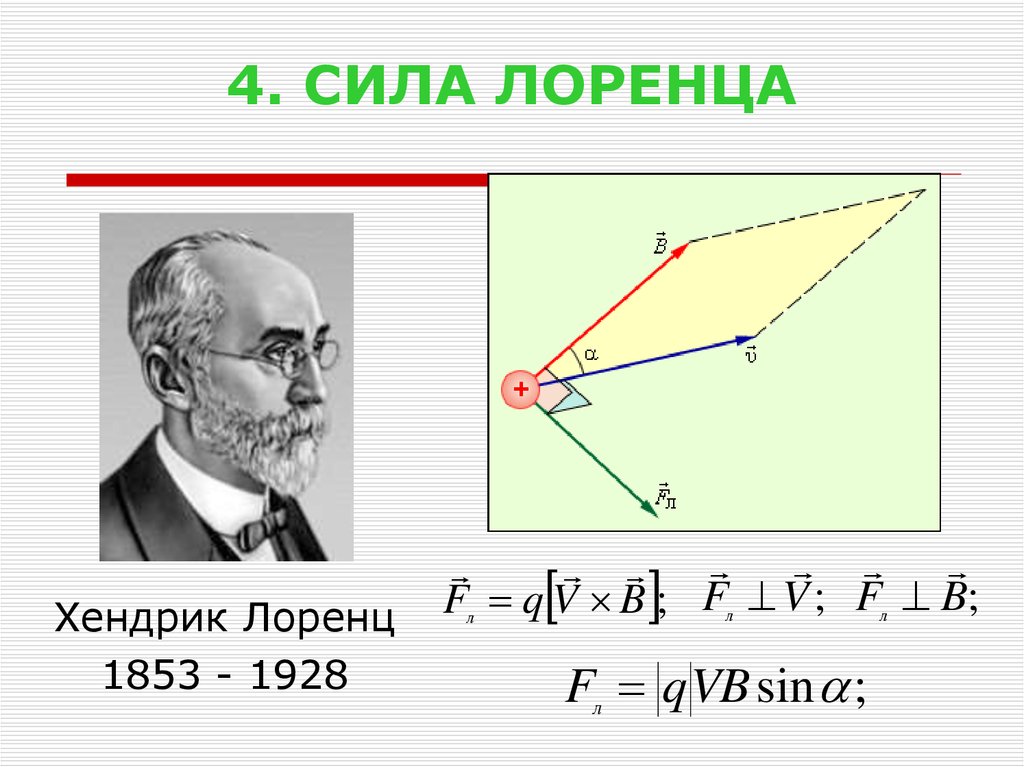
19. 4. СИЛА ЛОРЕНЦА
Хендрик Лоренц1853 - 1928
Fл q V B ; Fл V ; Fл B;
F q VB sin ;
л
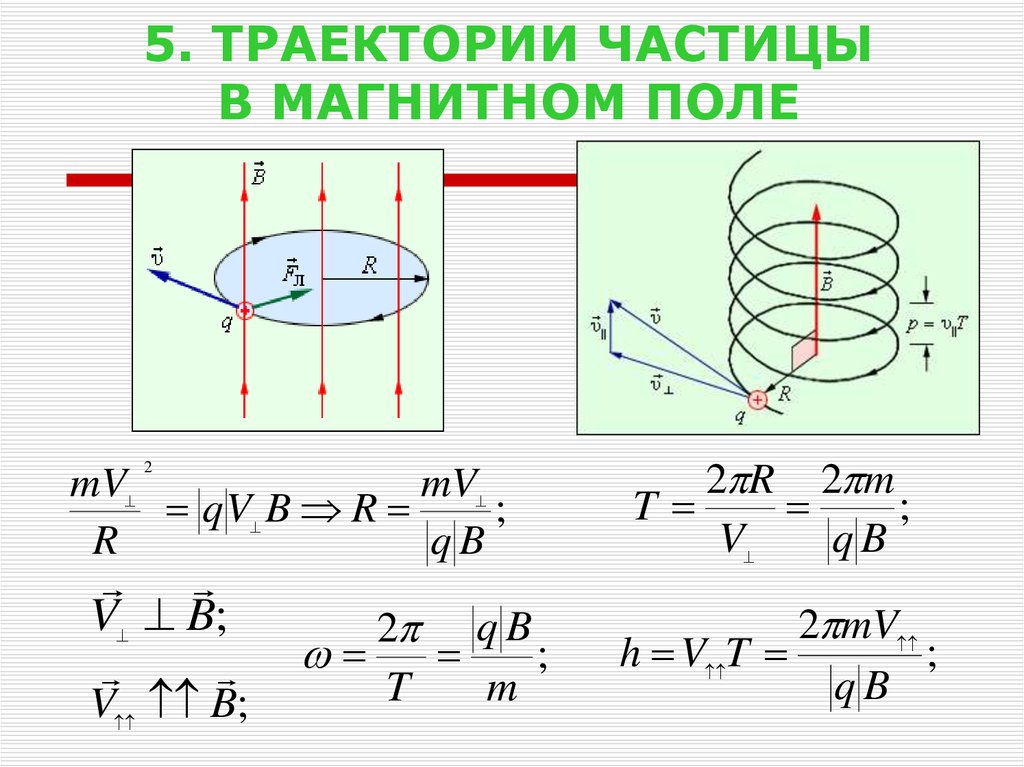
20. 5. ТРАЕКТОРИИ ЧАСТИЦЫ В МАГНИТНОМ ПОЛЕ
2mV
mV
qV B R
;
R
qB
V B;
V B;
2 q B
;
T
m
2 R 2 m
T
;
V
qB
2 mV
h V T
;
qB
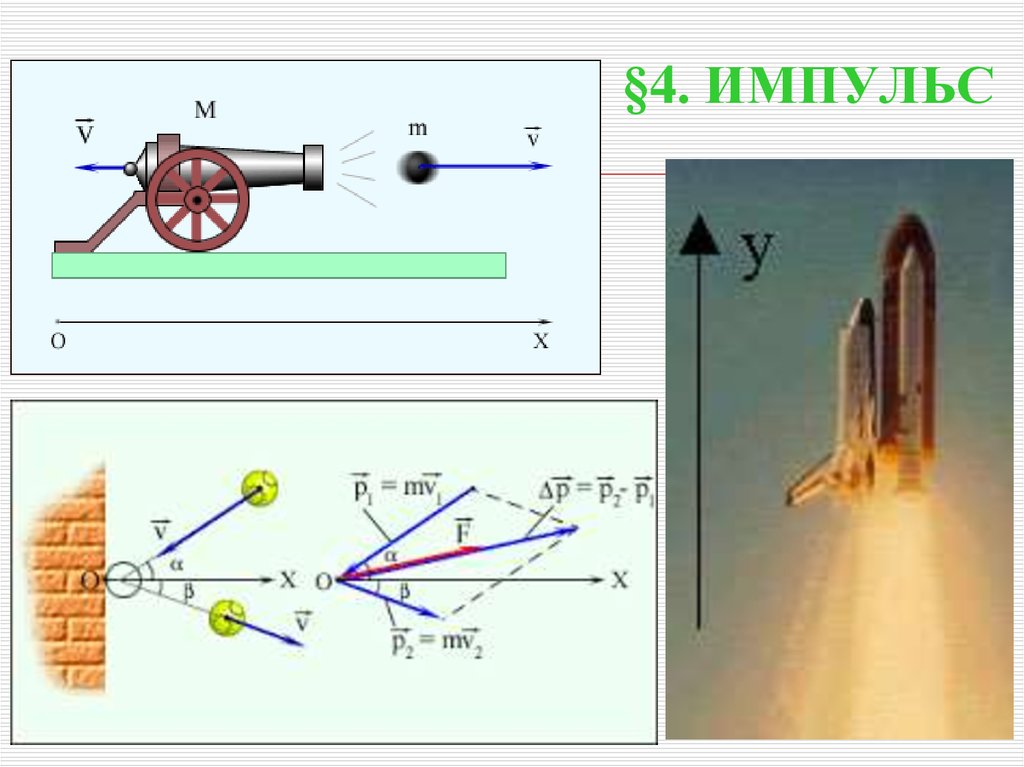
21. §4. ИМПУЛЬС
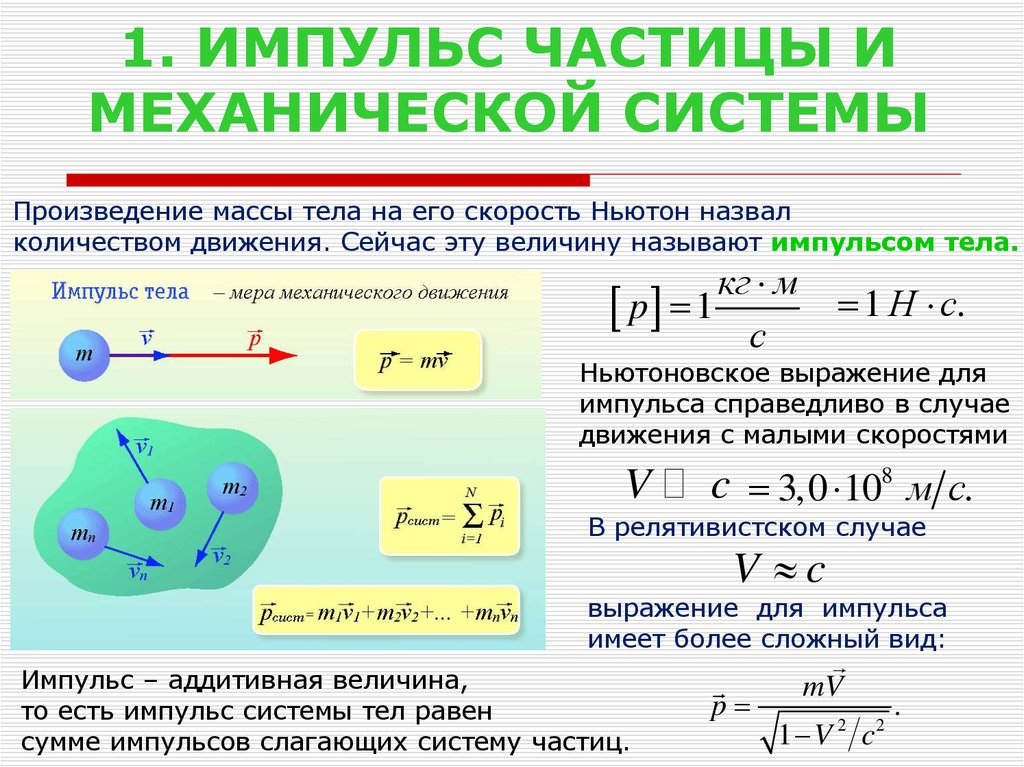
22. 1. ИМПУЛЬС ЧАСТИЦЫ И МЕХАНИЧЕСКОЙ СИСТЕМЫ
Произведение массы тела на его скорость Ньютон назвалколичеством движения. Сейчас эту величину называют импульсом тела.
кг м
p 1
с
1 Н с.
Ньютоновское выражение для
импульса справедливо в случае
движения с малыми скоростями
V
c 3,0 108 м с.
В релятивистском случае
V c
выражение для импульса
имеет более сложный вид:
Импульс – аддитивная величина,
то есть импульс системы тел равен
сумме импульсов слагающих систему частиц.
p
mV
1 V c
2
2
.
23. 2. ИМПУЛЬС СИСТЕМЫ И ЗАКОНЫ ДИНАМИКИ
Второй закон Ньютона гласит, что скорость измененияdp
dp Fdt.
импульса тела равно сумме сил, действующих на тело F
dt
Произведение силы на время её действия называется импульсом силы
Fdt dI dp dI ;
I 1 Н с,
I – импульс силы.
Проинтегрировав выражение для приращения импульса, получим
t
p p0 Fdt ;
0
t
px p0 x Fx dt.
0
Приращение импульса тела
равно импульсу силы,
действующей на это тело.
Для произвольной системы тел:
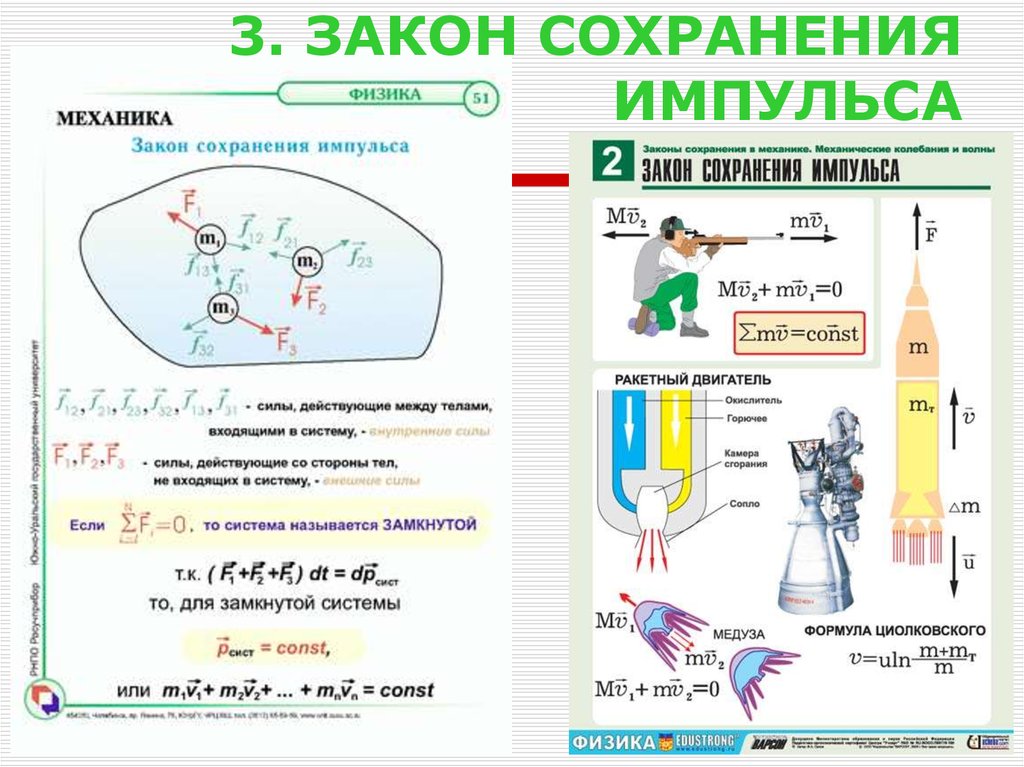
24. 3. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
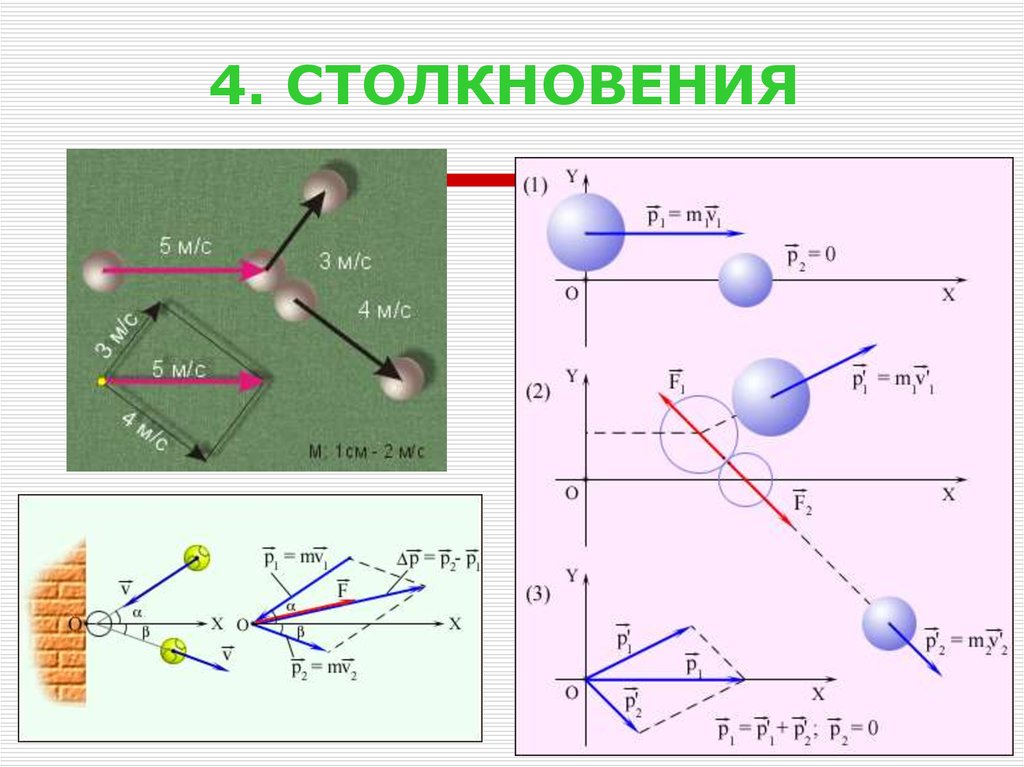
25. 4. СТОЛКНОВЕНИЯ
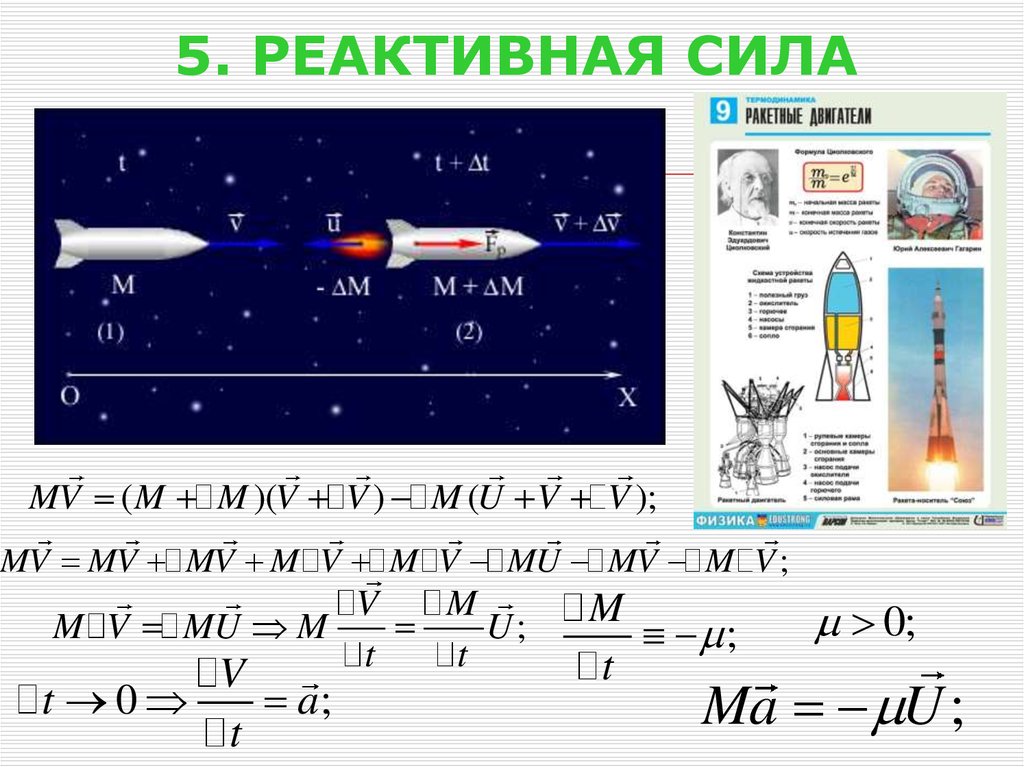
26. 5. РЕАКТИВНАЯ СИЛА
MV ( M M )(V V ) M (U V V );MV MV MV M V M V MU MV M V ;
V
M
M V MU M
U;
t
t
V
t 0
a;
t
M
;
t
0;
Ma U ;
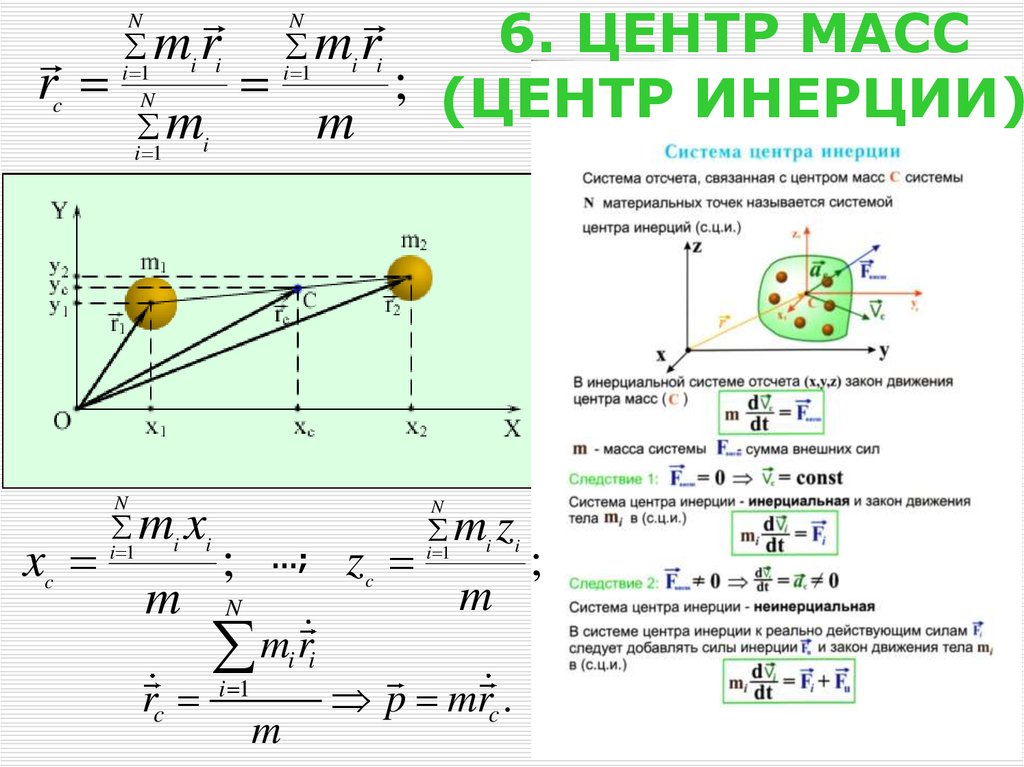
27. 6. ЦЕНТР МАСС (ЦЕНТР ИНЕРЦИИ)
rcmr
i i
i 1
mr
i i
i 1
6. ЦЕНТР МАСС
; (ЦЕНТР ИНЕРЦИИ)
m
m
N
N
N
i 1
i
N
xc
m
x
i
i
i 1
m
rc
N
;
…;
N
m r
i i
i 1
m
zc
m
z
i
i
i 1
m
p mrc .
;










 physics
physics








