Similar presentations:
Колебания материальной точки
1.
yO
x k x 0
2
x(t)
F
F c x ; mx F ; mx cx 0 m
круговая
c
c
2
c
частота
x
x
0
;
k
;
k
x
m
колебаний
m
m
– дифференциальное уравнение свободных колебаний материальной точки.
t
k 0; k i ;
Основная форма
x C1k sin kt C 2 k cos kt .
общего решения: x C 1 cos kt C 2 sin kt
Определение констант: Начальные условия: при t 0 : x x0 , x
v0 .
x0 C1 C 2 0 ;
v0
C1 x0 ; C2 k .
v0 C1k 0 C 2 k ;
Решение ищем в виде:
x e ;
Частное решение дифференциального уравнения
свободных колебаний материальной точки в
основной форме:
2
2
v0
x x0 cos kt sin kt
k
2.
x k x 02
Амплитудная форма
общего решения:
– дифференциальное уравнение свободных колебаний материальной точки.
Решение ищем в виде:
t
k 0; k i ;
x e ;
2
2
x A sin kt или x A sin cos kt A cos sin kt .
x C1 cos kt C 2 sin kt
C1 A sin ; C2 A cos .
2
0
2
v
А – амплитуда колебаний: A C C x
;
k
C 1 kx0
α – начальная фаза колебаний (изменяется в пределах [0,2π]): tg
;
C2
v0
2
1
2
2
Частное решение дифференциального уравнения
свободных колебаний материальной точки в
амплитудной форме:
2
0
v
kx0
x x
sin kt arctg
k
v0
2
0
2
0
2
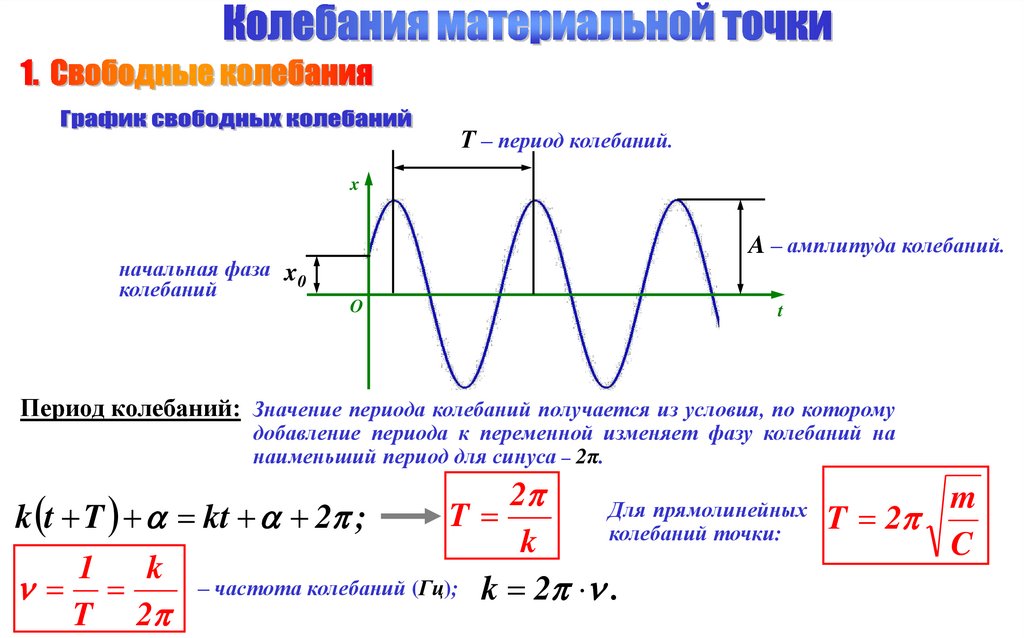
3.
Т – период колебаний.x
начальная фаза x0
колебаний
A – амплитуда колебаний.
O
t
Период колебаний: Значение периода колебаний получается из условия, по которому
добавление периода к переменной изменяет фазу колебаний на
наименьший период для синуса – 2π.
2
m
Для
прямолинейных
T
k t T kt 2 ;
T 2
колебаний точки:
k
C
1
k
– частота колебаний (Гц); k 2 .
T 2
4.
AF
B
C
P
x
Пружина АВ, закрепленная одним концом в точке А, имеет жесткость с =
19,6 н/м. В некоторый момент к нижнему концу В недеформированной пружины
подвешивают гирю С массой m = 0.1 кг и отпускают ее без начальной скорости.
Найти уравнение движения гири, амплитуду и период ее колебаний пренебрегая
массой пружины.
Решение: ma P F ;
mx mg F ; mx mg cx ; k c m ;
x k 2 x g – дифференциальное уравнение движения гири.
g mg
x x1 x2 ;
частное решение неоднородного дифуравнения: x2 2
;
2
y
c
1 k x1 0 ; k
общее решение однородного дифуравнения: x
характеристическое уравнение: 2 k 2 0
ki ;
x1 C1 cos kt C2 sin kt .
0 0.
начальные условия: при t 0 : x0 0 ;x
mg
определение
C1 mg c ;
x C1 cos kt C 2 sin kt
произвольных
c
C 2 0.
постоянных:
x C1k sin skt C2 k cos kt
mg
mg mg
x
cos
t
c
c
c
5.
Пружина АВ, закрепленная одним концом в точке А, имеет жесткость с =19,6 н/м. В некоторый момент к нижнему концу В недеформированной пружины
подвешивают гирю С массой m = 0.1 кг и отпускают ее без начальной скорости.
Найти уравнение движения гири, амплитуду и период ее колебаний пренебрегая
массой пружины.
Решение: ma P F . В положении статического равновесия: 0 P F ;
A
F c ст
F
F
B
C
mx mg F ; mx mg c x ст ;
начало
движения
статическая
ст деформация
λ
x
P
P
x
ст P c mg c
положение
статического
равновесия
y
x+λст
деформация
пружины
x mg k 2 x mg ;
k c m 14 ;
x k x 0 – дифференциальное уравнение
2
движения гири.
Характеристическое уравнение: 2 k 2 0
Общее решение однородного дифуравнения:
ki .
x C1 cos kt C 2 sin kt
6.
Пружина АВ, закрепленная одним концом в точке А, имеет жесткость с =19,6 н/м. В некоторый момент к нижнему концу В недеформированной пружины
подвешивают гирю С массой m = 0.1 кг и отпускают ее без начальной скорости.
Найти уравнение движения гири, амплитуду и период ее колебаний пренебрегая
массой пружины.
Решение:
A
x C1 cos kt C 2 sin kt x C1k sin skt C2 k cos kt ;
0 0.
Начальные условия: при t 0 : x0 ст ; x
Определение произвольных постоянных: C1 ст 0 ,05 ; C 2 0.
начало
движения
F
λст статическая
деформация
B
x
C
P
x
положение
статического
равновесия
y
x+λст
деформация
пружины
x 0.05 cos 14 t м – уравнение движения гири.
Амплитуда колебаний:
A C C 0.05 м .
Период колебаний:
T 2 k 0.45 c .
Ответ:
2
1
2
2
x 0.05 cos 14 t м ; A 0.05 м ; T 0.45 c .
7.
yO
F c x ; R x ; mx R F ; m
c
c
2
x x
2
n
;
x
x
0
;
k
;
R
m
m
m
m
x(t)
F
R
R
x 2 nx k x 0
2
Решение ищем в виде:
t
x e ;
– дифференциальное уравнение затухающих
колебаний материальной точки.
2 n k 0 ;
2
2
Три случая решения дифференциального уравнения:
n k;
2. Предельный случай:
n k;
3. Случай большого сопротивления: n k ;
1. Случай малого сопротивления:
n n k ;
2
2
8.
n k1 ,2 n k1i , где
k1 k n
2
2
c
m
2
2m
круговая частота
Затухающих колебаний
C1 cos k1t C2 sin k1t
nt
nt
x ne C1 cos k1t C 2 sin k1t e C1k1 sin k1t C 2 k1 cos k1t .
Основная форма общего решения:
x e
nt
Определение констант: Начальные условия: при t 0 : x x0 , x
v0 .
x0 1 C1 C 2 0 ;
v0 nC1 C 2 k1 ;
Частное
решение
дифференциального уравнения затухающих
колебаний материальной точки в
основной форме:
1
C1 x0 ; C 2 v0 nx0 .
k1
x e
nt
1
x0 cos k1t k v0 nx0 sin k1t
1
9.
n kАмплитудная форма
общего решения:
или
x e
nt
x Ae
nt
sin k1t
A sin cos k1t A cos sin k1t .
x e nt C1 cos k1t C 2 sin k1t
v0 nx0
x
;
C1 A sin ;
C2 A cos .
2
Амплитуда колебаний: A
C C
2
1
2
2
2
0
2
1
k
α – начальная фаза колебаний (изменяется в пределах [0,2π]):
Частное решение дифференциального уравнения затухающих колебаний материальной
точки в амплитудной форме:
C1
x0 k1
tg
;
C 2 v0 nx0
v0 nx0
x
sin kt arctg
2
x
2
0
2
1
k
x0 k1
v0 nx0
10.
n kТ1
x
A1
e
Т1
nt
x0 – начальная фаза колебаний;
T – период колебаний;
A1 , A2 – амплитуда колебаний;
Условный период колебаний (c):
2
T1
k1
2
c
m
2
2m
Частота колебаний (Гц):
x0
O
A2
e
t
nt
Декремент затухания:
Логарифмический
декремент затухания:
A1
D
e
A2
nT
2
1
k1
1
T1 2 2
;
nT
ln D
2
Q 0.25
2
c
m 2m
2
k
Добротность: Q
2n
11.
n k1 , 2 n . Общее решение: x e nt C1t C 2 x ne nt C1t C 2 e nt C1 .
Определение констант:
Начальные условия: при
x0 1 C1 0 C 2 ;
v0 nC2 C1 ;
t 0 : x x0 , x v0 .
C 2 x0 ;
C1 v0 nx0 .
Частное решение дифференциального
уравнения
затухающего
движения
материальной точки :
x e
nt
v0 nx0 t x0
x
v0 > 0
v0 = 0
x0
t
O
v0 < 0
12.
1 ,2 n k2 , где k2 n k2
x ne
nt
2
n k
2
c
.
2m
m
Общее
решение:
C e C e e k C e C e .
k2 t
k2 t
1
2
Определение констант:
x0 C1 C 2 ;
nt
v0 n C1 C 2 k2 C1 C 2 ;
1
1
2
2
Начальные условия:
при t 0 : x x0 , x v0 .
x0 n k2 v0
x n k2 v0
C1
; C2 0
.
2 k2
2 k2
Частное решение дифференциального уравнения
затухающего движения материальной точки :
nt
C e C e
k2 t
k2 t
k2 t
k2 t
2
x e
nt
e
k2 t
k2 t
k2 t
k2 t
x
x0 e
e v0 e
e
2 k2
x
v0 > 0
v0 = 0
x0
t
O
v0 < 0
13.
AПластина C массой m = 0.1 кг , подвешенная на пружине АВ, движется между полюсами
магнита. Вследствие вихревых токов движение тормозится силой, пропорциональной скорости. Сила
сопротивления движению R = fФ2v Н, где f = 0,001, Ф = 10√5 [Вб] — магнитный поток между
полюсами магнита. В начальный момент скорость пластинки равна нулю и пружина не растянута;
жесткость пружины с = 19,6 н/м.
Найти уравнение движения пластины.
Решение: ma P F R ; mx
mg F R ; mx mg c x ст x ;
k c m 14 c 1 ; 2 n m 5 c 2 ; ст mg c 0.05 м .
x 2 nx k x 0 – дифференциальное уравнение движения пластины.
2
B
CR
F
положение
статического
равновесия
y
Характеристическое уравнение:
x
n k1i ;
k1 k 2 n2 13.77 c 1 .
Общее решение:
Скорость:
P
2 2 n k 2 0
x e
nt
C1 cos k1t C2 sin k1t .
x ne nt C1 cos k1t C 2 sin k1t e nt C1k1 sin k1t C 2 k1 cos k1t .
14.
AПластина C массой m = 0.1 кг , подвешенная на пружине АВ, движется между полюсами
магнита. Вследствие вихревых токов движение тормозится силой, пропорциональной скорости. Сила
сопротивления движению R = fФ2v Н, где f = 0,001, Ф = 10√5 [Вб] — магнитный поток между
полюсами магнита. В начальный момент скорость пластинки равна нулю и пружина не растянута;
жесткость пружины с = 19,6 н/м.
Найти уравнение движения пластины.
Решение:
C1 cos k1t C2 sin k1t
x ne nt C1 cos k1t C 2 sin k1t e nt C1k1 sin k1t C 2 k1 cos k1t .
x e
R
B
C
x
nt
Начальные условия: при
F
положение
статического
равновесия
P
y
t 0 : x0 ст 0 ,05 м; x 0 0.
C1 0.05 ;
n
C2 ст 0.0091.
k1
2 . 5 t
0.05 cos 13.77 t 0.0091 sin 13.77 t м .
x e
Определение
произвольных
постоянных:
Ответ:
x e 2.5 t 0.05 cos 13.77 t 0.0091 sin 13.77 t м .
15.
yO
x(t)
F
x
HH
F c x;
H N sin pt ;
mx F H ; mx cx N sin pt m
Дифференциальное уравнение вынужденных колебаний материальной точки:
x k x h sin pt
2
x x1 x 2 ;
x1 C1 cos kt C2 sin kt ;
16.
x2 B sin pt ;2
x 2 Bp cos pt ; x 2 Bp sin pt ;
Bp 2 Bk 2 h sin pt 0 ;
B k 2 h p 2 ; x2 k 2 h p 2 sin pt ;
p k
Основная форма
общего решения:
x C1 cos kt C2 sin kt k 2 h p 2 sin pt
x C1k sin kt C 2 k cos kt k 2 p 2 cos pt .
hp
Определение констант:
при t 0 : x x0 , x v0 .
Начальные условия:
x0 C1 k 2 h p 2 sin ;
C1 x0 k 2 h p 2 sin ;
v0
hp
C 2 k k k 2 p 2 cos .
v0 C 2 k k 2 p 2 cos ;
Частное решение дифференциального уравнения свободных колебаний материальной точки в основной форме:
hp
x
x0 k 2 h p 2 sin
cos kt
v0
hp
k k 2 p 2 cos
k
sin kt k 2 h p 2 sin pt
17.
x2 B sin pt ;2
x 2 Bp cos pt ; x 2 Bp sin pt ;
Bp 2 Bk 2 h sin pt 0 ;
B k 2 h p 2 ; x2 k 2 h p 2 sin pt ;
p k
Амплитудная форма
общего решения:
x A sin kt k 2 h p 2 sin pt
Амплитуда собственных колебаний:
A С С
2
1
2
2
x
0
h
k 2 p2
sin
2
2
1
hp
2 v0 k 2 p 2 cos .
k
C1
x0 k 2 p 2 h sin
Начальная фаза собственных колебаний: arctg
arctg k v k 2 p 2 hp cos .
0
C2
Частное решение дифференциального уравнения свободных колебаний материальной точки в основной форме:
x
x
0
h
k p2
2
sin
2
2
1
x0 k 2 p 2 h sin
hp
2 v0 k 2 p 2 cos sin kt arctg k v k 2 p 2 hp cos k 2 h p 2 sin pt
0
k
18.
p kx
T1 – период собственных колебаний;
x01 – начальная фаза собственных колебаний;
А – амплитуда собственных колебаний.
T2 – период вынуждающей силы;
x02 – начальная фаза вынуждающей силы;
B – амплитуда вынуждающей силы.
Т1
Вынуждающая сила
B
x02 x
Собственные колебания
A
01
O
t
Т2
Вынужденные колебания
19.
x2 Bt cos pt ;p k
x 2 B cos pt Bpt sin( pt ); x 2 2 Bp sin pt Bp2 t cos pt ;
B 2hp ; x2 2htp cos pt 2htp sin pt 2 ;
2 Bp h sin pt 0 ;
Основная форма
общего решения:
x C 1 cos kt C 2 sin kt 2htp sin pt 2
x C 1k sin kt C 2 k cos kt 2hp sin pt 2 ht2 cos pt 2 .
Определение констант:
x0 C1 ;
v0 C 2 k 2hp cos ;
Начальные условия:
при t 0 : x x0 , x v0 .
C1 x0 ;
C 2 vk0 2 hpk cos .
Частное решение дифференциального уравнения свободных колебаний материальной точки в основной форме:
x x0 cos kt
v0
k
h
2 pk
cos sin kt 2htp sin pt 2
20.
p kx2 Bt cos pt ;
x 2 B cos pt Bpt sin( pt ); x 2 2 Bp sin pt Bp2 t cos pt ;
B 2hp ; x2 2htp cos pt 2htp sin pt 2 ;
2 Bp h sin pt 0 ;
Амплитудная форма
общего решения:
x A sin kt 2htp sin pt 2
Амплитуда собственных колебаний:
A
Начальная фаза собственных колебаний:
2
2
С1 С 2
2
x0 k12
v0 2hp cos
.
2
C1
2 pk x0
arctg
arctg 2 p v0 h cos .
C2
Частное решение дифференциального уравнения свободных колебаний материальной точки в основной форме:
x x
2
0
1
k2
v cos sin kt arctg
0
h
2p
2
2 pk x0
2 p v0 h cos
sin pt
ht
2p
2
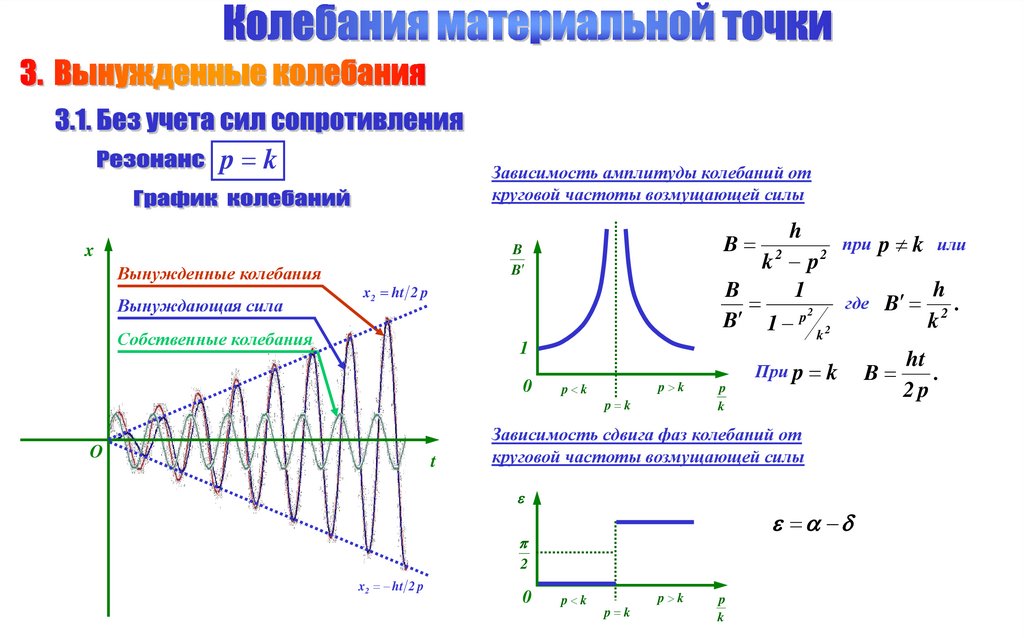
21.
p kЗависимость амплитуды колебаний от
круговой частоты возмущающей силы
x
Вынужденные колебания
Вынуждающая сила
h
при p k или
2
2
k p
h
B
1
где
B 2.
2
p
B 1 2
k
B
B
B
x2 ht 2 p
Собственные колебания
k
1
0
O
t
p k
p k
p k
p
k
Зависимость сдвига фаз колебаний от
круговой частоты возмущающей силы
2
x2 ht 2 p
При p k
0
p k
p k
p k
p
k
ht
B
.
2p
22.
AМагнит C массой m = 0.1 кг подвешен на пружине АВ жесткостью с = 19,6 н/м движется в поле
соленоида, по катушке которого идет переменный ток i = 20sin(8πt). Ток идет с момента t = 0,
втягивая стержень в соленоид; до этого момента магнит висел неподвижно. Сила взаимодействия
между катушкой и магнитом T = 0.016πi Н.
Определить уравнение дальнейшего движения магнита.
Решение:
B
ma P F T ; mx mg c x ст 0.32 sin 8 t ;
1
mx mg F T ; k c m 14 c ; ст mg c 0.05 м .
1
p 8 25.12 c ; h 0.32 m 10.05 м.
C
x k x h sin pt – дифференциальное уравнение движения магнита.
2
F
y
x x1 x 2 ;
x1 C1 cos kt C2 sin kt ;
p k x2 2 h 2 sin pt ;
x
0
.
023
sin
8
t
2
k p
положение
статического
равновесия
T P
x
– вынужденные
колебания
магнита.
23.
AМагнит C массой m = 0.1 кг подвешен на пружине АВ жесткостью с = 19,6 н/м движется в поле
соленоида, по катушке которого идет переменный ток i = 20sin(8πt). Ток идет с момента t = 0,
втягивая стержень в соленоид; до этого момента магнит висел неподвижно. Сила взаимодействия
между катушкой и магнитом T = 0.016πi Н.
Определить уравнение дальнейшего движения магнита.
Решение:
B
ma P F T ; mx mg c x ст 0.32 sin 8 t ;
1
mx mg F T ; k c m 14 c ; ст mg c 0.05 м .
1
p 8 25.12 c ; h 0.32 m 10.05 м.
C
x k x h sin pt – дифференциальное уравнение движения магнита.
2
F
y
x x1 x 2 ;
x1 C1 cos kt C2 sin kt ;
p k x2 2 h 2 sin pt ;
x
0
.
023
sin
8
t
2
k p
положение
статического
равновесия
T P
x
– вынужденные
колебания
магнита.
24.
Ry
O
x(t)
F
x
R HH R
F c x ; H N sin pt ; R x ;
mx F H R ;
mx x cx N sin pt m
c
c
N
2
x x x 0 , где k ; 2 n ; h .
m
m
m
m
m
Дифференциальное уравнение вынужденных колебаний материальной точки с учетом сил
сопротивления движению:
x 2 nx k x h sin pt x x1 x2 ;
2
Три случая частного решения однородного дифференциального уравнения:
n k : x1 e C1 cos k1t C 2 sin k1t .
nt
2. Предельный случай
C1t C2 .
x
e
n k: 1
k2 t
k2 t
nt
3. Случай большого сопротивления n k : x1 e
C 1e C 2 e
.
1. Случай малого сопротивления
nt
25.
Дифференциальное уравнение вынужденных колебаний материальной точки с учетом силсопротивления движению:
x 2 nx k x h sin pt x x1 x2 ;
Частное решение неоднородного дифференциального уравнения: x2 B sin pt ;
x2 Bp cos pt ; x 2 Bp 2 sin pt ;
2
2
Bp sin pt 2 nBp cos pt Bk sin pt h sin pt ;
2
h sin pt h sin pt h sin cos pt h cos sin pt ;
B k p h cos sin pt 2 Bnp h sin cos pt 0 ;
B k p h cos 0 ; 2 Bnp h sin 0 ;
2
2
2
B
2
h
k p 4 n2 p 2
2
2 2
tg k 22 npp 2 , 0
x2
h
k 2 p 4 n2 p 2
2 2
sin pt arctg k 2 p 2
2 np
26.
На пружине АВ жесткостью с = 19,6 н/м подвешены магнит C массой m = 0.05 кг ,движущийся в поле соленоида, по катушке которого идет переменный ток i = 20sin(8πt) и
пластина D массой m = 0.05 кг, движущаяся между полюсами постоянного магнита.
Сила взаимодействия между катушкой соленоида и магнитом T = 0.016πi Н. Ток идет с
момента t = 0, втягивая стержень в соленоид.
Сила сопротивления движению пластины R = fФ2v Н, где f = 0,001, Ф = 10√5 [Вб] —
магнитный поток между полюсами магнита. В начальный момент магнит и пластину подвесили
к концу нерастянутой пружины и сообщили скорость v0 = 0,05 м/с , направленную вниз.
A
B
R
F
C
Определить уравнение дальнейшего движения магнита с пластиной.
Решение:
y
положение
статического
равновесия
P
DT
m m1 m2 0.1 кг ; k c m 14 c ; ст mg c 0.05 м .
1
fФ 0.5 ; 2 n m 5 c 2 ; p 8 25.12 c 1 ; h 0.32 m 10.05 м.
2
x 2 nx k x h sin pt – дифференциальное уравнение движения системы.
2
x
ma P F T R ; mx mg F T R ;
mx mg c x ст x 0.32 sin 8 t ;
27.
На пружине АВ жесткостью с = 19,6 н/м подвешены магнит C массой m = 0.05 кг ,движущийся в поле соленоида, по катушке которого идет переменный ток i = 20sin(8πt) и
пластина D массой m = 0.05 кг, движущаяся между полюсами постоянного магнита.
Сила взаимодействия между катушкой соленоида и магнитом T = 0.016πi Н. Ток идет с
момента t = 0, втягивая стержень в соленоид.
Сила сопротивления движению пластины R = fФ2v Н, где f = 0,001, Ф = 10√5 [Вб] —
магнитный поток между полюсами магнита. В начальный момент магнит и пластину подвесили
к концу нерастянутой пружины и сообщили скорость v0 = 0,05 м/с , направленную вниз.
A
R
B F
Определить уравнение дальнейшего движения магнита с пластиной.
Решение:
y
C
x x1 x 2 ;
x 2 nx k 2 x h sin pt
частное решение неоднородного дифуравнения: x2 B sin pt
общее решение однородного дифуравнения:
P
T
D
x
;
x1 e C1 cos k1t C 2 sin k1t .
2
2
2
2
1
k1 k n 14 2.5 13.77 c ;
0 v0 0.05 м c .
Начальные условия: при t 0 : x0 ст 0 ,05 м ; x
– случай малого сопротивления n k :
nt
28.
На пружине АВ жесткостью с = 19,6 н/м подвешены магнит C массой m = 0.05 кг ,движущийся в поле соленоида, по катушке которого идет переменный ток i = 20sin(8πt) и
пластина D массой m = 0.05 кг, движущаяся между полюсами постоянного магнита.
Сила взаимодействия между катушкой соленоида и магнитом T = 0.016πi Н. Ток идет с
момента t = 0, втягивая стержень в соленоид.
Сила сопротивления движению пластины R = fФ2v Н, где f = 0,001, Ф = 10√5 [Вб] —
магнитный поток между полюсами магнита. В начальный момент магнит и пластину подвесили
к концу нерастянутой пружины и сообщили скорость v0 = 0,05 м/с , направленную вниз.
A
R
B F
Определить уравнение дальнейшего движения магнита с пластиной.
Решение:
y
C
P
T
D
x
x2
h
k 2 p 4 n2 p 2
2 2
sin pt arctg k 2 p 2 0.022 sin 25.12 t 0.28 ;
2 np
x e nt C1 cos k1t C 2 sin k1t 0.022 sin 25.12 t 0.28 ;
x ne nt C1 cos k1t C 2 sin k1t k1e nt C1 sin k1t C 2 cos k1t
0.022 25.12 cos 25.12 t 0.28 ;
29.
На пружине АВ жесткостью с = 19,6 н/м подвешены магнит C массой m = 0.05 кг ,движущийся в поле соленоида, по катушке которого идет переменный ток i = 20sin(8πt) и
пластина D массой m = 0.05 кг, движущаяся между полюсами постоянного магнита.
Сила взаимодействия между катушкой соленоида и магнитом T = 0.016πi Н. Ток идет с
момента t = 0, втягивая стержень в соленоид.
Сила сопротивления движению пластины R = fФ2v Н, где f = 0,001, Ф = 10√5 [Вб] —
магнитный поток между полюсами магнита. В начальный момент магнит и пластину подвесили
к концу нерастянутой пружины и сообщили скорость v0 = 0,05 м/с , направленную вниз.
A
R
B F
Определить уравнение дальнейшего движения магнита с пластиной.
Решение:
y
C
P
T
D
x
Определение
произвольных
постоянных:
x e
2.5 t
0.05 C1 0.022 sin 0.28 ;
0.05 nC1 k1C2 5.53 cos 0.28 ;
C1 0.044 ;
C2 0.043;
0.044 cos 13.77 t 0.043 sin 13.77 t 0.022 sin 25.12t 0.28
Ответ: x e 2.5 t 0.044 cos 13.77 t 0.043 sin 13.77 t 0.022 sin 25.12 t 0.28
30.
Вынужденныеколебания
при
линейном
сопротивлении
являются
незатухающими. Амплитуда их постоянна как при отсутствии резонанса, так и
при резонансе.
Линейное сопротивление не влияет на частоту вынужденных колебаний,
которая совпадает с частотой возмущающей силы.
Вынужденные колебания как при линейном сопротивлении, так и при его
отсутствии не зависят от начальных условий.
Амплитуда вынужденных колебаний стремится к нулю с увеличением
относительной частоты возмущающей силы, причем при наличии линейного
сопротивления – быстрее.
31.
: mv P sin ; v l ; ; ml mg sin ;O
φ
g
sin 0
l
l
n
τ
M
– дифференциальное уравнение движения
g
В случае малых колебаний ( sinφ ≈ φ ):
0
l
A sin kt
M0
P
k
A
T
2
g
2
– круговая частота колебаний;
l
k
– амплитуда колебаний;
– начальная фаза колебаний;
математического
маятника
–
не
интегрируется в элементарных функциях.
– общее
решение
дифференциального
уравнения
малых
колебаний
математического маятника .
l – период малых колебаний.
g
В случае обычных колебаний:
1 sin sin ...
T 2
l
g
T 2
l
g
1 2
2
1
A2
16
2 A
2
1 3 2
2 4
4 A
2
– колебания не являются гармоническими,
период колебаний зависит от амплитуды.
– приближенная формула вычисления периода негармонических колебаний
математического маятника.
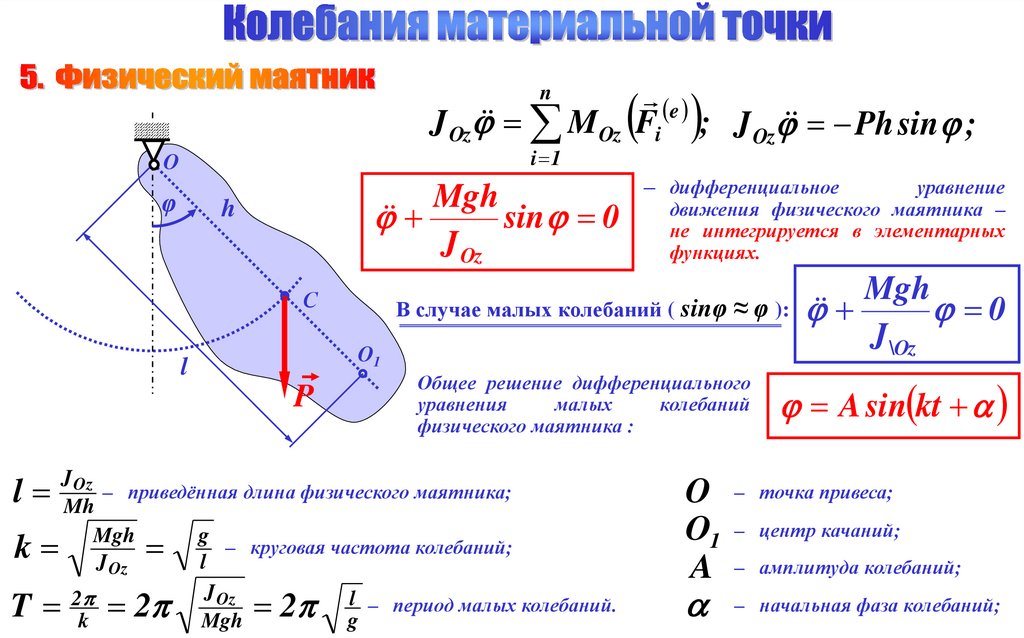
32.
eJ Oz MOz Fi ; J Oz Ph sin ;
n
i 1
O
φ
Mgh
sin 0
J Oz
h
С
P
Mgh
В случае малых колебаний ( sinφ ≈ φ ):
0
J
\Oz
O
l
Общее решение дифференциального
уравнения
малых
колебаний
физического маятника :
J Oz
– приведённая длина физического маятника;
Mh
Mgh
g
– круговая частота колебаний;
J Oz
l
J Oz
2
T k 2 Mgh 2 gl – период малых колебаний.
уравнение
движения физического маятника –
не интегрируется в элементарных
функциях.
1
l
k
– дифференциальное
A sin kt
O – точка привеса;
O1 – центр качаний;
A – амплитуда колебаний;
– начальная фаза колебаний;
33.
Приведенная длина физического маятника больше расстояния от точкипривеса до центра масс – l > h .
Применяя теорему Штейнера получим:
J Cz
J Oz J Cz Mh
J Cz
l h 0.
l
h h, так как O1C
Mh
Mh
Mh
Mh
2
Центр качаний и точка привеса обратимы (взаимозаменяемы).
Если то же тело подвесить за ось, проходящую через центр качаний параллельно первоначальной оси,
то приведенная длина полученного нового физического маятника будет равна приведенной длине
старого l1 = l .
Применяя теорему Штейнера получим:
J Cz M l h
J Cz
l1
l h l , так как J Cz Mh l h .
M O1C
M l h
M l h
J O1z
2






























 physics
physics








