Прямолинейные колебания точки

1. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ.

ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
ДИНАМИКА
ЛЕКЦИЯ 2

2. КОЛЕБАНИЯ

движения точки, которые характеризуются
определенной повторяемостью по времени.
Осциллятор — система,
совершающая колебания
Линейный осциллятор — система,
движущаяся под действием
возвращающей силы, то есть
силы, пропорциональной
отклонению от точки, называемой
положением равновесия и
направленной к этой точке
2
Колебания

3. ЦЕЛЬ ЛЕКЦИИ

На примере прямолинейных колебаний точки
познакомиться с колебательным движением в механике
Физические явления:
- механические колебания
- электромагнитные волны (оптические, радио, инфракрасные…)
- акустические волны (звук)
Природные явления:
- суточное вращение Земли
- землетрясения
- приливы и отливы
Биологические системы:
- сердечно-сосудистая система
- ухо + голосовые связки
3
Колебания

4. КОЛЕБАНИЯ В СТРОИТЕЛЬСТВЕ

Основные факторы
- природные явления
- промышленность
- транспорт
Виды колебаний
- механические
- акустические
- электромагнитные
- тепловые
4
Колебания

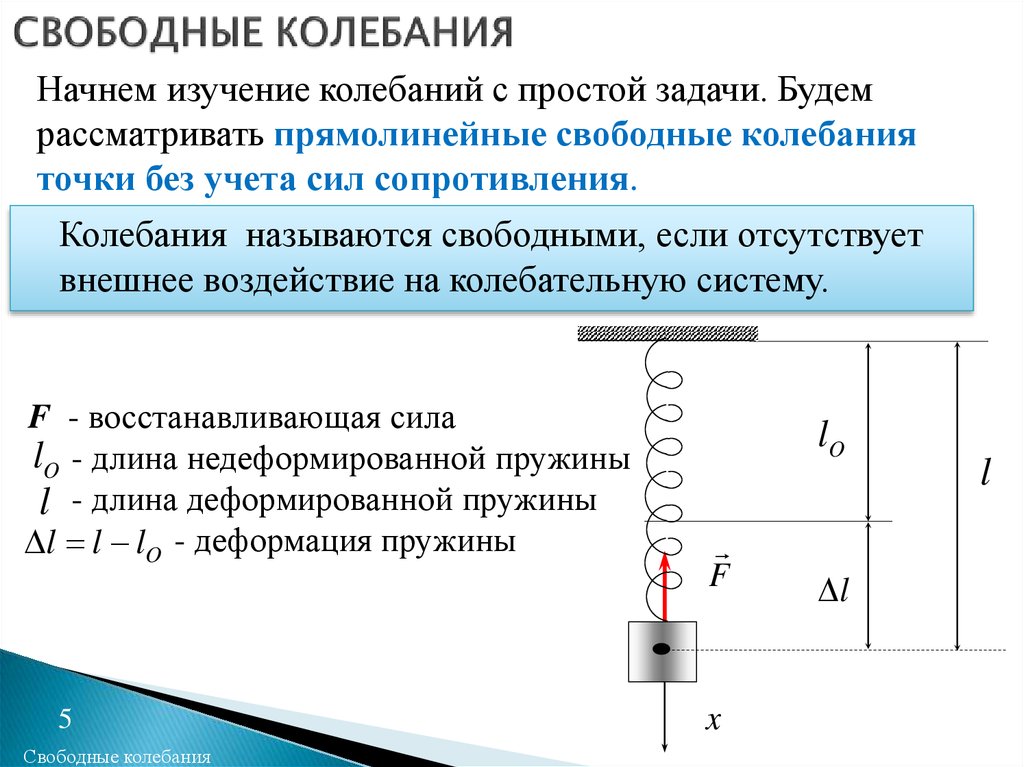
5. СВОБОДНЫЕ КОЛЕБАНИЯ

Начнем изучение колебаний с простой задачи. Будем
рассматривать прямолинейные свободные колебания
точки без учета сил сопротивления.
Колебания называются свободными, если отсутствует
внешнее воздействие на колебательную систему.
F - восстанавливающая сила
lO - длина недеформированной пружины
l - длина деформированной пружины
l l lO - деформация пружины
5
Свободные колебания
lO
F
x
l
l

6. СВОБОДНЫЕ КОЛЕБАНИЯ

lO
F
l
l
Рассматриваем прямолинейное
движение точки массой m под
действием силы упругости F.
Силу тяжести не учитываем.
F c l
- закон Гука
c - коэффициент жесткости
пружины
x
Закон Гука справедлив только для малых
колебаний! В общем случае
F c l c3 l c5 l ...
3
6
Свободные колебания
5

7. СВОБОДНЫЕ КОЛЕБАНИЯ

Начало отсчета – в положении
равновесия
lO
F
l
0
l
m x cx
c
m x cx 0 x x 0
m
c
k
m
2
Свободные колебания
Запишем ДУ движения точки
m x F
x
7
F c l cx
k – частота колебаний [рад/c]

8. СВОБОДНЫЕ КОЛЕБАНИЯ

x k 2 x 0
ДУ свободных колебаний
при отсутствии сил сопротивления
линейноe
однородное
второго порядка
x e
t
x e
t
x 2 e t
В результате подстановки решения получим
2 t
2 t
e k e 0
t
e ( k ) 0
2
2
характеристическое уравнение
8
Свободные колебания
2 k 2 0

9. СВОБОДНЫЕ КОЛЕБАНИЯ

k 0
2
2
1t
Корни уравнения мнимые
x D1e D2e
2t
1, 2 k 2 ik
D1eikt D2e ikt
используя формулу Эйлера
x C1 sin kt C2 cos kt
C1 ,C2 - постоянные интегрирования
Можно получить другую форму решения,
если ввести две другие постоянные A,
C1 A cos
9
Свободные колебания
C2 Asin

10. СВОБОДНЫЕ КОЛЕБАНИЯ

x C1 sin kt C2 cos kt
C1 A cos
C2 Asin
x A(sin kt cos cos kt sin )
Воспользуемся тригонометрической формулой
sin( ) sin cos cos sin
Получим решение уравнения свободных колебаний в форме
x A sin( kt )
A,
10
Свободные колебания
- постоянные интегрирования

11. СВОБОДНЫЕ КОЛЕБАНИЯ

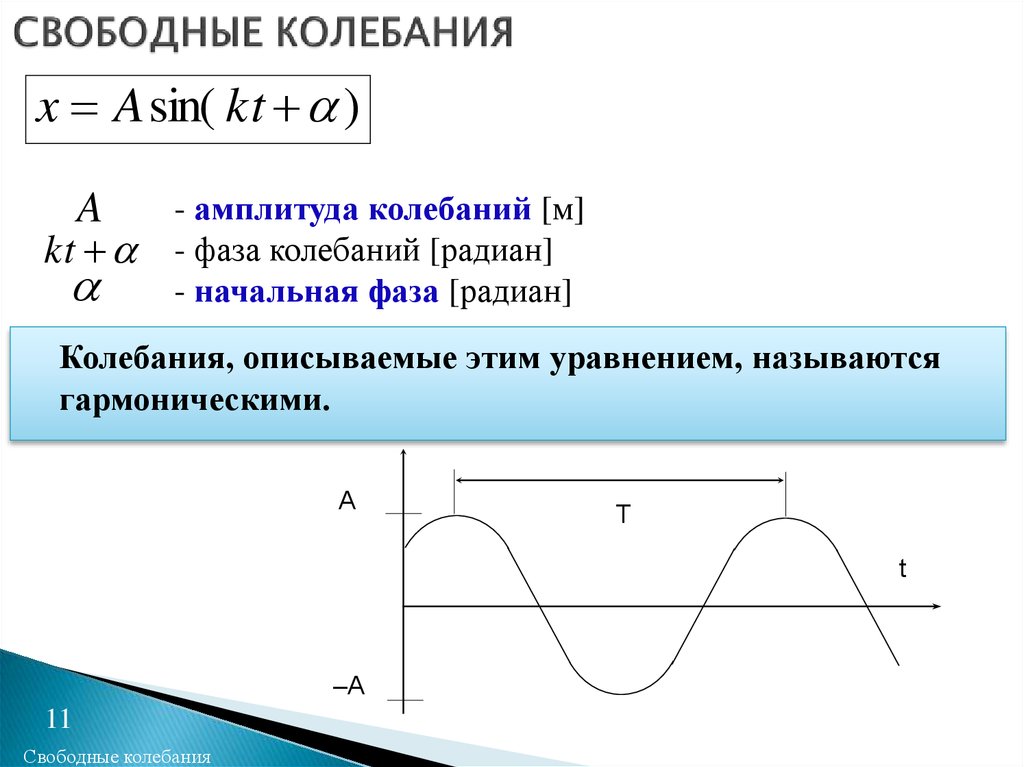
x A sin( kt )
A
kt
- амплитуда колебаний [м]
- фаза колебаний [радиан]
- начальная фаза [радиан]
Колебания, описываемые этим уравнением, называются
гармоническими.
A
T
t
–A
11
Свободные колебания

12. СВОБОДНЫЕ КОЛЕБАНИЯ

A
T
t
–A
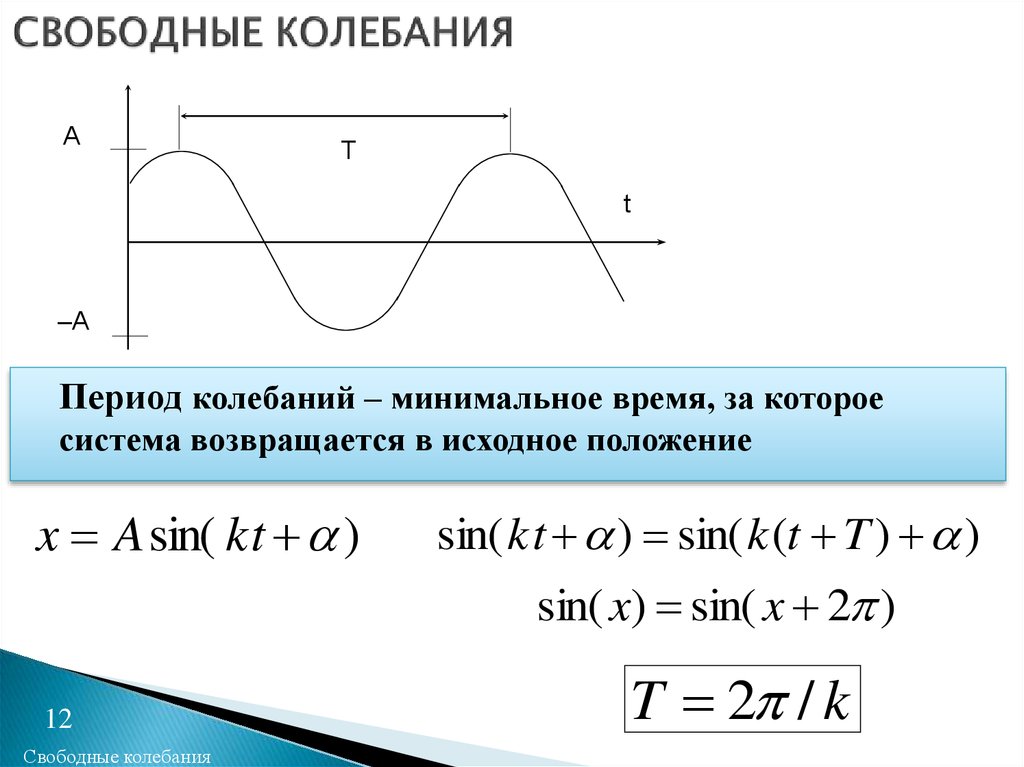
Период колебаний – минимальное время, за которое
система возвращается в исходное положение
x A sin( kt )
sin( kt ) sin( k (t T ) )
sin( x) sin( x 2 )
12
Свободные колебания
T 2 / k

13. СВОБОДНЫЕ КОЛЕБАНИЯ

Найдем постоянные интегрирования
A,
Подставим начальные условия
t 0 : x(0) x0 , v(0) x (0) v0
в общее решение
Получим
x A sin( kt )
x0 A sin , v0 x (0) Ak cos
tg sin / cos ( x0 /A) /( v0 / Ak ) kx0 /v 0
2
2
sin cos 1
( x0 /A) ( v 0 / Ak ) 1, A x v / k
2
13
Свободные колебания
2
2
0
2
0
2

14. СВОБОДНЫЕ КОЛЕБАНИЯ

1. Амплитуда и начальная фаза колебаний зависят от
начальных условий задачи
A x02 v02 / k 2 , tg kx0 /v 0
2. Частота и период колебаний не зависят от
начальных условий задачи и полностью определяются
параметрами самой колебательной системы
k c/m
14
Свободные колебания
T 2 / k

15. СВОБОДНЫЕ КОЛЕБАНИЯ С ПОСТОЯННОЙ СИЛОЙ

lO
s
0
mg
F
x
Рассматриваем прямолинейное
движение точки массой m.
Силу тяжести учитываем.
Условие равновесия
l
mg c s 0 s mg / c
Fx c( x s )
m x c( x s ) mg
m x cx
Постоянная сила, не изменяя характер колебаний,
смещает центр колебаний в сторону ее действия на
величину статической деформации
15
Свободные колебания