Прямолинейные колебания точки. (Лекция 2)

1.

Новосибирский Государственный Архитектурно-Строительный
Университет (Сибстрин)
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
ДИНАМИКА
ЛЕКЦИЯ 2.
ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ
Кафедра теоретической механики

2. План лекции

Времена меняются, и мы меняемся
вместе с ними.
Гораций
• Введение. Колебания в природе и технике
• Свободные колебания (без учета и с учетом
сопротивления среды)
• Вынужденные колебания (без учета и с
учетом сопротивления среды)
• Рекомендации к решению задач на
колебательное движение
• Примеры решения задач
• Заключение

3. На предыдущей лекции

Динамика
материальной
точки

4. Цель лекции

На примере прямолинейных
колебаний точки познакомиться
с колебательным движением в
механике

5. Колебания в природе и технике

Физические явления:
- механические колебания (вибрация, волны на воде)
- электромагнитные волны (оптические, радио,
инфракрасные…)
- акустические волны (звук)
Природные явления:
- суточное вращение Земли
- землетрясение и цунами
- приливы и отливы
Биологические системы:
- сердечно-сосудистая система
- ухо + голосовые связки
- эволюция биологического мира
Общество:
- промышленно-технологические циклы
- экономические циклы

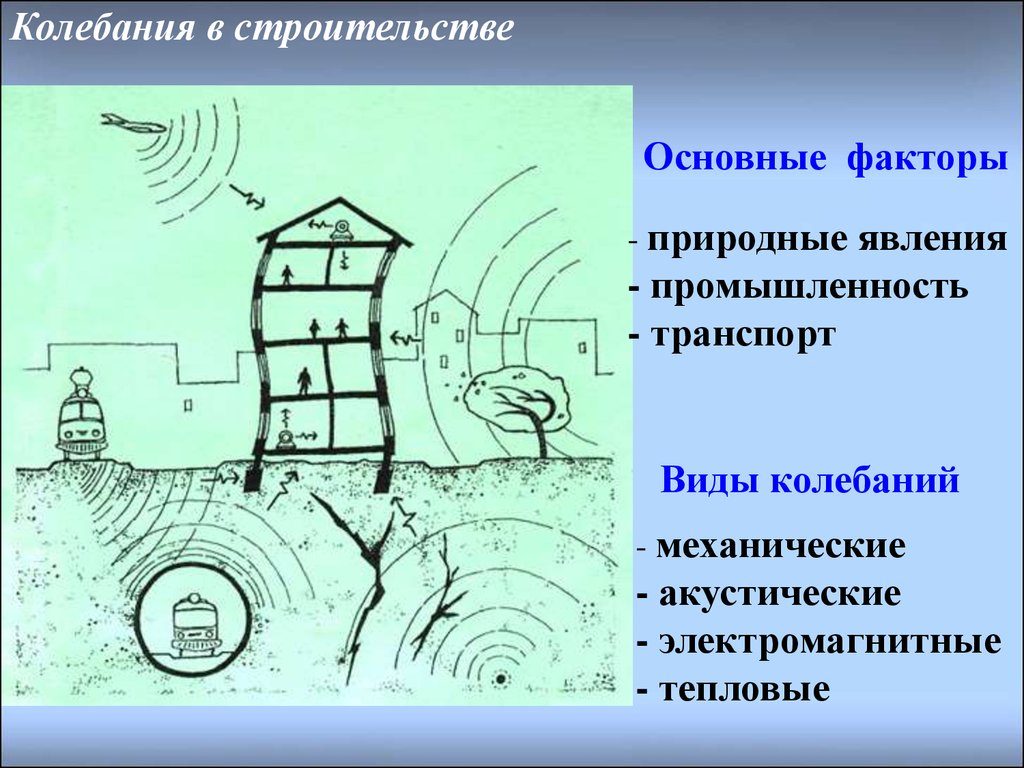
6. Колебания в строительстве

Основные факторы
- природные явления
- промышленность
- транспорт
Виды колебаний
- механические
- акустические
- электромагнитные
- тепловые

7.

Вред от колебаний:
- разрушение конструкций: мосты, перекрытия
зданий, трубопроводы, крылья самолетов, лопатки
турбомашин и т.д.
Примеры: трагедия такомского моста, меч статуи
Родины-Матери, шахтные вентиляторы.
-нарушение условий эксплуатации: вибрации станков
при обработке металлов, потеря точности приборов.
-вредное влияние на организм человека: работа с
вибраторами, шумы на производстве, морская болезнь
при шторме, игра музыкантов на определенных
частотах, …

8.

Колебания на службе человека:
Создание вибрационных машин (диапазон их
мощностей - от долей ватта у зубопропезного бора, до
тысячи киловатт у вибратора ледокола).
- вибропогружение и вибровыдергивание свай
- измельчение, дробление, уплотнение материалов
- вибротранспортировка сыпучих материалов
- виброобработка металлов с целью упрочнения их
поверхностей
- вибротерапия в медицине для восстановления
нормального давления
- вибромассаж
- физиолечение (токи Бернара, …)

9.

Свободные колебания точки
Начнем изучение механических колебаний с
наиболее простой задачи. Будем рассматривать
прямолинейное движение точки, а именно,
свободное колебание точки без учета сил
сопротивления.
Колебания называются свободными, если они
совершаются за счет первоначально запасенной
энергии. В последующие моменты времени
отсутствует внешнее воздействие на
колебательную систему.

10.

Свободные колебания точки
Рассматриваем
прямолинейное движение
l0
c
точки массой m под действием
l
восстанавливающей силы F.
O
Силу тяжести не учитываем.
Δ l=x
Ось x – направим в сторону
удлинения пружины
m
F
o - начало отсчета в конце
x
недеформируемой пружины
F – сила упругости пружины
c - коэффициент жесткости пружины,
lO - длина недеформированной пружины,
l - длина деформированной пружины,
l l lO x - деформация пружины

11.

ДУ свободных колебаний
Силу упругости пружины F еще называют
восстанавливающей силой
- всегда направлена в сторону восстановления
пружины
- ее модуль равен:
F c l
Составим ДУ движения точки в проекции на ось х
m x F m x c l cx
2
m x cx 0 x k x 0 (3)
c
k
m
2
k – частота колебаний точки, [рад/c]

12.

Решение уравнения свободных колебаний
Решение уравнения (3) в форме
x C1 sin kt C2 cos kt
(5)
C1 ,C2 - постоянные интегрирования
Можно получить другую форму решения:
x A sin( kt )
(7)
Связь между константами C1 A cos
C2 Asin
A, - постоянные интегрирования
A
- начальная фаза [радиан]
- амплитуда колебаний точки [м]
Колебания, совершаемые точкой по формуле (7)
называются гармоническими колебаниями.

13.

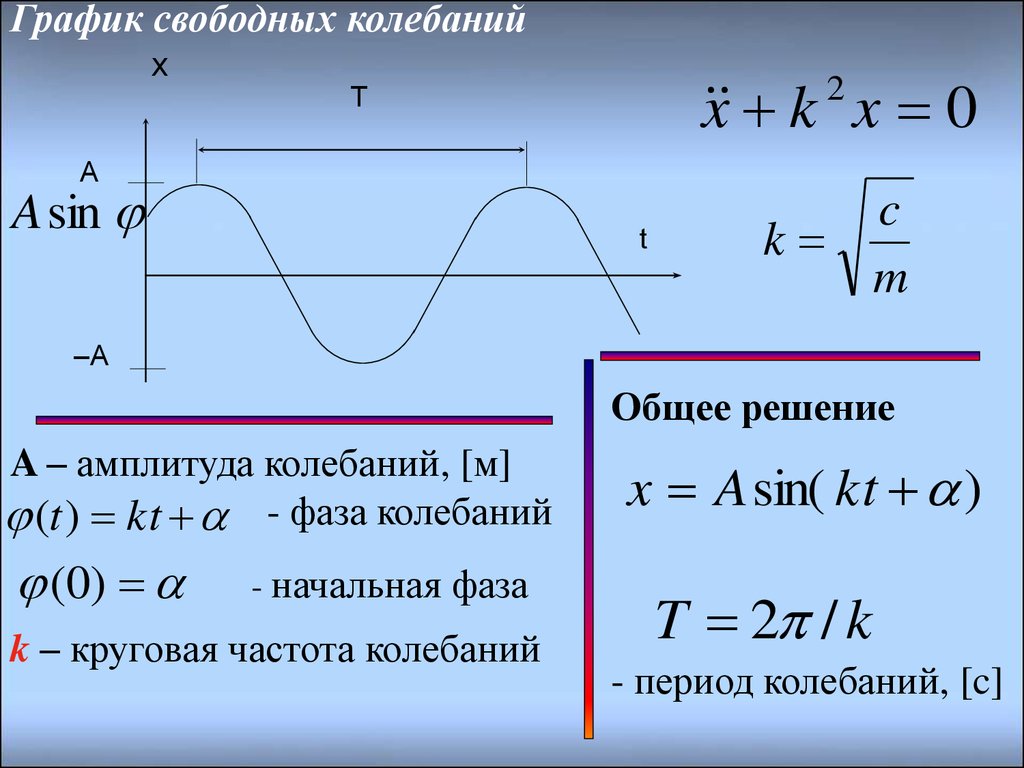
График свободных колебаний
x
x k x 0
2
T
A
A sin
t
c
k
m
–A
Общее решение
A – амплитуда колебаний, [м]
(t) kt - фаза колебаний
(0)
- начальная фаза
k – круговая частота колебаний
x A sin( kt )
T 2 / k
- период колебаний, [c]

14.

Постоянные интегрирования
A,
Подставим начальные условия
t 0 : x(0) x0 , v(0) x (0) v0
в общее решение
x A sin( kt )
Получим
x0 A sin , v0 x (0) Ak cos
Найдем постоянные интегрирования A,
tg sin / cos ( x0 /A) /( v0 / Ak ) kx0 /v 0
sin cos 1
2
2
( x0 /A) ( v 0 / Ak ) 1, A x02 v 02 / k 2
2
2

15.

Свойства свободных колебаний
1. Амплитуда и начальная фаза колебаний
зависят от начальных условий задачи
A x v / k , tg kx0 /v 0
2
0
2
0
2
(8)
2. Частота и период колебаний не зависят от
начальных условий задачи и полностью определяются
параметрами самой колебательной системы
k c/m
T 2 / k
(9)
Если в задаче требуется определить амплитуду и
период колебаний, то можно воспользоваться (8-9), не
решая ДУ.

16.

Свободные колебания при наличии постоянной силы P
l0
c
O
O1
l
λs
x
Δl
F
m
Рассматриваем прямолинейное
движение точки массой m под
действием восстанавливающей
силы F.
Силу тяжести учитываем.
Условие равновесия
P
x
O1 - начало отсчета x, в положении равновесия груза
P mg - сила тяжести
s ls ls lo
статическая
деформация пружины
mg c s 0
s mg / c
Восстанавливающая сила
Fx c( x s )
m x c( x s ) mg

17.

Уравнение свободных колебаний (P=const)
m x c( x s ) mg
С учетом условия равновесия
m x cx
(10)
mg c s
Получим ДУ свободных колебаний при наличии
постоянной силы, аналогичное (3)
x k x 0
2
Общее решение
(11)
x C1 sin kt C2 cos kt
x A sin( kt )
Постоянная сила, не изменяя характер колебаний,
смещает центр колебаний в сторону ее действия на
величину статической деформации
s

18.

Свободные затухающие колебания
Силы: F , P, R
Сила сопротивления
l0
c
λs
O1
R
F
m
P
x
x
R v
l
Второй закон Ньютона
m x cx x
ДУ свободных затухающих
колебаний
x 2bx k 2 x 0
2
b / 2m k c / m
O1 - начало отсчета в положении равновесия груза

19.

ДУ свободных затухающих колебаний
x 2bx k x 0
2
b / 2m k c / m
2
1. Случай малого сопротивления среды
(12)
b k
Общее решение уравнения
x e
bt
x Ae
(C1 sin k1t C2 cos k1t )
bt
sin( k1t )
(13)
Выражение для скорости
v x Ae
bt
( b sin( k1t ) k1 cos( k1t ))

20.

Постоянные интегрирования
Используем начальные условия
x(0) x0 v(0) v 0
x0 A sin
v0 A( b sin k1 cos )
Найдем постоянные интегрирования
A x (v 0 bx0 ) / k
2
0
2
2
1
tg x0 k1 /( v 0 bx0 )
k1 k 2 b 2
частота колебаний
T1 2 / k1 2 / k 2 b 2 период колебаний

21.

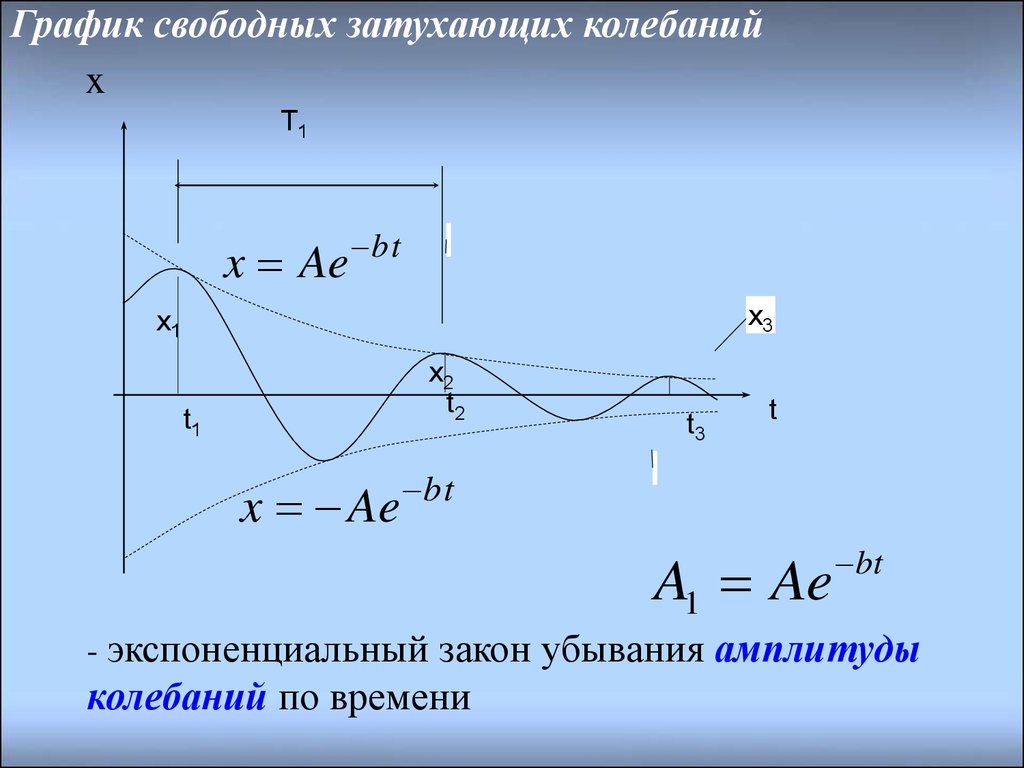
График свободных затухающих колебаний
x
T1
x Ae bt
x3
x1
x2
t2
t1
x Ae
t3
t
bt
A1 Ae
bt
- экспоненциальный закон убывания амплитуды
колебаний по времени

22.

Декремент затухания
Выясним, как меняется амплитуда колебаний за один
период
btn
x n Ae sin( k1t n )
btn 1
x n 1 Ae
sin( k1t n 1 )
с учетом
получим
t n 1 t n T1
x n 1 / x n e
bT1
(14)
Размах колебаний убывает по геометрической прогрессии
e
bT1
- декремент затухания
- логарифмический декремент затухания
Декремент затухания показывает, во сколько раз
уменьшается амплитуда колебаний за один период.
bT1

23.

Свойства свободных затухающих колебаний
x Ae
bt
b k
sin( k1t )
Основное влияние сопротивления среды (в случае b<k)
на свободные колебания сказывается в уменьшении
амплитуды колебаний по времени, т.е. в их затухании.

24.

b k
Свободные затухающие колебания
x 2bx k x 0
2
b k
2. Случай большого сопротивления среды
Общее решение уравнения
x C1e
q1t
C2 e
q2 t
(15)
q1 b b k , q2 b b k
q1 0 q2 0
2
2
2
2
- апериодическое движение точки, не является типично
колебательным, соответствует достаточно быстрому
затуханию по времени

25.

Свободные затухающие колебания
b k
x 2bx k x 0
2
b k
3. Случай
Общее решение уравнения
x e
bt
(C1 C2 t )
(16)
- движение точки апериодическое, соответствует
быстрому затуханию по времени

26.

Графики свободных затухающих колебаний в случае
большого сопротивления среды
b k
а)
б)
x
в)
x
x
m
x0
x0
t
x0 0, v0 0
t
x0 0, v 0 0
x0
t
x0 0, v0 0

27.

Вынужденные колебания
(без учета сопротивления среды)
O1 -начало отсчета в положении равновесия груза
Силы:
F , P, Q
Q Q0 sin pt - вынуждающая сила
01
F
Q0 - амплитуда,
M
P
Q
x
.
p - частота
Уравнение движения
m x cx Q0 sin pt
Q0
c
x x
sin pt
m
m
ДУ вынужденных колебаний (без учета сопротивления)
x k 2 x p0 sin pt
(17)
p0 Q0 / m

28.

ДУ вынужденных колебаний
(без учета сопротивления среды)
x k x p0 sin pt
2
(17)
Уравнение неоднородное и его решение можно записать
x1
x x1 x2
- общее решение однородного уравнения
x1 A sin( kt )
x2
- частное решение полного уравнения
x2 B sin pt
Подставляя это решение в (17), получим
p B sin pt k B sin pt p0 sin pt
2
2

29.

Решение ДУ вынужденных колебаний
p B sin pt k B sin pt p0 sin pt
2
2
Это равенство должно выполнятся для любого t
B(k p ) p0
2
B p0 /( k p )
2
Для случая
2
2
p k
x 2 ( p 0 /( k p )) sin pt
2
2
Общее решение:
x A sin( kt ) ( p0 /( k p )) sin pt
2
2
(18)

30.

Вынужденные колебания (резонанс)
Случай совпадения собственной частота колебаний с
частотой возмущающей силы называется резонансом.
k p
Подставим частное решение полного уравнения
x2 Ct cos pt в уравнение x p 2 x p0 sin pt
Получим
x2 ( p0 / 2 p)t cos pt или x2 ( p0 / 2 p)t sin( pt / 2)
- сдвиг по фазе между вынужденными колебаниями и
/2
возмущающей силой при резонансе равен
т.е. максимальному значению вынуждающей силы
соответствует положение равновесия и, наоборот, когда
значение силы равно нулю, отклонение от положения
статического равновесия максимальное

31.

График вынужденных колебаний при резонансе
x
p k
x p0t / 2 p
t
x k 2 x p0 sin pt
x p0t / 2 p
Общее решение
x A sin( kt ) ( p0 / 2 p)t cos pt
При резонансе (без учета сопротивления среды)
происходит линейный неограниченный рост
амплитуды по времени.

32. Свойства вынужденных колебаний (без учета сил сопротивления)

- Вынужденные колебания происходят с постоянной
амплитудой, которая не зависит от начальных
условий.
- Частота вынужденных колебаний равна частоте
возмущающей силы. То есть происходит “захват”
частоты вынуждающей силой (приложенная сила
“вынуждает” систему колебаться со своей частотой).
- Фазы вынужденных колебаний и возмущающей силы
совпадают при k>p и сдвинуты на 90° при k<p.

33. Вынужденные колебания при наличии сопротивления среды

O1 - начало отсчета в положении равновесия груза
01
Силы:
F
R
R v Q Q0 sin pt
Q
v
x
F cx
Уравнение движения
M
P
F , P, R, Q
m x cx x Q0 sin pt
Q0
c
x x x
sin pt
m
m
m
Введем обозначения
2b / m,
k c / m,
2
p0 Q0 / m

34. ДУ вынужденных колебаний при наличии сопротивления

x 2bx k 2 x p 0 sin pt
(19)
x x1 x2 - общее решение полного уравнения
- общее решение однородного уравнения b<k
x1 Ae
bt
sin( k1t )
x2 B sin( pt ) - частное решение полного уравнения
- постоянные
pt - фаза колебаний
Найдем B, , подставим частное решение в (19)
x Bp cos( pt )
x Bp 2 sin( pt )

35. Константы интегрирования

(20)
B( p 2 k 2 ) sin 2bpB cos p0 (cos sin sin cos )
Чтобы (20) выполнялось для любого t, коэффициенты
sin и cos должны быть равны,
при
следовательно
B(k 2 p 2 ) p0 cos
2bp p0 sin
Далее воспользуемся формулами из тригонометрии
sin cos 1
2
2
tg sin / cos
В результате получим
B p0 / (k 2 p 2 ) 2 4b 2 p 2
tg 2bp /( k 2 p 2 )

36. Решение ДУ вынужденных колебаний при наличии сопротивлении среды

Общее решение
x Ae
bt
sin( k1t ) B sin( pt )
Собственные
колебания
(21)
Вынужденные
колебания
Возмущающая сила все время поддерживает
колебательное движение точки, в результате чего
она колеблется с постоянной амплитудой B
B p0 / (k 2 p 2 ) 4b 2 p 2

37. Частота, период и амплитуда вынужденных колебаний

Сопротивление среды не изменяет частоту и период
вынужденных колебаний. Точка колеблется с частотой p
возмущающей силы.
Q Q0 sin pt
T 2 / k
В случае резонанса
p k
k c/m
2
амплитуда
Bres p0 / 2bp p0 m / p
Увеличение сопротивления среды приводит при
резонансе к уменьшению амплитуды колебаний
(это свойство часто используется в технике)

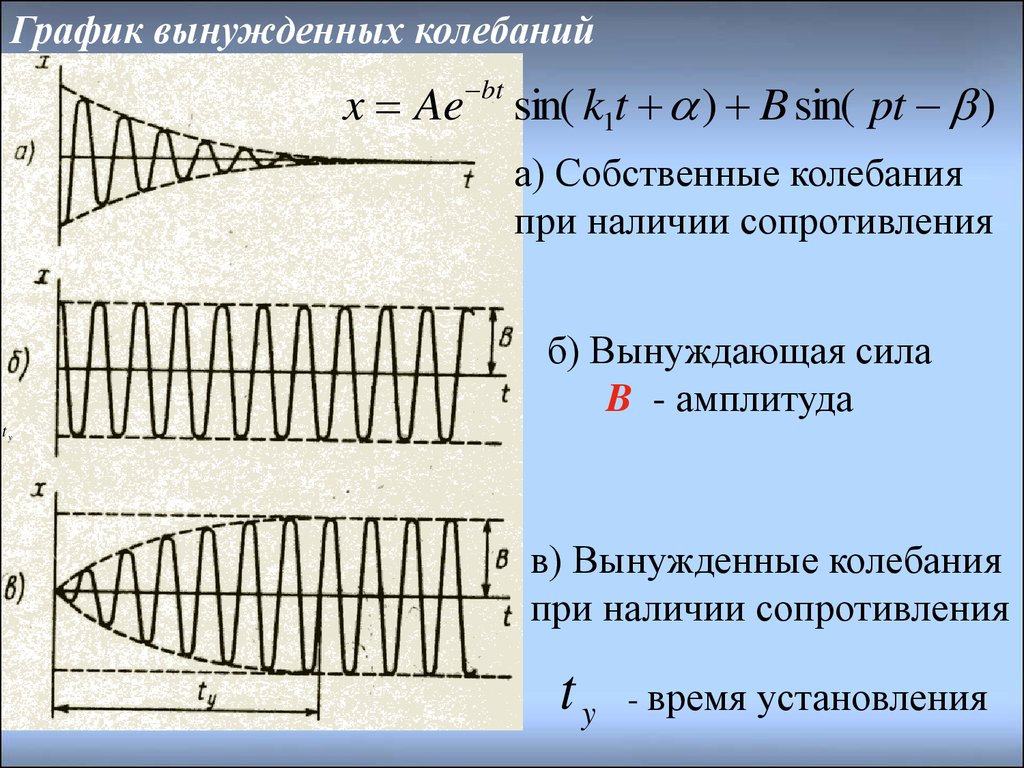
38. График вынужденных колебаний

x Ae bt sin( k1t ) B sin( pt )
а) Собственные колебания
при наличии сопротивления
б) Вынуждающая сила
B - амплитуда
ty
в) Вынужденные колебания
при наличии сопротивления
ty
- время установления

39. Коэффициент динамичности

p0 Q0
Bst 2
k
c
- статическое перемещение точки
под действием постоянной силы Q0
B / Bst
коэффициент динамичности показывает,
во сколько раз амплитуда вынужденных колебаний B
под действием возмущающей силы Q Q0 sin pt
больше статического перемещения Bst
при действии постоянной силы Q0
Подставим новые обозначения
z p/k
h b/k
в выражение для амплитуды и начальной фазы
B p0 / (k 2 p 2 ) 4b 2 p 2
tg 2bp /( k 2 p 2 )

40. Коэффициент динамичности

Получим коэффициент динамичности
1 / (1 z 2 ) 4h 2 z 2
z p/k
h b/k
- соотношение частот
- характеризует сопротивление среды
Важные характеристики колебательной системы
Амплитудно - частотная характеристика (АЧХ)
Фазо - частотная характеристика (ФЧХ)

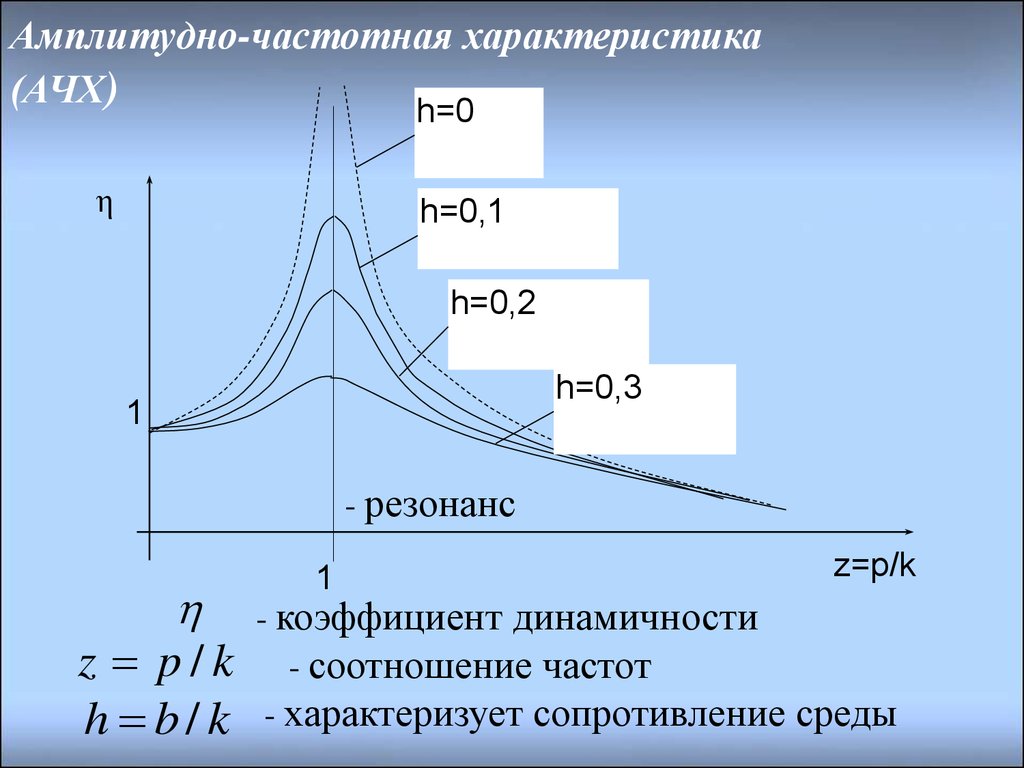
41. Амплитудно-частотная характеристика (АЧХ)

h=0
η
h=0,1
h=0,2
h=0,3
1
- резонанс
1
z=p/k
- коэффициент динамичности
z p / k - соотношение частот
h b / k - характеризует сопротивление среды

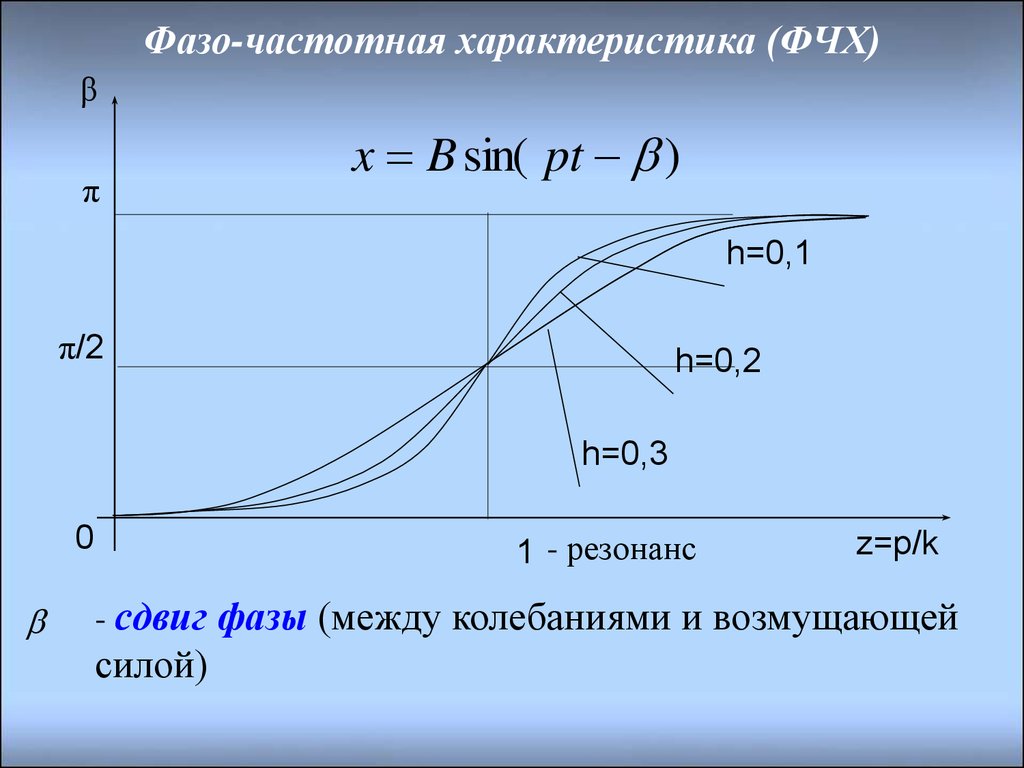
42. Фазо-частотная характеристика (ФЧХ)

β
π
x B sin( pt )
h=0,1
π/2
h=0,2
h=0,3
0
1 - резонанс
z=p/k
- сдвиг фазы (между колебаниями и возмущающей
силой)

43. Свойства вынужденных колебаний

1. Амплитуда вынужденных колебаний не зависит от
начальных условий задачи.
2. Вынужденные колебания при наличии
сопротивления не затухают.
3. Частота вынужденных колебаний равна частоте
возмущающей силы.
4. Даже при малой возмущающей силе можно
получить интенсивные вынужденные колебания,
если сопротивление мало, а частота p близка к k.
5. Даже при большой возмущающей силе можно
сделать вынужденные колебания сколь угодно
малыми, если частота p>>k.

44. Сложная колебательная система

- имеет набор собственных частот
k1 , k2 ,..., kn
- имеет набор возмущающих сил с частотами
p1 , p2 ,..., pm
- содержит много резонансов
pi k j
i 1,..., m,
j 1,..., n,
Применение резонансов на практике
Резонанс “полезен” – “настройка” колебательной
системы на резонанс.
Резонанс “вреден” – “отстройка” колебательной
системы от резонанса.
ЗАКЛЮЧЕНИЕ

45. Задача 1.

Замена нескольких пружин эквивалентной
a) Последовательное соединение пружин
c1
c2
m
Статическое удлинение пружин 1 и 2
s s1 s 2
s mg / c1 mg / c2
Статическое удлинение эквивалентной
пружины
s mg / c экв
В результате получим
1 / c экв 1 / c1 1 / c2
cэкв c1c2 /(c1 c2 )

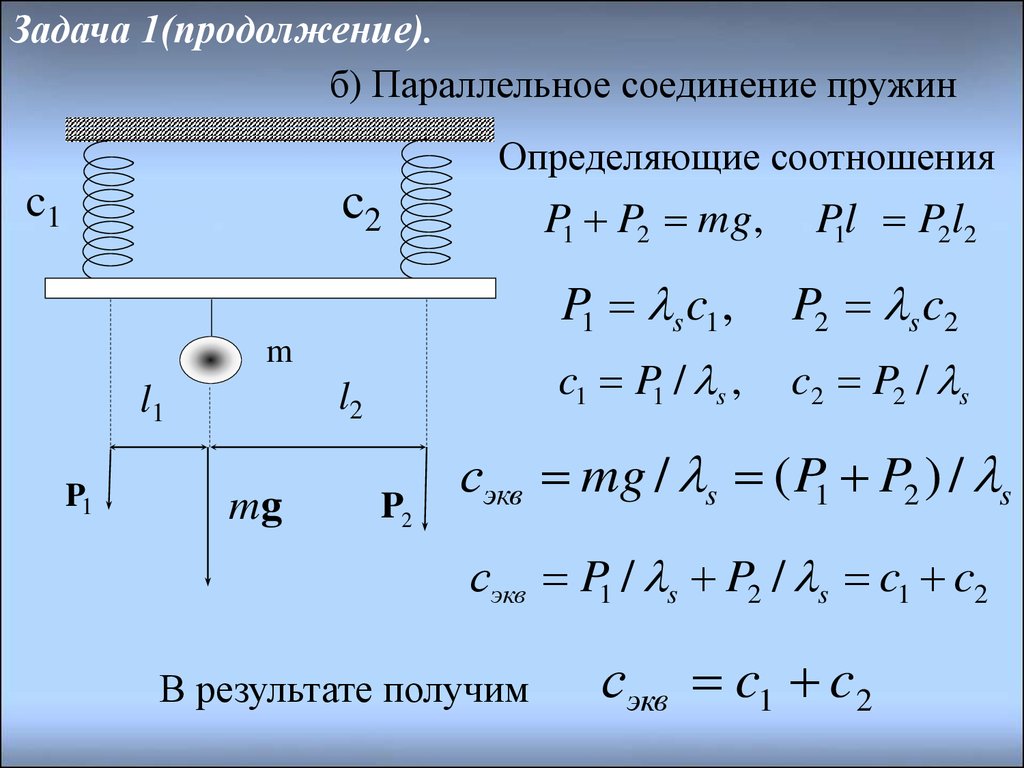
46. Задача 1(продолжение).

б) Параллельное соединение пружин
Определяющие соотношения
c2
c1
P1 P2 mg,
m
l2
l1
P1
mg
P2
P1l P2l2
P1 s c1 ,
P2 s c2
c1 P1 / s ,
c2 P2 / s
сэкв mg / s ( P1 P2 ) / s
сэкв P1 / s P2 / s c1 c2
В результате получим
сэкв c1 c2

47. Задача 2.

Груз массой 3кг совершает затухающие колебания с
периодом T1=0,3c и декрементом затухания λ=0,5.
Определить коэффициент жесткости пружины с и
коэффициент μ вязкого сопротивления. Во сколько нужно
уменьшить массу груза, чтобы движение груза стало
апериодическим?
Решение
T1 2 / k 2 b 2 ,
e bT ,
1
k c m
Подставим числовые значения
0.3 2 / k b , 0.5 e
2
2
bT1
, k c/3
Решаем эти уравнения относительно b, k, c
b 2,31 k 21,1 c 0,136

48. Задача 2 (продолжение)

Следовательно
c 0,136( Н / м) 2mb 13,86( Н с / м)
Пусть m1
новая масса, тогда a m / m1
b1 / 2m1 a / 2m, k1 c / m1 k a
Наименьшая масса при которой движение будет
апериодическим, находится из условия
b1 k1
Откуда находим
a m m1 (k 2m / ) 83
2

49. Уточнение рекомендаций к решению задач для случая колебательного движения точки

1. Выбрать систему координат.
Ось x направлять в сторону удлинения пружины,
начало – в положении равновесия груза
2. Изобразить все силы.
Силы: упругости пружины, сила тяжести, сила
сопротивления среды, вынуждающая сила
3. Написать второй закон Ньютона, получить ДУ.
Получить ДУ в “стандартном” виде, правильно
выразив l
через x.
x(0) x0 ; x (0) v0
4. Написать НУ.
xo
Не ошибиться при нахождении
5. Решить ДУ с использованием НУ.
Взять готовое решение “стандартного” ДУ

50. Заключение

Свободные незатухающие колебания:
1. Амплитуда и начальная фаза колебаний зависят от
начальных условий задачи
2. Частота и период колебаний не зависят от
начальных условий задачи и полностью определяются
параметрами самой колебательной системы
3. Постоянная сила, не изменяя характер колебаний,
смещает центр колебаний в сторону ее действия на
величину статической деформации
Свободные затухающие колебания:
Основное влияние сопротивления среды на свободные
колебания сказывается в уменьшении амплитуды
колебаний по времени, т.е. в их затухании.

51. Заключение (продолжение)

Вынужденные колебания:
1. Амплитуда вынужденных колебаний не зависит от
начальных условий задачи.
2. Вынужденные колебания при наличии сопротивления
не затухают.
3. Частота вынужденных колебаний равна частоте
возмущающей силы.
ЗАКЛЮЧЕНИЕ

52. Вопросы для самоконтроля

1. Как направлена и чему равна сила упругости пружины?
2. Какой вид имеют ДУ свободных колебаний точки?
3. Чем определяется амплитуда и начальная фаза свободных
колебаний точки?
4. От каких параметров зависят частота и период свободных
колебаний точки?
5. Записать ДУ свободных затухающих колебаний точки?
Привести вид его общего решения.
6. Привести график свободных и затухающих колебаний, а
также апериодического движения точки.
7. Как определяют декремент затухающих колебаний и что
он характеризует?
8. Каковы период и частота вынужденных колебаний?
9. Записать ДУ вынужденных колебаний.

53. Тема следующей лекции

Движение точки в неинерциальной
системе отсчета